An endogenous calcium oscillator may control early embryonic division

Abstract

Transient elevations in the concentration of free cytosolic calcium ion ([Ca²⁺]_i) promote cell phase transitions in early embryonic division and persist even if these transitions are blocked. These observations suggest that a [Ca²⁺]_i oscillator is an essential timing element of the early embryonic “master clock.” We explore this possibility by coupling a [Ca²⁺]_i oscillator model to an early embryonic cell cycle model based on the protein interactions that govern the activity of the M-phase-promoting factor (MPF). We hypothesize three dynamical states of the MPF system and choose parameter sets to represent each. We then investigate how [Ca²⁺]_i dynamics may control early embryonic division in both sea urchin and Xenopus embryos. To investigate both systems, distinct [Ca²⁺]_i profiles matching those observed in sea urchin embryos (in which [Ca²⁺]_i exhibits sharp transients) and Xenopus embryos (in which [Ca²⁺]_i is elevated and oscillates sinusoidally) are imposed on each of the hypothesized dynamical states of MPF. In the first hypothesis, [Ca²⁺]_i oscillations entrain the autonomous MPF oscillator. In the second and third hypotheses, where the MPF system rests in excitatory and bistable states, respectively, [Ca²⁺]_i oscillations drive MPF activation cycles. Simulation results show that hypotheses two and three, in which a [Ca²⁺]_i oscillator is a fundamental timing element of the master clock, best account for key experimental observations and the questions that they raise. Finally, we propose experiments to elucidate further [Ca²⁺]_i regulation and the fundamental components of the early embryonic master clock.

It has been suggested that a “master clock” controls early embryonic divisions because these divisions are relatively fast, synchronous, and not dependent on cell growth. Although several components of this clock are known, the essential timing elements are not yet established. The clock is characterized by the activity of the maturation or M-phase-promoting factor (MPF), a cyclin-dependent kinase, that when active indicates that the cell is undergoing mitosis. The master clock, therefore, is set by the factors that determine the activity of MPF. The protein components that determine the activity of MPF seem common among eukaryotic cells and have been labeled a “universal control mechanism” (1) that regulates the onset of M phase. In the present study we call these protein components the MPF system.

Studies in several systems also suggest that transient increases in the concentration of free cytosolic calcium ([Ca²⁺]_i) contribute to cell cycle regulation. However, the extent to which these transients regulate early embryonic division is under discussion. One possibility is that these transients are essential, and that the mechanism that controls variations in [Ca²⁺]_i is a fundamental component of the master clock. The following observations (among others) suggest this scenario: (i) [Ca²⁺]_i transients* accompany early embryonic cell cycles (2–7); (ii) the injection of calcium buffers into intact Xenopus blastomeres delays or blocks division (8); and (iii) in the absence of division, [Ca²⁺]_i transients appear with the same frequency as that of division (3, 5, 6).

A second scenario supposes that [Ca²⁺]_i transients are secondary. Here the master clock is timed chiefly through protein interactions. This scenario is supported by several experiments: (i) MPF activity in cycling extracts prepared from Xenopus laevis eggs is controlled by cyclin synthesis and destruction (9, 10); (ii) clam oocyte extracts continue cell cycle events in the presence of 5 mM EGTA (11), a strong calcium chelator; and (iii) in these extracts the addition of 1 mM CaCl₂ does not induce the destruction of cyclin. Observations in support of both scenarios are listed in Table 1 and reviewed below.

Table 1.

Summary of experimental observations concerning calcium and mitosis

The case for calcium involvement

1. [Ca2+]i oscillates in sinusoidal manner in Xenopus embryos at division frequency (5–7).

2. [Ca2+]i spikes at mitosis entry and mitosis exit in sea urchin embryos (2, 3, 12).

3. [Ca2+]i signals persist in absence of division in both Xenopus and sea urchin embryos (3, 5, 6).

4. Elevated [Ca2+]i induces nuclear envelope breakdown (mitosis start), presumably through activation of MPF (12, 13).

4′. [Ca2+]i may activate MPF through Cdc25 (14).

5. A [Ca2+]i signal is necessary to induce nuclear envelope breakdown, but it is effective only after sufficient protein synthesis (13).

6. Elevated [Ca2+]i induces cyclin destruction (mitosis exit), presumably through deactivation of MPF (11, 15, 16, 28).

6′. [Ca2+]i deactivates MPF through the ubiquitin-dependent proteolysis pathway (15).

7. BAPTA calcium buffers delay division in intact Xenopus blastomeres (8).

8. High-concentration calcium buffer injections block division cycles (8, 12, 13).

The case that MPF oscillations are independent of calcium

9. Addition of exogenous cyclin mRNA produces multiple cell cycles in Xenopus extracts (9).

10. Division cycles in clam embryo homogenates are not affected by injection of calcium buffers or CaCl2 (11).

Clearly the nature of calcium’s role in early embryonic cycles is under investigation. Here we mathematically study the possibility that an endogenous [Ca²⁺]_i oscillator regulates or drives early embryonic cycles. To investigate this proposition, we couple [Ca²⁺]_i oscillator models to an established early embryonic cell cycle model based on the protein interactions that govern the activity of MPF. We hypothesize several dynamical states of the MPF system and construct a set of kinetic equations for each hypothesis. We then investigate how each system responds to [Ca²⁺]_i variations similar to those observed in Xenopus and sea urchin embryos by numerically solving the kinetic equations.

The hypotheses differ in the degree to which [Ca²⁺]_i dynamics determine division rates and are listed in Table 2. Hypothesis 0, the protein-only hypothesis, postulates that an autonomous MPF oscillator acts as the master clock and that [Ca²⁺]_i transients are not involved. This hypothesis has been modeled by two variable (17, 18) and more comprehensive (19) cell cycle models. Hypothesis 1, the entrainment hypothesis, proposes that [Ca²⁺]_i oscillations regulate the appearance of MPF activation peaks by modulating the frequency of an otherwise autonomous MPF oscillator. Hypotheses 2 and 3, the induction hypotheses, suggest that [Ca²⁺]_i transients trigger a nonoscillating MPF system. Here [Ca²⁺]_i oscillations not only act as the timing mechanism but also are essential to cell cycle progression. In the absence of [Ca²⁺]_i (or at basal levels of [Ca²⁺]_i) the MPF system may have a single, but excitatory, steady state (hypothesis 2), or it may be bistable with active and inactive steady states (hypothesis 3). Hypotheses 2 and 3 imply that the elements governing [Ca²⁺]_i dynamics are central components of the cell cycle clock. All of the hypotheses are ordered on a scale of [Ca²⁺]_i involvement as listed in Table 2. Whereas previous studies have considered protein-only cell cycle control (hypothesis 0), in this study, we consider the hypotheses that include second messenger involvement (hypotheses 1, 2, and 3).

Table 2.

Hypotheses regarding [Ca²⁺]_i and the master clock

Hypothesis	Extent of [Ca2+]i control
0. Autonomous MPF oscillator	Limited
1. Autonomous MPF and [Ca2+]i oscillators	Entrainment
2. MPF system is excitable	Induction
3. MPF system is bistable	Induction

Hypotheses 1, 2, and 3 are constructed and simulated in this study.  

Our objectives are then fivefold. First, we review experiments for and against the supposition that [Ca²⁺]_i transients regulate early embryonic cell cycles. Second, we model experimental results—in particular, the results concerning calcium buffer injections. Third, we discuss the hypotheses insofar as they account for the experimental observations in Xenopus and sea urchin systems. Fourth, we discuss three relevant questions raised by the experimental review. Finally, we suggest experiments that may help answer empirically these questions and the possible role of a [Ca²⁺]_i oscillator in early embryonic division.

REVIEW OF EXPERIMENTS

The Case for Calcium Involvement.

[Ca²⁺]_i transients have been extensively studied in Xenopus (frog) and sea urchin embryos. In Xenopus embryos [Ca²⁺]_i oscillates sinusoidally with amplitudes of about 50–100 nM on an elevated, 400 nM, baseline ([Ca²⁺]_i before fertilization is 100–200 nM) and a period equal to that of cell division (observation 1) (5–7). One study indicates that in the absence of cellular division [Ca²⁺]_i oscillations cease (7); but more recent experiments using aequorin luminescence suggest that [Ca²⁺]_i oscillates even if the division cycle is blocked (5, 6) (observation 3). Furthermore, because oscillations persist in a calcium-free medium (6), the oscillator appears to be endogenous.

In sea urchin embryos, fura-2 studies (2, 3, 12) the investigators report that [Ca²⁺]_i transients or spikes appear at (i) cell cycle start, near the G₁/S transition, (ii) mitosis entry or nuclear envelope breakdown, (iii) mitosis exit near anaphase, and (iv) cytokinesis (observation 2). Furthermore, as in Xenopus embryos, [Ca²⁺]_i oscillations persist even when cell division is blocked (3) (observation 3).

The existence of [Ca²⁺]_i transients that accompany cell cycle events does not necessarily imply that [Ca²⁺]_i is essentially involved. But injection experiments (8, 12, 13, 20) and fertilization events attest that these transients are essential to induce transitions from phase to phase in the cell cycle. In particular, [Ca²⁺]_i transients induce both entrance into and exit from mitosis.

[Ca²⁺]_i induction of mitosis start has been demonstrated in several systems. Han et al. (20) injected Xenopus blastomeres with (i) a phosphatidylinositol 4,5-bisphosphate (PIP₂₎-directed antibody, which prevents PIP₂ hydrolysis by phospholipase C and subsequent formation of inositol 1,4,5-trisphosphate (IP₃); (ii) heparin, which competitively inhibits IP₃ receptor sites and presumably inhibits IP₃-induced Ca²⁺ release; and (iii) the calcium buffer dibromo-BAPTA. Each of these injections partially or completely arrested the cell cycle. Moreover, to various degrees each type of BAPTA buffer delays cleavage (observation 7) and at higher concentrations blocks cleavage for at least 4–6 hr (7–10 cleavage cycles) (observation 8) (8).

In sea urchin eggs injections of IP₃ [which releases calcium into the cytosol (3)] or CaCl₂ induce premature nuclear envelope breakdown (12, 13). But the cell responds to these signals only if the injection occurs at least 45 min after the preceding cleavage and protein synthesis is not inhibited (13). Furthermore, injection of BAPTA or EGTA blocks transient elevations in [Ca²⁺]_i and prevents nuclear envelope breakdown and mitosis onset (2, 12, 13). There is further evidence for the essential role of [Ca²⁺]_i transients at mitosis onset from other animal systems [see reviews by Hepler (4) and Whitaker (2, 14)]. These results suggest that [Ca²⁺]_i transients are essential to the cell cycle, and that they induce mitosis (MPF activation) (observation 4) provided that the cyclin synthesis requirement is met (observation 5).

These results do not reveal the downstream mitosis-inducing target of [Ca²⁺]_i. To this end, Whitaker (2) reports that the Ca²⁺/calmodulin-dependent kinase, CamK II, phosphorylates and activates Cdc25 in vitro and that mammalian cell lines arrested in G₂ by treatment with a calmodulin inhibitor lack the phosphorylated form of Cdc25 (observation 4′).

An essential role for [Ca²⁺]_i at mitosis exit has also been observed (observation 6). A burst of [Ca²⁺]_i at fertilization stimulates cell cycle onset in metaphase-arrested Xenopus oocytes by inducing the rapid destruction of cyclin (15). This [Ca²⁺]_i burst suggests that [Ca²⁺]_i transients are involved in subsequent embryonic cycles to destroy cyclin and to prompt mitosis exit. Lorca et al. (15) conducted a series of experiments showing that [Ca²⁺]_i acts through CamK II to inactivate the cytostatic factor and MPF in metaphase II-arrested Xenopus eggs. In a separate study, Lorca et al. (28) show that a calmodulin-dependent process is required for cyclin degradation in cell-free extracts prepared from metaphase-arrested Xenopus eggs. These studies also report that [Ca²⁺]_i-induced cyclin destruction is mediated by the ubiquitin-dependent proteolysis pathway. Furthermore, a high concentration calcium injection (5 mM) into clam embryo extracts results in rapid degradation of cyclin (11). (For further information see reviews cited above.) These results suggest that elevated [Ca²⁺]_i destroys cyclin by activating the ubiquitin-dependent proteolysis pathway (observation 6′), thereby deactivating MPF and inducing exit from mitosis (MPF deactivation).

The Case That MPF Oscillations Are Independent of Calcium.

There have been numerous investigations into the protein components that control division cycles in embryos. These studies have determined that mitosis is controlled, in part, by the activity of the cyclin-dependent kinase p34^cdc2. The activity of p34^cdc2 is determined by several regulatory enzymes and by the level of cyclin, which is maximal just preceding and during mitosis and falls rapidly at mitosis exit (for review see refs. 1 and 21). It has been shown that homologous proteins exist in a variety of species, prompting the “universal control mechanism” label (1).

While genetic investigations have begun to reveal the protein components that constitute the cell cycle machinery, further investigations suggest that only protein components control early embryonic division rates. Murray and Kirschner (9) have produced frog egg extracts which perform multiple cell cycles. They reported that when endogenous RNA is destroyed then cycles cease. However, if cyclin mRNA is reintroduced, the cycles return. These findings suggest that cyclin synthesis is essential to cell cycle progression and that cyclin is the only component needed to induce division in arrested homogenates (observation 9). A subsequent paper (10) revealed that a proteolysis-resistant form of cyclin prevents mitosis exit, which indicates that the destruction of cyclin is also essential to cell cycle progression. Luca and Ruderman (11) have developed a cell-free system from clam embryos that undergoes one or more rounds of cyclin synthesis and destruction. They tested a variety of agents for their effect on cyclin destruction. They showed that the addition of 5 mM EGTA, an effective calcium chelator, does not affect the timing or extent of cyclin destruction. They also showed that the addition of 1 mM CaCl₂ has no effect on cyclin destruction (observation 10). Furthermore, the introduction of the calcium buffer BAPTA in dividing embryos slows but does not kill division cycles (8). If it is assumed that EGTA and BAPTA prevent transient [Ca²⁺]_i increases, and that the addition of CaCl₂ produces a [Ca²⁺]_i transient, these results suggest that cyclin dynamics (and MPF activity) are not dependent on calcium. Last, earlier studies in Xenopus embryos did not indicate that [Ca²⁺]_i oscillates in the absence of division (7, 22).

Key Questions.

The above review raises several important questions: (i) how may the [Ca²⁺]_i and MPF systems function in tandem to yield successful division cycles; (ii) how can distinct calcium profiles (i.e., those observed in Xenopus and sea urchin systems) drive the conserved MPF system; and (iii) how can [Ca²⁺]_i transients activate and deactivate MPF in a nonfutile manner? We shall return to these questions in Discussion.

THE MODEL

Incorporating the Calcium Interaction.

Our model is constructed by coupling calcium oscillators to Novak and Tyson’s MPF model.† [Ca²⁺]_i activates MPF by means of Cdc25 (as suggested by observation 4′) and deactivates MPF through an intermediary enzyme, IE, in the ubiquitin-dependent proteolysis machinery (as suggested by observation 6′). CamK II (CamK), mediates both [Ca²⁺]_i interactions (as suggested by the experiments outlined in The Case for Calcium Involvement). These reactions are schematized in Fig. 1 and are mathematically modeled in a manner similar to that used by Dupont and Goldbeter (23). For example, the activation interaction is included by addition of the term

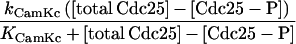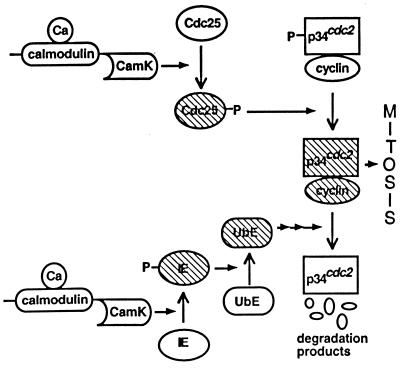
Figure 1.

Schematic showing details of [Ca²⁺]_i interaction points in our model. [Ca²⁺]_i acts through CamK II to phosphorylate and activate Cdc25 and the ubiquitin-conjugating enzyme, IE. The hatched enzymes represent active species. The CamK schematic represents the activation of CamK by calcium/calmodulin.

in the equation that determines the activity of Cdc25 (equation 7 of table 2 in ref. 19). The coefficient k_CamKc is a measure of the activity level of CamK (which depends on the level of calcium), and K_CamKc is the Michaelis constant associated with the CamK-induced phosphorylation of Cdc25 (which results in the molecule denoted Cdc25-P). There is a similar term in the equation for ubiquitin intermediary enzyme IE (equation 9 of table 2 in ref. 19) except that here the strength of interaction and the associated Michaelis constant are characterized by k_CamKu and K_CamKu, respectively. The subscripts c and u are used to denote the Cdc25 and the IE (ubiquitin system) interactions, respectively. We assume Michaelis–Menten kinetics because they adequately describe many enzymatic reactions and are consistent with the kinetics used in the Novak and Tyson model.

The term k_{CamK(c or u)} ideally should be determined by a set of differential equations dependent on [Ca²⁺]_i, the on and off rates of calmodulin, and the rates of the autophosphorylating reaction, including the homodecamer nature of CamK. However, because of a scarcity of experimental data, we simplify the [Ca²⁺]_i/calmodulin/CamK II interactions by using an algebraic cooperative binding term. For example, we use

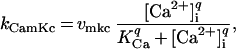where q is the Hill coefficient associated with cooperative calcium binding of calmodulin and K_Ca is the [Ca²⁺]_i at which CamK activity is half maximal. The symbols v_mkc and v_mku denote the maximum velocities associated with the Cdc25 and IE phosphorylations, respectively. This approximation has been used to simulate [Ca²⁺]_i-activated phosphorylation (23) and assumes that calcium binding and the reactions associated with [Ca²⁺]_i and CamK are fast relative to the MPF reactions.

The parameter q is set to represent the highly cooperative binding of calcium to calmodulin and calmodulin to CamK II. The parameter K_Ca is set so that it is not exceeded by [Ca²⁺]_i in our simulations. The parameters v_mkc and v_mku are chosen so that the [Ca²⁺]_i terms in the relevant differential equations are negligible at basal levels of [Ca²⁺]_i but dominate the other terms at elevated levels. The Michaelis constants, K_CamKc and K_CamKu, are chosen to be equal to the Michaelis constants of the phosphorylation and dephosphorylation reactions in the equations in which they appear.

The distinct [Ca²⁺]_i profiles observed in sea urchin and Xenopus systems are modeled with the IP₃–Ca²⁺ cross-coupling (ICC) model of Meyer and Stryer (24) and an ad hoc elevated sinusoidal signal, respectively. We use the ICC model because the concentration of IP₃ oscillates during early embryonic cycles (3), and IP₃ induces mitosis onset (12, 13, 20) in sea urchin embryos.‡ Xenopus embryo [Ca²⁺]_i dynamics are represented with the following equation: d[Ca²⁺]_i/dt = A2πf cos 2πft and [Ca²⁺]_i (at t = 0) = 500 nM.

The ICC model is modified to include buffering effects using mass-action kinetics. The rate constants approximate the binding rates of the rapid-equilibrium buffer dibromo-BAPTA (K_d = 1.5 μM = k_off/k_on, k_on = 200 μM⁻¹·s⁻¹). k_on and k_off are chosen so that larger values do not affect [Ca²⁺]_i simulation results and are several hundredfold greater than the binding rates associated with EGTA (k_on = 2.0 μM⁻¹·s⁻¹, k_off = 0.4 s⁻¹) (26). We also include a scaling parameter τ_scale that adjusts the frequency of ICC oscillations.

Generating Parameter Sets for Each Hypothesis.

The different dynamical states of the MPF system are constructed by adjusting the values of the kinetic terms V”_wee and k_h[PPase], where [PPase] represents the concentration of protein phosphatase. Since [Ca²⁺]_i is now an effector, the state of the MPF system is dependent on steady-state [Ca²⁺]_i. Accordingly, we compare the dynamical states of the different MPF systems at basal ([Ca²⁺]_i = 0.2 μM) and elevated ([Ca²⁺]_i = 0.5 μM) levels. The state at basal [Ca²⁺]_i suggests how the system might respond to the [Ca²⁺]_i profile observed in sea urchin embryos, whereas the state at elevated [Ca²⁺]_i suggests how the system might respond to the elevated sinusoidal signals observed in Xenopus embryos. In hypothesis 1 parameters are set to those used by Novak and Tyson (19) to model Xenopus extracts.§ In steady basal and elevated [Ca²⁺]_i the MPF system is oscillatory. The excitatory MPF hypothesis (hypothesis 2) is generated by raising V”_wee from 1.0 to 4.0. In basal [Ca²⁺]_i this system rests at a low active MPF stable state, and in elevated [Ca²⁺]_i the MPF system is transformed from an excitable to an oscillatory state. The bistable state (hypothesis 3) is generated by maintaining V”_wee at 4.0, but raising k_h[PPase] from 0.087 to 0.15. In basal [Ca²⁺]_i the system has low and high MPF activity stable states, allowing [Ca²⁺]_i transients to shuttle the MPF system between the two states. In elevated [Ca²⁺]_i this system becomes oscillatory. Therefore, in hypotheses 2 and 3, elevating [Ca²⁺]_i changes the MPF system from a nonoscillating state to an oscillating state whose frequency may be modulated by oscillating [Ca²⁺]_i.

RESULTS

We simulate [Ca²⁺]_i interactions with the three MPF systems outlined above. Each system interacts with a spiking [Ca²⁺]_i signal and a raised sinusoidal [Ca²⁺]_i signal. We examine the range of frequencies to which imposed [Ca²⁺]_i transients, whether spiking or sinusoidal, regulate division. We also simulate and discuss the effect of a rapid calcium buffer.

Hypothesis 1: MPF Is Oscillatory.

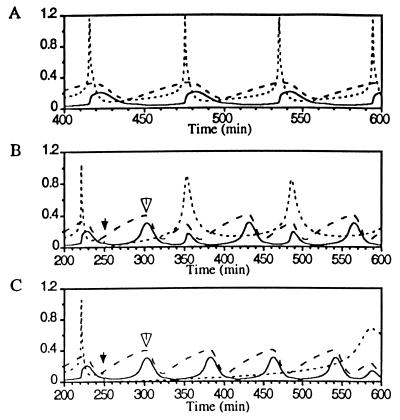
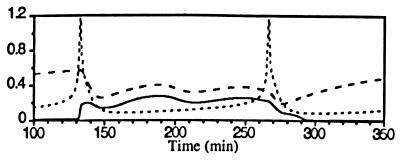
In Fig. 2 spiking [Ca²⁺]_i transients regulate an otherwise autonomous oscillatory MPF system. While this MPF system independently oscillates at 1.25 × 10⁻² min⁻¹, the [Ca²⁺]_i oscillator drives the division frequency up to 1.6 × 10⁻² min⁻¹ and down to 1.08 × 10⁻² min⁻¹ (data not shown). If the [Ca²⁺]_i spiking frequency is increased such that it is near an integral multiple of the MPF autonomous frequency, then [Ca²⁺]_i peaks appear between division cycles. In this case, the [Ca²⁺]_i peaks induce MPF activation only if a cyclin synthesis requirement is satisfied. Since MPF response is limited by the rate of cyclin synthesis it cannot be pushed to any arbitrary frequency. In Fig. 2 B and C, simulations show that injecting a rapid buffer greatly delays the [Ca²⁺]_i transient, but the MPF activation peak appears with little delay (open arrows in Fig. 2 B and C).

Figure 2.

Spiking [Ca²⁺]_i entrains the oscillatory MPF system (hypothesis 1). Here and in Figs. 3, 4, 5 the dotted line is [Ca²⁺]_i, the dashed line is active MPF/total p34^cdc2, and the solid line is total cyclin/total p34^cdc2. (A) [Ca²⁺]_i oscillations (spikes) at a frequency higher than the autonomous MPF oscillation frequency entrain and precede MPF activation peaks. τ_scale = 2.25 and f_Ca = 1.6 × 10⁻² min⁻¹. (B) The injection of 0.3 mM BAPTA (injection denoted by solid arrow) delays the subsequent calcium peak but has little effect on the subsequent MPF peak (hollow arrow). (C) The injection of 2.0 mM BAPTA delays the subsequent [Ca²⁺]_i spike, but active MPF peaks appear at nearly the autonomous MPF oscillation frequency until [Ca²⁺]_i rises to a level that modulates the MPF system.

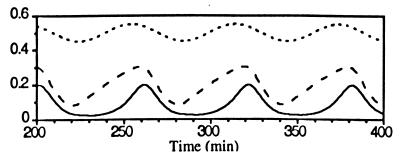
At constant elevated [Ca²⁺]_i, MPF activity oscillates at 1.47 × 10⁻² min⁻¹. In this state relatively small sinusoidal oscillations in [Ca²⁺]_i entrain the division frequency from about 1.2 × 10⁻² min⁻¹ to about 1.75 × 10⁻² min⁻¹ (Fig. 3). Note here that the elevation of [Ca²⁺]_i is not necessary to induce division cycles.

Figure 3.

Elevated sinusoidal [Ca²⁺]_i oscillations entrain the oscillatory MPF system. f_Ca = 1.3 × 10⁻² min⁻¹.

Hypothesis 2: MPF Is Excitable.

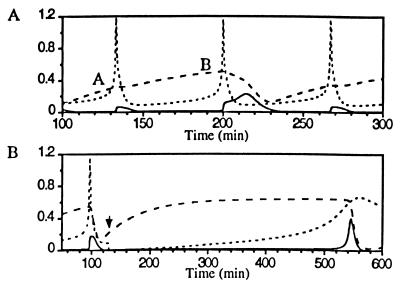
With MPF in an excitable state, spiking [Ca²⁺]_i induces an MPF activation peak if the cyclin synthesis requirement is met (Fig. 4A).¶ Because protein synthesis is relatively slow, a time lag following cyclin destruction is introduced, during which the system is primed for a [Ca²⁺]_i spike. Once primed—i.e., there is a sufficient concentration of the cyclin B/cdc2 dimer—the [Ca²⁺]_i spike triggers the autophosphorylation cycle that generates a rapid peak in MPF activity. In Fig. 4B the injection of 0.3 mM BAPTA delays MPF activation nearly 2-fold. The injection of 2.0 mM BAPTA blocks MPF activation through about three activation cycles (simulation not shown).

Figure 4.

Spiking [Ca²⁺]_i activates the excitable MPF system. (A) [Ca²⁺]_i spikes fail to induce MPF activation peaks (A) unless the cyclin synthesis requirement is met (B). τ_scale = 2.0, f_Ca = 1.44 × 10⁻² min⁻¹. (B) The injection of 0.3 mM BAPTA delays the subsequent [Ca²⁺]_i spike (injection denoted by solid arrow) and the [Ca²⁺]_i-induced MPF activation peak by nearly 2-fold.

Elevated [Ca²⁺]_i pushes the excitable MPF system into an oscillatory state. At elevated [Ca²⁺]_i the MPF system oscillates at 0.61 × 10⁻² min⁻¹. Small sinusoidal [Ca²⁺]_i oscillations then drive the division frequency from 0.45 × 10⁻² min⁻¹ to 0.86 × 10⁻² min⁻¹ (simulation not shown).

Hypothesis 3: MPF Is Bistable.

In Fig. 5 successive [Ca²⁺]_i spikes shuttle MPF between low and high activity levels. [Ca²⁺]_i-induced activation requires abundant cyclin (simulation not shown). The spike that destroys MPF activity is necessary to continue the cycles since, without it, MPF would remain in a high activity state.‖

Figure 5.

Spiking [Ca²⁺]_i shuttles the bistable MPF system between low and high activity. The second [Ca²⁺]_i peak is necessary to continue cycles. τ_scale = 1.0, f_Ca = 0.72 × 10⁻² min⁻¹.

The bistable system responds to elevated sinusoidal signals of [Ca²⁺]_i in a manner similar to the excitable system. At elevated [Ca²⁺]_i the MPF system is pushed into an oscillatory state with frequency 0.67 × 10⁻² min⁻¹. Small sinusoidal signals then drive the division frequency from 0.47 × 10⁻² min⁻¹ to 1.0 × 10⁻² min⁻¹ (simulation not shown).

DISCUSSION

The extent to which hypotheses 0, 1, 2, and 3 predict the list of experimental observations is summarized in Table 3 and below. All three of the hypotheses considered in this study predict the following observations: (i) spiking (observation 2; Figs. 2, 4, and 5) and elevated sinusoidal (observation 3; Fig. 3 and text) [Ca²⁺]_i signals regulate MPF activation frequencies; (ii) the appearance of a [Ca²⁺]_i transient at mitosis onset—MPF activation (observation 4; Figs. 2A, 4, and 5); and (iii) that a protein synthesis requirement must be met before the [Ca²⁺]_i transient can induce a division (observation 5; Fig. 4A and text). The oscillatory and excitable MPF hypotheses each imply that the signal at mitosis exit (observation 6) may occur; however, it is not essential, whereas in the bistable MPF hypothesis the [Ca²⁺]_i signal at mitosis exit signal is essential (Fig. 4). Hypothesis 1 and the protein-only hypothesis predict that in the absence of [Ca²⁺]_i signals the division cycles persist (observations 9 and 10). Only hypotheses 2 and 3 guarantee that buffers delay division cycles (observation 7), whereas hypothesis 1 predicts observation 7 only if [Ca²⁺]_i oscillations induce higher division rates than the autonomous MPF oscillation frequency; furthermore, in the protein-only hypothesis, buffers should have no effect. Also, only hypotheses 2 and 3 predict that super-threshold levels of buffer block divisions (observation 8).

Table 3.

How the hypotheses account for experimental observations

Hypothesis	Observation
	1	2	4	5	6	7	8	9, 10
0. Protein only	—	—	—	—	—	N	N	Y
1. MPF oscillates	Y	Y	Y	Y	M	M	N	Y
2. MPF excitable	(Y)	(Y)	(Y)	(Y)	(M)	Y	Y	(N)
3. MPF bistable	(Y)	(Y)	(Y)	(Y)	(Y)	Y	Y	(N)

Observation 3 is not included because [Ca²⁺]_i spikes or sinusoidal oscillations are imposed in all of the simulations. Y, simulation predicts or does not dispute observation; N, simulation disputes observation; M, simulation allows, but does not require observation; —, simulation does not consider observation. The entries in parentheses indicate that at elevated [Ca²⁺]_i (as in Xenopus) these systems are oscillatory and the MPF frequency is modulated by the sinusoidal [Ca²⁺]_i signal (see text for details). 

Now we address the questions posed in Key Questions. Question 1: The simulations suggest that the existence of two independent oscillators is not necessary to reproduce division cycles as long as [Ca²⁺]_i is included in the model. Nevertheless, the coupling of autonomous [Ca²⁺]_i and MPF oscillators predicts most of the experimental observations and a significant range frequency control. Question 2: Sinusoidal and spiking [Ca²⁺]_i profiles control division frequencies in all hypotheses studied here. In hypotheses 2 and 3 this is accomplished partly because elevated [Ca²⁺]_i pushes the MPF system into an oscillatory state. This may account for the elevated [Ca²⁺]_i in Xenopus embryos after fertilization. Question 3: [Ca²⁺]_i both acts to induce mitosis entry and mitosis exit and controls division frequencies in a nonfutile manner. This is especially apparent in hypothesis 3, where the action that prevails (activation or deactivation) depends on the state of the MPF system (Fig. 5). Furthermore, if we neglect either [Ca²⁺]_i-induced mitosis onset or exit, the extent to which [Ca²⁺]_i oscillations control division cycles is reduced (simulation not shown). Even though the calcium-dependent cyclin destruction pathway may not be essential to maintaining division cycles (hypotheses 1 and 2) it is essential to initiate onset of the cell cycle in metaphase-arrested Xenopus eggs, and it may act as a fail-safe mechanism should the cycle become arrested in mitosis.

In light of the experimental review, simulation results, and subsequent discussion we suggest that the machinery (membrane-bound stores, receptor proteins, channel proteins, etc) that regulates [Ca²⁺]_i is a component of the early embryonic cell cycle clock. The machinery may act by means of two distinct mechanisms in different systems. First, it may trigger sharp changes in MPF activity. Second, this machinery may, by altering the steady-state [Ca²⁺]_i, change the balance of kinase to phosphatase activity such that the MPF system moves from a stationary to an oscillatory state. In the second scenario, small sinusoidal [Ca²⁺]_i oscillations control the division frequency.

To help reconcile the apparent contradictions in experimental results concerning [Ca²⁺]_i dynamics and the cell cycle, we suggest several basic experiments. First, it is necessary to determine the total calcium present in and the calcium buffering capacity of extract and intact systems. This information should at the least provide insight into the effectiveness of [Ca²⁺]_i perturbations. A high buffering capacity probably explains why 5 mM CaCl₂ (as opposed to 1 mM CaCl₂ reported above) results in the rapid degradation of cyclin (9, 11). Second, with appropriate dye combinations and chamber design it should be possible to visually monitor [Ca²⁺]_i and nuclear morphology simultaneously in extracts. If a [Ca²⁺]_i oscillator is indeed a fundamental timing element, it should function in cycling extract systems. This apparatus than could be used to repeat in vivo experiments. For example, assuming it is possible to visualize [Ca²⁺]_i variations, one can add protein synthesis inhibitors and BAPTA to determine which is the driving oscillator. Such an apparatus may also help unravel the story concerning the existence and activity of localized calcium gradients (8).