A physiologically plausible spatio-temporal model for EEG signals recorded with intracerebral electrodes in human partial epilepsy

Abstract

Stereoelectroencephalography (depth-EEC signals) is a presurgical investigation technique of drug-resistant partial epilepsy, in which multiple sensor intracerebral electrodes are used to directly record brain electrical activity. In order to interpret depth-EEG signals, we developed an extended source model which connects two levels of representation: i) a distributed current dipole model which describes the spatial distribution of neuronal sources and ii) a model of coupled neuronal populations which describes their temporal dynamics. From this extended source model, depth-EEG signals were simulated from the forward solution at each electrode sensor located inside the brain. Results showed that realistic transient epileptiform activities (spikes) are obtained under specific conditions in the model in terms of degree of coupling between neuronal populations and spatial extent of the source. In particular, the cortical area involved in the generation of epileptic spikes was estimated to vary from 18 to 25 cm², for brain conductivity values ranging from 30 to 35×10⁻⁵ S/mm, for high coupling degree between neuronal populations and for a volume conductor model that accounts for the three main tissues of the head (brain, skull, and scalp). This study provides insight into the relationship between spatio-temporal properties of cortical neuronal sources and depth-EEG signals.

I. Introduction

About 0.5–1% of the population suffers from epilepsy, which is one of the most common neurological diseases.

Epilepsy is the result of abnormal synchronous discharges (paroxysmal discharges) from large ensembles of neurons in brain structures. Stereoelectroencephalography (SEEG) is a functional investigation method performed during presurgical evaluation of drug-resistant partial epilepsy. It consists in exploring the putative epileptogenic zone with multiple sensor intracerebral electrodes implanted under stereotactic conditions [1] [2]. Performed during long-term video-EEG monitoring, SEEG provides signals (referred to as depth-EEG signals) that correspond to electrical mean field potentials arising from brain structures directly explored by electrodes.

Progress in the interpretation of such signals is crucial for the understanding of functional properties of cerebral structures that are at the origin of paroxysmal discharges observed during interictal and ictal periods. Indeed, many questions about the information contained in depth-EEG signals remain open. These questions are related to the relationship between the properties of signals (morphological and spectral) and the underlying organization of populations of neurons involved in their generation: when cortical activity reflected in depth-EEG signals is changing from background activity to paroxysmal activity, how do excitation, inhibition and synchronization parameters change within neuronal subsets? How do source-related parameters (surface and 3D geometry) and source-sensor relationships (distance and orientation of sensors with respect to sources) influence the generation of potentials measured along intracerebral electrodes?

In this study, we address some of these questions through a biophysically- and neurophysiologically-relevant modeling of depth-EEG signals. The approach starts from the representation of local field potentials (LFPs) generated by coupled neuronal populations distributed over a patch of neocortex (folded surface obtained from anatomical imaging data). From this extended source model, the potential at each sensor location is then computed by solving the forward problem in the volume conductor under two assumptions (infinite and finite field), for comparison. Finally, quantitative comparison of real depth-EEG potentials recorded along intracerebral electrodes and corresponding simulated potentials allowed us to infer, from the model, knowledge about synchronization between neuronal populations and spatial extent of the distributed source during transient epileptiform activity (epileptic spikes).

II. Extended Source Model

At the level of the single cell, synaptic activation of a neuron causes changes in membrane conductance, which leads to the generation of primary currents through the membrane and causes a variation of the postsynaptic membrane potential (i.e. an excitatory or inhibitory postsynaptic potential, EPSP or IPSP). EPSPs cause active sink at the level of apical dendrites while IPSPs create active source at the soma. In both cases, extracellular currents (volume currents flowing in the surrounding medium) oriented in the same direction are generated and a dipolar source-sink configuration with the same polarity is created [3].

At the level of neuronal assemblies, these extracellular currents can only be measured at a distance from the sources when neurons are well organized both in space and in time. This is typically the case for cerebral cortex. Because of its columnar organization, it is admitted that the primary sources of EEG activity are the pyramidal cells in the cortical layer. Indeed, as neurons are distributed parallel to each other and perpendicular to the cortical surface, cells belonging to a same population activate coherently, resulting in the summation of extracellular currents and not in their cancellation. This principle allows us to consider the neuronal population as a whole and to represent its average electrical contribution by an equivalent current dipole whose time-varying moment depends on the time variations of average post-synaptic potentials generated at the population level.

These biophysical aspects justify our modeling approach: the model we developed to interpret signals recorded along intracerebral electrodes is based on the combination of both a model of coupled neuronal populations and a distributed current dipole model. The former allows for simulation of time-varying LFPs generated by coupled neuronal assemblies for meaningful modifications of physiological parameters like the balance between excitation and inhibition (i.e. variations of average PSPs) within populations, or like the degree of coupling between populations. The latter allows us to compute the electrical contribution of a patch of neocortex at any sensor for anatomically-relevant spatial distribution of these populations of neurons.

A. Temporal Dynamics of Neuronal Populations

LFPs primarily reflect summated postsynaptic potentials in activated main cells (mainly pyramidal neurons for the neocortex). In order to realistically represent their time variations, we used a physiologically-relevant model consisting in a network of coupled neuronal populations described elsewhere [4] [5]. The model is illustrated in Fig. 1. In brief, each neuronal population (Fig. 1a) contains two subsets of neurons that mutually interact via excitatory and inhibitory feedback: pyramidal cells and local interneurons. Each subset is characterized by i) a linear transfer function that changes the average pre-synaptic pulse density of action potentials into an average receptor-dependent postsynaptic membrane potential (either excitatory - EPSP - or inhibitory -IPSP-) and ii) a static nonlinear function that relates the average post-synaptic potential of a given subset into an average pulse density of potentials fired by the neurons. The influence from neighbourhood is modeled by an excitatory input p(t) that globally represents the average density of afferent action potentials. At each population, two parameters allow for adjustment of the amplitude of average EPSPs and IPSPs while synaptic efficacy is tuned using four connectivity constants. Since interconnections between neuronal populations are ensured by axonal projections between pyramidal cells, the model accounts for this organization by using the average pulse density of action potentials from the main cells of one population as an excitatory input to another population of neurons. A connection from a given population i to a population j is characterized by a parameter K_ij which represents the degree of coupling (Fig. 1b). Appropriate setting of parameters K_ij permits to build systems inside which neuronal populations can be unidirectionally and/or bidirectionally coupled.

Fig. 1.

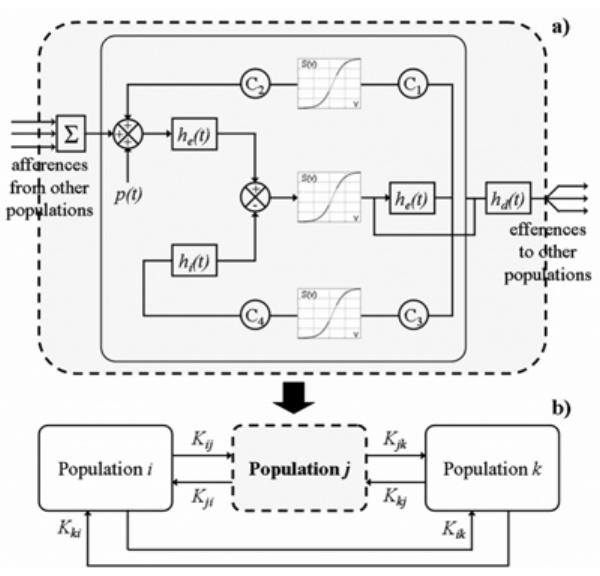
Structure of the model of multiple coupled neuronal populations, (a) Elementary model for a given population j within (b) the multiple coupled population model. Appropriate setting of parameters K_ij allows for neuronal populations to be unidirectionally and/or bidirectionally coupled. Each population of neurons produces a signal corresponding to local field activity.

In the absence of hypotheses about interconnection properties, couplings between populations were assumed to be bidirectional and all parameters K_ij were set to a same value K. In simulations, the effect of the degree of coupling between populations was analyzed by varying K. For standard parameter values, the model produces normal background activity. When model parameters are altered according to hypotheses related to epileptogenesis (increase of excitation/inhibition ratio or increase of coupling strength), it was already shown that transient epileptiform activities as spikes can be generated and that parameter K acts on the synchronization of these activities [5].

Model signal output α_i(t) represents the temporal dynamics of LFPs generated by neuronal population i. The amplitude of these LFPs is dealt with by the current dipole model (see section II-B).

B. Electrical Contribution of the Neocortical Patch

In this part, we consider a patch of neocortex composed by N coupled neuronal populations. Given its surface S, its total electrical contribution can be obtained from the elementary contributions of the N neuronal populations included in the patch. To compute each elementary contribution, we associated an elementary current dipole with each population i of surface s_i (Fig. 2). This dipole is defined by three parameters: position, orientation and norm.

Fig. 2.

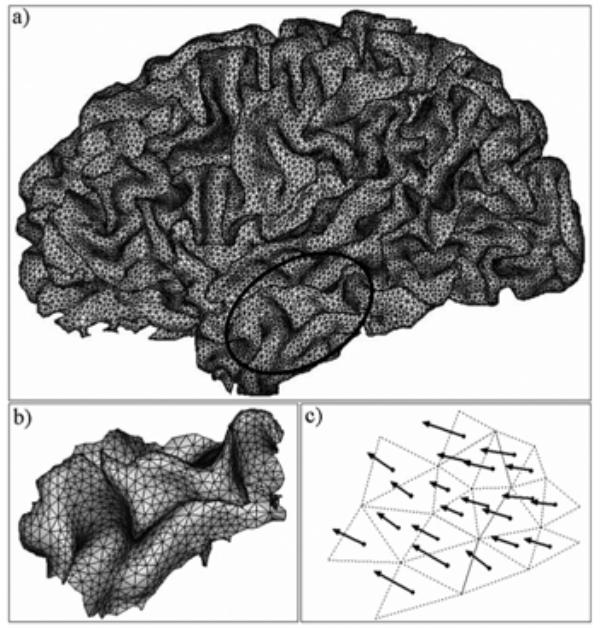
(a) A triangular mesh of the inner brain surface (grey-white matter interface) is built from the segmentation of 3D MRI data (~80000 triangles per hemisphere). In the extended source model, a surface element of neocortex is considered, as exemplified in the temporal lobe (ellipse), (b) This element of neocortex is composed of small elementary triangles (~1 mm² per triangle). Each triangle is assumed to represent a neuronal population, (c) The electrical contribution of each neuronal population is represented by an elementary current dipole which is placed at the barycentre of the triangle and which is oriented orthogonally to triangle surface. The moment of each elementary dipole is weighted by both the triangle area and the population time-varying field activity.

The two first parameters define the geometrical properties of the dipole and were set from an anatomically realistic triangular mesh of the neocortical patch (Fig. 2a). This mesh was built from the inner brain surface (grey-white interface) obtained from segmentation of three-dimensional magnetic resonance imaging (3D MRI) of the patient’s brain. Segmentation and triangulation of brain surface were performed using BrainVISA software (SHFJ, Orsay, France). A current dipole is located at the barycentre of each triangle of the mesh and oriented normally to its surface (Fig. 2b–c). The mesh resolution was adjusted so that the average surface s of triangles was equal to 1 mm², in accordance with [6].

The third parameter is the magnitude of the dipole moment m_i(t), which depends on the current density of the cerebral cortex and which temporal variations are imposed by those of LFPs generated by population i and represented by signal α_i(t). According to [6], an average value of the volume current density of the cerebral cortex is 175 nA/mm² (or nA.mm/mm³) for normal background activity. Assuming a cortical thickness of 3 mm, the average value of the corresponding surface current density is 525 nA/mm. Thus, at any time, an average value of the dipole moment m_i(t) associated to a neuronal population i of surface s_i is M = s_i × 525 (nA.mm). Finally, m_i(t) = M.α_i(t), i = 1…N. The temporal dynamics of m_i(t) are thus imposed by those of LFPs generated by population i and represented by signal α_i(t) in the neuronal population model. In order to keep m_i(t) in the correct range of values while preserving temporal dynamics, output signal α_i(t) was normalized between −1 and +1 for normal background activity.

In summary, the modeled neocortical patch behaves like a dipole layer whose local surface curvature complies with real anatomy. Its global surface S can be varied by steps of s mm². Given a seeding triangle, triangles are progressively added to the patch using local connectivity of the mesh, until total surface S is reached. Elementary dipole magnitudes reproduce time-varying dynamics of neuronal populations. The electrical contribution of this dipole layer at any arbitrary point in space (and thus at electrode sensor locations) is computed by considering all elementary dipoles (orthogonal to local surface) included in the patch, as described in the next section.

III. Reconstruction of Depth-EEG Signals

Stereoelectroencephalographic recording is performed during presurgical evaluation of patients with drug-resistant epilepsy. This technique allows for direct recording of brain structures using multiple sensor intracerebral electrodes (10 to 15 sensors, length: 2 mm, diameter: 0.8 mm, 1.5 mm apart) implanted according to Talairach’s stereotactic method [1]. The positioning of electrodes is determined in each patient from available non-invasive information and hypotheses about the localization of his/her epileptogenic zone. In general, electrodes are implanted orthogonally to the sagittal plane. Along the electrode trajectory, lateral (neocortical) and mesial (deep) structures are recorded. An example of intracerebral SEEG exploration is illustrated in Fig. 3.

Fig. 3.

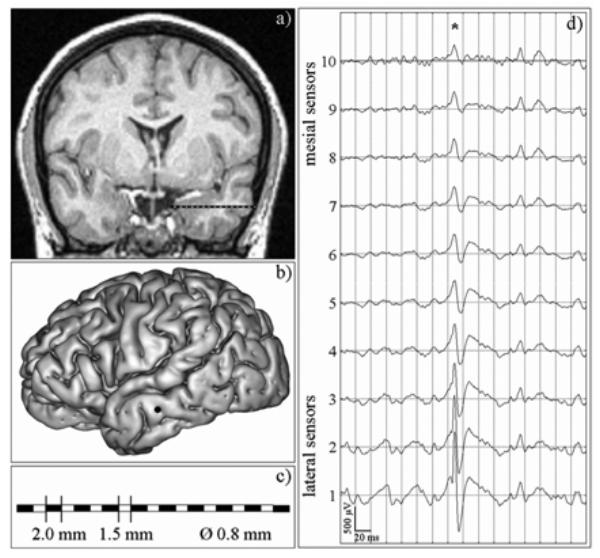
An example of SEEG exploration. For simplicity, only one intracerebral electrode is represented. However, during presurgical evaluation, the usual procedure uses 5 to 10 electrodes to explore brain regions that are supposed to be involved in epileptic activity, (a) MRI data of a patient suffering from lateral temporal lobe epilepsy. An intracerebral electrode is implanted in the left middle temporal gyrus, orthogonally to the sagittal plane, (b) Lateral view of the cortex, with surgical entrance point of the electrode in the left middle temporal gyrus. (c) Along each electrode, 10 to 15 cylindrical sensors (length: 2 mm, diameter: 0.8 mm, 1.5 mm apart) record signals from mesial (deep) and from lateral neocortical (middle temporal gyrus, superior temporal gyrus) structures, (d) An example of depth-EEG signals recorded by a 10-sensor intracerebral electrode, from mesial sensors (#7–10) to lateral, i.e. neocortical, sensors (#1–4). Asterisk indicates an interictal epileptic spike with maximal amplitude at lateral sensors and progressive amplitude decrease from lateral to mesial sensors.

Simulation of depth-EEG signals was performed from the extended source model by solving a forward problem in which both the characteristics of the intracerebral electrode (dimensions and location of sensors) and the properties of the surrounding media were taken into account. These properties were themselves represented in two different volume conductor models: an infinite volume conductor model and a 3-shell spherical head model. In the former, we only considered brain that was assimilated to an infinite and homogeneous volume conductor with constant isotropic conductivity. In the latter, we considered the whole head. Three media (brain, skull and scalp) were represented by a set of three concentric spheres, each of which was also assumed to be homogenous and to have constant isotropic conductivity. Radii of the three spheres were set to values identified from corresponding tissue boundaries extracted from real 3D MRI data.

In both cases, the calculation of electrical potentials is highly dependent on the conductivity values of the considered head tissues (see equations (1)–(5) below). In the past decades, several studies were performed to estimate these parameters, using both in vitro and in vivo measurements. It is generally admitted that brain and scalp can reasonably be assumed to have the same conductivity. However, reported brain conductivity values show a wide range of variations, as summarized in Table 1 which reports some conductivity values published over the past decades [7]–[14]. Moreover, the conductivity of the skull is known to be considerably lower than that of the brain and scalp, but the estimation of the ratio of brain and skull conductivities is still an open issue. Particularly, in a recently published study [14], Goncalves et al. showed that this ratio is lower than the commonly accepted value of 80[8]. Indeed, using an electrical impedance tomography method to perform in vivo measurements, authors found that the ratio of brain and skull conductivities is more likely to be in the range of 20–50. In this study, we used this result and we assumed skull conductivity to be 40 times lower than brain conductivity. This latter parameter was considered as free in our simulations, in order to analyze the effects of conductivity value changes.

Table 1.

Sample Selection of Brain Conductivity Values Reported in the Literature. These Estimates Were Performed Using Either in vitro or in vivo Measurements, in Animal or Human Tissues.

Reference	Brain grey matter (×10−5 S/mm)	Brain white matter (×10−5 S/mm)
Geddes and Baker (1967) [7]	35.21	14.66
Rush and Driscoll (1968) [8]	45.05
Hoseketal.(1978)[9]	33.33
Meijsetal. (1987) [10]	33.00
Haueisenetal.(1997)[11]	33.33	14.29
Oostendorp et al. (1999) [12]	20.25
Latikkaetal.(2001)[13]	28.49	25.58
Gon9alves et al. (2003) [14]	33.19
Average brain conductivity value: 30.08×10−5 S/mm (+/− 7.28 × 10−5)

As the power spectral density of mean field potentials arising from neuronal populations typically distributes over the 0–100 Hz frequency band, quasi-static approximation can be assumed to describe their conduction in a given medium. By linearity, the electrical potential generated by an arbitrary dipole layer at an arbitrary point in space can be written as the linear superposition of potentials generated by elementary dipoles. Hence, only one dipole is considered in the following theoretical expressions of the potential at a given time instant.

A. Infinite Volume Conductor Model

In the case of an infinite volume conductor, we considered a single current dipole represented by a dipole vector m in an infinite volume conductor characterized by its conductivity σ. The potential V(P) generated by this dipole at a point P located at distance r from the source is given by general electromagnetism principles [15] and can be written as follows:

$$\text{V}(\text{P})=\frac{\langle \mathbf{m},{\mathbf{u}}_r\rangle }{4\pi \sigma r^2}$$ (1)

where u_r is a unit vector oriented from source point to observation point, as shown in Fig. 4a.

Fig. 4.

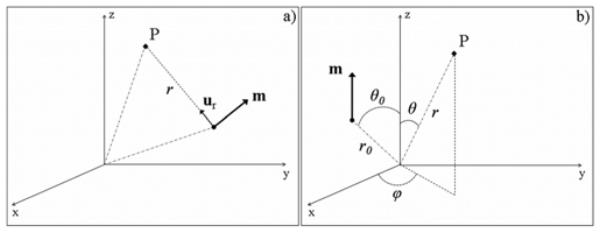
Coordinate systems, (a) Coordinate system for a dipole in the infinite volume conductor model, (b) Coordinate system for a dipole in the 3-shell spherical head model; particular case of a dipole of moment m located at (r_0,θ₀,0) and parallel to the z-axis.

B. 3-shell Spherical Head Model

In the case of a 3-shell spherical volume conductor, we considered a single current dipole m and an observation point P, both located inside the innermost sphere representing the brain. Potential V(P) can be related to the primary current density j_p(P) through the Poisson’s equation:

$${\nabla }^2\text{V}(\text{P})=\frac{\text{div}({\mathbf{j}}_{\text{P}}(\text{P}))}{\sigma }$$ (2)

where ∇² and div are the Laplacian and the divergence operators, and σ is brain conductivity.

Computation of potential V(P) requires to solve equation (2). The general solution to this linear non-homogeneous second order differential equation is V = V₁ + V₂ where i) V₁ is a particular solution to the non-homogeneous equation (2), and ii) V₂ is the general solution to the associated homogeneous equation (∇²V = 0).

1. As a particular solution, the Poisson’s equation (2) can be solved for a dipole embedded in an infinite region with a constant isotropic conductivity σ. Particularly, it has already been showed [16] that the potential due to a dipole m parallel to the z-axis and located at (r₀,θ₀,0) (Fig. 4b) can be written, in spherical coordinates, as in equations (3)–(4), where ${\text{P}}_k^l(.)$ is the associated Legendre polynomials.

   It is important to underline that this particular case is not restrictive as it can be reached from any dipole configuration by appropriate coordinate system transformation.

2. Assuming a solution of the form V₂ = F(r) G(θ) H(ϕ), the general solution of ∇²V = 0 was also shown [16] to be, in spherical coordinates, as in equation (6).

For the innermost sphere, terms B_kr^−(k+1) must be omitted as negative powers of r would cause a singularity at the origin (r = 0). Moreover, as the particular solution of equation (2) is only valid in the case where dipole is parallel to the z-axis and located in the xz-plane (ϕ₀ = 0) (Fig. 4b), the potential is ϕ-symmetric. Consequently, terms D_l.sin(lϕ) must be set to zero (i.e. D_l = 0, l = 0…k). Remaining coefficients A_k and C_l are determined from boundary conditions, which are specified in terms of the potential and the normal component of current density (σ∇ V) over the surfaces of the domain.

$${\text{V}}_1^{r<r_0}(r,\theta ,\varphi )=\frac{\parallel \mathbf{m}\parallel }{4\pi \sigma {r_0}^2}\sum _{k=0}^{\infty }\sum _{l=0}^k\left(2-{\delta }_l^0\right)(l-k-1)\frac{(k-l)!}{(k+l)!}{\left(\frac{r}{r_0}\right)}^k{\text{P}}_{k+1}^l(cos{\theta }_0){\text{P}}_k^l(cos\theta )cos(l\varphi )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{when\hspace{0.17em}}r<r_0$$ (3)

$${\text{V}}_1^{r>r_0}(r,\theta ,\varphi )=\frac{\parallel \mathbf{m}\parallel }{4\pi \sigma {r_0}^2}\sum _{k=0}^{\infty }\sum _{l=0}^k\left(2-{\delta }_l^0\right)(l+k)\frac{(k-l)!}{(k+l)!}{\left(\frac{r_0}{r}\right)}^{k+1}{\text{P}}_{k-1}^l(cos{\theta }_0){\text{P}}_k^l(cos\theta )cos(l\varphi )\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{when\hspace{0.17em}}r>r_0$$ (4)

$${\text{V}}_2(r,\theta ,\varphi )=\sum _{k=0}^{\infty }\sum _{l=0}^k\left(A_k{r}^k+B_k{r}^{-(k+1)}\right)(C_{l}cos(l\varphi )+D_{l}sin(l\varphi )){\text{P}}_k^l(cos\theta )$$ (5)

C. Simulation of Depth-EEG Signals and Comparison to Real Data

Along one intracerebral electrode, each sensor is a 2 mm long and 0.8 mm diameter cylinder. Sensors (10 to 15) are located 1.5 mm apart. In the real case, each sensor is a metallic conductor which has an equipotential surface. As sensors can be spatially close to sources, their dimensions are not negligible. In the simulation case, electrode sensors were divided into L observation points in order to account for the space they occupy in the cerebral tissue. Potentials generated by the extended source at each observation point were calculated by summing the contributions of the TV elementary dipoles of the neocortical patch. The value of the potential at each sensor (analogous to that actually reflected in depth-EEG signals) was then approximated by a spatial averaging of electrical potentials computed at each of the L equidistant points along the sensor axis.

For a given intracerebral electrode, simulated depth-EEG signals were quantitatively compared to real depth-EEG signals using a root mean square error (RMSE) between simulated and real maximal potentials, averaged over all sensor locations, and computed as follows:

$$\text{RMSE}=\sqrt{\frac{1}{n_s}\sum _{k=1}^{n_s}{\left({\stackrel{\sim }{\text{V}}}_k^{\text{real}}-{\stackrel{\sim }{\text{V}}}_k^{\text{sim}}\right)}^2}$$ (6)

where n_s is the number of sensors along the intracerebral electrode, and ${\stackrel{\sim }{\text{V}}}_k^{\text{real}}$ and ${\stackrel{\sim }{\text{V}}}_k^{\text{sim}}$ denote the maximal potential measured at sensor number k, in real and simulated data, respectively.

IV. Results

The model was used to interpret real depth-EEG signals recorded in a patient suffering from lateral temporal lobe epilepsy and candidate for epilepsy surgery (Fig. 3). The extended source of activity was modeled by a neocortical patch located in the middle temporal gyrus. Nearby activity (rising from more distant patches) was not considered. A 10-sensor (n_s = 10 in equation (6)) intracerebral electrode (orthogonally implanted) was considered. In the model, the seeding triangle (centre of the neocortical patch) corresponded to the surgical entrance point of the electrode in the neocortex.

In order to infer, from the model, information about synchronization between neuronal populations and spatial extent of the distributed source during transient epileptiform activity (spikes), we performed simulations by progressively increasing the surface S of the extended source model from 1 cm² to 40 cm² (by steps of 1 cm²). Surface values correspond to a number N of neuronal populations that typically ranges from 100 to 4000, as parameter s was set to 1 mm² per population. For each surface value, brain conductivity σ was varied from 20 to 40×10⁻⁵ S/mm (by steps of 5×10⁻⁵ S/mm) (Table 1), and parameter K (degree of coupling between neuronal populations) was varied from 0 to a maximal value (corresponding to the limit for which a change from sporadic spiking activity to rhythmic discharge of spikes is observed in the model). Simulated potentials were compared to those actually recorded at each sensor location for both volume conductor models (computation of the RMSE between simulated and real maximal potentials over all sensor locations). In both cases, for same K value, this RMSE was found to always converge to a global minimum. For epileptic spikes, “optimal” simulations were obtained for rather large areas of cortex and for high degrees of coupling between populations in both models. These results are detailed hereafter.

Fig. 5 illustrates the effect of increasing the degree of coupling (parameter K) between neuronal populations. For practical reasons, the behaviour of the model is illustrated on 10 populations only. Parameters of the N populations (excitation/inhibition ratio and local connectivity constants) were adjusted so that they all generated background activity, and remained unchanged. Hence, for null coupling between populations, the TV simulated signals reflected background activity (Fig. 5a). When parameter K was increased, sporadic spikes appeared randomly and independently in the N populations (Fig. 5b) and led to the appearance of either low amplitude spikes or slow waves in reconstructed signals (not shown). For high values of parameter K, synchronization between activities from populations was enhanced as a single spike within one population led to the generation of a spike in all populations in a 300 ms time interval (Fig. 5c). It is important to notice that this setting of parameter K constitutes a necessary condition, in the model, to simulate high amplitude transient activity that resemble epileptic spikes observed in depth-EEG signals.

Fig. 5.

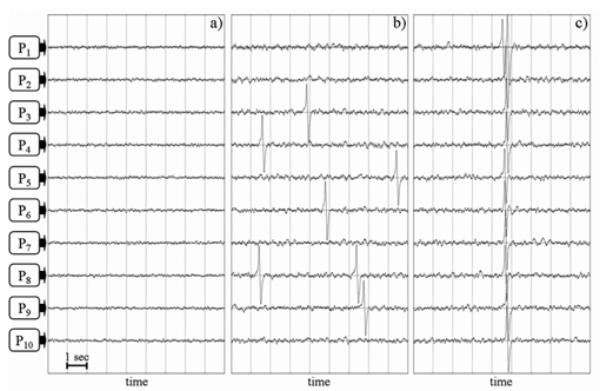
Influence of the coupling strength in a network often interconnected neuronal populations. All connections are bidirectional with identical strength K. (a) For null coupling (K=0), resulting signals correspond to normal background activity, (b) The increase of parameter K leads the model to generate sporadic spikes which appear randomly and independently from one population to another, (c) For high K values, synchronization is enhanced and single spikes that involve jointly all populations are produced.

For high K value, the RMSE was computed between simulated and real maximal potentials (equation (6)) for variations of the two other parameters (i.e. surface S of the extended source and brain conductivity σ and for both volume conductor models. Results are displayed in Fig. 6. Three main remarks can be made from the analysis of these results. First, one can notice that the relationship between parameter S and parameter σ is in accordance with physical principles in conducting media. For high conductivity value, electrical fields are more attenuated and higher source area is needed for simulated potential values to reach measured potentials. Second, in both volume conductor models, a minimal RMSE is present in all (S, σ) computed curves. Local minima were found to be less pronounced in the infinite case than in the spherical case. Third, and interestingly, we found a global minimum RMSE among all performed simulations in the infinite model and in the spherical model, denoted as RMSE_inf and RMSE_sph, respectively. In the infinite case (Fig. 6a), RMSE_inf = 56.67 was obtained for S_inf= 20 cm² and σ_inf= 25×10⁻⁵ S/mm. In the spherical case (Fig. 6b), RMSE_sph = 47.32 corresponded to S_sph = 22 cm² and σ_sph = 32.5×10⁻⁵ S/mm. Note also that RMSE_inf is slightly higher that RMSE_sph. This means the spherical model is more “appropriate” than the infinite model, regardless of the relevance of estimated surface and conductivity values which is discussed in the next section.

Fig. 6.

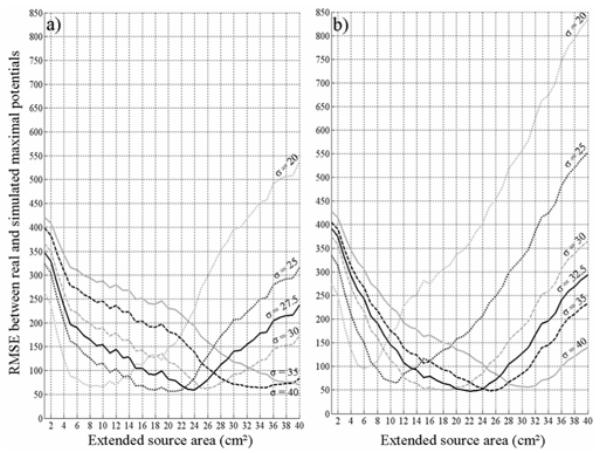
Root mean square error (RMSE) computed between simulated and real spike maximal potentials, with respect to variations of parameters S (extended source area) and σ (brain conductivity), for both volume conductor models, (a) In the infinite case, a global RMSE minimum (RMSE_inf = 56.67) was obtained for S_inf= 20 cm² and σ_inf= 25×10⁻⁵ S/mm (black dotted line), (b) In the spherical case, the global RMSE minimum (RMSE_sph = 47.32) corresponded to S_sph = 22 cm² and σ_sph = 32.5×10⁻⁵ S/mm (black solid line).

The reconstruction of electrical potentials corresponding to minimal RMSE in both volume conductor models (i.e. in the case where S = S_inf, σ = σ_inf and where S = S_sph, σ = σ_sph is illustrated in Fig. 7. Result analysis leads to two main remarks. First, the general morphology of simulated potentials, for both volume conductor models (Fig. 7b–c), was strikingly similar to that of actually recorded potentials (Fig. 7a). Second, as revealed by the plot of maximal amplitude of the spike with respect to space (sensor location along the electrode) shown in Fig. 7d, the model generated potential values that closely match those actually measured (in the order of 1 mV for the more lateral sensor at the spike maximum). Regarding amplitude gradients, results showed that potential versus distance curves obtained from simulated signals (Fig. 7d, square and triangle) were close to that obtained from real data (Fig. 7d, circle). As an interesting result, curve fitting showed these potential versus distance curves were hyperbolic and not parabolic. This indicates that real and simulated potentials are inversely proportional to source-sensor distance. This result shows that potential attenuation in the dipole layer model is less steep than the attenuation that would be obtained in the “ideal” single dipole model (for which voltage is an inverse function of the square source-sensor distance).

Fig. 7.

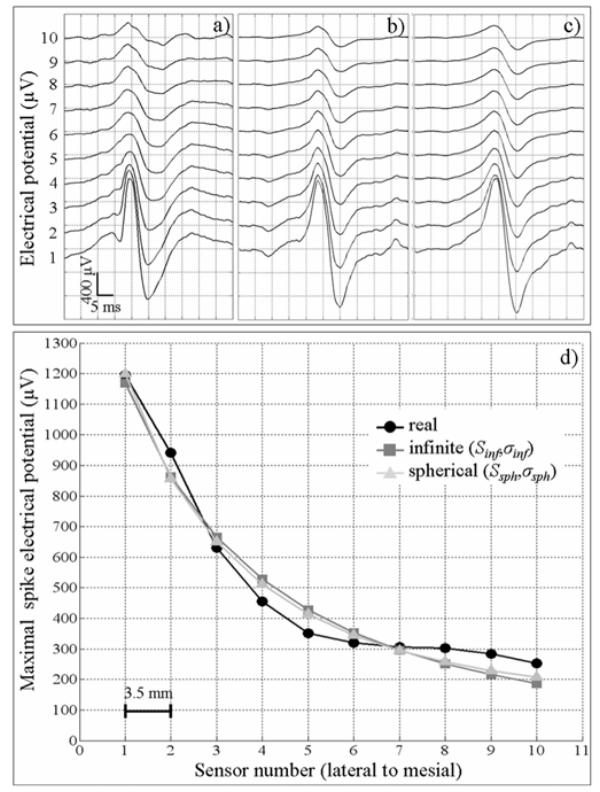
A simulation example of a transient epileptiform activity (spike), (a) Real depth-EEG signals were recorded by an intracerebral electrode implanted in the left middle temporal gyrus (from mesial - top - to lateral -bottom - sensors). Simulated signals obtained from the extended source model (patch of neocortex located in the left temporal lobe) in which surface and conductivity parameters (S, σ) are set to values corresponding to minimal RMSE (see Fig. 6), for infinite volume conductor model (b) and for 3-shell spherical head model (c). (d) Comparison of real (circle) and simulated voltages along the intracerebral electrode for both the infinite model (square) and the spherical model (triangle). Voltage estimator corresponds to the spike maximal potential.

Finally, regarding computation time, simulations performed in the 3-shell head model were 30 times longer than those performed in the infinite volume conductor model. This difference is due to the fact that potential computation involves an infinite expansion in the spherical case (equations (3)–(5)), while it is directly derived from a scalar product of two 3D vectors in the infinite case (equation (1)). As an example, the time required to reconstruct depth-EEG signals along the electrode for given K and conductivity values, and for average surface of 20 cm² was about 1 hour in the spherical case and about 2 min in the infinite case, on a standard PC computer (using C code, with no special optimization).

V. Discussion

From a cortical extended source model and from geometrical characteristics of multiple sensor intracerebral electrodes, depth-EEG signals were simulated and compared to real signals recorded in a patient with lateral temporal lobe epilepsy candidate to surgery. In order to represent both temporal and spatial features of depth-EEG signals, the modeling approach connects two levels of description. First, dynamics of neuronal assemblies included in a considered element of neocortex are represented in a model of coupled populations of neurons. Second, these populations are spatially distributed over the surface of this cortical patch. From this extended source model (dipole layer), signals are simulated from the forward solution, at each sensor location. Results showed that morphological features of simulated signals are very similar to those of real depth-EEG signals during transient epileptic activity (spikes) with simulated maximal potential amplitudes corresponding to real ones at the considered recording sites along the electrode. Regarding amplitude attenuation as a function of space, we found that potentials are inversely proportional to source-sensor distance according to a hyperbolic (1/x) and not a parabolic (1/x²) relationship that would be obtained with a single dipole model. This result adds further evidence that neocortical sources of epileptic interictal activity have an extended nature that can be hardly represented by only one equivalent current dipole.

In the extended source model, the main findings of this study showed that simulated transient epileptiform signals are similar to real depth-EEG spikes under two particular conditions: the degree of coupling between neuronal populations must be significantly high and the spatial extent of the neocortical source must be relatively large. These findings are discussed below.

The degree of coupling between neuronal populations in the model relates to excitatory cortico-cortical connection efficacy. To reach depth-EEG potentials measured during epileptic spike activity, an increase of coupling parameter is necessary. This increase enhances the synchronization of epileptic spikes generated at the level of neuronal populations. Actual depth-EEG potential values are only reproduced for near-synchronous spiking activity in neuronal populations. This condition in the model may also be interpreted as an augmentation of the global excitability of the modeled neocortical patch and corroborates the pathophysiological hypothesis of hyperexcitability in the neuronal tissue involved in the generation of epileptic activities (see review in [17]).

As far as the surface of the source is concerned, results showed that the neocortical surface involved in the generation of epileptic spikes is rather large, in both volume conductor models. Indeed, “optimal” simulations were obtained for surfaces ranging from 20 to 26 cm² in the infinite case, and from 18 to 25 cm² in the spherical case. Although estimated source areas are of same order of magnitude in both volume conductor models, results were found to significantly differ between these two models in terms of brain conductivity. Indeed, minimal RMSE between simulated and real maximal potentials of the spike were obtained for a brain conductivity value in the order of 25×10⁻⁵ S/mm in the infinite case against 32.5×10⁻⁵ S/mm in the spherical case. This latter value seems to be more relevant than the former value if one refers to the average value of brain conductivities given in Table 1. Following this idea, when we used a value of σ ranging from 30 to 35×10⁻⁵ S/mm in the infinite conductor volume model, we ended with less realistic values for source area S, ranging from 26 to 34 cm².

For these reasons, we think that, under infinite assumption for the volume conductor model, electrical potential values are underestimated by equation (1), which is compensated either by an overestimated source area or by an underestimated brain conductivity value. Results tend to confirm that volume conductor models accounting for the different tissues of the head are needed to accurately estimate potentials at each sensor position, even if these sensors are strictly located inside the brain.

In the 3-shell spherical head model, the cortical area involved in the generation of epileptic spikes was estimated to vary from 18 to 25 cm² for conductivity values ranging from 30 to 35×10⁻⁵ S/mm. These results corroborate those described in two recently published studies [18] [19] about the spatial extent of cortical sources in epilepsy. In [18], authors studied the generation of interictal spikes in 16 patients suffering from temporal lobe epilepsy from simultaneous scalp and cortical recordings (subdural electrode strips and grids). The spatial extent of cortical sources of interictal spikes was estimated from the number of subdural electrode contacts demonstrating concurrent depolarization. Those in vivo measurements showed that only few cortical sources with an area of < 10 cm² were able to generate scalp-recordable interictal spikes, whereas the activation of sources with an area ranging from 10 to 30 cm² commonly led recognizable scalp spikes. In [19], authors developed a spike generator to investigate the accuracy of dipole modeling during transient epileptic activity. As in the present study, the source of epileptic activity was realistically simulated by using a cortical patch with areas of different extents. The cortical patch was also built from 3D MRI data and consisted of a set of small triangles, each triangle having an elementary dipole oriented orthogonally to the cortical surface. Although they only considered the static problem (temporal dynamics of local field potentials are not represented as in the present study), their simulations showed that cortical areas ranging from 6 and 24 cm² were involved in the generation of scalp interictal epileptic spikes in temporal lobe epilepsy, for comparable surface current density value. At first sight, surfaces ranging from 18 to 25 cm² may appear as relatively large. However, it is important to note that this surface takes into account the cerebral convolutions, since the 3D anatomy of the neocortical patch is represented in the source model (Fig. 2a).

To simulate depth-EEG signals, we solved a forward problem, i.e. we computed electrical potentials at sensors from a definite set of current sources inside the brain. In the past decades, a tremendous amount of studies dealt with the forward solution in the field of electroencephalography and magnetoencephalography. In particular, several mathematical expressions have been established for electrical potentials, for both spherically and realistically shaped head models (see [20] and [21] for reviews). However, most of these studies considered scalp potential reconstruction only and few addressed the problem of describing potentials recorded in depth. To our knowledge, this study is the first attempt to model depth-EEG signals, as recorded by multiple sensor intracerebral electrodes used in the presurgical evaluation of patients with drug-resistant partial epilepsy.

As already mentioned, the approach reported here is based on the combination of two models (distributed current dipoles and coupled neuronal populations) which ensures a more accurate description of both spatial and temporal properties of neuronal sources of brain electrical activity. Although these two levels of representation are both widely used in contexts where hypotheses about neuronal sources are to be made, they are always considered separately. The only exception we found is the study by Jirsa et al. [22], who developed a model based on both a distributed current dipole model and a neuronal population model. On the one hand, a mesh of the cortical surface was built from 3D MRI data, which allowed for the positioning and the orientation of several elementary current dipoles. On the other hand, a macroscopic neuronal model was used to simulate neuronal field dynamics. Forward computations were performed in a single layer model (skull-brain interface) and in a spherical head model. Although the conceptual framework of our study is close to that reported in [22], the context and objectives of the two studies are different. Our goal is to use the model to reproduce depth-EEG signals recorded in epileptic patients and to infer, from “optimal” model parameters, knowledge about pathophysiological mechanisms involved in the generation of epileptiform activity. This intent differs from Jirsa’s, who used the model to establish a relation between function and behaviour in the human brain, in particular during cognitive tasks like the coordination of finger movements.

VI. Future Work

Perspectives of this study relate to the current limitations of the model that are to be addressed. First, the model is restricted to lateral neocortical sources of activity essentially because efficient segmentation of mesial structures (such as amygdala, hippocampus, and enthorinal cortex) from 3D MRI data remains a technically difficult issue. In the future, we plan to develop an approach similar to that presented here for deep structures, because they are known to play an important role in the generation of epileptic activities in temporal lobe epilepsy [23].

Second, at present, the head is represented by a set of three concentric spheres (brain, skull and scalp), in which each compartment is assumed to be homogeneous and isotropic, although electrical conductivities of head tissues are known to be anisotropic. It is the case, for example, for brain tissue in which the measured conductivity is different if transversal or longitudinal fibres are considered [7]. Volume conductor representation can be improved by use of realistically shaped models (for instance obtained from finite-element approach [24]). However, the striking similarity of simulated and real depth-EEG signals obtained for reasonable cortical surface values allows us to think that specific error introduced by the spherical head model is acceptable compared to that introduced by the infinite volume conductor model.

Third, in the present study, we only considered focal epileptic activities that were simulated from a restricted activated part of the cerebral cortex. In the case where epileptic activities arise from multiple generators, several extended sources distributed in different areas of the cortex will be considered to represent multi-focal events.

Finally, the use of the model for computing scalp EEG signals is straightforward. This extension will offer the possibility to identify the model from signals recorded at the surface of the scalp and simultaneously recorded within the underlying cerebral structures. On the long term, these works should participate to the identification of epileptic activity sources from non-invasive data only.

Biographies

D. Cosandier-Rimélé was born in France, in 1980. She received the Engineering Diploma in electronics and computer engineering from the Ecole Nationale Supéerieure des Sciences Appliquées et de Technologic, Lannion, France, in 2003, and the M.S. degree in signal processing and telecommunications from the University of Rennes 1, Rennes, France, in 2003. She is currently working towards the Ph.D. degree in signal processing at the Laboratory of Signal and Image Processing, INSERM, Rennes, France. Her research works deal with the reconstruction of surface and intracerebral EEG signals from physiologically-relevant models.

Jean-Michel Badier was born in France, in 1962. He received the Biomedical Engineering degree (1985) and the Ph.D. degree (1991) from the University of Technology of Compiegne (UTC), France. He is since 1997 a faculty member of the University of Aix-Marseille. He is particularly involved in the localisation of the sources of brain activity in the context of epilepsy surgery. He is now in charge of the Magnetoencephalography laboratory of Marseille that will start to operate spring 2007.

P. Chauvel is Professor of Clinical Neurophysiology at the University of Aix-Marseille II, and Consultant Neurologist at Hopital la Timone in the same medical campus. He trained in epileptology under Jean Bancaud, working with Bancaud and Talairach at a time when they were laying the foundation for much of what we know of the dynamics of onset and propagation of focal seizures. Continuing to work in the field of epilepsy surgery, he moved to Rennes in the early nineties, then to Marseille in 1997, founding a major epilepsy surgery unit. He is head of an INSERM Research Unit, named “Epilepsy and Cognition” (U751). As well as authoring many papers on the clinical features of seizures and their correlations with seizure discharges recorded using intracerebral electrodes, he has more recently published work on processing of EEG signals. He has regarded his work in epilepsy as an opportunity to study normal cerebral function: his unit in Marseille includes research teams working on language and memory processing and higher cognitive functions.

F. Wendling was born in France, in 1967. He received the Biomedical Engineering degree from the University of Technology of Compiegne, France (1990), the Master’s degree from the Georgia Institute of Technology, Atlanta, USA (1991) and the PhD degree in Signal Processing from the University of Rennes, France (1996). Since 1998, he has been working as a full-time researcher for the French NIH (INSERM) at the Laboratory of Signal and Image Processing (LTSI), in Rennes. Since 2001, he is responsible for a research project entitled “Dynamics of neuronal systems in epilepsy and cognition” at the LTSI. His research works deal with electrophysiological signal analysis and modeling of brain activity in the context of epilepsy.