Comprehensive Analysis of APOE and Selected Proximate Markers for Late-onset Alzheimer Disease: Pattern of Linkage Disequilibrium and Disease/Marker Association

Abstract

The ε₄ allele of APOE confers a two- to four-fold increased risk for late-onset Alzheimer’s disease (LOAD), but LOAD pathology does not all fit neatly around APOE. It is conceivable that genetic variation proximate to APOE contributes to LOAD risk. Therefore, we investigated the degree of linkage disequilibrium (LD) for a comprehensive set of 50 SNPs in and surrounding the APOE using a substantial Caucasian sample of 1100 chromosomes. SNPs in APOE were further molecular haplotyped to determine their phases. One set of SNPs in TOMM40, roughly 15 Kb upstream of APOE, showed intriguing LD with the ε₄ allele, and were strongly associated with the risk for developing AD. However, when all the SNPs were entered into a logit model, only the effect of APOE ε₄ remained significant. These observations diminish the possibility that loci in the TOMM40 may have a major effect on the risk of LOAD in Caucasians.

Introduction

Genetic variation in apolipoprotein E gene (APOE) confers risk for both coronary artery disease (CAD) [1] and Alzheimer’s disease (AD) [2]. The connection of this gene to CAD is apparent because the ApoE protein, as a component of serum lipoprotein particles, binds to cell surface receptors, mediates lipoprotein uptake, and thus has direct effects on lipid metabolism. In addition, both functional and regulatory variation in APOE account for population-level variation in metabolic lipid levels [3]. The connection between ApoE and AD pathogenesis is more obscure. The major APOE risk for AD is generally assumed to come from the ε₂/ε₃/ε₄ haplotype system with the ε₄ allele increasing risk for both disorders and the ε₂ allele is protective [4]. However, recent estimates of heritability of AD range from 57-78% [5], with ε₄ alleles accounting for only roughly 50% of that heritability.

The ε₂/ε₃/ε₄ haplotype system is defined by 2 non-synonymous single nucleotide polymorphisms (SNPs) in APOE exon 4. One is a C/T SNP (rs429358) that encodes either arginine (C) or cysteine (T) in ApoE at amino acid 112. The second site defining this haplotype system is a C/T SNP (rs7412), which again encodes arginine (C) or cysteine (T) at ApoE amino acid 158. The allelic compositions of the commonly investigated haplotypes are TT for ε₂, TC for ε₃, and CC for ε₄. The effects of these coding variants on ApoE function are well-defined [6]. Regulation of APOE expression is controlled by cis-acting elements both within the gene and in flanking sequences. The function of these regulatory elements could potentially be influenced by genetic variation. Variation in the 5’ promoter region of APOE alters its expression [7, 8], and some of these variants may be associated with AD [9], although their impact appears to be minor. In fact, it has proven difficult to provide good estimates of the effect of the 5’ regulatory variation on risk for AD, in part because these SNPs could be in linkage disequilibrium (LD) with ε₄. There are numerous non-coding SNPs within and immediately adjacent to APOE that may influence measures of lipid metabolism [10].

Variation just outside of the 3’untranslated region of APOE has also been reported to have a minor impact on risk for LOAD [11]. Again, LD potentially confounds interpretation of the association. Downstream regulatory elements include two copies of a multienhancer that control expression of APOE in adipocytes, macrophages and astrocytes (ME1 and ME2) [12, 13], two copies of a hepatic control region (HCR1 and HCR2) [14, 15] enhancer that control expression in the liver, and a potential brain control region 42 kb from APOE that may control expression in brain neurons and microglia [16]. It is unknown whether genetic variation in or near these elements controls APOE expression. What of the genes and genetic variants outside but potentially in LD with ε₄ of APOE? For example, based on results from cladistic analyses, Templeton [17] argued that variation in APOC1 causes risk to LOAD. Also unknown is whether there are additional cis-elements upstream of the APOE promoter that contribute to this risk.

Because of the strong association between the ε₂/ε₃/ε₄ variants of APOE and risk for AD, we investigated the LD structure of APOE and its surrounding region. Of particular interest are SNPs in potential regulatory regions both within and flanking APOE that could modify the risk associated with the ε₂/ε₃/ε₄ haplotypes. Also, APOE is an excellent model to explore the ability of genome-wide association methods to detect a causative gene when risk for a common disease is determined by a single, monophyletic, common variant therein. To characterize the APOE-region LD structure, we genotyped 50 SNPs in and surrounding APOE, with particular reference to the ε₂, ε₃, and ε₄ system of alleles. The 550 Caucasian samples genotyped were collected to evaluate the genetic basis of AD. Within APOE itself, we report on 21 SNPs that were molecularly phased using the methods reported in Yu et al. [18]. This set of SNPs overlaps substantially with those assayed by Fullerton et al. [19]. Outside of APOE, we relied on statistical methods to infer haplotypes or assess LD. In our study population, we assessed whether selection on ε₄ (or possibly other loci in the region) alters the pattern of LD found in the AD sample relative to that found in the control sample. Significant LD was observed between ε₄ and SNPs spanning 50 kb, a region containing multiple genes. Because of the LD patterns observed, it is difficult to distinguish the impact of ε₄ from highly correlated SNPs in the region. In terms of detecting APOE as an AD risk gene, there are numerous SNPs in the region that would detect AD risk, but interestingly, they are not necessarily in APOE. In fact, some of the SNPs with the greatest power to detect risk are in the adjacent gene TOMM40, while many others much closer to ε₄ would not be useful.

Results

Genotype data of fifty loci (Fig. 1, Supplementary Table) in the APOE region were generated from a clinical sample of 550 Caucasians. Among the subjects, 193 individuals had a clinical diagnosis of LOAD, 125 individuals had diagnoses of other neurodegenerative disorders, and 232 individuals were controls. For our combined samples, 16 of the 21 APOE loci were polymorphic, and 11 of 21 had a minor allele frequency (MAF) > 0.05 (Supplementary Table). The remaining 29 loci, those outside of APOE, were selected to have MAF > 0.02 in the samples. After Bonferroni correction for multiple testing, two loci violated Hardy Weinberg (HW) assumptions in the LOAD sample (SNP 8 [rs6857] and SNP 11 [rs11556505]); a different locus violated HW in the control sample (SNP 1 [rs2965118]); and all three violated HW when the data are combined to produce the full sample (data not shown). None of the loci within APOE violated HW in any of the samples. SNPs in APOE were further haplotyped by molecular methods to determine their phases. We used the Allele Discriminating Long and Accurate PCR Haplotyping (ADLAPH) method [18] to produce unambiguous molecular haplotypes for 21 loci in APOE (SNPs 17-37, Fig. 1, Supplementary Table) from our study samples.

Fig. 1.

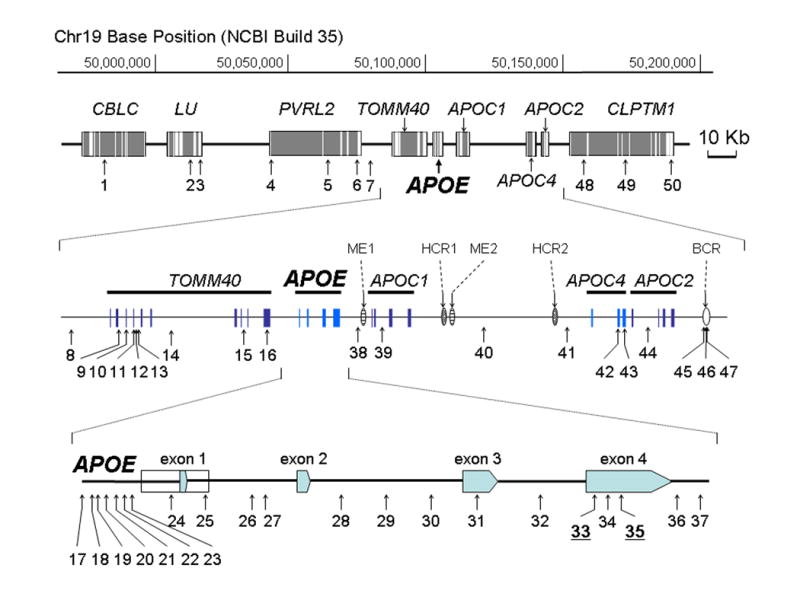
SNP map of APOE and its surrounding region. A 215 Kb genomic section containing nine genes, five APOE regulatory elements and 50 SNPs analyzed in this study is shown. APOE and its flanking region are further enlarged. Detail information of the 50 SNPs is described on Supplementary Table.

LD Pattern Within APOE

Genotyping error

Of the 550 individuals genotyped and 1,100 haplotypes determined for 21 APOE loci, 12 were singleton haplotypes. We reasoned that some of these singleton haplotypes could result from genotyping error because an error would have a non-negligible probability of producing a novel, albeit pseudo-haplotype. To address the question of the rate of genotyping error, we performed two analyses, one computational and the other molecular (for details, see Methods section). We estimate a per-locus error rate of 0.0003 with an upper 95% confidence interval of 0.0006.

Corrected haplotype distribution

If the APOE loci were in linkage equilibrium, then we would expect hundreds of different haplotypes. Because these SNPs fall within a 5300 bp region, we do not expect such a substantial set of haplotypes. Only 35 unique haplotypes are observed in the distribution, and the distribution is distinctly skewed toward a few common haplotypes (Table 1). Five haplotypes account for over 75% of the haplotype distribution, and 13 haplotypes account for over 95% of the haplotype distribution. The common haplotypes are common in both the LOAD and control samples, although individual haplotypes clearly differ in frequency (Table 1), especially with respect to presence/absence of ε₄. After accounting for errors, nine singleton haplotypes occur in the 1100 haplotypes. These singletons are evenly distributed across the samples: for the LOAD sample, the relative frequency of singletons is 0.008; for the control sample, it is 0.006; and for the miscellaneous sample it is 0.008.

Table 1.

Haplotypes and frequencies for all individuals (All), only individuals diagnosed with LOAD (LOAD) and only individuals who serve as controls for LOAD patients (Controls). “All” contains others samples in addition to LOAD and Controls. Embedded in the 21-locus (Figure 1 and Supplementary Table, SNP 17-37) haplotypes, in bold, are the two-locus haplotypes that encode the ε₂/ε₃/ε₄ system of alleles

No	Complete Haplotype		All		LOAD		Controls
			Count	Freq	Count	Freq	Count	Freq
1	CCACACTGGGCGATTCTCCAT	ε3	241	0.2191	70	0.1814	116	0.2500
2	CCACACTTCGCGGTTCTCCAT	ε3	213	0.1936	53	0.1373	107	0.2306
3	CCACACTTGGCAGTTCCCCAT	ε4	204	0.1855	111	0.2876	52	0.1121
4	CCACTCTTCGCGGTTCTCCAT	ε3	92	0.0836	23	0.0596	43	0.0927
5	CCACACTGGGCGATTCTCCAC	ε3	91	0.0827	26	0.0674	37	0.0797
6	CCACACTGGGCGGTTCCCCCT	ε4	59	0.0536	34	0.0881	14	0.0302
7	CCACTCTGGGCGGTTCTCTAT	ε2	40	0.0364	8	0.0207	25	0.0539
8	CCACACCTCGTGGTTCTCCAT	ε3	33	0.0300	13	0.0337	14	0.0302
9	CCACTCTGGGCGATTCTCCAT	ε3	26	0.0236	9	0.0233	15	0.0323
10	CCACACCGGGCGGTTCTCTAT	ε2	18	0.0164	3	0.0078	11	0.0237
11	CCACACCTGGCAGTTCCCCAT	ε4	17	0.0155	9	0.0233	2	0.0043
12	CCACACCGGGCGATTCTCCAT	ε3	10	0.0091	4	0.0104	5	0.0108
13	CCACACCTCGCGGTTCTCCAT	ε3	9	0.0082	3	0.0078	5	0.0108
14	CCACACTGGGCGGTTCCCCAT	ε4	5	0.0046	4	0.0104	0	0
15	CCACACTTCGCGGGTCTCCAT	ε3	4	0.0036	1	0.0026	3	0.0065
16	CCACACTGCGCGGTTCTCCAT	ε3	4	0.0036	1	0.0026	2	0.0043
17	CCACACCGGGCGATTCTCCAC	ε3	3	0.0027	1	0.0026	2	0.0043
18	CCACACTTGGCAGTCCCCCAT	ε4	3	0.0027	1	0.0026	2	0.0043
19	CCACACTGGGCGGTTCTCTAT	ε2	3	0.0027	0	0	3	0.0065
20	CCACACTTGGCAATTCTCCAT	ε3	3	0.0027	1	0.0026	0	0
21	CCACTCTGGGCGGTTCTCCAT	ε3	3	0.0027	2	0.0052	0	0
22	CCACTCCTCGCGGTTCTCCAT	ε3	2	0.0018	0	0	2	0.0043
23	CCGCTCTTGGCGGTTCCCCAT	ε4	2	0.0018	1	0.0026	1	0.0022
24	CCACACTTGGCGGTTCTCCAT	ε3	2	0.0018	2	0.0052	0	0
25	CCGCTCTGGGCGGTTCCCCAT	ε4	2	0.0018	1	0.0026	0	0
26	CCACACCGGGCGGTTCCCCAT	ε4	2	0.0018	2	0.0052	0	0
27	CCACACTGGGCGGTTCTCCAT	ε3	1	0.0009	0	0	1	0.0022
28	CCACTCCGGGCGGTTCTCCAT	ε3	1	0.0009	0	0	1	0.0022
29	CCGCACTTGGCGGTTCCCCAT	ε4	1	0.0009	0	0	1	0.0022
30	TCACACTGGGCGGTTCTTCAT	ε3	1	0.0009	1	0.0026	0	0
31	CCACACTTCGCAGTTCCCCAT	ε4	1	0.0009	1	0.0026	0	0
32	CCACACTGGGCGGTTCCCCAC	ε4	1	0.0009	1	0.0026	0	0
33	CCACTCTTGGCGGTTCCCCAT	ε4	1	0.0009	0	0	0	0
34	CCACTCCTCGTGGTTCTCCAT	ε3	1	0.0009	0	0	0	0
35	CCACACTTCGTGGTTCTCCAT	ε3	1	0.0009	0	0	0	0

In the total sample, 61 chromosomes carry ε₂ on three different haplotypes (Table 1); 741 chromosomes carry ε₃ on 20 different haplotypes; and 298 chromosomes carry ε₄ on 12 different haplotypes. Contrasting the case and control samples (Table 1), the case sample contains 11, 210 and 165 haplotypes bearing ε₂/ε₃/ε₄ alleles (n = 386), respectively, whereas the control sample contains 39, 353 and 72 haplotypes bearing ε₂/ε₃/ε₄ alleles (n = 464).

LD

To analyze the “haplotype-block” structure of APOE, as measured by the diversity of the haplotype distribution [20], we restricted the data to the 11 SNPs with MAF > 0.02 (see Supplementary Table). Results from this analysis are congruent with the restricted distribution of haplotypes in Table 1, suggesting that all but the last locus of APOE form a single haplotype block. Analyses for a recombination hotspot are more ambiguous: some runs of Phase 2 find no evidence for a recombination hotspot within these loci (mean posterior likelihood of 1.0 across the region); whereas other runs place a hotspot in the vicinity of loci 21-23 (rs449647 and rs769446, mean posterior likelihood of 276.7). The pattern of pairwise LD in the gene – as measured by a common metric D’ [21] is compatible with the haplotype structure of the gene (Supplementary Figure 1), suggesting complete LD for most pairs of loci.

The complementary results of limited haplotype diversity, substantial D’, and limited evidence for recombination hotspots suggest that recombination has not been a major evolutionary factor within APOE. By contrast, another common measure of pairwise LD, namely r² or Δ² [21] – is not uniformly large; instead pairwise LD varies substantially and is often small (Fig. 2). This measure is also a function of recombination, but is sensitive to a host of other factors, including homoplasy [21, 22]. Homoplasy in APOE has been demonstrated by Templeton et al. , who described the occurrence of a particular mutation on more than one haplotype background in the APOE region [22, 23].

Fig. 2.

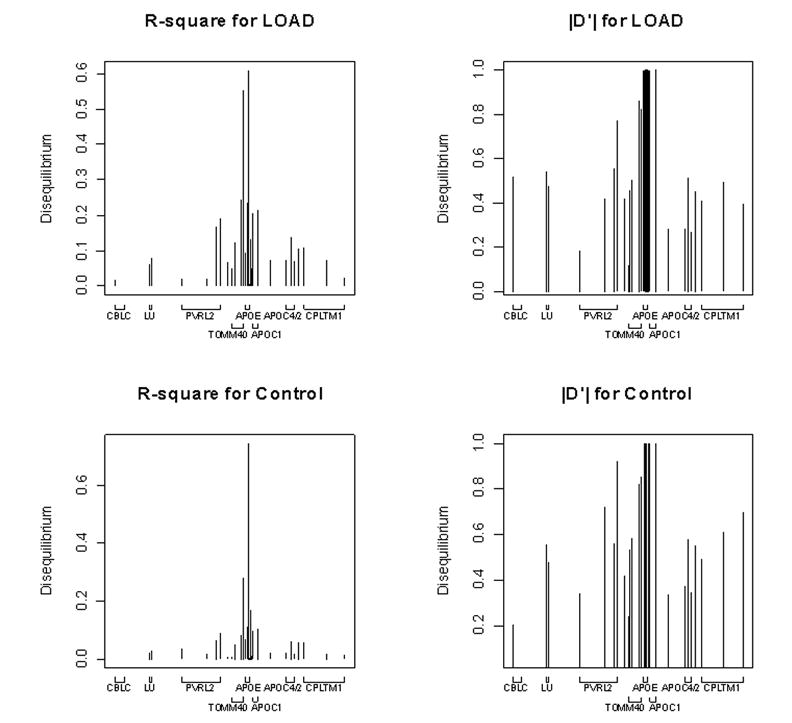
Pairwise LD between SNP 33 alleles (defining ε₃/ε₄ dichotomy) and all other loci across the region (except SNP 35, which defines the ε₂/ε₃ dichotomy). Left versus right show different equilibrium measures (r² versus |D’|) and top versus bottom contrast the LOAD sample versus the sample of control individuals.

LD Pattern in Loci in and surrounding APOE

Pairwise LD

In this subsection we focus largely on the ε₂/ε₃/ε₄ system of alleles, because of their presumed central role in the risk for LOAD. We also use the data from individuals diagnosed with LOAD and contrast those data to the controls. Fig. 2 shows the pairwise LD between the ε₂/ε₃/ε₄ system and other loci. Because of the relative rarity of ε₂, we centered the LD analysis on SNP 33, which defines the ε₄ versus ε₃ dichotomy. When measured by r², LD between alleles at SNP 33 and alleles outside of APOE shows notable variation (Fig. 2), much like the loci in APOE. Only one SNP in APOE shows a substantial r² with SNP 33, SNP 28, whereas a much larger number of SNPs 5’ of APOE show substantial r² (Fig. 2). LD tends to be unpredictable near the ε₃/ε₄ locus, but seems essentially absent at more substantial distances (Supplementary Table , Fig 2). The pattern is similar for both the LOAD and control samples. When LD is measured by |D’| (Fig 2), however, the values for most loci around SNP 33 are large (close to or equal 1), and are predictably small only at substantial distances from SNP 33 (Supplementary Table, Fig 2). Again the pattern is similar for both the LOAD and control samples. We do not report hotspot analysis for the larger region because we could not discern a consistent pattern in the results; it appears that numerous regions show some evidence for elevated recombination rates.

Tag SNPs

To summarize multivariate LD across these loci, as well as identify tag SNPs, we used the hierarchical cluster methods proposed by Rinaldo et al. [20]. Tag SNPs were selected using a bound of 0.8. Cluster analysis identifies only a few substantial clusters, and shows similar clustering features for both the LOAD and control samples (Supplementary Figure 2). SNPs spanning roughly 50 Kb and covering APOC4, APOC2 and CLPTM1 show substantial joint LD (SNPs 41-50 in Supplementary Fig. 2). This cluster, however, has no noteworthy correlation with SNPs 33 and 35, which define the ε₂/ε₃/ε₄ system. In terms of clustering by LD, SNPs 33 and 35 do not fall in the same cluster regardless of whether the LOAD or control samples were evaluated. Not only are SNPs 33 and 35 largely independent, they do not cluster strongly with other SNPs in APOE, with the exception of SNP 28, which clusters with SNP 33. Interestingly, SNP 33 clusters tightly with SNPs in TOMM40, especially SNPs 10-12 (Fig. 1), which are separated from SNP 33 by roughly 16 Kb. SNPs 10 and 11 occur in TOMM40 exon 3 and 4 respectively. SNP 35, defining the ε₂ versus ε₃ dichotomy, shows modest clustering with SNP 5, roughly 38 Kb away, in the second intron of PVRL2.

HapMap SNPs

To contrast our results with data from HapMap, we downloaded the data from release #21a (phase II Jan07 on NCBI B35 assembly, dbSNP b125; see HapMap in Electronic-Database Information). This version contains 219 SNPs spanning the same region we evaluated. Notably, neither SNP 33 (rs429358) defining the ε₃/ε₄ dichotomy nor SNP 35 (rs7412) defining ε₂/ε₃ dichotomy has genotypes in the CEU population of this version of HapMap. Nonetheless, genotypes for two other SNPs that we have shown are highly correlated with SNP 33 (r² > 0.5) are contained therein, namely SNPs 8 (rs6857) and 16 (rs10119), as well as others SNPs that are more moderately correlated. Because genotypes of SNPs 8, 16 and 33 are available in both Yoruba (YRI) and Japan (JPT) samples in HapMap, we evaluated these SNPs’ correlation in the two ethnic groups. Results indicated that both SNPs 8 and 16 do not correlate well with SNP 33 (r² = 0.0 and 0.029 respectively for SNPs 8 and 16 in YRI, and r² = 0.08 and 0.101 in JPT). Therefore, LD patterns in this region do not appear to be consistent across the different ethnic groups, although since SNP 8 was one of the SNPs which deviated from Hardy Weinberg equilibrium, we cannot exclude the possibility that there are as yet unrecognized genotyping artifacts, which could affect this conclusion.

Notably, the HapMap CEU data recapitulate the pattern of LD and clustering in Caucasians shown in Supplementary Fig. 2. Strong clustering emerges over a 50 Kb region, which contains the genes APOC1, APOC2, APOC4 and CLPTM1, while the roughly 60 Kb proximal shows no substantial clustering (data not shown). Clustering the HapMap CEU SNPs by H-clust reveals another SNP that should be highly correlated with SNP 33, specifically rs2075650, which has an r² of roughly 0.85 with SNP 8. Tag SNP selection using H-clust and the HapMap data always draws a SNP highly correlated with SNP 33, for a wide range of stringency of SNP selection, even to r² = 0.20 (data not shown). Therefore a genome-wide or local association scan built from HapMap data would very likely detect association to LOAD for regional SNPs, assuming the scan were adequately powered.

Disease Marker Association

APOE and ε₄ count

As has been demonstrated for many different samples, the distribution of ε₄ alleles (Table 2) differs substantially between AD and control samples (Chi-square = 78.6605, df = 2, p-value = < 2.2e-16). When evaluated by sex, the distribution of ε₄ alleles did not differ between men and women diagnosed with AD (Chi-square = 0.23, df = 2, p-value = 0.89) or between men and women in the control samples (Chi-square = 2.01, df = 1, p-value = 0.16). Analysis of age at AD diagnosis, performed using a Cox Proportional Hazards model, shows time to diagnosis is strongly dependent on ε₄ count (β = -1.07; SE = 0.111; z = 9.67; p ~ 0.0). Survival analysis models with gender and ε₄/gender interaction reveal no additional significant covariates.

Table 2.

AD status versus count of ε₄ alleles

Sample	Count of ε4 alleles
	0	1	2
All AD	58 (30.9)	105 (54.4)	30 (15.5)
All Control	162 (61.8)	68 (29.3)	2 (0.9)
Women AD	32 (30.9)	55 (54.4)	15 (15.5)
Women Control	91 (61.8)	45 (29.3)	2 (0.9)
Men AD	26 (30.9)	50 (54.4)	15 (15.5)
Men Control	71 (61.8)	23 (29.3)	0 (0.9)

Other SNPs in APOE

Within APOE, 11 SNPs were sufficiently polymorphic for inference using MHA [24] analysis. MHA uses inferred evolutionary relationships among haplotypes, specified in the form of a cladogram, to structure the tests of association. The network relating all haplotypes with one step mutations is given in Fig. 3a; only one haplotype is not connected in this network, and it differs from three other haplotypes by 2 mutational steps. Evolutionary rules [23] break the cycles in the network to produce a cladogram (Fig. 3b) of haplotypes connected by one-step mutations. The cladogram has the plausible feature of clustering ε₄ and ε₃-containing haplotypes, but the three ε₂-containing haplotypes are implausibly separated in the evolutionary space. The latter is of little concern given the modest impact of ε₂, and in fact the results do not differ if the haplotypes are grouped (results not shown). We simplify the cladogram for statistical inference by consolidating rare haplotypes with more common haplotypes, because the impact on risk of rare haplotypes – even if it were substantially different from adjoining haplotypes – could not be distinguished statistically.

Fig. 3.

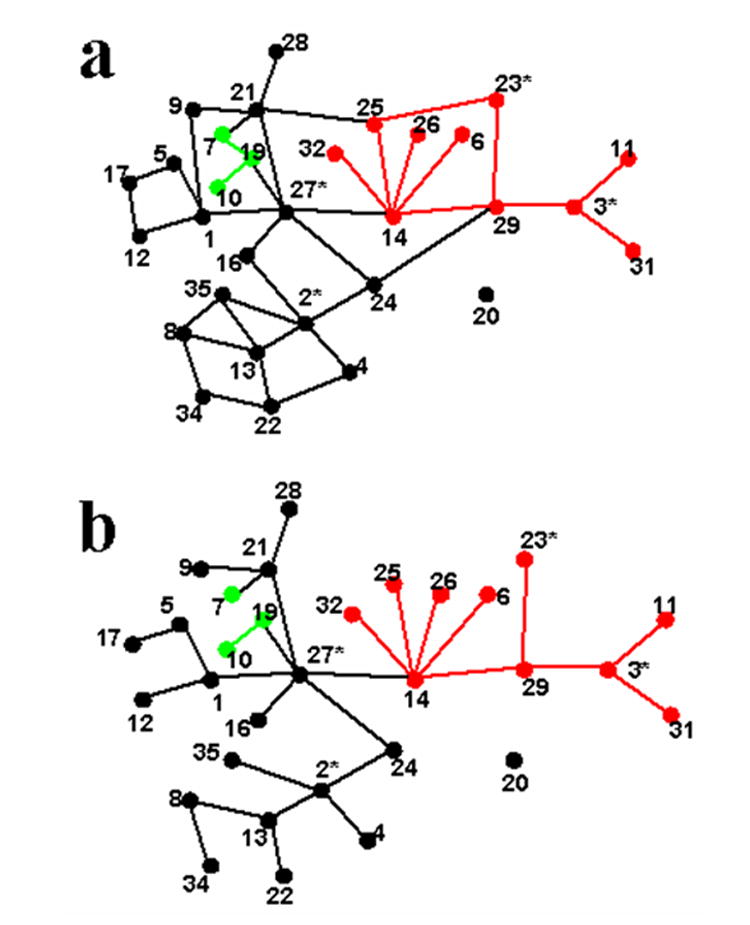
Network (a) and cladogram (b) representing relationships between 11-locus haplotypes of APOE.

We also performed a cladistic analysis using eHap for ε₂/ε₃/ε₄ haplotypes as a simple contrast of haplotypes on the cladogram ε₄ – ε₃ – ε₂. When ε₄ is contrasted to ε₃, while estimating the effect of ε₂ as a nuisance parameter, the contrast is highly significant, and thus the nodes remain distinct (Chi-square = 79.75; DF = 1; p ~ 0). When ε₂ is contrasted to ε₃, while estimating the effect of ε₄ as a nuisance parameter, the contrast is not quite significant, and thus the nodes collapse for purposes of estimation (Chi-square = 3.48; DF = 1; p = 0.062). The latter result is typical for samples of this size; the small protective effect of ε₂ is evident in the odds, but it is not significant. The odds of AD for the combined set ε₂ and ε₃ haplotypes is roughly fivefold less than that for ε₄.

SNPs inside/outside of APOE

Using MHA we find a cluster of high-risk haplotypes, all of which contain ε₄ alleles, and another cluster of low risk haplotypes that contain either ε₂ or ε₃ alleles. Thus, for these data and MHA, we find no evidence that SNPs elsewhere in APOE, such as in its regulatory region, have a significant impact on risk for AD. We would reach the same conclusions fitting AD status to two SNP models in which one SNP is always represented by ε₄ allele count, as we show now.

We imagine two scenarios, one in which one analyzes association with AD status without knowledge of ε₄ status, and one in which one appropriately conditions on ε₄ count. Forty SNPs were informative enough in the AD and control samples to produce valid tests (see Supplementary Table). It is apparent that, in the absence of information about ε₄ count, many loci in the region show significant association with AD status even after Bonferroni correction (Fig. 4). In fact, of the 40 informative loci, 28 SNPs have p ≤ 0.05 and 12 are less than the Bonferroni cut-off of 0.00125. Multiple SNPs in TOMM40 and APOE, and at least one SNP in LU, PVRL2, APOC1, APOC4 and CLPTM1 were associated with AD risk. In our sample, the association with AD was significant (p < 0.05) for APOE SNPs −491 (SNP 21) and +113 (SNP 25), but not for −427 (SNP 23), −219 (SNP 24) and +5361 (SNP 37). However, when ε₄ count is incorporated into the model and after Bonferroni correction, no locus has a significant, independent effect on AD status (Fig. 4).

Fig. 4.

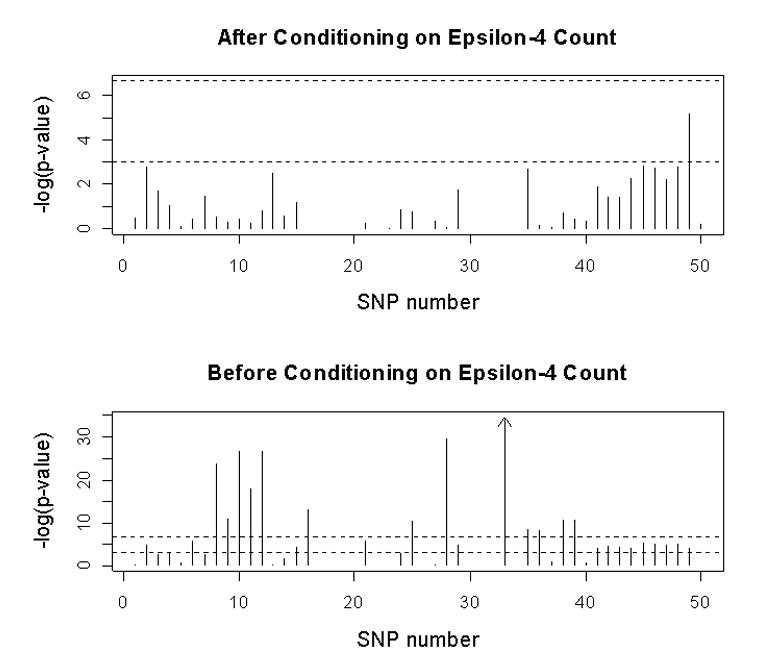
Results of association analyses for AD status versus individual SNP genotypes, with or without taking count of ε₄

MHA for logical units across this region, such as genes, produces the same conclusion (data not shown). In general, when MHA is performed without conditioning on ε₄ count, certain portions of the cladogram do not ‘collapse’ into a single node, suggesting some haplotypes were different in their impact on AD risk. However, when ε₄ count is introduced as a covariate, the cladograms always collapsed into a single node, consistent with the null hypothesis that haplotypes had no impact on risk for AD.

TOMM40 SNP 10 versus APOE ε₄

Of these results, the association of SNPs in TOMM40 with AD, especially SNP 10 (rs157581), is arguably most intriguing. The C allele of SNP 10 in TOMM40 is in very strong LD with the C allele of SNP 33 in APOE, which defines the ε₄ allele. The correspondence is so strong (Table 3) that one might wonder how the statistical models favor ε₄ as the risk allele. But there is information to distinguish the effects. For an additive (allele) logit model, the odds ratio for presence of ε₄ versus the status of AD is estimated to be 4.1; whereas the odds ratio for AD status using the alleles of SNP 10 is 2.88. Moreover, when variables representing both SNPs are entered into the logit model, either with or without an additional interaction term between the two SNPs, only the effect of APOE ε₄ count is significant.

Table 3.

Number of AD and control subjects by TOMM40 SNP 10 and APOE ε₄ genotypes

TOMM40, SNP 10	APOE
	Cases		Controls
	CC	CT or TT	CC	CT or TT
CC	24	8	1	9
CT or TT	5	144	0	217

Perhaps the effects of the TOMM40 SNP 10 alleles are not additive, but they are expressed recessively. Consider individuals who are doubly homozygous for C alleles (at TOMM40 and APOE), homozygous only for C alleles at SNP 35 of APOE, homozygous only for C alleles at SNP 10 of TOMM40 or homozygous for neither. The case/control counts for these multilocus genotype classes are 24/1, 5/0, 8/9, and 144/217. From the contrast of 5/0 to 8/9, it appears that risk solely or predominantly arises from ε₄ homozygotes, because the SNP 10 CC homozygotes are about equally likely to occur in case and control individuals who are not homozygous for ε₄.

Discussion

The ε₂/ε₃/ε₄ system of alleles in APOE appears to play a crucial role in risk for LOAD. In fact, as much as 50% of the population risk for LOAD could be attributable to ε₄ alone [4]. For the past decade, however, other loci in APOE and surrounding genes have also been associated with risk for LOAD. For instance, variation in the 5’ region of APOE has been shown to alter the expression of the gene, to produce population-level variation in metabolic lipid levels [3], and to have a weak impact on risk for LOAD [9]. Among the APOE promoter SNPs, the −491 A, −427 C and −219 T variants have a higher frequency in AD cases than in controls in some, but not all, studies [25-30]. Nonetheless, the impact of other loci has proven difficult to define because of their known or potential LD with SNP 33, which defines the ε₃/ε₄ dichotomy. Surprisingly, only a few studies have undertaken a comprehensive assessment of the patterns of LD in the APOE region [31], and none of those have used molecular methods to ensure accuracy of phased chromosomes. We provide a comprehensive assessment of LD by using molecular haplotyping to phase 21 SNPs in APOE itself [18], and complementary statistical methods for additional 29 SNPs surrounding APOE.

In our Caucasian sample, the association with AD was significant for APOE promoter SNPs -491 (SNP 21) and +113 (SNP 25). However, when ε₄ count is incorporated into the model and after Bonferroni correction, no locus has a significant, independent effect on AD status. As for SNPs outside of APOE, one locus in our comprehensive analysis, a synonymous SNP in the TOMM40 gene, accounts for increased risk for developing AD. Again, when ε₄ status is accounted for in the model, no single SNP explains a significant portion of the risk. Therefore, while tight LD between APOE and TOMM40 raises the possibility that the latter locus may contribute to the risk for developing AD, ε₄ remains the most likely LOAD allele in the region.

Within APOE itself, we genotyped 21 previously reported SNPs, but found only 16 to be polymorphic in our samples of 550 individuals, of which 11 had MAF > 0.02. These 11 SNPs cover 4,802 bp of genomic sequence. Thus, within APOE, a SNP with MAF > 0.02 occurs every 437 bp, on average. This density of SNPs is slightly higher than what is observed, on average, from completely-sequenced genes in general [32]. For the ε₂/ε₃/ε₄ system of alleles, we found that ε₄ is embedded in 12 different haplotype backgrounds; ε₃ is embedded in 20 different haplotype backgrounds; while ε₂ is embedded in only 3 backgrounds (Table 1). Because there were 298 haplotypes bearing ε₄ and 741 bearing ε₃, there is proportionately more variety in ε₄–bearing haplotypes than ε₃–bearing haplotypes (on average, 24.8 copies per ε₄-haplotype versus 37.1 copies per ε₃-haplotype). This observation is consistent with the conjecture that ε₄ is ancestral to ε₃, based on analyses of other primates [33], all of which carry the ε₄ allele. Nonetheless, the fact that ε₃ is now far more common in human populations worldwide led to conjecture that ε₃ has been under positive selection since its introduction in early humans [19]. Consistent with our observation that variation in APOE is at least as large as that seen in other genes, however, Fullerton et al. [19] could find no statistical evidence for selection, which would be expected to reduce regional variation.

If ‘haplotype block’ structure is measured by the distribution of haplotypes, our analyses suggest most of the SNPs in APOE exist in a single block. In fact only 5 haplotypes account for over 75% of the chromosomes in the sample. On the other hand, if LD is measured pairwise by r² (Supplementary Fig. 1), or even by multivariate assessment of LD based on pairwise r² (Supplementary Fig. 2), our analyses suggest much less LD. This result suggests that this contrast underscores the superiority of assessing multivariate LD, such as by analysis of the distribution of haplotypes.

To make the drawback of pairwise LD more concrete, we offer a simple example. Imagine there exists (or historically existed) a population in which there are five linked SNPs, with alleles named ‘1’ and ‘2’. Alleles at the loci are independent and thus all 32 possible haplotypes occur. From this population a sample is drawn to found a new population. The sample contains only four haplotypes (Table 4), each of which occurs with probability = ¼. As can be seen in Table 4, while the haplotype distribution is limited, the founder haplotypes set up a peculiar pattern of pairwise LD, regardless of the measure of LD used (see Devlin and Risch [21] for discussion). Pairs of adjacent loci are pairwise independent, while more distant pairs of loci are either in absolute LD or independent. While artificial, this scenario makes two points: pairwise LD can fail to capture higher-level LD, even in very simple instances (known in statistics as Simpson’s paradox) and comparisons of pairwise LD across and within genomic regions potentially confound an evolutionary parameter of interest, namely the recombination rate, with founder effect. This confounding will be most important for recently-founded populations, but we suspect it is also important for other populations, such as those of European and Asian decent.

Table 4.

Heuristic example of the failure of pairwise LD to capture higher-level LD. The four haplotypes occur with equal probability ¼ in the population. Pairwise LD, as measured by r² (but true also of any measure of LD reviewed by Devlin and Risch 1995) fluctuates in a peculiar pattern and fails to capture the higher-level features of LD, namely that only 4 of the possible 32 haplotypes occur in the population

	Loci
Haplotypes	a	b	c	d	e
1	1	1	1	1	1
2	1	2	1	2	1
3	2	1	2	1	2
4	2	2	2	2	2
Disequilibrium
Loci	a	b	c	d	e
a		0	1	0	1
b	0		0	1	0
c	1	0		0	1
d	0	1	0		0
e	1	0	1

Our experimental design over-samples for individuals diagnosed with LOAD. Devlin and Risch [21] and Devlin et al. [34] have shown that various measures of pairwise LD can be biased in the face of this over-sampling. Due to this bias, one might expect the patterns of LD to differ substantially between the LOAD and control samples. Instead we see similar patterns for both samples (Fig. 2, Supplementary Figs. 1 and 2), although the controls show somewhat stronger LD. These patterns are probably due to the fact SNPs 33 and 35, defining the ε₂/ε₃/ε₄ system, are not in high LD with many other genotyped SNPs in the region. If they were tightly linked, we would expect more divergent patterns in the two samples.

As described in more detail by North et al. [31], the pattern of LD in the region has implications for the power to detect the association between ε₂/ε₃/ε₄ and LOAD, assuming that this system of alleles was not genotyped but other SNPs in the region were. Two cross-currents complicate predictions about detection. As seen in Fig. 2, LD as measured by r² is not large, yet this is the natural measure for power due to its direct connection to the chi-square statistic [35]. On the other hand, the strength of the association between LOAD and the ε₂/ε₃/ε₄ system is substantial. Assuming an odds ratio for ε₄ versus ε₃ in the LOAD versus control samples is about 2.0, and the frequency of ε₄ in the population is 0.12. To detect the association with ε₄ with 80% power at a significance level of 0.05 would require roughly 100 individuals diagnosed with LOAD and an equal number of controls. To detect the ε₄ association by genotyping a locus in LD would require samples of size of roughly N/r² [35]. Even if r² were as small as 0.1, the required sample size for 80% power under these assumptions is only about 1000 cases and controls.

Scanning the region within and around APOE, there is only one set of SNPs that show large LD, as measured by r², with ε₂/ε₃/ε₄ system of alleles (Fig. 2, Supplementary Figs. 1 and 2). These loci fall in TOMM40, roughly 15 Kb 5’ of APOE. SNPs within this region (SNPs 8-12, Fig. 1) have some of the strongest genetic association with the risk of AD in our Caucasians AD samples (Supplementary Table). TOMM40 encodes a subunit of the multisubunit translocase of the outer mitochondrial membrane, the TOM complex [36], which plays a role in protein transport into mitochondria. In fact, the TOM40 protein forms the critical pore and actively sorts protein for sub-mitochondrial locations [37]. Because structural abnormalities and oxidative stress of the mitochondria are known to increase risk for AD, and defects in mitochondrial energy metabolism have been observed in AD [38-41]. This raises the possibility that part of the liability to LOAD commonly ascribed to ε₄ might have been caused by TOMM40, on the basis of its strong LD. However, contrasting the effects of all 50 loci in this region on the risk of AD, with and without conditioning on ε₄ status, our findings diminish the possibility that TOMM40 and other loci near APOE may have a major effect on the risk of LOAD in Caucasians.

Our results support the idea that associations can be detected at SNPs near a complex disease gene when the causative mutations are essentially monophyletic, as for APOE ε₄. However, high density of SNPs will be necessary to ensure the detection of such association with causative disease changes. Our study provided an excellent scenario to support this point of view. Because TOMM40 has functional implication in the AD pathogenesis and it shows strong genetic association with LOAD. If the APOE ε₄-defining SNP (SNP 33 [rs429358]) was not genotyped and analyzed in the study, one could have mistakenly selected the TOMM40 to be the candidate gene for LOAD. Thus, enormous research effort could be in vain by studying the incorrect genes. Moreover, our study further demonstrated that the haplotype based analysis can provide additional information with respect to tests of significance and fine localization of the most critical causative variants.

Materials and Methods

Study samples

Human subjects were collected by the University of Washington Alzheimer’s Disease Research Center. All were unrelated individuals of European ancestry. The samples consist of 193 individuals diagnosed with LOAD, 232 similarly-aged subjects with no cognitive impairment, and 125 individuals with various other neurodegenerative disorders, including possible LOAD, dementia with Lewy bodies, Parkinson disease, progressive supranuclear palsy, and frontotemporal dementia.

SNPs genotyped

Fifty potentially-variable sites were genotyped in this study, as mapped in Fig. 1. Twenty-one of these SNPs fall in APOE and its potential 5’ regulatory region, which covers roughly 5300 bp of genomic sequence, and were genotyped by primer extension assays using the SNuPE assay reagents [18]. SNPs within APOE were selected according to the study of Fullerton et al. [19] and described in detail previously [18]. An additional 29 SNPs were chosen to evaluate other genes/genomic elements that were proximate to APOE and plausibly could affect risk to LOAD. Sixteen fall in roughly 114 Kb 5’ to APOE; the remaining 13 fall in roughly 82 Kb 3’ to APOE (Fig. 1, Supplementary Table). These proximate SNPs were genotyped by TaqMan allele discrimination assays (Applied Biosystems, CA).

Genotyping Error

By our computational analysis, we wished to estimate the probability that a single error introduced into a naturally-occurring haplotype – defined to be a haplotype that occurred at least twice in the sample – would produce a pseudo-haplotype instead of a naturally-occurring haplotype. To estimate this probability PSH we iteratively performed this experiment: (1) randomly draw a haplotype from the distribution of naturally-occurring haplotypes; (2) randomly select one of the L = 11 polymorphic loci; (3) change the selected base pair to its complement; and (4) determine whether the resultant haplotype was also in the naturally-occurring haplotype list. Performing this experiment a million times yielded the estimated probability of producing a pseudo-haplotype by error, which was P_SH = 0.792. If this experiment were performed using all variable loci, L = 16, it would yield a slightly higher probability estimate; if more than one locus were altered on a haplotype, the estimated probability would be substantially larger.

To determine if any of the singleton haplotypes were pseudo-haplotypes, we started with the genomic DNA from the 12 samples containing singleton haplotypes. These samples were scored by direct sequencing instead of primer extension reactions, which allowed us to generate completely independent results from the previous experiments. Among the 12 samples, 9 were consistent with the previous results. Three subjects, however, showed inconsistency at a single SNP. Two of these errors were clerical, occurring when the data were entered by hand; the other error was due to a rare SNP that disrupted one of the priming sites for primer extension reaction. Thus from our data we would estimate the probability of drawing a singleton haplotype with a single error, P_E,S to be 3/1100 ≈ 0.00272, with 6 out of 12 singleton chromosomes representing an upper 96% confidence interval on the number of errors, given binomial sampling, to give a 96% upper confidence interval of ≈ 0.00544. Two of these errors occurred for SNPs with MAF > 0.02.

If we assume that errors are independent across loci on a haplotype and across haplotypes, it is straightforward to develop an estimator for the probability ε of an error on an individual SNP, namely ε ≈ P_E,S / (L* P_SH). Taking L = 11, and plugging in our estimates obtained from the molecular and computational analyses, we estimate a per-locus error rate of 0.00031. Two observations also follow from these calculations: the probability of haplotypes, natural or pseudo, with 2 or more errors on them is negligible; roughly 4 other haplotypes are expected to be erroneous, but they mimic naturally-occurring haplotypes and cannot be corrected.

Molecular haplotyping methods

To produce molecular haplotypes for 21 loci in APOE from our study samples, we used the Allele Discriminating Long and Accurate PCR Haplotyping (ADLAPH) method described in Yu et al. [18]. Briefly, ADLAPH combines allele-discriminating primers and long-range PCR amplification to amplify long genomic fragments from only 1 of the 2 chromosome homologues of a particular subject. The phase-separated long-range PCR product is then genotyped by standard methods to yield one haplotype. Contrast with the original diploid genotypes is then carried out to provide the complementary haplotype. Comparisons between molecular and computational haplotyping methods have been previously discussed in our other studies [18, 42]. For a small region with tight LD (such as the entire APOE gene), the computational methods do not differs substantially in its estimates of haplotype distributions [18]. However, when a larger region without tight LD was analyzed, the molecular haplotypes increased the linkage information by as much as 9% over the unphased SNPs [42]. In this example, marker phase resolution via molecular haplotyping led to modest increases in the evidence for linkage in these data. Yet, larger gains may be possible in datasets with greater inherent phase ambiguity, such as in studies with larger numbers of markers, more polymorphic markers, or weaker LD between markers.

Statistical methods

Haplotype frequencies comprised of SNPs outside of APOE were inferred by using maximum likelihood as implemented in the eHap program [43] (see CompGen in Electronic Database). To account for the phase-known haplotypes of APOE, we recoded haplotypes as alleles and the eHap program was specifically tailored to account for absolute haplotypes. Single SNP and haplotype-based statistical analyses were performed by using the eHap program [43]. eHap relates haplotypes to phenotypes by using likelihood techniques that account for haplotype uncertainty. The program offers a flexible set of hypothesis tests, including goodness-of-fit or omnibus tests and specified contrasts of association between haplotypes and phenotypes.

To estimate haplotypes at all 50 loci and to infer regions of greater than expected frequency of recombination (recombination hotspots), we used Phase (Version 2.0) [44-46]. Phase uses Bayesian methods for inference, based on the assumption that the evolutionary relationships among haplotypes can be imputed from their degrees of similarity. LD block structure was defined in the sense of Rinaldo et al. [20], namely blocks are regions of limited haplotype diversity. To identify blocks, we used Entropy Blocker (CompGen). Using output from Phase 2, its algorithm identifies those regions that exhibit substantial multi-locus disequilibrium, ranging over a substantial number of SNPs, while allowing one or more SNPs to separate blocked regions or adjacent blocks. The model computes the likelihood of the data minus a penalty for model complexity, using the criteria that blocks should have very low haplotype diversity and the LD with SNP’s outside a block should be small. Entropy Blocker was also used to visualize pairwise LD.

To select ‘tagging SNPs,’ we used H-clust [20] (CompGen). The algorithm in H-clust identifies highly correlated sets of SNPs and chooses a SNP within each correlated cluster to represent the cluster. Input data are multilocus genotypes, which are transformed into a per-locus count of the minor alleles (0, 1 or 2). This transformed matrix of multilocus genotypes is then itself transformed to a correlation matrix, from which clusters of SNPs are identified by hierarchical clustering. Within each cluster, the SNP that is most highly correlated with other SNPs in the cluster is chosen as its tag SNP.

We use measured haplotype analyses or MHA [24] to evaluate haplotype associations with AD. MHA uses inferred evolutionary relationships among haplotypes, specified in the form of a cladogram (an unrooted evolutionary tree), to structure the tests of association. Procedures for MHA are described in Templeton et al. [24] and Seltman et al. [43]. To perform this cladistic analysis, the cladogram is divided into subgroups (clades): individual haplotypes occurring as leaves (terminal nodes) on the tree represent 0-step clades; 1-step clades are produced by moving backward one mutational step from the 0-step clades toward internal nodes; and then this procedure is repeated to produce the 2-step clades and so forth. For inference, a series of 1 degree-of-freedom tests are performed in a sequential fashion based on the clades, from zero step clades onward. At each step in the algorithm, a full model is fit. The full model is the same within each step, but changes between steps, conditional upon the results of the previous step, with the goal of testing whether clades differ in their impact on phenotype, in this case risk of AD. MHA has been used in a variety of settings [47-50].

Results for MHA are reported in detail only for the molecularly-haplotyped SNPs in APOE. For SNPs outside of APOE, we performed MHA analyses for SNPs occurring in logical clusters, such as genes, and we fit additive logit models based on the count of alleles at the locus of interest; for both kinds of analyses, we ‘conditioned’ on ε₄ genotype by entering the count of ε₄ alleles as a covariate in the models.