Interpretation of Normalized Spectral Heart Rate Variability Indices In Sleep Research: A Critical Review

Abstract

The normalized spectral heart rate variability (HRV) measures low-frequency (LF)nu and high-frequency (HF)nu are frequently used in contemporary sleep research studies to quantify modulation of the sympathetic and parasympathetic branches of the autonomic nervous system. The purpose of this tutorial and methodologic critique is to concisely demonstrate the structural algebraic redundancy inherent in the normalized spectral HRV measures with respect to each other, and also with respect to the well-known HRV index of sympathovagal balance, LF:HF ratio. The statistical problems and interpretational paradoxes related to the mathematical definitions of LFnu and HFnu are briefly outlined. Examples of use of normalized spectral HRV measures in recent articles from the sleep-relevant research literature are critically reviewed. LFnu, HFnu, and LF:HF ratio should be considered equivalent carriers of information about sympathovagal balance.

Citation:

Burr RL. Interpretation of normalized spectral heart rate variability indices in sleep research: a critical review. SLEEP 2007;30(7):913-919.

NORMALIZED SPECTRAL BAND POWERS/VARIANCES ARE DERIVED MEASURES REFLECTING AUTONOMIC ACTIVITY, COMMONLY COMPUTED IN MANY HEART rate variability (HRV) data analysis software packages available to sleep researchers, particularly for the low-frequency (LF: often 0.04–0.15 Hz) and high-frequency (HF: often 0.15–0.40 Hz) spectral power/variance bands. The normalized (or normalized unit) spectral indices are usually defined as

LFnu = LF / (LF + HF)

and

HFnu = HF / (LF + HF)

.

Note that the normalized measures are derived or computed indices that are not directly estimated from the raw R-R interval data themselves but are computed as a second step after the initial statistical estimation of the power in the LF and HF bands of the HRV spectrum.

Less commonly, the normalizing denominator includes the power/variance in the very low frequency (VLF: frequencies < 0.04 Hz.) band, eg, LFnu = LF/(VLF + LF + HF). Alternatively, the denominator may include power in regions of the spectrum above the HF band (VHF: often frequencies > 0.40 Hz.), eg, LFnu = LF/ (LF + HF + VHF), or power contributions from both the VLF and VHF bands, eg, LFnu = LF/(VLF + LF + HF + VHF). All 4 versions are “unitless” ratios, due to the cancellation of the units in the equation of definition (ms² / ms²). This report will concentrate primarily on the characteristics of the indices defined using the first of these 4 forms, although similar arguments about the simplex structure of normalized measures are relevant to all 4 definitions.

Another decision in the practical definition of normalized HRV spectral indices is whether to compute proportional (fractional) values or percentage values (proportion×100%). The discussion in this report will be with respect to normalized values expressed as proportions, but it should be obvious that exactly the same arguments bear on normalized spectral band power values expressed as percentages.

The most common notational acronyms for the normalized spectral HRV measures used in the sleep research-relevant literature are based on the conventions of either adding a “nu” as a suffix (eg, LFnu, HFnu) or an “n” or a “%”as a prefix (eg, nLF, nHF, %LF, %HF). Some authors simply use the standard power band symbols (LF, HF) but make it clear in the narrative that the quantities have been normalized.

Part of the appeal of the normalized spectral HRV measures is that the normalization process expresses the quantities on a more easily understood proportion (0–1) or percentage (0%–100%) scale basis. Normalization removes most of the very large within-and across-subject variability in the total raw HRV spectral power, which theoretically and empirically tends to follow a long-tailed right-skewed exponential statistical distribution. The range of the normalized values is strictly bounded, so within-and across-subject statistical averages of normalized spectral indices tend to have distributions that converge more quickly to normal distributions, than do the raw measured spectral band powers, as study sample sizes increase. Normalized HRV spectral indices often have much smaller coefficients of variation when evaluated in repeatability/reproducibility studies.

Normalization also tends to produce values that are more exchangeable across different laboratories, research studies, and spectral analysis algorithms. Many of the differences in the computed band power that are related to the practical issues of spectral analysis block length, pseudo-sample interpolation density, zero padding, windowing, and algorithm family (eg, discrete/fast Fourier transform versus autoregressive model-based spectrum) are significantly mitigated by normalization.

Searching several of the major online biomedical research citation databases (MEDLINE, CINAHL, BIOSIS) for the years 1990 to 2006, it is apparent that normalized spectral HRV measures have been employed in more than 300 recent research reports in a sufficiently salient manner to have been specifically mentioned in the article title, abstract, or keywords. This includes a number of important recent contributions to the sleep research literature. The normalized spectral indices are almost always interpreted in sleep studies in a manner that is equivalent to the raw unnormalized versions of the same variables (LF band power, and HF band power).

• HFnu: index of modulation of the parasympathetic branch of the autonomic nervous system (ANS) as it influences the sinoatrial node of the heart,

• LFnu: usually viewed as an index of modulation of the sympathetic branch of the ANS, although some modern researchers prefer to view it as a general indicator of aggregate modulation of both the sympathetic and parasympathetic branches of the ANS.

• In applied research reports describing sleep studies, the 2 normalized spectral HRV power band measures LFnu and HFnu are almost always presented together, or in conjunction with the LF:HF ratio = (LF/HF), a widely used HRV index of sympathovagal balance between the 2 branches of the ANS. The rationale usually given for using the set of 3 variables together is to explore the potentially differentiated behavior of the sympathetic and parasympathetic branches, and their interaction.

However, there is an inherent paradox associated with the normalized spectral HRV measures that seriously confounds the naive physiologic interpretations presented in the preceding paragraph. In fact, the 3 indices LFnu, HFnu, and LF:HF ratio are algebraically pairwise redundant at the level of definition, with implications for both statistical analysis and clinical/physiologic interpretation.

The purpose of this paper is to give a terse but self-contained tutorial account of the structural redundancy of the normalized spectral HRV measures and the LF:HF ratio, to outline the statistical and interpretational problems induced by the mathematical form of the equations defining LFnu and HFnu, and to briefly review contemporary usage of these indices in applied science articles in the generalized sleep research literature.

Linear Redundancy between LFnu and HFnu

The relationship between LFnu and HFnu can be exposed by algebraically expanding their sum:

(LFnu + HFnu) = (LF/(LF + HF)) + (HF/(LF + HF)) = (LF + HF)/(LF + HF) = 1.

Therefore,

LFnu = 1 − HFnu,

and

HFnu = 1 − LFnu

.

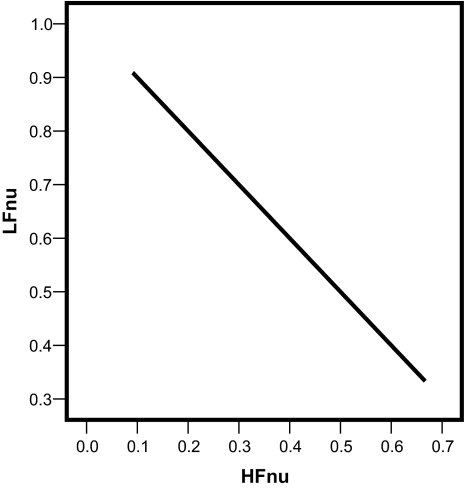
In other words, each of the normalized spectral values is exactly predictable from the other by means of a simple linear transformation, as shown in Figure 1. The information content of both variables is exactly the same.

Figure 1.

LFnu (often described in research articles as an index of sympathetic modulation of the autonomic nervous system) and HFnu (commonly interpreted to be an index of parasympathetic modulation of the autonomic nervous system) are perfectly predictable from each other by means of a simple linear relationship. This is not an empiric finding reflecting physiologic reciprocity, but an analytic result based on the mathematical forms defining normalized measures. These 2 normalized spectral heart rate variability indices are mutually redundant and equivalent carriers of the same information content. LF refers to low frequency; HF, high frequency.

Relationship of the normalized spectral HRV indices to LF:HF ratio

As noted earlier, one or the other or both of the normalized spectral HRV summaries are frequently presented in research articles in conjunction with the spectral ANS sympathovagal balance index LF:HF ratio. For example, it is very common to see HFnu and LF:HF ratio presented jointly in research papers, with the content interpretation that HFnu is an index of the parasympathetic branch modulation and LF:HF ratio is an index of the balance of the activity in the 2 autonomic branches. The typical semantic implication is that there are 2 conceptually independent mathematical degrees of freedom, each with a distinct physiologic interpretation. In fact, the LF:HF ratio is also algebraically redundant with respect to each of the normalized spectral measures separately, as will be shown below.

Some researchers using normalized spectral HRV measures seem to grasp that

(LFnu / HFnu) = (LF / HF)

at the level of definition, but few seem to realize that the normalized spectral HRV indices LFnu and HFnu are each linked to the LF:HF ratio with simple reversible 1-to-1 algebraic mappings. If we expand the inverse of HFnu:

(1/HFnu) = (LF + HF) / HF = (LF / HF) + (HF / HF) = 1 + (LF /HF)

. Therefore,

HFnu = (1 + (LF / HF))⁻¹,

and

(LF / HF) = ((1 − HFnu) / HFnu)

.

Similarly, if we expand the inverse of LFnu,

(1/LFnu) = (LF + HF) / LF = (LF / LF) + (HF / LF) = 1 + (HF /LF)

. Therefore,

LFnu = (1 + (LF / HF)⁻¹)⁻¹,

and

(LF / HF) = (LFnu / (1 − LFnu))

.

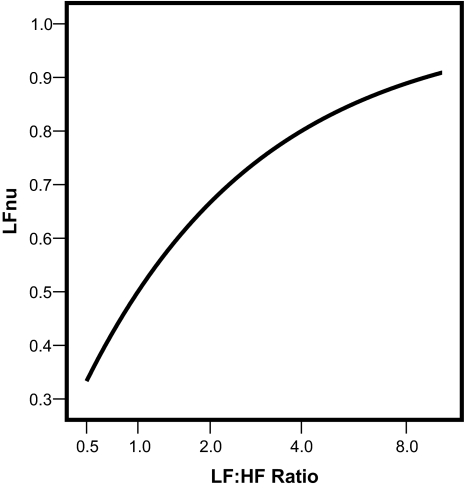
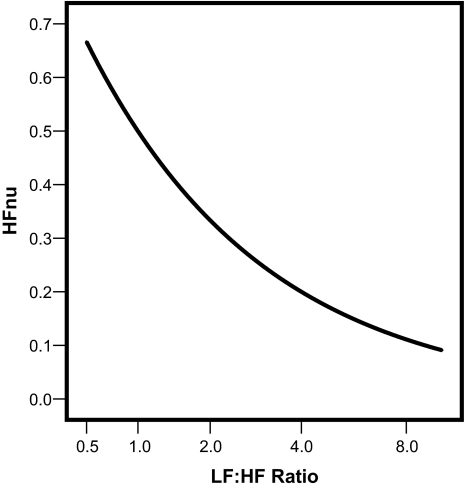
Although the relationships are not linear, nevertheless, as shown in Figure 2 and Figure 3, the curvature in each case is mild and strictly monotonic (always either consistently increasing or decreasing). LFnu and HFnu are each exactly predictable from the LF:HF ratio and vice versa. Thus, there is only 1 free mathematical parameter among the set of the 3 variables {LFnu, HFnu, and LF: HF ratio}. Once any 1 of these values is specified, the others are completely determined.

Figure 2.

As demonstrated in the text, LFnu (often interpreted as an index of sympathetic modulation of the autonomic nervous system) is perfectly predictably from the LF:HF ratio (usually interpreted as a marker of sympathovagal balance) through a simple reversible strictly monotonic-increasing nonlinear mapping. This implies that the 2 spectral analysis-derived indices quantify the same physiologic phenomenon and are exactly equivalent with respect to any empiric analysis based on order statistics. LF refers to low frequency; HF, high frequency.

Figure 3.

Similarly HFnu (usually interpreted in the recent research literature as a marker of parasympathetic modulation of the sinoatrial node) is also perfectly predictable from the LF:HF ratio, in this case, through a simple reversible strictly monotonic-decreasing nonlinear mapping. Clearly HFnu and LF:HF ratio are different quantifications of the same underlying physiological phenomenon, and apart from a change of sign coding the direction of the relationship, are exactly equivalent with respect to any empirical analysis based on order statistics. LF refers to low frequency; HF, high frequency.

Aggregation effects

The preceding discussion pertains to the interrelationships of LFnu, HFnu, and LF:HF ratio defined at the same level of aggregation. In sleep studies, these quantities may be defined at the level of the individual subject, based on a single spectrum, a within-subject average spectrum, or within-subject averaged spectral band powers Mean LF and Mean HF. Statistical procedures for comparing the resulting normalized HRV spectral measures between groups of subjects (eg, insomnia subjects vs normal subjects) will effectively aggregate these measures into means and/or nonparametric (e.g. rank-based) summaries. Because the 2 normalized spectral measures and the LF:HF ratio are all defined as ratios of correlated random variables, there is potential for the reciprocal nonlinearity to be noncommutable with the aggregation operation (often the arithmetic average). For example, the across-subject aggregate Mean(LF/HF) does not in general equal the ratio of the 2 band power aggregates Mean(LF)/Mean(HF). The variations from equality of these 2 quantities will depend on the empiric distributions of the LF and HF band power variables and their correlation.

When we focus, not on the values of the 3 measures per se, but on their interrelationships, some exact analytic connections remain. LFnu = (1 − HFnu) is a linear relationship at the level of definition (perhaps per subject). The operation of taking a mean or arithmetic average value is also a linear operation, and the order of sequences of linear operations can generally be interchanged. Therefore Mean(LFnu) = (1−Mean(HFnu)) and Mean(HFnu) = (1−Mean(LFnu)). Therefore, taking the averages of the normalized HRV spectral indices LFnu and HFnu does not alter their algebraic relationship.

The same logic cannot be extended to the relationships of LFnu and HFnu with respect to the LF:HF ratio. The order of linear operations, like the arithmetic average, cannot in general be interchanged through the nonlinear equations of definition. The aggregate Mean(LF/HF) may not exactly equal (1−Mean(HFnu))/Mean(HFnu). However, the relationship between LF/HF and HFnu, albeit nonlinear, is strictly monotonic. Therefore the relationships of rank-order based summaries, including the sample median, will be preserved. Thus Median(LF/HF) will exactly equal (1−Median(HFnu))/Median(HFnu).

In typical sleep research studies, the situation may be complicated by the presence of 1 or more additional levels of within-subject aggregation. For example, suppose one computed HRV spectra corresponding to each 5-minute block of stage 2 non-rapid eye movement (NREM) sleep across a subject's night, integrated the LF and HF power for each block's spectrum, and computed the LFnu, HFnu, and LF:HF ratio for each block. It might then be reasonable to aggregate these block estimates into a within-subject mean or median to represent the typical value of each of the indices in stage 2 NREM over the whole night, or perhaps separately for the first, second, third, and fourth NREM cycle/period. The previously described algebraic relationships between LFnu and HFnu will continue to hold for any multilevel combination of aggregation by means and medians (or other rank order-based statistics). But the perfect monotonic relationships of LFnu and HFnu with respect to LF:HF ratio will not necessarily be preserved if aggregation by arithmetic means is used at any level. Therefore, the invariance of the P value of a nonparametric test to the choice of {LFnu vs LF:HF ratio} or {HFnu vs. LF:HF ratio} at the across-subject group level will not necessarily hold if there was an intermediate level of within-subject averaging using the arithmetic mean.

Statistical Implications

The implications of the exact collinearity between HFnu and LFnu for statistical analysis include

• When used as dependent variables in univariate parametric or rank-based nonparametric statistical tests, parallel analyses of these 2 variables should result in exactly the same effect sizes (except for sign), and exactly the same P values.

• The Pearson product moment correlation and the Spearman rank order correlation between these 2 normalized variables should be a perfect r = −1.0, in both within- or across-subject analyses.

• The correlations of these 2 variables to any other study variables should have exactly the same magnitude but differ in sign, in both within- or across-subject analyses.

• The perfect collinearity implies that LFnu and HFnu should not both be present as simultaneous independent variables in a multiple regression or in any other statistical procedures that rely on matrix inversion.

• Because of the linearity and monotonic ordering of the relationship between the 2 variables, aggregate means and medians taken over a consistent study sample should also follow the same relationships as individual samples. That is, Mean(LFnu) = 1 − Mean(HFnu), Mean(HFnu) = 1 − Mean(LFnu), Median(LFnu) = 1 − Median(HFnu), and Median(HFnu) = 1 − Median(LFnu), both within and across cases.

The implications of the exact monotonic relationship of LF: HF ratio with respect to HFnu and LFnu for statistical analysis include

• The complete mathematical redundancy in the set of 3 measures creates potentially serious statistical problems when LF:HF ratio is used in conjunction with either or both of the normalized spectral HRV indices as independent or dependent variables within the same analysis.

• Because of the gentle nonlinearity, LFnu and HFnu will each have very strong but not perfect Pearson product moment correlations with respect to LF:HF ratio.

• They should, however, demonstrate perfect Spearman rank order correlations with respect to LF:HF ratio because of the exact monotonicity of their mathematical relationships.

• If the LF:HF ratio and either of the normalized spectral indices are simultaneously entered as independent variables in a multiple linear or logistic regression, the nonlinear curvature might seem to mitigate any technical multicollinearity, but the resulting regression coefficients will almost certainly be uninterpretable.

• Because of the modest nonlinearity of the relationship between the variables, aggregate arithmetic means of LF:HF ratio taken over a consistent study sample will not exactly follow the same equality relationships constraining individual samples. That is, depending on the empiric distribution of the data, Mean(HFnu) will not necessarily exactly equal (1 + Mean(LF / HF))⁻¹, and Mean(LFnu) will not necessarily exactly equal (1 + (Mean(LF / HF))⁻¹)⁻¹.

• However, because of the strict monotonic ordering of the relationships, aggregate medians and other order statistics will exactly follow the same relationships as individual samples. That is, Median(HFnu) = (1 + Median(LF / HF))⁻¹, and Median(LFnu) = (1 + (Median(LF / HF))⁻¹)⁻¹.

Implications for physiologic or clinical content interpretation

Because LFnu and HFnu are exactly predictable from each other, once 1 value is known, the other is completely determined. There is only 1 mathematical degree of freedom inherent in these 2 summary measures.

• Thus, it would be illogical and inconsistent to simultaneously interpret HFnu as an index of parasympathetic modulation and LFnu as a marker of sympathetic modulation. If a physiologic interpretation is correct for 1 of these variables, then the other variable must just be an additive inverse mathematical coding of the same phenomena. A different physiologic interpretation should not be separately ascribed for these 2 indices.

• Because the normalized spectral HRV indices can be exactly predicted from the LF:HF ratio, it is illogical and theoretically inconsistent to consider the latter to be an index of sympathovagal balance and, at the same time, regard HFnu, for example, to be an index of parasympathetic modulation.

• When these 3 variables are presented in a research report, only 1 interpretable phenomenon is being expressed in 3 mathematically redundant ways.

• It is probably most appropriate to consider all 3 HRV measures to be more or less exchangeable indices of the ANS balance.

Other Normalizations

The preceding presentation has focused on the use of the normalizing denominator (LF + HF). This is the form most often found in published papers, although sometimes the denominator is equivalently described as (Total Power − VLF), when the “Total Power” is specified to be the integrated power/variance in the observed spectrum between the lower frequency edge of the VLF band and the upper frequency edge of the HF band. That is, “Total Power” = (VLF + LF + HF), and the normalizing denominator becomes ((VLF + LF + HF) − VLF) = (LF + HF).

The situation is slightly more complicated when (LF + HF + VHF), (VLF + LF + HF), or (VLF + LF + HF + VHF) themselves are employed as the denominator to define the normalized spectral band powers under different interpretations of the term “Total Power.” The 2 carriers LFnu and HFnu thus created are no longer necessarily algebraically redundant. However, it is important to recognize that the innovation information that distinguishes LFnu and HFnu from each other in these cases comes exclusively from the VLF and/or VHF bands, neither of which is susceptible to a simple autonomic branch interpretation. The meaning of the normalized band powers thus defined becomes influenced as much by what is in the denominator as what is in the numerator. The presumption that LFnu necessarily has the same autonomic branch implications as LF, or that HFnu means the same thing as HF power, is not always tenable.

Critical review of recent sleep-related articles

Table 1 lists 17 recent influential articles that have used normalized spectral HRV measures to explore the activity of the autonomic nervous system. This list is not a complete census, nor a random sampling, of the papers in the generalized sleep literature using these measures. Instead, it is a subjective selection of papers that were judged to be representative, founded on good science, and diverse in application and whose primary conclusions were not controversially dependent on the critiques presented in this methodologic review. It is important to note that the normalized spectral indices were often not the only HRV measures presented in many of these articles, nor were they necessarily the conceptually most important to the essential rhetoric of the authors' arguments and interpretations.

Table 1.

Examples of the Application of Normalized Spectral Measures in Recent Sleep-Relevant Research Publications

Author (Year)	Measures	Physiologic Interpretation	Normalizing Denominator	Comments
Sforza et al7 (2007)	LFnu,	SNS+PSNS	Total Power−VLF = (LF+HF)	See Note E
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance	(LF+HF)
Robert et al6 (2006)	LFnu,	SNS		See Note C
	HFnu,	PSNS		See Note E
	LF:HF ratio	Sympathovagal Balance
Busek et al8 (2005)	LFnu,	SNS+PSNS	Total Power−VLF = (LF+HF)	See Note E
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance
Sforza et al.15 (2005)	LFnu,	SNS+PSNS	Total Power−VLF	= (LF+HF)
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance	(LF+HF)
Sacha et al9 (2005)	LFnu,	(Not stated)		See Note E
	HFnu,	(Not stated)		See Note F
	LF:HF ratio	(Not stated)
Brandenberger et al4 (2005)	LFnu,	Sympathovagal Balance	(LF+HF)
	HFnu,	Sympathovagal Balance
Dumont et al16 (2004)	LFnu,	(Not stated)	(LF+HF)
	HFnu,	PSNS
Kuo et al17 (2004)	LFnu,	SNS	(LF+HF)
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance
Hall et al10 (2004)	HFnu,	PSNS	(Not stated)	See Note D
	LF:HF ratio	Sympathovagal Balance		See Note E
Jurysta et al11 (2003)	LFnu,	SNS	(LF+HF)	See Note E
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance
Brandenberger et al5 (2003)	LFnu,	Sympathovagal Balance	(LF+HF)
	HFnu,	Sympathovagal Balance
Catai et al18 (2002)	LFnu	SNS	Total Power−VLF = (LF+HF)
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance
Ito et al1 (2001)	LFnu,	SNS	(LF+HF+VHF)	LFnu+HFnu < 1
	HFnu,	PSNS	(LF+HF+VHF)	See Note E
	LF:HF ratio	Sympathovagal Balance	(LF+HF+VHF)
Miyamoto et al12 (2001)	LFnu,	SNS	(LF+HF)	See Note E
	HFnu,	PSNS		See Note F
	LF:HF ratio	Sympathovagal Balance
Villa et al2 (2000)	LFnu,	SNS	Total Power−VLF = (LF+HF)	LFnu+HFnu < 1
	HFnu,	PSNS		See Note E
	LF:HF ratio	Sympathovagal Balance
Salo et al13 (1999)	LFnu,	(Not stated)	Total Power = (LF+HF)	See Note E
	HFnu,	(Not stated)
	LF:HF ratio	(Not stated)
Huikuri et al3 (1994)	LFnu,	SNS	Total Power−VLF = (LF+HF)	LFnu+HFnu < 1
	HFnu,	PSNS
	LF:HF ratio	Sympathovagal Balance

SNS refers to autonomic sympathetic nervous system activity; PSNS, autonomic parasympathetic nervous system activity; LF, low frequency; HF, high frequency.

C. May have used {%LF, %HF, LF:HF ratio} simultaneously in multivariate statistical procedure. Specified computing percentage format of normalized indices in Methods section, but presented descriptive graphics of values in proportion format and graph labels in percentage format.

D. Specified use of only HFnu and LF:HF ratio in Methods section, but presented only descriptive graphics of values of HF in what appears to be raw milliseconds-squared units.

E. Reported P values or statements of significance for LFnu and/or HFnu are not identical in parallel analysis to those reported for LF:HF ratio. (May be due to aggregation effects or alternative denominator.)

F. Reported P values or statements of significance for LFnu are not identical in parallel analyses to those reported for HFnu.

Most of the papers listed in Table 1 used a normalizing denominator of (LF+HF), or the equivalent, such that LFnu + HFnu = 1 (or 100%). In 3 studies,^1–3 the descriptive means for LFnu and HFnu add up to a value that is somewhat less than unity. This may be due to the use of a denominator that incorporates spectral power over a slightly broader bandwidth. For example, Ito et al¹ define Total Power as the integration of the HRV spectrum from 0.01 to 0.50 Hz but define HF power as the integration from 0.15 to 0.40 Hz. Thus, some power in the VHF band (> 0.40 Hz) will be present in the denominator but will not be part of either the LF or the HF components, and the LFnu and HFnu thus defined will sum up to a value that is a few percentage points less than 100%.

None of the published articles referenced in Table 1 explicitly acknowledges that LFnu and HFnu are linearly redundant (or nearly so), nor do any of them note that both of these normalized spectral indices have simple monotonic nonlinear algebraic relationships with the LF:HF ratio. Only the 2 papers by Brandenberger et al^4,5 explicitly describe LFnu and HFnu as markers of ANS sympathovagal balance. Almost all of the remaining articles interpret LFnu, HFnu, and LF:HF ratio as simultaneously indexing different physiologic processes, typically sympathetic nervous system activity, parasympathetic nervous system activity, and sympathovagal balance, respectively.

All of the research reports listed in Table 1 evaluated at least 2 of the derived measures in the set (LFnu, HFnu, LF:HF ratio), and most computed all 3. Most of these studies reported parallel parametric or nonparametric univariate statistical analyses for the multiple measures. The exception to this pattern was Robert et al,⁶ who may have treated the 3 algebraically redundant indices (LFnu, HFnu, LF:HF ratio) simultaneously as a dependent multivariate set in an omnibus multiple analysis of covariance, followed by univariate analyses for each of the normalized measures.

A number of the research reports listed in Table 1 include P-value discrepancies between parallel analyses of the normalized measures and the LF:HF ratio.^1,2,6–13 For example, Sforza et al,⁷ (Table 3, page 47) using a 3-group Kruskal-Wallis nonparametric analysis of variance, found robustly significant (P = 0.009) group differences in mean rank for the LF:HF ratio measure but no significant differences (P=NS) for the LFnu and HFnu normalized spectral measures. Robert et al⁶ noted substantive differences in the levels of statistical significance for the univariate analyses of HFnu versus LF:HF ratio during the rapid eye movement sleep stage condition (Figures 2 and 3, page 2125). Similarly Busek et al⁸ (Table 3, page 372), in the wakefulness condition, noted significant differences for LF:HF ratio (P < 0.01) but found no significant differences for LFnu and HFnu. These substantial interpretational differences in conclusions between the normalized measures and the LF:HF ratio are probably due to nonlinearity and within- and across-subject mean averaging aggregation effects. More difficult to explain are discrepancies in P values for parallel analyses of LFnu and HFnu, which have a linear relationship and are not subject to mean averaging aggregation effects, such as the small differences reported by Sacha and Pluta⁹ (Table 1, page 51; P = 0.07 for nHF, P = 0.03 for nLF, and P = 0.02 for LF:HF ratio), or Miyamoto, et al.,¹² (Table 1, page 1792, P = 0.0008 for HFnu, P = 0.0048 for LFnu, and P = 0.0080 for LF:HF ratio).

DISCUSSION

In 1996, the ESC/NASPE Task Force issued an influential set of guidelines for measurement and interpretation of HRV indices, which included the following statement about normalized spectral HRV measures: “The measurement of VLF, LF, and HF power components is usually made in absolute values of power (milliseconds squared). LF and HF may also be measured in normalized units, which represent the relative value of each power component in proportion to the total power minus the VLF component. The representation of LF and HF in normalized units emphasizes the controlled and balanced behavior of the two branches of the autonomic nervous system. Moreover, the normalization tends to minimize the effect of the changes in total power on the values of LF and HF components. Nevertheless, normalized units should always be quoted with absolute values of the LF and HF power in order to describe completely the distribution of power in spectral components.”¹⁴

The Task Force statement¹⁴ above, cited by many of the articles listed in Table 1, does not explicitly discuss the simple algebraic redundancies at the level of definition that exist between LFnu, HFnu, and LF:HF ratio as they are typically defined in applied sleep research. The third sentence in the quoted paragraph might possibly be interpreted as hinting that the normalized spectral measures are more akin to an ANS balance measure than to isolated sympathetic and parasympathetic indices. It is important to note that most of the articles listed in Table 1 have followed the advice given in the last sentence and have presented LF and HF power in absolute units as well as in the normalized unitless form.

The statistical and interpretational challenges of the normalized spectral HRV measures are similar to those of normalized sleep EEG spectral band powers, with which many of the technical readers of this journal will already be acquainted. If the total spectral power in a given bandwidth of the electroencephalogram is partitioned into M bands, and the power in each band is divided by the total power to create a set of M-normalized band powers, then there are only (M-1) nonredundant variables in the set. Any single 1 of these M-normalized band powers can be exactly predicted from the remaining (M-1) variables in the set. If all M-normalized band powers are entered as independent variables into a multivariate statistical procedure, the analysis will be compromised by the multicollinearity. In addition, the interpretation of each normalized band power is subtly altered because the denominator is not a constant, but the sum of a set of M random variables.

For the normalized HRV spectral measures, this redundancy is less disguised than the electroencephalogram analogue presented in the preceding paragraph because there are usually only 2 bands considered, LF and HF, and the normalization is typically with respect to the sum of the 2 band powers. Nevertheless, as noted in Table 1, many modern authors contributing to the generalized sleep research literature are treating LFnu and HFnu as if they are distinct statistical variables reflecting distinguishable physiologic phenomena.

In conclusion, the 2 normalized spectral HRV indices LFnu and HFnu are algebraically redundant, and each can be considered a monotonic nonlinear transformation of the LF:HF ratio at the level of definition. It is important to recognize that this conclusion is based on the fundamental mathematics of the computational definitions of the measures and is not dependent on physiologic reciprocity. If the LF:HF ratio has valid interpretability as an indicator of ANS sympathovagal balance, then, by virtue of the tautologic relations discussed in this report, it is probably inappropriate to consider the HFnu to be a simple measure of vagal modulation, or LFnu to be a simple measure of sympathetic modulation. In principle, all 3 indices reflect the same aspects of ANS balance and, in particular, will be exactly statistically equivalent in nonparametric statistical analyses based on rank-order properties of the dataset, with the caveat that aggregation by arithmetic averaging above the level of definition may somewhat alter the relationships of LFnu and HFnu with respect to the LF:HF ratio. Despite the structural redundancy at the level of definition, it is still often appropriate and useful in sleep research articles to display descriptive summary statistics for all 3 representations, so long as it is clear to reviewers, editors, and readers that only 1 unique dimension of information is being communicated.

ABBREVIATIONS

HRV

Heart rate variability (usually measured as summaries of heart period variability).

LF power

Power in the Low Frequency band of the HRV spectrum, often between 0.04 – 0.15 Hz, often reported in units of milliseconds-squared.

HF power

Power in the High Frequency band of the HRV spectrum, often between 0.15–0.40 Hz, often reported in units of milliseconds-squared.

VLF power

Power in the Low Frequency band of the HRV spectrum, often with band limits strictly greater than 0.00 Hz and less than 0.04 Hz, often reported in units of milliseconds-squared.

LFnu

Normalized power in LF band, a derived index that is computed by dividing LF by some suitable denominator representing the total relevant power, as discussed in the text.

HFnu

Normalized power in HF band, a derived index that is computed by dividing HF by some suitable denominator representing the total relevant power, as discussed in the text.

LF:HF Ratio

Spectral HRV index computed as (LF/HF).

ANCOVA

Analysis of Covariance.

MANCOVA

Multivariate Analysis of Covariance.

ESC/NASPE

European Society of Cardiology and North American Society of Pacing and Electrophysiology.

ANS

Autonomic nervous system.

SNS

Autonomic sympathetic nervous system.

PSNS

Autonomic parasympathetic nervous system.

SA node

Sino-atrial pacemaker node of the heart.