Repeated challenge with prion disease: The risk of infection and impact on incubation period

Abstract

Natural exposure to prion disease is likely to occur throughout successive challenges, yet most experiments focus on single large doses of infectious material. We analyze the results from an experiment in which rodents were exposed to multiple doses of feed contaminated with the scrapie agent. We formally define hypotheses for how the doses combine in terms of statistical models. The competing hypotheses are that only the total dose of infectivity is important (cumulative model), doses act independently, or a general alternative that interaction between successive doses occurs (to raise or lower the risk of infection). We provide sample size calculations to distinguish these hypotheses. In the experiment, a fixed total dose has a significantly reduced probability of causing infection if the material is presented as multiple challenges, and as the time between challenges lengthens. Incubation periods are shorter and less variable if all material is consumed on one occasion. We show that the probability of infection is inconsistent with the hypothesis that each dose acts as a cumulative or independent challenge. The incubation periods are inconsistent with the independence hypothesis. Thus, although a trend exists for the risk of infection with prion disease to increase with repeated doses, it does so to a lesser degree than is expected if challenges combine independently or in a cumulative manner.

It is known that increasing the level of exposure to transmissible spongiform encephalopathy or prion disease agents increases the risk of infection. It is unclear, however, how separate, successive doses combine over time to determine the outcome of infection. The risk of infection could simply be determined by total dose, which accumulates with each challenge (the cumulative hypothesis), or could increase as if each challenge acts independently (the independence hypothesis). These hypotheses can be compared with the alternative that multiple exposures decrease or increase the risk relative to that expected from cumulative or independent models in some (unspecified) way. By comparing how each hypothesis describes the data from prion diseases, we may shed light on the underlying process of the establishment of an infection and the replication of the infectious agent. This question is particularly important given that the fundamental unit of infectivity remains unknown.

The different hypotheses also have practical implications for risk assessment. The needs for assessment of low-dose risk are pressing. Even for single-exposure scenarios the dose–response curves are poorly understood at very low levels (1). In human exposure to bovine spongiform encephalopathy or variant Creutzfeldt–Jacob disease, it is difficult to assess the large-scale impact of exposure to low-risk materials such as gelatin and surgical instruments (2). The issue is clouded further by the potential for exposure to take the form of successive rather than single challenge, as may be the case for multiple blood transfusions (3).

In this article, we analyze data from the only large-scale experimental investigation of how repeated doses of transmissible spongiform encephalopathies affect the incidence of disease (4). First, we analyze risk of infection in terms of the cumulative and independence hypotheses. We then provide sample size calculations for future experiments involving repeated exposure data. Last, we analyze previously unpublished incubation period (IP) data. IPs are potentially powerful indicators of effects of dose on disease outcome; however, their analysis is less straightforward than for the probability of infection. We illustrate this by using traditional survival analysis and introduce IP models that can be used to interpret the data in terms of the hypothesis of independent challenges.

Methods

The Data. Outbred Syrian hamsters were given pellets of feed that had been soaked in dilutions of brain homogenate from hamsters in the terminal stage of scrapie. Groups of animals were given a specific dose and feeding schedule. Five different total doses (10-fold dilutions) and three feeding schedules were used. Animals in schedule 1 received all materials on one occasion. Animals in schedules 2 and 3 received the 10 pellets as single pellets given at intervals of 1 and 4 days, respectively. These data were made available by H. Diringer (Robert Koch-Institut, Berlin), and full details of the experiment are given in ref. 4.

In total, 681 animals (Table 1) were observed for up to 506 days after the first infection. Scrapie cases after the periods of observation were judged to be unlikely. Nine non-scrapie-related deaths are excluded. Trends in the data suggest that the risk of infection is greatest if a fixed total amount of infectivity is consumed on one occasion. For example, at dose 4, 72.5% of animals became infected if the dose was given once (schedule 1). If the same total dose was divided among 10 separate feeds the risk of infection was 55.9% and 44.8%, if exposure was daily and every 4 days, respectively (schedules 2 and 3).

Table 1. Probability of infection in each dose/schedule group (4).

Dose level	Schedule 1	Schedule 2	Schedule 3	All
5	0.97	1.0	1.0	0.99 (n = 147)
4	0.73	0.56	0.45	0.59 (n = 197)
3	0.11	0.08	0.04	0.08 (n = 197)
2	0.01	0.00		0.01 (n = 100)
1	0.00			0.00 (n = 40)

Dose levels are 10-fold dilutions (5 is the highest dose). Rows represent exposure with equivalent total dose. Challenge occurred on one occasion (schedule 1), 10 occasions at daily intervals (schedule 2), or 4-day intervals (schedule 3).

Diringer et al. (4) fitted a model in which the probability of not developing scrapie when the same total dose is given in 10 separate doses is the same as for a single 1/10th of that dose raised to the 10th power (see model 7). They concluded that repeated dosing caused disease at a higher incidence than single dosing and that the risk of infection decreased with the intervals between repetitive dosing.

Statistical Models for the Risk of Infection. For i = 1,..., 5and j = 1,..., 3, let p_ij denote the probability of infection in an experimental group with feeding schedule j and dose level i, where i corresponds to the total dose. For example, if dose i represents 10 “units” of infectivity, 10 units would be given all at once in schedule 1, or 1 unit would be given 10 times for schedules 2 and 3. Note that only 12 dose/schedule combinations were used. We consider first the full model (Model 1) that allows a different and unrelated probability of infection at every dose/schedule combination. This model may be restricted in a number of ways, imposing relationships between different doses (the form of the dose–response) or between the schedules. The latter relationships describe how consecutive challenges interact and are our primary focus. Parameters of each model were estimated by maximizing the binomial likelihood, and 95% confidence intervals were based on the profile likelihood. Comparisons of model fit were based on likelihood ratio tests (5). Brief headings for each model are given in Table 2.

Table 2. Log-likelihoods (I) for risk-of-infection models.

Model	Parameters	Description of model	I
1	12	Full model, schedule effect and unspecified dose—response	-13.75
2	5	Cumulative model (no schedule effect), unspecified dose—response	-22.70
3	7	Independent-challenges model, unspecified dose—response	-14.09
4a	6	Schedule and dose effects plus interaction, logistic dose—response	-17.85
4b	4	Schedule effect, logistic dose—response (common slope)	-19.24
5	2	Cumulative model (no schedule effect), logistic dose—response	-25.25
6	4	Independent-challenges model, logistic dose—response	-14.84
7	3	Schedule effect, independent dose—response	-21.68
8	1	Cumulative model, independent dose—response	-25.46
9	4	Independent challenges model, independent dose—response	-20.57

The cumulative and independence hypotheses. The cumulative hypothesis is that the probability of infection depends only on the total dose, that is, on i, and so does not depend on schedule. This is given by a restricted model with five parameters:

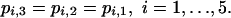[Model 2]

An alternative hypothesis is that the repeated challenges (schedules 2 and 3) act independently. At dose level i + 1, each individual challenge is at 1/10th of the total dose, and this is the same dose as the total challenge at dose level i. Hence, under independence, the probabilities of infection depend on five parameters and are given by

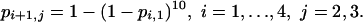In a more general form we consider the model

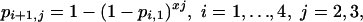[Model 3]

where the probability of infection at total dose i + 1 in schedule j, j = 2 or 3 is set equal to that of x_j independent challenges at the 10-fold lower dose in schedule 1. If x_j is <10, the infection risk of the overall challenge is less than that expected from the independence hypothesis.

Dose–response models. Models 2 and 3 impose relationships between schedules, but not between doses. It is often useful to assume a form for the dose–response relationship, reducing the number of parameters and allowing probabilities at intermediate doses to be inferred. A commonly used form is the logistic. Avoiding any assumption about the relationship between the different schedules, we may fit three separate logistic curves, each having two parameters α_j and β_j, j = 1, 2, 3, so that the probabilities of infection are

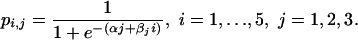[Model 4a]

A more restricted model assumes a common slope for the logistic dose–response curves for the different schedules, so that

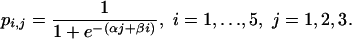[Model 4b]

This model allows a schedule effect but no interaction between schedule and total dose.

If, in addition to the logistic dose–response form, the cumulative hypothesis relating the schedules is assumed, i.e., models 2 and 4 are combined, the probabilities of infection are given by a single curve:

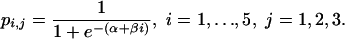[Model 5]

Alternatively, we may assume a logistic dose–response with the assumption that repeated challenges act like x_j independent challenges, combining models 3 and 4 to give

[Model 6]

An alternative to the logistic is given by supposing that, within each schedule, the probability of infection at a given dose is the same as that from 10 independent challenges from a 10-fold lower dose. This supposition leads to a model with three parameters corresponding to the three schedules:

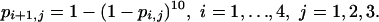[Model 7]

Model 7 may be combined with the cumulative hypothesis (model 2) to give

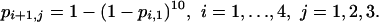[Model 8]

Generalizing model 7 to allow an exponent other than 10, and combining this with model 3, gives a model in which the probabilities of infection depend on four parameters and are given by

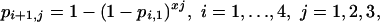[Model 9]

in which the value of x₁ determines the form of the dose–response relationship within each schedule, whereas x₂ and x₃ determine the relationship between the probabilities of infection for the different schedules, i.e., the repeated-challenge effects.

Experimental Design: Distinguishing Hypotheses for the Risk of Infection. The ability to distinguish between the cumulative and independence models for the risk of infection clearly depends on the number of challenges, the dilution factor, and the location and slope of the dose–response curve. We provide power calculations for the experimental sample sizes required to distinguish the cumulative and independence hypotheses. Using a logistic dose–response, we first calculate how the probability of infection under each hypothesis varies with the number of doses applied in an experiment then explore the relationship between required sample size and chosen number of challenges for a range of assumed dose–response curves.

Statistical Models for the Incubation Period. Survival analysis. Proportional hazards regression (6) was performed with dose as a continuous variable and three schedule categories. Doses 1 and 2 were excluded because of their extremely low scrapie incidence. Model assumptions were checked with log-cumulative hazard plots, and the fit was assessed by using Cox–Snell residuals (7).

Although proportional hazards regression is a standard analysis of IP, there is a problem in its interpretation. The comparison of interest is between schedules for a fixed total dose, and the outcome is the time until scrapie occurs. However, by the nature of the experiment, the total dose is not applied at the same time in each schedule. The total dose is given on day 1 in schedule 1 but not until day 10 in schedule 2 (day 37 in schedule 3), leading to a question of when an IP should be assumed to begin for each schedule.

If all IP are defined to start at the onset of the experiment, the IP in schedule 2 may be 9 days longer than in schedule 1 simply because it is 9 days before the animals have received equivalent doses. Although relevant in other circumstances, this finding may not represent a “schedule effect” as we wish to investigate here. At the other extreme, each IP could be corrected to begin only when all animals have received the full dose. This change may obscure differences between schedules. A compromise may be to adjust the IP relative to the halfway point of the exposure period. This adjustment is an ad hoc attempt to avoid the bias inherent in the experimental design, and it is hoped it will generate more realistic estimates of the hazard ratios, which in truth are more complicated functions of dose and time.

An explicit model for IP after repeated doses. As a more specific analysis of the IP data and test of the independence hypothesis, we developed a new statistical model that expresses the IP after 10 challenges in terms of the IP after a single dose, assuming that each challenge is independent. The comparisons of interest are therefore between schedule 1 at dose i and schedules 2 and 3 at dose i + 1.

First, we assume a normal distribution for the single-challenge IP. In an analysis of 117 experiments with rodent scrapie, incubation-period distributions were surprisingly symmetrical and well approximated by the normal (1). This finding contrasts with other diseases, which commonly show a log-normal pattern (8). Although a log-normal pattern was considered, it did not provide a better fit to the single-dose data and led to similar overall conclusions.

Model 10 consists of two components. For schedule 1 we assume

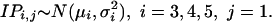If each dose acts independently, in schedules 2 and 3 the observed IP will be the minimum of 10 normally distributed random variables. These variables will be assumed to have the same normal distribution as that for a single, 10-fold lower dose in schedule 1, adjusted only by the time of challenge, so that

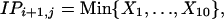where

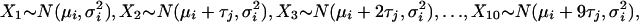[Model 10]

where τ_j is the interval between challenges (1 and 4 days for j = 2 and 3, respectively). To avoid treatment groups of small size, we focus on doses 3, 4, and 5 in schedule 1 and, correspondingly, doses 4 and 5 in schedules 2 and 3. Only confirmed scrapie cases are included.

For comparison we use a generalization of model 10 in which the IP is the minimum of 10 unrelated, normally distributed random variables. The model can be parameterized in several ways and is intended to represent an unspecified interaction between successive challenges.

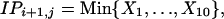where

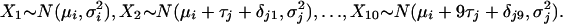[Model 11]

Note that the first distribution (X₁) for dose i + 1 under schedules 2 and 3 is identical with that for dose i under schedule 1, because immediately after the first challenge, these animals have had exactly the same exposure. The values of the parameters δ_j quantify the extent to which the multiple challenges generate IP in excess of or below that expected under the hypothesis of independence (under which δ_j = 0). The parameters δ_j cannot, however, be easily interpreted because many δ_j combinations lead to the same model.

For schedule 1, the likelihood is obtained from the relevant normal distribution. For the repeated-challenge schedules, let T = Min{X₁,..., X₁₀}, where X_i has probability density function f_i and distribution function F_i. The distribution function for T is given by 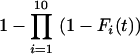, and the density is given by

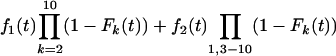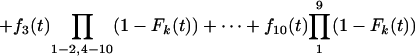Log-likelihoods for the two models were maximized numerically to obtain parameter estimates and perform the likelihood ratio test.

Results

Risk of Infection. The cumulative hypothesis. Log-likelihoods for the risk-of-infection models are given in Table 2. The cumulative model was first tested without assuming a specific dose–response relationship. The estimates of the parameters for models 1 and 2 are simply the cell and marginal row proportions in Table 1, respectively. A significant effect of schedule, indicating departure from the cumulative hypothesis, is shown by the improvement in the fit of model 1 over model 2 (P = 0.012).

By assuming a logistic dose–response, a significant schedule effect is again shown by the comparative fit of models 4b and 5 (P = 0.0025). Comparing models 4a and 4b, no significant dose/schedule interaction occurred (P = 0.25), suggesting that the preferred logistic model has three dose–response curves with the same slopes and different intercepts. Summarizing in terms of ID₅₀, the total dose required to infect half the population under schedule 2 is 50% higher than that under schedule 1. For schedule 3, the increase in ID₅₀ is more than 2-fold greater than the single-challenge schedule. In comparison with the full model, the logistic dose–response relationship gives a reasonable fit to the data (χ² = 11.0, 4 df, P = 0.2) (Fig. 1).

Fig. 1.

Fit of logistic dose–response model (4b). A significant difference in the probability of infection occurs across schedules for a fixed total dose. Data are given by symbols. Dotted line, schedule 1 (single dose, ▪); thick line, schedule 2 (10 daily doses, ▴); thin line, schedule 3 (10 doses, every 4 days, *). Parameter estimates (SE): α₁ = –11.78 (0.94); α₂ = –12.37 (1.00); α₃ = –12.86 (1.03); and β = 3.20 (0.25).

By assuming the dose–response relationship given by model 7, analysis of deviance for models 7 vs. 8 again confirms that the risk of infection is affected by schedule (P = 0.023) and is not cumulative. In comparison with the full model, the change in deviance by using this assumption approaches significance (χ² = 15.9, 9 df, P = 0.07), and the logistic dose–response appears to be a better description of the data.

Independence of challenges. Parameter estimates for the models that test the independence hypothesis are given in Table 3. Model 9 shows that 10 doses in schedule 2 result in a probability of infection expected from about six independent challenges. The infection risk of repeated doses is therefore less than that expected under the hypothesis of independence. The effect in the extended-exposure schedule 3 is more dramatic, the risk being that expected from only 4.5 independent doses.

Table 3. Parameter estimates (95% confidence interval) for independence models.

Parameter	Model 9	Model 3	Model 6
X1	7.97 (6.1, 10.8)
X2	6.13 (3.9, 10.2)	7.32 (4.4, 12.5)	6.5 (3.9, 11.5)
X3	4.54 (2.9, 7.4)	5.10 (3.1, 8.8)	4.6 (2.8, 8.0)

Nuisance parameter estimates were as follows: model 3, p₁₅ = 0.97 (0.9, 1.0), p₁₄ = 0.73 (0.6, 0.8), p₁₃ = 0.11 (0.1, 0.2), p₁₂ = 0.01 (0.004, 0.02), p₁₁ = 0.00 (0.0, 0.01); model 6, α = -10.4 (-12.2, -8.9), β = 2.8 (2.4, 3.3); model 9, p₁₁ = 0.002 (0.0, 0.01).

The interpretation of the dose–response parameter (x₁) is more difficult. It is included to confirm that the effect across schedules is more dramatic than simply the dose–response relationship within schedules (x₁ > x₂ > x₃). That the estimate of x₁ is <10 (although not significantly so) suggests that independence may not be a good model for the basic dose–response curve (as also implied above by comparison of model 7 with the full model and the better fit of the logistic).

If no specific dose–response (model 3) or a logistic (model 6) is assumed, similar conclusions are drawn (Table 3). The fit of model 9 shows some deviation from the full model (χ² = 13.6, 8 df, P = 0.1), and a better fit is given by models 3 and 6 (χ² = 0.68, 5 df, P = 0.98; χ² = 2.2, 8 df, P = 0.98).

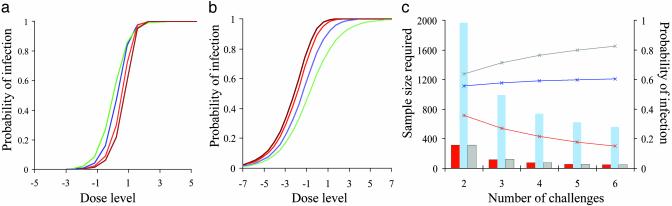
Experimental Design: Distinguishing Hypotheses for the Risk of Infection. The difference between the cumulative and independence models depends on the dose–response curve. For a dilution factor, n, if the probability of infection at dose d/n is p_(d/n) = 1 – (1 – p_(d))^1/n, the models coincide. If the probability at dose d/n is smaller/larger, then the probability of infection for the cumulative model is larger/smaller. For some dose–response curves, therefore, differentiation between the models can be difficult. In Fig. 2a the steep dose–response curve shows higher toxicity under the cumulative model, and declining probability of infection (at a fixed total dose) as the number of independent challenges increases. The picture is reversed in Fig. 2b for a dose–response curve for which the probability of infection changes less rapidly with the dilution.

Fig. 2.

Comparison of cumulative and independent models. With a logistic dose–response, the toxicity of repeated challenges may be higher (a) or lower (b) for the cumulative model. Probabilities of infection are for one challenge (green, cumulative model) and two (blue), four (red), and six (brown) challenges under the independent model. In a, the dilution required to reduce toxicity from 50% to 20% is 2 (logistic parameters: α = 0, β = 2); in b the dilution factor is 10 (α = 0, β = 0.6). (c) Total sample size in each group (bars) to distinguish the cumulative and independence hypotheses (80% power, 5% significance level) and the probability of infection with the independence model (lines) for three scenarios. Dilution factors are 4 (blue), 2 (red, independence model less toxic), and 10 (gray, independence model more toxic). The specific dose for each value of the required dilution factor was chosen to minimize the total sample size required (see text; e.g., the dose for the red scenario is the single-challenge ID₅₀).

The total sample size, at a single dose level to distinguish cumulative and independence hypotheses and based on a normal approximation for the difference between two binomial proportions, therefore depends strongly on the shape of the dose–response curve and on the ID₅₀. Minimum required sample sizes are achieved with doses chosen to give response rates of about 0.5, 0.9, and 0.8 when the shape of the response curve is such that the dilutions required to reduce the probability of infection from 50% to 20% are 2, 4, and 10, respectively.

In general, the required sample size is reduced as the number of repeated challenges is increased. Fig. 2c shows that, under a range of circumstances, the numbers of experimental units required to distinguish these two models may be impractical. It is straightforward to extend these methods to aid in the design of further experiments that might aim to quantify the level of interference between successive doses.

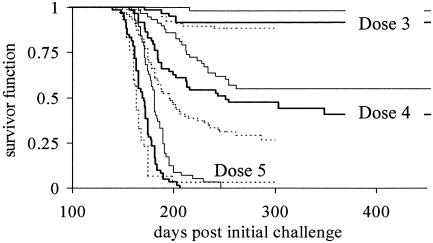
Statistical Models for the IP. Survival analysis. Estimated survivor functions for each dose/schedule combination are given in Fig. 3. A large dose effect occurs on the time to scrapie, with higher doses leading to shorter IPs. Within each dose, the probability of surviving beyond a specific time was greater if the dose was spread over 10 challenges. At the highest dose, median survival times in schedules 1, 2 and 3 were, respectively (95% confidence interval): 163 days (160, 167), 170 days (165, 174), and 181 days (176, 184). Similarly, at dose 4, the 25th percentile event times were 174 days (167, 181), 184 days (174, 202), and 213 days (202, 241).

Fig. 3.

Survivor functions for each dose/schedule group. Within the three distinct dose levels the functions refer to schedules 1 (dotted line, challenge all at once), 2 (thick line, 10 daily challenges), and 3 (thin line, 10 challenges at 4-day intervals). Survival times are shortest for dose 5 and longest for dose 3.

The survival analysis shows, as expected, a significant dose effect (P < 0.0001). A 10-fold increase in dose generates an estimated 8-fold (6.2, 9.7) increase in hazard. The effect of schedule was also significant (P < 0.0001). For a fixed total dose, and relative to schedule 1, the hazard ratios are 0.7 (0.5, 0.9) for the daily challenge, and 0.4 (0.3, 0.5) for challenge every 4 days. No significant dose/schedule interaction occurred. After adjustment of the starting point to midway through the exposure period, the hazard ratio for dose was unchanged. The effect of schedule remained significant (P = 0.026), but the hazard ratios increased to 0.8 (0.6, 1.0) for schedule 2 and 0.7 (0.5, 0.9) for schedule 3.

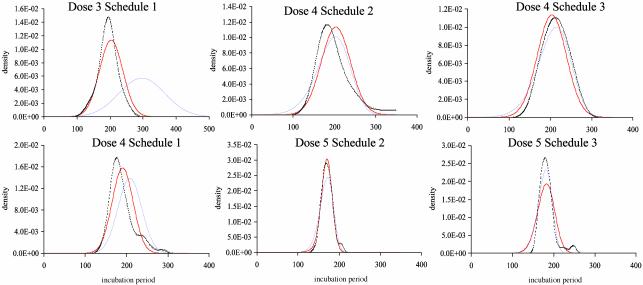
An explicit model for IP after multiple doses. A significant improvement occurred in the fit for model 11, and, hence, a rejection of the hypothesis that challenges act independently (χ² = 94, 40 df, P < 0.0001). The estimated IP distributions from the two models and parameter estimates are given in Fig. 4. The nonindependence model provides a good description of the data in all cases. The independence model fails to fit the IP simultaneously for schedules 1 and 2 or schedule 3. The result is a large overestimate of the single-challenge IP.

Fig. 4.

IP models. Observed IP at each dose/schedule combination is given by the dotted line (kernel density estimate by using s-plus software, Insightful, Seattle). The fit of the independence model is given in blue, and the alternative model is in red. Estimated distributions [N(μ_i, σ_i)] for the independence model at dose levels 3, 4, and 5 are N (296, 70), N (208, 29), and N (164, 10), respectively. For the alternative model, the distributions for doses 3, 4, and 5 in schedule 1 are N (204, 35), N (191, 25), and N (164, 10). The deviation from independence is quantified by the parameters δ_j1,..., δ_j9. For schedule 2, the parameters are, respectively, 301, 298, 296, 294, 292, 290, 289, 287, and 286 at dose 4 (σ = 34) and –18, 376, 265, 1,150, 367, 99, 98, 101, and 96 at dose 5 (σ = 13). For schedule 3, the parameters are 330 for all δ at dose 4 (σ = 28) and 7, 148, 410, 722, 1,027, 1,285, 1,471, 1,580, and 1,618 at dose 5 (σ = 24). Log-likelihoods are –1,256 (model 10) and –1,208 (model 11).

The results indicate that IPs in schedules 2 and 3 are significantly longer than would be expected if each challenge were independent. This finding can be illustrated by considering the expected repeated-dose IP given the observed values in schedule 1. Under the independence model, if the IP at dose 3, schedule 1(IP₃₁) is 194 days (as recorded in the experiment), IP₄₂ and IP₄₃ would average 161 and 170 days, respectively. The actual values are considerably longer, at 200 and 212 days. Similarly, given IP₄₁ = 188 days, we would expect that IP₅₂ and IP₅₃ would average 148 and 158 days, whereas observed values are 170 and 183 days.

Discussion

The data analyzed here result from the only large-scale investigation of how the risk of infection after exposure to prion disease depends not only on total dose but also on whether that dose was given as one or a series of challenges. Using a range of statistical models, we have shown that the probability of infection is highest when all infectivity is given at once, and declines as the interval between successive challenges increases. A useful model for the data is a logistic dose–response curve with common slope and different intercepts. The effect of multiple challenges can be represented in terms of ID₅₀ values. In comparison with a single challenge, the total dose required to infect 50% of animals was 1.5 times higher for the daily schedule and 2 times higher for the 4-day-interval schedule. The rates of infection for a total dose equal to the ID₅₀ for a single challenge were 36% and 25% under the two repeated-challenge schedules. This finding clearly demonstrates that the risk of infection does not simply increase in line with cumulative dose and that such a model for the risk of prion infection is inappropriate.

A different hypothesis is that successive doses act independently. We present several models of how independent doses might combine to affect probability of infection. We show that the independence models are also not consistent with the observed probabilities, with lower infection rates than would be expected if challenges acted independently. In schedule 2, the 10 oral doses generate a probability of infection equivalent to about six independent challenges. In schedule 3, the doses are equivalent to 4.5 independent challenges.

Many potential hypotheses exist for how repeated challenges combine, ultimately reflecting the underlying population dynamics of the infectious agent. The use of statistical models can help to clarify the precise meaning of the hypotheses and provide a means of testing them. That the risk of infection is lower than for either the independent or cumulative hypotheses indicates an interaction between the agent in successive challenges, in this case an interference rather than synergism. Such an effect has been noted in studies that demonstrate competition between scrapie strains (9). These studies gave rise to the hypothesis of the blocking of sites used for replication of the agent; however, the competition occurred after a delay in several weeks between challenges with two strains. The time window during which interference between doses of the same strain may occur could also depend on route of challenge (intracerebral vs. oral) and represent different mechanisms of interaction.

Even in the absence of data, such models can be used to help design experiments, in terms of both sample size and dose levels. The need for modeling repeated doses is mirrored in a wide range of fields, including environmental contamination (e.g., radiation, pesticide) and evaluation of the benefits of repeated treatments and vaccinations. The cumulative and independence models derived here could be applied to such studies. Our calculations show that infection risk can be greater under either the cumulative or independent model, depending on the shape of the dose–response curve, so that many hundreds of experimental units may be needed to distinguish the hypotheses with high power. For risk that changes rapidly over a 10-fold dilution, the cumulative model corresponds to higher infection risk.

IPs potentially provide considerably more information than the probability of infection alone. IPs are used as part of “strain typing” (10) and for the estimation of infectivity titer (11). However, the analysis here is not straightforward. By using survival methods, the infection hazard was significantly higher if the dose was given all on one occasion and lowest when the interval between challenges was greatest. This effect is valid in certain circumstances, such as estimating survival time from a given starting point, but does not address whether an extended IP is a true effect of repeated doses or a simple artifact of the extended exposure period. We provide an alternative approach based on a model for the IP, assuming each challenge acts independently, and we reject the hypothesis of independence. The IPs after multiple challenges are significantly longer than expected from 10 independent challenges. For quantitative transmissible spongiform encephalopathy studies, IPs have a clear advantage over the proportion infected and should be the focus of data-orientated modeling of prion population dynamics.

These analyses are clearly relevant to public health issues. A decade-long undetected phase of the bovine spongiform encephalopathy epidemic in the United Kingdom will have led to multiple exposures of the British public to the bovine spongiform encephalopathy agent, hopefully at low doses. This new analysis of the best available data on repeated dosing in an animal model sheds important light on the question of how the risk of infection changes with successive doses. Although such experiments are by necessity large-scale, it is crucial that they are repeated, if possible with low dose levels (to test the dose/schedule interaction). The statistical models produced here provide the framework for the rational design of such further experiments that will quantify the magnitude of the effect of consuming doses of transmissible spongiform encephalopathy agents over prolonged periods.