Identification of human-induced changes in atmospheric moisture content

Abstract

Data from the satellite-based Special Sensor Microwave Imager (SSM/I) show that the total atmospheric moisture content over oceans has increased by 0.41 kg/m² per decade since 1988. Results from current climate models indicate that water vapor increases of this magnitude cannot be explained by climate noise alone. In a formal detection and attribution analysis using the pooled results from 22 different climate models, the simulated “fingerprint” pattern of anthropogenically caused changes in water vapor is identifiable with high statistical confidence in the SSM/I data. Experiments in which forcing factors are varied individually suggest that this fingerprint “match” is primarily due to human-caused increases in greenhouse gases and not to solar forcing or recovery from the eruption of Mount Pinatubo. Our findings provide preliminary evidence of an emerging anthropogenic signal in the moisture content of earth's atmosphere.

“Fingerprint” studies, which seek to identify the causes of recent climate change, involve rigorous statistical comparisons of modeled and observed climate change patterns (1). Such work has been influential in shaping the “discernible human influence” conclusions of national and international scientific assessments (2–4). Most fingerprint studies have focused on temperature changes at the earth's surface (5, 6), in the free atmosphere (7, 8), or in the oceans (9), or have considered variables whose behavior is directly related to changes in atmospheric temperature (10).

Despite a growing body of empirical evidence documenting increases in moisture-related variables (11, 12), and climate model evidence of a number of robust hydrological responses to global warming (13, 14), there have been no formal fingerprint studies involving changes in the total amount of atmospheric water vapor, W. Other aspects of moisture changes have received attention in recent fingerprint work, with identification of an anthropogenic signal in observed records of continental river runoff (15), zonal mean rainfall (16), and surface specific humidity (17).

Warming induced by human-caused changes in well mixed greenhouse gases (GHGs) should increase W (11, 12). Under the assumption that relative humidity remains approximately constant, for which there is considerable empirical support (13, 18, 19), the increase in W is estimated to be ≈6.0–7.5% per degree Celsius warming of the lower troposphere (13, 18). The observed increase in W over the global ocean, as inferred since late 1987 from microwave radiometry measurements made with the satellite-borne Special Sensor Microwave Imager (SSM/I), is broadly consistent with theory (12, 18, 20).

Observational and Model Data

The SSM/I atmospheric moisture retrievals are based on measurements of microwave emissions from the 22-GHz water vapor absorption line. The distinctive shape of this line provides robust retrievals that are less problematic than other types of satellite measurement. For example, the signal-to-noise ratio (S/N) for detecting moistening in the lower troposphere by a measurement of water vapor is several times larger than for measurements of air temperature obtained directly from the Microwave Sounding Unit (18). Because SSM/I moisture retrievals are unavailable over the highly emissive land surface (18), our focus is on the total column water vapor over oceans, W_o, for a near-global domain.

Here, we attempt to identify in the relatively short SSM/I record the spatial pattern of human-caused changes in W_o. Before performing formal pattern comparisons, we analyze trends in 〈W_o〉, the spatial average of W_o (the brackets denote a spatial mean).^k We examine whether model estimates of internal climate “noise,” obtained from control integrations with no forcing changes, can explain the observed 〈W_o〉 increase over 1988–2006. We also consider whether the observed high-frequency variability of 〈W_o〉 is reliably captured in 20th century (20CEN) simulations with historical changes in external forcings.

We use control and 20CEN results from 22 climate models. Model results are from the World Climate Research Program's Coupled Model Intercomparison Project (CMIP-3) archive of simulations. The external forcings imposed in the 20CEN experiments differed between modeling groups. The most comprehensive experiments included changes in both natural external forcings (solar irradiance and volcanic dust loadings in the atmosphere) and a wide variety of anthropogenic influences (such as well mixed GHGs, ozone, sulfate and black carbon aerosols, and land surface properties). Details of the models, 20CEN experiments, and control integrations are given in supporting information (SI) Text.

Observational and Modeled Water Vapor Time Series

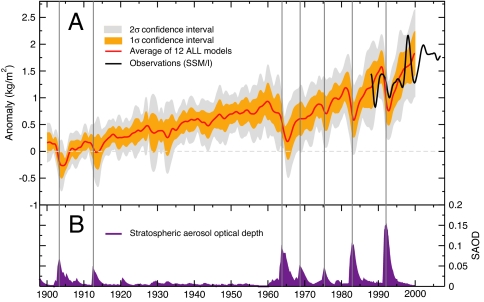
The model 20CEN runs yield overall increases in 〈W_o〉 in response to the imposed external forcings (Fig. 1). We discuss runs that include anthropogenic forcing only (ANTHRO) and runs with combined forcing by both human influences and natural external factors (ALL).^l The inclusion of volcanic effects in the ALL runs leads to slightly smaller 〈W_o〉 increases over the 20th century^m and causes pronounced decreases in 〈W_o〉 for several years after major eruptions (21). Such decreases are consistent with volcanically induced cooling of sea surface temperatures (SSTs) and with the strong coupling of interannual fluctuations in tropical SSTs and water vapor (18, 22–24).

Fig. 1.

Anomaly time series of monthly mean 〈W_o〉, the spatial average of total atmospheric moisture over near-global (50°N–50°S) oceans (A) and an estimate of the stratospheric aerosol optical depth (SAOD) (21) (B). Observations of 〈W_o〉 are from the SSM/I data set (20). Simulated 〈W_o〉 data are from 49 realizations of 20th century climate change that included combined anthropogenic and natural external forcing (ALL), performed with 12 different models. Model results were averaged over realizations and models (see footnote l). Both model and observational data were smoothed by using a filter with a half-power point at ≈2 years (see SI Text). The yellow and gray envelopes are the 1σ and 2σ confidence intervals (respectively) for the multimodel average, calculated at each time t with a sample size n = 12. Most of the 20CEN experiments end in December 1999, and the multimodel average is displayed until that month only. All model anomalies were defined relative to climatological monthly means over 1900–1909. The choice of reference period has no impact on subsequent trend analyses or variability estimates. SSM/I anomalies were forced to have the same mean as the ALL average over the period of overlap between the simulated and observed time series (1988–1999). Note that the amplitude of 〈W_o〉 variability is not directly comparable in the observations and ALL model average because the latter was damped by averaging over different realizations and models. Vertical lines denote the times of maximum SAOD after major volcanic eruptions.

In the SSM/I data, 〈W_o〉 increases over the period 1988–2006 by 0.41 kg/m² per decade, with a 95% confidence interval of ±0.21 kg/m² per decade (20). This trend is significantly different from zero (12). As in the ALL models, 〈W_o〉 decreases for several years after the eruption of Mount Pinatubo in June 1991 (Fig. 1). The observed post-Pinatubo decrease is partly masked by the effect of a small El Niño event in 1992 and is therefore smaller than in the ALL model average.

Comparison of Observed and Unforced Water Vapor Trends

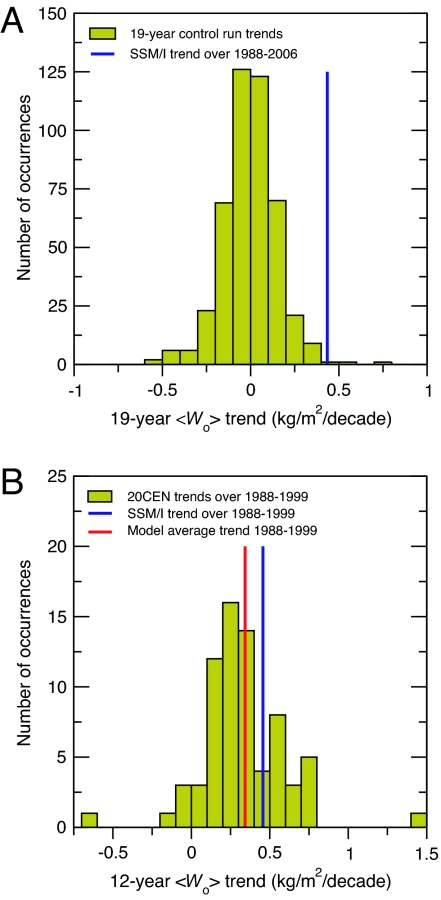
The “masking” described above illustrates a fundamental problem: observed climate changes represent a complex mixture of internally generated noise and responses to external forcing, and unambiguous separation of the two is difficult. Even if such separation were feasible, the short (19-year) SSM/I record provides only one sample of multidecadal noise. In contrast, climate models can provide multiple estimates of “pure” internally generated variability. The 22 model control runs analyzed here comprise a total of 8,848 years of data, and they yield 459 independent samples of the unforced variability of 〈W_o〉 on time scales of 19 years. This is the information we use to determine whether the SSM/I 〈W_o〉 trend over 1988–2006 could be due to noise alone.

To address this question, we calculate 〈W_o〉 from each model control run, fit linear trends to 19-year nonoverlapping segments of the 〈W_o〉 time series, and then pool results from the 22 models to form a multimodel distribution of unforced trends (Fig. 2A). If these noise estimates are reliable, internal variability is highly unlikely to be the sole cause of the observed increase in 〈W_o〉 over the SSM/I period: <1% (3 of 459) of the unforced trends in 〈W_o〉 exceed the observed trend over 1988–2006. When model experiments include estimates of anthropogenic and natural external forcings, the observed 〈W_o〉 trend of 0.46 kg/m² per decade over 1988–1999 (the period of overlap between the SSM/I record and the majority of the model 20CEN experiments) is not significantly different from the mean trend of 0.34 kg/m² per decade in the model 20CEN results (Fig. 2B).

Fig. 2.

Comparison of observed 〈W_o〉 trends with model simulations of unforced (A) and externally forced (B) trends. The sampling distribution of unforced 19-year trends was calculated as described in the text. Residual control run drift was not subtracted before estimation of the trend sampling distribution, thus inflating the standard error of the distribution and making it more difficult to reject the null hypothesis that internal variability alone could explain the observed trend. Forced 〈W_o〉 trends over 1988–1999 were estimated from 71 realizations of the 20CEN experiment performed with 22 models (see SI Tables 2 and 3). The SSM/I trend over 1988–1999 is larger than the mean of the model distribution of forced trends, in part because of the effects of the large observed El Niño event in 1997/1998 (Fig. 1A), which is close to the end of the trend period used in B.

Model Performance in Simulating Variability

The credibility of these results depends on the reliability of model noise estimates, particularly on multidecadal time scales. This is difficult to assess given the short observational record length and the large uncertainties inherent in partitioning that record into signal and noise components. The SSM/I data are of adequate length, however, to evaluate model performance in simulating the observed month-to-month and year-to-year 〈W_o〉 variability.

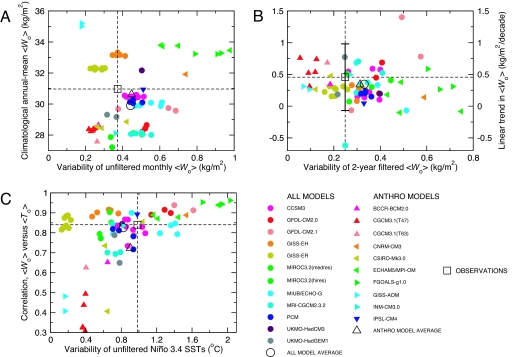
On both monthly and interannual time scales, the average temporal standard deviations of 〈W_o〉 for the ALL and ANTHRO models are actually slightly larger than the observed values (Fig. 3 A and B). Furthermore, we find no indication that the models systematically underestimate either the variability of SSTs in the Niño 3.4 region (25) or the strength of the coupling between SST and 〈W_o〉 fluctuations (Fig. 3C).ⁿ These results enhance our confidence in the ability of models to capture some of the basic physics necessary for reliable simulation of the multidecadal noise relevant to our detection study.

Fig. 3.

Comparison of basic statistical properties of simulated and observed means, variability, and trends for atmospheric moisture over near-global oceans. Scatterplots show the relationships between the temporal standard deviation of unfiltered 〈W_o〉 anomalies and climatological annual mean 〈W_o〉 (A), the temporal standard deviation of 2-year filtered 〈W_o〉 anomalies (see SI Text) and linear trends in 〈W_o〉 over 1988–1999 (B), and the standard deviation of SST anomalies in the Niño 3.4 region (12) and the temporal correlation between anomalies of 〈W_o〉 and 〈T_o〉 (where 〈T_o〉 is the spatially averaged SST anomaly over 50°N–50°S) (C). Model results are individual 20CEN realizations and are partitioned into ALL and ANTHRO models (circles and triangles, respectively). Observations are from SSM/I for 〈W_o〉 and from version 2 of the Extended Reconstructed SST (ERSST) data set of the National Oceanic and Atmospheric Administration (NOAA) for 〈T_o〉 (25). All calculations involve monthly mean, spatially averaged anomaly data for the period January 1988 through December 1999, with anomalies expressed relative to climatological monthly means over this period. Standard deviations and correlations were estimated from linearly detrended data. The dashed horizontal and vertical lines in A–C are at the locations of the SSM/I values (SSM/I and ERSST in C) and facilitate visual comparison of the modeled and observed results. The error bars on the observed 〈W_o〉 trend in B are the 2σ trend confidence intervals, adjusted for temporal autocorrelation effects (see SI Text).

Fingerprint Identification

Most formal detection and attribution (D&A) work has been performed in a “single-model” framework, where one or at most two models are used to estimate both the climate response to an imposed forcing change (the fingerprint) and the background noise of internal variability (5–10). The multimodel CMIP-3 archive offers unique opportunities and challenges for D&A research. A key opportunity is that the archive contains information from models with different resolution, physics, parameterizations, and forcings, enabling analysts to assess the robustness of D&A results. A key challenge is how best to exploit this wealth of information. Implementation of a single-model approach with 22 individual models and many different processing options (10) would generate a very large matrix of results.

A more elegant approach (26), which we follow here, is to estimate the fingerprint and noise by pooling information from multiple models. We use a standard optimal detection method (1) that has been applied successfully in studies of other climate variables (5, 10). All such methods seek to optimize the fingerprint relative to the noise and to enhance detectability of the fingerprint in observations (1). Optimization is often performed by using information on both the spatial and temporal behavior of signal and noise (6, 9, 15–17, 26). Here, given the short length of the SSM/I record, there is little low-frequency structure to estimate, and we apply spatial optimization only. We also consider whether the model fingerprints are identifiable without any optimization.

We employ two sets of moisture fingerprints, estimated separately from the ALL and ANTHRO 20CEN runs (see SI Text). The fingerprints are the leading empirical orthogonal functions (EOFs) of the atmospheric moisture changes over 1900–1999 in the ALL and ANTHRO multimodel averages. Use of W_o data for the entire 20th century (rather than simply for the period of overlap with SSM/I) provides a less noisy estimate of the true W_o response to slowly varying external forcings. It also provides a response that is more similar across models (see SI Fig. 6).

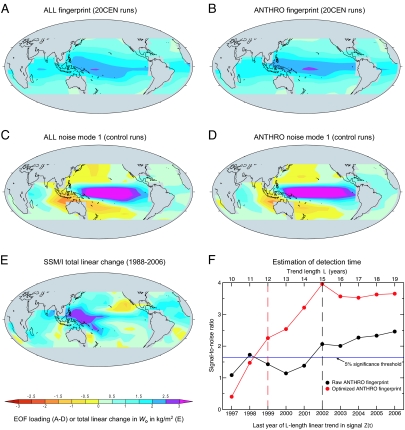
The ALL and ANTHRO fingerprint patterns are very similar, and primarily reflect the large mean changes in W_o over the 20th century (Fig. 4 A and B). In both fingerprints, W_o increases over the entire domain and varies smoothly along bands of latitude, with the largest increases close to the equator and the smallest increases toward the extratropics. The single realization of observed W_o changes over the short SSM/I period is noisier than the model fingerprints, but it also shows coherent increases in W_o over most of the worlD&Apos;s oceans, with the largest increases occurring in the western equatorial Pacific (Fig. 4E).

Fig. 4.

Simulated and observed spatial patterns of changes in W_o and estimation of detection time (10). Multimodel averages of the 20th century changes in W_o were used to calculate the ALL (A) and ANTHRO (B) fingerprints we search for in the observations. Also shown are the leading noise modes of the concatenated ALL (C) and ANTHRO (D) model control runs and the observed pattern of total linear changes in W_o over 1998–2006 (E). All calculations were performed on the common 10° × 10° latitude/longitude grid used for the fingerprint analysis. The method used for estimation of detection time (F) is illustrated for one specific example, in which W_o changes from both SSM/I data and the concatenated ANTHRO model control runs were projected onto the ANTHRO model fingerprint patterns. We fit trends of increasing length L to the resulting “signal” and “noise” projection time series, Z(t) and N(t), respectively; form a trend S/N as described in SI Text; and then determine the time at which this ratio exceeds and remains above a stipulated 5% significance threshold. This is the detection time. The dashed vertical lines denote the detection times for the raw and optimized fingerprints (1999 and 2002, respectively). In this example, data from the concatenated ALL model control runs were used for fingerprint optimization.

The leading noise modes have similar structure in the ALL and ANTHRO model control runs (Fig. 4 C and D) and primarily capture the effects of El Niño/Southern Oscillation (ENSO) variability on atmospheric moisture over the Pacific. The noise patterns resemble the leading EOF estimated from the SSM/I data (12). The observed pattern of W_o changes corresponds more closely to the model fingerprints than to the dominant noise modes.^o

Even without optimization, and despite the short observational record length, the ALL and ANTHRO fingerprint patterns are consistently identifiable in the SSM/I data. Detection of a signal that is statistically significant at the 5% level occurs by 2002, after only 15 years of monitoring atmospheric moisture with SSM/I, and is insensitive to different analysis choices (Table 1). Optimization enhances the detectability of the fingerprint, yielding detection by 1999. The optimized fingerprints have their largest loadings off-equator (see SI Fig. 7), where the raw fingerprints have relatively high loadings (Fig. 4 A and B) but the noise is relatively low (Fig. 4 C and D).

Table 1.

Detection times for model-predicted atmospheric moisture fingerprints in observational data

Noise	Fingerprint
	Raw		Optimized
	F⃗ALL	F⃗ANTHRO	F⃗ALL*(t)	F⃗ANTHRO*(t)
Mean retained
C⃗ALL(t)	2002	2002	1999	1999
C⃗ANTHRO(t)	2002	2002	1999	1999
Mean removed
C⃗ALL(t)	ND	ND	2000	2000
C⃗ANTHRO(t)	ND	ND	1999	1999

Detection times were calculated as described in SI Text. Results are given for both raw and optimized fingerprints and for analyses with the spatial mean included and removed. Detection times are shown for all four possible combinations of the fingerprints F⃗_ALLand F⃗_ANTHRO (and their optimized counterparts) and the noise data sets C⃗_ALL(t) and C⃗_ANTHRO(t). All optimized results are for a truncation dimension m = 15. Results are relatively insensitive to the choice of ALL or ANTHRO data for fingerprint or noise estimation. ND indicates that the fingerprint was not detectable before the end of the SSM/I record in 2006.

A specific example of how we estimate detection time is given in Fig. 4F and in SI Fig. 8. This example shows that calculating trends over longer time intervals generally increases the S/N used to define detection time. The growth in S/N arises primarily from the progressive decrease in the standard error of the noise trends with longer trend length L.

To test whether positive identification of the model-predicted fingerprints is driven by the mean increase in W_o (rather than by pattern correspondence at smaller spatial scales), we subtracted spatially averaged changes in W_o from all data sets and repeated the entire detection analysis (see SI Text). Subtraction of spatial means leads to greater similarity between the fingerprints and the dominant noise modes and results in failure to identify the nonoptimized fingerprint in the observations (Table 1). Optimization of the “mean-removed” fingerprint rotates it away from high-ENSO noise directions and transforms this null result to detection by no later than 2000. Temporal filtering of all data sets to damp ENSO variability has a similar effect, and it yields detection of the mean-removed fingerprint even without optimization (see SI Fig. 9).^p

Single-Forcing Experiments

Although the W_o fingerprints are highly similar in the ALL and ANTHRO experiments (Fig. 4 A and B), and both fingerprints are identifiable in the SSM/I data, these results alone do not allow us to make reliable inferences about the relative contributions of anthropogenic and natural external forcing to the observed W_o increase over 1988–2006. There are at least two reasons for this. First, the partitioning of the CMIP-3 20CEN results into ALL and ANTHRO groups does not cleanly isolate the effects of natural external forcings; there are also important differences in some of the anthropogenic forcings that were applied in the two groups (see SI Table 2). Second, it is likely that the large-scale spatial structure of the water vapor feedback will be similar for any spatially coherent surface warming signal. This implies that there may be degeneracy (24, 26) between the W_o response patterns caused by solar irradiance changes, GHG increases, and the slow recovery from the cooling induced by massive volcanic eruptions. The latter is of particular concern here because the “rebound” of W_o from the 1991 Pinatubo eruption occurs near the beginning of the SSM/I record.

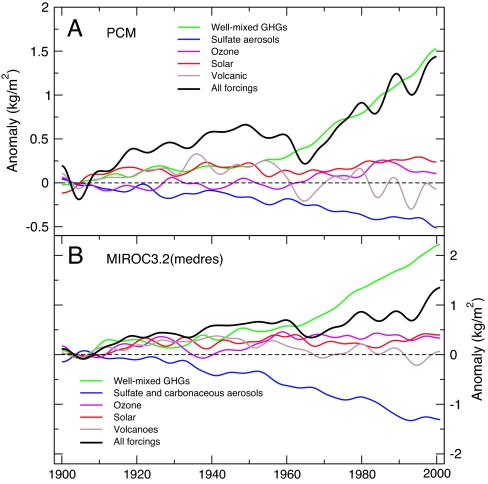
As noted above, purely statistical approaches do not permit unambiguous separation of the short SSM/I W_o record into volcanic, solar, anthropogenic, and unforced components (27). Here, we use results from single-forcing experiments performed with the Parallel Climate Model (PCM) (28) and the MIROC3.2(medres) model (29) to quantify the contributions of various factors to the simulated changes in atmospheric moisture (Fig. 5). Our focus is on the period of overlap between the SSM/I data and the PCM and MIROC experiments (1988–1999 and 1988–2000, respectively). In both models, the 〈W_o〉 trends in the “volcano only” experiment are slightly negative,^q and in absolute terms they are approximately a factor of 5 smaller than the moisture change caused by GHG increases (SI Fig. 10). Solar-induced changes in 〈W_o〉 are four to eight times smaller than the GHG component of 〈W_o〉 increase. In PCM and MIROC, therefore, forcing by natural external factors alone cannot explain the large post-1988 increase in 〈W_o〉.

Fig. 5.

Precipitable water changes in model single-forcing runs. Shown are column-integrated changes in monthly mean 〈W_o〉 in experiments performed with the Parallel Climate Model (PCM) (28) (A) and the MIROC3.2(medres) model (29) (B). For each model, there are a total of six experiments. In the first five, climate forcings were varied individually according to estimates of their historical changes over the 20th century. The five forcings considered were changes in well mixed GHGs, anthropogenic aerosol effects, tropospheric and stratospheric ozone, solar irradiance, and volcanic aerosols. These forcings were varied simultaneously in the sixth experiment (ALL). In PCM, the anthropogenic aerosol forcing involves only the direct (scattering) effects of sulfate aerosols. The MIROC anthropogenic aerosol experiment considers forcing by both the direct and indirect effects of sulfate and carbonaceous aerosols (29) (see SI Table 2). All changes in 〈W_o〉 were defined relative to climatological monthly means over 1900–1909. Results are ensemble averages and were decadally filtered (K = 145 months) to damp high-frequency noise (see SI Text). The ensemble size was 10 for the MIROC ALL integration and 4 for the PCM ALL experiment and for each PCM and MIROC single-forcing run (except the PCM volcanic forcing case, for which only two realizations were available).

Conclusions

In summary, model fingerprints of the response of atmospheric moisture to external forcings are identifiable in observations with high statistical confidence, despite the short length of the SSM/I record. Single-forcing experiments performed with two different models (28, 29) suggest that the large increase in 〈W_o〉 is primarily due to human-caused increases in GHGs (Fig. 5) and not to solar forcing or the recovery from the Pinatubo eruption. Our analysis of model control run data illustrates that internally generated variability is also a highly unlikely explanation for the observed 〈W_o〉 changes.

The credibility of these conclusions depends on the reliability of model-based noise estimates. On monthly and interannual time scales, where SSM/I data are of sufficient length to make such reliability assessments, the models used here do not systematically underestimate the amplitude of variability in 〈W_o〉 or the strength of the correlation between SSTs and 〈W_o〉. In fact, the simulated variability of 〈W_o〉 is, on average, slightly larger than observed, both with and without interannual filtering.

These findings, together with related work on continental-scale river runoff (15), zonal mean rainfall (16), and surface specific humidity (17), suggest that there is an emerging anthropogenic signal in both the moisture content of earth's atmosphere and in the cycling of moisture between atmosphere, land, and ocean. Detection and attribution studies have now moved beyond “temperature-only” analyses and show physical consistency between observed and simulated temperature, moisture, and circulation changes. This internal consistency underscores the reality of human effects on climate.

Abbreviations

CMIP

Coupled Model Intercomparison Project

EOF

empirical orthogonal function

GHG

greenhouse gas

S/N

signal-to-noise ratio

SSM/I

Special Sensor Microwave Imager

SST

sea surface temperature.