Water pulls the strings in hydrophobic polymer collapse

The molecular mechanisms of chemical reactions and conformational transitions are captured by their transition states and reaction coordinates. Transition states can be thought of as being intermediate between the reactant and product states, typically at elevated potential energy and correspondingly low popu lation yet visited on transition paths between the two metastable states. Reaction coordinates are measures of the progress of a reaction.

To define transition states and reaction coordinates, one would like to invoke simple structural criteria, such as the length of a certain chemical bond or the value of a torsional angle. Such geometric approaches work well for low-dimensional reactions in gas phase. From maps of the energy surface, transition states can be identified as low-energy saddles connecting the reactant and product minima. Reaction coordinates then parameterize the paths connecting the minima along the valleys and over the low-lying saddles.

For reactions in solution, one may try to retain such simple geometric descriptions. The gas-phase energy surface would then be replaced by the free-energy surface (or potential of mean force) in the relevant solute degrees of freedom. The role of the solvent would be reduced to generating an effective friction along the valleys and saddles on that surface, leading us from transition state theory toward Kramers' theory of diffusive barrier crossing. However, electron transfer, arguably one of the simplest reactions in solution, shows the hazards present on this route. In the highly successful Marcus theory of nonadiabatic electron transfer (1), it is precisely the solvent medium that plays the dominant role. More specifically, solvent motions govern the fluctuations of the energy gap between the reactant and product states and thereby determine the reaction rate (2, 3).

Whenever solvent coordinates contribute to the reaction, simple intuition is prone to fail and finding appropriate transition states and reaction coordinates becomes extremely challenging. In effect, among all of the motions in the high-dimensional space of the solvent coordinates, one needs to identify those that are coupled to the reaction. Moreover, this coupling has to be causal (i.e., the motions in the solvent are essential for the reaction to proceed and are not just a response to the progress of the reaction). Remarkably, even in molecular simulations of reactions, in which one can in principle follow every degree of freedom, it is far from trivial to identify the relevant solvent motions, simply because they are hidden in a sea of thermal noise (4, 5).

In a recent issue of PNAS, Miller et al. (6) study the collapse of a hydrophobic polymer in water from an extended, fully hydrated state to a compact state that largely excludes water (Fig. 1). They show that this seemingly simple molecular transition, driven by the hydrophobic effect, is closely connected to fluctuations in the local water density. Specifically, the hydrophobic collapse is found to be triggered by a transient local de wetting event in the elbow of a slightly kinked, but otherwise extended, polymer. A fluctuation in the local water density thus turns out to be the major rate-limiting event.

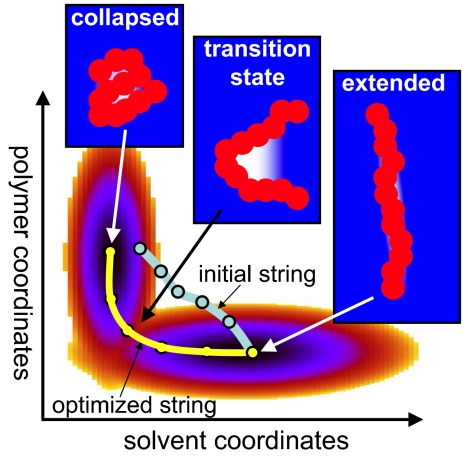
Fig. 1.

Schematic free-energy surface of hydrophobic polymer collapse as a function of polymer and solvent degrees of freedom. At the transition state, water (blue) recedes from a kink near the middle of the polymer (red), forming a small “vapor bubble” (white). In the string method (6, 14), an initial guess for the reaction path (light blue), consisting of a sequence of configurations (circles), is iteratively optimized to find the string representing the dominant reaction path (yellow).

Hydrophobic polymer collapse has long served as a paradigm of the molecular self-assembly processes in biology, in particular the folding of proteins (7–11). Previous studies have focused on the thermodynamics of polymer collapse, finding that the collapse is driven by water-mediated hydrophobic interactions. In essence, water is a poor solvent for nonpolar solutes such that a compact collapsed state of the hydrophobic polymer is favored over an extended, fully solvent-exposed state (12).

The central role of water in the thermodynamics of collapse leads one to ask whether water plays an equally important role in the kinetics of collapse, beyond providing the driving force. Indeed, ten Wolde and Chandler (13) showed some time ago that the formation of a “vapor bubble” was the key event at the transition state to collapse, a result obtained by using transition path sampling of polymer collapse in a coarse-grained, lattice-model solvent.

By studying polymer collapse in a detailed molecular model of water, Miller et al. (6) face multiple challenges: Collapse is a rare event; the transition time between extended and collapsed states is relatively long, reflecting the diffusive character of the transition; and there is no evident reaction coordinate describing the relevant solvent fluctuations. To overcome the resulting sampling issues, these authors use an elegant formalism that allows them to identify the dominant reaction paths. In the so-called “string method” of Maragliano et al. (14), the dynamics of the detailed molecular system is projected onto a space of chosen coarse coordinates, and one attempts to find the “string” that best represents the ensemble of reactive trajectories in this projected space. Such a string consists of a sequence of molecular conformations whose coordinates have been collectively optimized, primarily to follow valleys of low free energy in the coarse coordinates between the reactant and product states (Fig. 1). For polymer collapse, reactive trajectories connect extended conformations with compact ones. Following earlier work (13), Miller et al. project the solvent motions onto coarse-grained local water densities that jointly describe the fluctuating water density field. Overall, this procedure results in a representation with >100,000 coarse-collective coordinates in addition to the coordinates describing the polymer configuration.

The choice of the coarse coordinates is critical. On one hand, these coordinates have to capture the kinetically relevant motions in the solvent. This aspect is closely connected with the assumption of Markovian dynamics in the coarse space (i.e., the lack of memory, so that the future time evolution depends only on the present state and not on the preceding history). If one leaves out coordinates that are not relaxing fast relative to the process of interest, the projected motion will suffer from strong memory effects. In general, increasing the dimensionality of the space will make the projected dynamics more Markovian. Ultimately, in full phase space, Langevin or Newtonian dynamics are initial-value problems and, thus, are strictly Markovian. On the other hand, the coordinates should be coarse enough so that the assumption of a single dominant pathway (or string) in the projected space (or, at least, of a single dominant saddle over which most of the reaction paths cross) is valid. Increasing the dimensionality makes it less likely that a single path or saddle dominates, because the resulting free-energy landscape will become more structured with many local minima and saddles.

If the coarse coordinates are relevant and sufficient, then a string representing the dominant reaction path can be found iteratively (6, 14). By using restrained simulations, similar to what is done in coarse molecular dynamics (15, 16), estimates are obtained for local gradients in free energy and various geometric terms. The resulting string is represented by configurations in the space of coarse-collective coordinates. Along the string, one also obtains an estimate of the gradient in free energy and of the splitting or commitment probability (17). The resulting reaction pathway can thus be validated by running trajectories from the calculated transition state and comparing the fraction ending up on the two sides (here,

The choice of the coarse coordinates is critical.

extended and compact) with the theoretical prediction of 50%. Indeed, Miller et al. (6) find a splitting of 30%/70%, which is remarkably close to the optimum considering the fact that the commitment probability changes very rapidly from 0% to 100% near the transition state (or stochastic separatrix) (5, 18, 19).

A relevant question for the string and other methods focused on the “most likely” paths (20–22) is how unique the resulting paths are. The number of paths in high-dimensional space is enormous. For a polymer in which each of the N bonds can be in, say, cis or trans, one would estimate 𝒪(N!) distinct advancing paths between the all-cis and all-trans state in the polymer coordinates alone. With the number of paths being large, degeneracy in path space is likely, and it seems possible that the most likely path, as defined by a certain integration measure (22), is not always a “typical” path. To address this question for the collapse of the hydrophobic polymer, Miller et al. (6) invoke the high symmetry of the resulting transition state structure. Starting from an asymmetric initial configuration, the string method produces a symmetric transition state with the bend at the center of the polymer. The authors thus argue that the string represents an important reaction path that accurately captures the average transition state configuration.

How relevant are solvent fluctuations in the kinetics of collapse, folding, and binding of proteins beyond the evident role of water in mediating the molecular interactions (23)? Despite advances in single-molecule techniques (24, 25), direct experimental investigations of this question face formidable challenges, simply because any rate-determining solvent fluctuations are likely small and highly transient. However, by using string methods (14, 26), path optimization (20–22), transition path sampling (4, 27), reaction coordinate optimization (5, 28), direct simulation (29, 30), or simple models (31, 32), theoretical studies will be able explore the relevance of local solvent motions in proteins and other molecular systems.