A Unit Price Evaluation of Severe Problem Behavior

Abstract

We evaluated problem behavior exhibited by 6 individuals with developmental disabilities using the behavioral economic conceptualization of unit price. Descriptive observations were conducted during interactions between the participants and their primary care providers in a clinical laboratory, the participants' homes, or school. Data were recorded on potential reinforcers and problem behavior. After identifying reinforcers for each participant's problem behavior by way of functional analysis, the descriptive data were analyzed retrospectively, using the cost–benefit ratio described by the concept of unit price. Results showed that demand was elastic and produced monotonic response output curves. The results represent an extension of the concept of unit price to severe problem behavior under naturally occurring environmental conditions.

Behavioral economics is an area within behavior analysis in which responses are viewed as analogous to one's income, and reinforcers are viewed as analogous to commodities available for purchase (Hursh, 1980, 1984). As defined by Madden (2000), behavioral economics involves the combination of microeconomic concepts, principles, and measures, as well as behavior-analytic methods and principles. This amalgamation has yielded a fruitful body of experimental research (see, e.g., the November, 1995, special issue on behavioral economics in the Journal of the Experimental Analysis of Behavior). The implications for application of behavioral economic conceptualizations of consumption were suggested by Kagel and Winkler (1972), particularly for the design and evaluation of the familiar token economy or token system (e.g., Phillips, Phillips, Fixen, & Wolf, 1971). More recently, behavioral economic approaches have been applied to evaluate response allocation, in applied contexts, under open and closed economies (Roane, Call, & Falcomata, 2005), response allocation under increasing effort requirements (e.g., Perry & Fisher, 2001), and reinforcer demand under increasing price requirements (e.g., Kerwin, Ahearn, Eicher, & Burd, 1995; Roane, Lerman, & Vorndran, 2001; Tustin, 1994), to name only a few applications. The current investigation focuses on evaluations of spending (problem behavior exhibited by individuals with developmental disabilities) and consumption (of reinforcers for problem behavior identified via functional analysis) under naturally occurring price, or response requirement, increases.

Behavioral economic analyses focus attention on two measures: consumption (how much of the reinforcer is obtained) and spending (how much responding, or currency, is allocated to obtain the reinforcer; Madden, 2000). When combined, these measures produce a cost–benefit ratio made up of the number of responses emitted per reinforcer (i.e., unit price; e.g., Foster & Hackenberg, 2004). Alternatively, stated in economic terms, unit price is the amount of income expended to access a commodity. For example, if a 1-l bottle of juice costs $4.00 and the 2-l bottle of the same juice costs $5.50, the price per unit (i.e., liter) is cheaper for the larger bottle (i.e., $4.00 per liter vs. $2.75 per liter). Basic and applied research on reinforcement parameters (e.g., rate, quality, delay, effort) has shown that these variables may interact to influence overall consumption (e.g., Hursh, Raslear, Shurtleff, Bauman, & Simmons, 1988; Neef, Shade, & Miller, 1994). Thus, conceptualizations of unit price can also be arranged to accommodate variables other than reinforcers per response. For example, the juice choice may be influenced by the effort associated with obtaining the larger bottle (e.g., reaching to a higher shelf), the delay associated with obtaining the larger bottle (e.g., waiting for the stock person to refill the shelves), and so on.

The behavioral economic concepts of consumption, spending, and unit price may be used to quantify demand and demand elasticity. Demand refers to the function relating the amount of the commodity consumed to the prevailing price for each unit of the commodity (Hursh, 1980). The effects of changes in price (on consumption) are predicted to follow the economic law of demand, which states that, with all other things being equal, consumption of a commodity (reinforcer) decreases as its price increases (Chaloupka & Pacula, 2000). Demand elasticity is the extent to which consumption of a commodity is influenced by alterations in price for that commodity (Green & Freed, 1993). Further, demand elasticity can be broadly characterized as elastic or inelastic. Elastic demand describes a superproportional change in consumption as a function of changes in price. For example, if the price of tomatoes increased from $1.00 per kilogram to $2.00 per kilogram, this would represent a 50% increase in price. To characterize demand for tomatoes as elastic, consumption would necessarily decrease by more than 50% (i.e., a demand curve with slope between −1 and −∞). Inelastic demand describes a subproportional change in consumption as a function of changes in price. Thus, in the tomato example, if the price of tomatoes increased from $1.00 per kilogram to $2.00 per kilogram and consumption of tomatoes decreased by a mere 25%, then consumption for tomatoes would be characterized as inelastic (i.e., a demand curve with slope between 0 and −1). Frequently, experimental behavioral economic research has shown that the left portions of consumption and spending curves illustrate inelastic demand (subproportional changes in consumption), and the right portions of both curves illustrate elastic demand (superproportional changes in consumption). In other words, under initial price increases, spending increases such that a similar level of the commodity is produced. However, when increases in price reach a critical value (termed P_max; Hursh, 2000), consumption shifts from inelastic to elastic.

The extent to which the slope of the demand function changes from one unit price to the next describes the type of demand (e.g., elastic or inelastic; Allison, 1983), because as noted by Hursh (1980), demand curves tend to slope downward, thus producing a slope less than zero. Therefore, demand curves can be used as a means to assess stimulus value, in that flatter functions suggest higher value stimuli because consumption changes little as price increases. Further, if a stimulus is highly valued and the demand curve is flat, response output would be expected to increase dramatically with increasing price in order to maintain the level of consumption observed at lower unit price values.

Tustin (1994) evaluated demand functions obtained from 3 individuals with developmental disabilities using qualitatively different stimuli (e.g., auditory, visual) and button pressing as the operant. Participants were exposed to a concurrent-schedules arrangement in which one stimulus (e.g., a visual stimulus) could be obtained for a constant price (e.g., five responses produced one reinforcer, Unit Price 5), and the second stimulus (e.g., an auditory stimulus) could be obtained under increasing schedule requirements. For example, while the visual stimulus could be obtained for five responses, auditory stimuli were evaluated under fixed-ratio schedules of 1, 2, 5, 10, and 20. Characteristic decreases in consumption were obtained across increasing prices for one of the concurrently available stimuli. An apparent preference reversal was also observed in that a stimulus initially preferred at relatively low prices (i.e., response requirements) was relatively less preferred when the price for that stimulus increased.

More recently, Madden, Bickel, and Jacobs (2000) tested three predictions of unit price using chronic smokers as participants and cigarette puffs as reinforcers. Most germane to the current study was the prediction that increases in the price per puff would produce decreases in overall consumption (reinforcers obtained) and spending (response output) would produce a bitonic function with increasing prices, both on double logarithmic coordinates. Participants were required to pull plungers according to a predetermined schedule to produce cigarette puffs, and unit price was systematically altered. Consistent with prior research, decreases in consumption were observed under increasing price requirements.

Hursh (1984) suggested that the utility of economic concepts rests in part on the validity of findings obtained in laboratory contexts with individuals (and not large-group evaluations). This is clearly a position espoused by behavior analysts and is evidenced by the relatively large basic experimental and growing applied experimental literature testing the utility of behavioral economic concepts. Similarly, conceptualizations of a variety of a problematic responses (e.g., severe problem behavior, substance abuse) as consumer demand allow analyses informed by economic concepts known to influence consumer demand, for example, unit price (Madden, 2000). However, the extent to which economic concepts, in particular the concept of unit price, are of utility in nonexperimental (descriptive) contexts, at the level of the individual, has been the subject of appreciably less behavior-analytic research (see Oliveira-Castro, Foxall, & Schrezenmaier, 2006, for a recent notable exception). Clearly, economic theory is rooted in the prediction of consumer behavior under relatively uncontrolled contexts. Classic economics does not control price and observe changes in consumption; rather economists observe natural variations in price and then relate them to variations in consumption. For example, a change in the price of gasoline serves as an appropriate independent variable to measure an array of dependent variables (e.g., gas consumption, spending, the use of public transportation as an alternative form of reinforcement). However, such evaluations typically assess the behavior of large groups (e.g., residents of a particular region in the United States).

The purpose of the present study was to assess the concept of unit price using the conceptual orientation employed by J. C. Borrero and Vollmer (2002). Borrero and Vollmer conducted descriptive observations of caregiver–participant interactions and recorded instances of problem behavior, appropriate behavior, and various environmental events (e.g., periods of low attention). Next, the researchers conducted functional analyses to identify reinforcers for problem behavior, and then retrospectively evaluated relative response and reinforcer rates using the strict (Herrnstein, 1961) and generalized (Baum, 1974) matching equations. The experimental demonstration of reinforcers for problem behavior was important in that interpretations of the data via the matching equations could be related to those from basic and applied experimental work in which reinforcers are known and not assumed. In the current study, the same sequence of events was followed, including the experimental identification of reinforcers for problem behavior, and evaluated levels of response output (problem behavior), given changes in the price of events shown to reinforce problem behavior. The purpose of the current study was to assess work and demand functions under naturally occurring increasing price values at the level of the individual and at the level of a group of 6 participants.

Method

Participants

Six individuals participated in various portions of this study.1 Mandy was a 24-year-old woman who had been diagnosed with Sticklers syndrome and mild mental retardation. Her problem behavior consisted primarily of self-injurious behavior (SIB) including head banging, nose punching, chin punching, and head hitting. Bruno was an 11-year-old boy who had been diagnosed with autism. His problem behavior consisted of aggression, disruptive behavior (e.g., throwing academic materials), and SIB (head and face hitting). Dan was a 9-year-old boy who had been diagnosed with moderate mental retardation and cerebral palsy. His problem behavior consisted of aggression (e.g., hitting and kicking others) and disruptive behavior (e.g., throwing materials). Todd was a 9-year-old boy who had been diagnosed with moderate mental retardation and fetal alcohol syndrome. His problem behavior consisted of aggression (e.g., hitting and kicking others). Walsh was a 7-year-old boy who had been diagnosed with mild mental retardation and a seizure disorder. His problem behavior consisted of aggression and disruption. Antoine was an 8-year-old boy who had been diagnosed with autism and moderate mental retardation. His problem behavior consisted of aggression and disruption.

Sequence of Events

Descriptive Analysis and Settings

Descriptive data were gathered for each participant using methods described by Vollmer, Borrero, Wright, Van Camp, and Lalli (2001). Observers used a computerized data-collection system to record three potential reinforcers (instruction termination, access to tangible items, and attention) and problem behavior (individually defined for each participant). The term potential reinforcer was used to describe events that occurred subsequent to problem behavior because at the time of the descriptive observations, functional analyses had not been conducted for any participant (thus, functional reinforcers were not known). Descriptive analyses were conducted before functional analyses to capture behavior in the natural environment prior to exposure to experimental contingencies in the functional analysis. Attention was defined as physical or verbal interaction between the participant and his or her primary care providers. Instruction termination was defined as removal of demands and instructional materials for a period of at least 3 s, or the absence of instructions if the participant disengaged from a previously specified task for at least 3 s. Access to tangible items was defined as availability of previously restricted items for manipulation. Potential reinforcers and potential establishing operations were recorded as duration measures, and instances of problem behavior were recorded as a frequency measure.

Descriptive observations for Mandy, Todd, and Walsh were conducted on an inpatient hospital unit during interactions with their primary care providers. The inpatient hospital facility was furnished with a couch, chairs, tables, and a television. Descriptive observations for Dan and Antoine were conducted in their homes, throughout various rooms of the house, during interactions with their biological parents and siblings (for Dan). Descriptive observations for Bruno were conducted in his classroom during regularly scheduled activities with his classroom teachers.

Functional Analysis

The problem behavior of each participant was exposed to functional analysis using procedures similar to those described by Iwata, Dorsey, Slifer, Bauman, and Richman (1982/1994). Trained clinical therapists or trained graduate students conducted all functional analyses. Four test conditions and a control condition were alternated in a multielement design.

In the attention condition, the participant had access to a task or activity but did not have access to attention in the absence of problem behavior. Instances of problem behavior resulted in 30 s of attention from the therapist (in the form of statements of concern). The attention condition was designed to test behavioral sensitivity to adult attention as a reinforcer.

During the tangible condition, the participant received brief access to a preferred tangible item (or food item for Todd) that was subsequently restricted and returned contingent on problem behavior. Given an instance of problem behavior, the participant received access to the item for 30 s (or a bite of food). Attention was delivered throughout tangible conditions, irrespective of problem behavior (on a continuous or nearly continuous schedule). The tangible condition was designed to test behavioral sensitivity to tangible items as reinforcement.

In the escape condition, the participant received instructions to complete tasks approximately twice per minute. Instances of problem behavior resulted in a 30-s break from the instructional sequence. In the absence of problem behavior, the instructional sequence continued. The escape condition was designed to test for behavioral sensitivity to escape from instructions as reinforcement.

An alone condition (Mandy) and a no-consequence condition (Bruno) were also included. In the alone condition, the participant was escorted into a room with no tangible materials provided, and no programmed contingencies were in place for SIB. The no-consequence condition was similar to the alone condition in that no programmed contingencies were arranged for problem behavior and no tangible items were provided. However, due to the arrangement of the setting (his classroom), Bruno was not alone during these sessions. The alone and no-consequence conditions were designed to evaluate response persistence in the absence of programmed social contingencies.

Each test condition was compared to a control condition in which no programmed contingencies were arranged for problem behavior, no instructional demands were delivered, and therapist attention and preferred tangible items were freely available (on a continuous or nearly continuous schedule). Functional analyses were either 5 min (Bruno and Antoine) or 10 min (Mandy, Dan, Todd, and Walsh) in duration.

Interobserver Agreement

Interobserver agreement was assessed by having a second observer simultaneously but independently record data on problem behavior, potential establishing operations (e.g., low attention), and potential reinforcers (e.g., attention). Agreement was calculated using partial agreement within intervals (e.g., Iwata, Pace, Cowdery, & Miltenberger, 1994). Each observation was divided into 10-s intervals, and agreement between both observers was assessed across each interval. The smaller number (in each 10-s interval) was divided by the larger number, and all values were averaged for the entire observation. Interobserver agreement was assessed during 37% of all descriptive observations. Interobserver agreement data for reinforcers are reported for relevant conditions only (i.e., those conditions shown to reinforce problem behavior, as demonstrated via functional analysis). For Mandy, agreement averaged 84% for attention, 100% for access to tangible items, and 84% for problem behavior. For Bruno, agreement was 87% for escape from instructional demands (range, 80% to 99%), 98% for access to tangible items (range, 97% to 98%), and 100% for problem behavior. For Dan, agreement was 91% for access to tangible items (range, 82% to 99%) and 96% for problem behavior (range, 86% to 100%). For Todd, agreement was 99% for access to tangible items (range, 98% to 100%) and 95% for problem behavior (range, 91% to 98%). For Walsh, agreement was 97% for attention (range, 93% to 100%), 93% for escape from instructional demands (range, 91% to 95%), 98% for access to tangible items, and 97% for problem behavior (range, 93% to 100%). For Antoine, agreement was 92% for access to tangible items (range, 76% to 100%) and 96% for problem behavior (range, 72% to 100%). Interobserver agreement was assessed during 50% of all functional analysis sessions. Interobserver agreement for problem behavior exceeded 80% for all participants.

Data Preparation (descriptive Analysis)

Descriptive data were partitioned into three equal intervals. For example, if the entire descriptive observation was 3 hr in duration, each data point represented 1 hr of observation. Data were also examined in 10- and 30-min increments. However, results were more variable when evaluated in 10- and 30-min increments (i.e., consumption was not well described by changes in unit price). Unit price values were determined individually for each participant. Given the partitioning of the descriptive observations, each participant's data yielded three unit price values. Once partitioned, we calculated the total number of reinforcers delivered and the instances of problem behavior emitted during each equal interval. The unit price for each interval was then calculated by dividing the total number of responses emitted by the total number of reinforcers obtained. An event counted as a reinforcer if (a) it was an event identified via functional analysis as a reinforcer, and (b) the event was available within 10 s of problem behavior. The use of 10-s window was based on prior work (C. S. W. Borrero, Vollmer, Borrero, & Bourret, 2005; J. C. Borrero & Vollmer, 2002). If the functional analyses showed that problem behavior was sensitive to multiple sources of reinforcement (e.g., attention and tangible items), provision of either attention or tangible items was scored as a reinforcer. Only one event had to be delivered within 10 s to be scored as a reinforced response. For example, if 20 instances of problem behavior were observed and 10 of the 20 responses were reinforced (as previously defined), the unit price (responses per reinforcer) was 2. Having determined the unit price, we plotted consumption (demand functions) and spending (work functions) at each unit price.

Finally, we also calculated a single unit price value for each participant using the entire descriptive observation. For example, if the entire descriptive observation for 1 participant was 2.5 hr, we calculated the unit price for the entire 2.5 hr of descriptive observation and plotted the total number of reinforcers obtained and total number of responses emitted at each unit price value. In this way, we were able to evaluate a larger range of unit price values. This method of analysis was designed to be analogous to that used by J. C. Borrero and Vollmer (2002) in evaluations of matching relations in the natural environment.

Results

Table 1 provides a summary of the assessment findings, for all participants; however, note that functional analysis results for Mandy, Dan, Todd, Walsh, and Antoine were reported in prior work (see Footnote 1). Functional analysis results for all participants showed that the problem behavior of each participant was sensitive to socially mediated events as reinforcement.

Table 1.

Functional Analysis Results for All Participants

Participant	Results
Mandy	Attention and tangible items
Bruno	Tangible items and escape
Dan	Tangible items
Todd	Edible items
Walsh	Attention, tangible items, and escape
Antoine	Tangible items

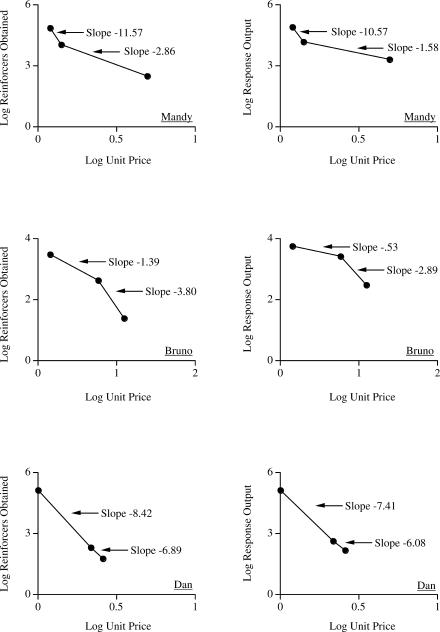
Figure 1 depicts the results of the demand functions and work functions for Mandy, Bruno, and Dan on double logarithmic coordinates. Double logarithmic coordinates were used in keeping with prior experimental behavioral economic research and because differences between consumption and spending at different unit price values are accentuated on double logarithmic axes (compared to arithmetic axes). For 3 participants (Todd, Walsh, and Alfonzo), reinforcers were not delivered during one of the three segmented intervals. Thus, data for these participants are not included in Figure 1. Overall, consumption and spending decreased as a function of increasing unit price (producing monotonically decreasing functions, or functions that move in only one direction as unit price increases). We also calculated the slope for each change in unit price. In this way, changes in the slope of the function could be interpreted in terms of demand elasticity. Results for all participants demonstrated elastic demand (all had a slope with absolute value greater than −1), but for 2 participants (Mandy and Dan) the largest decrease in consumption occurred between transitions from Unit Price 1 to Unit Price 2. Results for Bruno produced a steeper slope during transitions from Unit Price 2 to Unit Price 3. This finding replicates prior experimental work; however, the functions obtained for response output did not produce the bitonic function that would have been expected based on prior experimental work (e.g., Madden et al., 2000). This may have been a result of the rather limited range of unit price values, the limited number of data points, or both.

Figure 1.

Demand functions (left) and work functions (right) for Mandy, Bruno, and Dan in logarithmic coordinates.

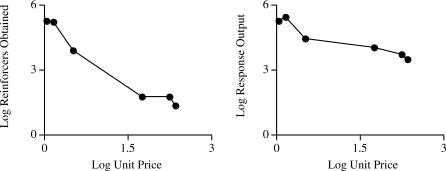
In addition to evaluating consumption and spending for 3 individual participants, overall consumption and spending were also evaluated when the entire descriptive observation was considered as a single observation. This yielded a single unit price and a single work and demand function. Each data point in Figure 2 represents data for 1 participant on double logarithmic coordinates. When evaluated in this way, the same monotonically decreasing function was obtained for consumption and spending. A rather minimal increase in spending was observed between the two leftmost data points (right panel), which arguably approximates the bitonic function frequently reported in the experimental literature. However, the global shape of the function is monotonically decreasing.

Figure 2.

Demand functions (left) and work functions (right) for all participants. Each data point represents data for a single participant, in logarithmic coordinates. In both panels, the data points represent (from left to right) Dan, Mandy, Bruno, Todd, Walsh, and Antoine.

Discussion

The concept of unit price was extended to severe problem behavior exhibited by 6 individuals with developmental disabilities. Descriptive observations provided the data necessary to evaluate unit price under natural environmental conditions that met the general criteria of a descriptive analysis (Bijou, Peterson, & Ault, 1968; Iwata, Kahng, Wallace, & Lindberg, 2000). Reinforcers were then empirically determined by way of functional analysis, and descriptive data were then retrospectively evaluated using the economic conceptualization of unit price. Results of individual participant data and the group analysis showed decreases in overall consumption as a function of increasing price.

The present study adds to the existing behavioral economic literature by extending the concept of unit price to severe problem behavior exhibited by individuals with developmental disabilities, under naturally occurring environmental conditions. However, the finding that demand was completely elastic, and thus resulted in monotonic response output curves, warrants some consideration. The typical outcome of such analyses in traditional laboratory evaluations in the behavioral economic literature is considerably different. As noted previously, demand is typically inelastic on the left side of the demand curve, and correspondingly, the response output curve is bitonic with increases in response output initially followed by a decrease in response output. In terms of the present study, as reinforcers were provided less frequently for problem behavior, problem behavior could have increased to maintain the same level of reinforcement. Returning to the tomato example, if the price of tomatoes were to increase from $1.00 per kilogram to $3.00 per kilogram, total money spent (response output) could increase even if demand (tomatoes purchased) declines slightly. That is, if 10 kg of tomatoes are purchased at $2.00 per kilogram, total spending is $20.00. But if only 8 kg are purchased at $3.00 per kilogram, total spending is $24.00. This is in the inelastic portion of the demand curve and is represented by the ascending limb of a bitonic response output curve. At further increases in price, response output may eventually decline (e.g., at $4.00 per kilogram, perhaps only 4 kg are consumed, and total spending is $16.00). This represents the elastic portion of the demand curve, and is represented by the descending limb of a bitonic response output curve. Notably, this was not observed in the present study. Response curves were not bitonic, and there was no inelastic portion on the left of the demand curve. Clinically, this can be viewed as a preferred outcome because at even the lowest unit price values in the present study, problem behavior decreased with increasing price. Perhaps if lower unit price values had been observed in the present study, an inelastic portion of the demand curve and bitonic response output function may have been apparent. If that were the case, then problem behavior may have initially increased with increasing unit price. Future research might involve evaluations of conditions under which a bitonic function would be apparent. This may represent an important clinical situation, similar to an extinction burst, in which attempts at eliminating problem behavior are initially met with increases in problem behavior.

Economic concepts such as the simple formulation of unit price used in the current investigation, as well as more complex iterations involving response effort (e.g., Hursh et al., 1988) and delay (e.g., Madden et al., 2000), represent examples of quantitative models. Quantitative modeling encourages descriptions of behavior that are precise and succinct while capturing relevant features of the phenomenon under investigation (Shull, 1991). In recent years, there has been a revitalized interest in one particular quantitative model of behavior in the context of naturally occurring interactions: the matching law (e.g., Oliver, Hall, & Nixon, 1999). Recent work has shown that the matching law (in its various iterations) effectively describes the allocation of problem and appropriate behavior based on relative reinforcement rates. The current investigation adds to the existing literature on quantitative modeling by demonstrating that problem behavior exhibited by individuals with developmental disabilities replicates some features of the behavior of consumers in laboratory contexts under increasing price requirements. However, the current investigation is not without its limitations.

First, we evaluated consumption and spending under a rather limited range of unit price values (three for 3 participants, one for the remaining 3 participants). The experimental literature on unit price typically involves many more unit price values and repeated measures of behavior under each value. In addition to the analyses reported in the present study, we also evaluated the descriptive data in smaller intervals (e.g., 10 min and 30 min). Results of those analyses did not produce orderly data, and it was not until descriptive data were partitioned into equal thirds that any semblance of order was obtained. However, the finding that consumption and spending decreased given increases in price across such a small range of unit price values speaks to the generality of unit price as a useful concept in applied behavior analysis.

Future research may be designed to arrange unit prices experimentally, based on those values derived from descriptive observations as well as additional unit price values. For example, if analyses from descriptive observations produce responses to reinforcer ratios of 3, 6, and 9 (across an extended observation period), experimentally arranged unit price values that mimic those obtained via descriptive observations may provide a stronger demonstration of the utility of the model. The recent work of Madden et al. (2000) suggests that the way in which unit price is manipulated (manipulations of amount while holding response requirement constant, manipulations of response requirement while holding amount constant, or proportional increases of both amount and response requirement) may produce differential effects on response output. Therefore, future research may also be designed to assess the effects of experimental manipulations of unit price based on values obtained from descriptive data while arranging a range of absolute values that determine a unit price. For example, if a unit price of 9 were obtained via descriptive observations, an experimental arrangement of the same unit price could be arranged by provision of one reinforcer for every nine responses or five reinforcers for every 45 responses. Such evaluations would also extend the applicability of unit price and provide a larger amount of data for consideration.

A second limitation is that only one reinforcement parameter (frequency) was evaluated. Other factors, such as the duration or magnitude of reinforcement likely contribute to overall consumption. For example, if each instance of SIB produces one reinforcer (unit price  =  1) but instances of a particularly high intensity produce a larger duration of reinforcement, price may likely be determined by response effort (associated with self-injury), reinforcer frequency, and reinforcer magnitude. Future research may be specifically designed to evaluate multiple parameters of reinforcement in determining price, because prior descriptive research has shown that reinforcement parameters may influence overall response output (C. S. W. Borrero et al., 2005).

Third, the method of assessing consumption in the present study is consistent with classical economic conceptualizations (there was no experimental manipulation of price). However, the elaborate covariate models used in econometrics were not employed to statistically control for confounding factors (e.g., settings, alternative reinforcement and activities). Were such statistical control procedures employed, more characteristic demand and work functions might have been obtained. The present study should be evaluated in light of this omission and considered a preliminary endeavor, leaving such methods available for future investigations on the concept of unit price as it relates to problem behavior in the natural environment.

Finally, consumption was evaluated using problem behavior as the unit of currency. However, this type of analysis could also be applied to evaluate appropriate behavior (e.g., communicative responses). Further, choice between two or more available response forms could be evaluated using the procedures described in the current investigation. Hursh and Natelson (1981) evaluated overall response output of rats responding on variable-interval (VI) schedules for food and electrical brain stimulation (either high or low electrical charge). As VI values increased, responses allocated to the alternative associated with brain stimulation decreased while responses allocated to food reinforcers increased. In a similar vein, future unit price evaluations in descriptive contexts may be designed to evaluate responses allocated to communicative behavior and problem behavior across increasing unit price values. For example, at relatively low unit price values, demand for a functional reinforcer may be high for communicative responses but low across increasing price values. Analyses of this sort may also be designed to evaluate additional reinforcement parameters, as suggested previously.

Evaluations of quantitative models, as applied to severe problem behavior in the natural environment, are predicated on the experimental identification of reinforcers. Behavior analysts have evaluated numerous quantitative models in experimental contexts (Mazur, 2006). Such models include (a) the contextual choice model (Grace, 1993), (b) the metaphor of behavioral momentum (Mace et al., 1988; Nevin, Mandell, & Atak, 1983), (c) the delay-reduction hypothesis (Fantino & Abarca, 1985), (d) the matching law (Herrnstein, 1961, 1970), (e) the hyperbolic value-added model (Mazur, 2001), and (f) economic concepts of substitutability and complementarity (Hursh, 1980, 1984). We suggest that a more general framework for assessing the utility of these models is needed to assess the extent to which these models provide a reasonable account of behavior in the natural environment and extend the generality of these models to uncontrolled environments. Evaluations of the aforementioned models, including evaluations of unit price, may be cumbersome in uncontrolled settings. However, the relevance of behavioral economic theory, matching, delay reduction, and behavioral momentum could be enhanced by applications of such models to human behavior that occurs in uncontrolled settings.