A Simplified Two-Component Model of Blood Pressure Fluctuation

Abstract

We propose a simple moving-average (MA) model that uses the low-frequency (LF) component of the peroneal muscle sympathetic nerve spike rate (LF_{spike rate}) and the high-frequency (HF) component of respiration (HF_Resp) to describe the LF neurovascular fluctuations and the HF mechanical oscillations in systolic blood pressure (SBP), respectively. This method was validated by data from eight healthy subjects (23–47 yr old, 6 male, 2 female) during a graded tilt (15° increments every 5 min to a 60° angle). The LF component of SBP (LF_SBP) had a strong baroreflex-mediated feedback correlation with LF_{spike rate} (r = −0.69 ± 0.05) and also a strong feedforward relation to LF_{spike rate} [r = 0.58 ± 0.03 with LF_SBP delay (τ) = 5.625 ± 0.15 s]. The HF components of spike rate (HF_{spike rate}) and SBP (HF_SBP) were not significantly correlated. Conversely, HF_Resp and HF_SBP were highly correlated (r = −0.79 ± 0.04), whereas LF_Resp and LF_SBP were significantly less correlated (r = 0.45 ± 0.08). The mean correlation coefficients between the measured and model-predicted LF_SBP (r = 0.74 ± 0.03) in the supine position did not change significantly during tilt. The mean correlation between the measured and model-predicted HF_SBP was 0.89 ± 0.02 in the supine position. R² values for the regression analysis of the model-predicted and measured LF and HF powers indicate that 78 and 91% of the variability in power can be explained by the linear relation of LF_{spike rate} to LF_SBP and HF_Resp to HF_SBP. We report a simple two-component model using neural sympathetic and mechanical respiratory inputs that can explain the majority of blood pressure fluctuation at rest and during orthostatic stress in healthy subjects.

various rhythmic oscillations in human blood pressure (BP) have been proposed to reflect the action of different physiological mechanisms on BP regulation. For instance, it has been suggested that very low-frequency (VLF) trends (period >25 s, frequency <0.04 Hz) in BP represent the influence of hormonal regulation and thermoregulation and that high-frequency (HF, 0.15–0.4 Hz) fluctuations mark the effect of respiration on BP. A more hotly debated issue is the idea that low-frequency (LF, 0.04–0.14 Hz) BP oscillations with a 10-s periodicity, generally referred to as Mayer waves, reflect sympathetically mediated vasomotor BP modulation. It has been proposed that the origin of these waves is a resonance phenomenon of the baroreflex pathway (12), and the LF power has been used as a marker of sympathetic activity (34, 35, 37), although this practice remains controversial (31, 48).

Several lines of indirect evidence have been used to associate the oscillations in BP with oscillations in these other physiological rhythms. For example, physiological maneuvers have identified changes in the oscillatory patterns of sympathetic nerve activity and respiration that correspond to those in BP during sympathetic activation (20). During head-up tilt (HUT), 1) LF oscillations are evident in the nerve activity and BP, 2) HF oscillations are expressed in each of the three signals, i.e., respiration, BP, and nerve activity, and 3) relative changes in the LF component of spike rate (LF_{spike rate}) and the HF component of respiration (HF_Resp) are also reflected in the BP (Fig. 1). Coherence analysis has objectively shown that the frequency-domain relations between these signals are significant under normal physiological conditions (18, 20, 40).

Fig. 1.

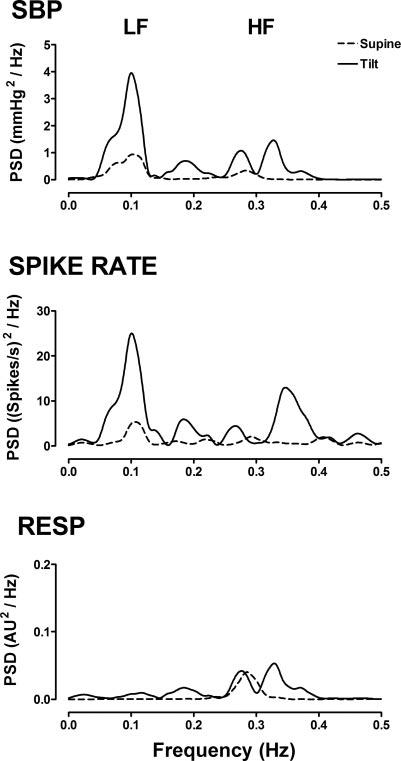
Spectral characteristics [power spectral density (PSD)] of systolic blood pressure (SBP), sympathetic spike rate, and respiration (Resp) at rest in the supine position and at 60° head-up tilt (HUT) in a representative subject. AU, abitrary units.

Similarly, pharmacological interventions and the study of autonomic pathologies have also indirectly supported the idea that sympathetic activity and respiration contribute to the oscillations in BP. The LF component of BP (LF_BP) oscillations is attenuated during ganglionic blockade in healthy subjects (15, 32, 56) and is absent in patients with pure autonomic failure with peripheral sympathetic nerve lesions (15, 19), suggesting a sympathetic origin for this rhythm. On the other hand, the HF component of BP (HF_BP) fluctuations is unaffected by ganglionic blockade (15, 32, 56) and remains after thoracic sympathectomy in transplant patients (27). Additionally, the neurovascular interface has been suggested to possess low-pass characteristics that effectively filter out the HF components of sympathetic activity (12, 25, 43, 55). These findings indicate that the HF_BP rhythm is not neurally mediated but, instead, largely the result of the mechanical interaction between BP and respiration or cardiac output (CO).

Although there is much indirect evidence, a mathematical model may provide a more direct description of the relation between the BP oscillations and fluctuations in other cardiovascular parameters. A number of models using heart rate (HR) and respiration (12, 29, 30, 47) have been developed to help explain the fluctuations in human BP. One limitation of most models is that they do not include sympathetic activity as a direct input parameter. Modeling of BP fluctuations from sympathetic activity in animals has been successfully applied using a system identification approach (5, 22, 24). Kamiya et al. (23) adapted a transfer function approach used in rabbits to explain the LF fluctuations in human BP and sympathetic activity during tilt but applied this model only to simulated data. In their explanation of human BP fluctuations, Myers et al. (31) used a linear model with integrated sympathetic activity as an input parameter, which yielded less accurate results than the transfer functions used in animals. However, the primary concern of this model was explanation of LF_BP; it utilized integrated burst areas with arbitrary units to quantify sympathetic activity, rather than the spike rates typically found in animal models, and involved euglycemic clamping to enhance sympathetic activation, a procedure that induces vasodilation through increased insulin release and may alter the neurovascular coupling (11).

We propose a different mathematical model that combines subbands of the sympathetic spike rate and respiration to explain the LF and HF oscillations in human BP. A technique to detect action potentials in raw human sympathetic nerve recordings has been recently introduced and can be used to form a spike rate density series to quantify sympathetic activity (3, 14). Using the spike rate density along with measured respiratory patterns, we examine the accuracy of a two-component linear model that attempts to describe the LF-neurovascular interaction and the HF mechanical effects of respiration on the fluctuations in human BP.

METHODS

Subjects and Clinical Conditions

Eight healthy subjects (6 male, 2 female; 23–47 yr old) were recruited from the Vanderbilt University General Clinical Research Center volunteer database. All subjects underwent extensive physical examination and had no signs of cardiovascular disease or history of syncope before the study. The subjects abstained from all drugs, including caffeine and nicotine, for ≥72 h before testing. Their body mass index was 26 ± 1.7 kg/m², resting HR was 61 ± 2 beats/min, and BP was 111 ± 2/65 ± 2 mmHg.

Protocol

Straps were used to secure the subjects to a tilt table. The subjects were instructed to remain relaxed and quiet throughout all studies and were monitored for any signs of presyncope during all tests (53). After 15 min of supine rest, the subjects were tilted by 15° increments every 5 min until an angle of 60° was reached. All studies were conducted at Vanderbilt University General Clinical Research Center, and all procedures were approved by the local Institutional Review Board.

Instrumentation

The following variables were measured: electrocardiogram (ECG), BP, respiration, and muscle sympathetic nerve activity (MSNA). The ECG of lead II was recorded with an ECG/Biotach amplifier (Gould Electronics, Cleveland, OH). The continuous finger BP waveform was measured by a photoplethysmograph-based volume-clamp method (39) with a finger cuff (Finapres, Ohmeda, Englewood, CO) on the middle finger of the nondominant hand and verified by brachial BP, which was obtained by an automated auscultometric device (Dinamap BP monitor, model 1846SX, Critikon, Tampa, FL) on the contralateral arm. The hand with the Finapres sensor was fixed at heart level. Respiration was measured by a pneumobelt (Pneumotrace II, UFI, Morro Bay, CA).

Microneurography

MSNA of the peroneal nerve was recorded randomly in either of the legs (51). A unipolar tungsten electrode with a 1- to 5-μm-diameter uninsulated tip and a 200-μm-diameter shaft (Frederick Haer, Bowdoinham, MA) was inserted into the muscle nerve fascicles of the peroneal nerve at the fibular head for multiunit recordings. Raw nerve activity was amplified with a total gain of 100,000, band-pass filtered from 0.7 to 2 kHz (662C-3 Nerve Traffic Analysis System, University of Iowa, Iowa City, IA). Satisfactory recordings of MSNA were defined by 1) heart pulse synchronicity, 2) facilitation during Valsalva straining and suppression during the hypertensive overshoot after release, 3) increases in response to breath holding, and 4) no change during tactile or auditory stimulation (13).

Data Preprocessing

Data were acquired at 5,000 Hz, 14-bit resolution using the Windaq data acquisition system (DI-720, DATAQ Instruments, Akron, OH) and analyzed off-line with custom software written in the PV Wave (Visual Numerics, Houston, TX) and MATLAB (Mathworks, Natick, MA) environments. QRS detection was performed using a modified Pan-Tompkins algorithm (38). Systolic and diastolic values in the continuous BP recordings were automatically identified as the maxima and minima for each cardiac cycle. All detections were visually verified.

A modified form of a technique described elsewhere (4, 14) was used to detect action potential spikes in raw MSNA recordings. A stationary wavelet transform with the Symlet 7 wavelet was used to decompose the MSNA into four bands of wavelet detail coefficients. Regions dominated by normally distributed noise in each band were identified as those with a kurtosis value <4. A kurtosis value of 3 indicates an ideal Gaussian distribution, and signal episodes with spike activity usually have higher kurtosis values. All coefficients with an absolute value less than four times the standard deviation of the identified noise regions were set to zero, and the denoised signal was reconstructed using the inverse stationary wavelet transform. Action potential spikes were then automatically detected from the denoised signal using a peak detector with a 3-ms time window.

We analyzed diastolic (DBP), systolic (SBP), and mean blood pressure (MBP) series, continuous respiration, and MSNA spikes detected over 200-s periods after 100 s of stabilization in the supine position and at 15°, 30°, 45°, and 60° HUT. DBP, SBP, and MBP variability series were formed by linear interpolation of the detected values onto regular 200-ms intervals (5 Hz). The detected MSNA spikes were used to form a spike rate series as previously described (3, 45). Briefly, a binary spike train was formed by insertion of delta functions into a 5-kHz sampled series at the detected spike times. The spike train was converted to a spike rate series by convolution with a Gaussian filter with a 3-Hz cutoff frequency (3). The spike rate signal was decimated by iterative convolution with an antialiasing Gaussian filter with a corner frequency of 0.4 times the current sample rate and downsampling by 2 until a sample rate of 4.88 Hz was reached. The resultant series was linearly interpolated at 5 Hz. The respiration signal was also decimated to 5 Hz after application of an eighth-order, antialiasing, Chebyshev type I low-pass filter with a corner frequency of 2 Hz. Each series was detrended by removal of the mean offset plus the VLF (0–0.04 Hz) components by filtering with a high-pass, finite-impulse response filter with a corner frequency of 0.04 Hz before any analysis or comparisons.

LF and HF time series were formed using a set of band-pass filters based on the Meyer wavelet, a modulated sinusoid with compact support (10), with approximate respective pass bands of 0.04–0.15 Hz (LF) and 0.15–0.5 Hz (HF) (see Ref. 49 for details of wavelet filtering).

Data Analysis

For study of the relation between each BP series (SBP, DBP, and MBP) and the MSNA spike rate and respiration, time-based cross-correlations were performed. In general, during the cross-correlation procedure, one time series, x, was delayed between the time constants τ_start and τ_end (in seconds) while the other series, y, remained stationary. After each delay, correlation between the two series was determined. First, the LF components of each series were compared, with LF_{spike rate} and LF_Resp as x and LF_SBP, LF_DBP, and LF_MBP as y. The procedure was repeated using the HF components of each series. For the HF_{spike rate} and respiratory series, the maximum absolute correlation was recorded for time delays between τ_start = 10 s and τ_end = 0 s, meaning that our only interest was the relation in which changes in respiration and HF_{spike rate} preceded changes in the BP. For the LF_{spike rate} and LF components of the BP series, two relations were investigated. The minimum negative cross-correlation value, termed the baroreflex-feedback relation, was studied between τ_start = 2 s and τ_end = −2 s. In this case, a negative time delay (e.g., τ = −2 s) would indicate that the spike rate is advanced in time. The positive maximum cross-correlation value, termed the feedforward relation, was studied between τ_start = 10 s and τ_end = 0 s.

Before the BP fluctuations were modeled, LF_{spike rate} was delayed by an amount equal to the feedforward delay and HF_Resp was delayed by an amount equal to the time shift that produced the maximum absolute correlation to HF_BP.

Data Predictive Modeling

The LF oscillations in sympathetic nerve activity and the HF fluctuations in respiration were used in a two-component, MA linear model to predict the fluctuations in BP. First, the LF model predicts the current value of LF_BP with use of the MA model, in which the output is a linear combination of p previous values of the LF components of the spike rate series (LF_{spike rate}). The term w_{spike rate} is added to indicate the presence of randomly distributed noise in the measurement of sympathetic spike rate

$${\mathrm{LF}}_{\mathrm{BP}}\left(n\right)=\sum _{p=0}^{p-1}a\left(p\right){\mathrm{LF}}_{\text{spike rate}}(n-p)+w_{\text{spike rate}}\left(n\right)$$ (1)

Similarly, the HF model predicts the current value of the HF BP series (HF_BP) with use of a linear combination of k previous values from the HF respiration series (HF_Resp). The term w_Resp is added to indicate the presence of random noise in the recording of respiration

$${\mathrm{HF}}_{\mathrm{BP}}\left(n\right)=\sum _{k=0}^{k-1}b\left(k\right){\mathrm{HF}}_{\mathrm{Resp}}(n-k)+w_{\mathrm{Resp}}\left(n\right)$$ (2)

The proposed total model (Fig. 2) is a summation of the outputs of the LF and HF models and predicts the current value of the detrended BP series.

Fig. 2.

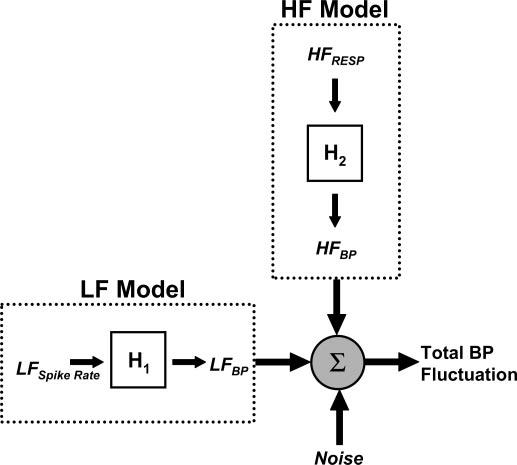
Components used to predict fluctuations in blood pressure (BP). H₁, moving-average (MA) model used to convert low-frequency (LF) spike rate (LF_{spike rate}) to LF_SBP; H₂, MA model used to convert high-frequency (HF) respiration (HF_Resp) to HF_BP. Sum of LF and HF models predicts total BP fluctuation.

The coefficients for each model were computed using the Steiglitz-McBride method (44), and the optimal values for p or k (model order) were selected as those that minimized the final prediction error (FPE) (42) with a maximum order of 25 coefficients, or 5 s of past data. The model is based on equidistant data because of the continuous nature of the spike rate and respiratory input signal

$$\mathrm{FPE}\left(p\right)={\sigma }_{\mathrm{E}}^2\frac{n+p+1}{n-p-1}$$ (3)

where ${\sigma }_{\mathrm{E}}^2$ is the mean squared error between the model and true output, n is the total number of points in the signal, and p is the current model order. This modeling technique was applied to components of the signals recorded during a baseline period and over increasing orthostatic load during graded HUT. The values predicted by each model were compared with the corresponding measured values by point-by-point linear regression analysis and by comparison of their power spectral density (PSD) in specific frequency ranges.

PSD

The Welch periodogram method (54) is used to compare the estimated PSD of the measured BP series with that of the BP series predicted by the total model. The 200-s signals, which were recorded and predicted during each angle of tilt, were divided into 60-s segments that overlapped by 50%. Each segment was detrended, multiplied by a Hamming window, and zero padded to the next power of 2. The power in the LF (0.04–0.15 Hz) and HF (0.15–0.5 Hz) ranges was estimated as the area under the PSD curve.

Statistics

Regression analysis was performed using a linear least squares fit, and the Pearson correlation coefficient (r) or the coefficient of determination (R²) was used to quantify the goodness of fit. Wilcoxon's signed ranks test was used to test for significant differences in the correlation between the components of three different BP series (SBP, DBP, and MBP) and the components of the sympathetic spike rate and respiration. This test was also used to determine whether significant differences existed between measured and model-predicted BP values at different degrees of HUT. P = 0.05 was defined as the significance level. Unless otherwise noted, values are means ± SE.

RESULTS

Correlations Between Oscillatory Components

A representative temporal relation between SBP and MSNA spike rate is shown in Fig. 3. The sample-to-sample correlation between the unfiltered SBP and spike rate does not reveal an inherent linear relation between the two series (r = −0.37; Fig. 3A, bottom). However, their LF components appear to have two distinct relations. A shift in the LF_{spike rate} series back in time by 0.4 s results in a strong negative correlation to LF_SBP (r = −0.87; Fig. 3B, bottom), which indicates the strength of the baroreflex-mediated feedback (high spike rates during low BP). A shift in the LF_{spike rate} series back in time by 5.2 s yields a strong positive correlation to LF_SBP (r = 0.70; Fig. 3C, bottom), which suggests a feedforward relation between the two series, meaning that an increase in LF_{spike rate} will produce a corresponding increase in LF_BP.

Fig. 3.

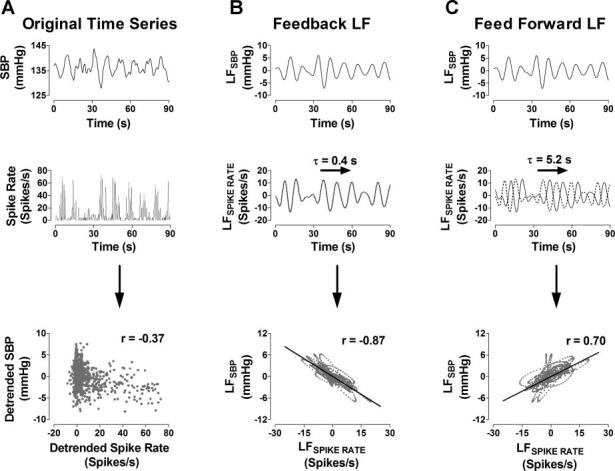
A: correlation between SBP and spike rate time series. B: baroreflex-mediated feedback relation between LF_SBP and LF_{spike rate}. C: feedforward relation between LF_SBP and LF_{spike rate}. Dashed lines, unshifted LF_{spike rate} time series. τ, Time constant.

A similar relation can be found between SBP, respiration, and their HF components (Fig. 4). The unfiltered time series have a lower correlation coefficient (r = −0.41; Fig. 4A, bottom), but after application of an HF-band wavelet filter, the sample-to-sample correlation improves significantly (r = −0.86; Fig. 4B, bottom).

Fig. 4.

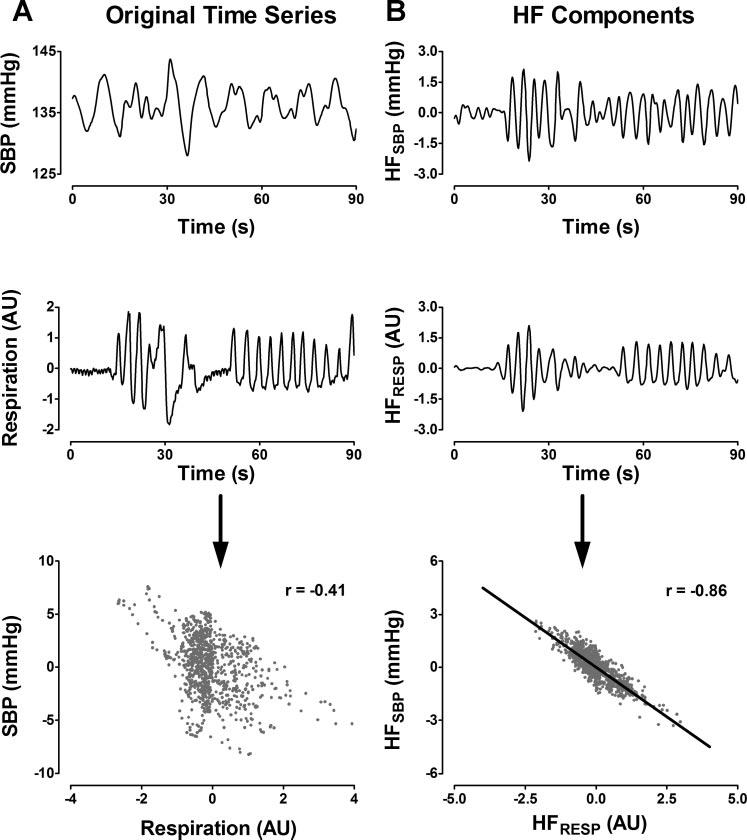
A: correlation between SBP and respiration time series (positive direction is inspiration). B: correlation between HF components of each time series. AU, arbitrary units.

A complete correlation analysis was performed between the LF and HF components of the SBP, MSNA spike rate, and respiration for all eight subjects during the baseline period (Fig. 5). The baroreflex-mediated feedback correlation (r = −0.69 ± 0.05) was significantly greater than the feedforward relation (r = 0.58 ± 0.03; Fig. 5, top left) between LF_SBP and LF_{spike rate}. However, the feedforward time delay (τ = 5.625 ± 0.15 s, increases in spike rate lead to increases in BP) was used in favor of the feedback time delay (τ = 0.375 ± 0.10 s, spike rate decreases with increase in BP) in the predictive model, because the intention of this model is to predict LF changes in BP from the LF changes in spike rate. HF_{spike rate} and HF_SBP are not significantly correlated (r = −0.22 ± 0.04; Fig. 5, top right). Conversely, HF_Resp and HF_SBP are highly correlated (r = −0.79 ± 0.04; Fig. 5, bottom right), whereas LF_Resp and LF_SBP have a significantly lower and less consistent correlation across subjects (r = 0.45 ± 0.08; Fig. 5, bottom left).

Fig. 5.

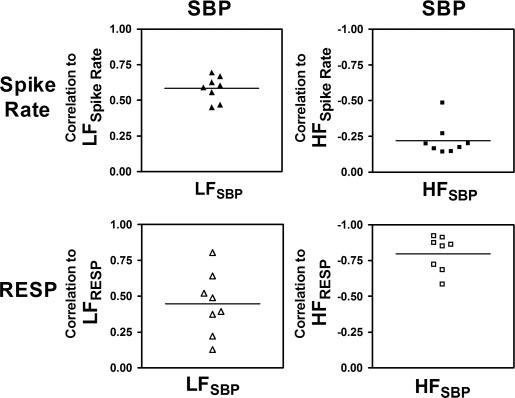
Correlations between LF (left) and HF (right) components of SBP and LF and HF components of spike rate (top) and respiration (bottom) at baseline.

When the correlation analysis was repeated using DBP and MBP, the feedback and feedforward correlations to LF_{spike rate} did not differ significantly from those of SBP (P > 0.05 in each case). LF_SBP (r = −0.58 ± 0.03, τ = 5.625 ± 0.15 s), LF_DBP (r = 0.62 ± 0.05, τ = 5.1 ± 0.14 s), and LF_MBP (r = 0.62 ± 0.04, τ = 4.8 ± 0.17 s) also had statistically similar feedforward correlations to LF_{spike rate}. However, the correlations between HF_Resp and HF_DBP and HF_MBP were significantly less than the correlation between HF_Resp and HF_SBP (P < 0.01 in both cases). Consequently, LF_SBP and HF_SBP will serve as the output of the predictive model.

Predictive Modeling at Rest in the Supine Position

The LF model (Fig. 2) used previously determined values of LF_{spike rate} to predict the current values of LF_SBP. The results of this model at baseline are displayed in Fig. 6A. The oscillations in the predicted LF_SBP follow those in the measured LF_SBP (Fig. 6A, top), and the two series have a strong linear correlation (r = 0.80; Fig. 6B, top). The HF model (Fig. 2) used previously determined values of the HF_Resp time series to predict the current values of the HF_SBP series. This model also demonstrates an ability to follow the measured HF_SBP (Fig. 6A, middle), and the measured and predicted sequences show a high positive correlation (r = 0.94; Fig. 6B, middle). When the outputs of the LF and HF models were summed, the resultant series was able to predict the total fluctuations in SBP (Fig. 6A, bottom). The sum of the LF and HF models produces a greater correlation to the measured SBP (r = 0.78; Fig. 6C, bottom) than either the individual LF (r = 0.70; Fig. 6C, top) or HF (r = 0.37; Fig. 6C, middle) models. (Statistical analyses for the supine model are discussed in the following section.)

Fig. 6.

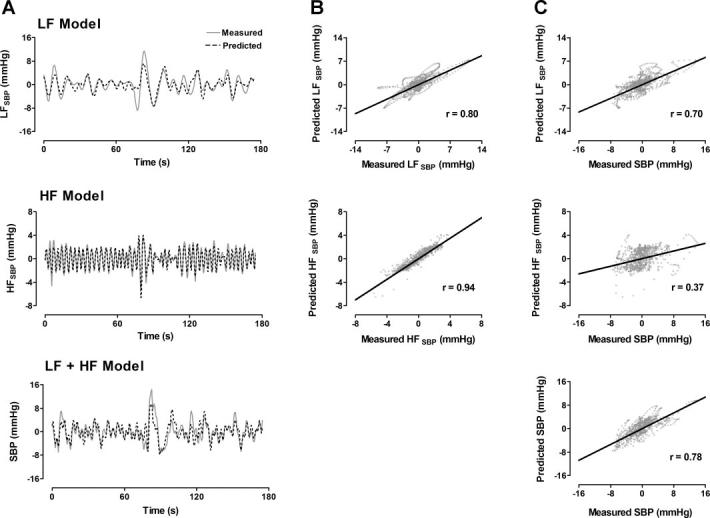
A: measured and model-predicted time series for LF component (top), HF component (middle), and total (LF + HF, bottom) detrended SBP. B: correlations between measured and predicted LF and HF time series in A. C: correlations between predicted time series in A and measured total SBP. LF_{spike rate} and HF_Resp were used as LF and HF model inputs, respectively (see Fig. 2).

Predictive Modeling During Orthostatic Stress

The LF, HF, and total models were also tested over increasing degrees of orthostatic stress during HUT. Two methods were used to predict the BP fluctuations during HUT: 1) the unmodified model coefficients computed at baseline were applied to the spike rate and respiratory sequences during HUT, and 2) the optimal coefficients were recomputed for each degree of HUT. Method 2 achieved significantly higher correlation coefficients than method 1 (P < 0.01 in all cases). Consequently, optimal model coefficients were computed separately during each degree of HUT.

The model is effective in predicting the total oscillations in the SBP components (Fig. 7, left), and the correlation between measured and predicted SBP fluctuations remains strong during increasing orthostatic load (Fig. 7, right).

Fig. 7.

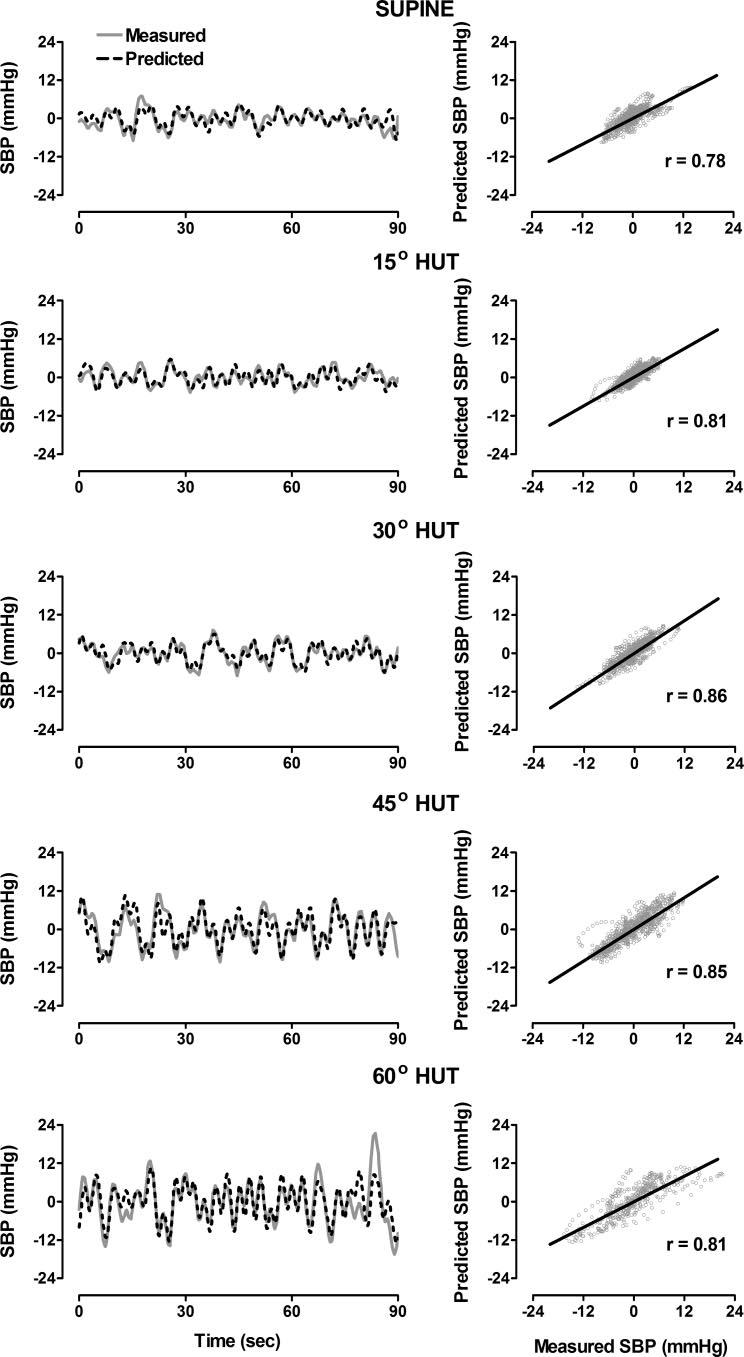
Left: measured and model-predicted detrended SBP in supine position and at 15°, 30°, 45°, and 60° HUT. Right: correlations between measured and predicted time series.

The mean value of the correlation coefficients between the measured and model-predicted LF_SBP for eight subjects at rest in the supine position (r = 0.74 ± 0.03) did not change significantly during increased orthostatic load (P > 0.05 in all cases). The average order used for the LF model was 14–19 coefficients (from 2.8–3.8 s of past data) but did not differ significantly (P > 0.05) over all degrees of HUT. The mean correlation for the measured and predicted HF_SBP (r = 0.89 ± 0.02) at baseline in the supine position was significantly reduced during 30° (r = 0.68 ± 0.04, P < 0.01) and 45° (r = 0.74 ± 0.06, P < 0.05) HUT but was not statistically different from baseline at 15° or 60° HUT. The average HF model order varied between 14 and 18 coefficients (from 2.8–3.6 s of past data) but did not differ significantly (P > 0.05) over all degrees of HUT. Figure 8 displays the correlation between total measured and model-predicted fluctuations in SBP during supine and graded tilt conditions. The mean correlations between the measured and model-predicted SBP fluctuations during each degree of tilt (r = 0.68 – 0.79) were not statistically different from one another. (Three subjects fainted during 60° HUT and were not included in the results at this tilt angle.)

Fig. 8.

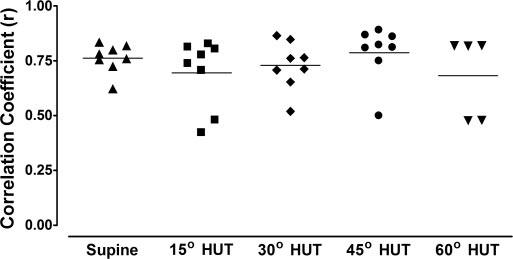
Correlations between measured and model-predicted SBP in supine position and at 15°, 30°, 45°, and 60° HUT.

The relation between the LF and HF power of the measured and predicted SBP signals for each subject during each degree of HUT is shown in Fig. 9. The slope of both regression lines is near 1 (0.9 for LF power and 1.1 for HF power) and the y-intercepts are 0, indicating a close identity of the model-predicted and measured values. The respective R² values for the regression analysis of the LF and HF powers indicate that 78% and 91% of the variability in power can be explained by the linear relation.

Fig. 9.

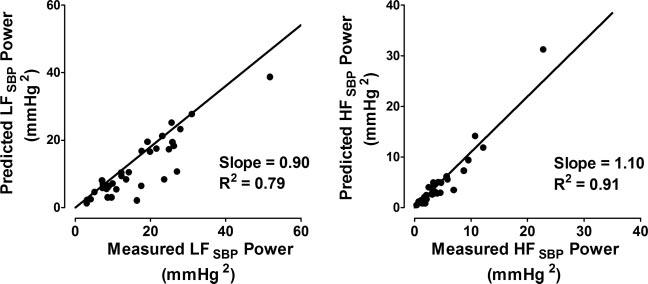
Cumulative relation between LF (left) and HF (right) power derived from measured and model-predicted SBP series in supine position and at 15°, 30°, 45°, and 60° HUT.

Zero-Order vs. Optimal-Order Model

When a simple slope model (model order = 0, 1 coefficient) was used to predict the components of the SBP from the components of the spike rate and respiration, the correlation between the measured and predicted values still indicated a strong linear relation (mean r = 0.60 for total model), but the correlations were significantly less than those computed using the optimal model order defined by the minimum FPE (P < 0.01).

DISCUSSION

In this study, we report three main findings: 1) LF_BP has a strong, linear, temporal correlation to LF_{spike rate}. 2) HF_SBP and HF_Resp also have a strong temporal correlation. 3) A large portion of the fluctuations in human BP can be explained using LF_{spike rate} and HF_Resp as the inputs to linear MA models.

LF_SBP-LF_{spike rate} Relation

A great deal of indirect evidence supports the hypothesis that LF changes in MSNA contribute to the LF changes in BP. For example, LF_SBP has been shown to increase during sympathetic activation, including orthostatic stress, such as lower body negative pressure (7, 41, 52) and upright tilt (9, 20), infusion of vasoactive drugs such as nitroprusside (41), and hypovolemia (26). Similarly, LF_SBP power has been shown to decrease significantly during ganglionic blockade in normal subjects (15, 32, 56) and in patients with essential hypertension and multiple system atrophy (15), indicating that it is largely mediated by the sympathetic nervous system. Finally, LF_SBP and LF_MSNA power exhibited similar increases and decreases during pharmacological infusions of sodium nitroprusside and phenylephrine, respectively (36), and coherence analysis has quantifiably demonstrated that patterns in LF_SBP and LF_MSNA are correlated at baseline (18, 20) and during HUT in humans (20), whereas HF_SBP and HF_MSNA are not highly correlated (18).

Conversely, a model of human BP by Myers et al. (31) showed that the sympathetic activity contributes little to the LF oscillations in BP. In the present work, however, we have demonstrated a strong temporal forward and feedback correlation between the LF fluctuations in SBP and the LF changes in MSNA spike rate in healthy humans at rest. The relation also improves when past values of LF_{spike rate} are incorporated to predict the present value of LF_SBP (Fig. 6, top) and is unaffected by increased orthostatic load.

The discrepancy in these results may be explained by several differences in protocol. 1) The previous model used normalized arbitrary units of integrated sympathetic burst area to form a sympathetic activity series, whereas our process involved detected sympathetic action potentials. The action potential detection is not based on arbitrary units and is less sensitive to the pass-band noise and artifacts that influence the burst area. 2) We used a physiological maneuver (HUT), rather than vasoactive or metabolic drugs, to induce an increased sympathetic state. These pharmacological agents may block or reduce the ability of the vasculature to accept modulatory sympathetic input, particularly at high doses when operating on the nonlinear portion of the baroreflex curve. 3) For the LF range, Myers et al. (31) elected to use 0.05–0.20 Hz, which is broader than the range recommended by the Autonomic Task Force (0.04–0.15 Hz) (46), although breathing was controlled at a higher frequency (0.25 Hz).

In the present work, we have identified two distinct time constants between LF_BP and LF_MSNA. The strongest linear relation between LF_SBP and LF_{spike rate} occurred near 0 s (average τ = −0.375 s), which results in a highly negative correlation between the two (MSNA is high at low BP, and vice versa). We have termed this the baroreflex “feedback” relation, although the change in LF_MSNA often precedes or occurs concurrently with changes in LF_SBP. Although several authors have computed the transfer function between sympathetic activity and BP in humans, the phase relation between these components is rarely reported (18, 20). Interestingly, Myers et al. (31) also identified the strongest linear relation between LF_SBP and LF_MSNA near 0 s and also reported a negative correlation. This finding is also consistent with the 180° neural arc phase relation reported in closed- and open-loop identification of the MSNA-BP relation in animals (22, 25). We hypothesize that this could be a sympathetic response to the change in BP (first deviation), rather than the absolute BP itself (17). This is supported by animal studies that have shown a strong response of baroreceptor afferents to changes in pressure (28).

In this previous model of LF_SBP using LF_MSNA, Myers et al. (31) chose to use this inverse, feedback relation as the input to their model, which necessitated the use of a negative model coefficient. Instead, we have elected to use the feedforward relation, defined as the maximum positive cross-correlation between LF_{spike rate} and LF_SBP (high values of MSNA ultimately leading to high values in BP). This relation is more closely related to the peripheral arc of the closed-loop model used in animal studies (25). The feedforward time delay was found to be ∼5.6 s, meaning a peak in LF_SBP occurred 5.6 s after a peak in LF_{spike rate}. This finding supports the reported peripheral arc phase values for animals, which are generally near 180° in the LF range (a 5-s time shift in a 10-s cycle) (25). It has been suggested that this phase shift is the combined result of the fixed physiological processing and transmission times from the baroreflex pathways, along with the slow response of the vascular smooth muscle to increased sympathetic activity (21). However, use of the feedback relation as the input to the LF model results in significantly higher correlations between the measured and predicted LF_SBP (r = 0.744 ± 0.03 vs. 0.81 ± 0.03, P < 0.025 for the mean feedforward and feedback time shifts).

HF_SBP-HF_Resp Relation

Oscillations in BP corresponding to respiratory rhythms have been well documented using spectral methods (2, 8, 16). The HF range of the BP variability contains the range of frequencies associated with normal breathing rhythms. Ganglionic blockade has little or no effect on HF_BP, suggesting that these oscillations are unrelated to the sympathetic activity and primarily due to changes in intrathoracic pressure caused by the mechanical aspects of respiration (15, 32, 56).

Here we report similar findings. We show that the temporal correlation between HF_SBP and HF_{spike rate} is low (r = −0.22 ± 0.04), meaning that vessels act as a neural low-pass filter (55), blocking transmission of the HF oscillations in MSNA to the arterial pressure. On the other hand, respiration has a strong mechanical influence on BP, evidenced by the high temporal correlation (r = −0.79 ± 0.04) between HF_SBP and HF_Resp at rest in the supine position.

The correlation of HF_SBP to HF_Resp was significantly higher than the correlation of HF_DBP or HF_MBP to HF_Resp (r = −0.45 ± 0.06 and 0.56 ± 0.08, respectively) at rest. This is consistent with the model proposed by Saul et al. (40), which showed that the mechanical effects of breathing would have a larger impact on SBP than on DBP because of the increased capacitance of the ventricles during systole.

Predictive Model

We have described how the fluctuations in SBP can be predicted by summing an optimized linear combination of past LF spike rate values, which predict LF_SBP, and past HF_Resp values, which predict HF_SBP. Using this approach, we were able to generate predicted SBP fluctuation series with good correlations to the measured values at baseline and during graded HUT. The relation between the power of the predicted and measured SBP also indicated that the models were able to explain a large majority of the fluctuations.

The optimized models produced predicted values that were more strongly correlated to the measured SBP fluctuations than a simple slope model, suggesting that some past information from the respiration and sympathetic spike rate contributes to the fluctuations in the SBP. Also, when model coefficients computed at baseline were used to predict the SBP oscillations during varying degrees of HUT, the correlations between measured and predicted SBP values were reasonable but significantly less than those predicted with the optimal models for each recording. This indicates that the relation between BP, sympathetic activity, and respiration changes during orthostatic load and cannot completely be explained by models created during baseline conditions. Indeed, some evidence suggests that the properties of the cardiac baroreflex (HR-BP relation) change during upright tilt (1, 33), but limited information about the sympathetic branch of the baroreflex has been reported during tilt. The results of the current model should be interpreted with caution, however, since a model will always have greater predictive value when its coefficients are reoptimized during each condition, as is the case here.

Limitations

VLF (0.004–0.04 Hz) fluctuations were excluded from the present model mainly because the length of each segment analyzed was too short (∼200 s) for accurate calculation of the influence of oscillations at this frequency range on the SBP. In this study, all subjects maintained a spontaneous breathing rate above 0.15 Hz (in the HF range); however, respiratory frequencies below 0.15 Hz would cause additional respiratory input in the LF range, and an LF model based solely on LF_{spike rate} could not accurately predict changes in LF_SBP. The present model takes into account only open-loop properties of the baroreflex system and ignores its closed-loop properties, i.e., feedback from the baroreceptors, which may also contribute to changes in BP and spike rate fluctuations (24). It has also been suggested that CO contributes to mean sympathetic activity (6) and BP fluctuations (31, 50). HR, one of the determinants of CO, has been associated with Mayer wave fluctuations (31). It has also been shown that respiratory fluctuations in BP can largely be explained by respiratory variation in the stroke volume (the other determinant of CO), independent of the vagally mediated changes in HR (50). Therefore, the addition of CO as an input parameter may help explain the remaining variability in the BP oscillations.

In conclusion, we have shown that a simple two-component model of neural sympathetic and mechanical respiratory input can explain the majority of BP fluctuation at rest and during orthostatic stress in a healthy subject.