Stability and Phase Separation in Mixed Monopolar Lipid/Bolalipid Layers

Abstract

The phase stability of a fluid lipid layer that is a mixture of conventional monopolar lipids and C₂₀ bipolar bolalipids was studied using a mean field theory that explicitly includes molecular details and configurational properties of the lipid molecules. The effect of changing the fraction of bolalipids, as well as the length of the hydrocarbon chain of the monopolar lipids, was probed. A phase separation between two liquid lipid phases was found when a mismatch exists in the optimal hydrophobic thicknesses of the pure bolalipid and monopolar lipid layers. The lipid mixture phase separates into a thin bolalipid-rich layer and a thicker monopolar-rich layer. The thin membrane phase is mainly composed of transmembrane bolalipid molecules whose polar heads are positioned at opposite membrane-water interfaces. In the monopolar lipid-rich phase, bolalipids are the minor component and most of them assume a looping configuration where both headgroups are present at the same membrane-water interface. For mixed layers that form a single lipid phase across all bolalipid concentrations, the hairpin-transmembrane ratio strongly depends on the hydrocarbon chain length of the monopolar lipid and the bolalipid concentration. The C-D bond order parameters of the different species have been calculated. Our findings suggest that the concentration-dependent phase transition should be experimentally observable by measuring of the order parameters through quadrupolar splitting experiments. The driving force for the phase separation in the monopolar lipid/bolalipid mixture is the packing mismatch between hydrophobic regions of the monopolar lipid hydrocarbon chains and the membrane-spanning bolalipid chains. The results from the molecular theory may be useful in the design of stable lipid layers for integral membrane protein sensing.

INTRODUCTION

Supported membrane-based sensors present a great opportunity for the functional characterization of integral membrane proteins (1–8). Successful realization of integral membrane protein sensors, however, requires the appropriate design of a supported lipid layer that is both stable and fluid. Since supported bilayer membranes are, in general, weakly bonded at the bilayer midplane, a significant failure mode is their delamination into monolayers under the environmental conditions encountered by the sensor (4). Therefore, mechanical stabilization of the lipid layer that will host the protein is needed as an initial step in sensor fabrication; however, the lipid layer must retain fluidity to enable the dynamic processes of most integral membrane proteins.

Archae are single-cell microorganisms whose lipid membrane combines stability and fluidity, allowing them to live in a variety of extreme habitats such as those containing high salt concentrations, low dissolved oxygen concentrations, and very high or low temperatures (9,10). The molecular origin of their unusual survival qualities is attributed to the presence of significant amounts of bolalipids in their membranes (11–13). Bolaform amphiphiles or bolalipids consist of two polar headgroups anchored by one, or more, flexible hydrocarbon chains. The robustness of bolalipid membranes suggests that bolalipid layers are excellent candidates for integral membrane protein sensor design and other biological applications requiring high membrane stability. Bolalipids derived from Archae are characterized by one or more membrane-spanning alkyl chains that are ether-linked to two glyceryl polar headgroups (14). The alkyl chains are typically derived from isoprenoid units. Synthetic bolalipid mimics share many of these structural motifs, including membrane-spanning chains and glyceryl ether linkages (4,11,15). Asymmetric bolalipids, which have different polar headgroups, were suggested to be potentially useful for biosensing and drug delivery applications (16).

In addition to the relevance of bolalipids to a variety of practical applications and to the understanding of the ability of Archae to survive in extreme environments, the behavior of bolalipid presents a very interesting fundamental question: How does the packing and the thermodynamics of lipid layers change by having two hydrophilic headgroups attached to one, or two, hydrocarbon chains? Having to place both headgroups in contact with water presents very stringent constraints on the conformational degrees of freedom of the chain molecules. The aim of the work presented here is to show how the restricted conformational degrees of freedom result in limited miscibility in mixtures of liquid monopolar lipids and bolalipids.

When analyzing lipid layer stability for integral membrane protein-sensing applications, two main factors should be addressed: permeability and prevention of delamination. Permeability in lipid membranes is related to the packing of the hydrocarbon chains. In the case of bolalipids, it was found that the permeability of the bolalipid layer is reduced as compared to that of a monopolar lipid bilayer (11). The molecular mechanism for the reduction of the permeability is, however, still not clear. Delamination can also be prevented by using bolalipids because they have the ability to adopt a transmembrane configuration that completely spans the hydrophobic region of the lipid layer by placing the polar headgroups at opposite membrane-water interfaces (4,15). In nature, bolalipids are generally macrocyclic structures, which increases the elastic modulus of the lipid layer (17). Structurally simple bolalipids, however, can also modify the lipid layer function and structure (18). It has also been found that the addition of short bolalipids to DMPC bilayers softens the membrane (19), presumably due to the packing mismatch described below.

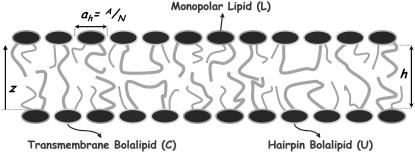
In a lipid aggregate, bolalipids have sufficient conformational flexibility to adopt a transmembrane or crossing configuration and a U-shaped or hairpin configuration in which the polar headgroups are in the same leaflet (see Fig. 1). The configuration that bolalipids assume has an enormous impact on the properties of the lipid aggregate. It has been shown that low concentrations of bolalipid molecules in a phospholipid vesicle can promote the flip-flop (i.e., membrane translocation) of the lipids if the bolalipids are in the transmembrane configuration (20). Bolalipids in the appropriate configuration can be used to place, with orientation and depth control, probes of membrane environment (21). Lipid interface mapping and determination of transmembrane protein regions using fluorescently-labeled bolalipids has also been demonstrated (21).

FIGURE 1.

Schematic representation of the mixed bolalipid-monopolar lipid system. The drawing represents a lipid layer that is a mixture of two different lipids: a bolalipid in concentration X_B and a monopolar lipid in concentration 1 − X_B. Bolalipids can assume two main configurations: a transmembrane configuration and a hairpin configuration, depending on the relative position of the polar headgroups.

A number of studies show that bolaform amphiphiles, when the flexible chain is long enough, assume a hairpin configuration at the air-water interface (11,22,23). The same was observed for bolaform electrolytes of the form R₃N ⁺ − (CH₂)_n − N ⁺R₃, with R = Me, n-Bu, when n = 12; this U-configuration was not observed when n = 4 or 8, simply because the molecules are more water-soluble and the alkyl chain is not long enough for a loop to exist (23). Flexible (eicosanedioyl 1,20-bis(pyridinium bromide) (C₂₀Py₂)) and rigid-group containing (phenyl 1,4-bis(oxyhexyl trimethyl ammonium bromide) (C₆PhC₆) and phenyl 1,4-bis(oxydecyl trimethyl ammonium bromide) (C₁₀PhC₁₀)) cationic bolalipids both adopt a hairpin conformation at the air-water interface when mixed with the conventional surfactant sodium dodecyl sulfite (24).

In contrast, bolaform amphiphiles preferentially assume a stretched configuration in micellar aggregates in aqueous solutions (25,26). Chemical relaxation, density, conductivity, and EMF experiments on C₁₂(NMe₃)₂ bolaform detergent micelles in aqueous solutions ruled out the possibility of an equilibrium between U- and stretched configurations and suggested that the latter will be preferred (25). A dominant stretching configuration was also observed in aqueous micellar dispersions of α,ω-type bolaform surfactants (26). In that study, the low capacity for solubilizing hydrophobic substances is attributed to the fact that the surfactants are unable to significantly swell due to their predominantly transmembrane configuration.

More recently, ²H NMR spectroscopy experiments were conducted to determine the relative transmembrane-hairpin population in planar C₂₈ bolalipid aggregates (27). The comparison of the spectra between lipid layers composed of different types of molecules suggests that the relative transmembrane-hairpin population in the bolalipid layers is 9:1.

Mixed lipid aggregates are of particular interest because of the design flexibility they provide and the superior properties they often possess (24). The design of mixed lipid-based devices requires a detailed knowledge of the behavior of the mixture as a function of composition. For example, a theoretical study of mixtures of C₁₁ and C₅ linear lipid chains showed that the aggregate composition plays a key role in determining the preferred geometry (28). The majority of bolalipid studies found in the literature deal with pure aggregates; there are only a few studies of mixed bolalipid and conventional monopolar surfactants (20,24,29). In this work, we show that the differential preferential packing between bolalipids and linear lipids is enough to drive phase separation between two liquid lipid layers.

In this study, a molecular mean field theory is used to evaluate the stability and concentration-dependent optimal properties of planar, fluid phase mixtures of bolalipid-monopolar lipids. The molecular theory explicitly incorporates conformational degrees of freedom of the lipid molecules as well as molecular details of the different lipid species. The length of the hydrocarbon chain of the monopolar lipid is varied to study the influence of hydrocarbon size mismatch between the linear and bolalipids on the stability of the mixture. The theory accounts for the inhomogeneous interactions felt by molecules within the lipid layer resulting from the hydrophobic packing repulsions as well as the interfacial energy between the hydrophobic lipid core and the hydrophilic regions that confine the lipid layer. The theory has been previously shown to quantitatively predict the structure and conformational properties of lipid layers (30–33), in agreement with experiments and molecular simulations.

In the next section, the molecular theory is presented. It follows a description of the numerical methodology used to solve the equations derived. A thermodynamic analysis approach was then used to evaluate the stability of the layer. Representative results obtained from this approach are presented for stable bolalipid-monopolar lipid mixed layers as a function of bolalipid concentration. Average conformational and structural properties for different-concentration mixed layers are then presented. Directions for future work are described in the final section.

THEORETICAL APPROACH

We are interested in studying the molecular packing of mixtures of monopolar and bolalipids. To this aim, we apply a molecular theory that enables the study of the conformational and thermodynamic properties of the mixtures. The theory is applied to the study of single phases of planar lipid layers. The stability of the mixtures, and thus the possibility for phase separation, is obtained by analyzing the thermodynamic stability of the mixtures. Namely, the curvature of the free energy as a function of composition, as it will be shown in detail below. Thus, when we describe two phases at coexistence or the onset of phase separation, we refer to conditions in which at a given composition the free energy of the homogeneous mixture is higher than that of two separated phases at different compositions. Therefore, we are not considering the interface (line) between the two phases, but concentrate on the stability of the homogeneous phases. The relevance for the experimental systems is that the possibility of domain formations of one phase in the other, can only occur when the homogeneous single phase system is predicted to be unstable. This type of approach has been recently applied to study liquid-ordered/liquid-disordered phase separation in saturated lipids-unsaturated lipids-cholesterol mixtures (34). We first derive the molecular theory followed by the thermodynamic analysis used to obtain the phase diagrams.

Molecular theory

Consider a fluid planar lipid layer system of thickness h, that is composed of N molecules of which a fraction, X_L, are monopolar or linear lipids and a fraction X_B are bolalipids (X_B + X_L = 1). To treat this problem, the contributions to the free energy of the lipid hydrophobic hydrocarbon chains and the hydrophilic polar headgroups are separated. The total free-energy density per lipid, 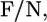is given by

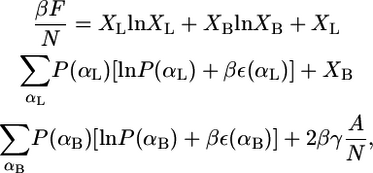(1)

where the two first terms represent the ideal entropy of mixing of the different lipids. The third and fourth terms are the conformational entropy of the monopolar and bolalipids, respectively. This contribution to the free energy results from the fact that lipids are flexible molecules and can assume many conformations depending on the state of each of their bonds, e.g., gauche-trans. P(α_I) is the probability of finding the molecular species I (I = L, B) in conformation α_I, while ε(α_I) is the total trans-gauche energy of that chain configuration and These two terms are the nonideal contribution to the entropy of mixing and the driving force for phase separation. The packing of the lipids depends very strongly on the overall composition of the mixture and therefore the distribution of conformers and the resulting conformation entropies are going to vary with composition (see Eqs. 4 and 5 below and discussion thereafter). The last term in Eq. 1 accounts for the interfacial free energy, at both interfaces, between the hydrophobic region within the lipid layer and the aqueous environment outside the layer. A is the total area of the interface, and γ is the water-hydrocarbon interfacial tension. The headgroup contribution to the free energy as expressed in the last term of Eq. 1 only accounts for the attractions between the hydrophilic headgroups.

Because there are two polar headgroups for each bolalipid molecule, 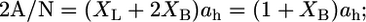where a_h is the average area per headgroup. Thus, the total free energy per lipid can be written as

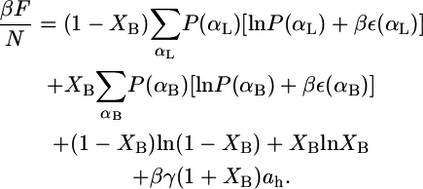(2)

The repulsive interactions within the hydrophobic core are modeled as hard-core repulsive interactions. This implies that the total lipid segmental density is assumed to be constant inside the fluid hydrophobic layer (i.e., the hydrocarbon chains of the lipid molecules completely fill the hydrophobic region of the lipid layer), leading to the packing constraint

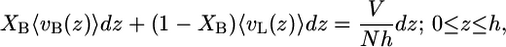(3)

which accounts for the repulsions within the hydrophobic region. The left-hand side terms of Eq. 3 are the fraction of the total volume per molecule occupied by bolalipid and monopolar lipids between z and z + dz. The expression 〈v_I(z)〉 dz is the total volume that species I chains occupy between z and z + dz. The brackets, 〈〉, represent ensemble averages over the corresponding probability density functions (pdfs).

The pdfs for the bolalipid and monopolar lipid molecules are obtained through minimization of the free energy (Eq. 2), subject to the hydrophobic packing constraint (Eq. 3). For this, Lagrange multipliers, βπ(z), are introduced to yield the pdf of bolalipid molecules

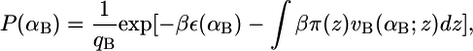(4)

where q_B is the partition function defined as 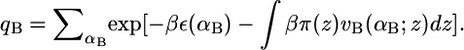This ensures that the probability density function of the bolalipid species is properly normalized. The expression v_B(α_B; z)dz is the volume that the hydrocarbon bolalipid chain in configuration α_B occupies between z and z + dz, such that 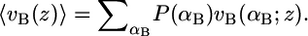A similar expression is obtained for the pdf of the monopolar lipids

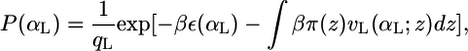(5)

where q_L is the partition function of the monopolar lipids and v_L(α_L; z)dz is the volume that a chain in configuration α_L occupies in the region between z and z + dz.

The Lagrange multipliers, βπ(z), can be interpreted as the z-dependent mean field-repulsive interactions acting on the molecule necessary to keep the density of hydrophobic region constant at the hydrocarbon value. They are associated with the inhomogeneous distribution of the different species. The βπ(z) values determine the optimal packing and they are a function of the composition of the film, having a direct consequence in the nonideal entropy of mixing in the film. For more detailed discussions of the interpretation of the Lagrange multipliers and the thermodynamic consequences of the incompressibility assumption, the reader is referred to the literature (28,30–32).

Lipid models and numerical methodology

The calculation of the total free energy of the system and, consequently, any quantity of interest, essentially reduces to the numerical evaluation of the z-dependent Lagrange multipliers, βπ(z). These are obtained by replacing the expressions for the pdfs of both lipids (Eqs. 4 and 5), into the packing constraint equation (Eq. 3). In practice, the z-direction is discretized into layers of thickness, δ, and integrals are replaced by sums over these layers. Thus, 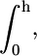where h is the lipid layer thickness, is replaced by 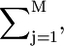where M is the number of layers in which the z-direction has been discretized. As a result of this discretization, a finite set of equations is obtained. These equations require as inputs the bolalipid concentration (X_B) and the volume distribution for the different configurations of both lipids. For the latter, a molecular model for the lipid species needs to be introduced. The lipid molecules are modeled as saturated hydrocarbon chains with a given number of carbon segments. Each CH₂ group has a volume, v = 27 ų, while the CH₃ groups are modeled as having a volume equal to 2v (35). The monopolar lipids have a principal chain with n_L carbon segments and a side chain containing n_L,s segments, bearing n_L − 1 and n_L,s − 1 CH₂ groups, respectively, and terminal CH₃ groups. Bolalipids, on the other hand, have a principal chain with n_B CH₂ groups and two side chains each having n_B,s − 1 CH₂ groups and a terminal CH₃ group. The number of carbon segments in a lipid principal chain, namely either n_B or n_L, is referred to as the size of the lipid. An example of the experimental system modeled here is a planar-supported bilayer that is a mixture of C₂₀BAS (4) and (18:0–16:0)PC. In our model, that is n_B = 20, n_B,s = 10, n_L = 18, and n_L,s = 16.

Since the goal of this study is to analyze the behavior of C₂₀ bolalipid-monopolar lipid mixtures as a function of the monopolar lipid size, the size of the monopolar lipid, n_L, is varied, keeping n_L,s = n_L − 2, while maintaining n_B fixed at 20.

The lipid chains are modeled using a rotational isomeric model (36) in which each carbon bond can assume three different configurations trans, gauche+, and gauche−. The gauche energy is higher relative to the trans conformation by k_BT. (The measured value of the difference between gauche and trans conformers is ∼0.8 k_BT at room temperature. However, previous work has shown that the exact value of this difference has no effect on the packing and thermodynamics of hydrocarbon chains packed in amphiphilic aggregates (37).) Thus, the internal energy of the conformation, ε(α_I), is the number of gauche bonds multiplied by k_BT. After a chain configuration, α_I, for species I is generated, the discretized volume distribution v_I(α_I, j), j = 1, 2, …, M is obtained by simply counting the number of segments contained within each layer and multiplying this by the volume of the group. In other words, v_I(α_I, j) = n_I(α_I, j)v, where n_I(α_I, j) is the number of segments contained within the planes z = (j − 1)δ and z = jδ for that particular chain and δ is set equal to 2 Å.

To generate the principal chains of the lipids, the first step is to generate the whole set of bond sequences for the given number of segments (n_I or n_I,s ; I = L, B). The Cartesian coordinates of each segment, for a given sequence, are obtained by matrix multiplication (36). Then, the first segment is translated to the origin and self-avoidance is checked. For bolalipid chains, attempts are made to translate the last bond to either the plane z = 0, for hairpin configurations or z = h, for transmembrane configurations. After this step, a number of rotations (typically 12 or 24) are attempted for both types of lipid molecules. Finally, if the chain is completely contained within the planes z = 0 and z = h, the configuration is accepted and the distribution of volumes is calculated.

For both lipid types, the side chains are generated independently as self-avoiding saturated linear chains of a given (n_B,s or n_L,s) number of segments. The total probability of a configuration is the product of the probabilities of the principal chain and its side chain(s). The contribution of the hydrophilic polar headgroups of the lipids is included as the surface tension term in the free energy (see Eqs. 1 and 2). The value γ is taken as 0.1 k_BT Å⁻², which corresponds to 41 dyne/cm at T = 300 K. This value is on the order of the experimental values for the oil-water interfacial tension (38).

The equations to be solved after discretization of the set of Eq. 3 are

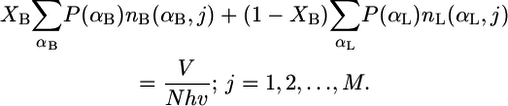(6)

Note that for a particular calculation at constant X_B, the right-hand side of Eq. 6 is constant for all j = 1, 2, …, M. The pdf of the bolalipid molecules reduces in its discrete form to

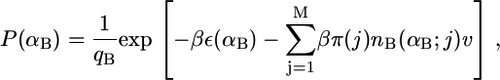(7)

and the partition function is now 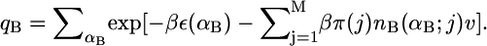A similar expression is obtained for the pdf of the monopolar lipid species.

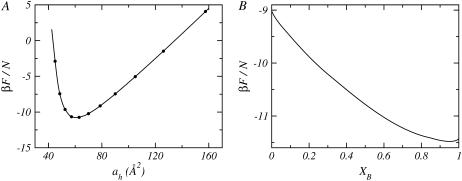
A single calculation for a given mixture, n_B − n_L, corresponds to a fixed bolalipid concentration and lipid layer thickness. This also fixes the area per lipid headgroup, a_h. At constant X_B, calculations for different thicknesses are performed. In this way, the free energy of the mixture can be represented as a function of the area per lipid headgroup, for each bolalipid concentration, as shown in Fig. 2 A. The optimal mixed lipid layer will be that which minimizes the free energy as a function of the area-per-lipid headgroup at the given X_B. If this procedure is repeated for different bolalipid concentrations, it is then possible to obtain the free energy as a function of X_B, which is displayed in Fig. 2 B. A graph similar to the one shown in Fig. 2 A, is obtained for each bolalipid concentration, from X_B = 0 to 1 using a step size of ΔX_B = 0.01. Since small concentration steps were used, the graph in Fig. 2 B is shown as a continuous curve rather than one containing discrete points. Any configurational or thermodynamic property of the lipid layer shown in this study is that of the optimal system at the given concentration, i.e., it corresponds to the area per lipid, at each composition, that minimizes the free energy (see Fig. 2 A).

FIGURE 2.

(A) Free energy per molecule as a function of the area per lipid headgroup, a_h, for a mixed lipid layer with n_L = 14 and X_B = 0.50. (B) The optimal free energy per molecule as a function of the layer bolalipid concentration, X_B, for a mixed lipid layer with n_L = 14. The optimal free energy is obtained from the minimum of a curve (as shown in A) for each composition.

Thermodynamic stability of the mixed lipid layer

The Helmholtz free energy for this two component system is given by

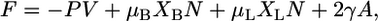(8)

where μ_B and μ_L are the chemical potentials of the bolalipid and monopolar lipids, respectively.

The packing constraints reduce the number of independent thermodynamic variables by one. Namely, the volume is completely filled by the hydrophobic tails of the lipids, then

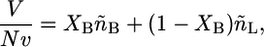(9)

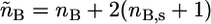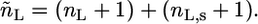where and The expressions 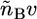and 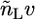are the total volumes occupied by a bolalipid and a monopolar lipid, respectively, while V = Ah is the total volume of the layer. By defining 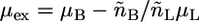and 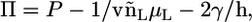the Helmholtz free energy reduces to

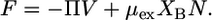(10)

The expression given by Eq. 10 is the Helmholtz free energy of an effective one-component system of X_BN molecules occupying a volume V with chemical potential μ_ex and pressure Π. It can be shown that the effective pressure, Π, and the excess chemical potential, μ_ex, must satisfy the same stability criterion as do the pressure and chemical potential in a one-component system. Therefore, analysis of Π − μ_ex curves provides a way to evaluate the stability of the lipid layer.

RESULTS

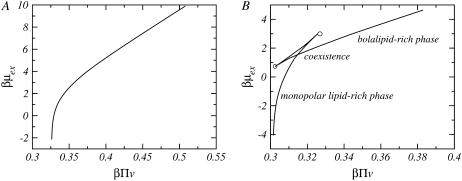
Fig. 3 shows the chemical potential as a function of the effective pressure for two different mixtures. The length of the monopolar lipids differs in the two cases shown. Each point along the curves in Fig. 3 corresponds to a unique calculation at a given bolalipid concentration, where the bolalipid concentration increases from left to right. For a short monopolar lipid (Fig. 3 A), there is only one value for the chemical potential for each pressure. Thus, the system is thermodynamically stable at all bolalipid concentrations. For a longer monopolar lipid such as n_L = 18 (Fig. 3 B, corresponding to 18:0–16:0 PC), there is a region where there are three possible values of the chemical potential for each pressure. At each pressure, the equilibrium system is the one with the minimal chemical potential. The intermediate chemical potential corresponds to a metastable region and the high chemical potential is the unstable region since the isothermal compressibility is negative in that region.

FIGURE 3.

The exchange chemical potential, βμ_ex, as a function of the effective pressure, βΠv, for n_B = 20 and two different monopolar lipids: (A) n_L = 12 and (B) n_L = 18. 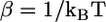and v is the volume of a CH₂ group. The concentration of bolalipids changes along the curves. In panel B, the points corresponding to coexisting phases and the onset of metastability are explicitly denoted.

There are two branches of lower chemical potentials; the one at lower pressures, Fig. 3 B, corresponds to monopolar rich layers while the one at higher pressures is for bolalipid rich layers. The intersection point between the two branches corresponds to the coexistence between the two phases. The two compositions of the intersection point, in the chemical potential-pressure curve, mark the coexistence between the two phases that define the binodal.

The two branches with intermediate values of chemical potentials shown in Fig. 3 B correspond to metastable regions. Namely, the free energy has the correct curvature with respect to the composition; however, there is a state of the same pressure with lower chemical potential that corresponds to the equilibrium state of the system. The two end-points of the metastable region, marked by circles in the figure, correspond to the beginning of the unstable region. The points that mark the boundary between the unstable and metastable region define what is called the spinodal. To summarize, if a layer has a concentration that is inside the spinodal, it is unstable and it will immediately phase-separate. A layer with a composition between the spinodal and the binodal is metastable and, therefore, it can be long lived; however, it will eventually phase-separate into two phases with the compositions marked by the binodal.

As an example, there is a pressure interval in Fig. 3 B, between β Πv values of 0.31–0.325, where there are three possible values of the chemical potential for each pressure. Each value of the chemical potential corresponds to a lipid layer containing a different bolalipid concentration. The equilibrium systems correspond to the lowest of the three values of chemical potential. The crossing point corresponds to the coexistence between the two phases (binodal), one rich in bolalipids and the other rich in monopolar lipids. The higher of the three chemical potentials corresponds to unstable systems with negative isothermal compressibilities. The intermediate values of the chemical potential are the metastable states that end in the spinodal points, marked as circles in Fig. 3 B.

To study the stability of the layer as a function of the size of the monopolar lipid, n_L is varied from 18 carbons with the side chain being 16 carbon segments (for example, 18:0–16:0 PC) to a very short lipid with 10 and 8 carbons in its principal and side chain, respectively (for example, 10:0–8:0 PC). The bolalipid is always n_B = 20 with two 10 carbon side chains n_B,s = 10 (for example, C₂₀BAS). The mixture is stable at all bolalipid concentrations when the monopolar lipids are short, i.e., n_L ≤ 14; however, when n_L ≥ 15, the system becomes unstable (or metastable) in a given range of bolalipid concentrations.

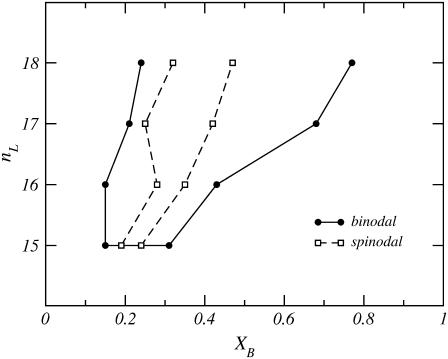
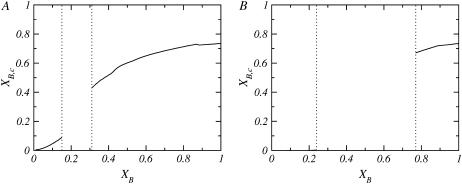
Fig. 4 shows a stability diagram of monopolar lipid and C₂₀ bolalipid. The mixed lipid layer shows a coexistence between two liquid phases of different compositions. The binodal of the phase coexistence is depicted as a solid line, while the dashed line represents the spinodal of the transition. The binodal curve separates the stable and metastable phase regimes, while the spinodal separates the metastable and unstable regions of the stability diagram. For example, if a mixed monopolar lipid-C₂₀ bolalipid layer is prepared where n_L ≥ 15 and X_B is within the binodal, the system is either unstable or metastable and will phase-separate into two different liquid phases of different bolalipid composition. At coexistence, the bolalipid concentration of each phase is given by the corresponding point in the binodal curve. One of these coexisting phases is rich in monopolar lipids; for a given n_L this composition is described by the point on the left side curve 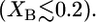The other liquid phase, described by the right side of the binodal curve, is enriched in bolalipids. It is important to mention, however, that the graphs in Fig. 4 are not real phase diagrams because n_L is a discrete parameter rather than a thermodynamic variable.

FIGURE 4.

Stability diagram for fluid phase mixtures of C₂₀ bolalipid (X_B) and monopolar lipids of varying chain length (n_L). The solid line joining the solid circles is the binodal and the dashed line connecting the open squares is the spinodal. The region outside the binodal corresponds to concentrations at which the mixture is stable. Inside the spinodal, the system is unstable. In the region in between the spinodal and binodal the system is metastable. The points in the binodal curve represent the bolalipid concentrations of stable mixed layers at coexistence.

The stability of the layer depends on the size of the monopolar lipid, n_L, and the concentration of bolalipids, X_B. For n_L ≥ 15, the mixture is always stable at high or low bolalipid concentrations, but in between it becomes nonstable. The width of the range of bolalipid concentrations for which the mixture is not stable increases as the size of the monopolar lipid increases. The fact that the mixture is stable when n_L ≤ 14, and that the size of the unstable region increases with the length of the monopolar lipid chain, suggest that the driving force for the phase separation is the size matching of both lipids in the layer and the constraint that one of those lipids is a bolaform molecule. This hypothesis is supported by the theoretical evidence presented below.

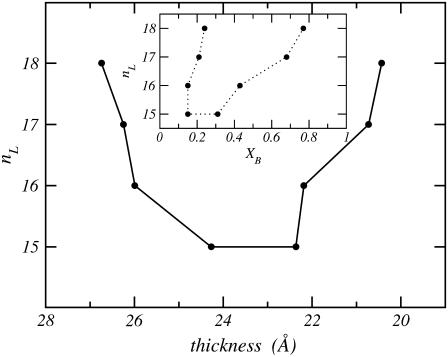
Fig. 5 shows the thickness of the layer in the two phases at coexistence for each length of the monopolar lipid. Note that the x axis is inverted, so that the bolalipid-rich phase is displayed on the right. The graph shows that for a given n_L, the point on the right is the thickness of the bolalipid-rich layer at coexistence, while the point on the left is the thickness of the monopolar-rich layer at coexistence. The corresponding composition of the two phases can be obtained by looking at the binodal, shown in the inset.

FIGURE 5.

The thickness of the mixed lipid layer corresponding to different monopolar lipid chain length, n_L, for concentrations that correspond to coexistence between the two liquid phases. The x axis is inverted so that points on the right correspond to the bolalipid-rich phase as in the binodal stability diagram (i.e., Fig. 4, also shown in the inset).

Figs. 4 and 5 demonstrate that for n_L ≥ 15, the phase separation occurs between a thin bolalipid-rich layer and a thicker monopolar lipid-rich layer. The thickness of a stable layer is found to be a monotonic function of the composition (results not shown) taking smaller values in the bolalipid-rich phase than in the monopolar lipid-rich phase. In other words, for a given n_L, the points in Fig. 5 are, from left to right, the minimum thickness for a monopolar lipid-rich layer and the maximum thickness for a bolalipid-rich lipid layer, respectively. This cannot be seen in Fig. 5, where only the thicknesses of the layers at the coexisting concentrations are shown. The thickness of a pure bolalipid n_B = 20 is calculated to be 18.8 Å, while those of pure monopolar lipid bilayers are 30.1, 28.4, 27.1, 26.1, 24.3, 22.7, 21.2, 20.1, and 18.4 Å for n_L from 18 to 10, respectively. These values for the thicknesses of the lipid layers represent the size of the hydrophobic region only, and are not to be compared with experiments reporting the total thickness of lipid layers that include both the hydrophobic and hydrophilic regions of layers which are in contact with an external aqueous medium.

The difference in thickness between the coexistence values in Fig. 5 decreases as the hydrocarbon chain-length size of the monopolar lipid decreases, further supporting the idea that the phase transition is associated with the relative size of the lipids.

Since bolalipids can adopt two different sets of conformations, hairpin or transmembrane, their preferred conformation should, in principle, be composition-dependent. Fig. 6 shows the fraction of transmembrane bolalipids, X_B,c, as a function of bolalipid concentration for two cases where the lipid mixture is composed of different monopolar lipids, n_L = 15 (Fig. 6 A) and n_L = 18 (Fig. 6 B). The empty region between the dotted lines corresponds to the region where the system is not stable. In both cases, the concentration of transmembrane molecules is very low in the monopolar-rich phase, being zero in the case of the monopolar lipid where n_L = 18 (Fig. 6 B). In the bolalipid-rich phase, for both cases, the majority of the bolalipids are in the transmembrane configuration. The rest of the monopolar lipids studied for which phase separation is predicted, show a behavior similar to the n_L = 15 and n_L = 18 cases (shown in Fig. 6).

FIGURE 6.

Fraction of transmembrane bolalipids, X_B,c, as a function of the total fraction of bolalipids in the layer, X_B, for different monopolar lipids: (A) n_L = 15 and (B) n_L = 18. In both cases, the region between the vertical dotted lines corresponds to the concentrations where the layer is nonstable.

The thickness of the mixed lipid layer also determines the conformation that the bolalipids assume within the mixed aggregate. Consider, for example, the case where n_L = 18. The mixed layer comprises one type of molecule that, when pure, forms a layer ∼19 Å thick and another that forms a bilayer ∼30 Å thick. When a few n_B = 20 molecules are added to a bilayer composed of n_L = 18 molecules, the bolalipid molecules will be forced to assume a hairpin shape, since the fully stretched length of the bolalipid is shorter than the thickness of the layer. The mixed layer incorporates a small amount of the bolalipid molecules undergoing a slight reduction in layer thickness. When the concentration of bolalipids reaches the binodal value (X_B ∼ 0.2), however, this compromise in membrane thickness is no longer favorable for the monopolar lipids. Since a thicker membrane is preferred by the monopolar lipids, the system must phase-separate into layers of different membrane thicknesses, lipid compositions, and bolalipid conformations. The same argument is also valid starting from pure bolalipid layers. Bolalipid-rich membranes are thinner because the majority of the bolalipid molecules are in the membrane-spanning configuration. The addition of monopolar lipid molecules to a bolalipid-rich layer results in a membrane thickness increase. Transmembrane bolalipid molecules are not as compliant with respect to changes in membrane thickness, as are hairpin bolalipid conformations or monopolar lipids. Then some compositions in the monopolar lipid-rich phase are too thick for even the fully extended all-trans bolalipid conformation to exist. Thus, when the concentration of monopolar lipids is sufficiently high, increasing the membrane thickness becomes unfavorable for the bolalipids and the system phase-separates.

The situation is completely different for n_L ≤ 14, where the mixed lipid layer is stable at all bolalipid concentrations. Here, the pure layers of the two lipid components of the mixture are of comparable thickness. For example, for a mixture where n_B = 20 and n_L = 10, the difference in hydrophobic thickness between the pure layers is <0.5 Å. Therefore, these mixtures can accommodate any bolalipid concentration by just slightly changing the thickness of the lipid layer. This thickness change may also be accompanied by a variation in the transmembrane/hairpin conformation ratio.

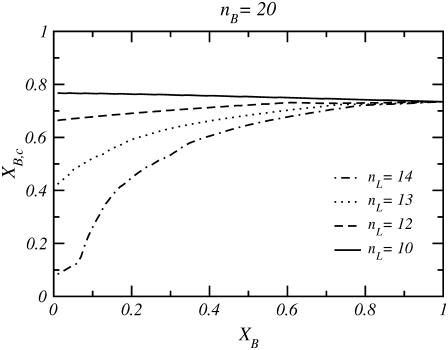
Fig. 7 shows the fraction of transmembrane bolalipid conformations, X_B,c, for cases where the monopolar lipid is short enough that the mixed layer is stable at all X_B values. In all cases, when the concentration of bolalipid molecules is high, the fraction of transmembrane bolalipids is also high (X_B,c ∼ 0.75) and independent of the size of the monopolar lipid. This behavior arises from the fact that as X_B goes to one, X_B,c has to converge to the value of a layer composed of only bolalipids. At lower bolalipid concentrations, X_B,c is highly dependent on the length of the monopolar lipid such that X_B,c decreases as n_L increases. Two cases are particularly interesting. The first is the n_L = 10 case, where X_B,c is almost constant for all bolalipid concentrations because the thickness of the mixed layer changes very little (<0.5 Å) from X_B = 0 to X_B = 1. The second is for n_L = 14, where a dramatic decrease in X_B,c is observed for bolalipid concentrations less than X_B ∼ 0.2; as X_B decreases, the transmembrane configuration becomes increasingly unfavorable. In this case, the thickness mismatch between the pure lipid layers, X_B = 0 and X_B = 1, starts to be significant.

FIGURE 7.

Fraction of transmembrane bolalipids, X_B,c, as a function of the total fraction of bolalipids in the layer, X_B, for four different short monopolar lipids. In these cases, the layer is stable at all bolalipid concentrations.

There is little experimental data on the relative transmembrane-hairpin populations in pure bolalipid planar layers and none on mixed lipid layers. Cuccia et al. (27) performed ²H NMR spectroscopy experiments to evaluate the transmembrane-hairpin ratio in bolalipid layers. Two DMPC molecules (n_L = n_L,s = 14) were coupled to form a bolalipid molecule with n_B = 28 and n_B,s = 14. Their results show that in a fluid lipid layer formed by these bolalipids, 90% of them adopt the crossing configuration. Our theoretical calculation is that in a n_B = 20 and n_B,s = 10 pure layer, a fraction X_B,c ∼ 0.75 will assume the transmembrane conformation. This result is in good agreement with the results of Cuccia et al. (27), the estimate of ∼80% transmembrane conformation determined by Raman spectroscopy of a bisphosphate C₂₀ bolalipid (11) and the expectation that X_B,c be a function of n_B.

The orientation of each carbon segment in the bolalipid molecule depends on the order within the layer and, in principle, on whether the lipid adopts a transmembrane or hairpin configuration. The carbon-deuterium order parameters, S_CD, can be used to quantify the orientation of the different bonds within each molecular species in the lipid layer (39–41). Quadrupolar nuclear magnetic resonance can be used to measure the order parameters of selectively deuterated C-H bonds (27,42). S_CD is a local chain property, meaning that it changes from bond to bond. The order parameter for the k^th CH₂ is defined as 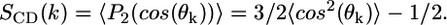θ_k is the angle between the z axis (perpendicular to the surface) and a vector from the k^th carbon in the chain to the ²H bound to it. P₂ is the second Lagrange polynomial. When −2S_CD(k) is close to 1, then bond k is preferentially oriented perpendicular to the plane of the surface. On the contrary, if −2S_CD(k) has a value near 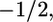the k^th bond is oriented parallel to the surface. When −2S_CD(k) is close to zero, the bond is randomly oriented. In principle, the complete spectrum of order parameters for a particular lipid chain can be obtained by performing a set of experiments in which different carbons along the hydrocarbon chain have been deuterated.

Fig. 8 shows the orientational order parameters of a mixed layer of lipid molecules given by n_B = 20 and the shortest monopolar lipid studied in this work, n_L = 10. For this mixture, the layer is stable at all bolalipid concentrations because the thickness of pure layers of each component roughly match. Two different bolalipid concentrations are shown in Fig. 8. The orientation of the different species do not vary in a significant fashion from a 90% bolalipid layer (Fig. 8 A) to a 10% bolalipid layer (Fig. 8 B). This fact is directly related to the stability of the layer at all bolalipid concentrations and it shows that the packing of both types of lipids is very similar at all compositions.

FIGURE 8.

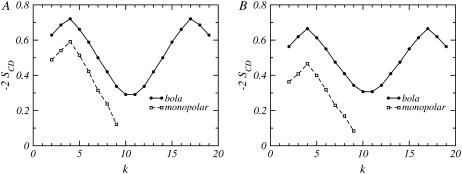
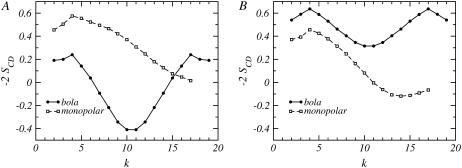
The orientational bond order parameter, −2S_CD, as a function of the carbon number along the lipid chains, k, for a mixture where n_B = 20 and n_L = 10, and the bolalipid concentrations are (A) X_B = 0.1 and (B) X_B = 0.9. Circles joined by a solid line correspond to the bolalipid while the values for the monopolar lipid are represented by open squares joined by a dashed line.

Fig. 9 represents the orientational bond-order parameters for a bolalipid-monopolar lipid mixture where n_B = 20 and n_L = 18. The two concentrations shown in Fig. 9 correspond to different stable liquid phases (see Fig. 4). The concentrations of the mixtures shown in Fig. 9 are stable since they do not correspond to the coexistence compositions. For illustrative purposes, concentrations in the middle of each phase have been chosen. Our results show that there is a small change in the shape of the curves for the monopolar lipid, between the two very different compositions shown in Fig. 9, A and B. The overall order is smaller and the change is most noticeable for the segments at the very end of the linear chain for the monopolar lipid in the layer with a large concentration of bolalipids (Fig. 9 B). The change in packing for the monopolar lipid is due to fact that the two cases shown in Fig. 9 correspond to very different hydrophobic thicknesses. Essentially, the monopolar chains adapt to layers of different membrane thicknesses with only a minor reduction in the degree of ordering along the chain. In contrast, there is a qualitative and large quantitative difference in the order parameters of the bolalipid chains for these two compositions. In the monopolar lipid-rich phase, the carbon segments close to the headgroups are oriented slightly perpendicular to the surface, while the middle segments are mostly parallel to the water-air interface. The preferred orientation for all the carbons of the bolalipid is perpendicular to the surface in the bolalipid-rich phase.

FIGURE 9.

The orientational bond order parameter, −2S_CD, as a function of the carbon number along the lipid chains, k, for a mixture where n_B = 20 and n_L = 18 for (A) a monopolar lipid-rich phase at X_B = 0.1 and (B) a bolalipid-rich phase at X_B = 0.9. The solid line joining the circles represents the bolalipid and the dashed line joining the open squares corresponds to the monopolar lipid.

The orientation of the bolalipid segments in the monopolar lipid-rich phase (Fig. 9 A) is due to the prevalence of hairpin conformers (see Fig. 6 B, at low X_B values), which causes the midsegments of the bolalipid to be oriented parallel to the surface. This is the only way that the bolalipids can pack in this film thickness. On the other hand, a majority of transmembrane bolalipids is predicted in the bolalipid-rich phase (see Fig. 6 B, for large X_B values), which leads to a large proportion of carbon segments that are preferentially perpendicular to the surface, as seen in Fig. 9 B.

The fact that the packing and the resulting bond-order parameters for the bolalipid chains differ so much in both phases suggests a way that the liquid-liquid phase separation can be experimentally observed. If a mixture is prepared containing a bolalipid concentration that produces an unstable mixed layer above the gel transition of both lipids, C-D bonds near the middle of the bolalipid chain (k ∼ 10) should produce ²H NMR spectra that have four frequency peaks corresponding to two different values of the order parameter of the deuterated group. Such a spectrum will be clear evidence of the presence of two immiscible liquid phases.

DISCUSSION AND CONCLUSIONS

A molecular mean field theory that enables the study of the structure and phase behavior of fluid lipid layers has been applied to study planar layers that are composed of a mixture of conventional monopolar lipids and bipolar bolalipids. The chain length of the monopolar lipid species is varied from n_L = 10 to n_L = 18, with a (n_L − 2)-long side chain, while the bolalipid size is maintained as a saturated chain of 20 carbon segments, n_B = 20, having two 10-carbon-long side chains.

The stability (phase) diagram for the bolalipid-monopolar lipid mixed layer has been predicted. For the short monopolar lipid cases where n_L ≤ 14, the lipid mixture is stable at all concentrations of bolalipids. For longer monopolar lipid cases where 15 ≤ n_L ≤ 18, a concentration-dependent phase separation between two liquid lipid phases is observed. The mixture is stable at both low and high bolalipid concentrations, whereas phase separation is predicted at intermediate concentrations. The two phases in which the system phase-separates are a phase rich in bolalipid molecules and another phase that is rich in monopolar lipids. The bolalipid concentration range in which the system is not stable increases as the size of the monopolar lipid increases.

The hydrophobic thickness of membranes has enormous importance in many biological processes. The fact that the size of the hydrophobic region of integral membrane proteins and host membrane must match (43) makes thickness matching a potential source of integral membrane protein activity regulation by cellular regulation of lipid synthesis (44). Membrane thickness is also associated with permeability, such that thinner membranes are more permeable (45). Using the molecular model presented in this study, the thicknesses of mixed bolalipid-monopolar lipid layers has been calculated for all bolalipid concentrations and for monopolar lipids where n_L = 10, …, 18. In particular, the relative thickness of the pure lipid layers plays a key role in the phase separation. The thicknesses of the coexisting lipid layers for the cases where there is a phase transition have been also calculated. The monopolar lipid-rich phase corresponds to a thicker lipid layer than that found for the bolalipid-rich phase. Phase separation is found for the monopolar lipids whose pure layer exhibits a mismatch in thickness relative to the ∼19 Å thickness of the pure bolalipid layer. The difference in thickness between the two phases decreases as the size of the monopolar lipid decreases, until the mixture becomes stable across all compositions when the thicknesses of the two pure lipid layers roughly match.

In the design of lipid layers for biotechnical applications, it may be necessary to know the conformation of the lipid constituents. Knowing the conformation of the bolalipid chains can be used, for example, to locate fluorescent groups or other probes with the desired depth and orientation to examine the hydrophobic region of the lipid layer (21). Thompson and co-workers (4) and Halter et al. (15) have suggested that lipids that span the hydrophobic layer are appropriate for several biotechnical applications because they can stabilize the membrane. Forbes et al. (20) showed that bolalipids in the transmembrane configuration promote membrane translocation, while hairpin conformations do not. The configurational properties of the bolalipid-monopolar lipid mixture depend on the size and concentration of the lipids. In particular, the configurational properties of the mixture in the bolalipid-rich phase are different from those in the monopolar lipid-rich phase. The bolalipid-rich phase is comprised of a majority of bolalipids in the transmembrane conformation. In the monopolar lipid-rich phase, the bolalipid fraction is small, but the overwhelming majority of these are found in hairpin configuration. Stable mixed lipid layers comprised of bolalipids and short monopolar lipids are found to contain predominantly transmembrane conformations of bolalipid at high X_B, regardless of the size of the monopolar lipid. For lower bolalipid concentrations, the fraction of transmembrane conformations decreases as the size of the monopolar lipid increases.

The physical phenomenon controlling the phase behavior of the system is directly related to the hydrophobic thickness of the pure lipid layers of each component. The C₂₀ bolalipid layer is thin relative to typical lipid bilayers due to the short transmembrane chain. Since the thickness of the bolalipid layer is roughly comparable to that of the shortest monopolar lipids in this study (C₁₀ to C₁₄), their binary mixtures are stable at all compositions. On the contrary, C₁₅-C₁₈ monopolar lipid bilayers are thicker than the C₂₀ bolalipid layer. In these mixtures, the layer is stable for bolalipid concentrations close to zero or one. This is because mixed layers with an excess of one component can slightly increase or decrease the membrane thickness of their layers to accommodate the minority component. The same argument explains why no phase separation was found for the short monopolar lipid mixtures where the membrane thickness of the pure bolalipid and pure monopolar layers are similar.

Another constraint that must be considered is the fact that one of the components is a bipolar molecule. In a bolalipid layer, most of the bipolar lipids prefer a transmembrane configuration, which has a dual effect: first, the thickness of the bolalipid layer will be much smaller than that of a lipid bilayer composed of a monopolar lipid with the same number of carbon segments. In addition, a stable, mixed lipid layer, rich in bolalipid molecules, cannot significantly increase its thickness when the concentration of monopolar lipids is increased because bolalipids in a transmembrane conformation do not easily fit large thicknesses. The influence of the transmembrane configuration is also reflected in the binodal curve shape. The curves that separate the bolalipid-rich and monopolar lipid-rich phases from the metastable region show different trends. A monopolar lipid-rich layer becomes metastable for n_L ≥ 15 when X_B ∼ 0.2. In other words, when X_B increases, the transmembrane configuration becomes increasingly favorable due to the mixed layer thickness decrease and hydrophobic mismatch between the monopolar lipids and the transmembrane bolalipids drives the phase separation. On the other hand, the concentration at which a bolalipid-rich layer becomes metastable strongly depends on n_L because the amount of monopolar lipids that a bola-rich membrane can accommodate depends on the size of the monopolar lipid molecule.

The C-D bond orientational order parameters for different deuterated species in mixed bolalipid-monopolar lipid systems have also been calculated. For mixtures that are stable at all compositions, the order parameters of both monopolar lipids and bolalipids do not significantly change at different bolalipid concentrations. For the longer monopolar lipids, when phase separation is predicted, there is a small but appreciable change in the order parameter of the bolalipid-rich and monopolar lipid-rich phases that is related to the different thicknesses of the lipid layers. In those cases, the change in the C-D order parameters of bolalipids residing in the two different phases is dramatic, which may be associated with the difference in transmembrane-hairpin populations present in the two phases. The large difference in the C-D order parameters of bolalipids in the different phases suggests that the liquid-liquid phase transition can be experimentally observed by quadrupolar NMR experiments.

The theoretical approach that we have used enables the study of liquid-liquid phase separation at a fixed temperature. This can be seen in the free energy expression where the only attractive term is the surface tension. Therefore, the phase diagram presented is not in the normal temperature-density plane, but in the chain length-composition plane. Clearly, chain length is not a thermodynamic variable, but it is a molecular property that can be controlled. The work presented here demonstrates the importance that packing has on the stability of lipid layer, and how the stability of liquid lipid layers depends on molecular architecture. The study of the phase diagram as a function of temperature and the ability to predict gel phases can be obtained as a straightforward generalization of the free energy expression (Eq. 1), as it was demonstrated elsewhere (33,34). This work is currently underway.

Though extremely controversial, coexistence between two liquid phases has been reported for mixtures of high melting point lipids and cholesterol (34,46–50), where the liquid-liquid coexistence is between two phases of different degrees of lipid order. The bolalipid- and monopolar lipid-rich phases also showed an important difference in the degree of order of the lipid constituents, although this is associated to different concentrations of the transmembrane bolalipids instead of cholesterol molecules. The two factors determining the coexistence of these liquid-liquid phases are the hydrophobic mismatch and the rigidity provided by the transmembrane configuration. Indeed, those factors are also present in the ternary lipid-lipid-cholesterol mixtures and the nature of the liquid-liquid coexistence between the bolalipid-rich and monopolar lipid-rich phases might be analogous to the liquid order-liquid disorder phase separation.

Currently, we are extending the theory described here to study the influence of chain length mismatching in mixtures of monopolar lipids (PCs). The question being addressed is whether the hydrophobic mismatch in mixtures of monopolar lipids is capable of forcing liquid-liquid coexistence, or whether a rigidity constraint such as the bipolarity of bolalipids is needed.