Analysis of Functional Signaling Domains from Fluorescence Imaging and the Two-Dimensional Continuous Wavelet Transform

Abstract

A technique that utilizes the one-dimensional (1D) continuous wavelet transform (CWT) of linearized fluorescence resonance energy transfer (FRET) microscopic images has been extended to identify signaling macro- and microdomains in cell plasma membranes by incorporating the two-dimensional (2D) CWT of time-lapse fluorescence and/or FRET images. Signaling domains were identified from differences in wavelet coefficient matrices, and there was good agreement between the 1D and 2D methods on examining a), static fluorescent images of COS1 cells expressing calmodulin kinase II fused with enhanced yellow fluorescent protein, and b), time lapse FRET images of reporters of protein kinase C (PKC) (PKC activity reporter) and adenylyl cyclase dynamics (cAMP) activity within COS1 plasma membrane confines after stimulation by phorbol-12,13-dibutyrate or forskolin, respectively. The proposed 2D wavelet-based image analysis effectively detected phosphorylation/dephosphorylation signaling microdomains (PKC) as well as those reflective of cAMP without the limitation of requiring linearized signals imposed by the 1D approach. Illustrating successful application to the analysis of intracellular compartments, the 2D CWT was further used to identify signaling domains of cAMP response element-binding (CREB)-induced transcriptional activation in the nuclei of COS1 cells, which could not be achieved with the 1D approach. This technique may be eventually used to characterize complex cellular signaling and protein-protein interactions within localized cytoplasmic domains.

INTRODUCTION

The plasma membrane of cells may be viewed as a fluid mosaic of functional microdomains implicated in a number of critical cellular processes, such as signaling, adhesion, and trafficking (1). Membrane components such as lipid rafts and caveloae serve as examples of nanometer-scale structures that provide environments rich in proteins and lipids that are involved in cell signaling pathways (2,3). A number of microscopic techniques are available to study compartmentalized cell surface microdomains in live cells. However each method is associated with specific limitations, in particular imaging resolution and a level of complexity that can be observed. For example, whereas conventional fluorescence imaging is useful for studying relatively large domains and static images, more sophisticated fluorescence resonance energy transfer (FRET) microscopy imaging may be used to monitor rapid and close proximity associations reflecting protein-protein interactions or conformational changes within single molecules coupled with biochemical processes (4,5). FRET microscopy involves detecting the efficiency of energy transfer between donor-acceptor fluorophores that occurs over distances of 1–10 nm. Despite the insights provided by such experimental techniques, methods for quantifying the spatiotemporal dynamics of functional signaling microdomains remain to be fully developed. This capability is necessary for modeling cellular processes and to achieve the goals of predicting or anticipating outcomes to various pathophysiological and/or pharmacological perturbations.

Previously, we introduced a wavelet-based approach for the identification of protein kinase C (PKC) signaling microdomains in plasma membranes from FRET microscopic images (6). The PKC activity reporter (CKAR) was expressed and anchored in the plasma membrane of COS1 cells to allow changes in FRET signaling to reflect the phosphorylation balance resulting from PKC activation and phosphatase activity (5). Images of corrected FRET in plasma membranes, before and after stimulation by phorbol-12,13-dibutyrate (PDBu) and acetylcholine, were subjected to linearization to generate one-dimensional (1D) signals from two-dimensional (2D) images. The 1D continuous wavelet transform (CWT) was applied to such 1D signals with the resulting coefficients representing correlations between the original signal and a wavelet basis function at different frequencies and positions in space (see Theoretical section in Materials and Methods). The wavelet transform is an extension of Fourier analysis but colocalizes in both the space and frequency domains to permit assessment of changes in spatial frequency content after pharmacological interventions. Differences in coefficient matrices as compared to controls were used to initially identify potential microdomains that were accepted or rejected based on a subsequent statistical comparison of corrected FRET values in these regions over time. In addition to the expected FRET temporal profiles that decrease in a relatively linear manner, transient activity was detected in several domains that were not observed in the time course of average spatial activity. This demonstrates the utility of the multiresolution properties of wavelet-based microdomain identification techniques in the analysis of local heterogeneity.

In this study, we extend this approach to include the 2D CWT to overcome the restrictions imposed by the linearization step required for the application of the 1D transform. First, static fluorescent images of COS1 cells expressing calmodulin kinase IIβ fused with enhanced yellow fluorescent protein (EYFP) were analyzed to compare the agreement between the 1D and 2D methods for examining microdomains. Second, time lapse images of FRET expression by CKAR and cyclic adenosine monophosphate (cAMP) activity were evaluated to identify signaling microdomains within COS1 cellular membranes after stimulation by PDBu and forskolin (an adenylyl cyclase activator), respectively. The good agreement between the 1D and 2D wavelet analyses suggests that the 2D approach is an effective alternative to the 1D method and circumvents the linearization step. To demonstrate the added value of the 2D CWT, intracellular signaling domains representing cAMP response element-binding (CREB)-induced transcriptional activation was identified in the nuclei of COS1 cells. This 2D extension should significantly expand the types of cellular signaling processes that can be evaluated using wavelet transform analysis.

MATERIALS AND METHODS

Materials

Plasmids coding for the plasma membrane targeting CKAR and a mutated PKC reporter (negative control) were kindly provided by Drs. R. Y. Tsien and A. C. Newton (University of California, San Diego, CA). The plasma membrane targeted reversible cAMP reporter (pm-ICUE1) was obtained from Drs. L. M. DiPilato and J. Zhang (Johns Hopkins University School of Medicine, Baltimore, MD). The Ca²⁺/calmodulin-dependent protein kinase-type IIβ construct (EYFP-CamKIIβ) was a gift from Dr. Y. Hayashi (Massachusetts Institute of Technology, Cambridge, MA). The plasmids of EYFP-labeled kinase-inducible domain (KID) domain of CREB and enhanced cyan fluorescent protein (ECFP)-labeled KIX domain of CREB-binding protein were gifts from Dr. M. R. Montminy (the Salk Institute for Biological Studies, La Jolla, CA). The PKC activator PDBu and forskolin were purchased from Calbiochem (La Jolla, CA). All other chemicals were obtained from Sigma (St. Louis, MO).

Cell culture and transfection

COS1 cells were grown on poly-D-lysine-coated coverslips (MatTek, Ashland, MA) in Dulbecco's modified Eagle's medium supplemented with 10% fetal calf serum. Cells were transfected with CKAR and cAMP reporter cDNA using the Effectene kit (Qiagen, Valencia, CA). Plasmids coding for the KID and KIX domains of CREB were coexpressed in COS1 cells at a ratio of 1:1.

Imaging

Images were recorded with a 14-bit Hamamatsu (Hamamatsu City, Japan) digital camera C9100-12 mounted on the Nikon (Tokyo, Japan) epifluorescent microscope TE200 (60 × 1.2 numerical aperture (n.a.) objective or 100 × 1.45 n.a. objective) equipped with multiple filter sets (Chroma Technology, Rockingham, VT) (pixel size = 200 nm). Excitation light was delivered by a 175 W Xenon lamp. Excitation filter sets were changed by a high-speed filter wheel system (Lambda 10-2, Sutter Instrument, Novato, CA). The Dual-View system (Optical Insights, Santa Fe, NM) was used for the simultaneous acquisition of two fluorescence images (donor and FRET). Images were obtained and analyzed using C-Imaging (Compix, Cranberry Township, PA) and MetaMorph (Universal Imaging, West Chester, PA) software. FRET was quantified with three filter sets: for the yellow fluorescent protein (YFP) cube, excitation filter 500/20 nm, dichroic beam splitter 515 nm, emission filter 535/30 nm; for the cyan fluorescent protein (CFP) cube, excitation filter 436/20 nm, dichroic beam splitter 455 nm, emission filter 480/40 nm; for the FRET cube (CFP/YFP), excitation filter 436/20 nm, dichroic beam splitter 455 nm, emission filter 540/30 nm. Regions of interest were selected using the C-Imaging software program. Corrected intensity of FRET was calculated from the three filter sets (CFP, YFP, and FRET) as described previously (6) using MATLAB (v.7.0.4, The Mathworks, Natick, MA). Briefly, corrected FRET values (FRET_c) were calculated according to

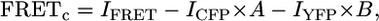(1)

where I is intensity, and the bleed through coefficients (A = 0.73, B = 0.08) were determined experimentally by calibration of the acquisition system according to Xia and Liu (7). Frame and light exposure time was 27 ms, and all experiments were conducted at room temperature (20°C–22°C). The mean of 10% of all pixels containing the lowest values within the image was used for background subtraction. Initially, either average intensity produced by nontransfected cells at the same particular gain and time exposure to the charge-coupled device (CCD) camera or an average intensity in the far corner of the image (manual selection) was used for background correction. These two cases resulted in similar values. It was therefore more convenient and practical to continue with the selection of background using the same image, particularly owing to the experimental variability requiring different gains of the CCD camera. To automate this process in an objective manner, we chose the best estimation by using control FRET experiments with a CFP/YFP pair with known FRET efficiency. Selection of the lowest 5%, 10%, 15%, and 25% for background subtraction was evaluated, and the lowest 10% produced the best results.

Synthetic images

To directly compare the performance of the 1D and 2D CWT algorithms, five 2D images of a single cell plasma membrane were generated, composed of only white noise (random numbers between 0 and 1). A total of six domains of 9–11 pixels each were arbitrarily placed around the cell (within the plasma membrane) by adding 0, 0.25, 0.5, 1, and 2 units to the domain elements. The 1D and 2D methods were applied to these test images and positive and false positive discoveries were identified.

Wavelet analysis

Theoretical

Given a linear 1D spatial signal h(x), the CWT is an extension of Fourier analysis, providing a windowing technique of variable-sized regions based on frequency, and is defined as

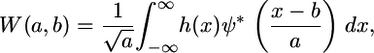(2)

where a represents scale (inversely related to frequency), b is the translation parameter (shift in space), and ψ is a wavelet basis function (* denotes complex conjugation). Thus, scale or frequency information is obtained, and the function simultaneously localizes in the spatial domain. The CWT can also be expressed in the Fourier domain, such that

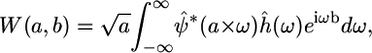(3)

with 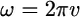(where v is frequency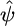) and and 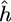represent the Fourier transforms of the wavelet and signal. Similar to Fourier analysis, where a signal is decomposed into a series of sin and cos functions, the CWT is the sum over all space of a signal multiplied by a), scaled, and b), shifted versions of the chosen wavelet basis function. The calculated coefficients, W(a,b), reflect the correlation between the original signal, h(x), and the wavelet basis function at specific scales (or frequencies) as a function of distance. Thus, the CWT can be viewed as a filter with a function of zero mean, where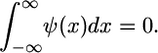

Considering an image as a 2D signal of finite energy, the CWT (Eqs. 2 and 3) can be readily extended to two dimensions (8):

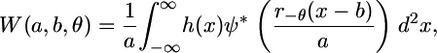(4)

with the wavelet basis function subject to rotation by an angle θ (r_−θ is the rotation operator) in addition to translation and dilation (as in the 1D case). For implementation purposes, it is more convenient to consider the 2D CWT in the Fourier domain. Note that a 2D signal h(x) may be transformed by translation, dilation, and rotation according to

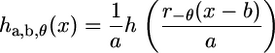(5)

and hence in the Fourier domain

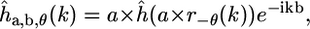(6)

where the hat denotes the 2D Fourier transform and k is a spatial frequency. Accordingly, Eq. 4 can be expressed in the Fourier domain as

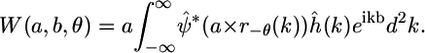(7)

For visualization and analysis purposes, the standard position or aspect-angle representation was chosen where positional snapshots (b_x and b_y) are considered at fixed scales (a) and angles (θ). As with the 1D CWT, several analyzing wavelets are available. Given the overall objective of performing a fine, pointwise analysis, the 2D Mexican hat wavelet was chosen, which is defined as the Laplacian of a Gaussian:

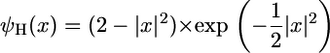(8)

This isotropic wavelet exhibits an additional feature of being rotation invariant (8).

Data analysis

The overall processing steps are depicted in a flow chart (see figure in online Supplementary Material). Both the 1D and 2D CWTs were applied to synthetic, static fluorescence and time lapse FRET images in MATLAB. For the 1D CWT, signals were modified using a common periodic signal extension technique to address the boundary condition problem or signal edge effects. The 2D CWT was implemented using the YAW toolbox (http://www.fyma.ucl.ac.be/projects/yawtb/) (9). For images generated from FRET microscopy, normalized temporal differences in wavelet coefficient matrices, as compared to coefficient matrices of control images, were used to identify potential microdomains as described previously (6):

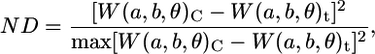(9)

where ND represents a normalized difference matrix and the subscripts C and t denote wavelet coefficients of control images and those obtained at sampling time, t. Although only a single control image was used for calculation purposes, images of control cells were stable over the duration of the experiments and no effects of photobleaching were observed (data not shown). Several scales of the 2D CWT were manually evaluated. The highest frequency, a = 1, largely contained noise (as is common) and was therefore excluded from further analysis. In addition, spatial localization rapidly diminishes for larger scales (e.g., a > 5). Thus, scales 2–5 were assessed independently and the highest relevant resolution (a = 2) was 400 nm. Initial domains were scrutinized by assessing corrected FRET values within each region using a one-way analysis of variance (ANOVA) with Dunnett's multiple comparisons, and only those regions of interest showing a statistically significant difference were accepted as microdomains (P < 0.05). For synthetic images, elements in potential domains at any one signal/noise level were compared to the control image (0 units added) using standard Student's t-test as there is no temporal relationship between levels. For the static images of calmodulin kinase IIβ fluorescence, initial regions of interest were identified by visual inspection of cumulative power plots (10) (1D CWT) or plots of normalized power (2D CWT), whereby signal power was approximated by W(a,b)².

RESULTS AND DISCUSSION

Here we incorporate a relatively new mathematical transform, the 2D CWT, to extend our previous wavelet-based approach to identifying and monitoring functional signaling microdomains in cellular plasma membranes (6). In contrast to the 1D CWT, the 2D transform can be applied to an entire image and does not require that regions of interest undergo a single-pixel linearization procedure. An additional advantage is that regions of interest do not have to be defined a priori, which is typically performed manually and subject to bias. The linearization step also implies a continuum or association among neighboring pixels, which can be assumed for structures such as the plasma membrane; however, this implication cannot be readily extended to global or local complex regions, such as the cytoplasm or endoplasmic reticulum, and restricts the prior approach to a limited range of cellular processes. In this proof of concept study, both the 1D and 2D algorithms were applied to synthetic, static fluorescent, and time lapse FRET images to evaluate the effectiveness of the 2D CWT and highlight the limitations and advantages of these methods.

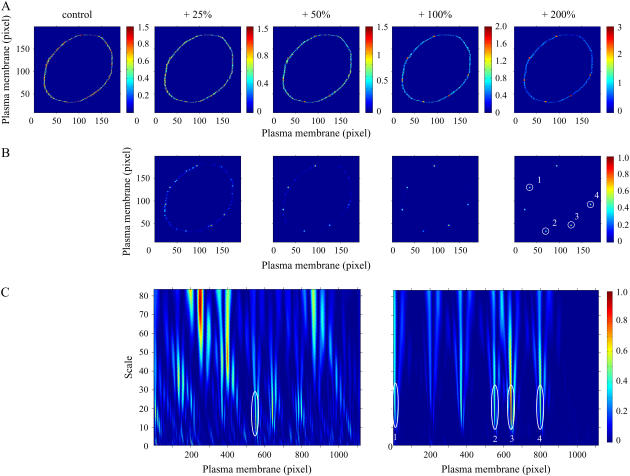
Synthetic computer generated images were constructed to directly assess the performance of the 1D and 2D wavelet methods (Fig. 1 A). The control image (0 units added) and four signal/noise levels are shown in Fig. 1 A and the locations of the six domains can be clearly identified in the far right panel (highest signal/noise ratio). Normalized wavelet coefficient difference matrices between control and individual signal/noise levels are shown in Fig. 1 B (scale a = 2). Whereas the six domains are clearly identified at the highest signal/noise ratio, additional potential domains are found at the lowest signal/noise ratio. After statistical comparisons, two false positive domains and only four true positives were found using the 2D CWT at the lowest signal/noise ratio (see table in Supplementary Material).

FIGURE 1.

Comparison of 1D and 2D CWT analysis of a model cell with different levels of signal/noise ratios. (A) Values were randomly generated in the plasma membrane (control, 0–1), and signal/noise level was set to gradually increase by 25%, level 1; 50%, level 2; 100%, level 3; and 200%, level 4; whereas noise level was not changed. Scale: arbitrary units (a.u.). (B) Normalized subtraction of squared 2D wavelet coefficient matrices revealing potential microdomains. 2D CWT Mexican hat function was applied at scale 2 to the corresponding noise-modified images shown in A. (C) Normalized subtraction of squared 1D wavelet coefficient matrices (see Materials and Methods) control: level 2 (left panel), control: level 4 (right panel). Plasma membrane microdomains identified by 1D CWT coincide with microdomains identified by 2D analysis shown as circled regions (B and C).

In contrast, no false positives and all six true domains were identified for all other noise levels. For the 1D CWT, one false positive was found for noise levels 1, 3, and 4, and the numbers of true positives discovered for increasing signal/noise levels were 0, 1, 3, and 4 out of 6, having failed to identify all six domains even at the highest signal/noise ratio level. Normalized difference matrices for the 1D CWT at the second and fourth noise level are shown in Fig. 1 C. A large number of potential domains are shown in the left panel and the only significant domain is marked by a white oval, which was one of the six true domains (Fig. 1 C). The difference matrix at the highest signal/noise ratio for the 1D CWT is shown in the right panel of Fig. 1 C and the four identified domains correspond with the four white circles in Fig. 1 B (far right panel; 2D CWT). The 2D algorithm was superior to the 1D approach for this simulated example, exhibiting a greater tolerance to noise and a lower false positive discovery rate. The linearization step of the 1D analysis is likely a major source of the limitations of this method.

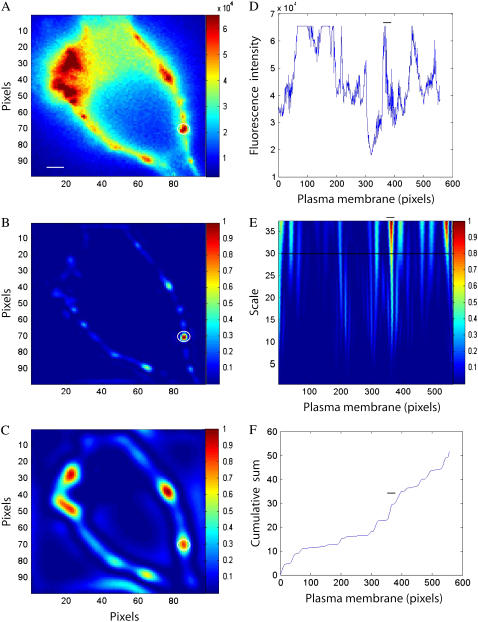
Single fluorescent images of COS1 cells (n = 5) expressing Ca²⁺/calmodulin-dependent protein kinase-type IIβ fused with EYFP were analyzed using both the 1D and 2D CWTs to compare their respective capacities to detect macrodomains that could be easily verified by visual inspection. The analysis results for a representative cell are shown in Fig. 2. The nonhomogenous distribution of fluorescence within the plasma membrane is clearly demonstrated (Fig. 2 A). As the intent of this analysis is to conduct a pointwise analysis or detection of discontinuities (as opposed to distinguishing directional features), the 2D Mexican hat wavelet was chosen as the basis function for the 2D CWT. Thus we assume that there are no oriented features relevant to compartmentalized signaling domains within the plane of the plasma membrane, and the rotational invariant property of this wavelet further simplifies subsequent visualization and analysis (8,9). An image of normalized square wavelet coefficients resulting from the 2D CWT at a relatively low scale (a = 2) is shown in Fig. 2 B.

FIGURE 2.

Comparison of 1D and 2D CWT analysis of static fluorescence images. (A) Fluorescence image of a COS1 cell expressing plasma membrane-targeted EYFP-labeled Ca²⁺/calmodulin-dependent protein kinase-type IIβ expressed in COS1 cells. (B,C) Comparison of 2D CWT analysis using the Mexican hat analyzing wavelet at different scales: low scale 2 (B), high scale 5 (C). (D) Fluorescence intensity values in the linearized plasma membrane region. (E) 1D normalized wavelet coefficient plot (db4 analyzing wavelet over scales 4–40); horizontal line indicates scale 30. (F) Cumulative sum of normalized 1D wavelet coefficients (db4 wavelet at scale = 30). The common identified microdomain is circled (A–C) or marked by horizontal bar (D–F). Scale bar is 2 μm.

At this high-frequency level (N.B.: frequency is inversely related to scale), a relatively small domain can be clearly identified, and the circled region corresponds to the enclosed area of fluorescence intensity shown in Fig. 2 A (white circle). On the other hand, a relatively large region of fluorescence in the original image (top left field of Fig. 2 A) went undetected. This region was subsequently detected from the normalized square wavelet coefficients calculated at a higher scale (or lower frequency; a = 5) (Fig. 2 C). Although the smaller domain shown in Fig. 2, A and B, is still identified at this higher scale, its definition (size and location) is less precise (circled region in Fig. 2 C). Similar to biosignal analysis with the 1D CWT, these results indicate that effective detection of signaling domains requires the careful consideration of wavelet coefficients across various spatial frequencies, with high and low frequencies providing information on local and global features of the original signal.

The corresponding analysis of the image shown in Fig. 2 C using a 1D CWT and the db4 wavelet basis function is shown in the right-hand panels of Fig. 2. Our previous analysis suggested that the results of the 1D approach to identifying domains of interest was relatively independent of the choice of the analyzing wavelet (6); however, other features of the Daubechies wavelets, such as compact support, make them ideally suited for this purpose (6,11). Linearization of the plasma membrane was conducted as previously described (6), and the fluorescence intensity along this 1D signal is plotted in Fig. 2 D. The heterogeneity of fluorescence intensity is readily apparent from “hot color” regions in the normalized square wavelet coefficients as a function of scale (a = 4–40) and space (Fig. 2 E). This assessment over spatial frequencies provides details of local and global features of the original signal simultaneously. Some regions of the fluorescence signal are saturated as shown in Fig. 2 D. In these saturated regions, the 1D CWT does not register a signal as indicated by the relatively low normalized wavelet coefficients in these regions shown in Fig. 2 E (although the edges appear to be highlighted). On the other hand, the 2D CWT at scale 5 (Fig. 2 C) readily detects the saturated regions, highlighting another advantage of the 2D approach over the 1D CWT. For time series analysis, fluorescence values in potential domains would be compared to a control image across time.

As this approach of domain analysis is not possible for static images, a cumulative power plot technique was used to improve visualization of potential regions of interest, where the cumulative sum of square wavelet coefficients at a given scale (a = 30 shown as a solid line in Fig. 2 E) is plotted as a function of pixels in the plasma membrane (Fig. 2 F). The cumulative power plot technique has been used previously to monitor tone of spectral content in specific frequency bands (10). Each “step” in this plot is associated with abrupt changes in fluorescence intensity and represents a potential domain of interest. For comparison purposes, the horizontal bars in Fig. 2, D–F, correspond with the domain identified by the 2D CWT as indicated by closed circles in Fig. 2, A–C. Across the 5 COS1 cell images, the absolute number of regions identified using the 1D CWT exceeded that of the 2D transform, with the 2D approach capturing 75% ± 6% of the potential domains detected using the 1D transform. The different number of domains identified using the 1D approach was expected as the linearization step likely introduces false positives that would ordinarily be rejected from a time series statistical analysis. Thus domains of high-intensity fluorescence in the plane of the plasma membrane can be adequately detected by both methods, and the 2D CWT approach has the advantage of providing a means for characterization of signaling domains of variable size and intensity without a potentially problematic linearization procedure.

The relative utility of the 1D and 2D CWTs to identify membrane microdomains in COS1 cells was evaluated from analyzing time-dependent changes in FRET microscopy after stimulation of two plasma membrane tagged FRET-based reporters of distinct signaling cascades. The reversible PKC reporter CKAR is composed of monomeric CFP, monomeric YFP, and a PKC substrate peptide tethered by a flexible linker to an FHA2 phosphothreonine-binding domain. Phosphorylation of the PKC substrate causes its binding to the FHA2 domain, and a subsequent conformational change results in a decrease in FRET signaling. This decrease of the FRET signal between the CFP and YFP fluorophores reflects an increase of PKC-mediated phosphorylation, whereas an increase of FRET corresponds to an increase of phosphatase activity (5,6). The CKAR construct can thus be used to reflect the dynamic balance in cellular phosphorylation-dephosphorylation (5), and we previously revealed heterogeneous signaling domains after stimulation with the phorbol activator PDBu from a 1D wavelet-based analysis (6). Various isoforms of PKC are involved with regulatory mechanisms of cell growth and differentiation and caveolae have been found to represent a major localization site for these proteins (12,13).

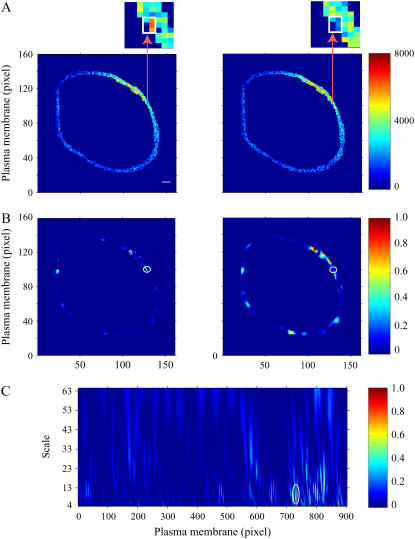
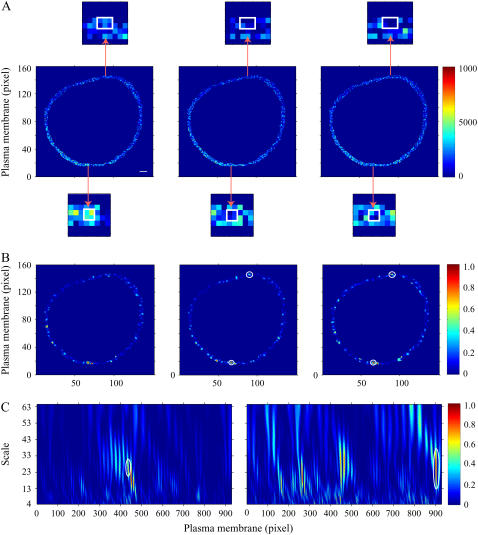
In this study, similar experimental procedures were followed, and corrected FRET values in the plasma membrane of a COS1 cell under control conditions or 3 min after PDBu exposure are shown in Fig. 3 A. A representative functional signaling domain identified by the 2D CWT approach is highlighted, showing relatively high FRET intensity in the control image and little to no FRET 3 min after stimulation by the agonist. Images of normalized 2D difference matrices between wavelet coefficients calculated for these two images at two different scales are shown in Fig. 3 B (a = 3 and 5 for the left and right panels, respectively). The final signaling domain indicated in Fig. 3 A, which reflects high PKC-induced phosphorylation activity, is clearly identified at a relatively low scale (high spatial frequency; left panel of Fig. 3 B), but is not clearly observed at lower frequencies (right panel of Fig. 3 B). This region (along with additional segments) was accepted as a signaling domain after a one-way ANOVA comparison over time (P < 0.05). The corresponding 1D analysis also identified this domain as indicated by the oval in the normalized difference matrix in Fig. 3 C. Complete overlap was found comparing the 1D and 2D methods, supporting the effectiveness of the 2D transform and the advantage of excluding a membrane linearization procedure.

FIGURE 3.

Comparison of 1D and 2D CWT analyses of FRET microscopy of PDBu-induced PKC activation in the plasma membrane of a COS1 cell expressing a PKC FRET reporter. (A) FRET image of the plasma membrane region of interest in control (left panel) and after 3 min of PDBu (200 nM) exposure (right panel). Arrows point to magnified regions of the plasma membrane (inset) containing identified PKC activity microdomains (white boxes). The color bar represents corrected FRET values. (B) Normalized subtraction of the 2D wavelet coefficient matrices (see Materials and Methods) before and after 3 min of PDBu exposure at low (a = 3; left panel) and high (a = 5; right panel) scales. Scale 3 was effective in revealing one microdomain (left panel), but scale 5 identified a region that was 2–3 pixels away (right panel). Potential PKC signaling microdomains are visualized by relatively high values. A statistically significant PKC signaling microdomain is shown by the white circle. (C) Normalized difference between squared wavelet coefficients of 1D wavelet coefficient matrices before and 3 min after PDBu application. The circled microdomain region corresponds with the region identified using the 2D transform in Fig. 2 B. The color bars represent differences between squared coefficient matrices normalized to the maximal values (B and C). Scale bar is 2 μm.

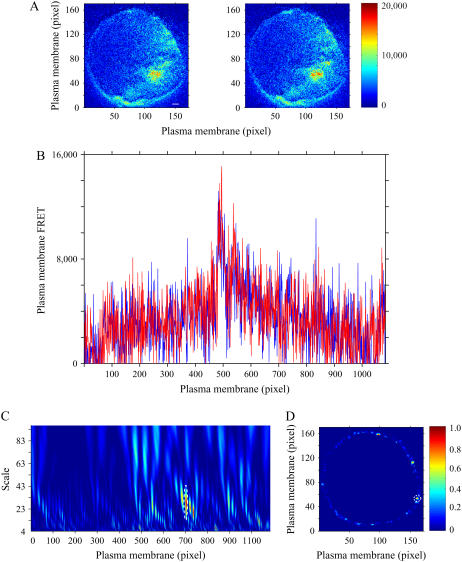
Specificity of the PKC phosphorylation analysis was verified using a mutated inactive PKC reporter, where the threonine phosphoacceptor in the PKC substrate sequence was changed to alanine (negative control). Application of PDBu to cells expressing this mutated reporter did not significantly affect FRET intensity (5). This mutated FRET-based PKC reporter was expressed in COS1 cells, and typical corrected FRET images of a representative cell under control conditions and 3 min after PDBu treatment are shown in Fig. 4 A. These images suggest that FRET intensity is relatively unchanged after PDBu exposure and is supported by examining FRET values within the linearized plasma membrane region (Fig. 4 B). Normalized wavelet coefficient difference matrices for the 1D and 2D transforms of the images in Fig. 4 A are shown in Fig. 4, C and D. Plasma membrane regions of potential PKC signaling changes were identified, and an example of overlapping membrane areas identified by both methods are indicated by dashed circles. Although potential domains composed of heterogeneous FRET values were identified by both methods, none of the plasma membrane regions showed significant changes in PKC signaling. Thus, good agreement between the 1D and 2D CWT analyses was observed, and false positives were not generated during the final assessment of this negative control.

FIGURE 4.

Application of PDBu (200 nM) to a COS1 cell expressing a mutated FRET-based PKC reporter producing no significant changes in the plasma membrane FRET signal. (A) Corrected FRET images of a representative COS1 cell expressing a plasma membrane-targeted mutated FRET-based PKC reporter before (left panel) and after 3 min (right panel) of PDBu treatment. The color bar represents corrected FRET values. (B) FRET values within the linearized plasma membrane of the identical COS1 cell before (blue line) and after 3 min (red line) of PDBu (200 nM) exposure. Normalized subtraction of 1D (C) and 2D (D) wavelet coefficient matrices (see Materials and Methods) of the 3 min time point after PDBu (200 nM) treatment from the control matrix. No potential domains visualized by large values were statistically significant (overlapping domain between the 1D and 2D methods is indicated by a dotted line). The color bar represents the difference between squared coefficient matrices normalized to the maximal value. Scale bar is 2 μm.

Another plasma membrane tagged reporter (pm ICUE1 cAMP) has been successfully used to identify changes in cAMP dynamics underneath the plasma membrane (14). This reporter of cAMP dynamics is the full-length cAMP receptor protein Epac1 (exchange proteins directly activated by cAMP), sandwiched between ECFP and citrine. Binding of cAMP to this reporter induces a conformational rearrangement that is associated with changes in FRET intensity. Zhang and colleagues have shown that application of forskolin, an activator of adenylyl cyclase, generates a transient appearance of cAMP signaling events at different cellular sites (15). We sought to identify such domains within the plasma membrane of a COS1 cell expressing the cAMP reporter using our 1D and 2D wavelet based methods. Fig. 5 A contains FRET images of the plasma membrane of this cell under control conditions (left panel) and 2 and 3 min (middle and right panels) after treatment with forskolin.

FIGURE 5.

Comparison of 1D and 2D CWT analyses of plasma membrane microdomains of cAMP production stimulated by forskolin (10 μM) in COS1 cells expressing a plasma membrane-targeted FRET-based cAMP reporter. (A) Corrected FRET images of the before forskolin application (left panel) and 2 min (middle panel) and 3 min (right panel) after forskolin treatment. Arrows point to magnified regions containing the plasma membrane microdomains of cAMP production (white boxes). The color bar represents corrected FRET values. (B) 2D wavelet coefficients plot of the plasma membrane region under control conditions (left panel) and normalized subtraction of squared 2D wavelet coefficient matrices (see Materials and Methods) after 2 min (middle panel) and 3 min (right panel) of forskolin application from the control matrix. The color bar represents the difference between squared coefficient matrices normalized to the maximal value. Potential microdomains of cAMP production are visualized by large values. Plasma membrane regions showing statistically significant changes are indicated by circles. (C) Normalized subtraction of squared 1D wavelet coefficient matrices (see Materials and Methods) after 2 min (left panel) and 3 min (right panel) of forskolin application from the control matrix. Plasma membrane microdomains identified by 1D CWT coincide with microdomains identified by 2D analysis (circled region on the left panel C coincides with the region in the bottom of the images presented on panel B; and the circled region on the right panel C coincides with the region in the top of the images presented in panel B). Scale bar is 2 μm.

Two microdomains revealed by both wavelet transforms are also highlighted in these images showing decreasing FRET intensity over time. A plot of the wavelet coefficients resulting from the 2D CWT of the FRET signal under control conditions is shown in Fig. 5 B (left panel; several scales were evaluated but only scale = 3 is shown). This figure also shows normalized difference matrices comparing changes in squared wavelet coefficients at 2 and 3 min after forskolin exposure (middle and right panels). Relatively large values in these plots were used to identify potential domains of transient cAMP activity, and statistically significant domains that correspond with those shown in Fig. 5 A are marked with circles. The analogous 1D method was applied to the same FRET images (Fig. 5 A), and normalized difference matrices are shown in Fig. 5 C. The identical microdomains were found (circles) but with only one domain identified from each matrix. Separate time points may have been needed for the 1D transform due to the need for the linearization step, whereas the 2D transform provides a more comprehensive analysis without altering the spatial relationships of original signals. Thus, plasma membrane microdomains reflecting spatiotemporal dynamics of cAMP signaling underneath the plasma membrane were successfully detected with the 1D and 2D transforms.

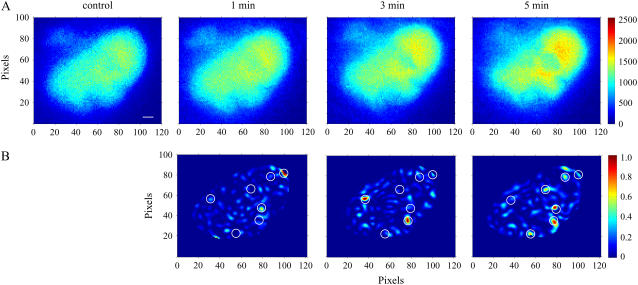
Finally, the unique advantage of whole image analysis using the 2D CWT was demonstrated through the identification of signaling microdomains of CREB-dependent transcriptional activation in the nuclear compartment of COS1 cells. CREB-dependent transcription has been shown to be regulated in part by the voltage-gated mobility of the Ca_v1.2 channel C-terminal tail (16). Corrected FRET images under control conditions, and 1, 3, and 5 min after treatment with forskolin are shown in Fig. 6 A where FRET signaling appears to increase with increasing time. Normalized difference matrices of the wavelet coefficients are shown in Fig. 6 B along with the seven identified domains (white circles). Interestingly, whereas some domains suggest a gradual increase in FRET, others show transient changes in time. Although our current 2D approach is designed only to identify signaling regions, spatiotemporal wavelets might be eventually used to follow spatial dynamics (e.g., diffusion/motion) in addition to changes in fluorescence/FRET signaling intensity over time (9).

FIGURE 6.

Identification of microdomains of CREB-dependent transcriptional activation in nuclei of COS1 cells. (A) FRET images of the interaction between KID and KIX domains of CREB and CREB-binding protein expressed in COS1 cells recorded before (control) and 1, 3, or 5 min after forskolin treatment (10 μM). (B) Intranuclear microdomains of CREB-dependent transcriptional activation identified by 2D CWT analysis. Normalized subtraction of squared 2D wavelet coefficient matrices (see Materials and Methods) after 1 min (left panel), 3 min (middle panel), and 5 min (right panel) of forskolin application from the control matrix. The color bar represents the difference between squared coefficient matrices normalized to the maximal value. Potential intranuclear microdomains of CREB-dependent transcriptional activation are visualized by large values. Circles indicate regions containing microdomains identified by 2D CWT analysis. Scale bar is 2 μm.

These data further support the role of coupling the wavelet transform with biophysical and imaging experiments to study complex cellular events such as compartmentalization and signal transduction. Wavelet analysis is relatively new, and there is a growing interest in its potential for bioinformatics and applications in computational biology (17,18). For example, Sosnovtseva and co-workers have developed a double-wavelet approach for analyzing interference microscopic images to reveal the time course of spectral content that is associated with several cell regulatory processes (19). Signals emanating from these as well as pharmacological response systems often exhibit complex nonlinear behavior, and significant information may be contained in the temporal aspects of their spectral density as opposed to their original waveform. Techniques such as those introduced in this study may provide a suitable platform for eventually achieving the goal of integrating standardized data into predictive models of cellular processes in four-dimensional space-time (20).

CONCLUSIONS

A new method of identifying functional signaling macro- and microdomains in cellular plasma membranes has been presented based on the 2D CWT of static and time lapse fluorescence microscopic images. The proposed 2D wavelet-based approach was shown to provide results in good agreement with our previous 1D method, and both effectively detected phosphorylation/dephosphorylation signaling microdomains (PKC) as well as those reflective of adenylyl cyclase dynamics (cAMP). The primary advantage of the 2D CWT is that it can be applied without the limitation of requiring linearized signals imposed by the 1D CWT. This serves to bypass the potential bias or false positives that might be linked to the linearization step and also may expand the locations of compartments that can be analyzed for spatiotemporal dynamics of cell signaling and protein-protein interactions.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.