Abstract
The electrophysiology of β-cells is at the origin of insulin secretion. β-Cells exhibit a complex behavior upon stimulation with glucose including repeated bursts and continuous spiking. Mathematical modeling is most suitable to improve knowledge about the function of various transmembrane currents provided the model is based on reliable data. This is the first attempt to build a mathematical model for the β-cell electrophysiology in a bottom-up approach that relies on single protein conductance data. The results of previous whole-cell-based models are reconsidered. The full simulation including all prominent transmembrane proteins in β-cells is used to provide a functional interpretation of their role in β-cell bursting and an updated vantage point of β-cell electrophysiology. As a result of a number of in silico knock-out and block experiments the novel model makes some unexpected predictions: single-channel conductance data imply that large-conductance calcium-gated potassium currents acquire the potential of driving oscillations at supralarge glucose levels. A more complex burst interruption model is presented. It also turns out that, depending on the species, sodium currents may be more relevant than considered so far. Experiments are proposed to verify these predictions.
INTRODUCTION
The electrophysiology of β-cells is most relevant for understanding possible regulatory targets of insulin secretion. Exocytosis of insulin-loaded granules is, among others, governed by intracellular calcium signaling. Calcium dynamics exhibits very specific patterns in reaction to increased glucose concentrations that include repeated bursting of the membrane potential. Bursting denotes oscillations of action potential-like depolarizations, which are regularly interrupted and set in again after a phase of silence. Thus, oscillations occur on two distinct timescales: Fast oscillation of the membrane potential on the scale of 100 ms and slow oscillations of intracellular calcium on the timescale of 10 (seconds to minutes), i.e., in the rhythm of the repetition of burst events.
In a minimal model of membrane potential oscillations (1) it was found that an activation delay between voltage-gated potassium and calcium channels gives rise to this bursting behavior. Sodium, the major player in neurons, is generally believed to be of minor importance (2). Therefore, modeling work was concentrating on potassium and calcium currents (3–5).
Initiation of bursting events was found to be related to ATP-driven potassium channels (6,7) that induce a relevant outflow of potassium under resting conditions. When glucose—and via glucose metabolism—ATP is increased, the channel conductance is inhibited (8,9), which leads to the initial depolarization. Then voltage-dependent calcium currents are activated and the delayed response of voltage-dependent potassium currents leads to the bursting event.
Simulations of the β-cell electrophysiology have shown how, in principle, repeated bursting can happen (1–3,5), and the found mechanisms are in agreement with experimental results. However, none of the presently existing models fulfill the following requirements: i), all important ions and membrane proteins are explicitly modeled including their activation and inactivation dynamics; ii), the β-cell exhibits a steady state and is stimulated by changes of glucose concentrations; and iii), the dynamics of the membrane protein activity are fully derived from protein experiment. Only if all these requirements are respected, the exact role of the different membrane proteins might be disentangled.
A major problem in developing such a complete simulation tool is related to the large variability of measured whole-cell conductances in β-cells. In fact the density of the membrane proteins is itself a dynamical quantity. Their dynamics vary for different cell types so that the data used for modeling are restricted to measurements in β-cells. Not all membrane proteins have been subject to quantitative measurements in β-cells. For example the sodium-calcium exchanger was intensively studied in neurons (10) but mathematically modeled in β-cells (11) (see Supplementary Material for a detailed discussion of membrane protein properties). Also the β-cells under consideration can be in various states of protein expression. Thus, modeling work was restricted to fit the activity dynamics of the membrane proteins to the behavior that was expected.
To overcome this problem, the present simulation exclusively relies on data of single protein activity. Such an approach was used in calcium modeling of neurons (12) before and is now applied for the first time to β-cell electrophysiology. Today there is a rather complete knowledge about single proteins conductance and opening dynamics available that allows a bottom-up approach starting from the single protein level.
To this end the single protein activity dynamics is separated from the protein density. It is assumed that the single protein dynamics is cell-independent. In other words a voltage-gated potassium channel has the same dynamical properties in a neuron and in a β-cell. This assumption might be set in question if cooperation of membrane proteins with other cell structures would change the activity dynamics. However, the universality of single membrane protein properties can be considered to be a good approximation because the measured characteristics of the cells show relatively small variations despite them stemming from different cell types (see “The basic model assumptions” and Supplementary Material).
The conductance and opening properties of single proteins are exactly implemented into the model and then are multiplied by the surface density of the respective proteins in β-cells. The latter are not precisely known and are the free parameters of the simulation. Some densities can be estimated from measured whole-cell currents. In comparison to the huge parameter space in simulations relying on whole-cell conductance measurements, this is a rather small set of unknown parameters. This improves the predictive power of the mathematical model. The behavior of the β-cell in terms of dynamics of membrane potential and ion concentrations is emerging from the single protein level, thus, coupling the molecular to the cellular level.
The framework of the simulation is presented in the Methods section. The single membrane protein properties are collected in the Supplementary Material. These define the current dynamics as used in the simulation. The full model as introduced in Methods contains the model of a most prominent original work (3). The bursting behavior as found in Sherman et al.'s (3) work is reproduced as a special case of the full model and is used as test for the simulation. Then the full simulation is employed to set up a steady state of the β-cell, and to allow for stimulation of the β-cell with glucose. The protein densities are determined to find a realistic behavior of isolated β-cells (13) where the single membrane protein properties are not touched. On the basis of this simulation various in silico experiments are performed and compared to real experiments if available.
The in silico experiments include knock-out experiments and partial or total block of membrane proteins. Large conductance calcium-driven potassium channels are phenomenologically modeled according to single protein activity data (14). The measured dynamics leads to the conclusion that this channel is of minor importance at normal glucose levels, while it is most important for the β-cell behavior at supralarge glucose levels. In this regime calcium-driven potassium channels may drive continuous spiking (7). Low-voltage activated (LVA)-channel inactivation, which has not been considered in other models, and plasma-membrane-calcium-ATPase (PMCA) are suggested to be important for the interruption of bursting events at elevated glucose levels. Also the importance of a dynamic reversal potential, which was mostly neglected in other work (1,3,5), is pointed out. It is found that the role of sodium currents might be underestimated so far, and their impact on β-cell behavior is explained. The article is concluded with a novel vantage point on the interplay of the different ion-conducting membrane proteins during repeated bursts and continuous spiking. Novel experiments are suggested to verify the new vantage point.
METHODS
Dynamics of ion concentrations and membrane potential
Rate equations are used to describe the dynamics of intracellular ion concentrations. External ion concentrations are assumed constant. The ions treated explicitly are sodium N, potassium K, and calcium C. The dynamics depends on the conductance of various membrane proteins that each correspond to one term in the following differential equations.
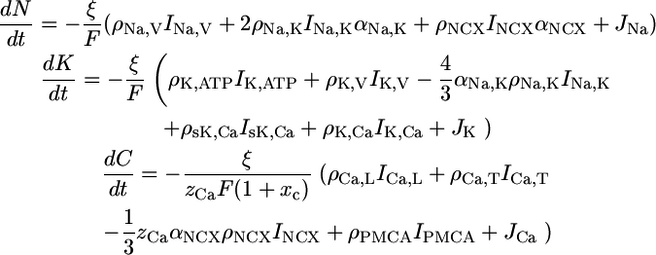 |
(1) |
Ix denotes the electrical single membrane protein currents, where x specifies the type of membrane protein as defined in Fig. 1 (see also Table 1 in Supplementary Material). Negative currents are defined to bring positive ions (charges) into the cell. Because the currents are not defined as ion currents but as electrical currents they have to be weighted by factors denoting the valence of the ion zCa = 2 and the stoichiometry of the protein αx. The single membrane protein currents and their dynamics are discussed in the Supplementary Material.
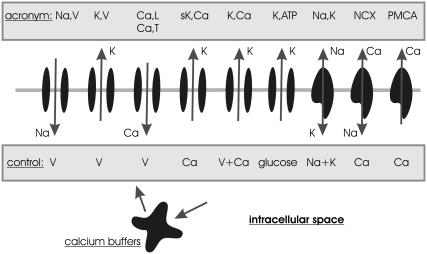
FIGURE 1.
Schematic representation of ion-conducting transmembrane proteins. The plasma membrane is visualized as horizontal gray line on which a set of transmembrane proteins are shown. The shaded boxes show the acronyms of the proteins and the quantities that control their gating/activity in the model introduced below. The ions attributed to the arrows denote the direction of ion flow (assuming normal electrochemical gradients). The calcium buffers symbolize all kinds of intracellular calcium binding sites, including calmodulin and organelles acting as calcium stores. The acronyms of the membrane proteins are also defined in Table 1 in the Supplementary Material, where also the activity dynamics are explained in detail.
ρx denote the corresponding surface densities of the membrane proteins. ξ is a surface to volume factor that relates the current through the membrane to a change of the ion concentration in the intracellular volume. The cell geometry is assumed to be approximately spherical, which implies ξ = 3/Rcell where Rcell is the cell radius.
Note that a calcium buffer is included in the equation for calcium. The calcium buffer is assumed to bind and dissolve calcium faster than the typical timescale of the ion dynamics. Thus, the kinetic equation for the buffer can be solved in the steady-state approximation (rapid buffer approximation). This implies an additional factor (1 + xc) in the equation for calcium, where
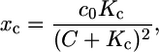 |
(2) |
with c0 the total concentrations of the buffering calcium binding sites. The most prominent buffer is calmodulin having more than one calcium binding site. Kc is the dissociation constant of the calcium binding sites. C is the free calcium concentration. The total calcium concentration is given by
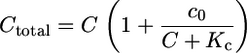 |
(3) |
The fraction of free calcium is 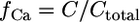 and adopts values between 0.1 and 1%.
and adopts values between 0.1 and 1%.
JK,Na,Ca denote the leakage currents. They are derived from the steady-state limit (see Eq. 27 in Supplementary Material) to guarantee a resting state of the cell. In the resting state all other currents are balanced by the leakage currents, so that the net current vanishes and the ion concentrations are constant.
The ions build up the membrane potential V. All nonelectroneutral currents introduced in Eq. 1 show up in the equation for V:
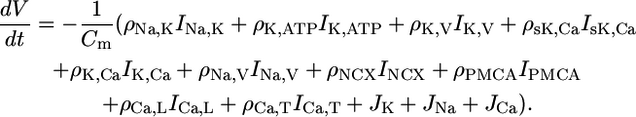 |
(4) |
No additional leakage current is needed because in the steady state the right-hand side vanishes by construction. Cm is the membrane capacitance that relates the electrical currents to changes of the membrane potential.
Reversal potentials
Reversal potentials depend on the chemical gradient and the membrane potential over the cellular membrane. They cannot be considered to be con-stant (as assumed in most other models, e.g., (1,3,5)). As the reversal potentials linearly enter Ohm's law (which is used to approximate ion current through open pores; see “The basic model assumptions” and Supplementary Material) this has to be accounted for. The Nernst equation is used to calculate the correct reversal potential during dynamical changes of the electrochemical constellation:
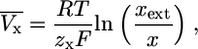 |
(5) |
where x = K, Na, Ca, and R = 8.315 J/(Kmol) the Rydberg (molar) gas constant. The temperature T is assumed to be the physiological temperature; xext is the external concentration of the ion (in thermic bath approximation). They are calculated from the intracellular ion concentrations at rest state to fit the known reversal potential VK = −75 mV, VNa = +80 mV, VCa = +128 mV.
The straight-forward application of Nernst equation, which is based on thermodynamical notions and only involves the electrochemical gradient of the ion under consideration, thus, neglecting other ions and not treating diffusion of ions correctly, is not always justified. In the case of calcium a more exact theoretical approach based on the Goldman-Hodgkin-Katz equation leads to a nonlinear I-V relationship (see, e.g., Hille (15)). This equation is derived from the theory of electrodiffusion through a membrane and involves the influence of other ions on the reversal potential. This more precise I-V relationship is approximated by an Ohm's-law-like current, which is only justified for the linear piece of the curve. A good approximation is to use a reversal potential that is corrected by a constant additive term in Eq. 5 to VCa = +50 mV. Up to this rather large membrane potential the I-V relationship is, indeed, approximately linear. However, one should keep in mind that for depolarization beyond 50 mV (thus of ΔV > 120 mV relative to the resting potential) the calcium currents are not correctly represented.
The basic model assumptions
The following list summarizes the most important features, assumptions, and limitations of the β-cell model:
Universality of single membrane protein measurements
It is assumed that the measured single membrane protein conductances and opening dynamics are valid irrespective of the cell type. This considerably increases the data basis of the simulation. In view of consistent measurements of the same protein in different cells this approximation is reasonable. For example the single channel conductance of T-type voltage-gated calcium channels (Ca,T) is consistently found between 8 and 10 pS in mouse, rat, and human β-cells (16,17), and also in neurons (18) (see also Plant (19) for a discussion of voltage-gated sodium channels in different species, and Supplementary Material for more details). These parameters are only varied to investigate robustness issues. Note that there might be differences in subtypes of membrane proteins that are expressed in different organs or species. These are not accounted for in the simulations.
Stability of the β-cell-resting state
The leakage currents are assumed to equilibrate all other currents if all cell properties are at their resting values. This implies that the cell exhibits a stable steady state and that the cell returns to this resting state after stimulation.
Glucose- and not ATP-mediated activation
Glucose is assumed to directly impact on the conductance of the K,ATP channel. Thus, the β-cell can be stimulated by changes of the glucose level. However, the dynamics of ATP (6,20), which mediates the effect of glucose on K,ATP channels (21), is not considered and left for future improvements of the simulation. Also any feedback between ATP and calcium is neglected (22).
Averaging over the whole cell
Inhomogeneities of the cell are averaged out. The ion concentrations are assumed to be average quantities over the whole cell. Thus, the model might underestimate the dynamics of currents if ion concentrations are much larger in the vicinity of the membrane (see Discussion).
Neglect of calcium-induced calcium release
Calcium-induced calcium release has been suggested to contribute to the calcium oscillations in response to glucose-induced potassium currents (23). However, blocking of related mechanisms does not affect observed oscillations in pancreatic β-cells (24,25). Oscillation in the stores might be or-chestrated with oscillations in the cytosol (25). The simulation neglects the effects of calcium-induced calcium release and assumes that the endoplasmatic reticulum acts mainly as an additional buffer. Thus, the binding site concentration c0 is assumed to be larger than expected by calmodulin alone.
Membrane channels follow Ohm's law
The ion flow through an open pore is assumed to follow Ohm's law, which implies a linear voltage-current relation. This is valid for most ion channels (see the discussion of each protein in Supplementary Material). Deviations are found only for extreme membrane potentials that are not considered here. In the case of ATP-controlled potassium channels (K,ATP) the assumption of Ohm's law is controversial in the literature (8,9,26,27).
The β-cell is isolated
In vivo β-cells are in the context of islets and connected with each others by gap junctions. This connection might influence the susceptibility of stimulation. Indeed, β-cell stimulation is more difficult in isolated cells (see, e.g., Kanno et al. (7)) and currents are larger. This simulation neglects effects stemming from being embedded into islets.
RESULTS
Evaluate the Sherman et al. (3) model
The model of Sherman et al. (3) can be considered as a classical reference model. It is characterized by the following properties:
The membrane potential follows a classical ordinary differential equation with capacity 5.31 pF and three ionic currents (no leakage and no sodium currents).
A voltage-gated potassium channel (corresponding to K,V here) is described by a sigmoidal function for its asymptotic value and a differential equation for the opening probability (same as here). Inactivation of K,V channels is not considered.
A calcium-gated potassium channel (corresponding to K,Ca here), which is described by a Hill function with Hill coefficient nK,Ca = 1.
A calcium channel (corresponding to Ca,L here) including inactivation and fast activation.
Constant reversal potentials are assumed (no Nernst equation is used).
The steady state of the system is defined as zero current of the three currents contributing to the voltage equation (thus no leakage currents are considered).
An equation for calcium ions including two terms and a constant factor f = 0.001 compensating for the buffer (thus, no buffer dynamics). One term accounts for Ca,L currents, the second for calcium removal (corresponding to PMCA here).
PMCA activity is not described by a Hill function but increases linearly with the calcium concentration. Note that in Sherman et al. (3) the calcium extrusion term is assumed to be electroneutral, which is not the case because calcium is mainly removed by the nonelectroneutral PMCA. Thus the PMCA current also enters the equation for the membrane potential Eq. 4 in this model.
The full model as introduced in Methods is reduced to these properties and the results in Sherman et al. (3) are reproduced (data not shown). In a second step some parameters are modified to experimentally known values: capacity, resting concentrations, reversal potential of calcium. All these changed values are collected in Tables 2–5 in Supplementary Material. Surprisingly, all modifications together only moderately alter the results (see Fig. 2).
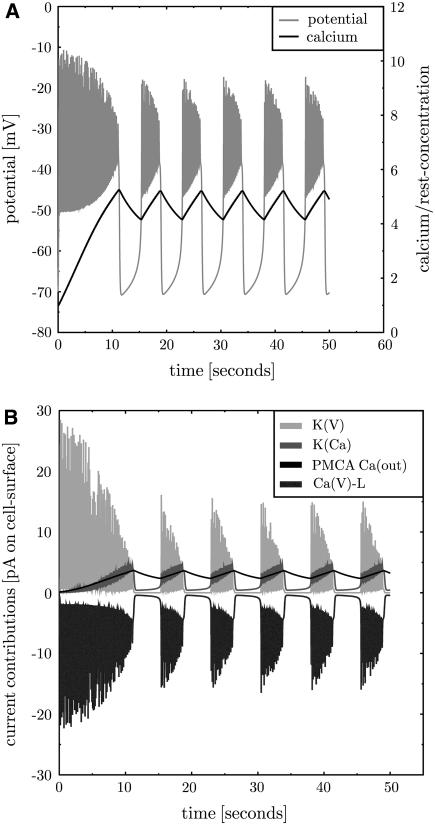
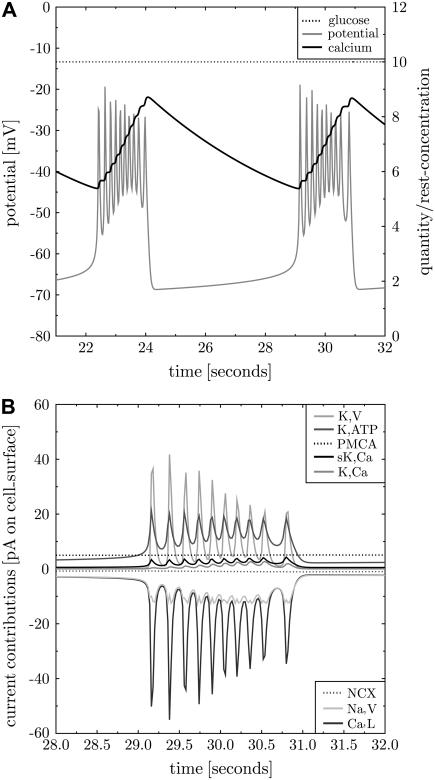
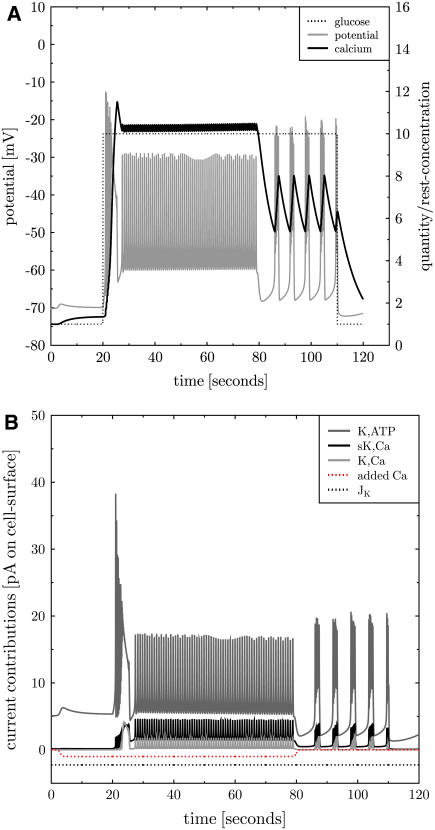
FIGURE 2.
The simulation is consistent with Sherman et al.'s (3) model. A simulation of the model of Sherman et al. (3) with adapted parameters (see Tables 2–5 in the Supplementary Material). The membrane potential (panel A, gray line) exhibits repeated bursts. Intracellular calcium is plotted as ratio to the resting concentration of 0.1 μM (panel A, black solid line). It rises during bursts and decreases during silent phases. The contributions of the transmembrane currents are shown in panel B (the inset lists the currents in the sequence of vertical appearance). Oscillations occur between voltage-gated potassium (K,V, panel B, light gray line) and calcium channels (Ca,L, panel B, dark gray line). K,Ca and PMCA activity follow the calcium level (panel B, medium gray and black line, respectively).
The channels in the initial state of the simulation are not equilibrated (thus not in a steady state). This induces a certain inflow of calcium through Ca,L, which depolarizes the cell. As the K,V current reacts with a delay the potassium outward current comes later and allows for an above-threshold depolarization. This leads to the oscillation on a higher voltage level. Now, free calcium accumulates in the cell due to repeated inflow. Note that the largest part of the incoming calcium is assumed to bind to the buffer, such that calcium accumulates much slower than according to the calcium inflow. More calcium induces increasing gK,Ca and PMCA activity, which in turn increases the potassium and calcium outflow, respectively. The oscillations are suppressed for some threshold K,Ca and PMCA conductance. From here the whole process restarts. The essential properties are the delay between Ca,L and K,V current, the calcium buffering that induces a slow calcium increase, and a membrane protein that reacts to the increased calcium level by interrupting oscillations.
The back reaction of PMCA activity on the membrane potential was neglected in Sherman et al. (3). If this is included into Sherman et al.'s (3) model, bursting disappears. The back reaction of PMCA activity on the membrane potentials induces hyperpolarization of the cell. This infers that K,V and K,Ca (in view of the reversal potential of 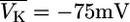 ) but more importantly Ca,L (because of very low opening probability) are almost inactive. In this situation PMCA reduces intracellular calcium below its resting state whereas further hyperpolarizing the cell. In conclusion, the neglect of a back reaction of the process, which removes calcium from the cell, on the membrane potential turns out not to be a justified approximation.
) but more importantly Ca,L (because of very low opening probability) are almost inactive. In this situation PMCA reduces intracellular calcium below its resting state whereas further hyperpolarizing the cell. In conclusion, the neglect of a back reaction of the process, which removes calcium from the cell, on the membrane potential turns out not to be a justified approximation.
β-Cell bursting with calcium, potassium, and sodium currents
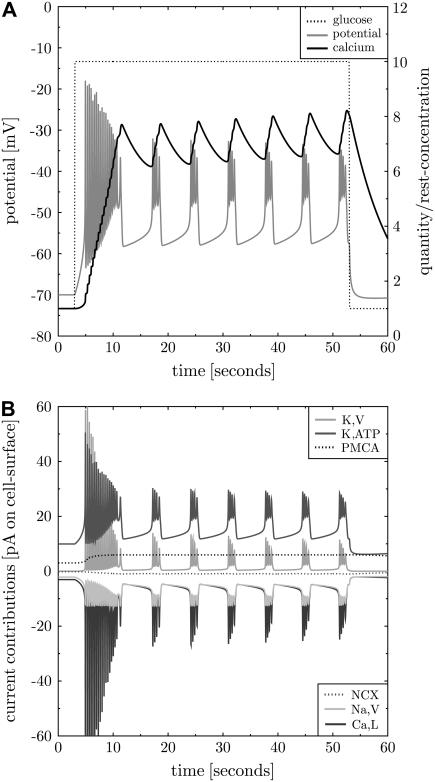
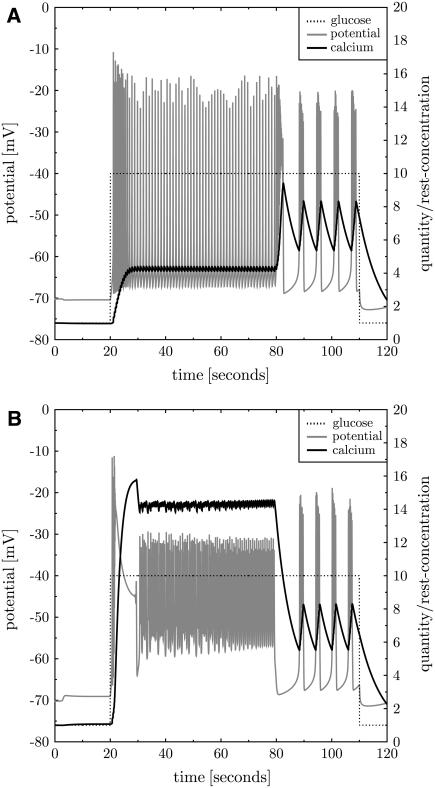
The second simulation includes all membrane proteins as introduced in Methods and, thus, extends the model (3). The characteristics of activation and inactivation are taken from single protein experiments. The densities are adapted to find reasonable electrical bursting and reasonable currents. Bursting shall be fast as found in isolated β-cells (13). The frequency is around six bursts per minute (see also Beauvois et al. (28) (Fig. 2 A measured in islets)). The spiking baseline (lower bound of bursts) shall be in the range of −50 mV and the peaks shall reach −20 mV (7). The bursts shall be shorter than the intermediate silent phases (7). The bursting baseline reached between the bursts is not allowed to exhibit hyperpolarization. The resulting set of densities is given in Supplementary Table 5 (full model). Thereby, some densities could be estimated from the whole-cell conductance (see below and references in Table 5, Supplementary Material). First, the steady state is established and then the cell is stimulated by 10 mM glucose. The result fulfilling the aforementioned constraints is shown in Fig. 3.
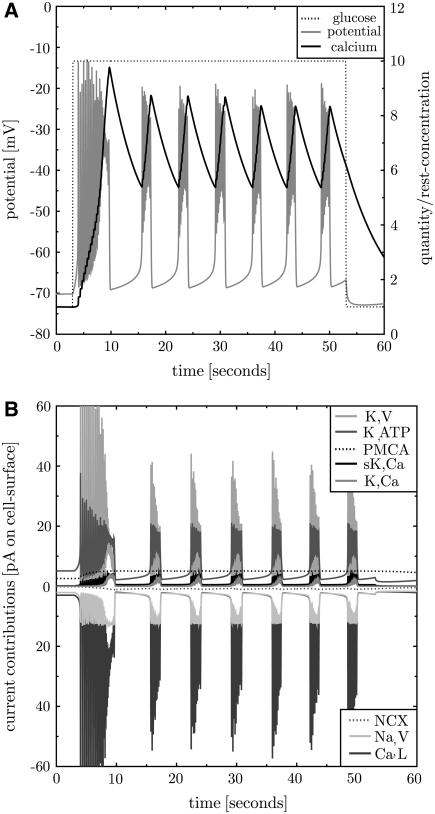
FIGURE 3.
Repeated bursting including all transmembrane proteins. The full model for the β-cell electrophysiology is used to simulate bursting after activation with glucose. Before stimulation the β-cell exhibits a stable steady state. Activation with 10 mM glucose at t = 3 s (panel A, dotted line) first leads to instabilities. Then the membrane potential (panel A, gray line) shows regular repeated bursting activity. The burst to silent ratio and the bursting frequency correspond to those observed in fast bursting isolated β-cells (13). The intracellular calcium level (panel A, black solid line) increases and decreases in cycles corresponding to the bursts. The whole-cell contributions of the different currents are shown in panel B (the proteins in the inset are given in the vertical sequence of the current contributions). Note that here and in the corresponding subsequent figures the electrical currents, not ion currents, are shown. Therefore the NCX current appears with negative sign.
The whole-cell peak ion currents are 12, 40, and 60 pA for sodium, calcium, potassium, respectively. Indeed, the peak potassium currents in human β-cells at depolarizations to −20 or −10 mV were measured in the range of 50 pA (29). This corresponds to a small open probability of K,V in both, the simulation (see Fig. 4) and the experiment. The whole-cell K,ATP conductance is 1 nS at 1 mM glucose (derived from Fig. 4 as 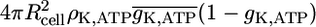 ), which compares to 1–3 nS in intact mice islets (26). The K,ATP conductance is reduced to 40% after increase of glucose to 10 mM (30) (in intact mouse islets), which is in perfect agreement with the model (see Fig. 4, panel A, dashed-dotted line starting at 0.5). Isolated β-cells were investigated with methyl succinate as a substitute for glucose (31). At the same time the K,ATP current increases from ∼5 pA to ∼20 pA after stimulation. A similar relation is found in Goepel et al. (30). At the end of a burst the ratio of sK,Ca to K,ATP currents is 4.2 pA/20 pA = 0.21, which is in good agreement with the value of 0.2 observed in mice islets (30).
), which compares to 1–3 nS in intact mice islets (26). The K,ATP conductance is reduced to 40% after increase of glucose to 10 mM (30) (in intact mouse islets), which is in perfect agreement with the model (see Fig. 4, panel A, dashed-dotted line starting at 0.5). Isolated β-cells were investigated with methyl succinate as a substitute for glucose (31). At the same time the K,ATP current increases from ∼5 pA to ∼20 pA after stimulation. A similar relation is found in Goepel et al. (30). At the end of a burst the ratio of sK,Ca to K,ATP currents is 4.2 pA/20 pA = 0.21, which is in good agreement with the value of 0.2 observed in mice islets (30).
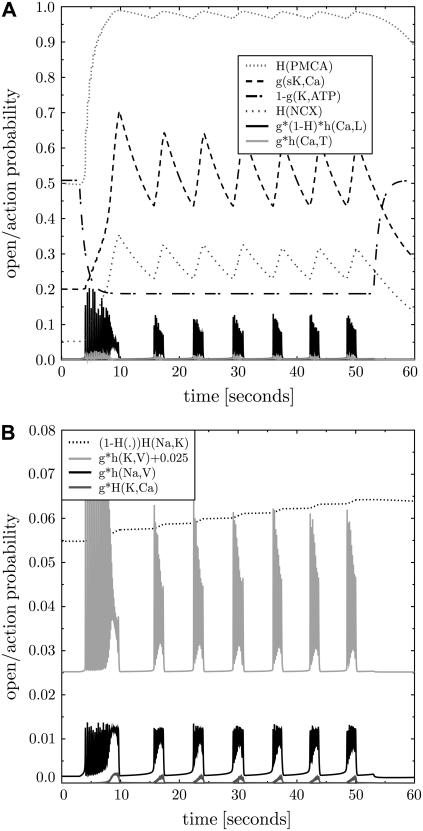
FIGURE 4.
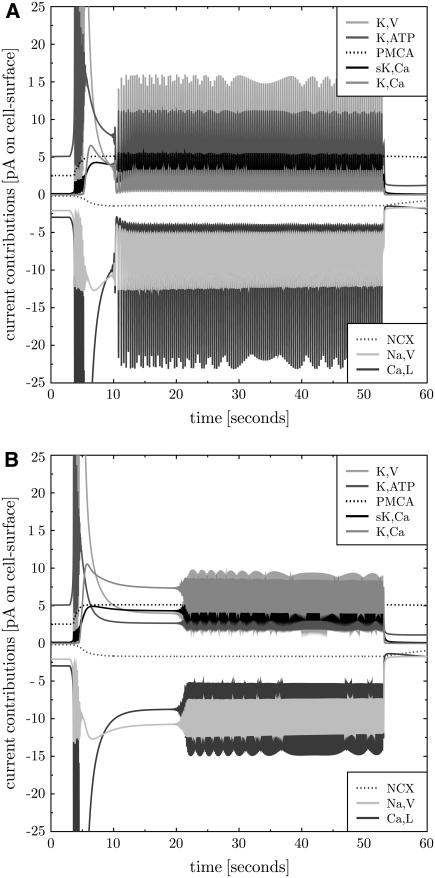
Opening/activity states of the membrane proteins. The states of the transmembrane proteins during bursting as given in Fig. 3 are shown as probability of activity or opening. Panel A collects all calcium-relevant proteins as well as sK,Ca and K,ATP channels. Panel B collects all sodium-relevant and other potassium-conducting proteins (note the different scale in the panel B and the shifted open probability for K,V channels). The inset lists the probabilities in the sequence of vertical appearance and gives a hint how the probabilities are calculated (see Supplementary Material for details). Note that the PMCA activity is at its limit in an actively bursting β-cell. The different kinetic single protein characteristics are reflected in two classes of protein response: fast spiking and slowly adapting ones.
Whole-cell calcium currents during bursts depend on the external calcium concentration (32). In isolated mouse pancreatic β-cells at depolarizations to −20 mV currents between 30 and 60 pA are found, which is consistent with the simulation results. However, the values vary between 10 and 350 pA per cell depending on the mode of stimulation and the species (26,29,32–35).
Sodium currents through noninactivated Na,V channels are in the range of 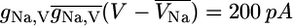 (see Eq. 9 in Supplementary Material) at V = −10 mV in mice and rats (19,33,26). In view of peak inactivations of hNa,V = 96% in the simulations (data not shown) these measurements correspond to currents in the range of 8 pA.
(see Eq. 9 in Supplementary Material) at V = −10 mV in mice and rats (19,33,26). In view of peak inactivations of hNa,V = 96% in the simulations (data not shown) these measurements correspond to currents in the range of 8 pA.
An analysis of the contributions of the different membrane proteins induces a picture that in part coincides with the one proposed by Sherman et al. (3). However, there are also some important modifications. The importance of specific proteins is analyzed and disentangled in subsequent knock-out, block, and overexpression experiments. The latter two correspond to the variation of protein densities.
High resolution of burst events
A single burst event in Fig. 3 is analyzed at high resolution in Fig. 5. The analysis is started when the membrane potential has reached its minimum. Because of the increased glucose level K,ATP conductance is reduced (8). This induces a slightly depolarized state of the cell. Depolarization is amplified by Ca,L and Na,V current. The K,V currents are suppressed in this phase of the burst event. This is not related to the delayed activation (which causes 50 ms at the most) but to the general single protein activation properties. These do not allow for a strong K,V current near the reversal potential of potassium. K,V currents become relevant only after strong depolarizations that are induced by strong Ca,L currents. The delay of K,V response with respect to the Ca,L dynamics leads to stable oscillations. Calcium levels increase with each depolarizing spike. This induces small K,Ca and sK,Ca currents, involving a slightly decreasing frequency of spikes during each burst event, which is in agreement with experimental data (7,28).
FIGURE 5.
High-resolution view on a burst event. The third bursting event in Fig. 3 is at higher resolution. All shown curves have the same meaning as explained in the legend of Fig. 3.
The interruption of bursts is related to proteins that rely on a slow variable. These are PMCA, K,Ca, and sK,Ca, where the slow variable is calcium. Also Ca,L activity contributes to burst interruption because of calcium-dependent inactivation (34). In addition, the reversal potential plays a role. For calcium it changes from 27 mV at the beginning of a burst to 22 mV at the end of a burst (see Fig. 14 in the Supplementary Material). This reduces the calcium currents through voltage-gated channels by ∼8% (at V = −40 mV) and is a contribution to the interruption of bursts. Consistently, replacing the Nernst equation by constant reversal potentials (the ones corresponding to the resting state) leads to continuous spiking (data not shown). However, bursting is also possible with a constant reversal potential.
Knock-out of K,Ca and sK,Ca protein
The calcium-gated potassium channel K,Ca is implemented according to single membrane protein characteristics (14), which differ in some important aspects from the values used in other β-cell models. The measured opening dynamics depends on the membrane potential and the calcium concentration in a complicated way. A detailed analysis of the measured data (see Supplementary Material (page 7)) has revealed that, in addition, the asymptotic opening probability for a given calcium concentration also depends on the membrane potential (see Supplementary Eq. 21 in the Supplementary Material; also Horrigan and Aldrich (36)).
In agreement with experiment (37) it is found that under normal conditions the K,Ca currents remain rather small because of a low opening probability. This finding suggests that K,Ca might even be unnecessary for repeated bursting. Indeed, K,Ca can be knocked out without altering the results at normal glucose levels up to 12 mM. The increased K,Ca currents at the end of a burst are fully replaced by sK,Ca currents.
The sK,Ca current is believed to abort burst events when calcium is sufficiently increased (38). It is found that in a double K,Ca and sK,Ca knock-out experiment, bursts are still interrupted. K,Ca and sK,Ca are switched off (ρK,Ca = ρsK,Ca = 0) and other densities have to be slightly adapted to ρK,ATP = 0.15/μm2 and ρPMCA = 1300/μm2 to keep regular bursting (see Fig. 6). Note that this simulation does not correspond to a block of calcium-gated potassium channels. The β-cell is constructed without K,Ca, thus, this simulation corresponds to a knock-out experiment.
FIGURE 6.
β-Cell bursting without calcium-gated potassium channels. Simulation without sK,Ca and K,Ca channels and with protein densities adapted to ρK, ATP = 0.15/μm2 and ρPMCA = 1300/μm2. A cell behavior comparable to Fig. 3 can be found without direct impact of calcium on potassium currents. Lines are explained in the legend of Fig. 3.
In the normal β-cell sK,Ca activity increases at high calcium levels at the end of each burst (see Figs. 3 and 4) leading to potassium efflux. This counterbalances the calcium influx and drops depolarization. In the simulation without K,Ca and sK,Ca, PMCA takes over this function. However, PMCA activity is already at its limits during bursts (see Fig. 4), which even more holds in the double knock-out experiment (not shown).
The K,Ca-sK,Ca double knock-out experiment suggests that for low calcium concentrations PMCA has an important role in burst interruption and can replace the function of sK,Ca channels. K,Ca channels only turn relevant for much larger calcium concentration of more than 1 μM. In this regime PMCA and sK,Ca are not sufficiently flexible to further increase activity and, thus, to interrupt bursting. It will be seen later that at high calcium concentration K,Ca acquires other functionality.
Stimulation by raising external potassium
The effect of increased external potassium levels on β-cells is investigated. Starting from a β-cell in its resting state at normal external potassium Kext = 5.7 mM, external potassium is increased to different values using a steep sigmoidal function. The β-cell that had adapted to the lower potassium level is stimulated because the reduced chemical gradient pushes potassium into the cell and depolarizes it.
For moderately increased external potassium the cell first exhibits a smooth depolarizing calcium current. Larger Kext then leads to K,ATP-induced action potential-like events involving potassium and calcium currents, and finally into a burst-like activity at Kext = 8 mM. However, this remains a unique event (data not shown). The burst is interrupted by sK,Ca and K,Ca currents at a rather high and constant calcium level around 1 μM. Despite a new depolarized equilibrium state that normally would induce action potentials, repeated bursting is prohibited by the constant strong activity of PMCA, K,Ca, and sK,Ca.
Stepwise increase of glucose levels
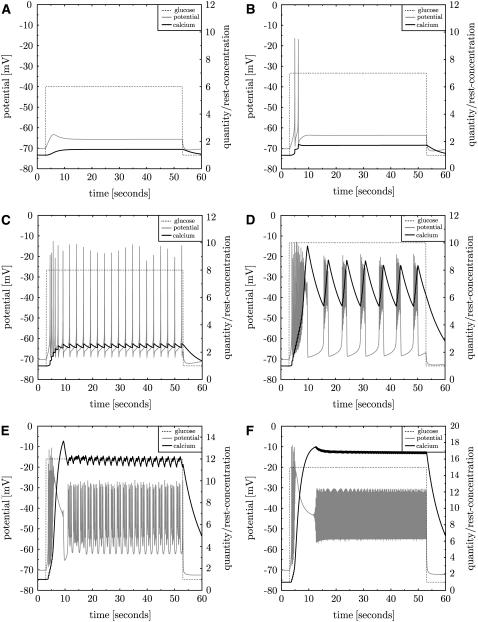
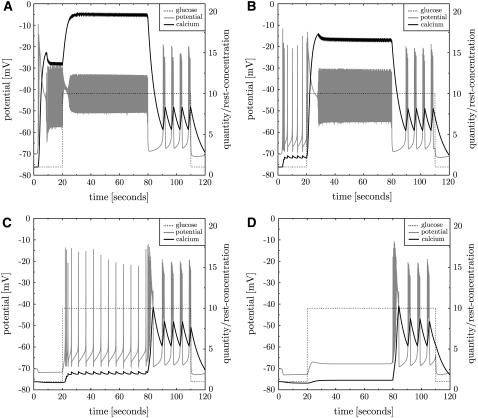
The full model is used to investigate the β-cell behavior after stimulation with various glucose levels between the resting value γ0 = 1 and 30 mM. The β-cell reaction is shown in Fig. 7 for some examples. As found in islets (28) calcium levels constantly increase with increasing glucose levels. Up to 6 mM glucose only a smooth increase of the membrane potential is found which then stabilizes on a higher level. This threshold for an effect of glucose on the calcium level is in agreement with data from islets (28). A single action potential appears around 7 mM. The spikes then turn into regular firing with increasing frequency between 7 and 9 mM. The high-frequency spikes then are interrupted and replaced by repeated bursting around 10 mM. For even larger glucose levels the burst/silent ratio is increased and finally continuous spiking is found (at 13 mM), which is also found in islets (7), even though at little higher glucose levels. Continuous spiking is suppressed for >25 mM glucose.
FIGURE 7.
The β-cell reaction to increased glucose levels. Glucose stimulation is increased in several steps γstimulation = 6, 7, 8, 10, 12, 15 mM (panels in reading order). The membrane potential (gray line) and the calcium concentration (black line) are shown. Repeated bursting is found for stimulation with ∼10 mM glucose. Less glucose only induces single spikes, more leads to continuous spiking.
Steepness of glucose increases
In experiments it is observed that the initial spike or burst is more intense than subsequent ones. According to the simulations this is related to the steepness of the switch to the higher glucose level. With smooth sigmoidal functions the initial spike can be fully suppressed. Similarly, long initial bursts can turn to a normal duration. However, the steepness of the glucose increase changes only the initial action potentials or prebursting events. The long-term bursting behavior does exclusively depend on the asymptotic glucose level irrespective of how quick it is reached.
The role of K,Ca currents at supralarge glucose
There is an unexpected diversity of model behavior at high glucose levels depending on the model assumptions. Continuous spiking for supralarge glucose levels is only found with the novel model for K,Ca activation (see Supplementary Material (page 7)). The simpler model for K,Ca activation leads to suppression of any spike for large glucose, which is in contradiction to experiment. The relevant single channel properties in this context are the large half-activation calcium concentration and the delayed activation (in analogy to K,V channels). This underlines the necessity to rely on the measured electrophysiology of single K,Ca channels. A rather weak role of K,Ca channels during normal electrical activity is inferred. K,Ca gets relevantly active only at very high calcium concentrations that are associated with high glucose concentrations.
A more detailed analysis of Fig. 7 reveals that continuous spiking at supralarge glucose levels is based on oscillations in the K,Ca current. Whereas at γ = 13 mM the K,V current is dominant, at 20 mM it is the K,Ca channel that provides the largest contribution to the potassium current (see Fig. 8). Instead of K,V and Ca,L it is now K,Ca and Ca,L that are swinging. Note that sK,Ca channels do not exhibit the potential to actively oscillate with Ca,L because of their independence of the membrane potential. This result suggests an additional role of K,Ca channel in the electrophysiology of the β-cell: it defines the electrical activity at supralarge glucose and calcium concentrations.
FIGURE 8.
K,Ca is the main oscillator at large glucose levels. The current contributions of K,Ca and K,V to continuous spiking for glucose levels of 13 (A) and 20 mM (B) are shown. Whereas at 13 mM the main contributors to the oscillations are K,V (light gray solid line, positive current) and Ca,L (dark gray solid line, negative current), these are K,Ca (medium gray solid line, positive current) and Ca,L at 20 mM glucose. The contribution of K,ATP channels is also strongly reduced at suprahigh glucose levels (dark graysolid line, positive current), whereas sK,Ca currents are almost unaltered (black solid line, positive current).
Addition of a constant calcium current
The behavior of β-cells in response to a small additional negative calcium current of −1 pA is investigated. This current corresponds to calcium flow into the cell. The involved depolarization increases K,ATP currents and the calcium baseline. The novel steady state at higher calcium can only be maintained with a higher PMCA activity. If then glucose is turned to γ = 10 mM continuous spiking is found. When the additional calcium current is turned off normal repeated bursting is recovered (see Fig. 9). Continuous spiking is also found when the additional calcium current is applied after onset of repeated bursting at high glucose levels. The sequence of stimulation events is not important. Thus, it is found that small additional calcium currents modify the effect of the glucose stimulus.
FIGURE 9.
Additional constant calcium current. An additional whole-cell calcium current of −1 pA (additional calcium influx) is applied after 3 s (panel B, gray dotted line). This increases the calcium baseline (panel A, black line). At t = 20 s glucose is turned to γ = 10 mM (panel A, black dotted line), which induces continuous spiking (panel A, gray line). At t = 80 s the additional current is switched off and repeated bursting (as in Fig. 3) is recovered. At t = 110 s glucose is turned back to its resting value. Panel B shows all but K,V whole-cell potassium currents.
Partial block of PMCA and NCX
A very similar result (to Fig. 9) is found when the PMCA current is reduced to 80%. The calcium baseline is increased and at 10 mM glucose continuous spiking is found. Substantially stronger inhibition of PMCA activity suppresses bursting after an initial burst event (data not shown).
A partial block of the sodium-calcium-exchanger (NCX) current leaves the duration of bursts invariant but increases the burst/silent ratio. This leads to continuous spiking when only 60% of the current is left. The characteristics of this continuous spiking differ from the one found after block of PMCA; the calcium baseline is slightly decreased and, instead of stronger calcium elevation during continuous spiking, the calcium elevation is reduced (data not shown; see Fig. 11 A for corresponding characteristics). Continuous spiking here resembles more fast repeated beating.
FIGURE 11.
Modulating Na,V currents. Na,V currents are inhibited to 90% (panel A) and increased to 140% (panel B) using the same protocol as in Fig. 9. The calcium baseline (solid black line before stimulation with glucose) is reduced and increased, respectively. At 10 mM glucose (see t > 20 s) fast and continuous spiking are found, respectively, with differing characteristics. Continuous spiking with increased calcium baseline is similar to Fig. 9 and reaches large calcium levels after glucose stimulation (panel B). Fast spiking with reduced calcium baseline exhibits a larger spiking amplitude and baseline, and the reached calcium level is lower (panel A).
Overexpression of NCX in a sK,Ca knock-out system leads to prolonged burst duration, as was also found in Gall and Susa (11). Such an effect is not observed in the full model including sK,Ca. NCX currents are not only depolarizing in this model. In addition, the intracellular calcium concentration is reduced, which has impact on the activity of other proteins leading to nontrivial effects.
Modulation of K,ATP with tolbutamide and diazoxide
Block of K,ATP currents was investigated in patch-clamp experiments with β-cells in intact islets (7). In silico the application of tolbutamide corresponds to a reduction of the K,ATP protein density ρK,ATP in a cell that has established its steady state in the presence of normal K,ATP densities. A reduction of K,ATP currents to 75% leads to a result almost identical to Fig. 9. An increased calcium baseline is established. This happens because the reduced potassium outflow depolarizes the cell which, in turn, partially opens voltage-dependent calcium channels. The new equilibrium state is, thus, established on a higher level of calcium influx.
When glucose is increased to 10 mM continuous spiking is induced. As in experiment (7) this is reversible: after release of partial K,ATP-block normal repeated bursting behavior is reestablished. This happens in the simulation without any additional stimulation. In Kanno et al. (7) the β-cell was depolarized several times in voltage-clamp mode.
It is possible to stimulate β-cells by partial block of K,ATP currents. Repeated bursting is induced at resting glucose level (see Fig. 10 B for a 50% block). When glucose is increased at t = 20 s repeated bursting turns into continuous spiking. Such a behavior was also found in β-cells (31). There also a mutation of the K,ATP channel (relevant to neonatal diabetes) was investigated, which exhibits substantially larger half-inhibition values γK,ATP. It was found that the electrical activity is suppressed with the mutated channel. When the K,ATP channels are blocked with tolbutamide continuous spiking is found. This behavior is consistent with the simulation (see Fig. 16 in Supplementary Material).
FIGURE 10.
Inhibition and overactivation of K,ATP. K,ATP is blocked to 25% at t = 3 s (A). This induces strong depolarization, calcium inflow, and continuous spiking. At t = 20 s glucose is turned to γ = 10 mM, which only weakly influences continuous spiking because of the K,ATP block. At t = 80 s the block is released and repeated bursting is recovered (as found in Fig. 3). At t = 110 s glucose is turned back to its resting value. Panel B shows the result of the same protocol with partial block of K,ATP channels to 50%. High-frequency repeated bursting is found at resting glucose levels. Overactivation of K,ATP with diazoxide hyperpolarizes the cell (C and D). At high glucose levels repeated single spikes are observed (C). For even stronger overactivation, the β-cell turns silent (D).
Interestingly, a block of K,ATP channels to 25% immediately leads to continuous spiking even at the resting glucose concentration γ0 = 1 mM (see Fig. 10 A). This supports that these channels trigger bursting events by inhibition of potassium outwards currents (8). Because only a small subset of K,ATP channels (the only points of impact of glucose) is left, the switch to high glucose level at t = 20 s has only minor consequences. ATP/ADP ratios are not explicitly monitored, which would also change ATPase activities.
An overactivation of K,ATP channels (with diazoxide) at normal glucose levels hyperpolarizes the cell. At high glucose this leads to continuous spiking with decreased calcium baseline (characteristics are those of fast beating like in Fig. 11 A). At 140% K,ATP activity regular single spikes (or beating) are observed. Even larger K,ATP activity suppresses any spike even at 10 mM glucose (see Fig. 10 C and D). This behavior was also found in vivo in mice islets (39).
Modulation of voltage-gated calcium channels
Overexpression, block, or knock-out of LVA calcium channels Ca,T have only minor effect on the bursting behavior. To see continuous spiking, LVA channels have to be overexpressed by a factor of 4. Inhibition only weakly modifies the calcium baseline before stimulation with glucose. The amplitude of spikes of the membrane potential is slightly increased and burst frequency is reduced (data not shown). According to these simulations, LVA has to be considered unimportant for β-cell bursting. Note that the simulation allows us to replace parts of the Ca,L currents by Ca,T currents without altering the results.
Moderately inhibited (80%) or strengthened (140%) Ca,L currents lead to continuous spiking combined with a lowered and increased calcium baseline, respectively (characteristics similar to those in Fig. 11). For stronger inhibition (20% remaining) spiking activity disappears, which is consistent with the dominant role of the Ca,L current for β-cell oscillations. Removal of calcium-dependent inactivation of Ca,L currents (see Supplementary Eq. 25) impacts on burst interruption (not shown).
Modulation of sodium currents
The sodium-potassium exchanger Na,K uses ATP to transport both sodium and potassium against their electrochemical gradient. Even though this membrane protein is only weakly active in the resting state, shows little dynamics upon β-cell stimulation (variations of intracellular potassium and sodium concentration are relatively small; see also Grapengiesser (40)), and induces only small currents, the bursting behavior is sensitive to partial block of the exchanger in the simulation. A corresponding effect was observed before in experiment with ouabain (41,40). Both inhibition and overexpression of Na,K increases burst frequency. The duration of bursts is increased when Na,K currents are increased. This is also reflected in the stepwise increase of Na,K activity after every burst (see Fig. 4 B, dotted line). At <60% and at >120% Na,K current continuous spiking is found, with increased and decreased calcium baseline before stimulation with glucose, respectively, which is in agreement with previous results (2). Due to the weak dynamics of Na,K currents corresponding effects are only found in Na,K block but not in Na, K knock-out experiments.
Similarly the voltage-dependent sodium channel Na,V is generally not considered to play a major role in β-cell electrophysiology. At a partial block to 90% (down to 70%) continuous spiking is found together with a slightly reduced calcium baseline (see Fig. 11 A). Continuous spiking is also found if the Na,V currents are increased by a factor 1.4 or higher together with a slightly increased calcium baseline (see Fig. 11 B). The different characteristics of fast or continuous spiking point to two underlying mechanisms (see Discussion).
Modulation of non-K,ATP potassium currents
Inhibition of K,Ca currents reduces the burst/silence ratio and the bursting frequency. Even if the K,Ca currents are fully blocked bursting is still observed. Increased K,Ca currents lead to increased burst/silence ratios and at 190% to continuous spiking (the characteristics correspond to those as found in Fig. 11 A). The calcium baseline and the membrane potential are not visibly altered by modulation of the K,Ca currents (data not shown).
Overexpression of sK,Ca leads to a reduced calcium baseline and to increased burst frequency. At 130% quasicontinuous spiking is found. Inhibition of sK,Ca currents increases the calcium baseline, reduces hyperpolarization, and increases burst frequency, as also expected from experimental results (38). Only for a total block continuous spiking is found.
Increased K,V currents to 110% lead to continuous spiking. A reduction of K,V currents reduces the burst/silence ratio. Surprisingly, even with totally blocked K,V currents, oscillations are still found with almost unaltered calcium baseline. The potassium current in the action potentials is then taken over by the K,Ca currents (not by sK,Ca currents). This shows that K,Ca proteins have the potential to drive the oscillations during burst events—similar to the scenario found for supralarge glucose levels.
Long-term stimulation
Stimulation by increased glucose levels not only induce repeated bursting, the β-cell is also shifted out of its resting state. If stimulation by glucose is applied for long durations, and assuming in a thought experiment all other cell properties unaltered during that period, the β-cell might find a novel stable resting state, which is in equilibrium with the high glucose level. The simulation in Fig. 3 is repeated with 10 mM glucose applied for 1 h. Due to limited responsiveness of Na,K exchangers each burst event (involving Na,V-current oscillations) increases the intracellular sodium level. After half an hour sodium reaches a novel resting state at 170% of its resting concentration adapted to the ongoing stimulation. Similarly the intracellular potassium concentration decreases to a new equilibrium state. Now, Na,K activity and sodium inflow at each bursting event get into equilibrium with a doubled Na,K current. Repeated bursting is still present at this higher sodium state with slightly modified spiking and bursting baselines, burst duration, and amplitude (see Fig. 15 in the Supplementary Material).
DISCUSSION
A bottom-up approach for the β-cell with quantitative ambitions
A simulation tool for the electrophysiology of β-cell was introduced. The model is strictly based on experimental data for single membrane protein activity or conductance measurements. This is considered to be a first step toward a quantitative modeling of β-cell electrical activity. Previous modeling work either structurally considered only those elements necessary to induce bursting or omitted some essential protein properties. All previous models relied on whole-cell experiments. Thus, this model can be considered to be the first bottom-up approach of the β-cell starting at the molecular level and predicting emerging properties on the cellular scale.
Improvements with respect to other modeling approaches
This model, besides relying on single protein characteristics, includes several β-cell properties that have been neglected in previous modeling approaches. It was found that the back-reaction of the PMCA currents on the membrane potential are very important and strongly alter bursting behavior as found in the literature (1–3). The inactivation properties (neglected in Fridlyand et al. (2)) of the channels turn out to be relevant for burst interruption and the stability of oscillation. Finally, the Nernst equation was used to dynamically calculate the reversal potential (which was assumed constant in the literature (1,3,5)) and turned out to substantially change the currents during burst events.
The endoplasmatic reticulum might change the dynamics
Even though a block of processes related to the endoplasmatic reticulum does not affect β-cell oscillations (25), calcium-induced calcium release might well modify the dynamics of raising calcium. These modifications might lead to adaptations of protein densities. Also the simple-minded cell geometry has impact on the protein densities. Thus, even though the resulting whole-cell currents are realistic, the protein densities used in the simulations (see Table 5 in the Supplementary Material) are not considered as a quantitative prediction in this stage of the model. Note that calcium pumps in the endoplasmatic reticulum will in first approximation act as an additional sink of free calcium, which, in this model, is effectively included in a large concentration of calcium binding sites.
Characteristics of glucose-dependent β-cell stimulation are reproduced
Despite the necessity for further improvement, the agreement with current experimental data is rather convincing and strengthens the relevance of the found results. The whole-cell currents are in the right range (19,26,29,33). Bursting is found in the same regime of glucose levels as in experiment (7,28). The glucose threshold for β-cell electrical response is quantitatively reproduced to be around 6 mM (28). The bursting frequency is in the range of experimental data for isolated fast oscillating β-cells (13). Although the spiking baseline is in the range of experiment (28), the potential is too strongly repolarized between the bursts (7,13,28). Continuous spiking is found for large glucose levels as in experiment (7).
In addition, the modulation of the activity of some membrane proteins leads to experimentally observed behavior (see Results). For example simulation of block and overactivation of K,ATP channels leads to continuous spiking and suppression of electrical activity, respectively, (39). The result that K,Ca channels are dispensable for β-cell bursting was also seen in mice and rats (37) despite being expressed in rat islet β-cell (42). The prominent role of sK,Ca and PMCA for burst interruption was also seen before (2,38). Thus, it can be stated that the simulation qualitatively respects the relevant characteristics of repeated bursting in β-cells.
Quantitative deviations
A more detailed analysis reveals quantitative deviations between simulation and experiment. The most relevant one concerns the range of glucose for which bursting is found. Although the simulation predicts 9–12 mM, in experiment the lower limit is at 7 mM (28) and the upper limit is at 15 mM (7). This discrepancy might be explained by a structural difference between the experimental setup and the simulation: the simulation models isolated β-cells, whereas both cited experiments investigate β-cell in a context of intact is-lets. Bursting is difficult to be induced in isolated β-cells (7), which can explain why the range of glucose is smaller in the simulations. It has to be evaluated in future research whether the gap-junction-mediated contact to other β-cells can enlarge the glucose regime for bursting. A similar reasoning holds for the result that continuous spiking is suppressed in the simulation for γ > 25 mM, which is not observed in experiment. Finally, the averaged intracellular calcium concentration reached in the simulation is too high and the potential baseline between the bursts is too low, both of which are likely to be related to spatial inhomogeneities of ions in the cell. Burst interruption can be achieved at lower average calcium concentrations if calcium concentrates at their site of entry.
A novel model of β-cell bursting
The fact that the main properties of β-cell electrophysiology are correctly described by the simulation encourages us to draw a novel picture of how β-cell bursting emerges. This picture is presented as a sequence of events:
Glucose inhibits K,ATP conductance. Increased glucose reduces the K,ATP conductance (8). This only induces a short pulse of inhibition of K,ATP currents. It slightly depolarizes the β-cell, which is further amplified by induced sodium and calcium entry through voltage-gated channels (Na,V; Ca,L; and Ca,T).
K,ATP currents increase again. Even though the opening of K,ATP channels is inhibited the current increases upon cell depolarization. According to Supplementary Eq. 14 (see Supplementary Material) inhibition is overcompensated by the increased electrochemical gradient.
Ca,L and Na,V cause electrical spiking. If the stimulus is overcritical a spike of cell depolarization is induced by voltage-dependent calcium and sodium currents.
Oscillations are induced by delayed K,V response. The potassium current repolarizes the cell, but this happens only with a delay τK,V. It is well known that delayed response can lead to stable fast oscillations.
Calcium rises during bursts. During a burst event calcium and sodium is constantly entering the cell while potassium is leaving it. Although the effect on potassium and sodium is small, calcium rises because of a strong electrochemical gradient and the small resting concentration. The speed of calcium increase is controlled by the intracellular calcium buffer, and is much slower than the oscillations.
The burst is interrupted by a concerted action of PMCA, K,Ca, sK,Ca, Ca,L inactivation, and Nernst reversal potential. During bursts calcium and sodium levels increase, inferring stronger repolarizing PMCA, sK,Ca, and K,Ca currents, where K,Ca currents play a minor role at normal calcium levels (14,37), and reduce depolarizing Na,V and Ca,L currents. Ca,L inactivation also relies on the slow variable calcium and contributes to burst interruption. In addition the calcium reversal potential is reduced further inhibiting calcium currents. At critical calcium and sodium concentrations oscillations are suppressed.
Restoration after burst events is governed by PMCA, NCX, and Na,K. In complete analogy to neuronal repolarization, ATPases and exchangers are needed to reestablish the resting concentrations.
Note that this model differs from older models in several aspects that are discussed in more detail in the following.
Two types of fast repeated spiking
Fast repeated spiking is found in two versions (see Fig. 11). One comes with a reduced, the other with an increased, calcium baseline (before stimulation with glucose). Why is fast-repeated spiking found with reduced calcium baseline? A reduced calcium baseline is induced when Na,K is overactivated, Na,V or Ca,L are inhibited, NCX is blocked, and K,ATP or sK,Ca are overactivated. All these modifications tend to polarize the cell. This reduces the calcium influx through voltage-gated calcium channels, and, in turn, reduces the calcium baseline. In the same way intracellular potassium levels are increased because of less potassium efflux. This corresponds to a stimulation in complete analogy to the inhibition by K,ATP channels with glucose.
Thus, we have to distinguish low and high calcium continuous spiking. β-cells become prone to oscillations either by increased calcium baseline or by increased potassium baseline. The equilibrium of both is regulated by the sodium currents. Despite the sodium-conducting proteins playing an unspectacular role in β-cell activity they nevertheless influence the electrophysiology.
Note that the characteristics of both types of fast spiking differ. Although in the case of increased calcium baseline the term continuous spiking is justified (see Fig. 11 B), the scenario with lowered calcium baseline more corresponds to a high-frequency bursting with individual spikes in each burst (see Fig. 11 A) and might be called “beating”. The duration of depolarization (integrated over a burst) is smaller in the case of beating, which induces the reduced calcium level compared to continuous spiking (see Fig. 11).
Sodium currents are important regulators of β-cell electrophysiology
In the presented simulations the Na,V currents directly participate in spikes and bursting events. The activity of the β-cell is responsive to all properties of the Na,V channel. Thereby the half-activation potential VNa,V has the greatest influence. Na,V currents facilitate onset of action potentials due to their fast dynamics (the reaction time is the fastest of all considered channels), participate in the interplay with delayed potassium currents to induce oscillations, and also facilitate the end of action potentials by relatively fast inactivation. The interpretation of a tightly controlled interplay of Na,V with other membrane proteins is supported by the observation that continuous spiking is observed for partially blocked and overexpressed Na,V proteins. The latter bursting is characterized by high calcium, the former by high potassium. It turns out that Na,V currents regulate the equilibrium between both ions in β-cell stimulation. Thus, according to the model results, sodium channels are more relevant for the β-cell electrophysiology than previously considered. This result has to be verified in space-resolved models.
However, it was shown in pancreatic islets of mice that the block of Na,V channels with TTX had no major effect on β-cell electrophysiology (19,43), which is in contrast to investigations in rats (33,44). It was hypothesized that the steepness of depolarization for stimulation might overinactivate sodium currents (33). In view of the similarity of sodium currents through noninactivated sodium channels in different species it is proposed here that the difference between the species might rely on the relative sodium and calcium currents. The latter ones are rather diverse in different species. From this vantage point the simulations correspond to low calcium currents as found in rats. An alternative explanation is that the assumption of universality of membrane protein properties is wrong for sodium channels. Then one might suspect that the inactivation properties of Na,V are different in rat and mice β-cells. The simulations have the potential to investigate the differences between the species, which is left for future research.
Long-term stimulation gives rise to a third timescale
The in silico experiment of long-term stimulation of β-cells with high levels of glucose has revealed three timescales of β-cell electrophysiology:
Delay of K,V or K,Ca currents with respect to calcium and sodium induced depolarizations (10–100 ms).
Slow increase in intracellular calcium level due to intense buffering, which keeps the fraction of free calcium low (10 s).
Even slower modifications of intracellular sodium and potassium levels (1–10 min) (2).
The third timescale was observed in measurements of sodium concentrations in mouse pancreatic β-cells (40), and may acquire a role in slow bursting (2).
Tiny inhibition of K,ATP currents by glucose
In the model the only effect of increased glucose levels is inhibition of K,ATP conductance (8). The relevant inhibition of conductance turns out to be a tiny effect on the currents, which quickly is hidden by the increased K,ATP currents in response to cell depolarization. This opens the possibility of alternative effects of glucose via ATP metabolism. Several channels and transporters rely on ATP concentrations and may alter their activity in response to changed glucose levels. Some might well initiate bursting as already established for K,ATP. This might explain the recently observed insulin secretion and calcium dynamics in islets of mice lacking K,ATP activity (45).
Bursts are interrupted by sK,Ca, K,Ca, PMCA, Ca,L inactivation, and the dynamic reversal potential
Interruption of bursting only weakly relies on K,Ca currents because of small activity at physiological calcium levels (14,37). Instead, interruption is strongly related to PMCA activity (2) and to sK,Ca currents (38,30). Interestingly, the observation of longer bursts for overexpressed Na,K currents suggests that also the slow increase of sodium is still sufficient to impact on burst interruption (2), even though the effect is small in this analysis of fast bursting. Ca,L inactivation, interestingly, is rather independent of voltage and mostly relies on the calcium level (34). Thus, Ca,L inactivation depends on the slow variable calcium and directly impacts on burst interruption. Mostly neglected in former research is the impact of a dynamic calcium reversal potential (see Eq. 5) that turns out to change the calcium currents by ∼8% during a burst and has an effect on burst interruption. This result is based on the average cytosolic calcium and might change when calculating the reversal potential on the basis of calcium concentrations near the calcium entry points at the membrane in a space-resolved model.
The inactivation dynamics of Na,V channels and LVA calcium channels Ca,T also modify burst interruption (46,47). However, Ca,T channels turned out to be dispensable for β-cell bursting. Their expression depends on the species: whereas in mice they are absent, they are found in rats and humans (16,48,17). In summary, burst interruption does not rely on a single type of membrane proteins but on a concerted action of various factors that depend on a slow variable. The delay-driven oscillation between Ca,L and K,V can be disturbed by different currents.
Calcium driven potassium channels K,Ca can drive oscillations
For the first time it is postulated that K,Ca can be an active part of the bursting behavior as well. Thereby the unknown K,Ca timescale of activation is relevant: if the K,Ca adapts faster to the membrane potential (thus using a smaller τK,Ca) the currents get out of phase and continuous spiking is inhibited. Therefore, the measurement of τK,Ca is most important to learn about this predicted functionality of K,Ca currents. According to the simulation results K,Ca acquires a major role for very large calcium concentrations where, in parts, it takes over the role of K,V in oscillations. Note that this is a direct consequence of the K,Ca single protein properties, and that a corresponding role cannot be attributed to sK,Ca channels. This is because K,Ca shows a voltage-dependent regulation of the open probability whereas sK,Ca does not and, thus, acts as a passive oscillator only.
Need for spatial resolution of the model
Even though most relevant characteristics of the cell could be reproduced there are some deviations from experiment that could not be explained by a space-averaged model. Most prominent is the calcium concentration reached in the simulations, which is about a factor 2 too high. The dynamics of the membrane proteins in this bottom-up approach are not subject to optimization. This implies that the average ionic quantities in the simulation have to some extent correspond to the quantities found near the membrane in real systems to generate the same dynamics. The same reasoning explains an overestimation of the reduction of potassium after bursts, which leads to an exaggerated repolarization by ∼10 mV in the simulation. Also the dynamics of the reversal potential might be altered in a space-resolved model.
Falsification of the predictions of the simulation
An improved version of the simulation model has to be developed to see whether the predictions of the simulations and the attributed roles of various membrane proteins for β-cell electrical activity are robust. The improved model shall include the impact of intracellular calcium stores and explicitly model the dynamics of ATP. As explained above the model has to be spatially resolved. In addition, different protein expression profiles are found in mice, rats, and humans, which shall be reflected in the model. Some of the presented in silico experiments were not yet executed in real systems. The simulation tool might serve as a guide for the design of very focused and conclusive experiments. This is not restricted to the proposed experiments. On the contrary the author welcomes the challenge of the simulation model with further suggestions for experimental setups.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
Michael Meyer-Hermann thanks Michele Solimena for pointing me to the subject. M.M.H. is indebted to Michele Solimena and Marc Thilo Figge for regular and fruitful discussion and for revising the manuscript. The executable of the simulation code is written in C++, compiled under Linux, and will be provided upon request by the author using the email: m.meyer-hermann@fias.uni-frankfurt.de.
Frankfurt Institute for Advanced Studies is supported by the ALTANA AG. M.M.H. is supported by the EC New-and-Emerging-Science-and-Technology (NEST) project MAMOCELL within FP6.
Editor: Peter C. Jordan.
References
- 1.Chay, T. R., and J. Keizer. 1983. Minimal model for membrane oscillations in the pancreatic β-cell. Biophys. J. 42:181–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fridlyand, L. E., N. Tamarina, and L. H. Philipson. 2003. Modeling of Ca2+ flux in pancreatic beta-cells: role of the plasma membrane and intracellular stores. Am. J. Phyisol. Endocrinol. Metab. 285:E138–E154. [DOI] [PubMed] [Google Scholar]
- 3.Sherman, A., J. Rinzel, and J. Keizer. 1988. Emergence of organized bursting in clusters of pancreatic beta-cells by channel sharing. Biophys. J. 54:411–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chay, T. R. 1997. Effects of extracellular calcium on electrical bursting and intracellular and luminal calcium oscillations in insulin secreting pancreatic β-cells. Biophys. J. 73:1673–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bertram, R., and A. Sherman. 2004. A calcium-based phantom bursting model for pancreatic islets. Bull. Math. Biol. 66:1313–1344. [DOI] [PubMed] [Google Scholar]
- 6.Keizer, J., and G. Magnus. 1989. ATP-sensitive potassium channel and bursting in the pancreatic beta cell. A theoretical study. Biophys. J. 56:229–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kanno, T., P. Rorsman, and S. O. Gopel. 2002. Glucose-dependent regulation of rhythmic action potential firing in pancreatic beta-cells by K(ATP)-channel modulation. J. Physiol. 545:501–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ashcroft, F. M., D. E. Harrison, and S. J. H. Ashcroft. 1984. Glucose induces closure of single potassium channels in isolated rat pancreatic β-cells. Nature. 312:446–448. [DOI] [PubMed] [Google Scholar]
- 9.Cook, D. L., and C. N. Hales. 1984. Intracellular ATP directly blocks K+ channels in pancreatic B-cells. Nature. 311:271–273. [DOI] [PubMed] [Google Scholar]
- 10.Blaustein, M. P., and W. J. Lederer. 1999. Sodium/calcium exchange: its physiological implications. Physiol. Rev. 79:763–854. [DOI] [PubMed] [Google Scholar]
- 11.Gall, D., and I. Susa. 1999. Effect of Na/Ca exchange on plateau fraction and [Ca]i in models for bursting in pancreatic β-cells. Biophys. J. 77:45–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Erler, F., M. Meyer-Hermann, and G. Soff. 2004. A quantitative model for presynaptic free calcium dynamics during different stimulation protocols. Neurocomputing. 61:169–191. [Google Scholar]
- 13.Zhang, M., P. Goforth, R. Bertram, A. Sherman, and L. Satin. 2003. The Ca2+ dynamics of isolated mouse β-cells and islets: implications of mathematical models. Biophys. J. 84:2852–2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Barrett, J. N., K. L. Magleby, and B. Pallotta. 1982. Properties of single calcium-activated potassium channels in cultured rat muscle. J. Physiol. 331:211–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hille, B. 1992. Ionic Channels of Excitable Membranes, 2nd Ed. Sinauer Associates, Sunderland, MA.
- 16.Ashcroft, F. M., R. P. Kelly, and P. A. Smith. 1990. Two types of Ca channel in rat pancreatic beta-cells. Pflugers Arch. 415:504–506. [DOI] [PubMed] [Google Scholar]
- 17.Yang, S. N., and P. O. Berggren. 2006. The role of voltage-gated calcium channels in pancreatic beta-cell physiology and pathophysiology. Endocr. Rev. 27:621–676. [DOI] [PubMed] [Google Scholar]
- 18.Magee, J. C., and D. Johnston. 1995. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J. Physiol. 487:67–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Plant, T. D. 1988. Na+ currents in cultured mouse pancreatic B-cells. Pflug. Arch. 411:429–435. [DOI] [PubMed] [Google Scholar]
- 20.Fridlyand, L. E., L. Ma, and L. H. Philipson. 2005. Adenine nucleotide regulation in pancreatic beta-cells: modeling of ATP/ADP-Ca2+ interaction. Am. J. Physiol. Endocrinol. Metab. 289:E839–E848. [DOI] [PubMed] [Google Scholar]
- 21.Hopkins, W. F., S. Fatherazi, B. Peter-Riesch, B. E. Corkey, and D. L. Cook. 1992. Two sites for adenine-nucleotide regulation of ATP-sensitive potassium channels in mouse pancreatic beta-cells and HIT cells. J. Membr. Biol. 129:287–295. [DOI] [PubMed] [Google Scholar]
- 22.Detimary, P., P. Gilon, and J. C. Henquin. 1998. Interplay between cytoplasmic Ca2+ and the ATP/ADP ratio: a feedback control mechanism in mouse pancreatic islets. Biochem. J. 333:269–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ämmälä, C., O. Larsson, P.-O. Berggren, K. Bokvist, L. Juntti-Berggren, H. Kindmark, and P. Rorsman. 1991. Inositol trisphosphate-dependent periodic activation of a Ca2+-activated K+ conductance in glucose-stimulated pancreatic beta-cells. Nature. 353:849–852. [DOI] [PubMed] [Google Scholar]
- 24.Liu, Y. J., E. Grapengiesser, E. Gylfe, and B. Hellman. 1995. Glucose induces oscillations of cytoplasmic Ca2+, r2+ and Ba2+ in pancreatic beta-cells without participation of the thapsigargin-sensitive store. Cell Calcium. 18:165–173. [DOI] [PubMed] [Google Scholar]
- 25.Gilon, P., A. Arredouani, P. Gailly, J. Gromada, and J.-C. Henquin. 1999. Uptake and release of Ca2+ by the endoplasmic reticulum contribute to the oscillations of the cytosolic Ca2+ concentration triggered by Ca2+ influx in the electrically excitable pancreatic B-cell. J. Biol. Chem. 274:20197–20205. [DOI] [PubMed] [Google Scholar]
- 26.Goepel, S. O., T. Kanno, S. Barg, J. Galvanovskis, and P. Rorsman. 1999. Voltage-gated and resting membrane currents recorded from B-cells in intact mouse pancreatic islets. J. Physiol. 521:717–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dunne, M. J., C. Ammala, S. G. Straub, and G. W. G. Sharp. 2001. Electrophysiology of the pancreatic B-cell and the mechanisms of inhibition of insulin release. In Handbook of Physiology: The En-docrine Pancreas and Regulation of Metabolism. L. S. Jefferson and A. D. Cherrington, editors. Oxford University Press, Oxford, UK. 79–123.
- 28.Beauvois, M. C., C. Merezak, J. C. Jonas, M. A. Ravier, J. C. Henquin, and P. Gilon. 2006. Glucose-induced mixed [Ca2+]c oscillations in mouse beta-cells are controlled by the membrane potential and the SERCA3 Ca2+-ATPase of the endoplasmic reticulum. Am. J. Physiol. Cell Physiol. 209:C1503–C1511. [DOI] [PubMed] [Google Scholar]
- 29.Kelly, R. P., R. Sutton, and F. M. Ashcroft. 1991. Voltage-activated calcium and potassium currents in human pancreatic beta-cells. J. Physiol. 443:175–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Goepel, S. O., T. Kanno, S. Barg, L. Eliasson, J. Galvanovskis, E. Renstroem, and P. Rorsman. 1999. Activation of Ca(2+)-dependent K(+) channels contributes to rhythmic firing of action potentials in mouse pancreatic beta cells. J. Gen. Physiol. 114:759–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tarasov, A. I., S. Welters, H. J. Senkel, G. U. Ryffel, A. T. Hattersley, N. G. Morgan, and F. M. Ashcroft. 2006. A Kir6.2 mutation causing neonatal diabetes impairs electrical activity and insulin secretion from IN-1 beta-cells. Diabetes. 55:3075–3082. [DOI] [PubMed] [Google Scholar]
- 32.Rorsman, P., and G. Trube. 1986. Calcium and delayed potassium currents in mouse pancreatic β-cells under voltage clamp conditions. J. Physiol. 374:531–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hiriart, M., and D. R. Matteson. 1988. Na channels and two types of Ca channels in rat pancreatic B cells identified with the reverse hemolytic plaque assay. J. Gen. Physiol. 91:617–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Plant, T. D. 1988. Properties and calcium-dependent inactivation of calcium currents in cultured mouse pancreatic B-cells. J. Physiol. 404:731–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Smith, P. A., F. M. Ashcroft, and C. M. Fewtrell. 1993. Permeation and gating properties of the L-type calcium channel in mouse pancreatic beta cells. J. Gen. Physiol. 101:767–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Horrigan, F. T., and R. W. Aldrich. 2002. Coupling between voltage sensor activation, Ca2+ binding and channel opening in large conductance (BK) potassium channels. J. Gen. Physiol. 120:267–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kukuljan, M., A. A. Goncalves, and I. Atwater. 1991. Charybdotoxin-sensitive K(Ca) channel is not involved in glucose-induced electrical activity in pancreatic beta-cells. J. Membr. Biol. 119:187–195. [DOI] [PubMed] [Google Scholar]
- 38.Tamarina, N. A., Y. Wang, L. Mariotto, A. Kuznetsov, C. Bond, J. Adelman, and L. H. Philipson. 2003. Small-conductance calcium-activated K+ channels are expressed in pancreatic islets and regulate glucose responses. Diabetes. 52:2000–2006. [DOI] [PubMed] [Google Scholar]
- 39.Gomis, A., and M. Valdeolmillos. 1998. Regulation by tolbutamide and diazoxide of the electrical activity in mouse pancreatic beta-cells recorded in vivo. Br. J. Pharmacol. 123:443–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grapengiesser, E. 1998. Unmasking of a periodic Na+ entry into glucose-stimulated pancreatic beta-cells after partial inhibition of the Na/K pump. Endocrinology. 139:3227–3231. [DOI] [PubMed] [Google Scholar]
- 41.Grapengiesser, E. 1996. Glucose induces cytoplasmic Na+ oscillations in pancreatic beta-cells. Biochem. Biophys. Res. Commun. 226:830–835. [DOI] [PubMed] [Google Scholar]
- 42.Tabcharani, J. A., and S. Misler. 1989. Ca2+-activated K+ channel in rat pancreatic islet B cells: permeation, gating and blockade by cations. Biochim. Biophys. Acta. 982:62–72. [DOI] [PubMed] [Google Scholar]
- 43.Ashcroft, F. M., and P. Rorsman. 1989. Electrophysiology of the pancreatic beta-cell. Prog. Biophys. Mol. Biol. 54:87–143. [DOI] [PubMed] [Google Scholar]
- 44.Vidaltamayo, R., M. C. Sanchez-Soto, and M. Hiriart. 2002. Nerve growth factor increases sodium channel expression in pancreatic beta cells: implications for insulin secretion. FASEB J. 16:891–892. [DOI] [PubMed] [Google Scholar]
- 45.Szollosi, A., M. Nenquin, L. Aguilar-Bryan, J. Bryan, and J. C. Henquin. 2007. Glucose stimulates Ca2+ influx and insulin secretion in 2-week-old beta-cells lacking ATP-sensitive K+ channels. J. Biol. Chem. 282:1747–1756. [DOI] [PubMed] [Google Scholar]
- 46.Cook, D. L., L. S. Satin, and W. F. Hopkins. 1991. Pancreatic B cells are bursting, but how? Trends Neurosci. 14:411–414. [DOI] [PubMed] [Google Scholar]
- 47.Keizer, J., and P. Smolen. 1991. Bursting electrical activity in pancreatic beta cells caused by Ca(2+)- and voltage-inactivated Ca2+ channels. Proc. Natl. Acad. Sci. USA. 88:3897–3901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yang, S. N., and P. O. Berggren. 2005. Beta-cell CaV channel regulation in physiology and pathophysiology. Am. J. Physiol. Endocrinol. Metab. 288:E16–E28. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.