Intrinsic Dynamics of the Partly Unstructured PX Domain from the Sendai Virus RNA Polymerase Cofactor P

Abstract

Despite their evident importance for function, dynamics of intrinsically unstructured proteins are poorly understood. Sendai virus phosphoprotein, cofactor of the RNA polymerase, contains a partly unstructured protein domain. The phosphoprotein X domain (PX) is responsible for binding the polymerase to the nucleocapsid assembling the viral RNA. For RNA synthesis, the interplay of the dynamics of the unstructured and structured PX subdomains is thought to drive progression of the RNA polymerase along the nucleocapsid. Here we present a detailed study of the dynamics of PX using hydrogen/deuterium exchange and different NMR relaxation measurements. In the unstructured subdomain, large amplitude fast motions were found to be fine-tuned by the presence of residues with short side chains. In the structured subdomain, where fast motions of both backbone and side chains are fairly restricted, the first helix undergoes slow conformational exchange corresponding to a local unfolding event. The other two helices, which represent the nucleocapsid binding site, were found to be more stable and to reorient with respect to each other, as probed by slow conformational exchange identified for residues on the third helix. The study illustrates the intrinsically differential dynamics of this partly unstructured protein and proposes the relation between these dynamics and its function.

INTRODUCTION

Many proteins contain unstructured regions of considerable length, some of which are entirely lacking a persistent tertiary structure (1). These proteins, or protein regions, with no stable fold play important roles in numerous cellular processes and signaling events, where they make efficient use of both their high flexibility and extensive conformational freedom (2). More specifically, the unstructured character allows low affinity interactions, promotes rapid degradation of the protein, enlarges the interaction surface, enables binding to numerous structurally distinct partners, and facilitates posttranslational modifications by leaving all side chains readily accessible (3–5). In addition, unstructured protein regions can function as a string or “fishing line” between distinct protein domains. Despite their functional importance, intrinsically unstructured proteins have long remained beyond the reach of classical structural biology. These proteins can be most readily described as an ensemble of interchanging conformations, and detailed descriptions of the sampled conformational space as well as the dynamics of such unstructured ensembles can contribute to a better understanding of the important biological processes in which they are involved.

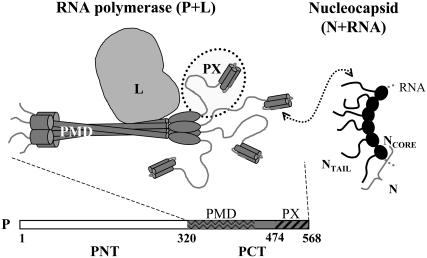
In this article we studied the dynamics of a partly unstructured protein from Sendai virus (SeV). This virus, also called murine parainfluenza virus (MPIV1), is a prototype negative-strand RNA virus. SeV belongs to the Paramyxoviridae family, which also contains measles, mumps, and human parainfluenza viruses. In these viruses the RNA genome is assembled in a nucleocapsid, where it is protected by many copies of the nucleoprotein N and where each copy of N is associated with exactly six nucleotides (6). The RNA polymerase for both replication and transcription of the viral RNA is a complex composed of the large protein L, which contains the polymerase activity and the phosphoprotein P, the tetrameric (7,8) cofactor, which places the polymerase on the N:RNA template (9) (Fig. 1). Positioning of the polymerase occurs through a highly dynamic interaction (10) of the C-terminal partly structured phosphoprotein X (PX) domain (11) of P (dotted circle in Fig. 1) and the unstructured tail of N (N_TAIL) that becomes structured upon binding to PX. Interestingly, PX is an independent protein, since it is also expressed as a sole (monomeric) domain in infected cells (12). PX comprises a disordered N-terminal subdomain (474–515) (13) and a C-terminal subdomain (516–568) having a three-helix bundle structure (14). Whereas this bundle forms the N_TAIL interaction site (15), the unstructured domain is supposed to play a pivotal role in the dynamics of RNA synthesis: RNA synthesis occurs one nucleotide at a time, whereas displacement of P on the N:RNA template occurs in steps of subunits of N. Therefore, the P tetramer is proposed to “cartwheel” across the N:RNAs, by on-and-off interactions of the PX domain with subsequent N_TAIL domains, whereas the polymerase transcribes or replicates the template RNA (10).

FIGURE 1.

Schematic representation of the SeV replicative complex. The RNA polymerase is composed of phosphoprotein (P) and large protein L, whereas L (light gray) contains the polymerase activity, and the P tetramer (dark gray) is the cofactor that interacts with L and that is responsible for the interaction with the nucleoprotein N that protects the RNA. These functions reside in the phosphoprotein C-terminus (PCT). More specifically, the phosphoprotein multimerization domain (PMD) contains the interaction site for L, and the structured part of PX contains the interaction site for the N_TAIL domain of N. For L to transcribe or replicate the RNA, P has to progress along the nucleocapsid by transient interactions of its four PX domains with successive N_TAIL domains of the nucleocapsid.

In this context we used NMR to study the dynamics of the PX domain. NMR has been shown to be a well-adapted technique for studying the dynamics of both structured and disordered protein states in solution at atomic resolution (16). Both ¹⁵N (17,18) and ²H (19,20) spin relaxation report on the fast fluctuation of the protein backbone and side chains, respectively. Slower motions, which are often related to conformational changes, can be probed by relaxation dispersion spectroscopy (21,22). In addition, experimental residual dipolar couplings (RDCs) can be reproduced remarkably well using a statistical coil model to define the conformational space explored by the unstructured peptide chain (13,23). NMR constraints are also used to direct conformational sampling in either restrained molecular dynamics or Monte Carlo simulations (24,25). Analysis of NMR relaxation data to extract timescales and amplitudes of the underlying motions is not straightforward in the case of an unstructured protein, since the common decoupling of global and internal motions no longer has any relevance. Several methods have been proposed to circumvent this problem, for example, determination of an effective correlation time per residue (26,27) or a distribution of correlation times (28). A more detailed interpretation of the relaxation rates of unstructured systems is provided by the iRED (isotropic reorientational eigenmode dynamics) method (29) developed by Brüschweiler and co-workers, which relies on a principal component analysis of the covariance matrix from a molecular dynamics trajectory, where the correlation times of the extracted eigenmodes are adjusted to optimally reproduce the experimental relaxation rates.

Here we used different NMR methods to describe the dynamics of this partly unstructured protein PX in detail. Backbone dynamics are probed by identifying infrequent events using hydrogen/deuterium (H/D) exchange experiments, ms-μs motions measured by relaxation dispersion experiments, and fast ps-ns fluctuations extracted from ¹⁵N relaxation rates. In addition, fast side-chain dynamics were identified from ²H relaxation in CH₂D methyl groups, where an optimized pulse sequence was designed. The partly structured nature of this protein allows the dynamics of the two domains to be investigated simultaneously and to relate them to their very distinct functions. Whereas the unstructured N-terminal subdomain acts as a flexible linker between the C-terminal subdomain and the P tetramer, the structured C-terminal subdomain forms a favorable interaction surface upon which the nucleocapsid N_TAIL domain can fold. There are not many examples of a detailed dynamic analysis of partly unstructured proteins, and this study highlights the importance of the intrinsic differential dynamics for the biological function of this class of proteins.

MATERIALS AND METHODS

Sample preparation

Isotope-labeled samples of the PX domain (474–568) of SeV phosphoprotein P, including an N-terminal His tag and a factor Xa cleavage site (MRGSHHHHHHIEGR), were prepared as described previously (30). A partially deuterated and uniformly ¹⁵N/¹³C-labeled sample was prepared using 70% D₂O in the growth medium and Escherichia coli BL21(DE3) that were adapted to grow in 70% D₂O. From an electrospray mass spectrum the portion of deuteration was determined to be 60%. For the backbone dynamics both a ∼1.3 mM and ∼0.2 mM ¹⁵N-labeled sample were used. Deuterium relaxation experiments were performed on the triple-labeled (60%) ²H/¹⁵N/¹³C PX sample with an approximate concentration of 0.8 mM. Stereospecific assignments of the methyl groups were obtained from a 1 mM 10% ¹³C-labeled sample as described by Neri et al. (31). All samples were prepared in potassium phosphate buffer (50 mM) pH 6 with 500 mM NaCl. Integrity of the samples was verified by comparison of heteronuclear single quantum coherence (HSQC) spectra before and after sets of NMR experiments.

NMR experiments

All spectra were recorded at 298 K on Varian Inova 600 MHz and/or 800 MHz spectrometers (Varian, Palo Alto, CA). The 800 MHz spectrometer was equipped with a cryogenically cooled probe. NMRPipe (32) was used to process the spectra, which were analyzed using NMRView (33). NMR assignments were previously reported (30) (BMRB-4999).

Hydrogen/deuterium exchange

A freeze-dried 1 mM ¹⁵N PX sample was dissolved in D₂O immediately before acquisition of a series of ¹⁵N-SOFAST-HSQC spectra (34). The dead time between dissolving the protein and the first NMR experiment was 3 min. For each amide group the signal intensities in a ¹H-¹⁵N correlation spectrum as a function of time were fitted to a single exponential decay to obtain the H/D exchange rates (k_ex). Exchange rates were converted into protection factors (log(k_ch/k_ex)) where k_ch are the intrinsic exchange rates for a specific residue in a certain sequence, as determined by Bai et al. (35,36):

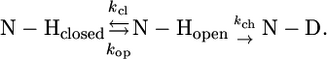In the same way equilibrium constants K_op (k_op/k_cl) where calculated from

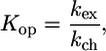(1)

which is true in the EX2 exchange regime (k_cl ≫ k_ch). From the average equilibrium constants for the three helices, average free energies were calculated according to

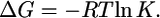(2)

¹⁵N auto- and cross-relaxation measurements

¹⁵N R₁, R₂ Carr-Purcell-Meiboom-Gill (CPMG) and heteronuclear nuclear Overhauser effect (hetNOE) relaxation experiments were recorded as described by Farrow et al. (37) using both the ∼1.3 and ∼0.2 mM ¹⁵N-PX samples. Details on the used delays, scans etc. are summarized in the Supplementary Material. For the hetNOE, recorded only at 600 MHz, a 1.7 kHz WALTZ16 decoupling scheme centered at the amide proton frequencies was used to saturate the amide proton signals. During the R₁ relaxation delays, cross correlated relaxation was suppressed by applying a 550 μs (600 MHz) or 350 μs (800 MHz) cosine-modulated 180° squared pulse every 5 ms with excitation maxima 2 kHz (600 MHz) or 2.8 kHz (800 MHz) from the carrier. The CPMG experiments were recorded with 180° ¹⁵N pulses applied every 1.25 ms (ν_CPMG = 400 Hz). R₂ relaxation rates at 800 MHz were also obtained from R_1ρ experiments using infrequent 180° ¹H pulses during the relaxation delay to suppress cross correlation pathways as proposed by Korzhnev et al. (38) and a 1.6 kHz on resonance ¹⁵N spin-lock pulse. For both CPMG and R_1ρ experiments on the 800 MHz spectrometer, which is equipped with a cryogenically cooled probe, compensation pulses were applied during the recycle delay to keep the amount of radio frequency (RF) power equal for all experiments. Moreover, pulse lengths and powers were calibrated while sending the same amount of RF power to the probe as used during the relaxation experiments as a slight detuning of the probe was observed. Spectra at 600 (800) MHz were recorded with spectral widths of 6000 (8200) and 1500 (1600) Hz, offsets of 4.77 (4.77) and 116.9 (118.8) ppm in the ¹H and ¹⁵N dimensions, respectively, and a recycle delay of 2 s.

Errors in the signal intensities were estimated from the duplicated points, with a minimal error of the standard deviation in the noise. Decay curves were fitted with the program Curvefit (http://cpmcnet.columbia.edu/dept/gsas/biochem/labs/palmer/software/curvefit.html) using a two-parameter single exponential and a Monte Carlo simulation to estimate the errors in the fitted parameters. A model-free (39) analysis of the relaxation rates was performed with modelfree4.0 (http://cpmcnet.columbia.edu/dept/gsas/biochem/labs/palmer/software/modelfree.html), using a value of 1.02 Å for r_NH and −170 ppm for the amplitude of the ¹⁵N CSA tensor. Error estimates were made from 300 Monte Carlo simulations.

Similarly ¹⁵N R₁ and R₂ relaxation rates of the triple-labeled sample were measured to accurately determine the rotational correlation time τ_c to be used for analysis of the ²H relaxation analysis.

¹⁵N relaxation dispersion measurements

¹⁵N relaxation dispersion measurements were performed with the ∼1.3 mM PX sample at both 600 and 800 MHz using a relaxation-compensated CPMG pulse sequence (40), where the CPMG period was implemented in a constant time (CT) manner (21). As discussed above, compensation pulses were applied during the recycle delay to keep the amount of RF power equal for all experiments on the 800 MHz spectrometer equipped with a cryogenically cooled probe. The CT period (T_CP) was set to 40 ms and by changing the number of 180° (5 kHz (600 MHz)/4 kHz (800 MHz)) pulses during T_CP, spectra with 10 different CPMG frequencies (ν_CPMG) were recorded: 25 (×2), 50, 75, 125, 200, 300, 400 (×2), 600, 800, and 1000 Hz, where ν_CPMG = 1/(4τ_CP) and 2τ_CP is the delay between two 180° ¹⁵N pulses. Spectral widths were set to 6980 (8800) × 1430 (1900) Hz and number of complex points to 480 (512) × 120 (160) for ¹H and ¹⁵N, respectively, at 600 (800) MHz. For the reference experiment, where T_CP was set to 0 ms, 16 (16) scans were used, whereas the CPMG experiments were recorded with 32 (24) scans. Using the signal intensity of the reference experiment (I_ref), the effective transverse relaxation rates for each experiment could be determined using 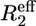(ν_CPMG) = (−1/T_CP)ln[I(ν_CPMG)/I_ref] (41). Since only residues in the structured part were found to have ¹⁵N relaxation dispersion decays, it seemed reasonable to analyze the data assuming exchange between two states:

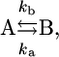with an exchange rate k_ex = k_a + k_b, populations p_a = (k_b/k_ex) and p_b = (k_a/k_ex), a chemical shift difference Δω = ω_a − ω_b, and transversal autorelaxation rates R_2a and R_2b. A simultaneous nonlinear least-squares fit of the data points at the two fields was performed using the following equation, where the autorelaxation rates were assumed to be the same in the two states, i.e., R_2a = R_2b = R₂:

(3)

This equation is valid for intermediate to fast exchange. In some cases, however, the exchange contribution was very small (<2 Hz) and fitting of the data points failed. For these residues only an estimation of the R_ex value was determined from the difference between R_2,eff(ν_CP = 25 Hz) and R_2,eff(ν_CP = 1000 Hz). The residues for which fitting of the decay curves succeeded were grouped according to the magnitude of their exchange rate and their location in the protein structure, followed by a simultaneous fit using one unique exchange rate per group. Only when the χ² of the simultaneous fit was not larger than 1.2 times the sum of the χ² values of the individual fits was the simultaneous fit considered relevant. Errors in the fitted parameters were estimated from 100 Monte Carlo simulations.

²H relaxation measurements

The five deuterium relaxation experiments were recorded both at 600 and 800 MHz using pulse programs provided by the group of L. E. Kay (19,42), where pulse scheme C (see Fig. 2 in Millet et al. (42)) was used for the R(D₊D_z + D_zD₊) experiment. In all cases, an “on the fly” correction for relaxation of the C_zH_z coherence was performed. The sequences to measure the three multiple quantum relaxation rates were slightly adapted to improve sensitivity, as discussed below. An overview of the acquired data sets at 600 and 800 MHz are given in Table S-I of the Supplementary Material. Spectral widths and offsets at 600 (800) MHz were set to 8000 [9804] × 3000 [4000] Hz and 4.76 [4.79] × 19 [19.5] ppm for ¹H and ¹³C, respectively. A ²H 670 (±45) [835 (±92)] Hz spin-lock pulse was used in the experiment to measure the R(D₊) relaxation rate. Calibration of the field strength was performed as proposed by Guenneugues et al. (43). ²H hard pulses had a field strength of 1.8 [1.4] kHz. All deuterium pulses were given centered at 1.8 ppm.

FIGURE 2.

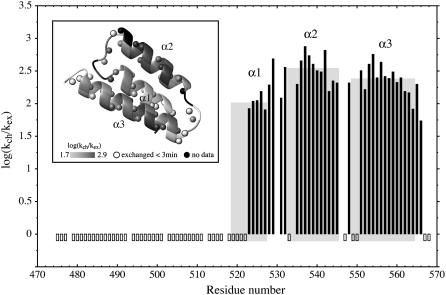
Protection factors of PX. Hydrogen/deuterium exchange rates were normalized using exchange rates of a random chain as proposed by Bai et al. (35,36) to obtain protection factors. These are represented by the black filled bars for the backbone amide protons. Open bars indicate exchange within the dead time (3 min) of the experiment. Gray squares indicate the three helices, where the height of the square indicates the average protection factor for the concerned helix. (Inset) Ribbon of the structured C-terminal subdomain of PX. Spheres represent backbone amide protons. Both the ribbon and the spheres are color coded from light gray (low protection factor) to dark gray (high protection factor). Black regions represent missing data due to overlap as well as one proline residue. White spheres with black rims are the amides that exchanged within the dead time of the experiment.

Duplicated points were used to determine errors in the signal intensities using a minimal error equal to the standard deviation in the noise. Decay curves were fitted using Curvefit. Peaks that partly overlap were left out of the analysis. However, in the case of complete overlap and a proper fit of the relaxation decay, the same relaxation rate was assigned to the overlapping methyls (i.e., A-504^β/A-507^β, I-470^γ2/I-481^γ2/I-490^γ2, I-481^δ1/I-490^δ1, and L-543^δ1/L-543^δ2). Apart from the quadrupolar contribution, Millet et al. (42) showed that dipolar interactions between carbon and deuterium within the methyl group, as well as between proton and deuterium, contribute significantly to the double quantum relaxation rate. Corrections for these contributions can be made using the R(C_zH_z) rates. These were measured using 16 scans; 512 × 84 complex points; 0.05, 5, 10, 15, 20, 30, 40, 60 (×2), and 80 ms relaxation delays at 600 MHz and 16 scans; 512 × 84 complex points; and 0.05 (×2), 4.5, 9.5, 15, 21, 28, 36, 48, and 63 ms relaxation delays at 800 MHz. In addition, evolution under the ¹J_CD coupling was shown to systematically reduce the measured double quantum relaxation rates but can be accounted for by a multiplication of the measured rates by a factor of 1.025. The ²H double quantum relaxation rates used in the analysis in this article and listed in the Supplementary Material were all corrected in this way. As was shown by Skrynnikov et al. (44), the five deuterium relaxation rates are dominated by the deuterium quadrupolar interaction and thus solely depend on the spectral density function at zero frequency (0) as well as the single (ω_D) and double (2ω_D) deuterium frequencies:

(4)

(5)

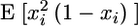(6)

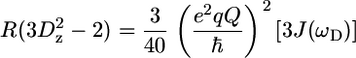(7)

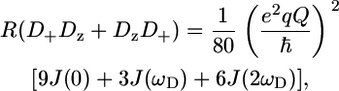(8)

where 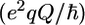is the quadrupolar coupling constant, which was experimentally shown to have a rather uniform value of 167 kHz (45). Using these equations, five (0, ω_D[600], ω_D[800], 2ω_D[600], and 2ω_D[800]) spectral density values were extracted from the 10 ²H relaxation rates via a least-squares minimization algorithm in octave. These spectral density values were concomitantly used in a model-free analysis, using the Lipari-Szabo (LS) (39) form for the spectral density function

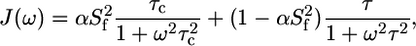(9)

with τ_c the correlation time for global rotational diffusion, 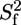the order parameter for fast internal motions with associated correlation time τ_e, 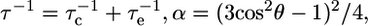and θ the angle between the C-D bond and the methyl symmetry axis. For the unstructured part as well as for some methyl groups in the structured part, an effective correlation time, which takes into account both overall tumbling and local ns motions, was used. When statistically relevant an extended form of the spectral density function was used, which accounts for the presence of both fast and slow internal dynamics (46):

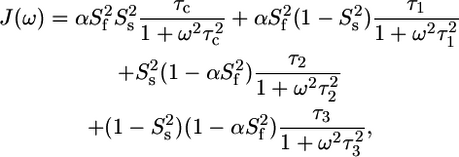(10)

where 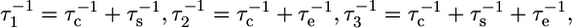and 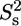is the order parameter for slow internal motions with associated correlation time τ_s. Extraction of the model-free parameters as well as model selection using an F-test were performed in Octave. A grid search was used to define the initial values of the parameters to be fitted, followed by a nonlinear least-squared minimization algorithm. Error estimates were made from 500 Monte Carlo simulations. The values for the order parameters were constrained between zero and one to improve stability of the fit.

Pulse sequence to measure R(D₊²), R(3D_z² − 2), and R(D₊D_z + D_zD₊)

In the experiments to measure both R(D_z) and R(D₊) relaxation rates (19), the delay during which the magnetization evolves due to the one-bond deuterium-carbon scalar coupling (¹J_CD) has a value of 1/(4¹J_CD). To measure the other three deuterium relaxation rates the coupling evolution time is adapted to 1/(2¹J_CD) according to Millet et al. (42) where different pulse schemes are used to select the coherence of interest. To refocus the ¹³C-¹³C coupling in a fully ¹³C-labeled protein, the total delay (2T_C; see Supplementary Material Fig. S1) before and after the relaxation period is adjusted to a multiple of (1/¹J_CC), i.e., ∼29 ms, whereas the time needed for the ¹J_CD coupling to evolve is only 1/2¹J_CD, i.e., ∼24 ms. Therefore during the remaining 5 ms the ¹J_CD needs to be refocused achieved by a 180° ²H pulse in the sequence by Millet et al. (42). We instead applied a decoupling scheme during this period (see Supplementary Material Fig. S1), as in the R(D_z) and R(D₊) experiments (19).

RESULTS

Hydrogen/deuterium exchange

H/D exchange experiments of PX were performed at pH 6.0. Under these conditions exchange rates are in the EX2 regime, and protection factors (log[1/K_op]) can thus be calculated using Eq. 1. These factors, calculated from the H/D exchange rates (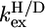) measured by dissolving freeze-dried ¹⁵N PX in D₂O, are shown in Fig. 2. All amide protons were exchanged within 2.5 h. Amide protons that exchanged within the dead time (3 min) of the experiment are indicated with negative bars. These amide protons were also exchanged within 200 s when mixing PX in H₂O with D₂O (see Supplementary Material Fig. S3). It could therefore be excluded that fast exchange resulted from slow protein refolding when dissolving the freeze-dried sample and validates the conclusion that these amide protons are not involved in stable hydrogen bonds.

All amide protons in the N-terminal part of PX exchanged within the dead time confirming the unstructured nature of this N-terminal subdomain. Several residues at the start of α1 helix also exchange within the dead time of the experiment. The lack of a suitable hydrogen-bond partner explains this finding for residues 519–521. In contrast, the hydrogen bond between the amide proton of L-522 and the carbonyl of T-518, which should be present based on the three-dimensional structure of PX, is apparently opening rapidly. The other amides in helix α1, including the turn that follows comprising S-528 and S-529, are protected, reflecting the HNⁱ-O^i-4 hydrogen bond pattern, as is also the case for helices α2 and α3. However, the average protection factor of 2.0 for helix α1 is significantly lower than the average values of 2.5 and 2.4 for α2 and α3, respectively, indicating that this first helix has a lower stability. In the loop between helix α1 and α2, both L-531 and S-532 are protected. The two amides are oriented toward the interior of the protein and although L-531 is hydrogen bonded with the carbonyl of S-529, S-532 is likely protected by the side-chain oxygens of E-535. Likewise, the amide of E-535 can be protected by the side chain of S-532. In the loop between helix α2 and α3, only T-548 is protected, which is pointing toward the hydrophobic core and can form a hydrogen bond with the side chain of E-551.

Fast ps-ns backbone dynamics of PX

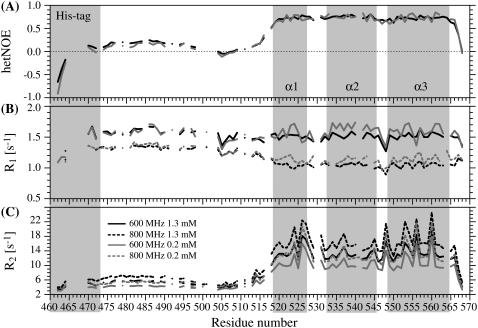
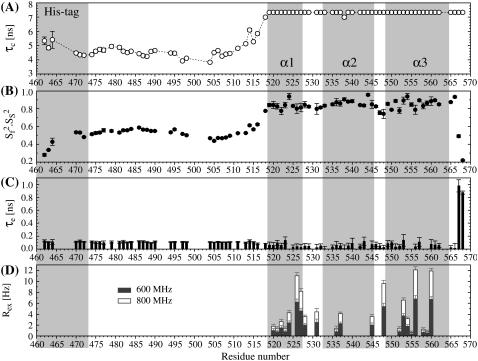
The ¹⁵N relaxation rates of PX at two fields and at two different protein concentrations are presented in Fig. 3. A dependence of the relaxation rates on the protein concentration is observed, with increased R₂ and decreased R₁ rates for the more concentrated sample. This indicates that PX, which was identified to be monomeric (14), starts to aggregate at higher protein concentrations.

FIGURE 3.

¹⁵N relaxation rates of PX at 298 K. Two sets of ¹⁵N hetNOE values (A), and four sets of R₁ (B) and R₂ (C) relaxation rates are presented that correspond to relaxation rates at a ∼1.3 mM (black) or ∼0.2 mM (gray) protein concentration and are recorded with a 600 MHz (solid) or 800 MHz (dashed) spectrometer. Error bars are omitted for clarity but can be found in the tables in the Supplementary Material. The three helices as well as the His tag are indicated by the gray areas.

As mentioned previously (14), low but mainly positive values of the hetNOE are found in the unstructured part of PX. We therefore postulated initially that there might be some residual structure causing the NOE values to be positive (14). Here residual structure is considered distinct from the inherent properties of the amino acid chain and implies the presence of persistent local or global interactions. Recently we demonstrated that the backbone RDCs in the unstructured region of PX can very well be reproduced by an ensemble of random structures, using a database of residue-selective φ/ψ propensities for coil regions (13). No persistent tertiary structure could thus be dissected from these data for this polypeptide chain.

Comparison with hetNOE values of other unstructured proteins or protein domains shows that although predominantly negative in some cases (phage λN (47), tropoelastin D26 (48), ATF-2 transactivation domain (49)), positive values, even up to 0.4, are regularly found (fibronectin binding protein (50), pro-peptide of subtilisin (51), unfolded ubiquitin (52)). This indicates that the positive hetNOEs may, rather, be a result of an inherent property of the individual nature of the amino acids along the sequence. Indeed, a high percentage of large and charged side chains is present in the N-subdomain of PX, and the stretch (470–498) that has positive hetNOE values lacks both Ala and Gly residues, which evidently slightly restricts the amplitudes of fast motions. The region that contains a series of relatively small residues (A-504, S-505, N-506, A-507, S-508) does display very low and even negative NOE values. Similarly, lower R₁ and R₂ values are found for the residues in this region. Zooming in on the R₂ relaxation rates in the unstructured part reveals that they follow a bell-shaped profile, with uniform values in the middle and lower values at both ends, as is expected for an unstructured polypeptide that has by nature a chain-like character (53). This bell-shaped profile tends to confirm the absence of residual structure, since the presence of local structure likely results in locally increased R₂ rates (54).

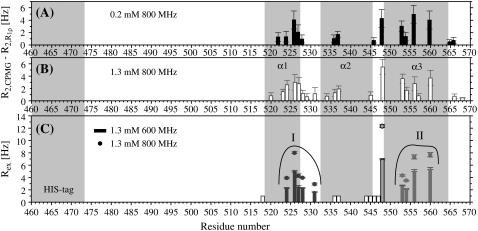
Several residues in the structured part of PX have high transverse relaxation rates, which indicate the presence of slow conformational exchange (R_ex). This is confirmed by the fact that lower transverse relaxation rates were found for these residues using a ¹⁵N spinlock field (R_1ρ) instead of a CPMG sequence during the relaxation period (see Fig. 5, A and B). This contribution has been quantified using relaxation dispersion measurements, as discussed in more detail below.

FIGURE 5.

Contribution of conformational exchange (R_ex) to the ¹⁵N transverse relaxation rates R₂ of backbone amide groups in PX, determined from (A and B) the difference between R₂ rates from CPMG and R_1ρ measurements at 800 MHz or from (C) ¹⁵N relaxation dispersion measurements at 600 (bars) and 800 (circles) MHz. Protein concentrations were ∼0.2 mM for A and ∼1.3 mM for B and C. In C, open bars represent residues for which dispersion curves were not fit due to low R_ex values. Gray bars/circles represent R_ex values extracted from fits of the relaxation dispersion curves. Curve fitting of residues in group I (L-524, I-526, E-527, S-528, and L-531) or II (K-553, A-554, M-556, and E-560) was performed simultaneously.

Fitting of the relaxation data at a high protein concentration using the LS model-free approach led to artificially high order parameters (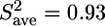) and long internal correlation times (>400 ps) for some of the residues in the structured part. These features are clearly related to the observed aggregation (26), which is not taken into account by the LS model and is only implicitly parameterized in an increased overall correlation time (8.9 ns). The relaxation rates at the low protein concentration could, however, be analyzed with the model-free approach (Fig. 4). For the structured part, an isotropic diffusion model, using a τ_c of 7.3 ns, was considered acceptable since D_par/D_per was found to be only 1.15.

FIGURE 4.

Model-free analysis of the PX ¹⁵N relaxation rates measured at both 600 and 800 MHz and a protein concentration of ∼0.2 mM. (A) Overall rotational correlation time τ_c. Isotropic rotational diffusion with a correlation time of 7.3 ns was assumed for the structured part (519–568), whereas a local diffusion model was used for residues in the unstructured part. (B) Product of order parameters for fast (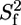) and slow (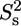) internal motions. An extended model including 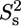was only used for T-567 (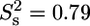) and N-568 (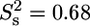). (C) Local correlation time (τ_e) for internal motion. (D) R_ex contribution to the R₂ relaxation rates.

The correlation time is slightly higher than what is expected for a 12.7 kDa globular protein. This might be due to the presence of aggregation, even at this low protein concentration. However, PX is not a globular protein, and another source of the higher correlation time might be the fact that in PX the two domains have rather similar mass, such that the overall diffusion of the structured part is dependent on the unstructured part. An extended conformation of the unstructured part would therefore result in completely different rotational diffusion of the protein than a conformation where the unstructured part is, for example, backfolded on the structured domain. Since the unstructured part is very flexible, these types of conformations are expected to interconvert rapidly. But since the timescale of this process is not a priori known, it is not necessarily true that the rotational diffusion of the structured part can be accurately described by one average correlation time. The order parameters (S²) in the well-structured area (excluding the C-terminus) have an average value of 0.85 ± 0.05, indicating a rather rigid structure. Only some residues located in the loops between the helices as well as in the C-terminus have lower order parameters. In this subdomain a large number of residues were fitted using a model including a contribution of conformational exchange (R_ex) to the transverse relaxation rate. These include all the residues for which the existence of conformational exchange was detected from the difference in CPMG and R_1ρ-derived transverse relaxation rates.

To fit the ¹⁵N relaxation rates in the unstructured part, three fitting parameters were used in the model-free analysis, i.e., an effective correlation time 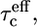an order parameter S², and a correlation time for fast local motions τ_e. We are aware of the fact that by using this form of the spectral density function we oversimplify the potentially complex nature of dynamics in an unstructured polypeptide chain. In particular, the assumed absence of correlation between overall tumbling and the internal dynamics is not evident. However, the small number of observables and the sparse knowledge concerning the nature of dynamics in unstructured proteins restricts the use of more sophisticated analyses at this stage. Therefore it is important to keep in mind that the extracted fitting parameters give only a simplified view of the dynamics. The fitted values for the correlation time τ_e for fast local motions are very similar over the whole of the unstructured chain (110 ± 7 ps).

The effective rotational correlation times as well as the order parameter, however, do slightly vary along the sequence. In particular, lower order parameters are found for residues 504–508. These are dictated by both the low hetNOE values and R₂ relaxation rates, as discussed above. More specifically, this region can be presented as a flexible hinge between the structured and unstructured subdomains. Although the effective correlation time also varies in this region (3.8–4.5 ns), which is also the case for the N-terminal end, a rather uniform value of 4.6 ± 0.2 ns is found for residues 474–495. This again shows that the unstructured subdomain can be regarded as an independent module whose dynamics are not correlated with the dynamics of the structured part. The average order parameter for the unstructured subdomain is 0.53 ± 0.04, excluding the residues of the His tag. Order parameters in the same range were also found for other unstructured proteins (51,55–57) or protein domains (58).

Slow μs-ms backbone dynamics of PX

From both the difference between the transverse relaxation rates determined using a CPMG or R_1ρ sequence (Fig. 5, A and B) and the model-free analysis (Fig. 4 D), it is clear that several regions in the C-terminal structured subdomain of PX undergo slow μs-ms conformational exchange. Since the R_ex contribution is independent of the protein concentration (Fig. 5, A and B), it can be excluded that the exchange originates from aggregation. To further characterize this conformational exchange we recorded ¹⁵N relaxation dispersion measurements at both 600 and 800 MHz, where for sensitivity purposes the higher concentrated sample was used. Fitted relaxation dispersion curves of three residues in different parts of the structured subdomain of PX are presented in Fig. 6. Fig. 5 C shows an overview of all the residues for which conformational exchange was detected from the relaxation dispersion measurements. These residues closely correspond to the ones for which a significant difference between R₂(CPMG) and R₂(R_1ρ) was also found. For some residues (black open bars in Fig. 5 C) fitting of the data points failed due to a small, but significant R_ex value (as determined from the difference between 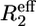(25 Hz) and 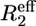(1000 Hz)). These residues are located in the middle and at the end of helix α2. The gray bars in Fig. 5 C represent residues for which curve fitting did succeed.

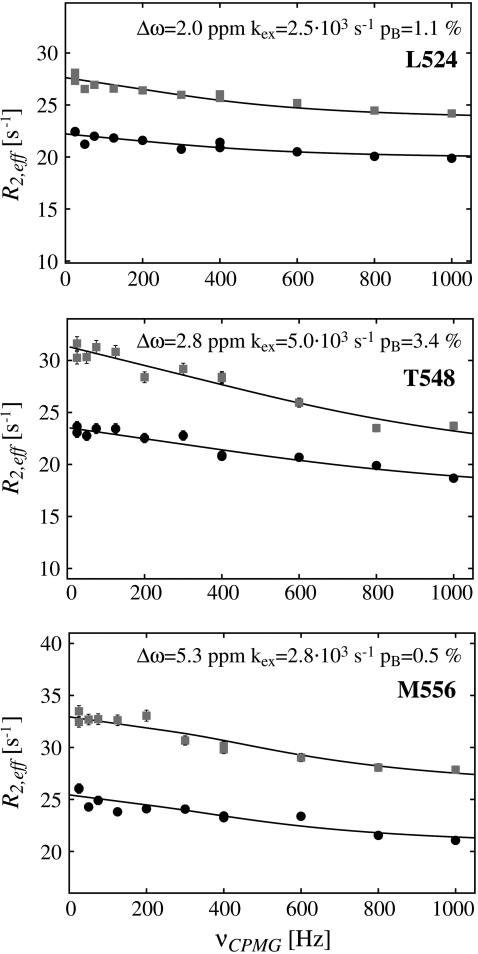
FIGURE 6.

¹⁵N backbone relaxation dispersion curves of three residues in the structured part of PX at 600 (circles) and 800 (squares) MHz. Fitting parameters are indicated on top of the graphs, where for L-524 and M-556 values from a simultaneous fit of residues in group I and II (see Fig. 5), respectively, are indicated.

The first group of residues (group I in Fig. 5 C) is located at the end of helix α1 (L-524, I-526, E-527) as well in the loop between α1 and α2 (S-528, L-531). Since exchange rates and populations after fitting the individual curves were in the same range, the dispersion curves of the five residues were fitted simultaneously, assuming that one process causes this exchange. The total χ² when fitting these five residues simultaneous increased only by a factor of 1.2 as compared to the sum of χ² of the individual fits. This resulted in an exchange rate of 2538 ± 142 s⁻¹ with a population of 1.1% ± 0.1% of the “excited” state (k_a = 30 ± 2 s⁻¹, k_b = 2508 ± 176 s⁻¹). This exchange very likely reflects an unfolding event of helix α1, which is also sensed by S-528 and L-531, whose amide protons are connected to this helix through their hydrogen bonds. The equilibrium constant of the exchange process can be extracted from the populations (K = p_a/p_b = 11.1 × 10⁻³ ± 1.0 × 10⁻³) and thus the free energy ΔG: 11.1 ± 0.2 kJ/mol. This value corresponds remarkably well to the free energies of these residues calculated from the H/D exchange rates using Eq. 2, ranging from 10.9 to 13.0 kJ/mol, confirming that the observed conformational exchange originates from the unfolding of helix α1. The absolute values of the chemical shift changes associated with the exchange process for the three residues at the end of helix α1 correspond reasonably well with the chemical shift differences between the observed chemical shifts and random coil values (Table 1).

TABLE 1.

Deviations from random coil of the ¹⁵N chemical shifts (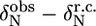) and absolute ¹⁵N chemical shift differences (Δ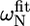) related to the exchange process

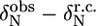		|Δ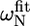|†			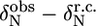|Δ|†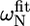
M-519*	−3.1 ppm	–	I-526*	−4.5 ppm	3.1 ppm
H-520*	−2.0 ppm	–	E-527*	−1.8 ppm	2.1 ppm
S-521*	−1.0 ppm	–	S-528	−4.1 ppm	2.0 ppm
L-522*	1.3 ppm	–	S-529	2.8 ppm	–
R-523*	−0.1 ppm	–	P-530	–	–
L-524*	−3.8 ppm	2.0 ppm	L-531	−4.3 ppm	1.7 ppm
V-525*	−0.5 ppm	–

^*Helix α1: 519–527.

^†Absolute chemical shift difference of exchange process.

Indeed, for two other residues at the end of helix α1 for which no exchange was observed (R-523, V-525), the chemical shift deviation from random coil is very low, possibly resulting in the presence of conformational exchange to be undetectable for these residues. In contrast, no exchange is observed for the residues in the beginning of the helix, whereas their chemical shifts do deviate from random coil. Presumably the exchange process in this part of α1 is faster than in the second half of the helix and therefore invisible. From the H/D exchange experiments we had concluded that the amides in this part of helix α1 are not involved in stable hydrogen bonds, as is the case for the residues that follow. The expected ¹H^N-¹H^N(i,i+1) NOEs are relatively weak for this part of helix α1 and long-range ¹H-¹H NOEs were only detected for L-552 on the hydrophobic side of helix α1 (14). In contrast, for the second part of helix α1 ¹H^N-¹H^N(i,i+1) NOEs are strong, and for both V-525 and I-526 many long-range NOEs with residues on both helix α2 (Y-539,V-540) and helix α3 (V-559) were identified (14). Taken together these observations indicate that at the beginning of helix α1 (519–522) fraying of the helix is a fast process due to the lack of stable hydrogen bonds and the absence of a strong hydrophobic network, which makes this process “invisible” for NMR relaxation measurements. The second part of the helix α1 (523–527) does contain hydrogen bonds detectable from H/D exchange as well as a strong hydrophobic network with the core of the protein, making it energetically less favorable to unfold this second part of the helix.

In the turn between helix α2 and α3 a large contribution of conformational exchange was observed only for the backbone nitrogen of T-548, and smaller R_ex values were found for some of the neighboring residues. The amide proton of T-548 is most probably hydrogen bonded to side chain oxygen in E-551, but it is possible that in this rather flexible turn a local backbone conformational change resulting in a φ/ψ flip of T-548 is allowed, which can cause the observed exchange.

In helix α3 four residues (K-553, A-554, M-556, and E-560) were found to have a relaxation dispersion decay. Fitting the curves simultaneously increased the total χ² only by 1.14 with respect to fitting the individual curves, resulting in a k_ex of 2857 ± 163 s⁻¹ (k_a 15 ± 1 s⁻¹, k_b 2842 ± 212 s⁻¹). The underlying mechanism is unlikely to be the unfolding of helix α3, which is rather stable according to the H/D exchange data. The amides of residues K-553, M-556, and E-560 are all located on the same side of the helix and not far from the single aromatic residue Y-539 of the structured subdomain that is located on helix α2. Both M-556 and E-560, which are closest to the aromatic ring, have downfield-shifted ¹⁵N chemical shift values. Moreover, the absolute value of the chemical shift differences extracted from the fit of the relaxation dispersion profiles is larger for M-556 and E-560 (5.3 and 5.6 ppm, respectively) than for K-553 (3.5 ppm) and A-554 (3.0 ppm). It is therefore tempting to speculate that the observed exchange results from a change in orientation of the Y-539 ring with respect to helix α3. However, Y-539 is located in the hydrophobic core of the protein, and its four aromatic ring protons all have different chemical shifts, indicating the absence of fast flipping of this ring. Rather than a reorientation of the aromatic residue, it would thus be more likely that a reorientation of the two helices with respect to each other is the underlying event of the observed exchange.

Methyl ²H relaxation

Pulse sequences to measure R(D₊²), R(3D_z²−2), and R(D₊D_z + D_zD₊)

Application of a ²H-decoupling scheme in the sequences to measure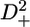 R(), R(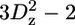), or R(D₊D_z + D_zD₊) shortens the existence time of the antiphase term C_xH_zD_z, which relaxes faster than the in-phase term C_yH_z. Considering that the R(D_z) rates for the protein in this study are on the order of 20 s⁻¹, shortening the existence of the antiphase term in both ¹J_CD evolution periods before and after the relaxation delay would roughly result in a signal increase of 20%. This corresponds well with the intensity gain of 20% found in practice (see Supplementary Material Fig. S1).

²H relaxation rates

A selection of ²H relaxation decays at both fields as well as the extracted relaxation rates are presented in Fig. 7. Note that the axes of the relaxation rate graphics are discontinuous because only the methyl groups are shown. In general the relaxation decays are of good quality, with only rather noisy double quantum signal decays. In addition, relaxation rates determined for L-522^δ1 have large error bars due to its low intensity broad signal in the ¹H-¹³C correlation spectrum. The relaxation rates are scaled to show that the R(D₊D_z) > 5/3R(D₊) > 5/3R(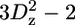) > 5/3R(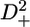) > R(D_z) trend is fulfilled (59), with the exception of some double quantum rates that exceed the quadrupolar rate, which is clearly caused by the lower quality of the data for the double quantum relaxation rates.

FIGURE 7.

²H relaxation decay curves and relaxation rates of PX. The relaxation curves at both 600 (A) and 800 (C) MHz are from two residues in the unstructured N-terminal subdomain (I-470 and V-494) and two in the structured C-terminal subdomain. The fitted relaxation rates are shown at 600 (B) and 800 (D) MHz are scaled for comparison as indicated on the graph.

In the unstructured part of PX the D₊D_z and D₊ coherences clearly relax much slower than in the structured part. These relaxation rates are the only two that depend on the spectral density function at zero frequency (J(0)), and the large difference in rates thus clearly reflects the difference in effective tumbling of the two subdomains. The entire set of 10 relaxation rates is a function of five spectral density values at different frequencies, i.e., J(0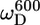), J(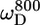), J(), J(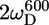), and J(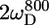). These spectral density values were extracted from the relaxation rates. Back calculation of the relaxation rates from these spectral density values shows that the 10 relaxation rates are self-consistent (see Fig. S2 of the Supplementary Material). Only the double quantum relaxation rates at 600 MHz are not well reproduced by the extracted spectral density values. As mentioned above, these rates suffer from noisy data points. However, omitting this data set results in nearly identical spectral density values, showing the robustness of this large set of relaxation rates.

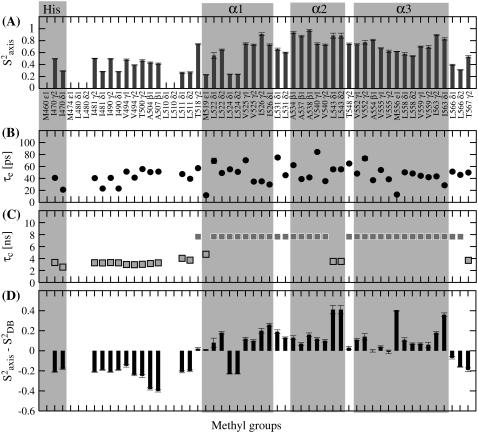
A model-free analysis of the spectral density values was performed. An overview of the extracted motional parameters for the side-chain methyl groups in PX is shown in Fig. 8. As in the model-free analysis for the ¹⁵N relaxation data, an effective residue-specific correlation time was used for residues in the unstructured part. Although this is an unrealistically simple model for side-chain motions in an unstructured protein chain, where a wide range of motions are likely superimposed, the extracted parameters are still indicative of relative amplitudes and timescales. For the structured part, the correlation time was fixed to 7.6 ns, as was determined from the ¹⁵N relaxation data on the same sample.

FIGURE 8.

Methyl axis model-free parameters from ²H relaxation measurements of PX. Order parameters for fast internal motion 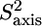of the methyl groups in PX are represented by the bars in A with the corresponding timescales τ_e in B. In C, the effective or global correlation times are represented by dark gray and light gray squares, respectively. The gray frames indicate the residues located in the His tag or the three α-helices. (D) The order parameters of PX in A were normalized by subtracting a residue-specific average order parameter.

Side-chain dynamics in the unstructured PX subdomain

In the unstructured part, the fitted residue-specific effective correlation times were found to be rather uniform, with an average value of 3.2 ± 0.1 ns for the residues 481–507. This confirms the modular behavior of this protein, as was also found from the ¹⁵N relaxation data analysis. From the ¹⁵N relaxation data a ratio of 1.6 between the rotational correlation time of the structured subdomain and the average effective correlation time in the unstructured subdomain was found. The higher ratio of 2.4 found from ²H relaxation data is likely caused by the fact that the effective correlation time reports not only on the overall tumbling but also on internal ns motion, meaning that the side chains as compared to the backbone experience additional slow ns motions. In the unstructured part the internal correlation times of fast methyl axis motion range from 20 to 60 ps and order parameters between 0.25 and 0.5. The variation in methyl axis order parameters is partly a result of the different lengths of the methyl-bearing side chains. As is found for globular proteins, lower 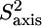values are found for the δ methyl groups of I and L in this unstructured chain than for the γ methyl groups of V, T, and I. However, two alanine residues (A-504 and A-507) have relatively low order parameters.

To account for the difference in side-chain length, Mittermaier et al. (60) have proposed to subtract a methyl-specific order parameter, as determined from a database analysis, and to use this normalized S² that no longer depends on the length of the side chain. The normalized 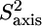values of PX are shown in Fig. 8 D. Negative normalized order parameters indicate flexibility, whereas positive values indicate rigidity. The two alanines A-504 and A-507 both have high negative normalized order parameters. They are located in the stretch (504–508), which from the backbone ¹⁵N relaxation data was identified as a very flexible linker between the unstructured and structured domain; and this highly flexible character is clearly also sensed by the alanine C^α-C^β axis. All other normalized order parameters in the unstructured part are also negative, meaning that the methyl groups are more flexible than on average in structured proteins. Remarkably, the order parameters of the two methyl groups in V-494 differ by 0.1. All the other valine order parameters in PX do not differ more than 0.05, and considering that the 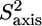error bars of the V-494 methyls are on the order of 0.01, the difference of 0.1 is probably significant.

Differences between valine methyl order parameters of this order or larger have in some cases been observed in well-folded proteins (61–63). They likely originate from complex dynamics due to steric hindrance. In a flexible unstructured protein the existence of complex asymmetric dynamics is, however, less intuitive. Choy et al. (20) measured methyl axis order parameters in Δ131Δ, an unstructured fragment of staphylococcal nuclease. To circumvent problems of overlap in the ¹H-¹³C correlation spectrum, the ²H relaxation rates were measured using an experiment where the magnetization is transferred from the methyls to the backbone NH groups. In this way, an average order parameter for the methyls in V, as well as in I and L residues, was measured, and a possible difference between the methyl axis order parameters thus remained unnoticed. V-494 in PX is adjacent to P-493 and Y-495. Previously it was noted from RDC data that the backbone root mean-square deviation around prolines of the calculated ensemble of the unstructured subdomain of PX is considerably lower than at other places in the peptide chain (13). This was explained by the fact that conformational sampling is restricted due to the presence of the proline residue. Valine residues preferentially have a χ₁ angle of 180° with C^γ1 closer to its own carbonyl and C^γ2 closer to the amide group. It might be that the restricted conformational sampling, as a result of the proline that is attached to the amide of V-494, makes the environment of the two methyls unequal, which can even be accentuated by the presence of a large aromatic side chain on the other side. This asymmetry might be the origin of a complex motion with an effective director other than the C^α-C^β axis, causing the difference in order parameters for the two methyl groups in V-494.

Side-chain dynamics in the structured PX subdomain

The normalized methyl order parameters in the structured part are mainly positive, with the exception of L-524, which is protruding into the solvent, as well as the C-terminal residues L-566 and T-567 (Fig. 8 D). The internal correlation times are all between 30 and 75 ps, with faster motions for the two methyl groups in the long methionine side chains, for which internal timescales are around 12 ps (Fig. 8). Methyls that are located in the hydrophobic core all have order parameters higher than 0.6. The two methyl groups of L-543 resonate at the same frequency. For analysis of their relaxation rates a three-parameter fit was performed using an effective correlation time. It should be kept in mind that this effective correlation time takes into account the global τ_c as well as both the amplitude and timescale of slow internal motions. Although ps timescale motions are rather restricted for the methyl groups of L-543 (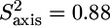), the methyls undergo a slower ns timescale motion. This motion most probably is related to rotameric jumps, whereby the two methyl groups occupy the same rotameric conformations, which results in both methyls resonating at the same frequency.

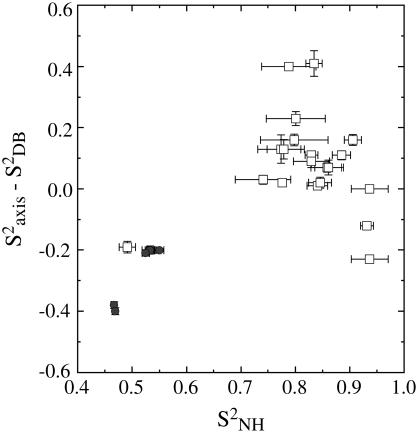
In Fig. 9 the correlation between the backbone and corrected side-chain order parameters is shown. An average value of the methyl axis order parameters of V, L, and I methyl groups is used. This graph shows that although a correlation between backbone and side-chain motions is virtually absent in the structured subdomain, which is generally found for structured proteins (64), the correlation is more pronounced when including the methyls in the unstructured part. It should be noted, however, that the two lowest data points are from the two alanine residues in the flexible linker, whose side-chain order parameters report on the C^α-C^β axis, which can be considered a backbone vector.

FIGURE 9.

Comparison of normalized methyl order parameters and backbone order parameters in PX. White squares represent residues in the structured part, and gray circles residues in the unstructured part.

Recently, we identified the interaction site on PX of the unstructured C-terminus (N_TAIL) of the SeV nucleoprotein to be located on the face created by helix α2 and α3 (65). All the methyl-bearing residues that are located on the N_TAIL interaction site (V-555, A-534, A-538, T-548, L-558) have zero or even positive normalized order parameters, creating a relative rigid interaction site. This is even the case for L-558, which is rather uncommon for such a long side chain that is solvent accessible.

DISCUSSION

Dynamics in unstructured proteins

This detailed analysis of the dynamics in a partly structured protein gives us the unique possibility to compare structured and unstructured protein motions within the same experimental system. Both ¹⁵N and ²H relaxation rates are in agreement with a protein that consists of two dynamically distinct parts. These two parts, one structured domain that does not display large-amplitude fast ps motions and one unstructured region that is very flexible on this timescale, are separated by a stretch of small residues. This stretch of residues displays even higher amplitude fast motions probably resulting from the fact that this part of the protein sequence lacks bulky residues and can therefore be considered as a flexible hinge that decorrelates the dynamics of the two domains. Describing PX as a two-domain protein when one of the domains has no structure may appear paradoxical since historically domains have been defined as having an independent persistent structure. For this kind of hybrid protein, however, differential dynamics are rather useful as a criterion for defining the different domains.

In the unstructured part of the protein the effective correlation times from both the backbone and side-chain relaxation analysis are rather uniform over a long stretch of residues. Only residues at the very N-terminal end, as well as residues close to the structured subdomain, have different effective correlation times. This may be interpreted in terms of a global motion with a certain persistence length (53), directed by the random coil polymer whose sequence in this region consists of several bulky amino and lacks both glycine and alanine residues. For the unstructured staphylococcal nuclease Δ131Δ fragment, a large spread of effective correlation times from ¹⁵N and ²H relaxation data was found (20,57). The presence of a significant amount of tertiary structure was, however, identified for Δ131Δ (66,67). This is, however, not the case for PX, where no residual tertiary structure has been detected in the unstructured part from both RDCs and small angle x-ray scattering data but can be represented as an ensemble of random conformers (13), which is in agreement with the relaxation data presented in this article. Comparison of the backbone and side-chain order parameters in the structured and unstructured subdomains of PX (Fig. 9) reveals that although no strong correlation between backbone and side-chain motions is found in the structured part, as was also shown for several other proteins (62), a weak correlation does exist in the unstructured part. Such a correlation was also found for Δ131Δ (20), and it seems that in contrast to structured proteins, the backbone in an unstructured polypeptide chain does, to a certain degree, direct the dynamics of its side chains.

Distinct dynamics in the subdomains of PX in view of its function

PX is the C-terminal domain of SeV protein P, the cofactor of the RNA polymerase. The unstructured part of PX connects the C-terminal three-helix bundle of PX to the tetrameric coiled-coil domain that binds to L. Although L is the protein that possesses the RNA polymerase activity, the four PX C-terminal three-helix bundles bind the polymerase to the nucleocapsid through an interaction with the unstructured N_TAIL domain (Fig. 1). Whether the four PX domains interact simultaneously or alternatively with the nucleocapsid is not yet known, nor is how the polymerase subsequently proceeds along the nucleocapsid so that L can then synthesize the RNA nucleotide per nucleotide. The highly dynamic character of both the backbone and side chains of the unstructured subdomain of PX, as identified by this study, must, however, be crucial for this process, as this domain forms a flexible linker between the nucleocapsid binding site of the polymerase cofactor and the protein L binding site.

We show here that the unstructured part has the typical dynamic characteristics of a polypeptide that has by definition a chain-like character and that the stretch of small residues in between the two subdomains creates a very flexible hinge which breaks the elongated chain. Although the unstructured chain is important to reach for the unstructured N_TAIL domain, the hinge region allows reorientation of the helix bundle without any hindrance. Tuckis et al. (68) investigated the effect of engineered mutations in the PX domain within the full phosphoprotein on the polymerase activity in both transcription and replication in vitro. Interestingly, mutation of both N-506 and R-509 in the hinge region to alanine residues resulted in a complete loss of polymerase activity, whereas the polymerase was still able to bind nucleocapsids. Likely these mutations altered the dynamics in this region, which might in turn have resulted in a drastic change in the ability of the polymerase to efficiently progress along the nucleocapsid.

The small helix α1 that follows the unstructured subdomain is not very stable, and the presence of a small percentage of an unfolded conformer was detected. In contrast, α2 and α3, which form the N_TAIL binding site, are more stable helices. Slow conformational exchange was identified in the turn between these two helices as well as on the hydrophobic site of α3. The exchange observed for the residues on helix α3 likely reflects a motion of helix α3 with respect to helix α2. This motion can be crucial for an optimal insertion of the induced helix of N_TAIL to form a well-packed four-helical bundle. The binding site contains several methyl-containing residues that, even though facing the solvent, display relatively restricted fast dynamics. This rather rigid interface forms a good mold for the N_TAIL to fold upon.

This study highlights the sophisticated design of proteins that optimally makes use of the wide range of dynamics that are possible in a polypeptide chain. Although in the unstructured subdomain both the flexibility and the elongated character of an unstructured chain are employed, the structured domain provides a rigid interaction surface that still allows small conformational changes for an optimal insertion.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.