A New Technique for Calculating Individual Dermal Fibroblast Contractile Forces Generated within Collagen-GAG Scaffolds

Abstract

Cell-mediated contraction plays a critical role in many physiological and pathological processes, notably organized contraction during wound healing. Implantation of an appropriately formulated (i.e., mean pore size, chemical composition, degradation rate) three-dimensional scaffold into an in vivo wound site effectively blocks the majority of organized wound contraction and results in induced regeneration rather than scar formation. Improved understanding of cell contraction within three-dimensional constructs therefore represents an important area of study in tissue engineering. Studies of cell contraction within three-dimensional constructs typically calculate an average contractile force from the gross deformation of a macroscopic substrate by a large cell population. In this study, cellular solids theory has been applied to conventional column buckling relationships to quantify the magnitude of individual cell contraction events within a three-dimensional, collagen-glycosaminoglycan scaffold. This new technique can be used for studying cell mechanics with a wide variety of porous scaffolds that resemble low-density, open-cell foams. It extends previous methods for analyzing cell buckling of two-dimensional substrates to three-dimensional constructs. From data available in the literature, the mean contractile force (F_c) generated by individual dermal fibroblasts within the collagen-glycosaminoglycan scaffold was calculated to range between 11 and 41 nN (F_c = 26 ± 13 nN, mean ± SD), with an upper bound of cell contractility estimated at 450 nN.

INTRODUCTION

Cell-mediated contraction plays a critical role in a number of physiological and pathological processes, notably organized wound contraction during wound healing after severe injury. In healing skin wounds, contractile myofibroblasts play a significant role in organized wound contraction and scar formation (1,2). In contrast to normal dermis, scar tissue is undesirable because of its inferior mechanical properties, potential to restrict the range of motion at joints, and physical disfigurement. Contractile cells have been identified in many tissues and have been implicated in scar tissue formation in a number of other wounded or diseased tissues such as injury to the dermis (2), transected peripheral nerve (1,3), injured anterior cruciate ligament (4), cirrhotic liver (5), and the conjunctiva (6). The importance of understanding cell contraction behavior in the context of wound healing and normal physiological behavior has prompted a multitude of studies of the contractile forces developed by cells using in vivo and in vitro models.

Studies of cell contraction in vitro have been performed using both two-dimensional and three-dimensional substrates. To study individual cell behavior, the cells are seeded onto a two-dimensional substrate and the deformation of the substrate by the cell is measured (7–12). The value of the contractile force is then determined using the modulus of the substrate (10,13,14). This technique also allows correlation of the development of the deformation (and force) with observed cell processes via microscopy techniques such as pseudopod extension and cell migration (13–16). Studies of cell behavior on two-dimensional substrates have shown that substrate modulus significantly modifies cell behaviors such as DNA biosynthesis, migration speed, directional persistence, and applied traction forces (12,16–27). Such experiments have provided valuable information concerning cell-extracellular matrix (ECM) interactions with, and cell behavior on, two-dimensional surfaces. Recently, a series of investigations has probed the relationship between cell behavior, contractility, and focal adhesion organization using a microfabricated post-array detectors system that attempts to better mimic biologically relevant structures as compared to completely two-dimensional substrates (19,28); these investigations have concluded that fibroblasts are able to generate contractile forces on the order of 100s of nanoNewtons. However, these techniques have only limited applicability in understanding cellular processes in three-dimensional tissues, particularly in the context of how cell contractility may differ in the fibrillar three-dimensional environment that defines most extracellular matrices in tissue and organs from those on microfabricated post-array detectors or two-dimensional substrates due to differences in cell morphology, cytoskeletal organization, and integrin-ligand complexes.

Choice of the experimental substrate may significantly influence cell morphology as well as measurements of cell mechanics and cell-ECM interactions. The amorphous, rounded shape of cells in suspension is quite different than the polygonal cell shape typically observed on two-dimensional substrates, and different still from the spindle-shaped cell often observed for contractile cells in the in vivo wound sites (1) and within three-dimensional constructs (29,30). Further, the cell stiffness estimated for cells within a three-dimensional bio-artificial tissue construct has been previously reported to be significantly higher than that estimated for cells in solution using local cell surface deformation techniques (i.e., poking, micropipette aspiration) (31), an effect likely due to the difference in cell, and therefore cytoskeletal, structure (31–33). By taking into account the effects of cell morphology, Zahalak et al. (33) estimated the contractile force generated by active fibroblast within a three-dimensional bio-artificial hydrogel to be 21 nN by combining experimental results from fibroblasts within a collagen-based ECM analog gel and an integral constitutive relation for bio-artificial tissue models.

Experiments utilizing three-dimensional constructs, each partial analogs of the extracellular matrix in various tissues such as gels and scaffolds, have recently made significant progress in studying cell contraction; however, these studies almost exclusively are at the scale of cell populations rather than the individual cell contraction assays that are traditionally used with two-dimensional substrates. Studies of populations of cells have generally involved seeding of the cells onto a porous three-dimensional lattice such as a collagen gel (29,30,34–43). The macroscopic deformation of the lattice is then measured, yielding an average response for the cell population. Again, forces are calculated based on the modulus of the construct and the measured deformations or scaffold (29,30,35–38,40). The benefits of measuring the macroscopic contraction and force of a population of cells are that the three-dimensional lattice more appropriately mimics the in vivo environment. This method, however, does not allow for a direct correlation of force with individual cell processes and more significantly, the population-averaged responses can conceal important cell-to-cell variation. Using this technique, the force developed by individual cells has been estimated by normalizing the macroscopic force value by the total cell number within the construct yielding an average force per cell of 0.1–9.8 nN/cell (22,29,30,36,38,40,44,45). Since not all cells actively contract together, and the contractile cells are likely acting in different directions, these values are a lower bound on the individual cell contractile force.

Tissue engineering scaffolds have been used extensively as a three-dimensional analog of the extracellular matrix (ECM) present in all tissues and organs. The scaffold acts as a physical support structure and as an insoluble regulator of cell biological activity. Implantation of a specific analog of the ECM has been linked to blocking organized wound contraction and scar formation and to inducing regeneration of physiological skin (1,2). Collagen is a significant constituent of the natural ECM. Scaffolds fabricated from type I collagen and a glycosaminoglycan (collagen-glycosaminoglycan, i.e., CG, scaffolds) have been used to study cell migration and cell population contraction in vitro (30,40,46,47) as well as induce regeneration of the skin, conjunctiva, and peripheral nerves in vivo (1,2,48,49). These low-density, open-cell foams are biodegradable and are characterized by an interconnected pore network defined by struts, providing an ideal environment for in vitro cell behavior studies.

The CG scaffold, fabricated via freeze drying, is an analog of the ECM that can induce in vivo regeneration of tissue (skin, peripheral nerve) after injury (1); the scaffold is typically of order 1% solid (99% air) and has an open-cell microstructure with pores of ∼100 μm in size defined by collagen-GAG fibers, termed struts. When seeded with contractile cells, the scaffold is observed to contract in vitro; the average cell contraction force generated by dermal fibroblasts within CG scaffolds, calculated by measuring gross changes in scaffold size when seeded with millions of cells, has been reported to be 1.4 ± 0.2 nN (30). Quantitative study of individual cell behavior within a three-dimensional construct such as the CG scaffold requires understanding the local extracellular environment of individual cells through accurate compositional, microstructural, and mechanical characterization. Comprehensive mechanical characterization of the CG scaffolds at the macroscopic and microscopic level has recently been completed; such characterization has determined the Young's modulus of the individual struts that define the pore microstructure and that are deformed by contractile cells (50).

In this investigation, we describe the development and use of a new method to calculate the cell-mediated contractile force generated by individual cells within a CG scaffold. Particular versions of the collagen-GAG scaffolds used here have been found to be especially bioactive and able to induce regeneration after severe injury (1), so an improved understanding of the populational versus individual cell contraction behavior of fibroblasts within the scaffolds is of significant importance in designing future bioactive scaffolds for tissue engineering applications. Additionally, the collagen-GAG scaffold provides a surface rich with natural ligands as opposed to a synthetic biomaterial with surface modifications. Additionally, the methodology developed here provides a technique to study individual cell contractile behavior within three-dimensional fibrillar networks. Such a technique may prove useful in studying differences in cell contractile behavior between cells on flat, two-dimensional surfaces, on quasi-three-dimensional or micropatterned two-dimensional surfaces (i.e., mPAD substrates), and in fibrillar three-dimensional surfaces. All of these experimental arrangements have applications in a variety of tissue engineering-based studies, so developing methods to study similar phenomena in all three could be especially useful in understanding cell-substrate interactions. Here we hope to provide motivation to add, and preliminary experimental results from, a new analytical method to the toolbox used for studying cell contraction. This new method calculates the individual cell-generated contractile force (F_c) directly from the observed strut deformation using the results of the mechanical characterization of the individual struts. This technique uses fewer experimental assumptions than previous studies of cell contraction in three-dimensional constructs, theoretically producing a more accurate estimate of F_c.

MATERIALS AND METHODS

Fabrication of CG scaffolds

CG scaffolds were fabricated using a freeze drying (lyophilization) technique (51–53) where a suspension of collagen and glycosaminoglycans is coprecipitated in acetic acid and is then subsequently solidified (frozen), resulting in a continuous, interpenetrating network of ice crystals surrounded by the collagen-glycosaminoglycan coprecipitate. Sublimation of the ice crystals produces the highly porous scaffold structure (2,51,53).

The CG suspension was produced by combining microfibrillar, type I collagen (0.5 wt %) isolated from bovine tendon (Integra LifeSciences, Plainsboro, NJ) and chondroitin-6-sulfate (0.05 wt %) isolated from shark cartilage (Sigma-Aldrich Chemical, St. Louis, MO) in a solution of 0.05 M acetic acid (pH 3.2).

The CG suspension was frozen using the quenching technique that has been previously described by this group (29,46,51,53,54). The CG suspension was poured into a 304 stainless steel tray (16.9 × 25.3 mm) (VirTis, Gardiner, NY) that was then placed into the chamber of a freeze dryer (Genesis, VirTis) held at −40°C; the depth of the suspension was ∼3 mm. The temperature of the freeze dryer shelf and chamber was held at −40°C for 60 min to complete the freezing process. The ice phase was removed via sublimation under vacuum (<100 mTorr) at 0°C for a period of 17 h to produce the porous CG scaffolds. The relative density (ρ*/ρ_s) of the CG scaffold variants was determined using the measured dry density of the collagen scaffold sheets (ρ*) and the known dry density of solid collagen (ρ_s: 1.3 g/cm³) (55,56).

CG scaffold crosslinking

A physical, dehydrothermal-based (DHT) process was used to crosslink the CG scaffolds. The DHT crosslinking treatment was carried out at 105°C in a vacuum oven (Fisher IsoTemp 201, Fisher Scientific, Boston, MA) under a 50 mTorr vacuum for 24 h (2,49,51,53); this treatment induced the formation of covalent bonds between the polypeptide chains of the collagen fibers without denaturing the collagen into gelatin (57).

Dermal fibroblast culture techniques

Dermal fibroblasts were isolated from New Zealand white rabbit skin explants as described previously (30). These cells were cultured in Dulbecco's modified Eagle's medium (GIBCO, Grand Island, NY) supplemented with 10% fetal bovine serum (Hyclone Laboratories, Logan, UT), 2% penicillin/streptomycin, 1% fungizone, and 1% L-glutamine (GIBCO) to the 5th to 12th passage. The fibroblast populations used to seed the CG scaffolds was isolated by removing the cells from the culture flask with trypsin-EDTA (Sigma, St. Louis, MO) and adding the appropriate amount of culture medium. Cell number was determined using Trypan Blue and a hemacytometer.

Live cell imaging

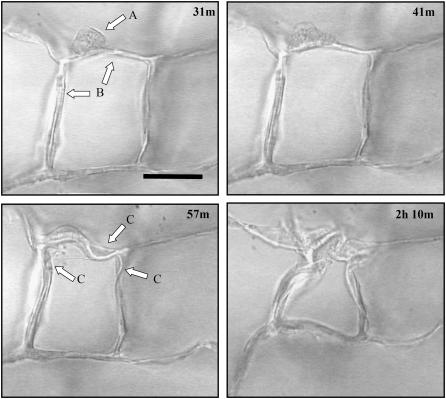
To continuously observe fibroblast elongation and contraction within the CG scaffold, dermal fibroblasts seeded into the scaffold were videotaped continuously over time, using a phase-contrast microscope (Optiphot, Nikon, Japan) (29). A section of ∼300-μm-thick CG scaffold was shaved from the full-thickness (∼3 mm) scaffold using a razor blade. This sample was then seeded with cells via submersion in a suspension of fibroblasts (∼1500 cells/mm³) for 10 min. The cell-seeded scaffold was placed into the well of a 3-mm-thick microscope slide (Erie, Cat. No. 48327-000, VWR Scientific, Bridgeport, NJ) filled with Dulbecco's modified Eagle's medium supplemented with 25 mM HEPES buffer. A glass coverslip was placed on top of the well, securing the scaffold sample on at least one side to prevent the entire scaffold sample from shifting during the imaging period. A heated stage (Biostage 600SM, 20/20 Technologies, Wilmington, NC) maintained the slide at 37°C throughout the imaging experiment. A CCD color digital camera (Optronics Engineering, Goleta, GA) attached to an Optiphot light microscope (Nikon) was used to image cell contraction at 30 images per second for up to 6 h. Output from the CCD camera was recorded directly to a VCR (AG-DS555 Panasonic, Rockville, MD). After each experiment, the video was replayed and discrete images were gathered via a frame grabber card (Snappy Video Snapshot, Play Inc., Rancho Cordova, CA) to show the mechanical interactions of the cell with the scaffold (Fig. 1).

FIGURE 1.

Time-lapse images of an individual dermal fibroblast within the CG scaffold. The sequence of images shows a dermal fibroblast (arrow in A) elongating and deforming the scaffold surrounding struts (arrows in B). Several struts are deformed over time (arrows in C). The number in the top-right corner of each image indicates the time, in hours and minutes, after cell seeding. Scale bar: 50 μm. Reprinted with permission (29).

Characterizing the scaffold strut

Combining mechanical characterization of the individual scaffold struts with the observed strut deformation during cell-mediated contraction (via light microscopy) allows calculation of individual cell-mediated contractile forces generated within the scaffold. The length of the strut being buckled was determined from each series of images obtained via live cell imaging (29). Digitized images from the start of each series, before the onset of cell contraction, were analyzed using the Scion Image (Scion, Frederick, MD) software to determine the length of the strut before it had been buckled by the dermal fibroblasts.

While strut length (order: 30–75 μm) was readily measured from the images obtained using live cell imaging, the strut thickness (order: 3–5 μm) was not readily obtained from these images due to resolution limitations. Instead, the average strut thickness of the CG scaffolds was determined from a series of histology images taken of scaffolds with mean pore sizes ranging between 96 and 151 μm (53); the strut thickness was measured for both the homogenous scaffolds, made using a constant cooling rate technique (51,53), and the heterogeneous scaffolds, made using the previous quenching technique (51), that were used in this investigation. The stereology technique used to measure the mean strut thickness has been previously described (51). Briefly, samples were removed from the CG scaffold sheets, embedded in glycolmethacrylate (Polysciences, Warrington, PA), and serially sectioned on a Leica RM2165 microtome (Mannheim, Germany) at a 5-μm thickness. The sections were stained using aniline blue and observed on an optical microscope (Nikon Optiphot) at 4× magnification; images of each section were digitized using a CCD color video camera (Optronics Engineering). The digitized images were analyzed using Scion Image to determine the mean thickness of the struts in each cross-sectional image.

The bending stiffness of the individual struts cut from a nonhydrated CG scaffold was measured via atomic force microscopy (MFP3D AFM, WaveMetrics, Portland, OR) using the supplied control and analysis software (IgorPro, WaveMetrics) (50). Individual struts of the CG scaffold were removed from the scaffold using microsurgical forceps and a scalpel under a dissecting microscope. The struts were attached to a standard glass slide using superglue with the strut cantilevered over the edge of the glass slide. Bending tests were performed on the cantilevered CG scaffold strut using an AC240TS AFM cantilever (Asylum Research, Santa Barbara, CA). To calculate the CG scaffold strut modulus (E_s), the strut-AFM cantilever system was simplified to a conventional beam bending system. Analysis of the linear unloading regime of each bending test was performed to calculate E_s. The unloading regime was used to determine E_s instead of the loading regime so as to obtain solely elastic deformations (50).

Calculating the contraction force generated by individual cells within a CG scaffold

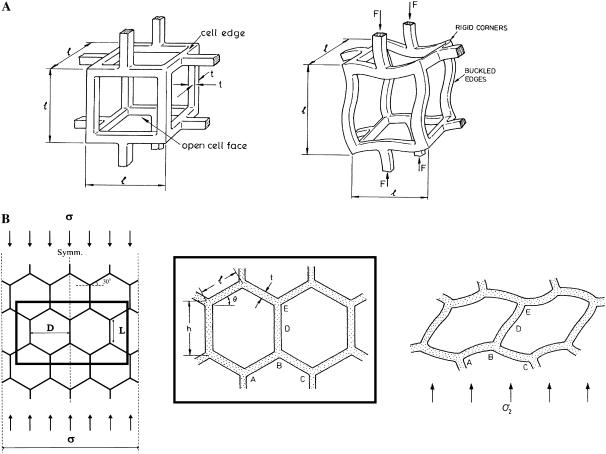
The magnitude of the cell-mediated contraction forces generated by individual dermal fibroblasts within the CG scaffold was then calculated from the strut characteristics (l, d, E_s) using an individual cell contraction assay. This calculation utilized detailed mechanical characterization of the CG scaffolds (50) and previous experimental and theoretical work describing the mechanics and collapse of open cell foams (58). The buckling load applied to an individual strut within the scaffold network was calculated using cellular solids theory to most appropriately model the boundary conditions of the buckled strut, incorporating the effect of the surrounding strut network. When an elastomeric cellular solid is loaded such that the cell edges (i.e., CG scaffold struts) are under compression, the edges first bend and then buckle; this buckling has been observed for many different classes of cellular solids such as elastomeric open-cell foams and hexagonal honeycombs (Fig. 2) (58,59).

FIGURE 2.

Schematic of elastic buckling of the struts of an open-cell foam (A) (58) and of the cell edges of a hexagonal honeycomb (B) (58,71) illustrating the rotational stiffness exerted by the strut vertices. Reprinted with permission (58,71).

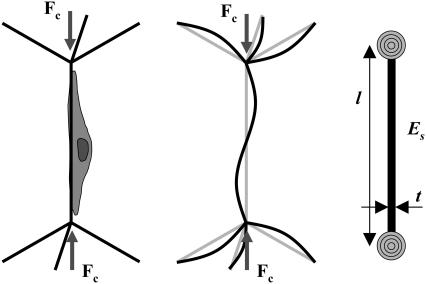
The effect of individual fibroblasts buckling the CG scaffold struts can be similarly described using these previously developed open-cell foam models for isotropic materials; for this analysis, an idealized CG scaffold structure described by a tetrakaidecahedron was used. In the tetrakaidecahedral unit cell, four cell edges meet symmetrically at each vertex in a tetrahedral arrangement. When a cell-generated contractile force is applied to the local strut network, the strut most nearly aligned with the axis of compression buckles (akin to the scaffold strut buckling under direct applied loads). This strut is restrained at its ends by the other struts where the other struts tend to reduce the rotation of the buckling strut ends. This restoring moment per unit rotation is most closely modeled by a rotational stiffness applied at the ends of the buckling strut by the three restraining struts (Fig. 3) (58).

FIGURE 3.

Schematic of a single cell applying a critical buckling load (F_c) to a scaffold strut within an idealized CG scaffold network (left). The surrounding struts inhibit rotation of the ends of the buckling strut (middle). A simplified model of CG scaffold strut buckling with the appropriate boundary conditions: the scaffold strut is restrained at its ends by a rotational spring that represents the surrounding strut network (right).

Using this description, the force per cell was calculated using a modified Euler column buckling model where care was taken to appropriately describe the system boundary constraints (end restraints of the buckling scaffold strut and the eccentricity of loading). While an eccentrically loaded column would most precisely describe the idealized case of a cell buckling a CG scaffold strut, there are a number of confounding issues to make the implementation of an eccentrically loaded column difficult. The nature of cell interactions with a scaffold strut involves many cell processes, making determination of the level eccentricity difficult. More significantly, calculation of the applied load using an eccentrically loaded column model requires measurement of the strut deflection at each time-point during cell-mediated contraction. A centrically loaded column buckling model was instead utilized to simplify the calculation.

The critical load (F_c) at which a scaffold strut of length l, Young's Modulus E_s, and second moment of area I, buckles can be calculated by Euler's formula:

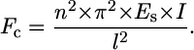(1)

For this analysis, strut geometry was approximated as a cylindrical fiber (I = π × d⁴/64), where scaffold diameter (d) was taken to be the average strut thickness of the CG scaffold. The factor n² describes the end constraint of the CG scaffold strut and depends on the surrounding mechanical environment. The effect of multiaxial loads applied to low-density, open-cell foams such as the scaffold network is to change the rotational stiffness of the vertices. Applied loads to the surrounding strut network bend the surrounding (restraining) struts, thereby reducing their rotational stiffness (58). The effect of such applied stress states on the degree of constraint has been previously described for many different cellular materials. For isotropic honeycombs under uniaxial compression, n_uni = 0.686. Under biaxial compression, the elastic buckling load (σ_el,bi*) and hence critical buckling load (F_c,bi) is ∼80% of that of the same honeycomb structure under uniaxial compression (σ_el,uni*, F_c,uni), and isotropic honeycombs under biaxial compression display n_bi = 0.61 (58). Similar calculations have been performed for isotropic open-cell foams, with values of the degree of constraint (n²) for uniaxial, biaxial, and hydrostatic compression reported: 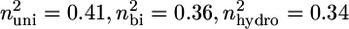(59).

During free-floating contraction of the isotropic CG scaffold, the random distribution of cells through the strut network and the randomly oriented contractile forces applied to the strut network suggest that hydrostatic compression most appropriately describes the loading conditions applied to the macroscopic scaffold. Therefore, the hydrostatic compression boundary condition was taken to most closely approximate the edge restraint applied to any particular strut within the scaffold network during contraction. The cell-mediated contractile force (F_c) was then calculated from Euler's buckling relation and the hydrostatic compression end restraint:

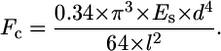(2)

This calculated cell-mediated contractile force is an upper bound for the applied force due to the likely eccentricity of the actual system. However, this calculation represents a new method for estimating the contractile force applied by an individual cell within a three-dimensional construct. Previous methods in the literature (29,30,35–38,40,44–46,60–63) have relied on calculating the average individual cell contractile force generated by cells in three-dimensional constructs from the observed macroscopic deformation of a construct and assumptions of the fraction of the cells that were contracting as well as their orientation within the construct. This technique generated a lower bound for the applied contractile load.

RESULTS

CG scaffold microstructural and mechanical properties

Mechanical and microstructural characterization of the CG scaffolds used in this investigation have previous been reported (50,51,53). Here we summarize the results of the previous characterization (50) and how it applies to the current investigation. The linear elastic modulus (E*), the elastic collapse stress and strain (σ_el*, ɛ_el*), and the collapse plateau modulus (Δσ/Δɛ) of the macroscopic homogeneous CG scaffolds are presented in Table 1; no effect of scaffold pore size (95–151 μm) was observed on CG scaffold mechanical properties (50). The hydrated (as opposed to dry) modulus of the individual struts that make up the CG scaffold microstructure (E_s,hyd) was calculated to be 5.28 ± 0.25 MPa based on the measured dry strut modulus (E_s = 762 ± 35.4 MPa) and the relative difference in the dry and hydrated CG scaffold elastic modulus (E_hydrated*/E_dry* = 0.00693) (50). This calculation was based upon the observed homogeneity of scaffold pore microstructure between the hydrated and dry phase as well as previously verified cellular solids theory; a much more complete analysis, including the experimental assumptions and modeling employed to determine the CG scaffold microscale and macroscale mechanical properties has been published by these authors (50).

TABLE 1.

Average (mean ± SD) mechanical properties of the homogeneous CG scaffold variants (96–151 μm; 0.006 relative density; DHT crosslinking at 105°C for 24 h; hydrated)

Property	Hydrated CG scaffold
E*	208 ± 41 Pa
σel*	21 ± 8 Pa
ɛel*	0.10 ± 0.04
Δσ/Δɛ	92 ± 14 Pa
Es	5.28 ± 0.25 MPa

The CG scaffold used in this investigation, fabricated via freeze drying using a quenching cooling process (51), exhibited a more heterogeneous pore structure than those more recently fabricated and described by this group (51,53), which were the subject of intense mechanical characterization (50). The mean pore size of the CG scaffold used in this study was measured to be 132 ± 25 μm (51), and the average strut thickness was determined via histological examination to be 3.9 ± 0.8 μm. A total of 463 strut thickness measurements, 2–3 measurements per strut, were made from four distinct scaffolds to determine the mean strut thickness. While some regions of pore heterogeneity were evident in the quenched scaffolds used in this experiment, no significant difference in the strut thickness of the homogeneous (mean pore sizes 95–151 μm) or the heterogeneous (mean pore size: 132 μm) scaffold microstructures was observed. Further analysis determined the variation in strut thickness along individual struts to better assay single strut uniformity. An average of 2.42 measurements were taken along each of 64 different struts from six distinct cross-sectional images of different scaffolds, and the coefficient of variation (CV = SD/Mean) of strut thickness within and between struts was compared. The variation of strut thickness within each strut (CV: 0.18) was less than the variation in strut thickness between struts (CV: 0.20), suggesting the measured average strut thickness (3.9 ± 0.8 μm) is an appropriate value to utilize for all the calculations within this work. The uniformity of the strut dimensions and scaffold microstructure has also been the foundation for the use of cellular solids modeling approaches to accurately describe scaffold specific surface area, permeability, and mechanics (50,53,64).

Due to the nonuniform, nonequiaxed pore microstructure, the heterogeneous scaffold used in this investigation does not exhibit mechanical isotropy and macroscopic mechanical characteristics (E*, σ_el*, ɛ_el*, Δσ/Δɛ) identical to the homogeneous scaffold variants (50). However, the measurements of Young's modulus of individual struts from the homogeneous scaffold (E_s = 5.28 ± 0.25 MPa) is an inherent characteristic of the CG scaffold strut that is independent of strut geometry and pore shape (i.e., whether or not the scaffold is heterogeneous or homogeneous). Both the heterogeneous and homogeneous scaffold variants were fabricated with an identical technique (freeze drying), relative density (0.006), crosslinking density (DHT 105°C, 24 h), and chemical composition (identical ratio of type I collagen:chondroitin 6-sulfate), so there is not expected to be a discrepancy between E_s for the homogeneous or heterogeneous scaffold struts. The measured strut modulus (E_s,hyd) for the homogeneous CG scaffold variants was therefore used to describe the strut modulus of the heterogeneous CG scaffold variants for this study.

Cell contraction in CG scaffolds: individual cell contraction assay measurement of cell-mediated contraction force

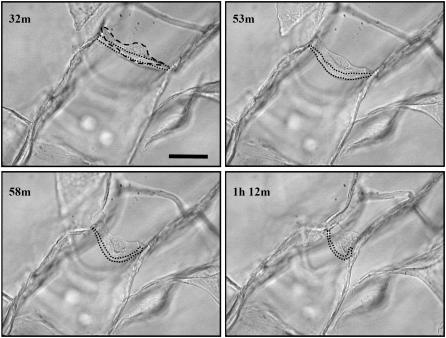
The contractile force generated (F_c) by individual cells within the CG scaffold was calculated using Eq. 2 from light microscopy images of dermal fibroblasts within CG scaffolds. The images that were analyzed were taken from datasets generated during previous investigations of cell-mediated contraction of CG scaffolds (29,30,65) (Figs. 1 and 4). Contractile cells on four struts from four distinct scaffolds were analyzed here. For each sequence of images that was analyzed for each contractile cell, the measured prebuckled strut length (l) for that particular image sequence, the mean strut thickness (d = 3.9 ± 0.8 μm) of the CG scaffolds, and the mean strut Young's modulus (E_s = 5.28 ± 0.25 MPa) for the CG scaffolds were utilized. The contractile force generated by individual dermal fibroblasts within the CG scaffold was calculated to range between 11 and 41 nN, with an average contractile force (F_c) of 26 ± 13 nN (mean ± SD) for cells that were able to buckle the strut they were attached on to. When considering the potential range of variation in strut thickness (t_Mean ± t_SD: 3.9 ± 0.8 μm), the contractile force could range from 11 ± 5 nN (t_Mean – t_SD) to 52 ± 27 nN (t_Mean + t_SD).

FIGURE 4.

Time-lapse light microscopy images of an individual dermal fibroblast buckling a CG scaffold strut (29). The dashed line highlights the fibroblast while the dotted line identifies the strut the fibroblast is buckling. The number in the top-left corner of each image indicates the time, in hours and minutes, after cell seeding. Scale bars: 50 μm. Reprinted with permission (29).

Cell contraction in CG scaffolds: upper bound of fibroblast contractile capacity in CG scaffolds

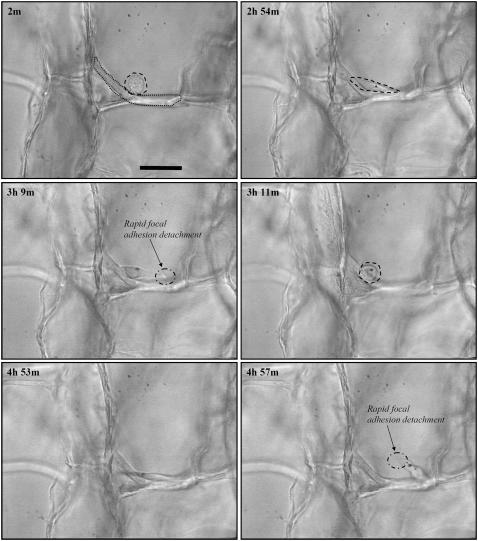
While the majority of contractile cells observed in this experiment were able to readily buckle the strut to which they were attached, in a few cases, cells appeared to be unable to contract the strut to which they were attached. While it is impossible to always determine the reason behind this failure, in one case, it appeared that the strut was much thicker than average strut, thereby increasing the flexural rigidity, and buckling load, of the strut (Fig. 5). Here, the cell starts (Fig. 5: 2 min) with a rounded morphology, then spreads in a manner characteristic of a contractile cell (29,36) and appears to apply tension to the strut (Fig. 5: 2 h, 54 min); however, the focal adhesions at one end of the cell rapidly detach from the strut (Fig. 5: 3 h, 9 min) and the cell returns to its original rounded morphology (Fig. 5: 3 h, 11 min). The cell makes a second attempt to buckle the strut (Fig. 5: 4 h, 53 min), only to have the opposite end of the cell rapidly detach (Fig. 5: 4 h, 57 min) in a similar manner as the first time, whereupon the cell returned to a more rounded morphology for the remainder of the imaging period.

FIGURE 5.

Time-lapse light microscopy images of an individual dermal fibroblast that was unable to buckle a CG scaffold strut (29). The dashed line highlights the fibroblast while the dotted line identifies the strut the fibroblast is buckling. The number in the top-left corner of each image indicates the time, in hours and minutes, after cell seeding. Scale bars: 50 μm. Reprinted with permission (29).

The buckling load of this strut provides an upper bound of the contractile capacity of the cell. Analysis of the local strut microstructure from these images determined that this particular strut was ∼10 μm in thickness and 130 μm in length so that the force required to buckle it was ∼450 nN. This suggests that 450 nN is an upper bound for the contractile force of dermal fibroblasts within a collagen-GAG scaffold.

DISCUSSION

This article describes a new method for estimating the contractile force applied by individual cells in open-cell foamlike porous scaffolds. Contraction of a wound site by cells has been found to be the primary mechanism responsible for the generation of scar tissue after severe injuries. Abrogation of organized cell contraction through the use of appropriately designed tissue engineering scaffolds has been shown to result in successful regeneration of some tissues after severe injuries. An improved understanding of the individual cell contractile behavior within scaffolds is significant for the design of future bioactive scaffolds for tissue engineering. The method developed here provides a technique for studying individual cell contractile behavior within three-dimensional fibrillar networks.

Dermal fibroblasts are observed to undergo morphological reorganization while generating contractile force within the CG scaffold. Initially rounded fibroblasts (diameter 20 μm), attached to the CG scaffold, elongated over time. The average aspect ratio increased from 1.4 to 2.8 during the first 15 h in culture (29). Scaffold deformation occurred simultaneously with cell elongation. The force generated by a population of dermal fibroblasts within the CG scaffold tends to reach an asymptote after ∼12 h (30); the time constant for population-averaged cell elongation was 5–7 h, similar to that for the force generated by the dermal fibroblast population (29,30). While cytoskeletal reorganization has not been studied within the CG scaffold, the observed cell elongation within the CG scaffolds and the correlation between cell elongation and populational force generation suggests the development of an elongated cytoskeleton during contraction. These results also suggest the development of significant mechanical anisotropy within the fibroblasts during cell-mediated contraction and that the stiffness of cells within a three-dimensional ECM analog may be significantly different from those estimated by conventional techniques that rely on localized cell surface deformation (i.e., cell poking or micropipette aspirations), as has previously been suggested (31).

The CG scaffold system allows measurement of the cell-mediated contractile forces generated within the scaffold at the individual and populational cell levels. Previously, the average cell contraction force generated by dermal fibroblasts with these CG scaffolds, calculated by measuring the gross dimensional change in the rectangular scaffold sample (58 × 28 × 3 mm) when seeded with millions of cells (2.3–10 × 10⁶ cells), has been reported to be 1.4 ± 0.2 nN (30). To make this calculation, two significant assumptions were made. The dimensional changes of the rectangular scaffold sample were measured in only one direction and the fraction of contractile cells within the scaffold was not characterized. So the average force per cell was calculated using the assumptions that all cells were contracting in the direction that dimensional change was measured and that all cells were contracting at the same time: F_c = 1.4 ± 0.2 nN is therefore a lower bound.

The individual cell contraction assay removes both these experimental assumptions by calculating the contractile force generated by a single cell within the mechanically characterized CG scaffold using a modified Euler buckling equation. The uniformity of the strut network (strut length, thickness, modulus) allows the modified Euler buckling equation to be applied to this system; the pore geometry and cell-seeding density are such that the individual cell contraction assay calculates the contractile force generated by an individual, isolated cell along a single fiber within a three dimensional fibrillar structure that acts as a bioactive extracellular matrix analog in vivo (1). Here, individual dermal fibroblasts that were able to contract CG scaffold struts were calculated to generate average contractile forces of 26 ± 13 nN (Mean ± SD; Range: 11–41 nN) (Figs. 1 and 4). As expected due to the removal of both experimental assumptions, the average force per cell calculated using the individual cell contraction assay was larger than that reported using the assay that measured the gross dimensional changes of the macroscopic scaffold (1.4 ± 0.2 nN) for the identical cell-scaffold system (29,30). The increased value of the calculated F_c for the individual cell contraction assay is likely due to the reduced experimental assumptions being made regarding the contractile behavior of a cell population within a three-dimensional substrate. However, the individual cell contraction assay did not take into account the effect of the eccentricity of the load applied to the strut by the fibroblast. It is likely that the cytoskeleton reorganizes to be aligned in the direction of cell elongation and contractile force generation, so future development of this model will attempt to integrate the influence of load eccentricity. In the case where the dermal fibroblast was unable to buckle the CG scaffold strut (Fig. 5), an estimated buckling force of 450 nN was required, suggesting that fibroblasts within a fibrillar collagen network are unable to develop contractile force at the level of 450 nN.

The results obtained here (F_c = 26 ± 13 nN) compare favorably with the estimates made by Zahalak et al. of the contractile force generated by individual, active fibroblasts within a three-dimensional bioartificial hydrogel using an integral constitutive relation for bioartificial tissue models (21 nN) (33). Additionally, while traditional individual cell contraction assays on two-dimensional and mPAD substrates typically report traction forces generated at specific focal adhesions within the cell, it is possible to integrate these reported traction forces to estimate the total contractile capacity of a single cell and compare these results with those form the individual contraction assay. From these studies on two-dimensional and mPAD substrates, fibroblasts can be estimated to be capable of generating contractile forces in the hundreds of nanoNewtons (19,27,28). The fact that the shape (and likely cytoskeletal organization) of cells on two-dimensional and mPAD substrates is significantly different than that those fibroblasts observed within the CG scaffold (spread polygonal versus elongated spindle) suggests that the contractile capacity of cells on these different substrates might be significantly different. However, the results of this investigation, while preliminary, seem to support these previous results on two-dimensional and mPAD substrates: dermal fibroblasts are readily able to generate contractile forces at the level of 25 nN (F_c = 26 ± 13 nN), and there is an upper bound to their contractile capability in the hundreds of nanoNewtons (F_ub = 450 nN).

The modulus of the CG scaffold struts (E_s,hyd) that the fibroblasts were contracting was measured to be 5.28 ± 0.25 MPa (50). This strut modulus can be placed along a continuum that considers biologically derived and relevant materials used to study cell behavior as well as natural tissues and extracellular matrix proteins and that spans six orders of magnitude. The range of elastic moduli for the natural ECM in tissues also spans a wide range: from 10 kPa for soft brain tissue to 20 GPa for cortical bone (66–68); however, as tissues are made up of a network of extracellular proteins and inorganic components, it is the mechanical properties of the individual fibrillar proteins within the tissue, to which individual cells attach, that are most important to consider. Significantly stiffer than the CG scaffold struts are many cytoskeletal and extracellular proteins such as actin (2.3 GPa), pure collagen fibrils (2 GPa), and tubulin (1.9 GPa), while keratin exhibits a modulus (2 MPa), is closer to the CG strut modulus. Stiffer still are materials used for conventional studies of cell behavior on flat substrates such as tissue culture plastic (3.5 GPa) and glass (50 GPa). And many studies of cell contraction on flat two-dimensional substrates have employed flexible polymeric substrates with moduli in the range of 10–50 kPa (27,68). The influence of substrate mechanics on cell contraction is therefore important to consider; such experiments involving two-dimensional substrates have shown significant influence of substrate mechanics on cell behavior and those utilizing three-dimensional constructs are an active and fertile area of current research.

Cell modification (i.e., degradation, matrix deposition) of the experimental construct is an issue that the individual cell contraction assay minimizes in comparison to traditional, population-level contraction assays in three-dimensional constructs. The CG scaffolds are degradable via endogenously produced proteases such as collagenase, which over time can solubilize and degrade the collagen network. However, the degradation kinetics of these CG scaffolds has been assayed both in vitro and in vivo as part of separate assays of induced regeneration and remodeling. The CG scaffolds used in this study have been used in vivo with observed degradation half-lives of ∼3 weeks (2,69), and cells have been cultured within them in vitro for periods of greater than 1 month with limited scaffold degradation (47,70). For the individual cell contraction assay, measurement of strut deformation was made within 5 h after the cells were first seeded into the scaffold. In contrast, measurements of gross scaffold deformation for population-level studies of cell contraction in these scaffolds require considerably longer time (12–20 h) to develop the necessary macroscopic scaffold deformation for reliable measurement (29,30,36). Therefore, it is unlikely that the cells could have significantly modified the scaffold strut geometry or mechanical properties via secreted proteases over the course of the experimental investigation.

Here, application of cellular solids theory and conventional column buckling relationships to the CG scaffold system allows the magnitude of individual cell contraction events within a three-dimensional porous biomaterial to be quantified. This new method represents an important advance in the field of studying cell interactions with their local environment; the analytical techniques that have previously been possible on two-dimensional substrates, where individual cell behaviors can be imaged and described in the context of the local extracellular properties, are now possible within a three-dimensional construct. The fibrillar nature of the CG scaffold provides an analog of the extracellular matrix environment in native tissues and organs that is significantly different from the environment of two-dimensional and mPAD substrates used for traditional individual cell contraction assays. Therefore, the results of analyzing cell contraction within these three-dimensional substrates is an improved experimental construct for assaying individual fibroblast contractile behavior, especially in the context of wound healing when considering the fibrillar structure of the natural ECM. The continued development of imaging techniques (i.e., confocal microscopy, nonlinear optics) will allow further expansion of this technique and will aid development of micromechanical models of cell behavior in three dimensions.

CONCLUSIONS

The individual cell contraction technique developed here adds a powerful new technique to the methods available to study cell contractility, particularly due to the ability to study individual cell contractility within a bioactive three-dimensional scaffold with direct in vivo applications for induced tissue regeneration where understanding cell contraction is critical (1). The main purpose of this investigation was to develop a new methodology that can be used to assess individual cell contraction events within three-dimensional materials, and is not meant to be a comprehensive study of cell contraction. Here, we introduce a new method, apply it to the CG system, and discuss how the results fit in with previous results from studies of entire cell populations contracting CG scaffolds and how they may relate to other studies of individual cell contraction. Future iterations of this work will attempt to provide a more comprehensive treatment of cell contraction within three-dimensional scaffolds and ECM analogs by integrating three-dimensional cell tracking using fluorescent technologies to incorporate the effect of loading eccentricity to this system and to better visualize cytoskeletal reorganization during contraction. Further modifying the mechanical properties (Young's modulus, flexural rigidity) of the CG scaffold struts would allow better estimation of the maximal contractile capacity of cells within a three-dimensional ECM analog. Lastly, comparing the individual and populational cell contractile capacity within the CG scaffold may allow aspects of cell cooperativity to be probed and may suggest techniques for modifying the scaffold microstructure or mechanics to prevent organized scaffold (and therefore wound) contraction during in vivo wound healing and regeneration studies.