Prediction discrepancies for the evaluation of nonlinear mixed-effects models

Abstract

Reliable estimation methods for non-linear mixed-effects models are now available and, although these models are increasingly used, only a limited number of statistical developments for their evaluation have been reported. We develop a criterion and a test to evaluate nonlinear mixed-effects models based on the whole predictive distribution. For each observation we define the prediction discrepancy (pd) as the percentile of the observation in the whole marginal predictive distribution under H₀. We propose to compute prediction discrepancies using Monte Carlo integration which does not require model approximation. If the model is valid, these pd should be uniformly distributed over [0, 1] which can be tested by a Kolmogorov-Smirnov test. In a simulation study based on a standard population pharmacokinetic model, we compare and show the interest of this criterion with respect to the one most frequently used to evaluate nonlinear mixed-effects models: standardized prediction errors (spe) which are evaluated using a first order approximation of the model. Trends in pd can also be evaluated via several plots to check for specific departures from the model.

INTRODUCTION

Nonlinear mixed-effects models in drug development

Nonlinear mixed-effects models are increasingly used for population analysis of pharmacokinetic or pharmacodynamic longitudinal data, especially during drug development (1,2). Several assumptions are needed to build these models: (i) for the structural model of the process under study, in most cases nonlinear with respect to the parameters, (ii) for the model of the inter-individual variability of the parameters, i.e. assumptions regarding the model and distribution of the random effects, (iii) for the error model. The model and estimated population parameters obtained from such analyses are now often used for simulation of clinical trials, an area which is also of growing importance in drug development (3–5). Providing evidence for the quality of the results is important for their use both in the different phases of drug development before registration and for dose recommendation for patients in routine clinical practice. We therefore fully agree with Yano, Beal and Sheiner who wrote (6): “As complex models depend on many assumptions, and their sensitivity to these is not immediately apparent, evaluation of such models is attaining new importance”.

In this paper, we restrict ourselves to the most popular statistical approach in this field: maximum likelihood estimation (MLE) with normality assumption for the distribution of the random-effects. Because the model is nonlinear, there is no closed form for the likelihood. The first estimation method proposed in the context of nonlinear mixed-effects models was the First-Order (FO) method, based on a linearisation of the model. There are now several estimation algorithms available (7–9), implemented in different software (10). Dedicated software, such as NONMEM (11), P-Pharm (12) or WinNonMix (Pharsight Corporation, Mountain View, CA), have been developed and more standard statistical packages also provide estimation tools, such as the nlme function (9) in Splus or the NLMIXED procedure (13) in SAS.

Model evaluation, validation, adequacy, assessment, checking, appropriateness, performance …

There is large statistical literature on model evaluation, especially from Bayesian statisticians. It is a complex issue in statistical modelling and it has several terminologies. Gelfand (14) started the chapter on model determination in a book on Monte Carlo Markov Chains applications by: “Responsible data analysis must address the issue of model determination, which consists in two components: model assessment or checking and model choice or selection. Since, in practice, apart from rare situations, a model specification is never ‘correct’ we must ask (i) is a given model adequate? and (ii) within a collection of models under consideration, which is the best?”. We focus here on question (i), model adequacy.

In 1997, Mentré and Ebelin (15) defined in population pharmacokinetics model validation as the assessment of the predictability of the model and estimates for further inferences. The same definition is used in the guidance on Population Pharmacokinetics of the Food and Drug Administration published in 1999 (16), in which there is a section devoted to model validation. Mentré and Ebelin (15) also noted that in chapter 6 about model checking in their book published in 1995, Gelman, Carlin, Stern and Rubin (17) wrote: “We do not like to ask, ‘Is our model true or false’, since probability models in most data analyses will not be perfectly true. The more relevant question is, ‘Do the model’s deficiencies have a noticeable effect on the substantive inferences?’”.

Yano, Beal and Sheiner proposed to use the term model evaluation as they explained in a note in their paper published in 2001 (6): “We use the weaker term ‘evaluation’ rather than the stronger one ‘validation’, as we believe one cannot truly validate a model, except perhaps in the very special case that one can both specify the complete set of alternative models that must be excluded and one has sufficient data to attain a preset degree of certainty with which these alternatives would be excluded. We believe that such cases are rare at best”.

Williams and Ette, in 2003, used the term model appropriateness in the title of their chapter in the book on Simulation for Designing Clinical trials (18), of which they then defined two different aspects: model evaluation and model validation. In the present paper, we rather follow the terminology of Yano, Beal and Sheiner (6), i.e. model evaluation, with the definition they gave: “The goal of model evaluation is objective assessment of the predictive ability of a model for domain-specific quantities of interest, or to determine whether the model deficiencies (the final model is never the ‘true model’) have a noticeable effect in substantive inferences.”

Methods of evaluation of nonlinear mixed-effects models

Although reliable estimation methods for non-linear mixed-effects models are now available, only a limited number of statistical developments for evaluation of the results or model checking have been reported in this area (15,6,18).

Model evaluation can be done either on the original data set used for estimation (usually called internal validation), or, preferably, on a separate data set (usually called external validation). For “internal validation” several methods have been proposed: one approach is to randomly split the initial data set, others are to use cross-validation approaches or bootstrap methods (15,6,18). It is not our purpose here to discuss whether random splitting, as proposed by the Food and Drug Administration (16), is the most appropriate approach for “internal validation”. This debate is beyond the scope of this paper, and has been the subject of more general discussion in the statistical literature on model checking, as for instance by Evans (19).

Here, we are interested in a criterion to evaluate the “distance” between the observed values and the model predictions in order to derive a statistical test of model adequacy. Most estimation software in nonlinear mixed-effects models evaluate the standardized prediction errors (spe). This criterion is currently the most frequently used for model evaluation in this area (18). The standardized predictions errors are derived, for each observation, from the mean predicted value and its variance, computed using a first-order approximation of the model like in the FO approach. A test is then often performed to see whether they follow a normal distribution, an assumption also based on the FO linearisation.

There have been several papers on the problem of investigating whether a given null model H₀ is compatible with data, in the situation where the assumed model has unknown parameters (20,21). These authors proposed and discussed several p-values for what they called composite null models in the frequentist or the Bayesian view. To our knowledge they did not address the issue of mixed-effects models. Lange & Ryan (22) developed a method to assess normality of random effects in linear mixed effects models using empirical cumulative distribution of the empirical Bayes estimates of the random effects.

Predictive distribution

The idea of using the whole predictive distribution for model evaluation has been proposed by Gelfand, Det and Chang (23) in a Bayesian framework and is also discussed by Gelman, Carlin, Stern and Rubin (17). It has been used for example by Best, Tan, Gilks and Spiegelhalter (24) to evaluate the model obtained in a population pharmacokinetic analysis in children on two separate data sets. Yano, Beal and Sheiner extended the idea to the non-Bayesian setting and defined posterior predictive check (PPC) which they applied and evaluated in individual nonlinear regression. They proposed three approaches to compute the posterior distribution of the parameters estimated through MLE. The simplest approach, which we use also here, is to use what they called a “degenerate” distribution: the posterior distribution is approximated by a discrete distribution with one location at the maximum likelihood estimate. That is to say, the estimation error is not taken into account, which can be reasonable in large enough data sets. This approach, based only on the maximum likelihood estimates, is called the “plug-in” approach in the papers by Bayarri and Berger (20) and Robins, van der Vaart and Ventura (21).

In the present paper, we propose a criterion to evaluate the predictability of an observation by a model without approximation. This criterion can be viewed as a “distance” between an observation and its prediction. It is an extension of the notion of residuals or of prediction errors which are the differences between observations and fitted or predicted values. We evaluate what we call the “prediction discrepancy” (pd) which is defined as the percentile of an observation in the whole marginal predictive distribution under H₀. This approach has already been applied for the evaluation of the population pharmacokinetic analysis of an anti-histaminic drug during its development after random splitting of the original data set with 2/3 of the patients for model building and 1/3 for model evaluation (25). In that study, a nonparametric estimation method was used (26) and the estimated distribution was discrete; there was therefore a closed form for the evaluation of the prediction discrepancies. In the more usual case of parametric MLE methods which we consider here, we propose to calculate the prediction discrepancies by Monte-Carlo integration. This approach has been successfully applied to detect the differences of the pharmacokinetics of S1, an oral anticancer agent, in Western and Japanese patients using NONMEM (27).

The method is described in details in the next section. Because the distribution of pd is uniform U[0,1] under H₀, a Kolmogorov-Smirnov (KS) test can be used to test model adequacy. In the following section, we illustrate the use of pd in the context of a basic population pharmacokinetic model and we evaluate by simulation the type I error and the power of the proposed test for a number of alternative hypotheses. We also compare the performances of the tests based on pd to those based on spe.

METHODS

Model

Let y_i be the n_i-vector of observations observed in individual i (i=1,…, N). We assume that there is a known function f describing the non-linear structural model and that the error model is additive. The individual regression model is then given by y_i = f(θ_i, ξ_i) + ε_i, where ξ_i = (t_i1,…,t_ini)^T is the n_i-vector of sampling times for individual i, θ_i is the p-vector of individual parameters and ε_i is the n_i -vector of random errors with ε_i ~ N(0, Σ_i(θ_i)). Σ_i(θ_i) are assumed to be n_i × n_i -diagonal matrices.

The model for the variance of the residual error of the j^th observation of individual i is assumed to be given by a known function h which may depend on θ_i but also on additional variance parameters σ and β: var(ε_ij) = σ² h(t_ij, θ_i, β). If a constant error model is assumed, the function h is equal to one and σ² is the variance of the residual error. If a constant coefficient of variation error model is assumed, h is equal to f² and σ is the coefficient of variation. In these two cases there is no additional variance parameter β, but more complex error models can be used.

As usual, ε_i | θ_i, i=1,…, N, are assumed to be independent from one individual to the other, and for each individual, ε_i and θ_i are also independent. The model for inter-individual variability of the parameters involves individual vectors of random effects, b_i, and a vector μ of fixed effects. The individual parameters are modelled either by θ_i = μ + b_i, for an additive random-effects model, or by θ_i = μ exp(b_i), for an exponential random-effects model. It is assumed that b_i ~ N( 0, Ω), with Ω defined as a p×p- matrix, where each diagonal element ω_kk represents the variance of the k^th component of the random effects vector.

Predictive Distribution

We assume that the population model and the population parameters, μ, diag(Ω), σ, β, are given and that they define the null model H₀. We want to evaluate the predictive distribution of the observations in an individual i. Assuming that the population parameters were obtained by maximum likelihood, we consider here only the point estimates and discard the estimation error as in the plug-in approach defined by Bayarri and Berger (20) and Robbins, van der Vaart and Ventura (21). For each vector of observation y_i, given the associated experimental design ξ_i, the model and the population parameters, we can compute the associated predictive distribution p_i(y), defined as:

$${\text{p}}_{\text{i}}(\text{y})=\int \text{p}(\text{y}\mid {\theta }_{\text{i}})\text{p}({\theta }_{\text{i}})\text{d}{\theta }_{\text{i}}.$$ (1)

Because of the assumptions on the error model, p(y | θ _i) is normal with mean f(θ _i, ξ_i) and variance Σ_i(θ_i) = diag(σ² h(t_ij, θ_i, β)). When the structural model is nonlinear, there is no analytical expression for the integral in p_i(y). This is a well known fact which has prompted the first-order approximations proposed for maximum likelihood estimation in that case.

We propose to approximate the distribution p_i(y) by a discrete distribution, by stochastic simulation of K values of b_k in N(0, Ω) and to evaluate θ_k with the appropriate model. The predictive distribution can then be estimated by Monte Carlo integration, and approximated by a mixture of K normal distributions with weights 1/K, means f(θ_k, ξ_i) and variances Σ_i(θ_k):

$${\text{p}}_{\text{i}}(\text{y})=\frac{1}{\text{K}}\sum _{\text{k}=1}^{\text{K}}\text{p}(\text{y}\mid {\theta }_{\text{k}})=\frac{1}{\text{K}}\sum _{\text{k}=1}^{\text{K}}\phi \left(\text{y};\text{f}({\theta }_{\text{k}},{\xi }_{\text{i}}),{\mathrm{\sum }}_{\text{i}}({\theta }_{\text{k}})\right),$$ (2)

where (φ)(x; μ, Ω) is the multivariate normal density function with mean μ, and variance Ω evaluated at x. This expression does not use a linearisation of the structural model but uses instead stochastic integration using random samples from the normal distribution, and K can be chosen large enough to provide a good approximation.

Prediction Discrepancy

We use the full predictive distribution to define the prediction discrepancy for the j^th observation of individual I, pd_ij. Let F_ij be the cumulative distribution function of the predictive distribution p_i(y_ij) given in Eq. (1). The prediction discrepancy is defined by the evaluation of F_ij at y_ij, and is given by:

$${\text{pd}}_{\text{ij}}={\text{F}}_{\text{ij}}({\text{y}}_{\text{ij}})={\int }_{\hspace{0.17em}}^{{\text{y}}_{\text{ij}}}\int \text{p}(\text{y}\mid {\theta }_{\text{i}})\text{p}({\theta }_{\text{i}})\text{d}{\theta }_{\text{i}}\text{dy}.$$ (3)

pd_ij is the percentile of the observation y_ij in the marginal distribution of the observations under H₀. If the model and population parameters are correct, these prediction discrepancies should follow a uniform distribution over [0, 1]. This well known result on the cumulative distribution function is always true under H₀ and does not require any approximation.

The prediction discrepancies can be evaluated by stochastic integration using a random sample of values θ_k as in Eq. (2). Then F_ij (y_ij) is evaluated by:

$${\text{F}}_{\text{ij}}({\text{y}}_{\text{ij}})=\frac{1}{\text{K}}{\int }_{\hspace{0.17em}}^{{\text{y}}_{\text{ij}}}\sum _{\text{k}=1}^{\text{K}}\text{p}(\text{y}\mid {\theta }_{\text{k}})\text{dy}=\frac{1}{\text{K}}\sum _{\text{k}=1}^{\text{K}}{\int }_{\hspace{0.17em}}^{{\text{y}}_{\text{ij}}}\text{p}(\text{y}\mid {\theta }_{\text{k}})\text{dy}.$$ (4)

Because of the error model, it can also be expressed as:

$${\text{pd}}_{\text{ij}}={\text{F}}_{\text{ij}}({\text{y}}_{\text{ij}})=\frac{1}{\text{K}}\sum _{\text{k}=1}^{\text{K}}\mathrm{\Phi }\left({\text{y}}_{\text{ij}};\text{f}({\theta }_{\text{k}},{\text{t}}_{\text{ij}}),{\sigma }^2\text{h}({\text{t}}_{\text{ij}},{\theta }_{\text{k}},\beta )\right),$$ (5)

where Φ(x; μ, ω) is the cumulative density function of a univariate normal distribution with mean μ, and variance ω evaluated at x. If the model f has an analytical expression, pd_ij in Eq. (5) can be easily evaluated by any statistical package in which Φ is available.

Standardized Prediction Error

Prediction errors for each individual are usually derived using a first order linearisation of the model, as in the FO estimation methods (15, 17, 16). Indeed, after linearisation, the predictive distribution can be obtained analytically. For instance, the linearisation in the case of additive random-effects model yields:

$${\text{y}}_{\text{i}}=\text{f}(\mu +{\text{b}}_{\text{i}},{\xi }_{\text{i}})+{\epsilon }_{\text{i}}\approx \text{f}(\mu ,{\xi }_{\text{i}})+\frac{\partial \text{f}(\mu ,{\xi }_{\text{i}})}{\partial {\text{b}}^{\text{T}}}{\text{b}}_{\text{i}}+{\epsilon }_{\text{i}}.$$ (6)

Because of this approximation, the predictive distribution is normal with mean:

$$\text{E}({\text{y}}_{\text{i}})\approx \text{f}(\mu ,{\xi }_{\text{i}}),$$ (7)

and variance V_i:

$${\mathbf{V}}_{\mathbf{i}}\approx \frac{\partial f(\mu ,{\mathbf{\xi }}_{\mathbf{i}})}{\partial {\mathbf{b}}^{\prime }}\mathbf{\Omega }\frac{\partial f^{\prime }(\mu ,{\mathbf{\xi }}_{\mathbf{i}})}{\partial \mathbf{b}}+{\mathbf{\Sigma }}_{\mathbf{i}}(\mathbf{\mu }).$$ (8)

Then, for a given observation y_ij, the prediction error is defined as pe_ij = y_ij − E(y_ij), where E(y_ij) is given in Eq. (7). The standardized prediction error is defined, in most software, as

$${\text{spe}}_{\text{ij}}=({\text{y}}_{\text{ij}}-\text{E}({\text{y}}_{\text{ij}}))/\text{SD}({\text{y}}_{\text{ij}})$$ (9)

where SD(y_ij) is the square-root of the j^th diagonal element of the variance V_i given in Eq. (8). In NONMEM, the full predicted variance V_i can be used to evaluate the “uncorrelated” vector of standardised prediction errors,

$${\text{spe}}_{\text{i}}={\text{V}}_{\text{i}}^{-1/2}\{{\text{y}}_{\text{i}}-\text{E}({\text{y}}_{\text{i}})\}.$$ (10)

This approach provides uncorrelated components spe_ij within an individual i, only if the normality of the predictive distribution, which is based on the linearisation, is assumed to be valid.

Under H₀ and based on the first-order approximation, the spe_ij should have a normal distribution with mean 0 and variance 1. It is however known that the linearisation around the mean is poor if the model is highly nonlinear or if the inter-patient variability is large, and then the distribution of spe_ij under H₀ is no longer normal.

Tests

We use the theoretical distributions under H₀ of prediction discrepancies and standardized prediction errors to provide a test of H₀ for a given data set of N individuals. The idea is to test whether the prediction discrepancies follow a uniform U[0,1] distribution and whether the standardized prediction errors follow a normal N(0,1) distribution. Several useful diagnostic plots that were defined for spe_ij can easily be applied also for pd_ij: quantile-quantile plots; histograms; plots of pd versus predicted mean concentrations or versus time.

A problem arises, when analysing real datasets, for the implementation of statistical tests to evaluate whether there is departure from the distributional assumption under H₀. Indeed, if all observations y_ij were independent, then all prediction discrepancies or errors would be independent and we could use the one-sample Kolmogorov-Smirnov (KS) test to evaluate the departure from the expected distribution under H₀. However, in most cases there are several observations within one individual, which are only independent given the individual random effects but not marginally. In that case the prediction discrepancies and the prediction errors (computed as in Eq. (9)) within an individual are not independent. When using NONMEM with the prediction errors computed as in Eq. (10) and assuming the first-order approximation is valid as in a linear mixed-effects model, then they can be assumed independent within individuals and this problem no longer holds. These correlations within individuals invalidate the previous distributional tests (both on pd or spe) because these tests assume a set of independent realisations. The KS test then might not be of the expected size, with a wrong type I error.

Correlations are often forgotten when validation is performed using spe_ij (15,6). To circumvent that problem we propose two approaches. The first one is to apply the test on only one randomly chosen observation per individual, but obviously this leads to loss of power because all observations are not used for model evaluation. The other approach is to use a Monte Carlo simulation under HO to define an empirical threshold for the test in order to get the chosen type I error. This is of course a computer-intensive approach.

EVALUATION BY SIMULATION

Model

The basic pharmacostatistical model used for the evaluation by simulation is similar to the one in Mentré and Gomeni (12). A one compartment pharmacokinetic model with first-order absorption is assumed, corresponding to the following equation:

$$\text{f}(\theta (\text{t}))=\frac{{\text{Dk}}_{\text{a}}}{\text{V}({\text{k}}_{\text{a}}-\frac{\text{CL}}{\text{V}})}({\text{e}}^{-\frac{\text{CL}}{\text{V}}\text{t}}-{\text{e}}^{-{\text{k}}_{\text{a}}\text{t}}).$$ (11)

It involves three pharmacokinetic parameters k_a, the rate-constant of absorption, Cl, the oral clearance of elimination, and V, the oral volume of distribution. The dose D is fixed to 10. Exponential random effects are assumed for these three parameters and the error model variance is a constant coefficient of variation model, i.e. the variance of the error is proportional to the square of the prediction: h(t, θ, β) = f²(θ, t).

For the basic model, i.e. under the null hypothesis, the following values are used. The fixed effects are 5, 5 and 2 for k_a, Cl and V, respectively. A coefficient of variation of 30% for interpatient variability is assumed, which corresponds to a variance of 0.09 for the distribution of the logarithm of the parameters. The coefficient of variation of the error model is 15% which corresponds to σ²= 0.0225.

Six sampling times are defined: 0.05, 0.15, 0.3, 0.6, 1 and 1.4 after dose administration. We simulated two types of data sets both with a total number of 300 observations. In the first case (Case I), simulated data sets are composed of N = 300 patients with only n = 1 observation at a sampling time randomly chosen among the six defined sampling times. In the second case (Case II), simulated data sets are composed of N = 100 patients with n = 3 observations at sampling times chosen randomly (without replacement within one individual) among the 6. The first case is not very realistic and is interesting only because there is no correlation between the observations. The second case is closer to real-life data and is used to evaluate the methods when there are correlations. We evaluate two approaches to handle the repeated observations within individuals in Case II: in Case IIa, all 300 observations are kept and an empirical threshold is computed; in Case IIb only one observation per individual is used, randomly chosen among the three available, which leads to a total of only 100 observations for model evaluation.

Simulation Setting

Data sets are simulated under H₀ with the basic model and parameters described above, and under several alternative hypotheses with modified parameters and/or models. For each alternative hypothesis studied, 1 000 datasets for Case I and 1 000 sets for Case II are simulated. Each set is simulated as follows. First, random effects are sampled from a normal distribution and individual parameters are derived. Second, sampling times are randomly chosen and predicted concentrations are calculated from the model. Third, concentrations are simulated by multiplying the predicted concentration by 1 + ε, where ε is a random sample of a zero-mean normal distribution with variance σ². Fig. 1 displays a typical set of pseudo-observed concentrations for the basic model with the prediction for the mean parameters overlaid.

Fig. 1.

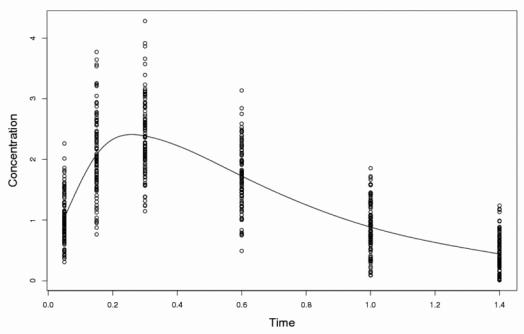
Typical data set containing 300 simulated pseudo-observed concentrations and mean-predicted concentrations for the basic model, in case IIa (N=100, n=3).

In a first stage, simulations are performed under H₀ to evaluate the type I error and to determine the empirical thresholds to be used in the evaluation of the power. The empirical threshold, for a given simulation, is defined as the 95% percentile of the KS distances under H₀, i.e. the 950^th value once the 1 000 KS distances are ordered.

In a second stage, data sets are generated under alternative assumptions corresponding to the same models but with successive changes in the value of the parameters. First, each fixed effect is separately multiplied or divided by two (6 cases). Second, the coefficient of variation of each random effect is separately multiplied or divided by two and then all together (8 cases). Third, the error coefficient of variation is multiplied or divided by two (2 cases). Thus we define a total of 16 alternative hypotheses based only on numerical modifications of the population parameters. The first group of simulations with changes on the fixed effects are mostly performed to check the approaches and their implementation. Indeed, such important changes in fixed effects can usually be seen visually and do not need such complex tests for which we expect a good power. We are indeed more interested in the other groups of simulations under H₁, where change are made on the variances or on the model (see below), because these changes are more difficult to check visually.

In a third stage, we assume an alternative pharmacokinetic model. We simulate data under a two-compartment model with first order absorption. The parameters of this model are chosen in order to be close to the one compartment model. We also chose typical values for Cl, V, and k_a and variabilities for these parameters similar to those from the basic model. The two inter-compartmental rate constants, k₁₂ and k₂₁, are fixed respectively to 2.1 and 2.4, without inter-patient variability. The two mean rate constants λ₁ and λ₂ are then respectively 6 and 1, compared to the mean elimination rate constant of 2.5 (k = Cl/V) in the one-compartment model.

In the fourth and last stage, we assume that the distribution of the random effects for Cl is a mixture of two normal distributions. More precisely, the distribution for log(Cl) under the null hypothesis is N(1.6; 0.09). The alternative distribution is a mixture of the same distribution N(1.6; 0.09) with a weight of 0.75 and of N(2.2; 0.0225) with a weight of 0.25. This intends to mimic a validation set where one fourth of the patients would come from a different population.

Evaluation method

The simulated sets are considered as validation sets and the null assumption is the basic model with the basic population parameters μ, Ω, σ. In a real-life analysis, these “basic” parameters could have been for instance those estimated on a separate data set (in the case of external validation) or on the same data set (in the case of internal validation). As already mentioned we do not take into account the estimation error in our predictive distribution, so that we do not need to perform estimation on the simulated datasets to evaluate the statistical properties of the prediction criteria.

The method proposed to evaluate prediction discrepancies given in Eq. (5), with K =10 000 Monte Carlo samples, is applied to each observation of a simulated set using the basic values for the population parameters. Similarly, the standardized prediction error for each observation of a simulated set is evaluated as in Eq. (9) using the analytical expression of the derivatives of the model. In order to get similar distributional assumptions for testing pd and spe, the latter are transformed using the normal cumulative density function Φ. More precisely, Φ(spe) are evaluated and, under the assumption that spe follow a N(0,1) distribution, Φ(spe) follow a U(0, 1) distribution.

A KS test for a U(0,1) distribution is then applied on the samples of pd or spe evaluated from the pseudo-observations of each simulated set. The distance limit of this test for 300 observations (Cases I and IIa) and a type I error of 0.05 is 0.078. For 100 observations (Case IIb) the distance limit is 0.136.

Numerical Implementation

All computations were done on a Sun Ultral Workstation. The procedures used in this paper were implemented in the Pascal programming language. The pseudorandom generator is that of Sun Pascal Compiler 4.2 release, for Solaris 5.1.1. The algorithm for generating normally distributed numbers is the routine named « gasdev » in Numerical Recipes. Descriptive statistical analyses were performed in SAS 8.1.

Results

Type I error

The type I errors evaluated on the 1000 replications for cases I (N=300, n=1), IIa (N=100, n=3) and IIb (N=100, n=1) are reported in Table I for both evaluation criteria (spe and pd). For spe, they are 25.3 %, 34.7 % and 11 % for cases I, IIa and IIb respectively, values that are much greater than the nominal 5% level. The increase of type I errors for spe in the two cases (I and IIb) when there is no correlation between observations is wholly attributable to the first-order approximation of the model. The highest type I error is observed for case IIa can also be explained by the correlation within individuals. With the method implemented in NONMEM (as in Eq. (10)) to evaluate uncorrelated WRES, the type I error would have been closer to those of the two other case. This method is, however, not evaluated here because, first it is only implemented in NONMEM and not in other statistical packages, and, second the main limitation of using spe is already apparent with independent observations (cases I and IIb)

Table I.

Type I error and power under several alternative assumptions (in %) of the KS test for standard prediction errors (spe) and for prediction discrepancies (pd) evaluated on 1000 simulated data sets under the 3 studied cases with various number of individuals (N) and number of samples per individual (n).

Assumptions	Case I (N=300, n=1)		Case II (N=100)
			Case IIa (n=3)		Case IIb (n=1)
	spe	Pd	spe	pd	spe	pd
H0	25.3	3.8	34.7	10.9	11.0	5.8
V × 2	100	100	100	100	100	100
Cl × 2	100	100	100	100	100	100
ka × 2	98.7	99.7	93.6	98.8	54.4	69.3
V/2	100	100	100	100	96.2	99.0
Cl/2	100	100	100	100	100	100
ka/2	100	100	100	100	94.4	96.5
CVv × 2	54.7	91.3	36.6	75.8	20.4	33.8
CVCl × 2	73.2	97.3	52.4	87.3	23.0	40.1
CV ka × 2	18.6	42.1	10.5	28.6	10.2	11.9
All CV × 2	100	100	99.8	100	85.1	96.6
CVv/2	14.2	21.5	7.6	15.4	4.3	5.1
CVcl/2	37.7	53.6	15.6	32.5	10.7	11.5
CVka/2	8.8	9.0	6.1	6.8	4.8	3.6
All CV/2	100	100	100	100	78.6	85.0
CVε × 2	25.1	59.2	15.5	38.8	10.5	16.8
CVε/2	7.7	8.2	4.7	8.7	3.3	4.8
2cp model	99.8	99.7	96.9	93.1	77.1	71.3
Cl mixture	96.8	98.0	85.9	98.1	58.8	30.9

Interestingly, for the prediction discrepancies in cases I and IIb (i.e., in the absence of correlation in the observations) the empirical type I errors are close to 5 %: 3.8 % and 5.8 %, respectively. We anticipated this good behavior because no approximation is made in pd evaluation. There is however an increase in the type I error to 10.9% in the case of correlated observations within individuals (case IIa), but the type I error still remains much lower than for spe. Fig. 2 displays several goodness-of-fit plots for spe and pd for one simulated set under the null hypothesis in case IIb.

Fig. 2.

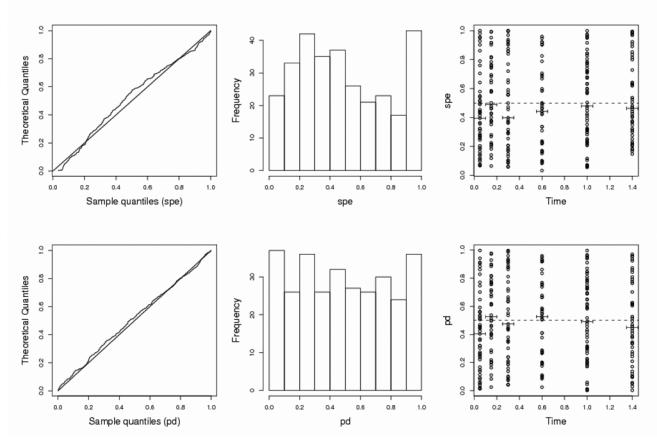
Goodness-of-fit plots under H₀, for standardized prediction errors (top) or for prediction discrepancies (bottom), for one simulation in case IIa (N=100, n=3). Left: quantile-quantile plot for a uniform distribution; middle: histograms of errors; right: box plots of the 50 errors at each sampling time versus time.

Power

The empirical thresholds of the KS tests estimated from the 1 000 simulations under H₀ are used for the evaluation of the power of the tests under several alternatives. They are .098, .111, .153 for spe in cases I, IIa and IIb respectively and .076, .088, .139 for pd.

The powers of the tests for the several alternatives are given in Table I. It can be seen that the power to detect a systematic deviation on the fixed-effect parameters (multiplied or divided by two) is, as expected, very high (greater than 99 %) for V and Cl regardless of the case and method used. The power is slightly lower for k_a probably because of the experimental design where only few samples during the absorption phase are available.

For all the alternative assumptions based on changes in the variability of the parameters or of the error, it can be seen that the power using spe is consistently lower than when using pd, and the loss is sometimes important, especially in case IIa. For instance, for increased variability on Cl or V in case IIa, the power is respectively 36.6 and 52.4 % for spe versus 75.8 % and 87.3 % for pd. This is partly due to the fact that the empirical threshold used in order to maintain a type I error of 5% is greater for spe than for pd. In general, the powers of tests based on pd to detect increased variability on Cl and V are satisfactory, except for case IIb where the loss of power compared to case I, and even to case IIa with a corrected threshold, is obvious and is due to the decrease of the number of samples. We note that the power to detect a decrease of variability for Cl or V is lower than for an increase of variability. This may be a consequence of the low variability assumed here, 30%, which is then reduced to 15%. However, when the variability changes for all three parameters (multiplied or divided by two), the power is again close to 100% for both methods. Fig. 3 displays the same goodness-of-fit plots than Fig. 2, but one simulated set of case IIa where variability on Cl is multiplied by two. These plots illustrate the use of pd also graphically without formal testing.

Fig. 3.

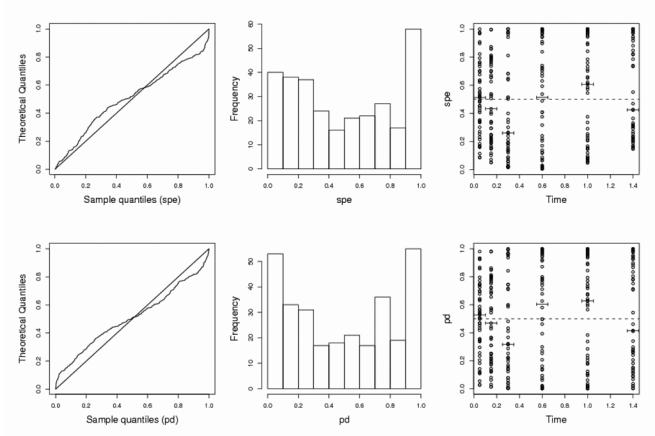
Goodness-of-fit plots under the alternative assumption that the variability of Cl is multiplied by two, for standardized prediction errors (top) or prediction discrepancies (bottom), for one simulation in case IIa (N=100, n=3) (see legend of Fig. 2 for more details).

The power to detect changes in the variability on k_a is smaller than for V and Cl, and again this could be explained by the experimental design. The power to detect changes in the variance of the residual error is lower than for the changes on the variability of the random effects, and again is much smaller when it is divided by two than when it is multiplied by two. It is also lower for spe compared to pd.

The last two lines of Table I report the power for changes not in the parameters values but in the population model itself. First, a two-compartment model is simulated instead of a one-compartment model. The power for cases I and IIa is high, greater than 90%, although the alternative hypothesis is chosen to be not too far from the null. It is interesting to notice that this is the only case where spe have similar (or even greater) power than pd. Fig. 4 displays the goodness-of-fit plots for spe and pd for one simulated set in case IIa with a two-compartment model. It can be seen in the graph of box-plot of errors versus time, a clear trend towards smaller errors for times just after the peak (0.3, 0.6) and larger errors for later times (1.4). The last alternative assumption is when Cl is distributed as a mixture on the validation set and the power is again very high, except for case IIb where the total number of observations is only one third that of cases I and IIa.

Fig. 4.

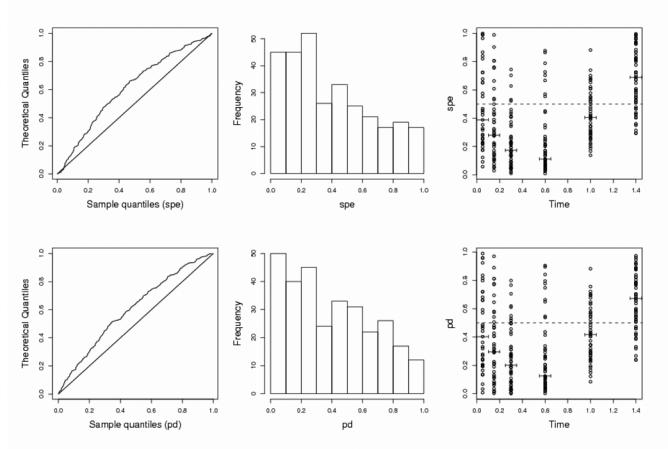
Goodness-of-fit plots under the alternative assumption that the pharmacokinetic model is a two-compartment model, for standardized prediction errors (top) or prediction discrepancies (bottom), for one simulation in case IIa (N=100, n=3) (see legend of Fig. 2 for more details).

DISCUSSION

We develop a criterion and a test for nonlinear mixed-effects model evaluation based on prediction discrepancies. The evaluation of these discrepancies by Monte Carlo integration, that is to say based on simulated samples from the distribution of the random effects, is not difficult, especially if the structural model f has an analytical solution. For more complex models, the pd in Eq. (3) can also be evaluated using the simulated capacities of the estimation software as for instance in NONMEM. In that case, K sets of observations with the same design features as the validation set are simulated under the null population model. Then, for each observation, its percentile on the sample of simulated observations is evaluated, and it is an estimate of the associated pd. This method was used by Comets et al (27) in a recent application of the use of prediction discrepancies for comparison of real pharmacokinetic data obtained in two different populations of patients.

We do not incorporate covariates in the method section and in the simulations, but it is straightforward to extend the method to models with additional fixed effects quantifying the relationship between parameters and individual covariates z_i. In the evaluation of the predictive distribution, the observed value z_i of each individual is then used.

To test a null model H₀ using pd, we propose to use a KS test to check for departures from a U[0, 1] distribution. We evaluate that test and compare its performance to a test based on spe in a simulation study. In the simulation study, we mimic the case where the validation data set is a separate data set and not the one used for model development and for parameter estimation. Therefore no estimation is performed during the simulation because the null model H₀ was given, and only validation sets are simulated. We also illustrate that prediction discrepancies can be used in graphs to visually assess the distance between model and data (similarly to graphs for residuals or for errors) without testing formally model’s correctness as suggested by Gelman (28). These diagnostic plots can help to detect where the model may fail.

The simulations under H₀ have shown, for validation sets with independent observations, a type I error close to the nominal level for the test based on pd. Using spe the type I error is greatly increased (25.3 % in Case I), which can be only explained by the poor statistical property of this criterion which uses a linearisation of the model. We do find an increased type I error, for both pd and spe, in the more usual case where there are repeated measurements within individuals (Case II.a), but less for pd (10.9 %) than for spe (34.7 %). The increased type I error is the result of the correlation between the errors within one individual, which invalidates the assumption of the KS test, and appears for both criteria since it is not related to model linearisation but to the distributional test itself. In this paper, we propose to solve that problem of repeated observations by using an empirical threshold estimated using a Monte Carlo simulation under H₀, a procedure that can be rather cumbersome.

The simulations show the satisfactory power of the proposed approach, for a validation sample of a total of 300 observations, to detect departure from H₀ either in the parameter values or in the model assumptions. It is interesting to note that the power is satisfactory in the case when there is only one observation per individual but in 300 patients (Case I). The power is much lower when only one third of the observations are used (case IIb). The power for spe is lower than for pd, and this could be simply a consequence of using a higher threshold for spe because of the increased type I error under H₀. Consequently, even though pd may be more complex to evaluate than spe, the use of the latter not only implies to always estimate an empirical threshold, but also leads to a lower power.

The main limitation of the proposed approach based on pd is that it does not take into account the correlation within individuals with repeated observations, which are the most usual cases in population PK. We did not perform simulations for a richer design with for instance 10 samples per individual, because the problem is already apparent with 3 observations per individual and it would have been even bigger. We did not computed uncorrelated spe as proposed in NONMEM, because spe showed rather poor properties even for only one observation per patient. It is fair to note that for Case II.a, doing a test based on uncorrelated spe as in NONMEM would have lead to a better Type I error than the one with standard spe as evaluated here. The tests could have performed better, in that case, than using pd. We propose here to use empirical thresholds, but we think that other statistical developments are needed. One idea would be to use a rather similar approach than in NONMEM, in order to obtain uncorrelated pseudo-observations in each patient. Using K simulated data sets under the null model, the expected variance matrix for each vector of observation of an individual could be empirically estimated without linearisation. Then using a Cholesky decomposition as in Eq. (10), uncorrelated vector of pseudo-observations could be derived. These vectors would have independent observations within one individual. Then, for each pseudo-observation a pd could be computed using the predictive distribution of the pseudo-observation instead of the predictive distribution of the real observation. This method should be implemented and evaluated. It could then be compared to spe as computed in NONMEM where the evaluation of the mean and variance are based on a linearization of the model.

We can also suggest a model evaluation “strategy” based on pd in order to try to avoid the computer intensive estimation of the empirical threshold in the present form of the test. In a first step, the KS test is performed with only one sample per individual randomly chosen in the validation set. If there is a significant departure from H₀, the model is rejected and no correction of the threshold is needed because there is no correlation between pd. If it is not rejected, then, in a second step, the approach should be applied to all observations, to avoid a lack of power of the previous test, using then a Monte Carlo p-value approach.

It should be noted that the null hypothesis in all the proposed approaches is that the model is correct, so that we can only invalidate a model when we reject H₀. When H₀ is not rejected, it can always be due to a lack of power because for instance of a poor design in the set used for ‘evaluation’. It is for instance illustrated here with a small power to detect changes in k_a. There is a strong link between design and model evaluation: for instance a linear model is only valid for a given range of doses. Therefore, as H₀ is never accepted, ‘Absence of evidence is not evidence of absence’, a model will never be significantly correct with these methods. Approaches based on the idea of equivalence testing could perhaps be developed, in which the alternative hypothesis would be that the observations are close enough to the model.

There are several similarities between the proposed criterion, i.e. prediction discrepancy, and the approach proposed by Yano, Beal and Sheiner (6). They also used random samples of the parameters to do Monte Carlo integration for evaluation of posterior predictive checks (PPC). The cumulative distribution of the predictive distribution for one observed statistic was also evaluated. Here we restrict ourselves to the observations themselves, which would correspond to a two-sided PPC. Like us, Yano Beal and Sheiner used a KS test (6). Other tests of distributional assumptions could be used like the Anderson and Darling test or the Cramer van Mises test, which would perhaps have greater power (29). There are also similarities with the approach proposed by Lange and Ryan (22) who tested the distributional assumption of the random effects in linear mixed-effects models by comparing the expected and empirical cumulative distribution functions of the random effects. They used weighted empirical cumulative distribution functions of linear combinations of random effects and they adjusted the covariance to take into account both the correlation within individuals and the estimation of the unknown parameters. This idea could perhaps be extended to empirical cumulative distribution functions on observations, as done here, in order to try to take account correlations within individuals. Again, the nonlinearity of the model makes it not straightforward to apply.

The present work concerns the evaluation of a composite null model where the parameters are unknown and have been estimated by MLE. As recalled in the introduction, we do not evaluate an exact predictive distribution. As in the plug-in approaches (20,21), the posterior distribution of the parameters is assumed to be located only at the MLE which is the simplest approach in this framework. This limitation is the same for errors based on pd or on spe but is perhaps not major. Indeed, in their evaluation by simulation of PPC in individual nonlinear regression, Yano, Beal and Sheiner (6) showed that this approach to evaluate the posterior distribution in the maximum likelihood framework was “as good as either of the others” and that the test was conservative. Also, Bayarri and Berger (20) pointed out the fact that the criterion mostly used by Bayesian statisticians, which is based on the full posterior predictive distribution, makes somehow a “double use” of the data. They concluded their paper by suggesting that, in practice, p-values based on this plug-in approach seem preferable over those based on the posterior predictive distribution, even though they may be conservative. This explains why both they and Robins, van der Vaart and Ventura (21) proposed, compared and evaluated new criteria based on partial predictive, conditional predictive or conditional plug-in distributions, which we do not study here.

The problem of how model evaluation should be performed when there is not clearly an external dataset is not clear. Prediction discrepancies can be evaluated either on observations used for model building and estimation or on separate observations. We believe that it is preferable to randomly split the data to perform model evaluation on data not used for model building. This is the approach we mimic in our simulation study. Evans (19) recommends that approach and proposes that the validation set be randomly chosen as 25% of the total data set. In the FDA guidance, random splitting is also suggested (16).

All these discussion points confirm that model evaluation is a difficult task which depends of the objective of the analysis. The best way to conclude may be to quote McCullag and Nelder who wrote in the introduction of their book on Generalized Linear Models in 1989 (30): “Modelling in science remains, partly at least, an art. A first principle is that all models are wrong; some, though, are more useful than others and we should seek those. A second principle (which applies also to artists!) is not to fall in love with one model to the exclusion of alternatives. A third principle recommends thorough checks on the fit of a model to the data. Such diagnostic procedures are not yet fully formalised, and perhaps never will be. Some imagination or introspection is required in order to determine the aspects of the model that are most important and most suspect.” We think that that prediction discrepancies as developed here could be helpful in these diagnostics steps and are a good alternative to usual standardized prediction errors.