Normalization Approaches for Removing Systematic Biases Associated with Mass Spectrometry and Label-Free Proteomics

Abstract

Central tendency, linear regression, locally weighted regression, and quantile techniques were investigated for normalization of peptide abundance measurements obtained from high-throughput liquid chromatography-Fourier transform ion cyclotron resonance mass spectrometry (LC-FTICR MS). Arbitrary abundances of peptides were obtained from three sample sets, including a standard protein sample, two Deinococcus radiodurans samples taken from different growth phases, and two mouse striatum samples from control and methamphetamine-stressed mice (strain C57BL/6). The selected normalization techniques were evaluated in both the absence and presence of biological variability by estimating extraneous variability prior to and following normalization. Prior to normalization, replicate runs from each sample set were observed to be statistically different, while following normalization replicate runs were no longer statistically different. Although all techniques reduced systematic bias to some degree, assigned ranks among the techniques revealed that for most LC-FTICR MS analyses linear regression normalization ranked either first or second. However, the lack of a definitive trend among the techniques suggested the need for additional investigation into adapting normalization approaches for label-free proteomics. Nevertheless, this study serves as an important step for evaluating approaches that address systematic biases related to relative quantification and label-free proteomics.

INTRODUCTION

Confident identification of many thousands of peptides is feasible in single experiments using liquid chromatography-Fourier transform ion cyclotron resonance mass spectrometry (LC-FTICR MS) and the accurate mass and time (AMT) tag approach¹ and has provided the basis for higher throughput proteomics measurements where the relative abundances of peptides are compared². Changes in relative peptide abundances (and by inference, protein abundances) can be viewed not only as a function of actual biological change, but also of bias and noise. Bias, resulting from systematic errors in experimentation, sample preparation, and instrumentation, is either independent of or dependent on the magnitude of the measured parameter denoting abundance. Noise often results from random errors in experimentation, sample preparation, and instrumentation. Both bias and noise lead to extraneous variability among replicate samples and can affect the accuracy and precision of biological research conclusions.

Isotopic labeling of peptides, either metabolically or chemically prior to mass spectrometric analysis, has been applied to reduce the effects of extraneous variability ^3–6. This practice has parallels in genomic studies that utilize microarrays in which cDNAs from conditions to be compared are labeled with different fluorophores. Both practices seek to nullify bias from sample/array preparation, as well as from instrumentation used to detect and measure arbitrary abundance. However, in cases where abundance data from multiple arrays or multiple LC-FITCR-MS runs are generated, e.g., as for the comparison of multiple conditions to a common condition, normalization of the data is still required to account for extraneous variability. Another practice in microarray studies is to use a single fluorophore for both conditions and multiple arrays (one array for each condition) to avoid bias associated with using two fluorescent reporters ⁷. This practice has a parallel in proteomics where peptides are not isotopically labeled prior to instrument analysis. In such a practice, data from one array or run (or replicates) that represents the common baseline is used to create the relative abundance comparisons ¹

Because proteomics labeling techniques have limitations associated with cost, often smaller proteome coverage due to labeling selectivity, applicability, and differences in labeling efficiency, ^{8, 9}, quantitative “label free” analyses are of growing interest ¹⁰. Such approaches may become more useful with very low flow rate separations that would allow electrospray ionization efficiency to be optimized and where response is projected to be more quantitative in nature, which has been demonstrated for simple mixtures ^{11, 12}. For more complex samples, normalization could be used as means of reducing extraneous variability that results from less than optimal ionization efficiencies. Other sources that could potentially introduce extraneous variability include LC carryover and different sample injected masses. Ideally, whether labeled or unlabelled samples are utilized the use of exogenous controls (spiking controls) would be an appropriate option for addressing extraneous variability. While these controls are available for microarray studies, a set of universally applicable proteomics controls is presently not available.

Herein, we present the results from an evaluation of four normalization techniques—1) central tendency (global normalization) ¹³, 2) linear regression ¹⁴, 3) local regression ¹⁵, and 4) quantile ¹⁶—used to reduce extraneous variability in high-throughput proteomics. These normalization techniques have been extensively applied to gene expression data obtained from laser or optical scanners that measure fluorescent emission from single- or dual-fluorescently labeled hybridized microarrays, where a variety of statistical methods are needed to deal with assumptions related to systematic biases. The same underlying assumptions, which include independent versus dependent systematic biases and the scale on which data should be included in the normalization process (global versus local scale), have application to high-throughput proteomics. Therefore, our evaluation of these techniques for relative quantification of non-isotopically labeled peptides was performed with the expectation that these results would prove useful for the development of more suitable normalization techniques for proteomics data.

In our study, normalization techniques were evaluated using data from three sets of samples that represented important levels of proteome complexity. The first sample set consisted of standard proteins. The second set consisted of two Deinococcus radiodurans samples, one taken during the early-log growth phase and the other taken during the stationary growth phase. The third set consisted of two striata samples, one taken from the brain of a control mouse and the other taken from a methamphetamine-stressed mouse. Replicate relative peptide abundance ratios obtained from each sample set were used to address normalization in both the absence and presence of biological variability.

EXPERIMENTAL SECTION

Sample preparation

Standard proteins

Fifteen commercially available proteins were combined (1 mg/ml in 8 M urea) to produce the standard sample of proteins described in Supplementary Table 1 online. This sample was incubated at 60° C for 1 hr in 8 M urea and 5 mM dithiothreitol (DTT) to denature and reduce the proteins. An additional incubation was carried out in the dark for 1.5 hr at 60° C in the presence of 20 mM iodoacetamide to alkylate cysteine residues. The sample volume was then increased 10-fold by addition of 100 mM NH₄HCO₃ (pH 8.4) and proteins digested overnight at 37° C by modified porcine trypsin (Promega). Following digestion, the sample was passed through a 1 ml SPE C18 column (Supelco) to remove salts. Eluted peptides were adjusted with 25 mM NH₄HCO₃ (pH 8.4) to a final concentration of 0.1 μg/μl.

Deinococcus radiodurans

Cells grown in tryptone/glucose/yeast extract (TGY) medium ¹ were harvested at ~ 16 hr (OD₆₀₀ 0.110) and ~46 hr (OD₆₀₀ 0.991) following inoculation. These harvesting times corresponded to early log phase growth and stationary phase growth, respectively. Harvested cells were concentrated by centrifugation, then immediately frozen in liquid nitrogen. For sample preparation, portions of the frozen cultures were suspended in 100 mM NH₄HCO₃, (pH 7.8) washed once using this buffer, and lysed by bead beating for 3 min using 0.2 mm zirconian beads. Proteins were separated from the lysed cells and digested into peptides according to previously published protocols ¹.

Brain tissue

The brain striata from both control mice and those in which a model of Parkinson’s disease had been induced by methamphetamine (MA) use were dissected for comparative analyses. The mouse Parkinson’s disease (PD) model was created by administrating toxic doses of methamphetamine (MA) to inbred C57BL/6J mice. Adult C57BL/6J male mice (10 wk, 25 – 31 g) received four i.p. injections of MA hydrochloride (10 mg kg⁻¹ injection⁻¹ using 1.5 mg ml⁻¹ solution) at 2 hr intervals ¹⁷. Control animals received vehicle alone. The mice were analyzed 7 days after either MA treatment or placebo. Brain material was solubilized using 99% formic acid and heat and then neutralized with ammonium hydroxide. Next, the acid-labile detergent RapiGest® (Waters) was added to 1% and the reducing agents, tributylphosphine and tricarboxyethylphosphine, were added to 40mM. The solution was digested with methyl-modified trypsin at a 1:20 ratio for 18 h at 37° C.

LC-FTICR MS analysis

Quadruplicate sub-samples taken from the standard proteins, early-log phase growth, stationary phase growth, control mouse striata tissue, and MA-stressed mouse striata tissue samples were consecutively analyzed ¹ using a capillary LC system developed in house coupled to a modified 9.4 tesla FTICR MS (Bruker Daltonics) ¹⁸. Separations on the LC system were achieved with 5000 psi reversed-phase packed capillaries (150 μm i.d. ×360 μm o.d.; Polymicro Technologies) using two mobile phase solvents: 0.2% acetic acid and 0.05% TFA in water (A) and 0.1% TFA in 90% acetonitrile/10%water (B). Flow through the capillary HPLC column was ~1.8 μl/min when equilibrated to 100% mobile phase A. Eluant from the HPLC was infused into the mass spectrometer by an electrospray ionization (ESI) interface to an electrodynamic ion funnel assembly coupled to a radio frequency (RF) quadrupole for collisional ion focusing and highly efficient ion accumulation and transport to the cylindrical ICR cell for analysis. Mass spectra were acquired with approximately 10⁵ resolution and analyzed using ICR-2LS software developed in our lab ². Measured peptide abundances where determined by integrating the areas under each peak of the spectra following deconvolution of ion currency measured by the FTICR instrument ². Only peaks with amplitudes larger than a signal to noise ratio (S/N) of at least 5 were used in calculating peptide abundances. At this S/N the impact of background on calculated peptide abundances was estimated as not being significant. Peptides common to all LC-FTICR MS runs for a given sample were used for normalization.

Normalization techniques

Normalization techniques remove systematic bias incorporated into abundances of peptides observed in the samples that can result from protein degradation, variation in sample loaded, measurement errors, etc. Before normalization, data was transformed into the log scale. Even though the relationship between peptide abundance and detector measurement is expected to be linear, log transformation has several advantages similar to those highlighted for microarray data ¹⁹. Using such a transform converts the distribution of ratios of abundance values of peptides into a more symmetric, almost normal distribution. This allows the use of several robust normalization techniques that have been developed for such data. Also, a log transform reduces the leverage of a low number of highly abundant species on the regression analysis used by these robust techniques.

In addition to the log transformation, all normalization methodologies, with the exception of the quantile approach, were carried out by plotting data in a ratio versus intensity plot (refs), or also commonly described as an M versus A (minus versus average) plot (refs.). Where, the ratio of peptide abundances is:

$$m_i={log}_2\hspace{0.17em}{x}_{i,j=1}-{log}_2\hspace{0.17em}{x}_{i,j=2}\hspace{0.17em}={log}_2\left(x_{i,j=1}/x_{i,j=2}\right),$$ 1)

with x_i,j as the arbitrary abundance obtained from summed peptide peak intensities measured by capillary LC-FTICR MS for the given peptide, i, in sample j. The intensity portion of the plot is calculated as:

$$a_i=\left({log}_2\hspace{0.17em}{x}_{i,j=1}+{log}_2\hspace{0.17em}{x}_{i,j=2}\right)/2={log}_2\left(x_{i,j=1}\hspace{0.17em}{x}_{i,j=2}\right)/2$$ 2)

The ratio versus intensity ordinate system is a re-scaling and counterclockwise rotation of the x versus y coordinate system, and allows for an easier observation of trends (both linear and nonlinear) resulting from biases ¹⁹. This easier observation of trends is due to the dependency of the ratio of abundances for a peptide d on the measured abundances, including bias, from both samples rather than just one sample as in the case of an x versus y coordinate system. After normalization, normalized values for $x_{i,j=1}^{\prime }$ and $x_{i,j=2}^{\prime }$ were found by de-convoluting $m_i^{\prime }$ and a_i, using ¹⁶:

$$x_{i,j=1}^{\prime }=2^{\left(m_i^{\prime }+2a_i\right)/2}\hspace{0.17em}\text{and}\hspace{0.17em}{x}_{i,j=2}^{\prime }=2^{-\left(m_i^{\prime }-2a_i\right)/2}.$$ 3)

Central tendency normalization

This normalization technique centers peptide abundance ratios around a mean, median, or other fixed constant to adjust for the effects of independent systematic bias and has often been defined as “global” or “total intensity” normalization by those performing microarray analyses because it utilizes all intensities of hybridized probes on the microarray ^{13, 20, 21}. Yet, this normalization technique can potentially utilize a subset of genes ²⁰ or peptides that target known conserved proteins. Therefore, in this study, we use the term “central tendency” instead of “global”. Proteomic analysis requiring central tendency normalization may occur, for example, when different peptide masses from different samples are injected into the LC system for comparative analysis. This mass difference results in the measured abundances of peptides from each sample being separated by a constant factor. In this study, all peptides with arbitrary abundances obtained from measured peptide peak intensities were utilized for normalization and normalized relative abundance ratio $m_i^{\prime }$ was calculated by subtracting the arithmetic mean of the population of peptide abundance ratios from the abundance ratio for each peptide ^{14, 22}:

$$m_i^{\prime }=m_i-\mu .$$ 4)

Linear regression normalization

This normalization technique assumes that systematic bias is linearly dependent on the magnitude of peptide abundances ^{14, 16}. For example, sample carry-over on an LC column can potentially result in inflation of measured abundances of selected peptides that elute from the system due to overlapping peaks. ^{16, 19, 23}. Linear regression normalization was performed by applying least squares regression to the scatter plot. The resulting first order regression equation was used to calculate each normalized peptide ratio:

$$m_i^{\prime }=m_i-m_i^{\ast },$$ 5)

where $m_i^{\ast }$ is the predicted peptide ratio calculated from the regression equation. The value of a predicted peptide ratio represents the deviation from the abscissa to the regression line. Therefore, a linear regression equation with a slope greater than zero indicates a proportionately larger amount of bias as the magnitude of a_i increases. As a result, a proportionately larger deviation is subtracted from the un-normalized peptide ratio.

Local regression normalization

This technique assumes that systematic bias is non-linearly dependent on the magnitude of peptide abundances ^{13, 14, 24}. This non-linearity potentially results from the effects of ion suppression on measured peptide abundances, or on measured peptide abundances approaching detector saturation or background. To adjust for this type of bias linear regression analysis was performed on localized subdivisions of the peptide populations using the 2D data smoothing object and LOWESS algorithm ¹⁵ packaged with SigmaPlot™ version 8.0 (SPSS Inc., Chicago, IL) to find the predicted value for each peptide ratio. Normalized peptide ratios were calculated in the same manner as the linear regression technique. The fraction of peptides for inclusion around the peptide ratio to be normalized was set at 0.4. The value of this fraction increases in magnitude up to 1.0 with an increasingly greater number of peptides included in the subdivision surrounding the peptide ratio to be normalized. Our selection of 0.4 was based on the observation that values <0.4 resulted in plotted regression lines not being smooth, while values >0.4 resulted in plotted regression lines being approximately linear.

Quantile normalization

This technique employs a nonparametric approach that was originally designed for multiple high density arrays, such as those created by Affymetrix GeneChip®, where measured intensities from a single fluorophore are normalized to a common distribution ¹⁶. This approach is based on the premise that the distribution of peptide abundances in different samples is expected to be similar and can be accounted for by adjusting these distributions. In our study, arbitrary peptide abundances measured across multiple FTICR runs were compared relative to a common base-line to create a set of replicates, which were then normalized using the quantile approach. Normalization was performed by:

1. Assigning each sample replicate to a column and placing the abundance values for peptides common to all replicates in the same row.

2. An index was assigned to each peptide abundance value in the column.

3. Each column was then sorted.

4. After sorting all replicates by abundance value, the mean arbitrary abundance for each row, was substituted for each abundance value in the row.

5. The normalized relative abundance for a given peptide was then found by restoring the original order of the assigned indexes for each replicate.

When adapted to the relative quantification of peptides, this normalized abundance represents the transformation m* = F⁻¹(G(m)), where G represents the empirically estimated distribution of each replicate and F is the mean of the quantile ¹⁶.

Evaluation of normalization techniques

A comparison matrix was created to evaluate the four normalization techniques and to observe the effect of different baselines on normalization. Each column within the matrix represented one of four sub-samples from one condition (early-log growth for D. radiodurans or control striata tissue from laboratory mice) and each row represented one of four sub-samples from a different condition (stationary phase growth for D. radiodurans or methamphetamine-stressed striata tissue from laboratory mice). Each element within the matrix represented the comparison of replicates relative peptide abundances created from the two conditions. To evaluate the normalization techniques in the absence of biological variability, both columns and rows of the comparison matrix contained sub-samples from the same condition.

Elements under a column (referred to as a block) were normalized using the sub-sample (i.e., LC-FTICR run) at the head of each block as the common baseline. An iterative process adapted from the normalization of multiple replicate microarrays ¹⁶ was applied to the central tendency, linear regression, and local regression normalization techniques, but was not required for normalization with the quantile technique. The iterative process for this technique was performed by subtracting the normalized m_i* from the previous un-normalized m_i. The original un-adjusted peptide abundance ratio was then replaced by the normalized abundance ratio and the iteration process continued until the difference between the mean of all abundance ratios from the previous iteration and current iteration was ≤0.005.

To compare the four normalization approaches, extraneous variability was estimated by: calculating the pooled estimate of variance (PEV) ²⁵ of peptide abundance ratios as:

$${\sigma }_p^2=\frac{(n_1-1){\sigma }_{m_1}^2+(n_2-1){\sigma }_{m_2}^2\hspace{0.17em}\text{K}}{(n_1-1)+(n_2-1)\hspace{0.17em}\text{K}}.$$ 6)

Where, ${\sigma }_{m_i}^2,$ is the variance across instrument runs for a given peptide and n_i is the number of runs. In the absence of biological variability, the log abundance ratios of peptides should equate to zero. Hence, the variance across sub-samples for a peptide used to calculate PEV in this case are based on a deviation from zero rather than the mean. The median coefficient of variation (CV) was also calculated for the population peptide abundances, x_i,j, to assess reproducibility of instrument analyses prior to and following normalization. All estimators used in this analysis have been previously applied to evaluate normalization approaches in microarray studies and have application here, as well ^{14, 26}.

RESULTS

Normalization in the absence of biological variability

Differences in LC-FTICR MS runs are is graphically depicted in Figure 1 for a block of elements selected from each sample set, i.e., standard proteins, D. radiodurans, and mouse striata tissue. Prior to normalization, little overlap was observed among the elements. Because we are comparing LC-FTICR analyses of non-isotopically labeled sub-samples we assume that the lack of agreement due to extraneous variability was introduced in the analysis. A noted lack of agreement was evident for the block elements created from the 4 runs representing the standard proteins sample (Figure 1a). In the raw data not only are the elements almost completely separated, but at lower intensities the ratios of relative abundance are shifted upward as indicated by local regression results. This upward trend may have e.g. resulted from the base-line abundances of these peptides subsiding in the lower region of the dynamic range of the instrument, i.e., close to instrument background. For these elements and for the other blocks of elements created from the replicate instrument analyses that corresponded to each sample type, we found that normalization improved agreement, although the degree of improvement varied depending on the normalization approach used.

Figure 1.

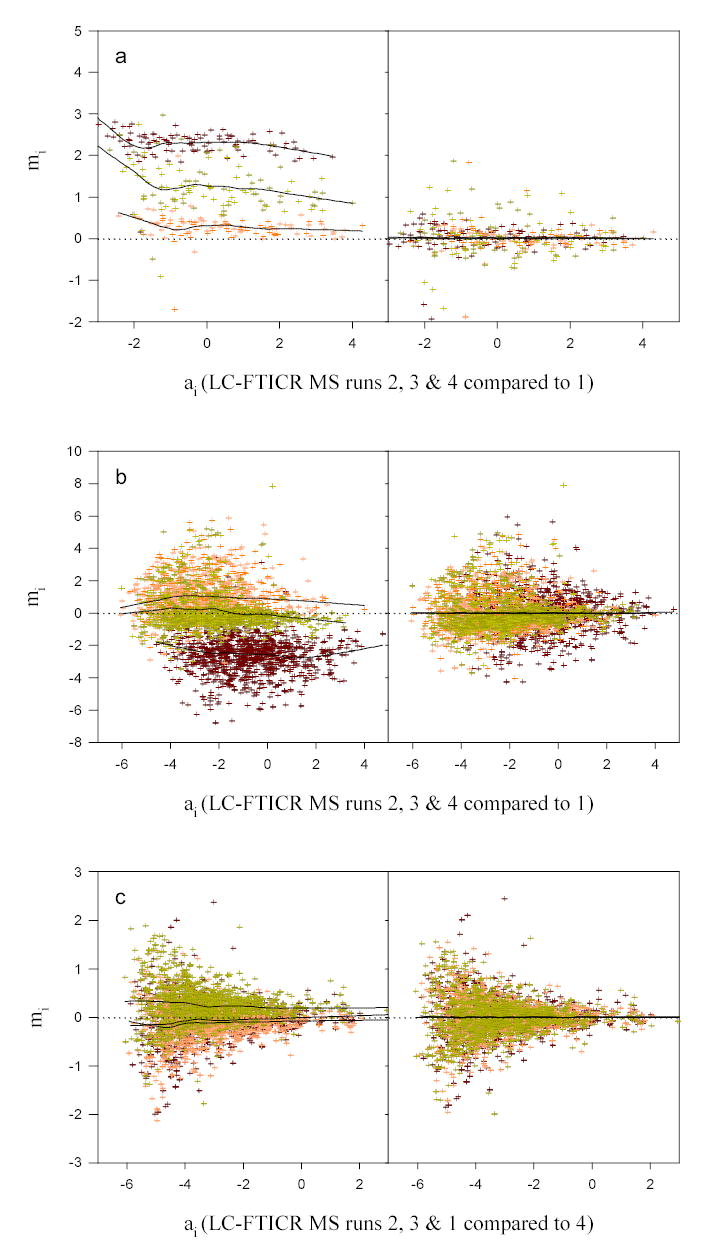
Comparison of triplicate sets of relative peptide abundances in the absence of biological variability prior to and following normalization with the local regression technique. Scatter plots represent peptide ratios (ordinate) versus their mean abundances (abscissa) for (a) 111 common peptides from the standard proteins sample, block 3, (b) 1032 common peptides from the stationary phase growth sample of D. radiodurans, block 2, and (c) 1605 common peptides from the methamphetamine induced mouse striata tissue sample, block 3. Solid lines represent potential non-linearly dependent systematic bias estimated from application of the locally weighted regression and smoothing scatter plots (LOWESS) function.

Pooled estimates of variance (PEV) and median CV values are presented in Table 1 prior to normalization and following normalization (separated by a dash). The approach that resulted in the largest percent reduction (provided in parentheses) is also indicated (superscripted letter). Evaluation in greater detail of the different sample blocks revealed which LC-FTICR MS run (used to create the relative comparisons) was the largest contributor to extraneous variability. For example, block 1 of the standard proteins sample (that consisted of Runs 2, 3, and 4, each relative to Run 1) had the largest PEV compared to the other blocks, indicating that Run 1 contributed the most to extraneous variability, possibly due to small amounts of peptides carried over from the previous run. (We observed that the first runs for the early-log phase and stationary phase D. radiodurans growth samples were also the largest contributors to extraneous variability.) However, for these two runs this observation was not unexpected since these samples were analyzed roughly three months prior to the other runs, during which time the LC column was also replaced.

Table 1.

Pooled estimate of variance (PEV) and median coefficient of variation (CV) used to estimate extraneous variability in the absence of biological variability of replicates of relative peptide abundances. Data are presented as: prior to normalization of blocks - following normalization of blocks; (% reductions), and superscript letters correspond to the normalization approach that resulted in the largest percent reduction.

			Deinococcus radiodurans				Mouse striata tissue
	Standard Proteins		Early-log Phase		Stationary Phase		Control Tissue		Stressed Tissue
Block	PEV(0)	CV	PEV(0)	CV	PEV(0)	CV	PEV(0)	CV	PEV(0)	CV
1	306 – 15.0 (95%)d	0.83 - 0.13 (83%)a	17087 – 3738 (78%)d	0.64 - 0.30 (53%)d	10296 – 1753 (82%)a	0.89 - 0.41 (53%)a	446 – 432 (3%)d	0.10 - 0.08 (20%)a	245 – 182 (25%)c	0.08 - 0.06 (25%)c
2	158 – 16.4 (89%)a	0.83 - 0.15 (81%)b	6332 – 1958 (69%)d	0.64 - 0.30 (53%)b	3732 – 1405 (62%)a	0.89 - 0.33 (62%)a	523 –423 (19%)d	0.10 - 0.08 (20%)b	240 – 155 (35%)d	0.08 - 0.06 (25%)c
3	207 – 16.6 (91%)a	0.83 - 0.16 (79%)d	6769 – 1993 (70%)d	0.64 - 0.29 (54%)b	6637 – 1912 (71%)c	0.89 - 0.38 (56%)b	406 – 360 (11%)a	0.10 - 0.07 (30%)a	206 – 168 (18%)d	0.08 - 0.06 (25%)c
4	126 – 24.1 (81%)d	0.83 - 0.14 (82%)a	6596 – 2428 (63%)d	0.64 - 0.29 (54%)b	4670 – 1929 (58%)c	0.89 - 0.42 (52%)d	372 – 303 (18%)a	0.10 - 0.07 (30%)a	360 – 221 (38%)d	0.08 - 0.05 (37%)c

^aLinear regression normalization

^bCentral tendency normalization

^cLocal regression normalization

^dQuantile normalization

A comparison among blocks within each sample, with the exception of the blocks corresponding to the early-log phase sample, did not obviously reveal one normalization approach that consistently resulted in the largest percent reduction of extraneous variability. For example, quantile normalization resulted in the largest percent reductions for Blocks 1 and 4 of the standard proteins sample, while for Blocks 2 and 3, linear regression resulted in the largest percent reduction (Table 1). This also demonstrated the impact of base-line selection on the normalization process. A similar observation was made when using the median CV as the estimator. For Blocks 1 and 4 of the standard proteins sample, linear regression resulted in the largest improvement in reproducibility, while for Blocks 2 and 3, central tendency and quantile normalization, respectively, out performed the other approaches.

As a means to reconcile the performance of the different normalization approaches each normalization approach for a given block was ranked by percent reduction, with the lowest rank assigned to the approach that exhibited the largest percent reduction. From these ranks, a mean rank for each normalization approach was calculated. Mean ranks based on PEV are presented in Table 2. For the standard proteins sample, normalization using linear regression received the lowest ranking, indicating on average deviations of peptide ratios from zero exhibited the largest reduction with this approach. This rank was significantly different than the ranks assigned to the central tendency approach (p-value 0.049, agr; = 0.05), which ranked third, and the local regression approach (p-value <0.001), which ranked fourth. Although the quantile approach ranked 2 on average its associated standard deviation suggested that this ranking could not be considered different among ranks for the other approaches. A similar scenario was observed for the control striata tissue sample. For the early-log phase sample, quantile normalization ranked highest among normalization approaches, and this ranking was significantly different than the assigned ranks for the other approaches. Quantile normalization also ranked highest among the approaches for the MA-stressed mouse striata tissue, although this ranking was only significantly different from the ranking assigned to central tendency normalization. For the stationary phase sample type, the best performing normalization methodology could not be identified.

Table 2.

Mean ranks assigned to approaches used in normalizing blocks of replicates containing relative peptide abundances in the absence of biological variability. Ranks were assigned on the percent reduction in the pooled estimate of variability (PEV) and median coefficient of variability (CV). The lower the value of the rank the greater the percent reduction. Values in parentheses represent the standard deviation of ranks.

Pooled Estimate of Variance (PEV)
	Standard	Early-log	Stationary	Control	Stressed	Sum of
	Proteins	Phase	Phase	Tissue	Tissue	Ranks
Central tendency	2.5(± 0.5)	3.2(± 0.5)	3.0(± 1.1)	2.5(± 0.5)	3.7(± 0.5)	15.0(± 1.4)
Linear regression	1.5(± 0.5)	2.2(± 0.5)	2.0(± 1.1)	1.5(± 0.5)	2.2(± 0.5)	9.5(± 1.4)
Local regression	4.0(± 0.0)	3.5(± 1.0)	2.0(± 1.1)	3.5(± 0.5)	2.2(± 0.9)	15.2(± 1.8)
Quantile	2.0(± 1.1)	1.0(± 0.0)	3.0(± 1.1)	2.5(± 1.7)	1.7(± 1.5)	10.2(± 2.7)
Median Coefficient of Variation (CV)
Central tendency	1.7(±0.5)	1.7(±1.5)	2.2(±0.9)	2.0(±0.8)	2.5(±0.6)	10.0(±2.0)
Linear regression	2.0(±1.2)	2.5(±0.6)	1.5(±0.6)	1.2(±0.5)	2.2(±0.5)	9.5(±1.6)
Local regression	4.0(±0.0)	3.7(±0.5)	4.0(±0.0)	2.7(±0.5)	1.0(±0.0)	15.5(±0.7)
Quantile	2.2(±0.9)	2.0(±0.8)	2.2(±0.9)	4.0(±0.0)	4.0(±0.0)	14.5(±1.5)

Ranking in terms of largest percent reduction in median CV is presented in Table 2. For the standard proteins sample, central tendency ranked better than the other approaches, indicating that on average peptide abundances exhibited greater reproducibility following application of this normalization approach. However, this rank was only statistically different compared to the rank assigned to the local regression approach (p-value 0.013), which consistently ranked worst (indicated by the standard deviation assigned to the average rank) for all blocks. A similar result was observed for the early-log phase sample type. For the stationary phase and control mouse striata tissue sample types, linear regression normalization ranked best, but the significance of this rank varied among the other approaches within these sample types. Only in the MA-stressed mouse striata tissue was the best ranking (assigned to local regression normalization) and worst ranking (assigned to quantile normalization) significantly different than the other ranks assigned to the normalization approaches.

To obtain a more general understanding of how the approaches compared, an overall rank was calculated from summed ranks across sample types for each estimator used in the evaluation (the last columns of Tables 2). The amount of uncertainty associated with each summed rank was calculated by propagating the deviations from the mean ranks, i.e., the square root of the summed deviations, with each deviation being raised to the second power before being summed. A plot of these summed ranks along with their uncertainties is presented in Figure 2. In terms of PEV (Figure 2A), summed ranks for linear regression normalization and quantile normalization were similar, but distinctly better than the summed ranks for central tendency and local regression normalization, which suggested that these two approaches performed generally better at reducing extraneous measurement variability than the other approaches. In terms of median CV (Figure 2B), summed ranks for linear regression and central tendency normalization were similar, but distinctly better than the summed ranks for local regression and quantile normalization. The observation that linear regression normalization ranked better among the four approaches for both estimators suggested that this approach was an appropriate starting point to address extraneous variability reduction in future proteomic studies.

Figure 2.

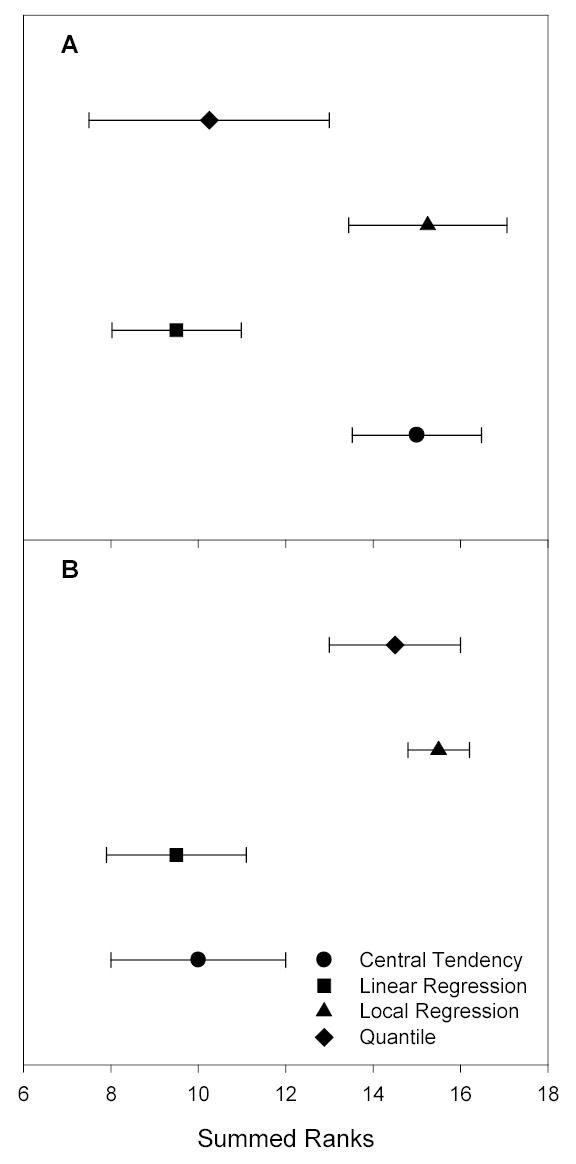
Comparison of summed ranks for central tendency, linear regression, local regression, and quantile normalization approaches applied to LC-FTICR MS runs without biological variability. (a) Ranks by percent reduction in extraneous variability estimated as PEV. Note that the lower the value of the summed rank, the greater the percent reduction in this estimate of extraneous variability. Linear regression and quantile normalization performed similarly and received better rankings than central tendency and local regression normalization. (b) Ranks by percent reduction in extraneous variability estimated by the median CV. Here, central tendency and linear regression normalization performed similarly, and better than local regression and quantile normalization.

Normalization in the presence of biological variability

The relative comparison of proteomes from multiple biological conditions adds to our variability model the additional dimension of biological variability. Here, normalization seeks to reduce biases and improve the conclusions from comparative analyses. We were interested in observing how the selected normalization approaches compared in terms of reduction in extraneous variability and improved reproducibility for replicates with this additional dimension. For this, columns of the comparison matrix represented one of four LC-FTICR MS runs (or sub-samples) taken from the stationary phase growth D. radiodurans sample, and rows represented one of four LC-FTICR MS runs taken from the early-log phase growth D. radiodurans sample. A similar comparison matrix was created for the control and MA-stressed striata tissue samples. For both sample sets, run comparisons within each block were normalized as above where biological variability was absent. Extraneous variability was estimated again by calculating the pooled estimate of variance (PEV) of peptide abundance ratios; however, the mean relative abundance ratio of each peptide common across elements within a block instead of a theoretical abundance ratio was used to estimate variance. The use of the mean relative peptide abundance ratio was chosen because the true relative abundance ratio for each peptide was unknown. Reproducibility of de-convoluted peptide ratios was also estimated by the median CV for the population of calculated peptide abundances common across sub-samples as described above.

Results prior to and following normalization for the growth phase and mouse striata comparisons, in terms of PEV and median CV, are presented in Table 3. The normalization approach that resulted in the largest improvement is indicated by the superscripts. Quantile normalization resulted in the largest percent reduction in PEV for all blocks of replicates and for both the D. radiodurans and mouse striata relative comparisons. Only one exception was observed with the early-log versus stationary phase growth comparison. Here, linear regression normalization for the replicates within Block 1 had a slightly greater percent reduction in PEV (73% versus 71%). In terms of median CV, central tendency normalization consistently resulted in the largest improvement in reproducibility of peptide abundances, also with the exception of one block in each condition where the quantile approach did better. It was interesting to observe, in contrast to the addition of biological variability, how in the absence of biological variability the normalization approach which performed best per block was not as consistent within a given sample type. Here, in the absence of biological variability, the random error component (noise) of the extraneous variability model may play a larger role than systematic bias.

Table 3.

Pooled estimate of variance (PEV) and median coefficient of variation (CV) used to estimate extraneous varibility in the presence of biological variability. Data are presented as: prior to normalization of blocks of replicates - following normalization of blocks of replicates of relative peptide abundances; (% reductions); and superscript letters correspond to the normalization approach resulting in the largest percent reduction.

	Early-log versus Stationary		Stressed versus Control Tissue
Block	PEV	CV	PEV	CV
1	1477 –398 (73%)a	0.82 - 0.49 (39%)d	101 – 68 (33%)d	0.078 - 0.063 (19%)b
2	1477- 339 (77%)d	0.82 - 0.30 (62%)b	101 – 67 (34%)d	0.078 - 0.064 (17%)d
3	1477 – 373 (74%)d	0.82 - 0.25 (69%)b	101 – 63 (38%)d	0.078 - 0.063 (19%)b
4	1477 – 352 (76%)d	0.82 - 0.30 (63%)b	101 – 67 (33%)d	0.078 - 0.063 (19%)b

^aLinear regression normalization

^bCentral tendency normalization

^cLocal regression normalization

^dQuantile normalization

Ranks assigned to each normalization technique in terms of percent reduction in PEV are provided in Table 4 to help evaluate the performance of all normalization approaches. Once again, a lower rank value indicates greater percent reduction. Here, central tendency normalization and linear regression normalization have similar rankings for both the growth phase comparison and striata tissue suggesting that neither method performed significantly different. On the other hand, local regression normalization ranked last for both condition comparisons, with a high degree of statistical significance for the stressed versus control striata tissue (p-values ranging from <0.001 to 0.002). This technique has performed well for normalization of microarray data, and we speculated that the poorer performance of this approach relative to the other normalization approaches may have been due to the number of peptides included in the subdivision around the peptide ratio to be normalized. To test this premise, normalization of the stressed versus control striata tissue was repeated using increasingly larger fractions (>0.4) and increasingly smaller fractions (<0.4). At a fraction of 0.9, the percent reduction in PEV for all blocks was similar to central tendency and linear regression normalization techniques (26% to 33% depending on the block). However, no improvements in percent reduction (22% to 33% depending on the block) were observed as the fraction was reduced to 0.2. This observation suggests that the systematic bias associated with this peptide data is more likely linearly rather than non-linearly related to the magnitude of measured abundances.

Table 4.

Ranks assigned to approaches used in normalizing blocks of replicates containing relative peptide abundances in the presence of biological variability. Ranks were assigned on the percent reduction in the pooled estimate of variability (PEV) and median coefficient of variability (CV). The lower the value of the rank the greater the percent reduction. Values in parentheses represent the standard deviation of ranks

Pooled Estimate of Variance (PEV)
	Early-log versus Stationary				Stressed versus Controlled Tissue
Block	CT	LinReg	LocReg	Quan	CT	LinReg	LocReg	Quan
1	3	1	2	4	3	2	4	1
2	3	2	4	1	2	3	4	1
3	2	3	4	1	3	2	4	1
4	2	3	4	1	3	2	4	1
Mean	2.5 (±0.5)	2.25 (± 0.9)	3.5 (±1.0)	1.75 (±1.5)	2.75 (±0.5)	2.25 (±0.5)	4.0 (±0.0)	1.0 (±0.0)
Median Coefficient of Variation (CV)
	Early-log vs Stationary				Meth vs Norm
Block	CT	LinReg	LocReg	Quan	CT	LinReg	LocReg	Quan
1	3	2	4	1	1	2	4	3
2	1	2	3	4	2	3	4	1
3	1	2	3	4	1	2	4	3
4	1	2	3	4	1	2	4	3
Mean	1.5 (±1.0)	2.0 (±0.0)	3.25 (±0.5)	3.25 (±1.5)	1.25 (±0.5)	2.25 (±0.5)	4.0 (±0.0)	2.5 (±1.0)

Table 4 also ranks each normalization approach in terms of percent reduction in the median CV (lower rank value indicates greater percent reduction). Central tendency and linear regression ranked significantly better than local regression and quantile normalization of data obtained from samples with biological variability. In contrast to the assigned ranks for the PEV estimator in which quantile normalization ranked first, this technique was ranked last for the growth comparison and second to last for the mouse striata tissue comparison. This may be understood, in part, by considering the procedure used for this normalization approach. For example, it is desirable that upon sorting relative peptide abundances for each element in a given block, peptides observed across each element should be positioned relatively close, i.e. should have a small magnitude of distance between their assigned indexes. However, if one element has a few relative peptide abundances that are extreme in terms of their magnitudes, then the proximity of peptides after sorting can be biased by these extremes. Thus, when the mean relative peptide abundance across each row of sorted elements is assigned and then the elements re-sorted by the original assigned index, a larger CV can result than what was originally present.

Figure 3 compares the performance of the quantile approach, in terms of the median CV estimator, with the other approaches for a given block of elements from the comparison matrix representing the growth phase relative comparison. Prior to normalization, element 1 exhibited significant deviation from the other elements plotted as quantiles. The box plot for this element (Figure 3a inset) shows a number of relative peptide abundances with values considerably larger than the other replicates. Interestingly, the arbitrary abundances of peptides relative to the baseline used to create this element were measured roughly three months prior the arbitrary abundances of peptides used as the common baseline, which helps to explain the poorer performance of the quantile technique in this case Following quantile normalization, the deviation of Replicate 1 from the other replicates is reduced (Figure 3b) representing an improvement in median CV. In comparison, normalization using central tendency resulted in a smaller deviation of elements plotted as quantiles in Figure 3c. Although the median CV was reduced by ~40% following quantile normalization, this reduction was significantly less than the percent reduction observed by central tendency normalization (~60%).

Figure 3.

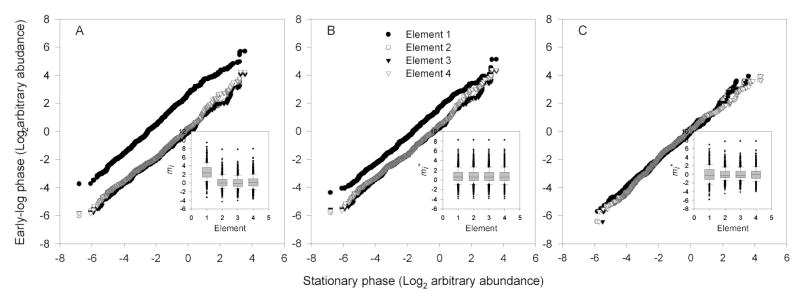
Quantile plots with box plots (inset) comparing elements (replicates) of relative peptide abundances for early-log phase growth of Deinococcus radiodurans relative to stationary phase growth. (a) Prior to normalization. (b) Following quantile normalization. (c) Following central tendency normalization. While quantile normalization resulted in the largest percent reduction in extraneous variability estimated using PEV, it ranked behind central tendency normalization in terms of extraneous variability estimated using the median CV of peptides common to all elements.

DISCUSSION

Ideally, the most appropriate normalization technique is selected after the causes of systematic bias are identified and characterized according to observed trends across the dynamic range of detection. However, this approach is seldom taken due to the challenge of identifying and defining the wide range of possible contributions in both sample processing and analysis to the overall bias. More commonly, different normalization techniques are compared, and the technique that best minimizes extraneous variability is selected. The use of isotopically labeled data can also prove useful in this comparison by evaluating the distributions of unlabeled abundance ratios to labeled abundance ratios of replicates prior to and following normalization. Unfortunately, isotopic labeled data for the experimental datasets used here was not available. However, 14N/15N and unlabeled samples from Shewanella oneidensis oxic and sub-oxic cell cultures has been published in connection to the demonstration of the AMT approach ^{27, 28}. We have included a distribution comparison of un-normalized and normalized replicates of unlabeled and labeled abundance ratios as Supplementary Figure 1. In general, the normalization evaluation presented here allows for the further adaptation of the selected techniques or development of a new technique, as additional knowledge concerning extraneous variability is obtained.

Of the four normalization techniques evaluated in this study, the quantile technique was the most unique in that an iterative process was not required for normalization. Additionally, this normalization technique does not force the means of replicate samples to converge upon a predetermined value, as was observed in the case of the other three normalization techniques (i.e., central tendency, linear regression, and local regression), where the mean of relative peptide abundances were forced to converge to zero. When the quantile technique was applied to our data, the mean of the common distribution following normalization fell within the range of means for the compared runs. This observation has an important implication related to the selection of a normalization technique and to the number of peptides common to all replicates runs used in the normalization process. Since we opted to perform central tendency, linear regression, and local regression normalization on a global scale, where measured abundances of all common peptides are used, we assumed that the leverage of peptide ratios containing biological variability on the mean relative abundance of the set of peptide ratios would not be significant. Such an assumption is commonly made for mRNA expression analysis where arrays are designed to target a large or complete set of open reading frames ²¹. In the case of high-throughput proteomics large number of peptides can be detected, but peptides can fail to be detected for many reasons (changes in the LC separation, the overshadowing of less abundant peptides by highly abundant peptides in the same spectrum, variations in MS performance, etc.) ^{3, 10}. Hence, the mean relative abundance of replicate sets of peptide ratios may indeed lie above or below zero. In such a case, quantile normalization would be more suitable for reducing variability among these replicate runs.

To test the validity of this assumption, peptides from a control set of proteins is required. However, in the absence of such a control set, evaluation of conserved proteins may add insight into the appropriateness of the applied normalization technique ²⁹. A few of these proteins were identified in the Deinococcus growth phase samples including glyceraldehyde-3-phosphate dehydrogenase (G3PDH), DNA polymerase, and ribosomal proteins. However, estimated protein ratios from the early-log and stationary phase growth samples ranged from 0.72 to 1.74, following quantile normalization. This was not surprising considering the comparison was made between extreme phases of growth where variation in abundances of conserved proteins, such as ribosomal proteins, and G3PDH, can occur. In the case of the different mouse tissues, protein ratios of conserved proteins following quantile normalization exhibited relatively no change. For example, average protein ratios of β- actins for the blocks of elements ranged from 0.85 to 1.04, while for the α – and β – tubulins average protein ratios ranged from 0.84 to 0.99 and 0.82 to 0.92, respectively. Future research into the validity of the global scale assumption for use in normalization of LC-FTICR MS data from different biological conditions is planned.

Observed trends among the four normalization techniques may also lie in the assumptions related to the bias independence/dependence on the magnitude of measured abundances. Central tendency normalization targets bias that is independent of the magnitude of measured abundances ¹⁴. Linear regression normalization is suited for reducing bias that is linearly dependent on the magnitude of measured abundances ^{7, 14, 22}, while local regression normalization is designed for bias that is non-linearly dependent ²¹. Linear regression normalization, in the absence of biological variability, ranked ahead of central tendency and local regression normalization in terms of PEV and ranked ahead of local regression normalization in terms of median CV, but was roughly equal in ranking to central tendency normalization. In the presence of biological variability, linear regression and central tendency normalization also ranked similarly in terms of median CV to ranks assigned in the absence of biological variability. This accounting, as well as the statistical analysis of assigned ranks presented earlier, suggests that normalization using the linear regression technique is more suitable for the proteomic data in this study than normalization using the local regression technique. It also suggests that the degree of linearity dependent bias that requires adjustment is small.

Although normalizing the data generally improved agreement between peptide ratios observed across instrument runs, the applied approaches are independent of or “blind” to the protein level. Hence, for example, evaluation of proteins targeted by multiple peptides in the D. radiodurans growth phase comparison, revealed that agreement among ratios did not significantly change. This was observed for the central tendency, linear regression, and local regression approaches. However, for the quantile approach, we observed that on average 98% of proteins with greater than 3 peptides showed improved agreement (data not shown). This was somewhat unexpected and possibly fortuitous because quantile normalization adjusts the width of the distribution of peptide ratios. In general, the observed difference in agreement on a peptide and protein level raises the question of on what level should normalization be performed? Because the instrument used in this evaluation makes measurements on the peptide level we performed normalization on this level and assumed that systematic biases were captured by the population of peptides. Ideally, for proteins targeted by multiple peptides, all peptide ratios should fall on a horizontal parallel to the ordinate in the M versus A environment, or on a line equidistant from the 45° in an X versus Y environment. The challenge in normalizing on a peptide level where multiple peptides for a given protein are also considered becomes knowing where the horizontal for a given protein should lie. Possibly the quantile approach is more suited to this challenge, or more sophisticate approaches that address this challenge need development.

While suggestive, the present findings do not provide direct evidence that a linearly dependent bias was the predominate effect on the observed extraneous variability e.g. of replicate data sets. Specific error(s) responsible for bias could include slight differences in masses from the sub-samples loaded onto the LC column, different degrees of contamination among samples collected under different conditions, LC carryover, etc. In addition, while the current evaluation was conducted using state of the art LC-FTICR instrumentation, there is no indication that these approaches could not find application and adaptation to other comparable high-throughput instrumentation platforms such as TOF MS or LTQ-FT MS. In general, these normalization approaches could benefit data analysis from platforms that produce sufficient ion statistics, resolution, and mass measurement accuracy. Indeed, normalization approaches comparable to central tendency normalization using global scale assumptions and conserved proteins have been applied to TOF MS data across multiple samples ^{30, 31}, and we are evaluating central tendency and linear regression approaches applied to LTQ-FT MS data. At present, relative quantification of peptides in a high throughput manner without isotopic labeling is promising, can be improved through the use of normalization methods, and will further improve as the sources of error and identified and reduced, and the most appropriate normalization technique(s) applied.

Supplementary Material

Supplementary Figure 1

Distribution comparison of replicate labeled (14N/15N) and unlabeled Shewanella oneidensis samples from oxic and sub-oxic cell cultures. Unlabeled abundance ratios were normalized using central tendency, linear regression, local regression, and quantile normalization techniques. Although all normalization techniques tended to align the unlabeled distributions, linear regression normalization appeared to approximate the labeled distributions more closely. The primary advantage of label-free proteomics is demonstrated in the overall frequency or number of peptides detected compared to the paired peptides from the labeled samples.