Abstract
The prevailing model of somitogenesis supposes that the presomitic mesoderm is segmented into somites by a clock and wavefront mechanism. During segmentation, mesenchymal cells undergo compaction, followed by a detachment of the presumptive somite from the rest of the presomitic mesoderm and the subsequent morphological changes leading to rounded somites. We investigate the possibility that minimization of tissue surface tension drives the somite sculpting processes. Given the time in which somite formation occurs and the high bulk viscosities of tissues, we find that only small changes in shape and form of tissue typically occur through cell movement driven by tissue surface tension. This is particularly true for somitogenesis in the zebrafish. Hence it is unlikely that such processes are the sole and major driving force behind somite formation. We propose a simple chemotactic mechanism which together with heightened adhesion can account for the morphological changes in the time allotted for somite formation.
Keywords: Somitogenesis, somite morphogenesis, mechanical forces, differential adhesion, chemotaxis
1 Introduction
The generation of a periodic pattern of segments, known as somites, along the anterior-posterior axis of vertebrate embryos is one of the major unresolved problems in developmental biology (Schnell et al., 2002). Later in development, somites govern the segmental organization of peripheral spinal nerves, vertebrae, axial muscles, and the metameric distribution of blood vessels (Stickney et al., 2000; Stockdale et al., 2000).
A large number of theoretical models have been proposed (see Schnell and Maini, 2000; Baker et al., 2003, for a review), including the clock and wavefront model (Cooke and Zeeman, 1976; Dubrulle et al., 2001; Baker et al., 2006), the reaction-diffusion model (Meinhardt, 1986), the cell-cycle model (Stern et al., 1988; Primmett et al., 1989; Collier et al., 2000) and the clock and induction model (Schnell and Maini, 2000). Each of these models captures certain essential features of the underlying biology but fails to satisfactorily explain a number of other observations. The clock and wavefront model proposed by Pourquié and co-workers (Dubrulle and Pourquié, 2002; Pourquié, 2004) incorporates several well-known aspects of somitogenesis better than most models (Baker et al., 2006).
All present models share one common property: they predict that the presomitic mesoderm (PSM) is periodically segmented into tissue blocks which coalesce to form somites. However the actual process of somite formation - how a somite pulls apart from the PSM and the ensuing morphological changes - are not well understood. In fact, they have not been the subject of modeling to date. All the models above are formalisms of somite specification not somite formation. The only mathematical model attempting to describe the bulk movement of somitic cells to form a somite is by Schnell et al. (2002). The major drawback of this model is that it does not take into account the intercellular mechanical forces involved in the process of somite formation. As a consequence, it cannot account for the morphological changes observed in somite formation.
The anterior portion of the PSM is the site of the forming somite; we shall refer to this as s0. Cells in s0 condense into somites by undergoing changes in their adhesive and migratory properties (Gossler and Hrabě de Angelis, 1998). These mechano-physical changes are brought about by an intricate pattern of gene activity and protein expression, a topic which is currently the subject of extensive research. Presently there are thought to be at least two distinct types of gene-driven processes which can individually or cooperatively lead to somite condensation: (i) differential-expression of cell adhesion molecules (ii) bidirectional activation of Eph receptors and ephrin-B proteins.
The differential expression of cell adhesion molecules is frequently associated with the development of organized patterns in embryogenesis (Takeichi, 1991; Gumbiner, 1996). For example, in the avian and mouse embryos somite formation is preceded by compaction of the s0 region (i.e. a reduction of the intercellular spaces between cells) and the simultaneous heightened expression of two types of cadherin molecules, N-CAM and N-cadherin (Duband et al., 1987; Kimura et al., 1995). These adhesion molecules are also expressed in the rest of the PSM but at reduced levels when compared to that in the s0 region. In mice somitogenesis (Kimura et al., 1995) it is found that cadherin-11 is strictly correlated with s0 and is not expressed in other parts of the PSM.
In the past few years, it has been suggested that Eph/Ephrin signalling is as well required for the development of inter-somitic boundaries and the subsequent epithelization process (Durbin et al., 1998). This signalling pathway was found to be responsible of boundary formation in the developing hindbrain (Mellitzer, 1999; Xu et al., 2000). In particular, it is observed that somite formation is accompanied by the differential expression of ephrin-B2 and EphA4 at the interface of the s0 region and the rest of the PSM (Bergemann et al., 1995; Nieto et al., 1992). The current experimental evidence shows that Eph/Ephrin signalling also regulates the mesenchymal-to-epithelial transition of the PSM during somitogenesis (Barrios et al., 2003). The bidirectional signalling between the Eph and ephrin proteins mediates a contact-dependent repulsive mechanism which may aid in the separation of the two cell populations in the PSM and the s0 region.
Though the genetic patterns underlying somite formation have been extensively studied during the last 10 years, it is not clear how these molecular patterns lead to the physico-mechanical processes responsible for sculpting a somite. In this article we present a study of how the coupling of molecular-level and cell-level processes may lead to somite formation. Our model suggests that independent of the actual molecular-level mechanism at play, the rounding typically exhibited by a somite during the time of its formation, is unlikely to be solely accounted by a minimization of tissue surface-tension. We suggest another mechanism based on chemotaxis which together with heightened adhesion and Eph/ephrin signalling may explain the observed morphological changes during somitogenesis.
2 The viscous liquid model of tissue dynamics
As previously mentioned, cells in the s0 region express various cadherins at the time of somite formation. Thus cell-cell adhesion in this region becomes particularly strong compared to the adjoining PSM. At the same time, the differential expression of Eph and ephrin also occurs across the boundary separating the forming s0 region and the PSM. It is indeed possible that these two seemingly different mechanisms do not act separately but rather are related or co-dependent on each other. For example, it has been found that Eph/ehprin signalling in certain neuronal processes leads to de-adhesion of cells at the boundaries by regulating cell adhesion molecules (Zisch et al., 1997).
The question we address in this work is how these molecular mechanisms lead to tissue rearrangement culminating in somite formation. For this we need a model of tissue dynamics, one which successfully captures the essential features observed experimentally. One of the most successful models is that originally proposed by Malcolm Steinberg, in which tissue is hypothesized to possess liquid-like properties (see Steinberg, 1963, for example). Amongst the theory’s achievements is its ability to account for:
how irregularly shaped tissue fragments have a tendency to round up towards a spherical shape.
the spontaneous sorting-out of experimentally intermixed embryonic cells of different types.
These two observations are easy to explain by analogy with liquids and their behavior. Molecules in the bulk of a liquid, being surrounded in all directions by many other molecules, experience zero net force. However, those molecules at the surface experience a net attractive force towards the center of the liquid. The potential energy associated with this net force (the surface tension) is minimized by minimizing the liquid’s surface area, a feat accomplished by the liquid drop assuming a spherical shape. In the same way, cells at the outer surface of a tissue will experience a weak (though significant) net attractive force towards the center in a tissue composed of cells interacting via cell-cell adhesion forces. This leads to eventual rounding of the tissue to minimize its surface tension. Note that the spherical configuration also results in the maximization of intercellular adhesion. This explains (i) above.
Observation (ii) can be explained by analogy with the behavior of a two-phase liquid system. There are four possible equilibrium configurations for an initial configuration of cells, in which two different spherically-shaped cell populations with different adhesion properties sit side by side. The determinants of the final configuration are the self-adhesion of cell type 1, the self-adhesion of cell type 2 and the cross-adhesion between cells of type 1 and 2. The possible configurations are (Foty and Steinberg, 2004): (a) if there is no cross-adhesion then the two cell populations will form separate detached spheres (Fig. 1a), (b) a low degree of cross adhesion weaker than either of the self-adhesion of the two cell types will result in a configuration in which the less cohesive population partially envelops the more cohesive population (Fig. 1b), (c) if the cross-adhesion is intermediate in strength then the less cohesive population will engulf the more cohesive population (Fig. 1c), and if the cross-adhesion is equal to or greater than the average of the two population’s self-adhesion then there will be intermixing (Fig. 1d).
Figure 1.
Equilibrium configurations of two different spherical cell populations which are initially placed side by side. The dark sphere is the population with high self-adhesion and the white sphere is the population with the smaller self-adhesion. The equilibrium configuration can be deduced by analogy to a two-phase liquid system. The final configuration is determined by the strength of the cross-adhesion between the two populations relative to the self-adhesion of the individual populations: (a) No cross-adhesion, (b) Relatively weak cross-adhesion, (c) Intermediate cross-adhesion, and (d) Preferential cross-adhesion. (e) The morphological changes caused by differential adhesion during somitogenesis, if the cross-linking between s0 (dark region) and the PSM (white region) is very small.
Now let us apply the viscous liquid model of tissue dynamics to somitogenesis. We consider first the case where the separation of the s0 region from the rest of the PSM occurs by Eph/ephrin bidirectional signalling. Ephrin-B2 is expressed in the posterior region of s0 (Bergemann et al., 1995) and also in the part of the PSM touching with the newly forming s0 region, while EphA4 is expressed in the anterior half of s0 (Nieto et al., 1992). Bidirectional signaling between the two different proteins across the boundary leads to local de-adhesion or repulsion. This prevents cells from s0 intermingling with those from the rest of the PSM, effectively leading to detachment. Once detached, the square or rectangular s0 region rounds up to minimize tissue surface-tension, thus completing the process of somite formation. Note that detachment and change of shape of the s0 region actually occur hand in hand and not sequentially (Kulesa and Fraser, 2002) and so what we have considered is a simplified process. It is important to point out that minimization of tissue surface tension is present before detachment, but its effect on the PSM is most probably quite small since tissue rounding time is proportional to tissue size (Gordon et al., 1972). Realistically we only expect the detached s0 region to experience rounding on timescales relevant to the formation of a somite.
Now we apply the liquid model to the second case. The hypothesis that the expression of different adhesion molecules and the modulation of cadherin quantity may be linked to the morphogenetic changes in somite formation has been previously proposed by Newman (1993) and more recently by Murakami et al. (2006). By analogy with the dynamics of a two-phase liquid system explained above, it is clear that s0 can detach itself from the PSM if the cross-adhesion is very weak compared to the self-adhesion of the cells in the two different pieces of the PSM. In other words the cadherin molecules expressed by the cells in the s0 region should not (or should very weakly) cross-adhere with the cadherin molecules of the rest of the PSM. Therefore, this mechanism can only be successful if different cadherin molecules are expressed on either side of the boundary separating s0 from the rest of the PSM. The mechanism would fail if there simply exists a quantitative difference in the expression level of one type of cadherin (Duguay et al., 2003). If detachment occurs then it would be accompanied by rounding of the separated region. This is schematically illustrated in Fig. 1e.
Thus we have shown that the viscous liquid model of tissue dynamics can qualitatively explain how the dynamical process of somite formation proceeds from the molecular pre-pattern initially induced by the two molecular mechanisms. The type of molecular mechanism influences solely the detachment process. The morphological changes, shape changes of the s0 region culminating in the spherical shape of somites, can only be driven by tissue-surface tension in both cases. Now we are left with the problem of determining whether tissue surface-tension driven processes can occur on a timescale relevant to somite formation.
2.1 Timescale of a somite formation
As we previously mentioned, detachment and change of shape of the s0 region do not occur sequentially but rather simultaneously. This is very difficult to model since it requires knowledge of the exact spatio-temporal expression of the major adhesion and signaling molecules and the subsequent response of cells. This information is not currently available in the literature. We opt for a simpler model which enables us to do some quantitative estimates. This model is valid for both types of molecular mechanisms considered in this work.
Let the somite formation time be T. Then at some time t* < T, detachment of the s0 region will be almost complete and the region itself will possess some ellipsoidal shape. As time approaches T, one expects the ellipsoidal s0 region to round up and hence form the final somite shape. Say that the ellipsoidal tissue has z semi-axis length rz, x semi-axis length rx and y semi-axis length rx. We also define r = rz/rx < 1 (i.e. an oblate ellipsoid). The volume will remain unchanged but the surface area will be minimized with the progression of time. As a consequence, r will approach one (note that r = 1 is a perfect sphere). Using the liquid model of tissue dynamics, we obtain an expression (see Appendix A) for the time taken by an ellipsoidal piece of tissue to change from an initial shape r = ri to a final shape r = rf:
| (1) |
In this formula the parameters determining the timescale of morphological deformation, tc, are the bulk viscosity of the tissue μ, the tissue surface tension σ, the diameter D of the final spherical aggregate which determines the somite volume v and the initial and final shape configurations determined by ri and rf respectively. We find D ≃ 50 μm for the zebrafish and D ≃ 100 μm for the mouse or the chick. The ratio σ/μ has been determined from a number of experiments for chicken embryonic tissue and for Hydra cells (see Appendix B for a detailed discussion). An average value is about 1.39±0.94 × 10-6 cm/s. We believe this value is representative for tissues. This will be discussed in more detail at the end of this section.
We shall now proceed to use Eq. (1) to predict how the shape of the s0 region changes during the somite formation period, according to the viscous liquid model. Our aim is to deduce whether surface-tension can really drive the morphological changes or if other physical mechanisms need to be postulated to explain the observations. We illustrate how we calculate the time progression with a practical example. Consider zebrafish somitogenesis. Assume a final shape for the somite which is slightly aspherical: rf = 0.95. The total somite formation time T is known to be 30 minutes. To find the shape of s0 at say 20 minutes, we substitute tc = 30 - 20 = 10 minutes, rf = 0.95 and the values of the morphological parameters (the ratio σ/μ and the somite volume) in Eq. (1) and then solve for ri. Now the latter quantity is the ratio of semi-axes of the oblate ellipsoid at 20 minutes, ri = rz/rx. To estimate rz and rx we use the fact that the volume of ellipsoidal tissue is constant throughout the somite formation period (surface-tension simply changes the surface area). Then solving simultaneously for rz and rx from the two equations, ri = rz/rx and , we obtain and , where D is the diameter of the final somite, a known quantity. Having determined the two radial axes of the ellipsoid, its shape is completely quantified at a given time. Repeating this process for different times generates the temporal variation in the shape of the s0 region.
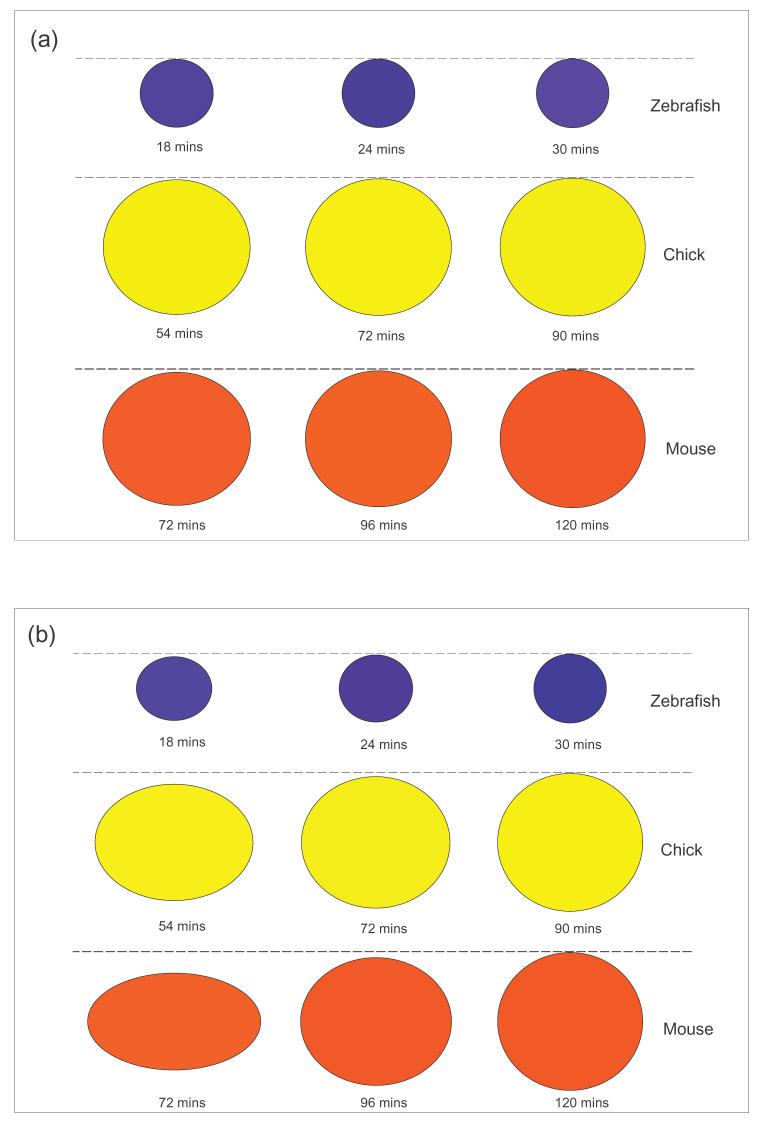
In Fig. 2 we illustrate the morphological changes of s0 for zebrafish, chick and mouse embryogenesis, using both average and high values of the ratio σ/μ. In these numerical experiments, the time t* at which almost complete detachment of the s0 region has occurred is taken to be equal to 60% of the somite formation time (T). T is 30, 90 and 120 minutes for zebrafish, chick and mouse somitogenesis, respectively (Dubrulle and Pourquié, 2004). For a typical value of σ/μ (see Fig. 2a), the tissue can only undergo very small changes in shape. However, substantial morphological changes occur for chick and mouse somites if the value of σ/μ is large (see Fig. 2b). The σ/μ value employed in Fig. 2b is 3.8 standard deviations away from the average value predicted by experiments. This makes it an unlikely value since 99.7% of all values in normally distributed data lie within 3 standard deviations of the mean (see Appendix B). Therefore, it is reasonable to conclude that it is improbable that somite formation in the zebrafish is driven by tissue surface tension. It seems more likely for the case of chick and mouse somitogenesis, though this would be only possible if the ratio σ/μ is unusually large. It is important to emphasize that the above estimates implicitly assumed that the forming somite is surrounded by water. In reality changes in the shape could be much smaller due to physical constraints imposed by the surrounding tissue and the acellular matrix fiber assembly surrounding a forming somite (Czirok et al., 2004).
Figure 2.
Morphological changes of a tissue due to cell movement driven by tissue surface tension for: (a) σ/μ = 1.5 × 10-6 cm/s (typical average value found in tissues) (b) σ/μ = 5 × 10-6 cm/s (a value particularly larger than found in most experiments). Given the final shape of the somite, we use the viscous liquid model, encapsulated by Eq. (1), to regress back in time and calculate the shape of the somite at times equal to 60% and 80% of the somite formation time. The somite formation time is 30 mins, 90 mins and 120 mins for zebrafish (blue), chick (yellow) and mouse (red) somitogenesis, respectively. Note that according to the model changes in shape are almost negligible for the zebrafish and they are significant for the chick and the mouse only when the ratio σ/μ is larger than the typical average found in experiments.
Morphological changes driven by the minimization of tissue surface tension are relatively slow since the bulk viscosity of tissues is large, typically 107-109 times higher than that of water (Gordon et al., 1972). Tissue viscosity is comparable to that of tar and pitch at normal temperatures. On the other hand, the typical tissue surface tension is about 100 times smaller than that of water (σ ∼ 1 mN/m, Mombach et al., 2005). In the case of embryonic cell sorting, morphological changes by the minimization of tissue surface tension occur over a period of days (Steinberg, 1963). Similar supporting evidence comes from the experiments of Mombach et al. (2005). They estimated that the time taken for aggregates of chicken embryonic neural cells in initially ellipsoidal shapes of various sizes to relax into a spherical one of radius 60 μm (typical radius of a chick somite) occurs in a time ranging 8-22 hours.
Of course, it can be argued that the values we employed for the ratio σ/μ are not typical for somitic tissue; they are only specific to the chick embryo. Unfortunately there are no measurements available in the literature for other types of embryonic tissue. However, there are two reasons which lead us to believe that the values used in this paper are typical for many tissues. First, experiments with Hydra cells (Rieu and Sawada, 2002) provide an estimate for σ/μ within the same range of chick embryonic tissue. Secondly the magnitude of the σ/μ ratio is driven by two physical processes: (a) sliding friction between cell membrane surfaces which is regulated by the expression of adhesion molecules, and (b) the rate at which cells break and reform adhesive contacts with neighboring cells. These facts combined with dimensional arguments (Forgacs et al., 1998), imply that σ/μ is proportional to a/τ, where a is the cell radius and τ is the characteristic lifetime of adhesive contacts. As a consequence, the ratio σ/μ is independent of the cadherin expression level. This result suggests that the magnitude of the ratio is similar for a broad range of tissues, provided that cell-cell adhesive forces are a primary distinguishing feature of the tissue.
Moreover, we now have an alternative way to estimate the ratio σ/μ for the zebrafish and mouse somitic tissue. The average cell diameters for zebrafish, chick and mouse cells in the presomitic mesoderm are, respectively, 8μm (Henry et al., 2000), 10μm and 25μm (personal communication, P. M. Kulesa, Stowers Institute for Medical Research). Since the time τ has to be proportional to the somite formation time T, then we estimate that the average σ/μ for zebrafish and mouse are 2.4 times and 1.9 times larger than the chick ratio, respectively. Using the average value for the chick (see Appendix B), these translate into σ/μ = 3.3 and 2.6 × 10-6 cm/s. These values are both smaller than the maximal value of σ/μ = 5 × 10-6 cm/s used in our simulations (see Fig. 2b). This reinforces our conclusion that surface tension driven processes cannot easily account for somite rounding in the zebrafish. Other processes are quite possibly driving somite formation.
This conjecture is also supported by experimental evidence. Kulesa and Fraser (2002) observed that during somite boundary formation cells from deep inside the PSM are recruited in the newly forming somite. The cells’ long-distance and directed movement cannot be explained by local processes such as those underlying morphological changes driven by tissue surface-tension.
3 A chemotactic mechanism
We propose a simple chemotactic mechanism which can account for: (i) somite detachment, (ii) somite rounding, (iii) long distance directed movement of cells from the PSM to the newly forming somite s0. This mechanism is compatible with both heightened adhesion and Eph/ephrin signalling, and it acts in conjunction with surface tension processes during the time of somite formation. As cells in the anterior-most region of the PSM (s0) are specified as somitic, we hypothesize that they release an instantaneous pulse of chemical. This chemical induces a positive chemotactic response from all cells in s0. The chemotactic response is only triggered in cells in the s0 region leading to the physical detachment of s0 from the rest of the PSM. Presently there is no evidence that cells in the PSM are chemotactically sensitive. However, it is plausible that a few cells could be - this would account for the long distance directed cell movement observed by Kulesa and Fraser (2002). In the next two subsections, we show that chemotaxis can induce significant cell movement in the time allotted for somite formation and that chemotactic forces sculpt a spherical or nearly spherical somite.
3.1 Estimating the time for chemotactic communication across s0
The implicit assumption of our chemotactic mechanism is that the chemotactic signal can diffuse through the s0 region in a time much less than the somite formation time. We can prove by calculation that this is possible. Suppose that a cell in the anterior-most part of s0 releases an instantaneous chemical pulse of M molecules of a certain molecule with diffusion coefficient D. What is the time taken for this pulse to reach the posterior-most part of s0? Let us assume that somitic cells will chemotactically respond if the concentration of the chemoattractant is larger than a threshold value C. The chemical concentration detected by cells will start increasing a short time after the pulse is released. It will reach a maximum and then decrease back to zero. The maximum concentration detected by a particular cell will depend on its distance from the cell secreting the chemical signal. The larger is this distance, the smaller will be concentration detected by the cell. By considering the isoconcentration surface represented by the threshold concentration C (Okubo and Levin, 2001, the approach in this book is correct but some constants have been calculated incorrectly, a mistake which we correct here), it can be shown that the maximum distance, Rm, over which cell-cell communication occurs is given by:
| (2) |
The chemical signal diffuses over this region in a time:
| (3) |
From these expression we find:
| (4) |
The distance Rm can be equated with the length of the s0 region. To use this expression we now need to estimate the chemical diffusion coefficient in vivo.
In vivo, diffusion is hindered by the extracellular matrix (ECM) between cells and by the presence of the cells themselves. The extracellular matrix consists mainly of two types of macromolecules: (i) glycosaminoglycans (GAGs), such as Hyaluronan which is typically abundant in early embryos (ii) fibrous proteins such as collagen and fibronectin (Alberts et al., 2002). Diffusive hindrance by these macromolecules implies that in vivo diffusion coefficients cannot be calculated using the Stokes-Einstein relation, since the latter is only valid in the limit of high dilution. A number of alternative models have been derived (see Section 2.2. Grima and Schnell, 2006, for a review of these models in the context of intracellular diffusion in the presence of obstacles). A number of popular models are based on the Brinkmann or effective medium approximation (Phillips et al., 1989, 1990). In these models, the extracellular matrix is considered a porous matrix characterized by its Darcy permeability and pore size. The predictions of these models agree well with the experimental diffusion coefficients of various solutes in gels (Pluen et al., 1999; Ramanujan et al., 2002).
In our case, we consider the diffusion coefficients obtained from FRAP (fluorescence recovery after photobleaching) in collagen gels and Hyaluronan solutions prepared at physiologically relevant concentrations (Ramanujan et al., 2002). This is most fitting to the cases considered here since as previously mentioned the extracellular matrix has significant amounts of both of these structural macromolecules. The diffusion coefficient of molecules with size in the range 2-20 nm is found to approximately vary between 1 and 100 μm2/s. This range encapsulates a large number of molecules. Hindrance is found to stem primarily from collagen. Hyaluronan molecules and the close-packedness of cells do not significantly contribute to the value of the diffusion coefficients. Substituting the minimum value for D in Eq. (4), it follows that the time tm for a chemical pulse to travel across s0 is typically less than 30 mins for the chick and the mouse, and less than 7 mins for the zebrafish. Now the lag time between the reception of a chemotactic signal by a cell and its subsequent chemotactic response is equal to the time taken for the stimulus to induce restructuring of the actin cytoskeleton. This time typically is less than a few minutes. For example, Dictyostelium discoideum cells increase significantly their level of polymerized actin within 10 seconds after detecting a chemical stimulus. After about a minute, these cells have already starting moving in the direction of the chemical gradient (Alberts et al., 2002; Bray, 2001). We can therefore infer that the total time from the release of the chemotactic signal to induced cell movement is significantly less than the time for somite formation. This establishes the chemotactic mechanism’s viability as a candidate for explaining somite sculpting processes.
3.2 Shape changes induced by chemotaxis
Now let us consider how the chemotactic mechanism can lead to a spherical or nearly spherical somite. We have assumed that the pulse of chemoattractant is released by all cells in s0 at approximately the same time. The initial result will be a compaction of the region, as the cells move towards higher concentrations by decreasing the intercellular spaces between them. If the cells are homogeneously distributed in s0, then the chemoattractant concentration will have a maximum in the middle of the s0 region. In other words, a chemical gradient is temporarily set up which is radially directed towards the center of the forming somite. This gradient is detected by chemotactic cells, which respond by extending filapodia in the direction of high chemical concentration while simultaneously retracting from the direction of relatively low concentration. This leads to a net chemotactic force towards the center of the s0 region. These forces cause the aggregate of cells to squeeze itself together. In this process, the s0 region reduces its surface area and assumes a nearly spherical shape. The chemical signal will degrade in a short time, but the cells will retain their new spherical configuration due to the heightened cell-cell adhesion which is typical of the region. Note that the same outcome will result if the cells secrete the chemical for a short period of time instead of releasing a single instantaneous pulse.
We have simulated the proposed chemotactic mechanism and the results corroborate our predictions above (see Fig. 3). The algorithm for cell movement is that expounded in Newman and Grima (2004). Briefly the cells are modeled as point particles experiencing forces due to chemotaxis, short-range repulsion and short-range cell-cell adhesion. The short-range repulsion forces effectively give the cells a certain radius and a certain compressibility; this is schematically shown by spheres of fixed radius in Fig. 3. The forces are modeled through appropriately chosen potential functions: the repulsion and adhesion are qualitatively captured by a potential qualitatively similar to a Lennard-Jones or Morse potential (see Newman and Grima, 2004, Fig. 12); chemotaxis can be modeled by a potential proportional to the chemoattractant concentration. This approach is qualitatively similar to that of Drasdo and Hohme (2003), which has been successfully applied to model a wide range of biological problems.
Figure 3.

Computer simulation of the proposed chemotactic mechanism in two dimensions. Grey colored cells form part of the PSM while blue colored cells form part of the region s0. The top represents the anterior part of the PSM and the bottom represents the posterior part of the PSM. The PSM is shown at three different times (A) just after chemoattractant pulses have been simultaneously secreted by all cells in s0 (B) an intermediate time, in which cells close-pack together (C) late time configuration, in which the s0 region has rounded up due to the cells experiencing a chemotactic centripetal force. At this time, the cells have stopped producing chemoattractant but the shape is preserved due to heightened cell-cell adhesion in s0.
The chemotactic process considered here can cause morphological changes on a timescale far shorter than that due to minimization of tissue surface tension. We can explain this by looking at the forces acting in both mechanisms. In the chemotactic process, cells experience a chemotactic force pulling them towards the aggregate’s center; whereas for the tissue surface tension minimization mechanism, only cells at the surface experience an inward weak force and in the bulk of the aggregate the net average force is zero. Of course, the timescale of the chemotactic mechanism will depend on the strength of the chemotactic forces. These forces are known to be proportional to the chemoattractant gradient across a cell, which itself is directly proportional to the amount of chemoattractant secreted. This implies that the dynamics of the somite shaping process can be easily controlled by cells through a regulation of the rate of chemoattractant secretion. Such a fine-tuning control is not possible through the passive dynamical process induced by the minimization of tissue surface tension.
4 Discussion
In this article we have investigated whether tissue rearrangement driven by tissue surface tension can completely account for the detachment of s0 and its subsequent morphological changes to form a somite. The differential adhesion between the two parts of the PSM can qualitatively explain the detachment and rounding of the s0 region, provided cross-adhesion is weak. Similarly Eph/ephrin signalling at the boundary of the forming somite leads to detachment of the somite. In both types of molecular mechanisms, the somite can be hypothesized to take its spherical shape due to short-range cell movement processes driven by tissue surface-tension.
Using the viscous liquid model for tissues, we have shown that the shape changes induced by such processes are usually small in a time equal to that of somite formation, particularly for the zebrafish. This suggests that the degree to which surface tension forces can account for the experimentally observed morphological changes varies strongly from one organism to another. Such processes are usually effective over a period of many hours, even days and thus are unlikely to play a major role in the short time in which somite formation occurs. Based on our results from the viscous liquid model, it seems likely that other processes may be at play. We have suggested a simple chemotactic mechanism which can account for somite detachment, rounding and long-range movement of cells and which is complementary to both the differential expression of adhesion and Eph/ephrin signalling.
Our analysis has some limitations since the viscous liquid model captures well the tissue’s bulk movement but does not take into account some microscopic cellular processes which may be pivotal to somitogenesis. For example, the viscous liquid model cannot account for how the assembly and remodeling of the ECM changes the large-scale mechanical properties of the tissue. It is possible to explain the long-range movement of cells across the forming boundary by postulating that cells preferentially follow oriented ECM fibres. This has been observed in fibroblasts by Dickinson et al. (1994). However this proposition cannot be straightforwardly related to heightened adhesion or the Eph/ephrin signalling. Our current knowledge of the molecular mechanisms underlying tissue-level ECM remodeling during somitogenesis is very limited (Czirok et al., 2004). Our chemotaxis mechanism can work on its own or in parallel with the above mechanism. It is also plausible that the chemical field we suggested in our model, instead of providing chemotactic cues to the cells, acts as a pre-pattern for fibre orientation, which consequently induces cell movement by contact guidance. This possibility we cannot presently exclude and will be explored in a future article.
Acknowledgements
The authors would like to thank Prof. Paul M. Kulesa (Stowers Institute for Medical Research) for providing presomitic mesodermal cell morphology data and two anonymous referees for helpful comments. The authors also gratefully acknowledge support by a grant from the Faculty Research Support Program from the OVPR, Indiana University (Bloomington Campus). SS would also like to acknowledge support from NIH grant R01GM76692. Any opinions, findings, conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the NIH.
Appendix A
In this appendix, we briefly describe the physical and mathematical basis of Eq. (1). Young (1939) developed a mathematical formalism to describe the shape changes exhibited by an initially ellipsoidal fluid drop as it minimizes the surface tension and approaches a more spherical configuration (see Gordon et al., 1972, for a more recent reference). Let the initial shape of the fluid drop be described by the ellipsoid of revolution generated by rotating the ellipse
| (5) |
about the z-axis. Furthermore let the ratio r = rz/rx be less than one, such that we have an oblate ellipsoid. Then the rate of deformation of the drop is given by:
| (6) |
where
| (7) |
It follows by direct integration of Eq. (6) that the time taken for the drop to change its axial ratio from r = r0 to r = r1 is given by:
| (8) |
The function τ can be obtained by numerical integration.
Appendix B
In this appendix, we discuss the experimental determination of the ratio σ/μ which is at the heart of the calculations using the viscous liquid model. This ratio has been measured directly or indirectly by a number of experiments for various chicken embryonic tissues. It has also been measured for aggregates of Hydra cells. These experiments can be subdivided in two types: (a) those determining directly the ratio from experimental data, and (b) those determining individual values of σ and μ using separate methods and from which we can then calculate the ratio. The first type of experiments is always preferable since errors in computing quotients can be large as they accumulate errors in the individual determination of the surface tension σ and the viscosity μ.
The first type of experiments have been pioneered by Gordon et al. (1972) and more recently performed by Rieu and collaborators (see Rieu and Sawada, 2002; Mombach et al., 2005, for details)). Gordon et al. (1972) measured the ratio σ/μ for four types of tissue: (i) seven 5-day embryonic chicken heart reaggregates of various radii with values σ/μ = 1.18, 0.71, 1.17, 1.66, 1.72, 1.01, 1.9 × 10-6 cm/s, (ii) 5-day liver reaggregates with σ/μ = 2.75 × 10-6 cm/s, (iii) rounded-up liver fragments with σ/μ = 0.72 × 10-6 cm/s (iv) 4-day forelimb bud cores with σ/μ = 0.44 × 10-7 cm/s. This data was obtained from the fusion of two rounded-up tissues placed in contact with each other. Thus the ratio is found to range from 0.44 to 2.75 × 10-6 cm/s. Rieu and collaborators using data obtained from the relaxation of initially elongated aggregates towards circular or spherical shapes obtained σ/μ = 0.1, 3.33 × 10-6 cm/s for chicken embryonic neural aggregates and 2D Hydra cell aggregates, respectively. Hence based on all the available data obtained from experiments of the first type, the average value of σ/μ is 1.39 ± 0.94 × 10-6 cm/s. In our calculations in the text, we use a value of 1.5 × 10-6 cm/s for the typical value of σ/μ for embryonic tissue and a value of 5 × 10-6 cm/s as the maximum realistically plausible value of σ/μ (this value is 3.8 standard deviations away from the mean).
The second type of experiments have to our knowledge been done only by Forgacs et al. (1998) using a compression plate apparatus. Aggregate relaxation after compression is analyzed in terms of a generalized Kelvin-body model of viscoelasticity, which yields various parameters, including the surface tension σ for chick neural retina, liver, heart and limb tissue. The viscosity μ cannot be obtained directly from the simple Kelvin model used in the data analysis. However a rough estimate can be made by relating it to a friction constant whose value is determined from experiment. Using these values (see Forgacs et al., 1998, Table I), we can estimate the range of the ratio σ/μ to be from 1.6 to 8.5 × 10-5 cm/s. Note that this range is about an order of magnitude larger than that from the first type of experiments. An analysis of the magnitudes of the individual values of σ and μ and of the method by which they are determined reveals the reason for the discrepancy. The range of values of the surface tension, σ = 1 - 20 dynes/cm is in very good agreement with the values estimated by the first type of experiments. However, the values of the viscosity are about an order of magnitude smaller. The viscosity in the second type of experiments is roughly estimated using the relation μ2 = Caμ, where μ2 is a friction coefficient. This friction coefficient is obtained directly from the data using the Kelvin model, a is cell radius and C is some unknown constant. To calculate the viscosity, the constant C is arbitrarily assumed to be of order unity (see Forgacs et al., 1998, Discussion). This explains the discrepancies of the computed range of the ratio σ/μ when compared with that obtained directly from experiments of the first type. Therefore, it seems very likely that the range of possible values of σ/μ is that directly determined by the first type of experiments and that the values of the ratio determined from the second type of experiments is artificially high.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alberts B, Johnshon A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. Garland Publishing; New York: 2002. [Google Scholar]
- Baker RE, Schnell S, Maini PK. Formation of vertebral precursors: Past models and future predictions. J. Theor. Med. 2003;5:23–35. [Google Scholar]
- Baker RE, Schnell S, Maini PK. A clock and wavefront mechanism for somite formation. Dev. Biol. 2006;293:116–126. doi: 10.1016/j.ydbio.2006.01.018. [DOI] [PubMed] [Google Scholar]
- Barrios A, Poole RJ, Durbin L, Brennan C, Holder N, Wilson SW. Eph/Ephrin signalling regulates the mesenchymal-to-epithelial transition of the paraxial mesoderm during somite morphogenesis. Curr. Biol. 2003;13:1571–1582. doi: 10.1016/j.cub.2003.08.030. [DOI] [PubMed] [Google Scholar]
- Bergemann AD, Cheng H-L, Brambilla R, Klein R, Flanagan JG. ELF-2, a new member of the Eph ligand family, is segmentally expressed in the region of the hindbrain and newly formed somites. Mol. Cell. Biol. 1995;15:4921–4929. doi: 10.1128/mcb.15.9.4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray D. Cell Movements: From Molecules to Motility. Garland Publishing; New York: [Google Scholar]
- Collier JR, McInerney D, Schnell S, Maini PK, Gavaghan DJ, Houston P, Stern CD. A cell cycle model for somitogenesis: Mathematical formulation and numerical simulations. J. theor. Biol. 2000;207:305–316. doi: 10.1006/jtbi.2000.2172. [DOI] [PubMed] [Google Scholar]
- Cooke J, Zeeman EC. A clock and wavefront model for control of the number of repeated structures during animal morphogenesis. J. theor. Biol. 1976;58:455–476. doi: 10.1016/s0022-5193(76)80131-2. [DOI] [PubMed] [Google Scholar]
- Czirok A, Rongish BJ, Little CD. Extracellular matrix dynamics during vertebrate axis formation. Dev. Biol. 2004;268:111–122. doi: 10.1016/j.ydbio.2003.09.040. [DOI] [PubMed] [Google Scholar]
- Dickinson R, Guido S, Tranquillo R. Biased cell migration of fibroblasts exhibiting contact guidance in oriented collagen gels. Ann. Biomed. Eng. 1994;22:342–356. doi: 10.1007/BF02368241. [DOI] [PubMed] [Google Scholar]
- Drasdo D, Hohme S. Individual-based approaches to birth and death in avascular tumors. Math. Comput. Model. 2003;37:1163–1175. [Google Scholar]
- Duband JL, Dufour S, Hatta K, Takeichi M, Edelman GM, Thiery JP. Adhesion molecules during somitogenesis in the avian embryo. J. Cell. Biol. 1987;104:1361–1374. doi: 10.1083/jcb.104.5.1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubrulle J, McGrew MJ, Pourquié O. FGF signalling controls somite boundary position and regulates segmentation clock control of spatiotemporal hox gene activation. Cell. 2001;106:219–232. doi: 10.1016/s0092-8674(01)00437-8. [DOI] [PubMed] [Google Scholar]
- Dubrulle J, Pourquié O. From head to tail: links between the segmentation clock and antero-posterior patterning of the embryo. Curr. Opin. Genet. Dev. 2002;12:519–523. doi: 10.1016/s0959-437x(02)00335-0. [DOI] [PubMed] [Google Scholar]
- Dubrulle J, Pourquié O. Coupling segmentation to axis formation. Development. 2004;131:5783–5793. doi: 10.1242/dev.01519. [DOI] [PubMed] [Google Scholar]
- Duguay D, Foty RA, Steinberg MS. Cadherin-mediated cell adhesion and tissue segregation: qualitative and quantitative determinants. Dev. Biol. 2003;253:309–323. doi: 10.1016/s0012-1606(02)00016-7. [DOI] [PubMed] [Google Scholar]
- Durbin L, Brennan C, Shiomi K, Cooke J, Barrios A, Shanmugalingam S, Guthrie B, Lindberg R, Holder N. Eph signalling is required for segmentation and differentiation of the somites. Genes Dev. 1998;12:3096–3109. doi: 10.1101/gad.12.19.3096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forgacs G, Foty RA, Shafrir Y, Steinberg MS. Viscoelastic properties of living embryonic tissues: A quantitative study. Biophys. J. 1998;74:2227–2234. doi: 10.1016/S0006-3495(98)77932-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foty RA, Steinberg MS. Cadherin-mediated cell-cell adhesion and tissue segregation in relation to malignancy. Int. J. Dev. Biol. 2004;48:397–409. doi: 10.1387/ijdb.041810rf. [DOI] [PubMed] [Google Scholar]
- Gordon R, Goel NS, Steinberg MS, Wiseman LL. A rheological mechanism sufficient to explain the kinetics of cell sorting. J. Theor. Biol. 1972;37:43–73. doi: 10.1016/0022-5193(72)90114-2. [DOI] [PubMed] [Google Scholar]
- Gossler A, Hrabě de Angelis M. Somitogenesis. Curr. Top. Dev. Biol. 1998;38:225–287. [PubMed] [Google Scholar]
- Grima R, Schnell S.A Mesoscopic Simulation Approach for Modelling Intracellular Reactions J. Stat. Phys 2006. DOI:10.1007/s10955-006-9202-z [Google Scholar]
- Gumbiner BM. Cell Adhesion: The Molecular Basis of Tissue Architecture and Morphogenesis. Cell. 1996;84:345–357. doi: 10.1016/s0092-8674(00)81279-9. [DOI] [PubMed] [Google Scholar]
- Henry CA, Hall LA, Hille MB, Solnica-Krezel L, Cooper MS. Somites in zebrafish doubly mutant for knypek and trilobite form without internal mesenchymal cells or compaction. Curr. Biol. 2000;10:1063–1066. doi: 10.1016/s0960-9822(00)00677-1. [DOI] [PubMed] [Google Scholar]
- Kimura Y, Matsunami H, Inoue T, Shimamura K, Uchida N, Ueno T, Miyazaki T, Takeichi M. Cadherin-11 expressed in association with mesenchymal morphogenesis in the head, somite, and limb bud of early mouse embryos. Dev. Biol. 1995;169:347–358. doi: 10.1006/dbio.1995.1149. [DOI] [PubMed] [Google Scholar]
- Kulesa PM, Fraser SE. Cell dynamics during somite boundary formation revealed by time-lapse analysis. Science. 2002;298:991–995. doi: 10.1126/science.1075544. [DOI] [PubMed] [Google Scholar]
- Meinhardt H. Models of segmentation. In: Bellairs R, Ede DA, Lash JW, editors. Somites in Developing Embryos. Plenum Press; New York: 1986. pp. 179–189. [Google Scholar]
- Mellitzer G, Xu Q, Wilkinson DG. Eph receptors and ephrins restrict cell intermingling and communication. Nature. 1999;400:77–81. doi: 10.1038/21907. [DOI] [PubMed] [Google Scholar]
- Mombach JCM, Robert D, Graner F, Gillet G, Thomas GL, Idiart M, Rieu JP. Rounding of aggregates of biological cells: Experiments and simulations. Physica A. 2005;352:525–534. [Google Scholar]
- Murakami T, Hijikata T, Matsukawa M, Ishikawa H, Yorifuji H. Zebrafish protocadherin 10 is involved in paraxial mesoderm development and somitogenesis. Dev. Dyn. 2006;235:506–514. doi: 10.1002/dvdy.20622. [DOI] [PubMed] [Google Scholar]
- Newman SA. Is segmentation generic? BioEssays. 1993;15:277–283. doi: 10.1002/bies.950150409. [DOI] [PubMed] [Google Scholar]
- Newman TJ, Grima R. Many-body theory of chemotactic cell-cell interactions. Phys. Rev. E. 2004;70:051916. doi: 10.1103/PhysRevE.70.051916. [DOI] [PubMed] [Google Scholar]
- Nieto MA, Gilardi-Hebenstreit P, Charnay P, Wilkinson DG. A receptor protein tyrosine kinase implicated in the segmental patterning of the hindbrain and mesoderm. Development. 1992;116:1137–1150. doi: 10.1242/dev.116.4.1137. [DOI] [PubMed] [Google Scholar]
- Okubo A, Levin SA. Vol. 14 of Interdisciplinary Applied Mathematics. 2nd Edition Springer-Verlag; New York: 2001. Diffusion and ecological problems: modern perspectives. [Google Scholar]
- Phillips RJ, Deen WM, Brady JF. Hindered transport of spherical macromolecules in fibrous membranes and gels. AIChE J. 1989;35:1761–1769. [Google Scholar]
- Phillips RJ, Deen WM, Brady JF. Hindered transport in fibrous membranes and gels: effect of solute size and fiber configuration. J. Colloid. Interface Sci. 1990;139:363–373. [Google Scholar]
- Pluen A, Netti PA, Jain RK, Berk DA. Diffusion of Macromolecules in Agarose Gels: Comparison of Linear and Globular Configurations. Biophysical J. 1999;77:542–552. doi: 10.1016/S0006-3495(99)76911-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pourquié O. The chick embryo: A leading model in somitogenesis studies. Mech. Dev. 2004;121:1069–1079. doi: 10.1016/j.mod.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Primmett DRN, Norris WE, Carlson GJ, Keynes RJ, Stern CD. Periodic segmental anomalies induced by heat shock in the chick embryo are associated with the cell cycle. Development. 1989;105:119–130. doi: 10.1242/dev.105.1.119. [DOI] [PubMed] [Google Scholar]
- Ramanujan S, Pluen A, McKee TD, Brown EB, Boucher Y, Jain RK. Diffusion and convection in collagen gels: implications for transport in the tumor interstitium. Biophys. J. 2002;83:1650–1660. doi: 10.1016/S0006-3495(02)73933-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieu JP, Sawada Y. Hydrodynamics and cell motion during the rounding of two dimensional hydra cell aggregates. Eur. Phys. J. B. 2002;27:167–172. [Google Scholar]
- Schnell S, Maini PK. Clock and induction model for somitogenesis. Dev. Dyn. 2000;217:415–420. doi: 10.1002/(SICI)1097-0177(200004)217:4<415::AID-DVDY8>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Schnell S, Maini PK, McInerney D, Gavaghan DJ, Houston P. Models for pattern formation in somitogenesis: a marriage of cellular and molecular biology. C. R. Biologies. 2002;325:179–189. doi: 10.1016/s1631-0691(01)01418-4. [DOI] [PubMed] [Google Scholar]
- Steinberg MS. Reconstruction of tissues by dissociated cells. Some morphogenetic tissue movements and the sorting out of embryonic cells may have a common explanation. Science. 1963;141:401–408. doi: 10.1126/science.141.3579.401. [DOI] [PubMed] [Google Scholar]
- Stern CD, Fraser SE, Keynes RJ, Primmett DRN. A cell lineage analysis of segmentation in the chick embryo. Development. 1988;104S:231–244. doi: 10.1242/dev.104.Supplement.231. [DOI] [PubMed] [Google Scholar]
- Stickney HL, Barresi MJF, Devoto SH. Somite development in zebrafish. Dev. Dyn. 2000;219:287–303. doi: 10.1002/1097-0177(2000)9999:9999<::AID-DVDY1065>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Stockdale FE, Nikovits WJ, Christ B. Molecular and cellular biology of avian somite development. Dev. Dyn. 2000;219:304–321. doi: 10.1002/1097-0177(2000)9999:9999<::AID-DVDY1057>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Takeichi M. Cadherin Cell Adhesion Receptors as a Morphogenetic regulator. Science. 1991;251:1451–1455. doi: 10.1126/science.2006419. [DOI] [PubMed] [Google Scholar]
- Xu Q, Mellitzer G, Wilkinson DG. Roles of Eph receptors and ephrins in segmental patterning. Phil. Trans. R. Soc. Lond. B. 2000;355:993–1002. doi: 10.1098/rstb.2000.0635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young G. On the mechanics of viscous bodies and elongation in ellipsoidal cells. Bull. math. Biophys. 1939;1:31–46. [Google Scholar]
- Zisch AH, Stallcup WB, Chong LD, DahlinHuppe K, Voshol J, Schachner M, Pasquale EB. Tyrosine phosphorylation of L1 family adhesion molecules: Implication of the Eph kinase Cek5. J. Neurosci. Res. 1997;47:655–665. doi: 10.1002/(sici)1097-4547(19970315)47:6<655::aid-jnr12>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]