A Theoretical Model for F-actin Remodeling in Vascular Smooth Muscle Cells Subjected to Cyclic Stretch

Abstract

A constrained mixture theory model was developed and used to estimate remodeling of F-actin in vascular smooth muscle cells that were subjected to 10% equibiaxial stretching for up to 30 minutes. The model was based on a synthesis of data on time-dependent changes in atomic force microscopy measured cell stiffness and immunofluorescence measured focal adhesion associated vinculin as well as data on stress fiber stiffness and pre-stretch. Results suggest that an observed acute (after 2 minutes of stretching) increase in cell stiffness is consistent with an increased stretch of the originally present F-actin plus an assembly of new F-actin having nearly homeostatic values of stretch. Moreover, the subsequent (after 30 minutes of stretching) decrease in cell stiffness back towards the baseline value is consistent with a replacement of the overstretched original filaments with the new (reassembled), less stretched filaments. That is, overall cell response is consistent with a recently proposed concept of “tensional homeostasis” whereby cells seek to maintain constant certain mechanical factors via a remodeling of intracellular and transmembrane proteins. Although there is a need to refine the model based on more comprehensive data sets, using multiple experimental approaches, the present results suggest that a constrained mixture theory can capture salient features of the dynamics of F-actin remodeling and that it offers some advantages over many past methods of modeling, particularly those based on classical linearized viscoelasticity.

Introduction

The cytoskeleton (CSK) not only provides a structural framework that determines cell shape and mechanical properties, it also influences many important cellular functions (Bray, 2000; Alberts et al., 2002). Within a tissue environment, a variety of extracellular stimuli, including fluid-induced shear or matrix-induced stretch, affect the distribution and organization of CSK filaments (e.g., Smith et al., 1997; Galbraith et al., 1998; Takemasa et al., 1998; Wang et al., 2000, 2001; Hayakawa et al., 2001; Costa et al., 2002; Yoshigi et al., 2003). Many different types of mathematical models have been developed to describe the associated cell mechanics (for a review, see, Zhu et al., 2000; Stamenović and Ingber, 2002; Bao and Suresh 2003; Huang et al., 2004; Lim et al., 2006). Such models are often based on either classical continuum approaches, and thus assumptions of material uniformity (e.g., linearized viscoelasticity), or microstructural approaches, and thus idealized distributions and material properties of the CSK filaments (e.g., tensegrity or percolation). Recently, Humphrey (2002) proposed a conceptually different approach based on the concept of a constrained mixture, which is a microstructurally motivated continuum approach that can account the different nonlinear properties, deformations, and rates of turnover of individual constituents. In particular, this approach allows one to include separate contributions and distributions of the primary CSK filaments and viscous cytosol without having to quantify possible momentum exchanges between constituents or to prescribe partial traction boundary conditions that are notoriously difficult to identify. That is, one can exploit certain advantages of the continuum theory of mixtures without having to solve separate linear momentum balance relations for each constituent. By providing details on locally averaged distributions of stresses and strains in cells, this approach can be useful in identifying mechanobiological correlations (cf. Humphrey, 2001) and in estimating the distribution and transmission of forces to sub-cellular components.

Recent studies show that a single step increase in substrate stretch can increase the stiffness of adherent cells (Mizutani et al., 2004) as well as alter the binding of multiple focal adhesion (FA) associated proteins (Sawada and Sheetz, 2002). Similar findings on stretch-induced changes in FA associated vinculin and paxillin have been reported for cyclic stretching (Cunningham et al., 2002). In recent experiments (Na, 2006), we found that rapid, time-dependent, stretch-induced changes in FA area correlated well with changes in cell stiffness. In this study, therefore, we sought to develop a constrained mixture model of CSK remodeling that is consistent with observed dynamic stretch-induced changes in cell stiffness and focal adhesion area. Toward this end, the model was fit to indentation force-depth data obtained from atomic force microscopy measurements on cyclically stretched vascular smooth muscle cells and was based on immuno-fluorescent measurements of FA areas.

Materials and methods

Details on cell culture methods, design of the cell stretching device, and data collection from atomic force and confocal microscopy experiments are in Na (2006). Below we simply provide a brief review as background, with Figure 1 illustrating the overall approach to synthesize the experimental data and modeling.

Fig. 1.

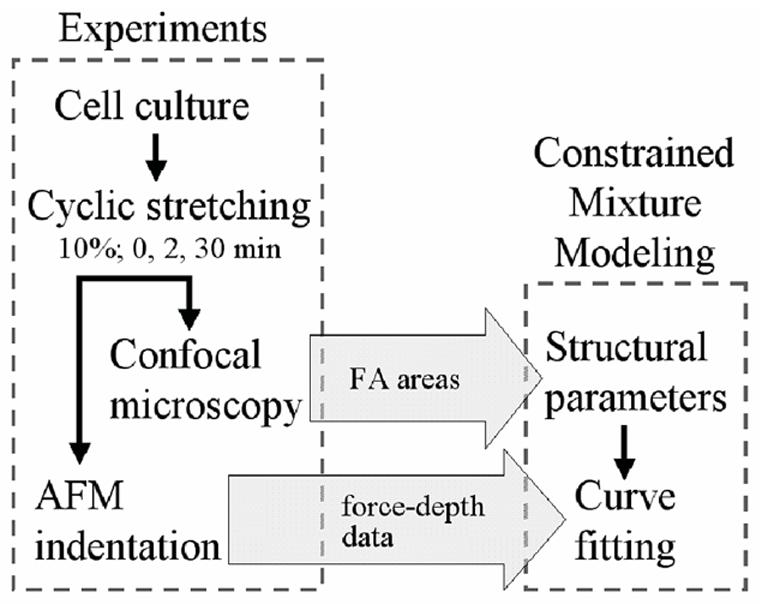
Flow chart showing the synthesis of experiments and modeling. In this study, results from previous experiments on vascular smooth muscle cells were used to model cytoskeletal (CSK) remodeling in response to cyclic stretching. Values of focal adhesion (FA) associated vinculin area obtained from immunostaining and confocal microscopy were used as parameters in a mixture model of CSK remodeling. The model was then fitted with indentation force-depth data obtained from AFM measurements to predict time-dependent CSK remodeling in response to cyclic stretching. Note that there are but a few basic assumptions in the general constrained mixture model (e.g., that energy stored in individual constituents are additive and based on 1-D relations), but many illustrative assumptions (e.g., particular stress-strain relations, distributions, pre-stretches, etc. for F-actin) are needed to fit data. We offer illustrative assumptions based on the best available data, but emphasize that the theory reveals the need for significantly more data.

Experimental protocols

Briefly, vascular smooth muscle cells (VSMCs) from first order feed arterioles within rat cremaster muscle were isolated and expanded through 3 to 10 passages. Cells were then cultured to ∼50% confluence in a serum-supplemented Dulbecco’s modified Eagle’s medium (DMEM/F-12) under static conditions, but within a custom stretching device that could subsequently be secured on the stage of an inverted microscope that is coupled to an atomic force microscope (AFM). The stretching device applies a cyclic, homogeneous, equibiaxial stretch to the central region of a circular silicone elastic membrane by dynamic infusion and withdrawal of air using a programmable syringe pump. VSMCs were cyclically stretched 10% at a frequency of 0.25 Hz for durations of 0 (control), 2, or 30 minutes.

A Bioscope System AFM (Model 3A; Veeco, Santa Barbara, CA) mounted on an Axiovert 100 TV inverted microscope (Carl Zeiss, Thornwood, NY) was used to obtain indentation force-depth curves for individual cells. AFM probes consisting of silicon-nitride cantilevers fused with a 5μm diameter spherical glass bead were allowed to repeatedly indent and retract from the surface of the VSMCs in a Force Mode Operation at 0.5 Hz. Tip velocity was 0.8 μm/s, which was slow enough to minimize viscous contributions from the cytosol (Mathur et al. 2001). Each cell was indented halfway between the nucleus and its periphery for 30 seconds to obtain 15 indentation curves per cell per duration (0, 2 or 30 min) of equibiaxial cyclic stretching, with the cell held at 10% equibiaxial stretch during indentation. Overall, 5 to 12 cells were selected per membrane, and two to five independent experiments were performed per duration of mechanical stretching for a total of 15 to 25 cells per condition.

Immunofluorescence staining was performed independently. After cyclic stretching for 0, 2, or 30 minutes, cells were immediately fixed with a 2% paraformaldehyde while held at 10% equibiaxial stretch and then quenched with a 0.1 mM glycine buffer. After washing, the cells were dual-labeled by incubation with a mouse anti-vinculin monoclonal antibody, an Alexa 488-conjugated anti-mouse IgG secondary antibody, and an Alexa 594-conjugated phalloidin. Fluorescently-labeled cells were visualized on a Leica SP2 laser confocal microscope using either a 63× oil or a 63× water immersion objective.

Quantitative analysis of focal adhesion proteins was performed on 6 or 7 cells each for two independent experiments per mechanical stretching condition (10% cyclic stretching for 0, 2 or 30 min, respectively). FA area ratio was calculated using ImageJ software as the projected total FA area divided by total basal cell area based on immunofluorescence staining of actin filaments (F-actin) and vinculin.

Cytoskeletal remodeling model

We employed a constrained rule-of-mixtures model for stresses in a remodeling CSK, which for the case of a single change in mechanical environment (i.e., from unstretched to 10% stretch) can be written as (Humphrey, 2002)¹

$$\mathbf{t}=-p\mathbf{I}+{\varphi }^{c}2\tilde{\mu }\mathbf{D}+{\varphi }_o^a{\mathbf{t}}^a\left({\mathbf{F}}_{{\kappa }_o^a}\right)+{\varphi }_o^i{\mathbf{t}}^i\left({\mathbf{F}}_{{\kappa }_o^i}\right)+{\varphi }_o^m{\mathbf{t}}^m\left({\mathbf{F}}_{{\kappa }_o^m}\right)+{\varphi }_n^a{\mathbf{t}}^a\left({\mathbf{F}}_{{\kappa }_n^a}\right)+{\varphi }_n^i{\mathbf{t}}^i\left({\mathbf{F}}_{{\kappa }_n^i}\right)+{\varphi }_n^m{\mathbf{t}}^m\left({\mathbf{F}}_{{\kappa }_n^m}\right),$$ (1)

where t is the Cauchy stress tensor for the mixture, p is a Lagrange multiplier that enforces overall incompressibility during transient loading, I is the identity tensor, μ̃ is a viscosity associated with the cytosol, D is the stretching tensor (i.e., $2\mathbf{D}=\stackrel{.}{\mathbf{F}}{\mathbf{F}}^{-1}+{\mathbf{F}}^{-T}{\stackrel{.}{\mathbf{F}}}^T$ where the over-dot denotes a time-derivative and F is the overall deformation gradient tensor), and the F_κ ’s are deformation gradient tensors for each constituent (a, i, or m) relative to individual natural configurations κ_o (with the subscript o denoting original, before 10% stretching) or κ_n (with the subscript n denoting new, due to 10% stretching). The φ ’s are mass fractions (i.e., constituent mass per total mass) for the individual constituents, which by definition are subject to the constraint

$${\varphi }^c+{\varphi }_o^a+{\varphi }_o^i+{\varphi }_o^m+{\varphi }_n^a+{\varphi }_n^i+{\varphi }_n^m=1,$$ (2)

where the superscripts c, a, i, and m denote cytosol, actin, intermediate filaments, and microtubules, respectively. Although new could refer to both newly synthesized (e.g., production and assembly of monomers that did not exist before the 10% stretching) and newly assembled (e.g., either via depolymerization and repolymerization of extant polymers or by assembly of extant monomers, each for purposes of forming a new structure due to 10% stretching), given the timescales of interest herein new will imply assembled or reassembled extant constituents. Finally, note that this basic framework admits nonlinear and anisotropic elasticity and viscoelasticity, different distributions and prestretches of individual constituents, and, most importantly, different rates and extents of turnover of individual constituents that can account for overall transitions from more solid-like to more fluid-like behaviors.

Although each family of CSK filaments plays a role in maintaining cell shape (Ingber, 1993), F-actin has been shown to impart the primary mechanical stiffness of many cell types, including SMCs (Wu et al., 1998; Rotsch and Radmacher, 2000; Wakatsuki et al., 2000), and to be physically connected to FA sites at the basal cell membrane (Gerthoffer, 2005; Mitra et al., 2005). Indeed, our previous modeling results showed that removal of intermediate filaments and microtubules reduced smooth muscle cell stiffness less than 10% (Na et al., 2004). Herein, therefore, we focus exclusively on F-actin for simplicity and illustrative purposes. Although VSMCs exhibit a viscoelastic character under various types of loading, our AFM experiments used a slow tip velocity compared to the viscoelastic time constants (cf. Mathur et al., 2001). Therefore, we restrict our attention to the elastic response of F-actin to estimate AFM measured CSK remodeling. In the absence of significant contributions from intermediate filaments, microtubules, and cytosol, Eq. 1 simplifies to

$$\mathbf{t}\cong -p\mathbf{I}+{\varphi }_o^a{\mathbf{t}}^a\left({\mathbf{F}}_{{\kappa }_o^a}\right)+{\varphi }_n^a{\mathbf{t}}^a\left({\mathbf{F}}_{{\kappa }_n^a}\right).$$ (3)

We emphasize again that there was not sufficient time to synthesize new actin in the 2 minute stretching experiments considered here, thus “new’ implies the reassembly of G-actin from disassembled filaments or the assembly from cytosolic stores of G-actin (note: cytosolic stores of G-actin may account for up to 50% of all actin; McGrath et al., 1998).

A general form for the mixture Cauchy stress is dictated by the Clausius-Duhem inequality for an isochoric, isothermal, elastic process (Truesdell and Noll, 1965):

$$\mathbf{t}=-p\mathbf{I}+2\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^T,$$ (4)

where W is a strain energy function and C is the right Cauchy-Green tensor (i.e., C= F^TF where superscript T denotes transpose). Consider a microstructurally-motivated (Lanir, 1983), but phenomenological strain energy function W for potentially evolving F-actin, namely at any point within the mid-portion of the cell (actually, averaged over a representative volume element consistent with the continuum assumption) let

$$W\equiv W_o^a+W_n^a=\sum _{k=1}^2{\varphi }_k^a{\int }_0^{2\pi }{\int }_{-\pi ∕2}^{\pi ∕2}{R}_k^a(\phi ,\theta )w^a\left({\alpha }_k\right)\cos \phi d\phi d\theta ,$$ (5)

where $w_k^a\left({\alpha }_k\right)$ is a 1-D strain energy function for F-actin and α_k is its stretch ratio relative to an individual, possibly evolving natural (i.e., stress-free) configuration. The subscript k denotes the constituent family, which is to say the related natural configuration of the F-actin (i.e., k = 1 and 2 denote original, prior to 10% stretching, and new, after 10% stretching). The function $R_k^a(\phi ,\theta )$ represents the distribution of orientations of F-actin in its natural configuration (which need not be physically experienced by the filaments) and ${\varphi }_k^a$ is the associated mass fraction².

Clearly, Eqs. 4-5 yield the same “model” as Eq. 3 (and thereby determine the constitutive relations for the stresses ${\mathbf{t}}_k^a$) provided that one accounts for relationships between the overall and the individual reference configurations (Baek et al., 2006). For illustrative purposes, and because of difficulties of measuring 3-D distributions of filaments in individual natural configurations, let R_k (φ,θ) =1/4π by assuming that all filaments would be distributed isotropically in natural configurations (which is likely the case in cell sphering, a convenient configuration, prior to cell adhesion and spreading on a membrane), although they will reorient and stretch in 3-D due to deformation. Substituting Eq. 5 into Eq. 4 gives

$$t_{ij}=-p{\delta }_{ij}+2\sum _{k=1}^2\frac{{\varphi }_k}{4\pi }\left({\int }_0^{2\pi }{\int }_{-\pi ∕2}^{\pi ∕2}\frac{\partial w}{\partial {\alpha }_k}\frac{1}{2{\alpha }_k}\frac{\partial C_{11}^{\prime }}{\partial C_{MN}}\cos \phi d\phi d\theta \right)F_{iM}{F}_{jN}.$$ (6)

where the 1’ (primed) coordinate axis coincides with the direction of a generic filament, and $C_{11}^{\prime }$ is obtained from a tensorial transformation of C_MN. Note, too, that the indices i, j, M, and N = 1,2,3 for the different components of stress in 3-D, with summation implied over repeated indices according to the usual Einstein convention.

Consistent with previous reports that the mechanical behavior of individual CSK filaments is nonlinear and qualitatively similar to those of soft tissue (Janmey et al., 1991; Liu and Pollack 2002; Deguchi et al., 2006), two specific functional forms of the first Piola-Kirchhoff stress-stretch relation ($\partial w∕\partial {\alpha }_k$) for individual stress fibers were compared (Humphrey and Yin, 1987; Misof et al., 1997):

$$\frac{\partial w}{\partial {\alpha }_k}=c{c}_1({\alpha }_k-1)\left[\exp \left(c_1{({\alpha }_k-1)}^2\right)\right];\text{exponential model},$$ (7)

$$\frac{\partial w}{\partial {\alpha }_k}=\frac{c{c}_1({\alpha }_k-1)}{{\alpha }_k(c_1-({\alpha }_k-1))};\text{molecular model},$$ (8)

where c and c₁ are separate material parameters. Note, here, that we assume that intrinsic material properties of “original” and “new” stress fibers are the same (e.g., F-actin is F-actin, which is to say that the same cross-linking proteins are operative); only the orientations, mass fractions, and natural configurations evolve. Hence, material parameters, c and c₁, are assumed to be constant during CSK remodeling.

Interrogation of cell stiffness via AFM indentation

Detailed analysis of an AFM indentation superimposed on a finite equibiaxial stretch was described previously (Na et al., 2004). Briefly, the force versus indentation depth (P-θ) relationship is (Beatty and Usmani, 1975; Green et al., 1952):

$$P=2\pi \frac{\Gamma \left(W\right)}{\Sigma \left(W\right)}\widehat{f}\left(\delta \right),$$ (9)

where Γ(W) and Σ(W) are functionals that depend on the strain-energy function W and the in-plane finite equibiaxial stretch μ whereas the function $\widehat{f}\left(\delta \right)$ depends on the geometry of the tip of the rigid AFM indenter and the penetration depth δ of the indenter. A spherical tip of radius a was used in this study, therefore (Beatty and Usmani, 1975),

$$\widehat{f}\left(\delta \right)=\frac{4}{3\pi }\sqrt{a{\delta }^3}.$$ (10)

To compute Γ(W) and Σ(W) using the results of Humphrey et al. (1991), we need the strain energy function W in terms of invariants I_i of the right Cauchy-Green tensor C. Because the proposed strain energy function for CSK remodeling is written in terms of filament stretch α_k (equation 6), which is related to C, we can easily find the requisite relations between derivatives with respect to the invariants I_i and those in terms of the components of C (Na et al., 2004). These results are used without restatement here.

Results

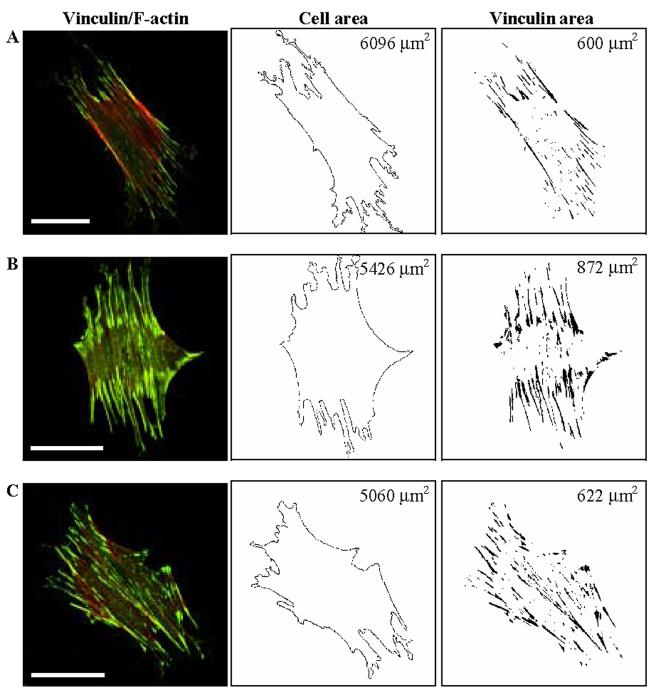
Representative immunofluorescence micrographs reveal changes in FA associated vinculin in response to 10% cyclic stretching for 0, 2, or 30 minutes (Figure 2); shown numerically are calculated total basal cell areas and FA associated vinculin areas for individual cells. Overall, the ratio of vinculin area to basal cell area in the unstretched state was 0.105 ± 0.002 (mean ± SEM). This area ratio increased to 0.156 ± 0.003 following cyclic stretching at 10% for 2 minutes, but returned toward the unstretched level (0.121 ± 0.004) after 30 min of stretching at 10%. Overall, therefore, the increase in focal adhesion area was ∼49% after 2 minutes of stretching but only ∼15% after 30 minutes of stretching, each relative to the unstretched control.

Fig. 2.

Effects of equibiaxial cyclic stretch on FA localization for three different, but representative cells. (A) Cell on an unstretched membrane. (B) Cell subjected to cyclic stretch (10%, 0.25 Hz) for 2 min. (C) Cell subjected to cyclic stretch (10%, 0.25 Hz) for 30 min. Note that stretching for 2 minutes in panel B induced a significant increase in FA associated vinculin staining, particularly at the periphery of the cell. Total basal cell area and the vinculin-containing FA area are shown in the middle and right column, respectively, but more importantly note that the FA-area ratios (FA area/total cell area) were 0.098, 0.161, and 0.123 for panels A, B, and C, respectively. Bars, 50 μm.

Since actin filaments make bundles to bear intracellular stresses (Byers and Fujiwara 1982; Zimerman et al., 2004), we used force-strain data from single F-actin bundles (i.e., stress fibers) isolated from vascular smooth muscle cells (Deguchi et al., 2006) to determine the material parameters c and c₁ (Eqs. 7 and 8). The first Piola-Kirchhoff stress-stretch relation for these data was described well by ∂w/∂α = 656α ² +138α - 794 (kPa) based on the reported radius of 100 nm for the fibers (Deguchi et al., 2006). The associated best-fit parameters were c=1837 kPa and c₁=0.8302 for the exponential model and c=1537 kPa and c₁=1.0699 for the molecular model (Figure 3).

Fig. 3.

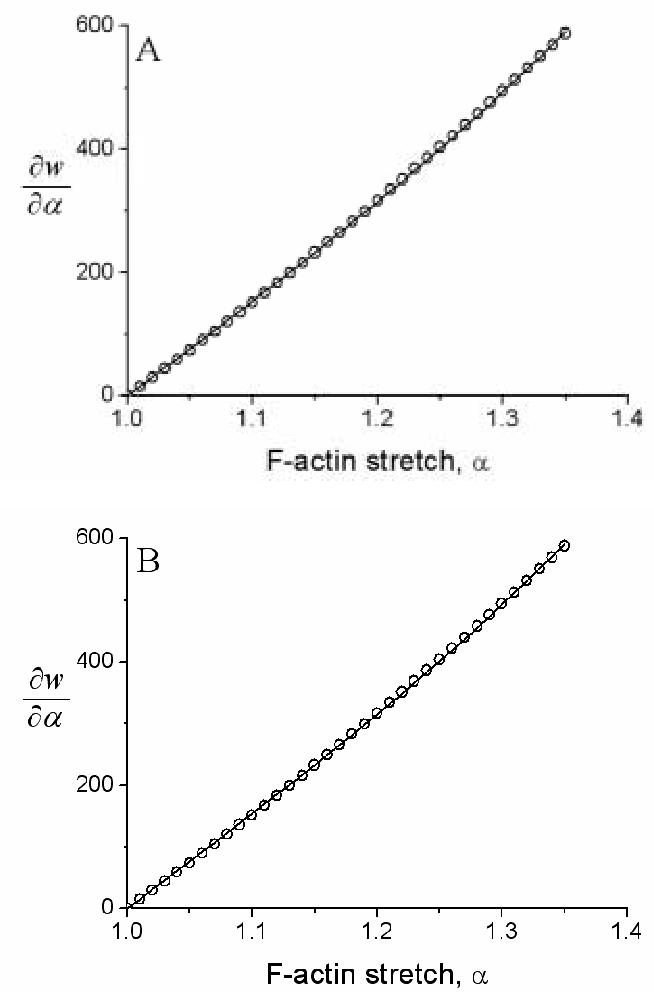
Shown as data (open circles) are results from a polynomial fit ∂w/∂α=656α²+138α-794 kPa to the Deguchi et al. (2006) data on stress fibers. Shown, too, are best-fits (solid lines) for (A) the exponential model of F-actin elasticity (Eqs. 6 and 7) and (B) the molecular model of F-actin elasticity (Eqs. 6 and 8). Note the comparable fits to data despite one model being phenomenological (panel A) and one being molecular (panel B). Note, too, the slight nonlinearity over this range of finite stretch, which could not be captured with a linearly elastic model.

The final two variables to determine for the unstretched cells were filament pre-stretch and mass fraction. The pre-stretch was assumed to be 1.2 based on data from Costa et al. (2002), which show that under “homeostatic” conditions the filaments are stretched 15 to 26%; this is consistent with the concept of cytoskeletal pre-stress (Ingber, 1993; Wang et al., 2002) and measurements by Deguchi et al. (2006). The mass fraction was then estimated by fitting indentation force-depth curves from AFM measurements using Eq. 9 along with Eqs. 7 and 8 and the corresponding material parameters noted above. Thirteen force-indentation curves for unstretched (i.e., control) cells whose stiffness values were close to the mean for the unstretched cells (1.30 kPa, which was reported in Na, 2006) were chosen for fitting (Figure 4). In this case, φ_n = 0 and total mass fraction, ${\varphi }_o(\equiv {\varphi \mid }_{\mathrm{con}})$, was found to be ∼0.005 for both models of F-actin stiffness. This value was ∼5% of the measured FA related area ratio (Table 1). Assuming the vinculin containing area ratio (Table 1) and the mass fraction of the stress fibers are proportional, evolving total mass fractions for cells subjected to cyclic stretch were then computed for both models (Table 1).

Fig. 4.

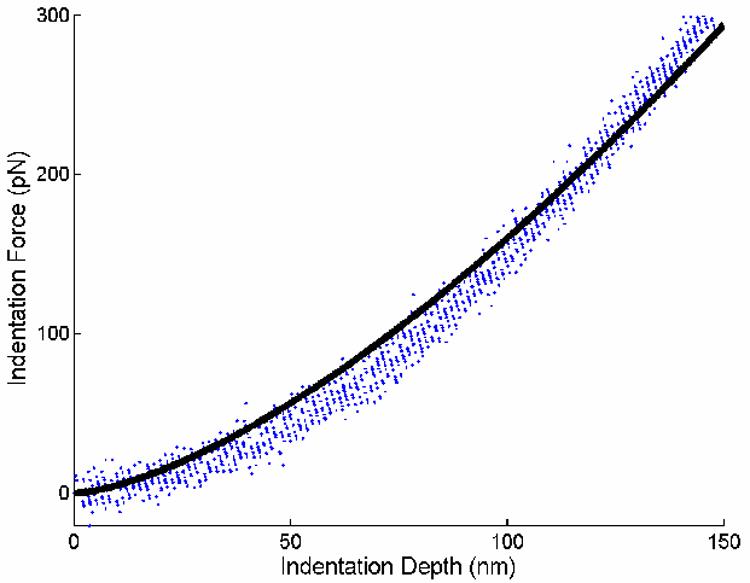
Data from thirteen indentation force-depth tests obtained from AFM indentations of unstretched cells were fitted with the CSK remodeling model (solid line) to estimate the mass fraction of F-actin in unstretched state. Experimental data were chosen from 3 cells each from 2 independent experiments. Although not shown, fits were similar in parameter sensitivity studies wherein the values of c in equations 7 and 8 were varied by ±10%.

Table 1.

FA associated vinculin area ratios and total mass fractions of F-actin in response to 10% cyclic stretching for three durations: 0, 2, and 30 minutes.

Stretching Time (min)	FA related Area Ratioa	Total F-actin Mass Fraction, φ
		Exponential Model	Molecular Model
0	0.105±0.002	0.00468b	0.00451b
2	0.156±0.003	0.00695	0.00670
30	0.121±0.004	0.00537	0.00518

^aFA associated vinculin area ratios were obtained previously. N=6 to 7 cells each for two independent experiments per condition. Results are mean ± SEM.

^bTotal mass fractions in the unstretched state were obtained from fitting 1 forceindentation curve per cell with the CSK remodeling model. N=5 cells.

Next, to estimate F-actin remodeling due to prior cyclic stretching, data from indentation tests on 5 different cells (one curve for each cell) were fit in a similar way to find α_n as well as φ_o and φ_n. These indentation data were chosen since the associated stiffness values were close to the mean values for each mechanical stretching condition: 2.42 and 1.46 kPa after 2 and 30 min of cyclic stretching, respectively (Na, 2006). Note, however, that the total mass fraction of F-actin after each mechanical stretching condition is the sum of the “original” and “new” F-actin mass fractions. Hence, one need only determine two parameters (α_n and either φ_o or φ_n) from the fit to AFM data. In summary, the following constraints were enforced for the 2 minute, 10% cyclic stretching condition: ${{\varphi }_o\mid }_{2\min }+{{\varphi }_n\mid }_{2\min }={\varphi \mid }_{2\min },{{\varphi }_o\mid }_{2\min }\le {\varphi \mid }_{0\min },{{\alpha }_n\mid }_{2\min }\ge 1.2$, and $1.2<{{\alpha }_o\mid }_{2\min }\le 1.32$ (=1.2×1.1 where 1.2 is the pre-stretch and 1.1 is the test-induced stretch). Recall that the pre-stretch of 1.2 in the unstretched state was based on the results of Costa et al. (2002) and Deguchi et al (2006). Constraints for the 30 minute stretching conditions were similar to those for 2 minutes. Computed changes in mass fractions and stretch ratios for F-actin following both mechanical stretching conditions are shown in Figure 5. Whereas the initial mass fractions of F-actin were ${\varphi \mid }_{0\min }$ ∼ 0.005 in the unstretched state for both the exponential and molecular models, after 2 minutes of 10% equibiaxial stretching μ, the predicted mass fraction of the original F-actin decreased by 53% and 51% (i.e., to φ_o ∼ 0.002) for the exponential and molecular models, respectively. Conversely, predicted values for the new F-actin were φ_n ∼ 0.005 for both models, consistent with a possible assembly of new actin filaments having a nearly “homeostatic” prestretch. After 30 min of cyclic stretching, most of the original F-actin was predicted to be disrupted, as revealed by a predicted mass fraction of φ_o ∼ 0.0007 for both models while the mass fraction of the newly assembled F-actin remained φ_n ∼ 0.005 for both models (Figure 5A). Stretch ratios computed for the new F-actin following 2 minutes of cyclic stretching were α_n ∼1.25 (in contrast to α_o = 1.2 in the unstretched state) for both models, which decreased slightly to α_n ∼ 1.23 for both models following 30 minutes of cyclic stretching (Figure 5B). Finally, to assess potential sensitivity of the fits to AFM data to the key parameters, we varied the values of c in Eqn 7 by ±10% and determined the associated best-fit values of c₁. It was found that neither the fit to the data of Deguchi et al. (2006) nor the fit to the AFM data changed significantly (not shown). Moreover, the predicted original mass fraction changed less than 1% in the worst case. Similarly, we found that the fits to AFM data were not significantly different for assumed values of the fiber pre-stretch ranging from 1.15 to 1.25. Yet, predicted original mass fractions were markedly different. For example, for the unstretched cells they were 0.00569, 0.00468, and 0.00403 for the 15, 20, and 25% pre-stretches, whereas for the cells cyclically stretched 10% for 2 minutes they were 0.00600, 0.00578, 0.00416 for the same 15, 20, and 25% pre-stretches. These results are sensible in that increased pre-stretch renders the fiber stiffer, thus one would need fewer fibers to carry the same load.

Fig. 5.

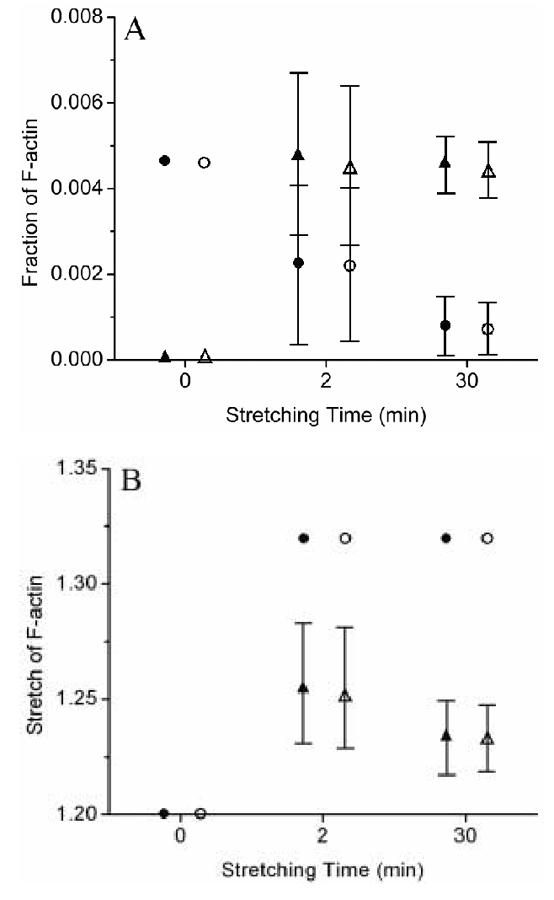
Possible CSK remodeling in response to cyclic stretching. Results show high-low-mean values. ●: original F-actin in the exponential model; ○: original F-actin in the molecular model; ▲: new F-actin in the exponential model; △: new F-actin in the molecular model.

In summary, results from the remodeling model, based on both exponential and molecular constitutive relations for stress fiber elasticity as well as immunofluorescence and AFM data, are consistent with the possible assembly of new actin filaments (∼0.5% of the total cell mass) soon after the onset of cyclic stretching with associated disassembly of original filaments: φ_n ∼ 0.005 after only 2 minutes, which was maintained for longer periods of cyclic stretching (Figure 5A). Moreover, the new (i.e., assembled, not synthesized) fibers were predicted to have different natural configurations, the predicted stretch being ∼25% after 2 minutes of stretching and ∼23% after 30 minutes in comparison to the “overly stretched” original F-actin that could have been stretched up to 32% (Figure 4B).

DISCUSSION

The importance of understanding well both cell mechanics and mechanobiology is undisputed, yet significant challenges remain. For a VSMC, for example, we ultimately need to know how macroscopic loads induced by blood pressure and blood flow within a vessel are distributed throughout the complex cell-cell and cell-matrix structures that define the vascular wall, how these loads are transferred to particular sites (e.g., specific integrins) on the surface of each cell, how these localized loads are distributed within the cytoskeleton (e.g., along actin filaments), and ultimately how these distributed loads affect cell signaling and altered gene expression. Because of the extreme structural complexity over many different times scales and length scales - from millimeters at the level of an artery, to microns at the level of collagen fibers and cells, to nanometers at the level of cell surface receptors and CSK constituents - mathematical modeling must range from continuum to microstructural to molecular biomechanics (e.g., see, Stamenović and Ingber, 2002; Humphrey, 2002; Bao and Suresh, 2003; Lim et al., 2006).

Continuum descriptions are well accepted at the vessel level, but can apply at the cellular level as well. For example, characteristic dimensions of a VSMC, on the order of 25 to 100 μm, are much greater than those of the CSK constituents, on the order of nm, which thereby motivates a continuum approach. Indeed, when one considers the large number of receptors or integrins on a cell surface (on the order of 10³ to 10⁵; Lauffenburger and Linderman, 1993) or the enormous number of actin molecules within a cell (on the order of 10⁶ to 10⁸; Lodish et al., 2000), there is considerable motivation to consider appropriately averaged field quantities. Finally, formulating continuum level models for both the vessel and the associated cells will facilitate the development of much needed multi-scale models.

The focus of this paper is a continuum biomechanical analysis of AFM data that reflect dynamic changes in the overall (local) stiffness of cyclically stretched vascular smooth muscle cells in the absence of complexities due to cell-cell and 3-D cell-matrix interactions. Whereas most prior AFM data have been collected using nm scale cantilever tips, we suggest that this is inconsistent with the continuum approximations typically used to interpret the associated stiffness data (e.g., even the Hertz solution). For this reason, we confined our analysis to data collected using larger (5 μm diameter) tips; we also used a more appropriate large strain formulation of the AFM boundary value problem (equation 9). Our AFM results cannot be compared directly to most prior results, therefore, which tend to yield larger estimates of stiffness due to the much smaller tips (e.g., see Mathur et al., 2001). Moreover, in contrast to prior continuum models of cells that assume a linear, isotropic, and materially uniform behavior (e.g., described by a Young’s modulus and Poisson’s ratio, or by a storage and loss modulus; Fabry et al. 2001; Mijailovich et al., 2002; Mack et al., 2004; Smith et al., 2005), we employed a geometrically and materially nonlinear constrained mixture model that mass averages contributions of the individual structurally significant CSK constituents, which in turn are allowed to remodel separately over time and to exhibit deformation-dependent anisotropy. Again, therefore, the present results cannot be compared directly to prior results even though our general model can recover many of the prior models as special cases. We emphasize, however, that one of the main contributions of new theoretical framework is that it can identify and guide new experiments. Whereas prior models that assume that the CSK is isotropic and materially uniform provide little guidance on what data are needed, or an ability to incorporate increasingly detailed data as they become available, our framework reveals a need for much more detail on all of the important parameters that define the constrained mixture (stress-strain behaviors, mass densities, distributions, cross-linking, pre-stretch, etc.) as it evolves during remodeling. To illustrate the potential utility of this approach, we invoked numerous illustrative assumptions based on the best data available.

Many families of CSK proteins contribute to overall cell stiffness, but F-actin tends to dominate in many cases (Pourati et al., 1998; Wu et al., 1998; Smith et al., 2003; Na et al., 2004; Huang et al., 2005) and thus was the focus herein. There is increasing information available on the elasticity of F-actin, including isolated filaments, networks having different degrees of cross-links, and stress fibers (e.g., Liu and Pollack, 2002; Gardel et al., 2004; Deguchi et al., 2006). Best-fit values of material parameters embodied in two different forms of the stored energy function $w^a\left({\alpha }_k^a\right)$, k = “o” or “n”, were determined directly from data available on isolated stress fibers (Deguchi et al., 2006), which provided suitable descriptions of the characteristically nonlinear force-length response. Because our overall predictions were not affected by the use of two different models (equations 7 and 8) or slightly different parameter values (determined via a sensitivity study of ±10% changes in parameter values), it appears that the data themselves played the critical role. Given that there has been only one study on the stress-strain behavior of stress fibers, there is a pressing need for additional experiments to verify or refine our understanding of this important property. The present mixture model can capture mass density directly via the evolving mass fraction ${\varphi }_k^a$ and orientation directly via the potentially evolving distribution function $R_k^a(\phi ,\theta )$; at present, the degree of cross-linking is correlated with the material parameter c, consistent with the results of Gardel et al. (2004). Perhaps least well known are mass densities for the different cytoskeletal filaments and in particular how they partition for “original” and “new” filaments. Herein, mass density of the load bearing actin was assumed to correlate with FA density, which is to say vinculin or paxillin (Saez et al., 2004), for which reliable data were available. Although it is expected that stress fibers will increase as the focal adhesions to which they anchor increase, this relationship is not known. We estimated changes in phalloidin-labeled actin at the basal surface and found that, qualitatively similar to changes in focal adhesion area, actin area increased (∼16% relative to control) after 2 minutes of stretching but decreased after 30 minutes of stretching (∼12% of control). These data were not used in the modeling, however, because of concerns with photobleaching the limitation of data to the basal surface. Quantifying changing mass fractions remains as an important need.

Noting that equibiaxial stretching preserves fiber orientations in plane, this negated the need for more detailed analyses of load-induced changes in fiber orientations. The original distribution of actin was assumed to be isotropic relative to a computationally convenient natural configuration (i.e., before the cell adhered and spread). This is probably a reasonable assumption, which could be assessed in part by measuring 3-D actin orientations in non-adherent spherical cells. This issue needs much more attention, however, as does measurement of spreading and deformation-induced changes in orientation. Cross-link density was not accounted for directly; rather we assumed that the material parameters remained constant despite changes in mass density and pre-stretch. Because cross-linkers play a key role in governing the overall mechanical properties (Wagner et al., 2006), this too needs increased attention. Notwithstanding these illustrative assumptions, Figures 4 and 6 reveal that the model was able to describe observed time-dependent changes in overall cell stiffness reasonably well, and therefore that the observed changes in stiffness are consistent with the concept that the actin cytoskeleton remodeled so as to restore a “tensional homeostasis”.

Fig. 6.

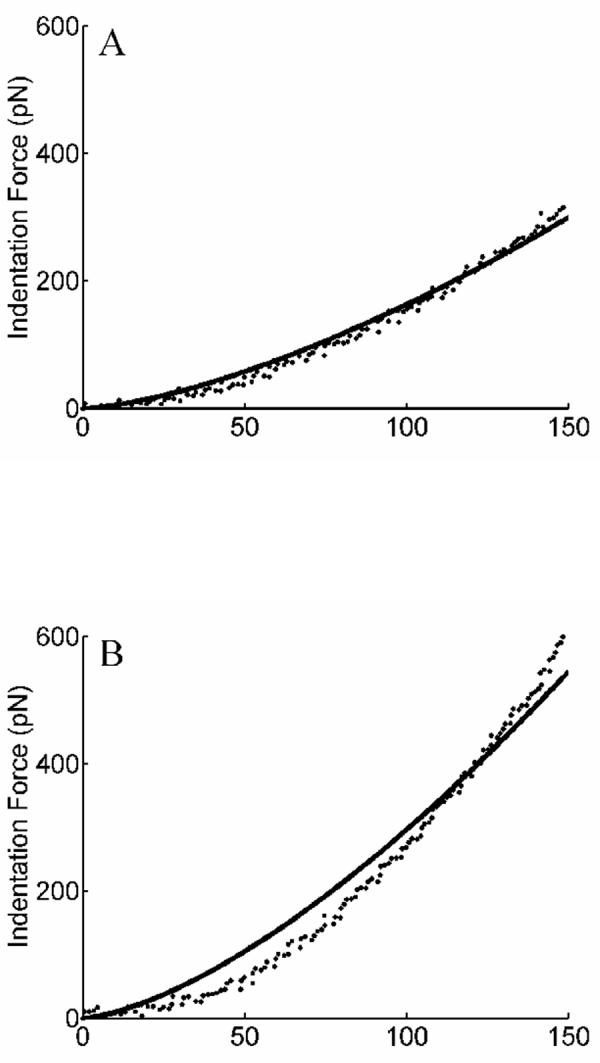
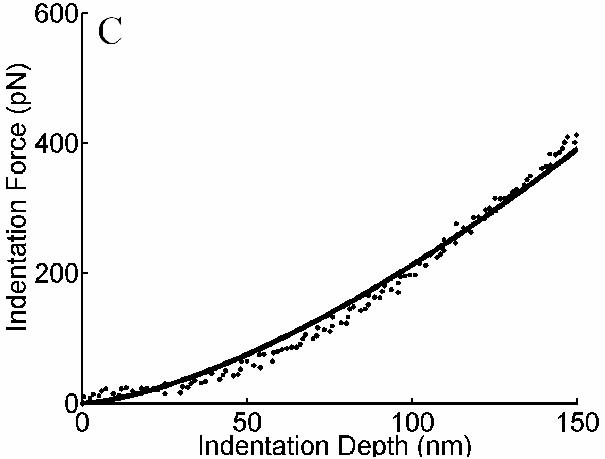
Representative indentation force-depth curves from AFM measurements obtained from independent experiments as well as best-fits obtained with the remodeling model: (A) unstretched cells; (B) cells subjected to 2 minutes of 10% cyclic stretch; (C) cells subjected to 30 minutes of 10% cyclic stretch. Note the increased stiffness after 2 minutes of stretching but the decrease after 30 minutes of stretching toward the original stiffness.

Note, therefore, that CSK constituents have been shown to turnover rapidly in response to perturbations in loading (e.g., Galbraith et al., 1998; Cunningham et al., 2002). Although the turnover of F-actin involves depolymerization/repolymerization (Cipolla et al., 2002), precise changes associated with such turnover remain unknown. Mizutani et al. (2004) recently suggested that just as fibroblasts appear to try to maintain a “tensional homeostasis” in collagen gels in which they are cultured (Brown et al., 1998), so too fibroblasts appear to try to maintain a tensional homeostasis within their CSK. That is, in response to increased (or decreased) mechanical loading, cells appear to modify both the extracellular matrix and their cytoskeleton so as to decrease (or increase) the stress and thereby restore “normalcy”. Indeed, this concept of a homeostatic tendency is consistent with vessel level responses to increased or decreased wall shear and intramural stresses (Taber, 1995; Gleason and Humphrey, 2004). The key question, however, is: How does the cell control mechanical homeostasis in different situations? Mizutani et al. found that in response to a single 8% step increase in uniaxial stretch, fibroblasts exhibited an increase in stiffness followed by a gradual (over tens of minutes) return toward the baseline value; moreover, this response was due entirely to actomyosin interactions. Peterson et al. (2004) similarly reported that focal adhesion area increases and then decreases in response to a contractile agonist (i.e., an increased tension), again with changes occurring over tens of minutes. As noted above, however, cell stiffness can also be changed by altering actin density, orientation, cross-linking, or stretch. Indeed, Pourati et al. (1998) showed that rapid increases in strain increased cell stiffness independent of actomyosin interactions but dependent on the integrity of the actin CSK; actin stretch, or tension, was thus increased by overall cell stretch. Although we did not control the contractility of the VSMCs in our experiments, based on the culture conditions used (passages 3 to 10 in serum), the rapidity of the observed changes, the lack of agonist stimulation, and findings in diverse reports in the literature (cf. Worth et al., 2001; Fabry et al., 2001; Saez et al., 2004; Peterson et al., 2004), it is unlikely that the AFM measured changes in stiffness were due to actomyosin effects alone. Of course, once data are available on the stress-strain behavior of individual stress fibers as a function of actomyosin interactions, then similar experiments on the effects of stretch on cells with different degrees of contractility would be useful to check further the model.

We suggest that the ability to rapidly depolymerize / repolymerize actin allows the cell to control stiffness by changing the length of individual filaments, which is to say by changing their degree of stretch (e.g., since stiffness is stretch dependent). In the context of tissue-level growth and remodeling, this is equivalent to saying that the natural configuration can change individually for each constituent, which has proved to yield predictions that are consistent with many empirical observations (Gleason and Humphrey, 2004). Indeed, based on Figure 5, the observed acute increase in stiffness in response to an increased cyclic stretch is consistent with both an increased stretch of the original filaments (cf. Pourati et al., 2005) and an assembly of new, less stretched filaments, whereas the subsequent decrease back towards normalcy is consistent with a replacement of the highly stretched original filaments with new less stretched (i.e., reassembled) filaments. That the stiffness did not return completely to baseline, similar to the report by Mizutani et al. (2004), may suggest that the “homeostatic target“ is actually an acceptable range (note: Brown et al. (1998) similarly suggest that cells respond only if the alteration in loading is outside a range of ±25% of normalcy). Costa et al. (2002) reported a clever experiment wherein endothelial cells were cultured on pre-stretched membranes that could subsequently be unstretched. They found that the actin stress fibers did not buckle, as would be expected of a thin compressed filament, until the membrane shortened significantly. They suggested that a distribution of ”pre-extensions“ (primarily from 15 to 26%) or pre-stresses exist in the filaments, which is consistent with the aforementioned concept of tensional homeostasis (Mizutani et al., 2004), the concept of pre-stress motivating the tensegrity model (Ingber, 1993; Pourati et al., 1998), and the concept of constancy of stress at focal adhesions (Balaban et al., 2001; Tan et al., 2003). Clearly, there is a need to quantify this homeostatic stretch, or distribution therein, in each type of cell and for each type of filament, particularly given the sensitivity of our modeling results to its value. Because of the highly nonlinear behavior of F-actin (Janmey et al., 1991; Liu and Pollack, 2002), it appears that small changes in stretch can significantly affect stiffness, thus returning it towards its homeostatic range. There is a pressing need for experiments to focus not just on the rates of assembly and disassembly, but also on the pre-stretch and orientations of the reassembled filaments in relation to normal values.

In conclusion, we emphasize that, regardless of the type of mathematical model used to reduce the data, a disadvantage of most current experimental techniques for studying cell mechanics, including AFM indentation force-depth tests and magnetic twisting cytometry (MTC), is that the resulting data are essentially 1-D and fitting such data is not a stringent test of any model. There is, therefore, a need to evaluate our model (as well as other models) using data from multiple experimental set-ups but the same cell conditions. Moreover, just as in tissue level mechanics, we must move towards multi-axial tests of cell mechanics, which provide significantly more information but also be significantly more difficult to perform and interpret. Finally, because CSK filaments remodel in response to mechanical perturbations, they may respond locally to changes in loading that are induced by our measurement tools, hence raising the question whether in vitro data actually reflect native properties or merely rapid adaptations to a local non-physiologic loading. There is, therefore, a need for real-time imaging of overall CSK changes during mechanical experiments wherein native cell-matrix and cell-cell interactions are maintained and the loading is both multidimensional and more natural.

Appendix

Mechanics is the study of forces and the associated motions. For continua, however, it has proven useful to quantify the mechanics in terms of force intensities (or, stresses) and gradients of the motion (or, deformation gradients). If we consider a small cuboid of material, it is easy to imagine the possibility of 3 components of force (a vector) acting on each of the 3 positive faces, which gives rise to 9 components of stress (i.e., forces per unit areas) at any point that can be represented succinctly by a 2^nd order tensor (the components of which can be represented by a 3×3 matrix). Two common measures of stress are the Cauchy stress tensor t (force per deformed area) and the first Piola-Kirchhoff stress tensor P (force per undeformed area). A key goal in continuum mechanics is to relate the 9 components of stress to the 9 components of deformation, including possible rates of change therein, via constitutive relations. Toward this end, the deformation gradient tensor F has proven useful; briefly, it maps differential position vectors from undeformed to deformed configurations, via dx = FdX, and thus contains information on both rigid body motion R and deformation U (i.e., F = RU). Because we intuit stress to result from deformation alone, not rigid body motion, the tensor C = F^TF = U^TR^TRU = U^TU (because R is an orthogonal tensor, R^T = R^-1) is very useful. It thus proves convenient to quantify elastic behaviors in terms of a strain-energy function W = W(C), for the second law of thermodynamics requires that the first Piola-Kirchhoff stress be determined from W via $\mathbf{P}=2\frac{\partial \mathbf{W}}{\partial \mathbf{C}}{\mathbf{F}}^T$ where t = FP/(det F). These general relations give equation 4 in the text with the exception of the reaction part of the stress, -pI, which allows a stress in the absence of deformation if the body is incompressible. A key challenge in biomechanics is finding appropriate forms of W, as postulated in equation 5 in the text (noting that certain viscoelasticity models can be extended from properly formulated elasticity models). Our particular form of W assumes that the energy stored in the CSK due to deformation results from the strain energy stored in each of the individual filaments, which may have individual mass fractions, orientations, uniaxial stress-strain responses (given by w(α), with α a uniaxial stretch and thus a component of U), and even unloaded lengths. Moreover, energy is only stored elastically in filaments that remain assembled.

Note, too, that an exact measure of strain is given by E = (F^T F-I)/2 whereas the common linearized measure of strain is ε = (F + F^T-2I)/2. E is insensitive to rigid body motion as desired of a measure of strain whereas ε varies with rotations and thus can only be used in the case of small strains and small rigid body rotations. In this very special case, with F∼I, the general nonlinear hyperelastic relation $\mathbf{t}=\mathbf{F}\frac{\partial W}{\partial \mathbf{E}}{\mathbf{F}}^T$ (since partial derivatives with respect to E and C are related easily via a 2) reduces to $\mathbf{t}=\frac{\partial W}{\partial \epsilon }$, which represents a general Hooke’s law if W is quadratic in the small strain ε. Note, therefore, that proper nonlinear relations can recover simpler relations as special cases, but the converse is not true - it is generally not possible to extend a linearized relation to a correct nonlinear relation. Note, too, for the simple case considered herein: if the prestretch is 20% and the applied stretch is 10%, the exact uniaxial strain is 0.371 whereas the linearized approximation is 0.3, hence resulting in a 19% error in strain calculation. The exact measure should be used whenever the strains are not small.

Finally, let us consider a simple 1-D case. Let W = Eε ²/2 whereby the single component of the Cauchy stress is t =∂W/∂ε = Eε and E is the Young’s modulus (note that stiffness is obtained by taking derivatives of stress with respect to conjugate strains, but in the linearized case this can sometimes be accomplished by taking ratios of stress to strain). It should be noted further that nonlinear and linearized viscoelasticity theories can build upon associated results from elasticity (Truesdell and Noll, 1965). As a simple example, analogous to 1-D Hooke’s law, t = Eε, let t(τ) = G* ε(τ) where G* ≡ G′ + iG^′′ is a complex modulus and τ is time. If we consider sinusoidal variations in strain and associated sinusoidal stress responses that may be out of phase (given by δ), then let $t=t_o\exp \left(i(\omega \tau +\gamma )\right)=(G^{\prime }+i{G}^{″}){∊}_o\exp \left(i\omega \tau \right)$, whereby we can show that G′ = t_o cosγ/ε_o and G″ = t_o sinγ/ε_o are the so-called storage and loss moduli (note that the loss modulus is zero if the material is elastic, γ = 0, and the stress and strain remain in phase during sinusoidal testing). Although these moduli can be derived in different ways, and are defined independent of a specific linearized viscoelastic model such as Maxwell, Kelvin-Voigt, etc., the key observation is that they only hold for linearized viscoelasticity and either 1-D or isotropic/incompressible cases. Storage and loss moduli have been used extensively in cell mechanics (e.g., Gardel et al., 2004; Smith et al., 2005; Wagner et al., 2006), and they have led to clever and intriguing interpretations in terms of soft glassy rheology (Fabry et al., 2001) that address transitions from fluid-like behaviors needed in cell migration to solid-like behaviors needed in cell contraction. Indeed, soft glassy rheology, sol-gel theories, and our current mixture theory (recall equation 2) can all address this interesting transition from fluid-like to solid-like behaviors. It is noted, however, that unlike current soft glassy rheology models, the current constrained mixture theory is not restricted to linear behaviors, small strains, isotropy, material uniformity, the absence of self-equilibrating pre-stresses in different constituents, the kinetics of turnover of individual types of filaments, evolving individual natural configurations, etc. Hence, although simpler models are attractive because of mathematical and experimental simplicity, more detailed models offer the possibility to address better the increasingly detailed biological information as it becomes available and they better point out associated experimental needs.

Nomenclature

t, tⁱ - Cauchy stress (force/current area) for mixture, constituent i

p - Lagrange multiplier (enforces overall incompressibility)

${\varphi }_k^i$ - mass fraction of constituent i, relative to state k

F, Fⁱ - deformation gradient for mixture, constituent i

D - stretching tensor for flow of cytosol

C - deformation tensor for mixture of structural constituents

$R_k^i(\varphi ,\theta )$ - filament distribution function for constituent i as a function of spherical coordinates (φ,θ)

W - total strain energy stored in the mixture

wⁱ - strain energy stored in individual filaments due to uniaxial deformation

α - stretch of a filament

P, δ - AFM indentation force and depth

μ̃, μ - cytosol viscosity and in-plane equibiaxial finite stretch, respectively