Treatment of High Blood Pressure and Gain in Event-Free Life Expectancy

Abstract

Objective

Consideration of absolute risk has been recommended for making decisions concerning preventive treatment in hypertension. We performed simulations to estimate the benefit of antihypertensive therapy over a life-time.

Methodology

The rate of nonfatal and fatal events of untreated hypertensives in the US population were estimated using data from Individual Data ANalysis of Antihypertensive drug intervention trials (INDANA; a meta-analysis on individual data in hypertension) and specific cause of death from national statistics. Disease-free survival curves until all patients have died were built using the “life-table” method. The treatment effect estimated from INDANA was applied to this curve to obtain the disease-free survival curve of the life-long treated population. Gains in event-free life expectancy (GLE) were estimated from survival curves. A sensitivity analysis was performed to assess the impact of possible death misclassifications.

Results

For a 40-year-old man, the gain in life expectancy without stroke and major cardiovascular events were 27 and 32 months, respectively, and were more substantial than those without coronary disease (19 months). The GLE decreased slowly with increasing age at the beginning of treatment, whereas short-term absolute risk reductions increase sharply with age.

Conclusions

Policies based on the selection of patients to treat according to absolute benefit do not maximize the GLE compared with strategies that treat low-risk patients.

Introduction

Since randomized clinical trials (RCTs) that included elderly patients have demonstrated that absolute risk reduction depends on the level of cardiovascular risk prior to treatment (MacMahon and Rodgers 1993; Lievre and Leizorovicz 1995), the use of absolute risk as a guide to individual treatment is generally recommended (JNC 1997; Boissel 1998; Chalmers 1999; Ogden et al 2000). With most treatments in cardiovascular prevention, absolute risk reduction is proportional to the baseline risk. Patients with a baseline risk above a pre-defined threshold, with a high probability of experiencing an event, tend to be defined as the therapy target population because they will on average benefit more from antihypertensive therapy than patients at low risk. The decision strategy based on absolute cardiovascular risk has been criticized (Jackson 1994; Levy 1995; Menard and Chatellier 1995; Krakoff 1996; Swales 1996; Zanchetti and Mancia 1996), particularly because age is a major determinant of cardiovascular risk favoring the treatment of elderly population. Yet, the use of RCTs of short-term duration (between 2 and 6 years) may not provide the best basis for a decision concerning long-term preventive therapy, particularly for young or middleage subjects.

Ideally, a prediction of the treatment effect after the average duration of RCTs should be available to define which hypertensive patients should be treated? As long-term RCTs encounter unresolved ethical issues, longterm follow-up after the end of the study has been used to measure the average life prolongation (Cucherat et al 1997; Swedberg et al 1999).

Another way to fill the gap between the evidence from short-term RCTs expressed in terms of risk reduction, and patient expectations of healthy life years, is to extrapolate the available data on treatment benefit to a life-long perspective using national vital statistics, which are regularly employed to measure life expectancy. The objectives of this investigation were to predict the impact of long-term antihypertensive therapy in the prevention of cardiovascular events. To this end we built a simple mathematical model, which takes into account the treatment effect beyond the usual duration of RCTs (life-long treatment for hypertension) and the life expectancy measured from national vital statistics. In addition, we explored the appropriateness of the absolute and relative gain in event-free life expectancy as comprehensive efficacy indices for quantifying the effect of long-term preventive treatment for each age from 40 to 90 years.

Methods

To estimate the rate of cardiovascular (CV) and non CV deaths in a hypothetical US population of untreated hypertensive patients, we used the following procedure: agespecific death rates in the US general population were obtained from national vital statistics (1994), and in untreated hypertensive population they were obtained from the control groups of the Individual Data ANalysis of Antihypertensive drug intervention trials (INDANA) database (Gueyffier et al 1995). This latter group represents a unique cohort of 14 942 untreated or placebo-treated hypertensive patients, aged 26–96 with an average followup of 5 years (Table 1). The INDANA death rate relative to the US death rate was calculated for each age category and summarized over all age groups using the Mantel Haenszel (1959) estimator (no heterogeneity was found between the age groups). US vital statistics were then multiplied by the Mantel Haenszel estimate to extrapolate the death rate in the US untreated hypertensive patients. The same procedure was used to estimate the ratio of the rate of nonfatal events, ie, stroke (ST), coronary heart disease (CHD), and major cardiovascular events (CVE = ST + CHD), from the rate of fatal events in the US general population. An illustrative example is presented in Table 2.

Table 1.

Baseline characteristics of population included in INDANA database

			Number of patients
Study	Follow-up (years)	Treatment allocated	Treated	Control	Male (%)	Age (mean)
MRC1	4.9	Placebo	8700	8654	52	52
EWPHE	4.7	Untreated	416	424	30	72
COOPE	4.4	Untreated	419	465	31	69
SHEP	4.5	Untreated	2365	2371	43	72
STOP	2.1	Untreated	812	815	37	76
MRC2	5.8	Placebo	2183	2213	42	70

Abbreviations: INDANA, Individual Data ANalysis of Antihypertensive drug intervention trials.

Table 2.

Illustrative example of calculation method

Age	INDANA hypertensive population stroke non fatal ratea	US stroke fatal rate	SMR	Estimated non fatal stroke rate in US untreatedb	Estimated non fatal stroke rate in US treatedc
26–50	0.00083	0.00007	11.03	0.00029	0.00018
51–60	0.00308	0.00037	8.35	0.00145	0.00090
61–70	0.00808	0.00099	8.14	0.00391	0.00242
71–93	0.01270	0.00576	2.21	0.02269	0.01407

^aRate for 100 000 patients per year.

^bNon fatal stroke rate in US untreated population was obtained by multiplying US fatal stroke rate by Mantel Haenzsel estimator (= 3.94).

^cNon fatal stroke rate in treated population was obtained by multiplying the rate in untreated population by the hazard ratio (= 0.62).

Abbreviations: INDANA, Individual Data ANalysis of Antihypertensive drug intervention trials; SMR, standardized mortality ratio.

The risk of death or cardiovascular events over time in the US hypertensive population was then estimated using the life-table method. Disease-free survival curves (ST, CHD, and CVE) were built from 40 years until all patients died (arbitrarily fixed at 101 years).

The treatment effect (hazard ratio) estimated from the control and treated group of INDANA was applied to this disease-free survival curve to obtain the disease-free survival curve of the life-long treated population. The treatment effect was considered constant over time.

The gain in life expectancy without ST, CHD, and CVE was estimated from the area between the two survival curves of treated and control groups (Naimark et al 1994). The relative gain in life expectancy was defined as the ratio of gain in life expectancy to life expectancy.

The secular trends in mortality rates in the US were integrated into our model using a linear regression model (R² = 0.89, p < 0.001) estimated from the US census (US DHHS 1995) of 1975–1997. The final models and estimators used in our simulation are presented in Appendix 1.

As the quality of reporting cause of death is dubious, a sensitivity analysis was performed to measure the possible impact of such classification errors in the estimation of GLE by our method. The GLE was estimated assuming an overestimation of 25% in cardiovascular death certification (Lloyd-Jones et al 1998; Coady et al 2001). (Simulations were carried out using Mathematica™ software.)

Results

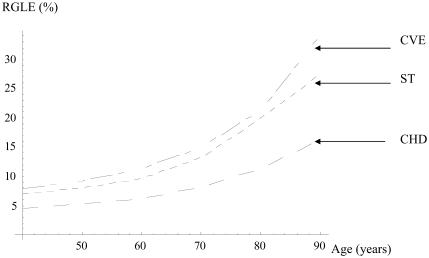
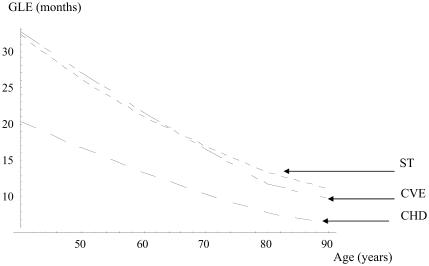
Results of the simulation are presented in Table 3. They show a modest GLE without CHD and a more substantial GLE without ST or CVE in both sexes. When hypertension is diagnosed and treated in a man at 40 years of age, the GLE is 20 months without CHD, 32 without ST, and 33 without CVE. These gains decrease slowly with increasing age at the beginning of the treatment. At 70 years, the GLE is 10 months without CHD and 17 months without ST. However, the relative gain in life expectancy (RGLE) increases with age. The RGLE without stroke for men rises from 7% at 40 to 13% at 70 years. Figures 1 and 2 illustrate how the GLE decreases and the RGLE rises with increasing duration of treatment in men.

Table 3.

Absolute and relative gain in life expectancy without events

		Age at treatment initiation
		40 years		50 years		60 years		70 years
		Women	Men	Women	Men	Women	Men	Women	Men
CHD	GLE (months)	9.0	20.3	10.0	16.6	10.6	13.3	10.3	10.3
	RGLE (%)	2.0	4.5	2.7	5.18	3.7	6.2	5.2	8.1
Stroke	GLE (months)	14.2	32.2	15.7	26.0	16.5	21.0	16.2	16.9
	RGLE (%)	3.1	7.0	4.3	7.9	5.9	9.6	8.5	13.2
CVE	GLE (months)	19.2	32.6	21.3	27.0	22.1	21.5	21.3	16.5
	RGLE (%)	4.3	7.8	5.9	9.2	8.4	11.2	11.5	15.0

Abbreviations: CHD, coronary heart disease; CVE, cardiovascular events; GLE, gain in life expectancy without events; RGLE, relative gain in life expectancy without events.

Figure 1.

Relative gain in event-free life expectancy (RGLE) (%) in men. Abbreviations: CVE, cardiovascular events; ST, stroke; CHD, coronary heart disease.

Figure 2.

Gain in event-free life expectancy (GLE) in men (months). Abbreviations: CVE, cardiovascular events; ST, stroke; CHD, coronary heart disease.

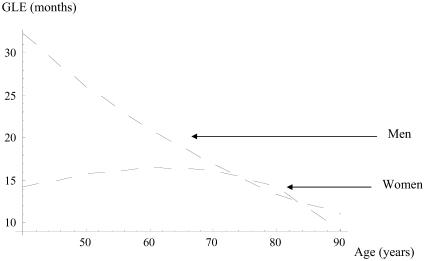
Both GLE and RGLE are higher in men than in women. Gains are generally modest in women for all outcomes (Table 2). On the other hand, as shown in Figure 3, when comparing the GLE without stroke between men and women, the GLE in women reaches a peak at 70 years, then decreases.

Figure 3.

Gain in life expectancy (GLE) without stroke (months).

In Tables 3 and 4, we compare the usual efficacy indices, ie, relative risk and absolute risk reduction computed after 10 years of treatment with the assumption of a constant treatment effect over time, with the GLE and RGLE at different ages in men. A 40-year-old man treated for hypertension has a relative risk of stroke of 0.80, an absolute benefit of 0.4% after 10 years, a GLE of 32 months or a RGLE of 6% without stroke for his whole life. The absolute benefit increases up to 6% and the GLE decreases to 15 months when hypertension is diagnosed and treated at 70 years.

Table 4.

Comparison between traditional efficacy indexes, Gle and RGle in men

	Coronary heart disease					Stroke
Age (years)	RRa	ABb (%)	NNTc	GLEd	RGLEe (%)	RR	AB (%)	NNT	Gle (months)	RGle
40	0.86	0.3	333	20	4.1	0.80	0.4	250	32	5.9
50	0.88	1.0	100	17	4.3	0.84	1.0	100	26	5.7
60	0.90	1.9	53	13	3.4	0.86	2.3	44	21	7.1
70	0.91	3.9	26	10	5.4	0.87	5.7	18	17	9.1

^aRelative risk at 10 years.

^bAbsolute benefit at 10 years.

^cNumber needed to treat to avoid one event.

^dGain in life expectancy in months without events.

^eRelative gain in life expectancy without events.

Sensitivity analysis

More than 99% of deaths occurring in the US are registered (US DHHS 1994). Thus, to perform a sensitivity analysis we took into account the possible misclassification of cause of death that occurred in the 1990s ten-year census. We assumed 25% overestimation in death from stroke, CHD, and CVE (stroke and CHD) classifications. The misclassification of cardiovascular causes of death had no major influence on the results (Table 5). The maximum variation observed in measured GLE was 3 months.

Table 5.

Sensitivity analysis for gain in life expectancy (months)

	Female age (years)				Male age (years)
	40	50	60	70	40	50	60	70
Stroke
Without misclassification	14.2	15.7	16.5	16.2	32.2	26.0	21.0	16.9
25% overestimation	16.7	18.7	19.1	18.5	29.3	23.7	19.2	15.5
CHD
Without misclassification	9.0	10.0	10.6	10.3	20.3	16.6	13.3	10.3
25% overestimation	9.5	10.3	10.3	9.6	21.2	17.2	13.8	10.8
Cardiovascular events
Without misclassification	10.5	11.8	12.4	10.7	32.6	27.0	21.5	16.5
25% overestimation	18.2	20.1	20.8	20.2	32.1	25.8	20.9	16.8

Abbreviations: CHD, coronary heart disease.

Discussion

We extrapolated a hypothetical US untreated hypertensive population from national vital statistics and individual patient data of untreated or placebo treated participants in RCTs. To estimate the GLE without cardiovascular events achieved with antihypertensive therapy we applied the treatment effect estimated from RCTs to these hypertensive patients.

National vital statistics are widely available and are used to measure the life expectancy of populations with life-table methods. However, one limitation of this approach is that cross-sectional data are used longitudinally (life-table method); ie, as if the rate for a 40-year-old individual after 20 years follow-up was the same as the one of a 60-yearold 20 years ahead. This computation assumes the absence of any secular trend. To decrease the impact of this drawback, we took into account the secular trends in all death rates from 1975 to 1997 in the US population. When available, cohort studies on secular trends can determine precisely whether age has the same effects on CV risk for those born in different decades (Lloyd-Jones et al 1999; Lloyd-Jones et al 2004), and their results could then be integrated into our model.

Extrapolating the risk of death or cardiovascular events in the general population from the control group of participants in RCTs, could also lead to unrealistic results, because study populations included in RCTs are not entirely representative of the population at risk. However, INDANA is a unique database because it includes data about hypertensive, untreated, or placebo-treated patients that are followed-up for on average five years. This provides the most reliable available measurement of the hazard of cardiovascular events.

Previous analyses with similar aims are based on the isotropy hypothesis. This hypothesis asserts that the preventive effect of antihypertensive or hypocholesterolemic treatments on clinical events is solely and entirely explained by the risk factor reduction (Taylor et al 1987; Tsevat et al 1991; Grover et al 1998; Ulrich et al 1999, 2000; Montgomery et al 2003). For instance, Tsevat et al (1991) have reported that reducing diastolic blood pressure to 88 mmHg if >88 mmHg will lead to 13 months GLE in a 35-year-old male. However, the isotropy hypothesis seems not to hold true in hypertension (Gueyffier and Boissel 1999). Our approach, assessing a patient's GLE by multiplying the baseline risk of death or cardiovascular events, by the treatment effect (hazard ratio) estimated from a systematic overview, performed on a large individual patient database, seems more realistic (Boissel et al 1998). With our method the estimated CHD-free GLE in a 35-yearold man is 22 months.

Further analyses must assess the impact of treatment-time interaction over the length of follow-up as well as the trend of hypertension self-aggravation (Psaty et al 1997). Variation of the treatment effect seems to be significant for stroke (Boutitie et al 1998) and vary between different classes of antihypertensives (ALLHAT 2002). However, because we were not able to quantify this variation, we considered the treatment effect constant over time. In a hypothetical hypertensive French population, an arbitrary increase or decline of treatment effect could highly influence the GLE (Kassai et al 2001).

To predict the benefit of starting treatment early, we must also take into account the risk associated with the history of hypertension. For instance, in the female subgroup, one cannot conclude that the GLE does not vary significantly, no matter what age treatment is begun.

The robustness of our results to sensitivity analysis for misclassification of causes of death shows that the use of largely available life-table data can be generalized to forecast gain in life expectancy, taking into account competing risks and population particularities.

Our results highlight two major consequences of longterm preventive therapy: first, the gain in life expectancy declines and the relative gain in life expectancy rises with age. These results balance guidelines based solely on the absolute risk in the decision-making process. Second, our simulation demonstrates the difficulty in estimating the benefit of long-term therapy in low-risk (young) patients, by short-term RCTs.

We believe that the absolute and RGLE calculated by our simple method is a relevant decision tool, when correctly understood by the patient and their healthcare providers (Naimark et al 1994). These tools should be available in daily practice through tables or a simple pocket calculator. The GLE seems more relevant to describe long-term benefit from preventive therapy than relative risk or absolute benefit (Wright and Weinstein 1998; Tan and Murphy 1999). At least, they helpfully complete the use of absolute benefit expected from various therapies, recommended in recent guidelines. There are few data available on whether the results of RCTs expressed in terms of probability of successful treatment could facilitate shared decision making (Barry et al 1995; Lenert and Cher 1999). Further work is needed to determine whether patients and healthcare providers correctly understand these efficacy indices.

Appendix 1

Mathematical model used for estimating the hazard of death or event in US hypertensive population.

$$\hat{\rho }=\frac{\sum _{x=1}^g\frac{k_{2}x{m}_{1}x}{Mx}}{\sum _{x=1}^g\frac{k_{1}x{m}_{2}x}{Mx}}$$

$\hat{\rho }$ = Mantel Haenszel estimator (mean weighted rate ratio between INDANA and US population)

k₁x = number of events in INDANA in age group x

m₁x = number of participants in US population in age group x

k₂x = number of events in US population in age group x

m₂x = number of participants in INDANA in age group x

Mx = m₁x + m₂x

Hazard Model used for estimating the hazard of death or event in US hypertensive

$$h_0\left(t\right)=({\hat{\rho }}_1\times h_0(t\left)NCV\right)+({\hat{\rho }}_2\times h_0(t\left)CV\right)+({\hat{\rho }}_3\times h_0(t\left)SCD\right)+f\left(t\right)$$

$$h_1\left(t\right)=({\hat{\rho }}_1\times h_0(t\left)NCV\right)+({\hat{\rho }}_2\times h_0(t)CV\times h{r}_1)+({\hat{\rho }}_3\times h_0(t)SCD\times h{r}_2)+f\left(t\right)$$

Where:

h₀(t) = Hazard of death or event in control group

h₁(t) = Hazard of death or event in treated group

h₀(t)ncv = Hazard of non cardiovascular death in US population

h₀(t)cv = Hazard of cardiovascular death in US population

h₀(t)scd = Specific causes of death i.e. Stroke, Coronary Heart diseases, Cardiovascular events

hr₁ = Hazard ratio estimated from INDANA for CV death

hr₂ = Hazard ratio estimated from INDANA for nonfatal CVE

${\hat{\rho }}_1$ = Weighted rate ratio between cardiovascular death in INDANA and cardiovascular death in US population

${\hat{\rho }}_2$ = Weighted rate ratio between non cardiovascular death in INDANA and non cardiovascular death in US population

${\hat{\rho }}_3$ = Weighted rate ratio between non fatal events (ST, CHD, CVE) in INDANA and fatal events (ST, CHD, CVE) in US population

f(s) = Linear function taking into account the secular trend in mortality over time

Abbreviations: INDANA, Individual Data ANalysis of Antihypertensive drug intervention trials; CHD, coronary heart disease; ST, stroke; CVE, cardiovascular events.