Abstract
During the past years there has been increasing interest in the development of cardiovascular disease functions that predict future events at individual level. However, this effort has not been so far very successful, since several investigators have reported large differences in the estimation of the absolute risk among different populations. For example, it seems that predictive models that have been derived from US or north European populations overestimate the incidence of cardiovascular events in south European and Japanese populations. A potential explanation could be attributed to several factors such as geographical, cultural, social, behavioral, as well as genetic variations between the investigated populations in addition to various methodological, statistical, issues relating to the estimation of these predictive models. Based on current literature it can be concluded that, while risk prediction of future cardiovascular events is a useful tool and might be valuable in controlling the burden of the disease in a population, further work is required to improve the accuracy of the present predictive models.
Keywords: cardiovascular disease, risk, models
Introduction
The statistical prediction of cardiovascular risk has received increased attention in recent years. The main goal of these prediction models has been to identify individuals at high-risk for a cardiac event and therefore, to identify patients who are likely to benefit from aggressive preventive treatment. Based on these models risk charts have been incorporated into guidelines for the prevention of cardiovascular disease and for treating risk factors (NCEP 2002; BCS et al 2003; De Backer et al 2003). Undoubtedly, risk modeling is an area with great opportunities for research and for the development of significant improvements in the efficiency of healthcare delivery. However, it should be underlined that the field of risk prediction is vast and the quality and focus of studies are broad and variable. Although the set of risk factors associated with cardiovascular disease is consistent between studies, some investigators advocate that the effort of risk prediction has not been very successful so far, because of the inaccuracy of forecasts, as well as of the problems observed by several investigators in daily clinical practice (Sing et al 1992; Haq et al 1999; Liao et al 1999; Menotti, Lanti, et al 2000; Menotti, Puddu, et al 2000; Pyorala 2000). A potential explanation was attributed to several factors such as geographical, cultural, social, behavioral, and genetic peculiarities between the investigated populations (Sing et al 1992; Haq et al 1999; Menotti, Lanti, et al 2000; Menotti, Puddu, et al 2000; Pyorala 2000). These differences among populations are of even greater epidemiologic interest than a major shift in the pattern of mortality within a particular population because of the added dimension of variation between populations. This review deals with the methodology of predictive risk models, the basic concept of the most widely used cardiovascular disease risk charts in primary prevention, as well as providing an evaluation of the efficiency of these models between different populations.
Available methods
Before discussing and comparing findings from the most widely used coronary heart disease (CHD) risk models and charts, an introduction to the theory of these models is appropriate. An often-used predictive risk model is the logistic regression model (Hosmer and Lemeshow 1989; Rothman and Greenland 1998). Once we have the model we can take the exponent of the regression model solution, which converts log-odds to odds and then converts the odds to the probability that an event will occur, ie, p=odds/(1 + odds). Although the logistic regression model is very often used in the epidemiologic research, it should be noted that the model does not take into account the time of an event to occur.
A predictive risk model that incorporates time is the Cox Proportional Hazards model (Kleinbaum 1996). The mathematical form of the hazard function that is used in the aforementioned model is the following:
where Z is a set of variables (X's) that considered as potential predictors of the event. Using this model and a minimum of assumptions (ie, proportionality of hazards) we can obtain the primary information desired from a risk prediction analysis, ie, hazard (risk) ratio and survival curves.
The models mentioned above have extensively been used in the development of risk charts of a disease, while other models, like the Weibull model, have rarely been applied in the production of charts (Kleinbaum 1996). Weibull models assume a particular form of probability distribution for the survival times (Weibull distribution) and this imposes a particular parametric form on h0(t) (baseline hazard function at time t), while in the Cox regression model the form of h0(t) is unspecified. The hazard of an event occurring at time t for the ith individual is given by the function:
where h0(t) = λγtγ−1 and Z is a set of variables (X's) that are considered as potential predictors of the event.
All the aforementioned risk models are based on classical statistical methods. To overcome the limitations that occurred in the previous models, other investigators proposed the use of decision-making algorithms (like the Classification And Regression Tree [CART]) and a multilayer perception (MLP) approach in order to predict cardiovascular risk [Colombet et al 2000]). CART analysis is a tree-building technique. For applying this analysis, one must have: a categorical outcome as “dependent” variable, “predictor”, or “independent” variables, a dataset, and a “prior” probability for each outcome. This tree consists of nodes containing a particular group of patients and each node can only be split into two others until each one contains only one patient or all patients are included in each node so to have the same distribution on independent variables. Each node is assigned a predicted class based on the assumed prior probability of each class, the decision loss or cost matrix, and the fraction of subjects with each outcome in the dataset that end up in each node. Some other investigators also used neural networks to predict future cardiovascular events (Voss et al 2002). They evaluated whether probabilistic neural networks improved the risk estimate of coronary events in the Prospective Cardiovascular Munster Study (PROCAM) compared with the classical logistic regression and MLP. The accuracy of the MLP was greater than that of the probabilistic neural networks (89.7% vs 87.2%), and both exceeded the accuracy for logistic regression (ie, 84.0%). Probabilistic neural networks, supervised networks that provide general solutions to a pattern classification problem, utilize larger numbers of coefficients, and take into account complex nonlinear relationships that exist within the data; therefore, they can produce a model of greater discrimination and a more accurate estimation of risk than classical statistical approaches.
Predictive risk models in cardiovascular disease epidemiology
The Framingham Heart Study models
The most well known predictive risk charts in cardiovascular disease prevention are the Framingham Heart Study models. The Framingham Heart Study (Kannel et al 1976; Wilson et al 1998) is one of the most important epidemiological studies that have been designed as a prospective, single-center study in the setting of a community-based cohort (ie, Framingham, US). The Framingham coronary prediction algorithm provides estimates of myocardial infarction, CHD, death from CHD, stroke, cardiovascular disease, and death from cardiovascular disease, over the course of 10 years (Anderson et al 1991). However, it has also been stated that the risk estimating scores were only for persons without known heart disease, the algorithm encompasses only CHD, and the population was almost all Caucasian and therefore may not map over other populations (Wilson et al 1998). Many physicians and public health policy makers have used the risk models in daily clinical practice and research since their first presentation.
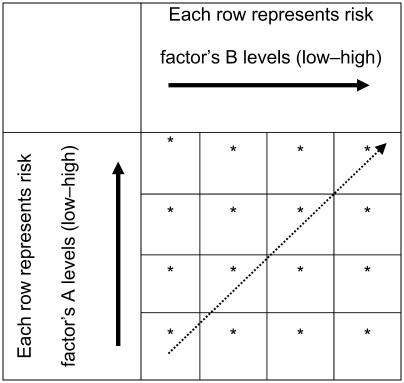
In the early 1990s, European recommendations on CHD prevention adopted the 10-year Framingham Heart Study equations. These equations were presented in a form of a Coronary Risk Chart (Pyorala et al 1994). The chart consisted of a table, where each entry concerns the levels of a risk factor and the content of each cell is the absolute risk level (Table 1). A few years later a colorful version of these charts were included in the European Society of Cardiology, European Atherosclerosis Society, European Society of Hypertension, International Society of Behavioural Medicine, European Society of General Practice/Family Medicine, European and Heart Network task force report (SJTFES 1998). More recently, Framingham projections of 10-year absolute CHD risk were used in Adult Treatment Panel III guidelines in order to identify certain patients with multiple (2+) risk factors for more intensive treatment (NCEP 2002).
Table 1.
Sample of a risk chart
Note: *Each cell represents the absolute risk for developing a disease.
Other risk models in the cardiovascular field
Several other investigators have attempted to evaluate cardiovascular risk through local studies (Assmann et al 1998; Menotti, Lanti, et al 2000). Menotti and colleagues (2000) predicted the risk for future CHD based on the sixteen cohorts of the Seven Countries Study. In particular, risk charts, based on age, smoking habit, levels of systolic blood pressure and total serum cholesterol, were constructed separately for northern and southern Europe, with estimated probabilities for the occurrence of CHD events over 10 years.
The PROCAM study (Assmann et al 1998) also produced risk algorithms and neural networks. Another well-known risk model is the “Dundee risk function” (Tunstall-Pedoe 1991), which measures modifiable CHD risk from smoking, blood pressure and blood cholesterol concentration, by sex and age. Moreover, Shaper and colleagues (1986) produced risk functions from the British Regional Heart study (BRHS) based on cigarette smoking, mean blood pressure, recall of ischemic heart disease or diabetes mellitus, history of parental death, and the presence of angina.
During 2000, a matched for age, sex, and region case-control study (the CARDIO2000 study) was conducted in Greece. Among others, the study's investigators have estimated a “predictive risk” model through the odds of developing non-fatal acute coronary syndromes (Panagiotakos et al 2002). This model included conventional cardiovascular risk factors (hypertension, hypercholesterolemia, diabetes mellitus, smoking, and sedentary life), as well as the effect of low educational status, the presence of short term depressive episodes, and the adoption of Mediterranean diet and alcohol consumption. The CARDIO2000 model included much more risk factors than the previously mentioned models (Panagiotakos et al 2002). It is possible that these factors add to the explanatory ability of the predicted model, as well as to its accuracy. However, only the prospective evaluation of the study's participants could confirm or refute the previous speculations.
Recently Yusuf and colleagues (2004) from the INTERHEART study presented a model that estimates the risk for non-fatal CHD, using data from 15 152 cases and 14 820 controls in 52 countries around the world. However, the cross-sectional design of this large case-control study cannot provide accurate measurements of the absolute or relative risk, but it can provide some information about the hierarchy of the risk factors.
Both INTERHEART and CARDIO2000 studies were case-control studies and it could be claimed that estimation of the relative risk through the odds ratios may be inappropriate.
The Systematic Coronary Risk Evaluation (SCORE) Project
The working group on epidemiology and prevention of the European Society of Cardiology conducted a research project for the development of risk prediction charts based on data from 12 European cohort studies (the SCORE project) (Conroy et al 2003). The outcome that was investigated in the latter study was cardiovascular mortality among 205 000 persons. During 2.7 million years of follow up 5652 deaths from CHD were observed. The estimated 10-year risk prediction model was based on the Weibull function. Age was used in this model as a measure of exposure time to risk, rather than a risk factor, as it has been done in log-linear models. This may improve the estimating ability of the model. Age and sex specific risk charts were developed based on cholesterol, smoking, and systolic blood pressure levels, separately for high and low risk European populations (ie, Northern and Southern cohorts). These risk charts were incorporated into the third European guidelines on cardiovascular prevention (Conroy et al 2003). The separation of the European countries as high and low risk was ingenuous. However, the inclusion of only 12 cohorts may raise several concerns about the suitability of the developed risk charts to estimate risk in various European populations.
Problems in estimating cardiovascular risk
Concerns exist when generalization of different predictive risk models for a specific population has been applied to the population at large. It is recognized that there are two elements that describe the reliability of risk prediction tools: calibration and discrimination.
Calibration
Calibration measures how closely predicted outcomes agree with actual outcomes. The Hosmer-Lemeshow χ2 statistic was the most widely used test for assessing the fit of predictive model on data (D'Agostino et al 2001; Brindle et al 2003; Liu et al 2004; Cooper et al 2005). A number of analyses have been conducted to evaluate the performance of Framingham functions in non-Framingham populations. D'Agostino and colleagues (2001) examined the validity of Framingham risk function for predicting absolute CHD risk in several US cohorts. Such analyses have revealed that the latter model overestimates the risk of 5-year CHD events in Japanese-American and Hispanic men and Native American women. Moreover, a recently published study demonstrates that Framingham CHD risk functions overestimate the absolute CHD risk in a large Chinese population (Liu et al 2004). Regarding the performance of Framingham functions on European populations, it has been observed that they overestimate CVD risk in low-risk southern European populations (Laurier et al 1994; Menotti, Puddu, et al 2000; Bastuji-Garin et al 2002; Empana et al 2003; Marrugat et al 2003). In Northern European populations, older studies suggested that Framingham functions predict with accuracy the number of observed CHD events (Schulte and Assmann 1991; Haq et al 1999; Ramachandran et al 2000). However, recently validation studies have shown that Framingham point-scoring systems overestimate the individual risk of CHD in a representative British population enrolled in the BRHS (Brindle et al 2003), as well as in healthy UK men from the second Northwick Park Heart study (NPHS-II) (Cooper et al 2005) and in a Denmark population (Thomsen et al. 2002).
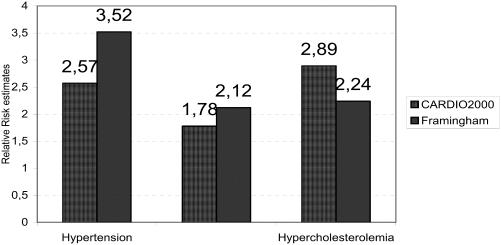
Based on the results from the follow up of the Seven Countries Study, Menotti, Lanti, and colleagues (2000) have found that the absolute risk was overestimated when applying the northern European model to southern European populations and vice versa, with ratios of about 1.5 and 0.5, respectively. When a hypothetical variable identifying areas in the risk model for hard coronary events was used, it gave a relative risk of 0.57 for southern Europe compared with northern Europe, which is in line with the ratio of observed to-expected cases (Menotti, Lanti, et al 2000). Furthermore, based on the risk charts for northern and southern Europe, it was observed that the probabilities of an event were systematically greater for northern Europeans than for southern Europeans, when the other factors remained constant (Menotti, Lanti, et al 2000). It is interesting that these differences in the incidence were not attributed to the differences in the incidence of the various manifestations of CHD (ie, fatal, hard, and mild) since the analysis showed that the ratios between each pair of the disease were practically the same within each region. Moreover, homogeneity analysis showed that these differences in absolute risk were not due to the differences observed in the baseline cardiovascular risk factors levels observed between the cohorts of the Seven Countries Study. An overestimation of absolute risk has also been identified using PROCAM risk functions for individual risk of CHD in UK men in the Second Northwick Park Heart Study and in men from Belfast as well as France (Empana et al 2003; Cooper et al 2005). Moreover, in a Greek sample of about 1000 cardiac patients and 1000 matched controls (Panagiotakos et al 2002), the point estimates of the relative risks of CHD events due to hypertension, hypercholesterolemia, and smoking habits, as calculated by the Framingham Risk model (SJTFES 1998), were overestimated by 36% for hypertension, by 19% for smoking, and underestimated by 29% for hypercholesterolemia in comparison with the CARDIO2000 risk model (Figure 1). However, it should be mentioned that the CARDIO2000 study is a retrospective one, thus recall bias may exist and overestimation of the risk may be a result of this bias.
Figure 1.
Comparisons between relative risk estimates for coronary heart disease events by hypertension, hypercholesterolemia status, and smoking habits.
To explain the inaccuracy in predictive risk models, some investigators claimed that it could attribute to the differences in the incidence (ie, absolute risk) of CHD between populations (Menotti et al 2000). In particular, the link between hazard ratios derived from Cox proportional hazards models and estimation of absolute risk is dependent on some form of “reference” level of risk (ie, average cardiovascular disease free survival of the population from which the model was derived). Thus, if the average survival varies between populations, then the prediction of absolute risk will also vary. This also assumes that the hazard ratios are homogenous between populations, an assumption which may not be correct. Reports from the World Health Organization confirm the variability of the absolute risk of cardiovascular diseases worldwide (Labarthe 1998; WHO 2002). It has been suggested that a calibration on the constants of the models be produced (ie, lambda [t]) to resolve the problem of estimating absolute risk. However, to achieve such a goal the incidence of an event in each population must be known. Therefore, the development of local epidemiological studies is considered essential. Other potential explanations can attribute to genetic differences (Sing et al 1992), eating habits, social and behavioral characteristics, or several unmeasured or unknown factors that prevail among populations. Finally, it is believed that interactions between the risk factors levels and several environmental conditions may cause the dispersion of the predictive models, at population level (Pyorala 2000).
On the other hand, it should be noted that others have suggested that there are no differences regarding the predictive ability of the cardiovascular risk models. For example Liao et al (1999) reported that the Framingham Heart Study score for the prediction of coronary mortality rates provides a reasonable rank ordering of risk for individuals in the US white population for the period 1975 to 1990. The investigators compared predictive CHD risk models derived from the major risk factors from Framingham and two more recent national cohorts: the first and second National Health and Nutrition Examination Surveys. It was revealed that significant heterogeneity existed among studies in the magnitude of the coefficients for individual factors (Liao et al 1999). However, when risk factors were considered together and applied to different cohorts, a similar ability to rank individual risk was observed. Similar results have been reported by Haq et al (1999) when coronary risk estimates for individuals derived from the Framingham, the PROCAM, Dundee, and British Regional Heart Study risk functions were compared.
Discrimination
Discrimination is the ability of analysis to assign, on average, a higher probability of an event to those who go on to experience an event, compared with those who do not. In most studies, this ability was quantified by calculating the C-statistic, analogous to the area under a receiver operating characteristic (ROC) curve. If C-statistic is 0.5, this means that the tool has no discriminatory ability and as it approaches 1, this ability improves. Most studies have shown that Framingham-based tools discriminate risk well in different populations (C-statistic>0.6), probably because the hazards of individual risk factors are broadly similar (D’Agostino et al 2001). For example, D'Agostino and his colleagues (2001) found that the area under the operating characteristic curve was between 0.63 and 0.83 using Framingham functions in different cohorts. Moreover, Hense and colleagues (2003) demonstrated that the area under the ROC curve was 0.78 and 0.73 for men in Monitoring of Trends and Determinants in Cardiovascular Disease (MONICA) Augsburg cohorts and PROCAM cohort, respectively, while the respective values for women were 0.88 and 0.77. The discriminatory ability of Framingham functions was found to be good in the Chinese population (C-statistic: 0.705 and 0.742 for men and women, respectively) (Liu et al 2004). When Framingham CHD risk functions were applied to men recruited in Belfast and France, the C-statistic was found to be 0.66 for the former and 0.68 for the latter, while using PROCAM risk model in the same cohorts, the area under the ROC curve was 0.61 and 0.64, respectively (Empana et al 2003).
The role of age and treatment in risk prediction
Another issue that needs further attention is the role of age in risk assessment. Until now, most investigators used age as a risk factor in the prediction of future cardiovascular events. In the past few years, it has been suggested to use age not as a single risk factor, but as a “condition at risk”. In other words, some investigators believe that predictions could be improved when we stratify for age and not account for it (Ridker and Cook 2005). By this approach the interaction between aging and various socio-demographic, lifestyle, and clinical conditions could be evaluated at individual as well as population setting (Ridker and Cook 2005). Therefore, a person that is currently experiencing low risk for cardiovascular events (ie, <2%), may substantially have an increased risk if he/she continues to have the same adverse health profile for the next years. Labeling such an individual as a high-risk would be a serious public health error (Brindle et al 2003).
Perspective
Estimation of CHD and other cardiovascular events is a dynamic field in epidemiological research. Risk estimation is also an important tool in primary and secondary prevention as it can be used to expedite the initiation of lifestyle changes or the use of an appropriate therapeutic intervention or both. The production of a single chart for the prediction of risk of CHD is still problematical when estimation from one population is applied to another. Most limitations in this field could be due to: (a) the existence of unknown risk factors and incidence rates of the disease, (b) factors that are not measured in some studies, and (c) factors that are difficult to reproduce in the everyday activity. Moreover, the presently used log-linear models are probably inadequate since they cannot accommodate many covariates and, mainly, highly correlated covariates, age should be used as a “risk condition” and not as a risk factor, and the linearity of these models for CHD risk prediction should be further evaluated. More national studies are needed and further methodological work should be carried out in the field of biostatistics and epidemiology to accurately estimate the incidence of cardiovascular disease in various populations. The cost of developing local, large scale, observational studies for the production of risk models might be high, but we strongly believe that the economic benefits for the health system and the society from the early detection of people “at risk” through these models may overlap the aforementioned cost. A challenge to healthcare policy makers is how to develop “front-end” tools based on these risk prediction models that can be integrated successfully into primary healthcare.
Acknowledgments
We would like to thank Miss Georgia Kurlaba for her assistance in reviewing some of the papers used in this work.
References
- Anderson KM, Odell PM, Wilson PW, et al. Cardiovascular disease risk profiles. Am Heart J. 1991;121:293–8. doi: 10.1016/0002-8703(91)90861-b. [DOI] [PubMed] [Google Scholar]
- Assmann G, Cullen P, Schulte H. The Munster Heart Study (PROCAM) – Results of follow-up at 8 years. Eur Heart J. 1998;19:A2–11. [PubMed] [Google Scholar]
- Bastuji-Garin S, Deverly A, Moyse D, et al. The Framingham prediction rule is not valid in a European population of treated hypertensive patients. J Hypertens. 2002;20:1973–80. doi: 10.1097/00004872-200210000-00016. [DOI] [PubMed] [Google Scholar]
- Brindle P, Emberson J, Lampe F, et al. Predictive accuracy of the Framingham coronary risk score in British men: prospective cohort. BMJ. 2003;327:1227–33. doi: 10.1136/bmj.327.7426.1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [BCS] British Cardiac Society, British Hypertension Society, Diabetes UK. JBS 2: Joint British Societies' guidelines on prevention of cardiovascular disease in clinical practice. Heart. 2003;91(Suppl 5):v1–52. doi: 10.1136/hrt.2005.079988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colombet I, Ruelland A, Chatellier G, et al. Models to predict cardiovascular risk: comparison of CART, multilayer perception and logistic regression. Proc AMIA Symp. 2000;1:156–60. [PMC free article] [PubMed] [Google Scholar]
- Conroy RM, Pyorala K, Fitzgerald AP, et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24:987–1003. doi: 10.1016/s0195-668x(03)00114-3. [DOI] [PubMed] [Google Scholar]
- Cooper JA, Miler GJ, Humphries SE. A comparison of the PROCAM and Framingham point-scoring systems for estimation of individual risk of coronary heart disease in the Second Northwick Park Heart Study. Atherosclerosis. 2005;181:93–100. doi: 10.1016/j.atherosclerosis.2004.12.026. [DOI] [PubMed] [Google Scholar]
- D'Agostino RB, Grundy S, Sullivan LM, et al. CHD Risk Prediction Group. Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA. 2001;286:180–7. doi: 10.1001/jama.286.2.180. [DOI] [PubMed] [Google Scholar]
- De Backer G, Ambrosioni E, Borch-Johnsen K, et al. Executive summary. European guidelines on cardiovascular disease prevention in clinical practice. Third Joint Task Force of European and other Societies on Cardiovascular Disease Prevention in Clinical Practice (constituted by representatives of eight societies and by invited experts. Eur Heart J. 2003;24:1601–10. doi: 10.1016/s0195-668x(03)00347-6. [DOI] [PubMed] [Google Scholar]
- Empana JP, Ducimetriere P, Arveiler D, et al. Are the Framingham and PROCAM coronary heart disease risk functions applicable to different European populations? The PRIME study. Eur Heart J. 2003;24:1903–11. doi: 10.1016/j.ehj.2003.09.002. [DOI] [PubMed] [Google Scholar]
- Haq IU, Ramsay LE, Yeo WW, et al. Is the Framingham risk function valid for northern European populations? A comparison of methods for estimating absolute coronary risk in high risk men. Heart. 1999;81:40–6. doi: 10.1136/hrt.81.1.40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hense HW, Schulte H, Lowel H, et al. Framingham risk function overestimates risk of coronary heart disease in men and women from Germany – results from the MONICA Augsburg and the PROCAM cohorts. Eur Heart J. 2003;24:937–45. doi: 10.1016/s0195-668x(03)00081-2. [DOI] [PubMed] [Google Scholar]
- Hosmer D, Lemeshow S. Applied logistic regression. New York: John Wiley & Sons, Inc; 1989. [Google Scholar]
- Kannel WB, McGee DL, Gordon T. A general cardiovascular risk profile: The Framingham Study. Am J Cardiol. 1976;38:46–51. doi: 10.1016/0002-9149(76)90061-8. [DOI] [PubMed] [Google Scholar]
- Kleinbaum D. Survival analysis. New York: Springer–Verlag Inc; 1996. [Google Scholar]
- Labarthe DR. Epidemiology and prevention of cardiovascular diseases. A global challenge. Maryland: Aspen Pub; 1998. [Google Scholar]
- Laurier D, Nguyen PC, Cazelles B, et al. Estimation of CHD risk in a French working population using a modified Framingham model. The PCV-METRA Group. J Clin Epidemiol. 1994;47:1353–64. doi: 10.1016/0895-4356(94)90079-5. [DOI] [PubMed] [Google Scholar]
- Liao Y, McGee DL, Cooper RS, et al. How generalizable are coronary risk prediction models? Comparison of Framingham and two national cohorts. Am Heart J. 1999;137:837–45. doi: 10.1016/s0002-8703(99)70407-2. [DOI] [PubMed] [Google Scholar]
- Liu J, Hong Y, D'Agostino RB, et al. Predictive value for the Chinese population of the Framingham CHD risk assessment tool compared with the Chinese Multi-provincial Cohort Study. JAMA. 2004;291:2591–9. doi: 10.1001/jama.291.21.2591. [DOI] [PubMed] [Google Scholar]
- Marrugat J, D'Agostino R, Sullivan L, et al. An adaptation of the Framingham coronary heart disease risk function to European Mediterranean areas. J Epidemiol Commun Health. 2003;57:634–8. doi: 10.1136/jech.57.8.634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menotti A, Lanti N, Puddu PE, et al. Coronary heart disease incidence in northern and southern European populations: A reanalysis of the seven countries study for a European coronary risk chart. Heart. 2000;84:238–44. doi: 10.1136/heart.84.3.238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menotti A, Puddu PE, Lanti M. Comparison of the Framingham risk function-based coronary chart with a risk function from an Italian population study. Eur Heart J. 2000;21:365–70. doi: 10.1053/euhj.1999.1864. [DOI] [PubMed] [Google Scholar]
- [NCEP] National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III) Third report of the National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, and Treatment of High Blood Cholesterol in Adults (Adult Treatment Panel III). Final report. Circulation. 2002;106:3143–421. [PubMed] [Google Scholar]
- Panagiotakos DB, Pitsavos C, Chrysohoou C, et al. Risk Stratification of Coronary Heart Disease, in Greece: Final Results from CARDIO2000 Epidemiological Study. Prev Med. 2002;35:548–56. doi: 10.1006/pmed.2002.1108. [DOI] [PubMed] [Google Scholar]
- Pyorala K, De Backer G, Graham I, et al. Prevention of coronary heart disease in clinical practice. Recommendations of the Task Force of the European Society of Cardiology, European Atherosclerosis Society and European Society of Hypertension. Eur Heart J. 1994;15:1300–31. doi: 10.1093/oxfordjournals.eurheartj.a060388. [DOI] [PubMed] [Google Scholar]
- Pyorala K. Assessment of coronary heart disease risk in populations with different levels of risk. Eur Heart J. 2000;21:365–70. doi: 10.1053/euhj.1999.1927. [DOI] [PubMed] [Google Scholar]
- Ramachandran S, French JM, Vanderpump MP, et al. Using the Framingham model to predict heart disease in the United Kingdom: retrospective study. BMJ. 2000;320:676–7. doi: 10.1136/bmj.320.7236.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridker PM, Cook N. Should age and time be eliminated from cardiovascular risk prediction models? Rationale for the creation of a new national risk detection program. Circulation. 2005;111:657–8. doi: 10.1161/01.CIR.0000154544.90488.52. [DOI] [PubMed] [Google Scholar]
- Rothman K, Greenland S. Modern epidemiology. New York: Lippincot Williams & Wilkins Pub; 1998. [Google Scholar]
- Schulte H, Assmann G. CHD risk equations, obtained from the Framingham Heart Study, applied to PROCAM Study. Cardiovasc Risk Factors. 1991;1:126–33. [Google Scholar]
- Shaper AG, Pocock SJ, Phillips AN, et al. Identifying men at high risk of heart attacks: strategy for use in general practice. BMJ. 1986;293:474–80. doi: 10.1136/bmj.293.6545.474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sing CF, Haviland MB, Templeton AR, et al. Biological complexity and strategies for finding DNA variations responsible for interindividual variation in risk of a common chronic diseases, CAD. Ann Med. 1992;24:539–47. doi: 10.3109/07853899209167008. [DOI] [PubMed] [Google Scholar]
- [SJTFES] Second Joint Task Force of European and other Societies. Prevention of coronary heart disease in clinical practice. Recommendations of the Second Joint Task Force of European and other Societies on coronary prevention. Eur Heart J. 1998;19:1434–503. doi: 10.1053/euhj.1998.1243. [DOI] [PubMed] [Google Scholar]
- Thomsen TF, McGee D, Davidsen M, et al. A cross-validation of risk-scores for coronary heart disease mortality based on data from the Glostrup Population Studies and Framingham Heart Study. Int J Epidemiol. 2002;31:817–22. doi: 10.1093/ije/31.4.817. [DOI] [PubMed] [Google Scholar]
- Tunstall-Pedoe H. The Dundee coronary risk-disk for management of change in risk factors. BMJ. 1991;303:744–7. doi: 10.1136/bmj.303.6805.744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voss R, Cullen P, Schulte H, et al. Prediction of risk of coronary events in middle-aged men in the Prospective Cardiovascular Munster Study (PROCAM) using neural networks. Int J Epidemiol. 2002;31:1253–62. doi: 10.1093/ije/31.6.1253. [DOI] [PubMed] [Google Scholar]
- Wilson PWF, D'Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97:1837–47. doi: 10.1161/01.cir.97.18.1837. [DOI] [PubMed] [Google Scholar]
- [WHO] World Health Organization. The atlas of heart disease and stroke [online] 2002 Accessed 28 April 2006. URL: http://www.who.int/cardiovascular_diseases/resources/atlas/en/
- Yusuf S, Hawken S, Ounpuu S, et al. Effect of potentially modifiable risk factors associated with myocardial infarction in 52 countries (the INTERHEART study): case-control study. Lancet. 2004;364:937–52. doi: 10.1016/S0140-6736(04)17018-9. [DOI] [PubMed] [Google Scholar]