Linking Neural Representation to Function in Stereoscopic Depth Perception: Roles of the Middle Temporal Area in Coarse versus Fine Disparity Discrimination

Abstract

Neurons selective for binocular disparity form the neural substrate for stereoscopic depth perception and are found in several areas of primate visual cortex. Presumably, multiple representations of disparity exist to serve different functions, but the specific contributions of different visual areas to depth perception remain poorly understood. We examine this issue by comparing the contributions of the middle temporal (MT) area to performance of two depth discrimination tasks: a “coarse” task that involves discrimination between absolute disparities in the presence of noise, and a “fine” task that involves discrimination of very small differences in relative disparity between two stimuli in the absence of noise. In the fine task, we find that electrical microstimulation of MT does not affect perceptual decisions, although many individual MT neurons have sufficient sensitivity to account for behavioral performance. In contrast, microstimulation at the same recording sites does bias depth percepts in the coarse task. We hypothesized that these results may be explained by the fact that MT neurons do not represent relative disparity signals that are thought to be essential for the fine task. This hypothesis was supported by single-unit recordings that show that MT neurons signal absolute, but not relative, disparities in a stimulus configuration similar to that used in the fine task. This work establishes a link between the neural representation of disparity in MT and the functional contributions of this area to depth perception.

Introduction

Neurons selective for binocular disparities form the neural basis of stereoscopic depth perception (Cumming and DeAngelis, 2001). Although early work focused on the primary visual cortex (V1), subsequent studies have described disparity-selective neurons in several extrastriate visual areas (Hubel and Wiesel, 1970; Maunsell and Van Essen, 1983; Burkhalter and Van Essen, 1986; Felleman and Van Essen, 1987; Poggio et al., 1988; Roy et al., 1992; Janssen et al., 2000b; Taira et al., 2000; Uka et al., 2000; Hinkle and Connor, 2001; Thomas et al., 2002; Tsao et al., 2003). Why should binocular disparities be represented in so many areas? One possibility is that each representation of disparity is specialized to serve specific functions, some of which include the localization of objects in depth, three-dimensional (3D) shape perception, scene segmentation, and guidance of eye movements. To clarify the functions of each area, we must examine the contributions that it makes to multiple tasks and relate these contributions to the underlying neural representation.

Previous work suggests that the middle temporal (MT) area is important for coarse discrimination of absolute disparities (DeAngelis et al., 1998; Uka and DeAngelis, 2003, 2004) (“coarse” task). Does this imply that MT is involved in all forms of depth perception? To address this question, we tested whether MT also contributes to fine depth discrimination. Monkeys were trained to discriminate small differences in the relative depth between two adjacent stimuli (“fine” task). This task requires neurons to be sensitive to small differences in disparity, whereas the coarse disparity task requires high sensitivity to image correlation between the two eyes.

We quantified the sensitivity of single MT neurons for discriminating among disparities. In the coarse task, we showed previously that the average MT neuron is as sensitive as the monkey (Uka and DeAngelis, 2003). Despite MT neurons having fairly broad disparity tuning compared with V1 (DeAngelis and Uka, 2003), we show here that many MT neurons also have sufficient sensitivity to account for psychophysical thresholds in the fine task. However, microstimulation of MT does not affect performance of the fine task, whereas microstimulation of the same sites in MT biases depth percepts in the coarse task.

We hypothesized that MT does not contribute to the fine task because MT neurons are selective for absolute, not relative, disparities. Absolute disparity refers to the difference in retinal positions (with respect to the foveae) between corresponding features in the two images, whereas relative disparity is defined as the difference in absolute disparity between two points in a scene (Cumming and Parker, 1999). An explicit neural representation of relative disparities may be needed for fine disparity discrimination because absolute disparities vary with fluctuations in vergence angle whereas relative disparities do not (Westheimer, 1979; Prince et al., 2000). Disparity-selective neurons in V1 code absolute disparities (Cumming and Parker, 1999), whereas a small fraction of V2 neurons signal relative disparities (Thomas et al., 2002). We show here that MT neurons signal absolute, not relative, disparities in a center-surround stimulus configuration. This supports our hypothesis and establishes a link between the neural representation of disparity in MT and the functional contributions of MT to stereoscopic depth perception.

Materials and Methods

Our general experimental procedures have been described in detail previously (DeAngelis and Uka, 2003; Uka and DeAngelis, 2003). Here, we briefly summarize aspects relevant to the present study.

Subjects and surgery

Experiments were performed using three male rhesus monkeys (Macaca mulatta). Two animals participated in recording/microstimulation experiments involving coarse and fine disparity discrimination, and three animals participated in recording experiments to distinguish between absolute and relative disparity coding. Animals were prepared for experiments using standard surgical procedures (Britten et al., 1992; DeAngelis and Newsome, 1999; DeAngelis and Uka, 2003). Scleral coils were implanted in both eyes for monitoring eye position, including both version and vergence (Judge et al., 1980). A cylindrical recording chamber was mounted over the occipital cortex ∼17 mm lateral and 14 mm dorsal to the occipital ridge. The long axis of the chamber resided in a parasagittal plane and was inclined 25° relative to the horizontal plane, such that area MT was accessed after passing through extrastriate visual areas in the lunate sulcus. All animal care and experimental procedures were approved by the Institutional Animal Care and Use Committee at Washington University and were in accordance with National Institutes of Health guidelines.

Visual stimuli

Monkeys sat in a primate chair and faced a flat-screen 22 inch color monitor [SONY (Tokyo, Japan) GDM-F500] placed at a viewing distance of 57 cm. The display subtended a visual angle of 40° × 30° and had a resolution of 1152 × 864 pixels. Random-dot stimuli were presented using an OpenGL accelerator board with quad-buffer stereo support (Oxygen GVX1; 3D Labs, Milpitas, CA). Random-dot stereograms (RDSs) were presented within a circular aperture. Dot density was 64 dots per square degree per second, with each dot subtending ∼0.1°. The starting position of each dot within the aperture was randomized for each trial. Precise disparities and smooth motion were achieved by plotting dots with subpixel resolution using hardware anti-aliasing.

Stereoscopic images were displayed by presenting the left and right half-images alternately at a refresh rate of 100 Hz. The monkey viewed the display through a pair of ferroelectric shutters (DisplayTech, Longmont, CO) that were synchronized to the video refresh such that one shutter was closed while the other was open. To minimize ghosting effects (stereo cross talk was <3%), the RDS consisted of red dots presented on a black background.

All dots within the RDS moved coherently (100% motion coherence) at a velocity tailored to each MT neuron or multiunit cluster. When they reached the boundary of the circular aperture, dots resumed motion from the opposite side of the aperture.

Tasks

Monkeys were required to fixate on a yellow spot (0.15° × 0.15°) within a 1.6° × 1.6° electronic window. In the fixation task, monkeys received a water or juice reward for maintaining fixation throughout the 1.5 s trial. When the monkey's conjugate eye position left the fixation window prematurely, the trial was aborted immediately without reward. In the discrimination tasks, the monkey was required to maintain fixation during stimulus presentation, and then to execute a saccade to one of two targets to signal his choice. Correct responses were rewarded with a drop (0.1–0.15 ml) of water or juice.

Monkeys were trained to perform two depth discrimination tasks (see Fig. 1). In the coarse task (see Fig. 1A), the disparity signal was titrated by manipulating the percentage of binocularly correlated dots in the RDS. Correlated (i.e., signal) dots were assigned one of two fixed disparities (one crossed, one uncrossed) during each trial, and the remaining (noise) dots were assigned random disparities within the range from −2 to 2° (see Fig. 1A, right). Dots retained their identities (signal or noise) throughout a trial; hence, the exact distribution of noise disparities was fixed within a given trial but varied across trials (Uka and DeAngelis, 2003). Monkeys reported whether the signal dots were near (crossed) or far (uncrossed) relative to the fixation point (i.e., they reported the sign of the absolute disparity). The two disparity values for signal dots were chosen based on the tuning of the recorded neurons, one disparity being preferred and the other antipreferred (null). In MT, preferred and null disparities are located on opposite sides of zero disparity in the vast majority of cases (DeAngelis and Uka, 2003); thus, only a few recording sites were discarded because the preferred and null disparities were both crossed or uncrossed. The monkey signaled his depth percept by making a saccade to one of two targets (located 5° below and above the fixation point, respectively) that appeared 200 ms after offset of the RDS (see Fig. 1A). The range of binocular correlations was chosen to bracket the monkey's psychophysical threshold (Uka and DeAngelis, 2003).

Figure 1.

Schematic illustration of the two depth-discrimination tasks. A, The coarse task. A random-dot stereogram was presented within a circular aperture over the receptive field (RF), and dots moved at the preferred velocity of the neuron (arrow). Filled and open dots represent left and right half images, respectively. The background was filled with dynamic zero-disparity dots (gray). Saccade targets were located 5° above and below the fixation point, corresponding to far and near choices, respectively. The strength of the depth signal was adjusted by varying binocular correlation. At 50% binocular correlation (right), half of the dots within the receptive field were presented at either the preferred disparity of the neuron (horizontal line inside gray oval) or the disparity that elicited a minimal response (null disparity). The remaining dots had random disparities. B, The fine task. A bipartite (center/surround) random-dot stereogram was presented. The center patch covered the RF, and contained dots moving at the preferred velocity (arrow). The surrounding annulus contained stationary dots presented (in most cases) at a nonzero disparity. A small patch of zero-disparity dots (gray) surrounded the fixation point to help anchor vergence. The monkey reported whether the center patch was in front of or behind the surround patch, and task difficulty was manipulated by finely varying the center disparity around the surround disparity. C, Trial timing. The fixation point (FP) first appeared, along with the zero-disparity background (Bgnd) dots. After a 1.5 s stimulus presentation, the fixation point and dots were extinguished, and two choice targets appeared. Monkeys reported depth by making a saccade to one of the two targets.

In the fine task (see Fig. 1B), a bipartite (center/surround) RDS was presented. The center patch moved at the preferred velocity of the neuron, whereas the surround patch remained stationary. The outer diameter of the surround patch was twice that of the center patch. Binocular correlation was fixed at 100% for both patches, and task difficulty was manipulated by changing the disparity of the center patch relative to the surround. Monkeys were trained to report whether the center patch was in front of or behind the surrounding annulus. Note that both patches of dots could have near or far disparities relative to the fixation point; the monkey's task was to judge the relative disparity of the two stimuli. The range of relative disparities was chosen to bracket the monkey's psychophysical threshold, and a typical range of center disparities was ±0.08° around the surround disparity. The disparity of the surround was chosen to lie at the point of steepest slope of the tuning curve of the neurons, such that neurons would be maximally informative to the monkey (Seung and Sompolinsky, 1993; Purushothaman and Bradley, 2005). For each task, all stimulus conditions were randomly interleaved. In microstimulation experiments, the two tasks were performed in separate blocks.

Both animals were initially trained to perform the coarse task and were involved in previous single-unit and behavioral studies (Uka and DeAngelis, 2003, 2004). They were subsequently transitioned to performing the fine task with the surround disparity set initially to zero. The range of center patch disparities was then gradually reduced over several sessions until the monkeys performed the task with thresholds well below 0.1°. When the surround disparity was subsequently moved away from the plane of fixation, both monkeys' psychometric functions (plotted as in Fig. 4C) shifted by approximately the amount of the surround disparity. In other words, when the surround disparity was nonzero, both monkeys initially reported the depth of the center patch relative to the fixation point, not relative to the random-dot surround. Thus, it was clear that both monkeys were initially reporting the absolute disparity of the center patch, presumably as a result of being extensively trained in the coarse task. Over several weeks of additional training, the monkeys gradually learned to report the relative disparity between center and surround stimuli, and their psychophysical thresholds improved dramatically when they began to report relative depth. At the end of training, relative disparity thresholds were ∼0.01–0.03° (see Fig. 3) at stimulus eccentricities of 5–10°. It is known that discrimination relying on absolute disparities alone results in thresholds that are roughly tenfold larger (Westheimer, 1979; Prince et al., 2000). In some preliminary experiments, we interleaved two different pedestal disparities in the same block of trials. Monkeys performed comparably on these interleaved pedestals, giving additional confidence that they were judging relative disparities in the fine task.

Figure 4.

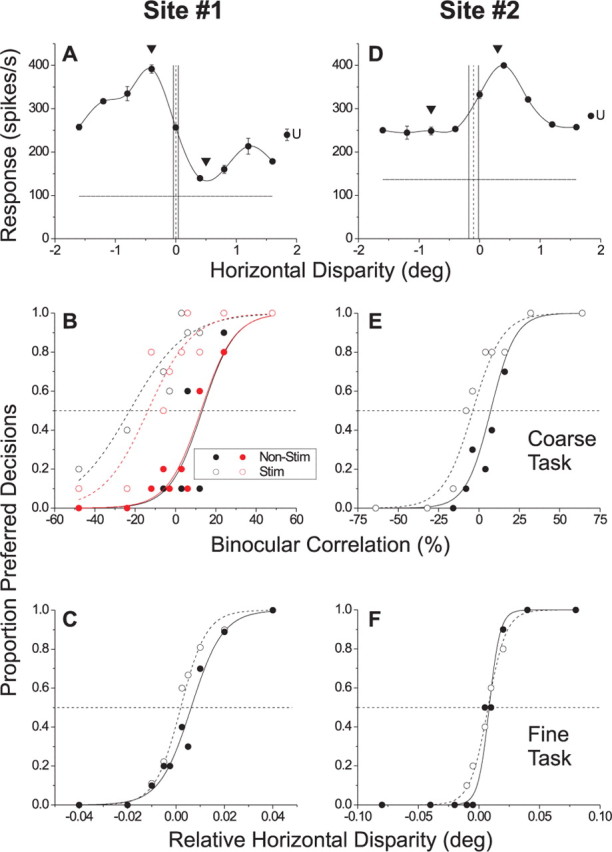
Example effects of MT microstimulation on the two depth-discrimination tasks. Each column shows data for a different stimulation site. A, Disparity-tuning curve of MU activity recorded at a near-tuned site (site 1). Arrowheads denote the preferred (−0.4°) and null (0.5°) disparities used in the coarse task. The dashed vertical line indicates the disparity of the surround patch (0.0°) and the solid vertical lines indicate the range of center disparities used in the fine task. The horizontal line shows the spontaneous activity level. The point labeled “U” denotes the mean response to binocularly uncorrelated dots. B, Effect of microstimulation of site 1 on performance of the coarse task. Filled circles and the solid line represent the psychometric function for nonstimulated trials, whereas open circles and the dashed line show data from stimulated trials. Black symbols show data from the first block of absolute disparity trials. Red symbols show data from a repeat experiment that was performed after an intervening block of relative disparity trials. The horizontal dashed line denotes chance performance. C, Effect of microstimulation of site 1 on performance of the fine task. D, Disparity-tuning curve of multiunit activity recorded at a far-tuned stimulation site (site 2). E, Effect of microstimulation of site 2 on performance of the coarse task. F, Effect of microstimulation of site 2 on performance of the fine task. Error bars indicate SE.

Figure 3.

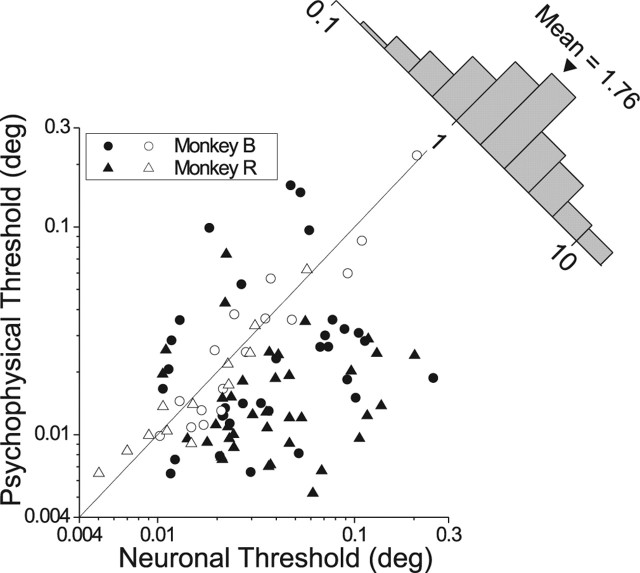
Population summary of neuronal and psychophysical thresholds for the fine task. Data are shown for 98 MT neurons (50 from monkey B and 48 from monkey R). Filled symbols indicate cases in which the neuronal and psychophysical thresholds are significantly different (p < 0.05). Circles and triangles indicate data from monkeys B and R, respectively. The histogram (upper right) shows the distribution of neuronal to psychophysical threshold ratios.

Experimental protocols and data acquisition

A tungsten microelectrode was advanced into the cortex through a transdural guide tube using a micromanipulator (MO-951C; Narishige, Tokyo, Japan) mounted on the recording chamber. Single-unit (SU) or multiunit (MU) activity was measured using a conventional amplifier, bandpass filter (500–5000 Hz), and window discriminator (Bak Electronics, Mount Airy, MD). Times of occurrence of action potentials and trial events were stored to disk with 1 ms resolution. Tasks and data acquisition were controlled by TEMPO software (Reflective Computing, St. Louis, MO), and data analyses were done using MATLAB (MathWorks, Natick, MA). The positions of both eyes were sampled at 1 kHz and stored at 250 Hz.

Comparison of neuronal and psychophysical thresholds.

After isolating an MT neuron, we used a custom software interface to carefully map the receptive field and to estimate stimulus preferences. Next, we quantitatively measured the direction, speed, size, and horizontal disparity tuning of each neuron as described previously (DeAngelis and Uka, 2003). In the first disparity-tuning run, disparities were tested from −1.6 to 1.6° in steps of 0.4° (see Fig. 2A). In the second disparity-tuning run, we focused on the slope of the disparity-tuning curve, and measured the tuning on a finer scale (see Fig. 2B) to determine the location of the steepest slope of the tuning curve. In some experiments, a third run was done at an even finer scale. All tuning measurements were done in blocks of randomly interleaved trials, and responses were averaged across three to five stimulus repetitions.

Figure 2.

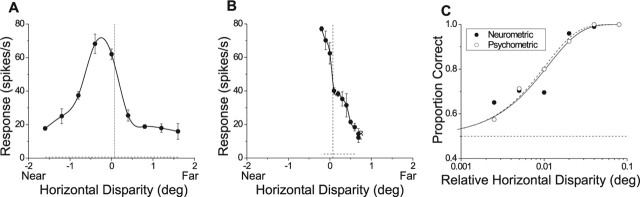
Example single-unit data. A, Disparity-tuning curve for a near-tuned neuron from monkey B. Filled circles show mean responses (±SE) to five repetitions of each disparity. The solid curve is a spline fit. The vertical dotted line denotes the disparity of the surround patch (0.075°), which was placed at the steepest slope of the tuning curve. B, Disparity-tuning curve of the same neuron using a narrower range of disparities. C, Neurometric (filled circles) and psychometric (open circles) functions obtained during performance of the fine task. Solid and dashed curves show Weibull fits to the neurometric and psychometric functions, respectively.

Next, we recorded while the monkey performed the fine task. The disparity of the surround was fixed at the steepest slope of the disparity-tuning curve, and the relative disparity between center and surround took the following typical values: 0, ±0.0025, ±0.005, ±0.01, ±0.02, ±0.04, and ± 0.08°. The majority of data sets (62 of 98) were collected using this fixed set of parameters. In other cases, it was necessary to increase the range of relative disparities because of the MT neuron having weak, broad, or noisy disparity tuning. In these cases, relative disparities of ±0.16° were usually added. Whenever possible, data were collected for 40 or more repetitions of each unique stimulus condition, and data sets were discarded if isolation was not maintained for at least 10 repetitions. Among the 98 neurons included in the analysis, the average number of stimulus repetitions was 36.4 ± 0.91 SE.

Microstimulation.

To identify microstimulation sites, we recorded MU activity and measured disparity tuning every 100 μm along oblique electrode penetrations through MT (DeAngelis and Newsome, 1999). When disparity tuning remained fairly constant over a span of ∼300 μm, the electrode was retracted to the middle of that span. We then explored the receptive field and tuning properties of the MU activity, followed by quantitative measurements of direction, speed, size, and horizontal disparity tuning (DeAngelis and Uka, 2003). From the disparity-tuning curve, we extracted the preferred and null disparities for use in the coarse task (see Fig. 4A, arrowheads), and the location of maximal slope for use in the fine task (see Fig. 4A, dashed vertical line). In some microstimulation experiments (32 of 78), monkeys only performed the fine task. In the remaining experiments (46 of 78), monkeys performed the two tasks in separate blocks of trials, with the order of the two tasks counterbalanced across experiments. Electrical microstimulation was applied at 200 Hz using biphasic pulses, cathodal pulse leading (Salzman et al., 1992; DeAngelis et al., 1998). Current amplitudes were 20 μA for monkey R and 40 μA for monkey B.

Representation of absolute and relative disparity signals.

To determine whether MT neurons code absolute or relative disparities, we recorded from isolated single units. In the main experimental run, a bipartite (center/surround) RDS was centered over the receptive field of the neuron. Dots moved in the neuron's preferred direction and speed. The diameter of the center patch matched the peak (or saturation point) of the size-tuning curve, and the outer diameter of the surrounding annulus was threefold larger. The horizontal disparity of the center patch usually varied from −1.6 to 1.6° in 0.4° intervals, and the disparity of the surround patch typically varied from −1.0 to 1.0° in 0.5° intervals (in some early experiments, we only used three surround disparities). All combinations of center and surround disparities (see Fig. 7A) were randomly interleaved in a single block of trials.

Figure 7.

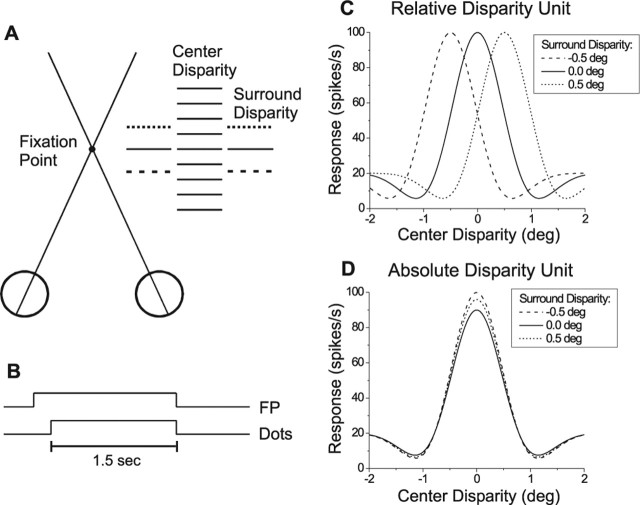
Schematic illustration of stimuli and predicted outcomes for tests of absolute versus relative disparity tuning. A, Top-down view of the stimulus configuration, consisting of a center patch of dots and a surrounding annulus. All combinations of nine center disparities and three to five surround disparities were presented in randomly interleaved trials. B, The bipartite stereogram was presented for 1.5 s during fixation. C, If a neuron signals relative disparity, the disparity tuning in response to the center patch should shift horizontally by an amount equal to the change in surround disparity. D, If a neuron signals absolute disparity, no shifts should be seen although amplitude variations may occur.

Eye calibration.

To measure small changes in vergence angle that might accompany disparity variations or the presence of microstimulation, we systematically calibrated the position of each eye before and after each experiment. In a separate block of trials from the main experiment, the fixation point was presented at nine different locations (on a 3 × 3 grid) separated by 5°. Each fixation point location was presented five or more times in a block of randomly interleaved trials. At the end of the block, we performed a least-squares fit to minimize the error between actual eye position and desired eye position. The calibration model was linear in horizontal and vertical position (use of a nonlinear model improved calibration fits very little). Parameters of the best-fit calibration were stored and were used on-line to calibrate eye position signals during the experiment. At the end of recording or microstimulation experiments, the eye calibration procedure was repeated to check that the calibration had not changed substantially. When some drift in calibration occurred during the experiment, it was usually a small (<0.25°) change in the position offset without any change in gain.

Data analysis

Calculation of neuronal thresholds.

To characterize neuronal sensitivity in the fine task, we used receiver operating characteristic (ROC) analysis similar to that used by Britten et al. (1992). For each magnitude of relative disparity, we constructed an ROC curve from the two distributions of responses corresponding to center disparities on opposite sides of the surround disparity (e.g., −0.02 vs +0.02°). Because the surround disparity was always at the steep slope of the tuning curve, disparities on one side of the surround were closer to “preferred” and disparities on the other side were closer to “null.” The area under the ROC curve is taken as the ability of an ideal observer to discriminate between the two disparities based on the responses of the recorded neuron and an assumed “antineuron” with an oppositely sloped tuning curve. A plot of the ROC area as a function of |relative disparity| defines the neurometric curve (see Fig. 2C, filled symbols), which is fit with a cumulative Weibull function given by the following:

where c is the relative disparity of the stimulus, p is the proportion of correct responses, α defines the threshold at 82% correct, and β gives the slope of the curve.

To test whether neurometric and psychometric thresholds differed significantly, we used a bootstrap technique (Uka and DeAngelis, 2003). For each relative disparity, spike counts and choices were resampled with replacement from the measured distributions. The number of random draws was equal to the number of trials done at each relative disparity. One such set of random draws of spike counts for all relative disparities defined a single “bootstrap” neurometric function, and an analogous set of draws of choices defined a single bootstrap psychometric function. These bootstrap functions were then fit with Weibull curves to extract thresholds, as described above. This process was repeated to compute 1000 pairs of bootstrap neurometric/psychometric functions from which we computed the 95% confidence interval of the threshold difference. Differences between neuronal and psychophysical thresholds were considered significant if the 95% confidence interval did not include zero.

Quantification of microstimulation effects.

Microstimulation effects were quantified as the leftward shift of the psychometric function at the midpoint (proportion preferred decisions = 0.5) of the stimulated and nonstimulated curves (see Fig. 4B) (DeAngelis et al., 1998). Statistical significance of the horizontal shift was determined using logistic regression (Salzman et al., 1992). To compare effects of microstimulation between the two disparity tasks, we normalized the horizontal shift of the psychometric function by multiplying it by the slope of the nonstimulated psychometric function. The resultant quantity is unitless and, thus, can be compared directly across tasks.

Calculation of shift ratios.

To determine whether MT neurons signal absolute or relative disparity, we fit the data (see Fig. 8A) with constrained Gabor functions and calculated shift ratios (Thomas et al., 2002). A disparity-tuning curve was generated for each surround disparity by calculating the mean firing rates (± SE) during the 1.5 s stimulus duration. For each pair of surround disparities at which disparity tuning was statistically significant (ANOVA, p < 0.01), we calculated the horizontal shift between the two curves by fitting the data with a pair of Gabor functions having the following form:

where d is the horizontal disparity of the center patch, R₀ is the baseline response level, A is the amplitude, d₀ is the center of the Gaussian envelope, σ is the SD of the Gaussian, f is the frequency of the sinusoid, and Φ is the phase of the sinusoid (relative to the center of the Gaussian). The Gaussian width (σ), frequency (f), and phase (Φ) parameters were shared between the two curves, whereas baseline response (R₀), amplitude (A), and Gaussian center location (d₀) were independent (see Fig. 8B, example fits). This constrains the two curves to have the same shape while allowing for horizontal and vertical shifts, as well as amplitude scaling. We refer to this as the “center-shift” model.

Figure 8.

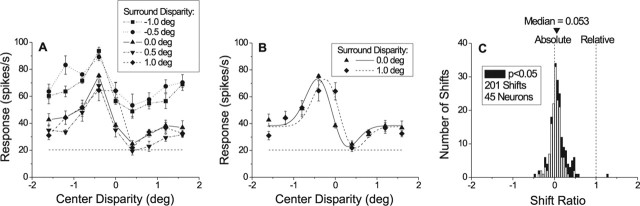
MT neurons signal absolute, not relative, disparities. A, Disparity-tuning curves for an example neuron are plotted for five different surround disparities. B, For each pair of surround disparities, we calculated the horizontal shift between disparity tuning curves by fitting a pair of Gabor functions. From this paired fit, we calculated a shift ratio (see Materials and Methods). C, Distribution of shift ratios for 201 surround pairings from 45 neurons. Note that shift ratios are distributed around zero, with a slight but significant bias toward positive values (sign test, p < 0.0001). Filled bars denote shift ratios that were significantly different from zero (Sequential F test, p < 0.05; 52 of 201 shifts). Error bars indicate SE.

The paired Gabor fits described above give us a quantitative estimate of the horizontal shift between disparity tuning curves obtained at a pair of surround disparities, in the form of the difference between d₀ parameters for the two curves. From these parameters, we calculated a shift ratio as follows:

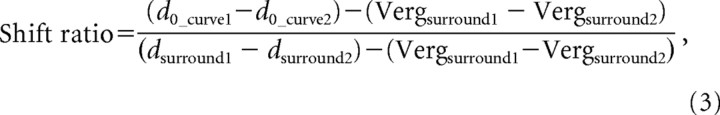where (d_{0_curve1} − d_{0_curve2}) is the horizontal shift between the pair of fitted curves and (d_surround1 − d_surround2) is the difference between the two surround disparities. To control for small variations in vergence angle with surround disparity, the shift ratio also incorporates a term, (Verg_surround1 − Verg_surround2), which represents the difference in mean vergence angle between the two surround disparities. A shift ratio of 0 indicates no shift in disparity tuning with changes in surround disparity, consistent with absolute disparity coding. A shift ratio of 1 indicates a shift equal to the difference between the two surround disparities, consistent with relative disparity coding.

To assess the statistical significance of shift ratios, a second fit was performed in which the center of the Gaussian envelope (d₀) was also shared between the two fitted curves (i.e., no horizontal shift was allowed). We refer to this as the “center-shared” model. Shift ratios were deemed to be significantly different from zero if the center-shift model provided a better fit than the center-shared model, as assessed using a sequential F test (Draper and Smith, 1966; Thomas et al., 2002). Monte Carlo simulations were performed to ensure that the sequential F test yielded appropriate error rates in this context. Shift ratios were calculated for all unique pairings of surround disparities that were tested for a given neuron (three surround disparities yield three pairings, five surround disparities yield up to 10 pairings).

The above analysis assumes that changes in surround disparity only cause horizontal shifts, vertical shifts, or amplitude scaling of the disparity tuning curves. To address this, we also fit the data from each neuron with a set of completely independent Gabor functions, one for each surround disparity. The quality of these independent fits was then compared with the center-shift model using a sequential F test. For the vast majority of surround pairings (201 of 239), the independent fits were not significantly better (p > 0.05) than the center-shift model, supporting the assumption that the shape of the tuning curve was unaffected by surround disparity. Data from the remaining surround pairings (38 of 239) were excluded from additional analysis.

Results

Data were collected from three male rhesus monkeys. In single-unit experiments examining the sensitivity of MT neurons to fine relative disparities, we recorded from 147 MT neurons in two animals (70 from monkey B; 77 from monkey R). Among these, 34 of 147 were excluded from analysis because isolation was lost prematurely (<10 repetitions per unique stimulus), 13 of 147 were excluded because of lack of disparity tuning, and 2 of 147 were excluded because the monkey's behavioral performance was clearly outside the normal range. Microstimulation experiments were performed at 78 additional recording sites in MT of the same two monkeys (see Materials and Methods for selection criteria). In single-unit experiments aimed at distinguishing between absolute and relative disparity coding, we recorded from 45 MT neurons from three animals (monkeys B, R, and J).

Sensitivity of single MT neurons to fine relative disparities

We examined whether single MT neurons carry disparity signals with sufficient fidelity to account for fine depth discrimination (Prince et al., 2000). In the fine task (Fig. 1B), a bipartite (center/surround) RDS was centered over the receptive field of the neuron, and monkeys discriminated the relative depth between the center patch and the surround patch. The center patch covered the receptive field and had the same size as the RDS used in the coarse task (Uka and DeAngelis, 2003, 2004). No disparity noise was added to the visual stimulus in the fine task; rather, task difficulty was manipulated by adjusting the difference in disparity between the center and surround stimuli. As the relative disparity approaches zero, task performance approaches the chance level (50% correct). The disparity of the surround patch was generally not zero; thus, the monkey could not base his decisions on the absolute disparity of the center patch to perform the task well. Several aspects of the animals' behavior during training indicated that they learned over time to rely on the relative disparity between center and surround stimuli (for details, see Materials and Methods).

Figure 2 shows data from an MT neuron that was strongly tuned for “near” disparities (Fig. 2A). In this and all experiments, the surround disparity was chosen to lie at the steepest point along the disparity-tuning curve (Fig. 2B), such that the sensitivity of each neuron was maximized for fine discrimination (see Discussion). Here, we chose 0.075° to be the surround disparity, and we varied the center disparity around this value in small steps (±0.0025, 0.005, 0.01, 0.02, 0.04, and 0.08°). To quantify neuronal sensitivity, we calculated an ROC curve (Green and Swets, 1966; Britten et al., 1992) from the two distributions of neuronal responses obtained for each magnitude of relative disparity (e.g., −0.02 vs +0.02°). The area under the ROC curve defines the proportion correct of an ideal observer whose “task” is to determine whether the center patch was in front of or behind the surrounding annulus, using only the responses of this neuron (and an assumed antineuron with an oppositely sloped tuning curve).

ROC values are plotted as a function of |relative disparity| in Figure 2C, to create a neurometric function (filled circles). These data were fit with a Weibull function (solid curve) to extract an 82% correct threshold. For this neuron, the threshold was 0.011°. This value was comparable with the psychophysical threshold of the monkey (0.010°), which was obtained by fitting the psychometric function (Fig. 2C, open circles, dashed curve) using identical methods. The difference between the two thresholds was not statistically significant (p > 0.05) in this experiment, as determined using a bootstrap analysis (see Materials and Methods).

Figure 3 summarizes results for a population of 98 MT neurons recorded from two monkeys during performance of the fine task. For 28 of 98 experiments (29%, open symbols), there was no significant difference between neuronal and psychophysical thresholds (bootstrap, p > 0.05). Among the remainder (filled symbols), 13 of 98 had neuronal thresholds significantly smaller than the corresponding psychophysical thresholds (p < 0.05), and the majority (57 of 98) exhibited neuronal thresholds that significantly exceeded behavioral thresholds. Overall, the neuronal:psychophysical threshold ratio was significantly larger than 1 (sign test, p < 0.001), with a geometric mean of 1.76 (1.44 for monkey B and 2.13 for monkey R). Thus, the modal MT neuron was roughly half as sensitive as the monkey.

These data show that at least some MT neurons are sufficiently sensitive to account for performance in the fine task. Moreover, the sensitivity of MT neurons is similar to that reported previously for V1 neurons (Prince et al., 2000) (see Discussion).

Effects of microstimulation on relative and absolute disparity judgments

Although Figure 3 shows that MT neurons might contribute to relative disparity judgments, this need not necessarily be true. Thus, we asked whether microstimulation could bias monkeys' perceptual judgments in the fine task. Furthermore, we directly compared the effects of microstimulating the same cluster of MT neurons on performance of both disparity tasks. In the coarse task (Fig. 1A), monkeys reported whether the perceived depth of an RDS was near or far relative to the plane of fixation, and task difficulty was varied by titrating the binocular correlation of the stereogram (i.e., the percentage of signal dots that were presented at either the preferred or null disparity of the neurons) (see Materials and Methods). This task is identical to the one that we have used in previous MT studies (DeAngelis et al., 1998; Uka and DeAngelis, 2003, 2004).

Figure 4A–C shows data from an example microstimulation experiment. Figure 4A shows the disparity tuning curve for MU activity recorded at the stimulation site; this site preferred near disparities. The monkey performed the two tasks in different blocks of trials while microstimulation was applied on half of the trials selected randomly. In this particular experiment, the monkey performed the coarse task first. Specifically, the monkey discriminated between the preferred (−0.4°) and null (0.5°) disparities of the neurons (shown by triangles in Fig. 4A) in the presence of disparity noise. In Figure 4B, the proportion of preferred (near) decisions is plotted as a function of signed binocular correlation. Positive binocular correlations indicate that signal dots were presented at the preferred disparity, whereas negative correlations denote signal dots at the null disparity. As expected if the monkey monitors the activity of this cluster of neurons to perform the coarse task, microstimulation increases the proportion of trials in which the monkey reports the stimulus as near (Fig. 4B, black symbols), causing a leftward shift of the psychometric function equivalent to 36% correlated dots. We measure this shift by fitting the behavioral data using logistic regression (Salzman et al., 1992). The effect is highly significant in this experiment (p < 0.001). This confirms previous observations (DeAngelis et al., 1998) that MT contributes to absolute disparity discrimination.

The critical question is whether microstimulation of MT also biases depth percepts in the fine task. Figure 4C shows data for the same stimulation site from a second block of trials in which the animal performed the fine task. Here, the monkey reported whether the center patch was in front of or behind the surround patch, which had a disparity of 0.0° such that it was centered at the steepest slope of the tuning curve (Fig. 4A, dashed vertical line). If MT carries signals used to perform the fine task, microstimulation should increase the proportion of trials in which the monkey reports the center patch to be in front of the surround. In Figure 4C, the proportion of preferred (i.e., near) decisions is plotted as a function of the relative disparity between center and surround stimuli. By convention, positive values of relative disparity indicate that the center patch is closer to the preferred disparity of the neurons. Figure 4C shows that microstimulation did not produce a significant shift of the monkey's psychometric function in this experiment (logistic regression, p = 0.18), suggesting that this cluster of MT neurons did not contribute to performance of the fine task.

Previous work has shown that effects of microstimulation can wane over time (Salzman et al., 1992). To ensure that this did not explain the difference in results between Figure 4, B (black symbols) and C, we performed a third block of trials in which the monkey repeated the coarse task. Red symbols in Figure 4B show that microstimulation again resulted in a large leftward shift of the psychometric function equivalent to 26% correlated dots (logistic regression, p < 0.001). This indicates that the lack of an effect in Figure 4C is attributable to differences between the two tasks and not to nonspecific changes in the efficacy of microstimulation.

In the experiment of Figure 4A–C, the surround disparity was 0° for the fine task, such that absolute and relative disparities were indistinguishable. It is interesting to note that microstimulation did not significantly influence performance of the fine task, despite the fact that the monkey could have performed the task based on absolute disparities in this instance. In most (53 of 78) experiments, however, the range of center disparities for the fine task did not include zero disparity, thus requiring the monkey to rely on relative disparities. Figure 4D–F shows data from one such experiment. MU activity at this site preferred far disparities, and the surround disparity for the fine task was placed at −0.1°. In this experiment, the monkey first performed the fine task (Fig. 4F) and there was no significant effect of microstimulation (logistic regression, p = 0.24). Subsequently, the monkey performed the coarse task (Fig. 4E) and microstimulation exerted a significant effect on performance equivalent to 11% correlated dots (logistic regression, p = 0.003).

For each experiment, the effect of microstimulation was quantified as the leftward shift of the psychometric function measured at the midpoint of the curves (proportion preferred decisions = 0.5) (Salzman et al., 1992). Figure 5A summarizes data from 78 experiments in which two monkeys performed the fine task. Leftward shifts of the psychometric function appear as positive values in Figure 5A and filled bars denote statistically significant effects. Only 19 of 78 sites showed significant effects of microstimulation (logistic regression, p < 0.05). Moreover, seven of the 19 significant effects were in the opposite direction to that predicted by the disparity tuning of MU activity at the stimulation site. The median microstimulation effect (0.00°) was not significantly different from zero (sign test, p = 0.81), indicating that microstimulation produced no overall bias in performance of the fine task. We can also rule out the possibility that microstimulation simply interfered with performance of the fine task. The slope of the psychometric function, an indicator of sensitivity, was significantly influenced by microstimulation at only 4 of 78 sites, as expected by chance (p < 0.05).

Figure 5.

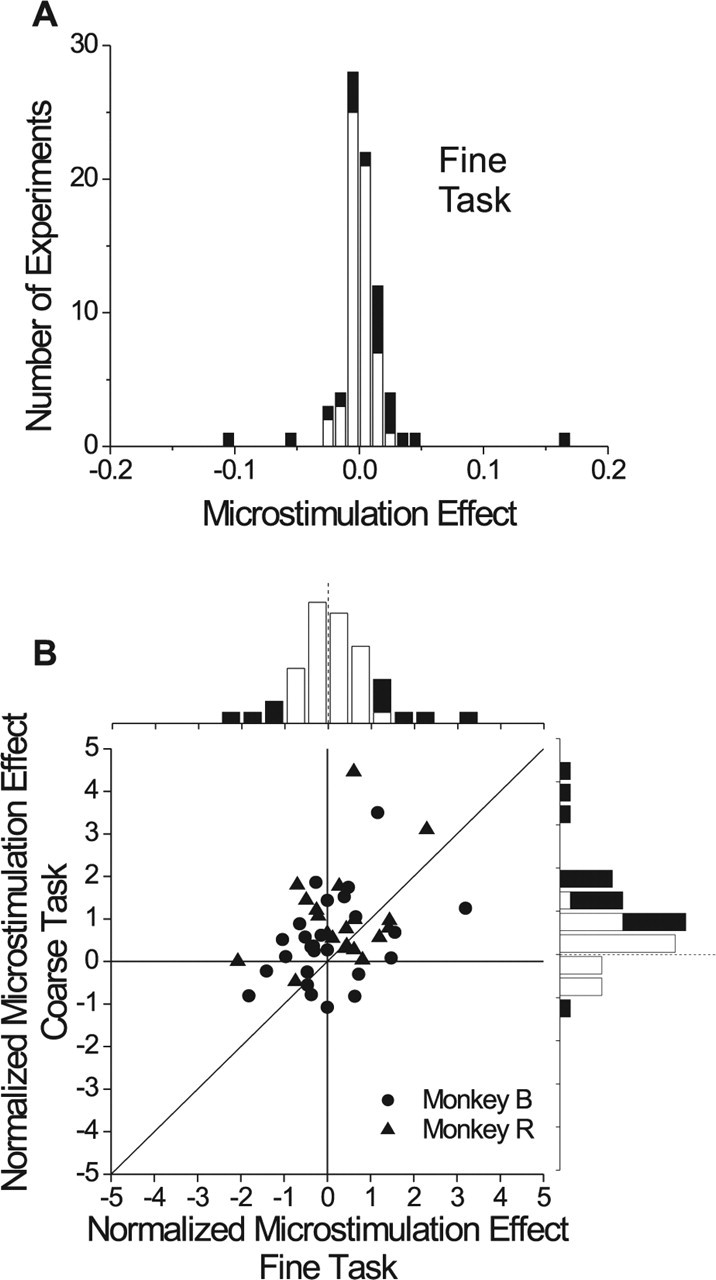
Population summary of microstimulation effects. A, Data are shown for 78 sessions of the fine task. This distribution shows the shift between stimulated and nonstimulated psychometric functions in degrees of visual angle. Black bars denote stimulation effects that were statistically significant (logistic regression, p < 0.05). B, Effects of microstimulation for 46 experiments in which both the coarse and fine tasks were performed in separate blocks. Microstimulation effects are normalized to the slope of the psychometric function (see Materials and Methods) to make the data comparable. Frequency histograms for the two tasks are shown along the top and right margins. Filled bars indicate significant effects (logistic regression, p < 0.05).

The result of Figure 5A lies in stark contrast to previous findings for the coarse task (DeAngelis et al., 1998), in which 43 of 65 experiments produced significant microstimulation effects and 42 of 43 of these significant effects were in the direction predicted by MU tuning curves. Direct comparison of Figure 5A with the data of DeAngelis et al. (1998) is hampered by the fact that experiments were performed on different animals in different laboratories. Thus, we trained two of our animals to switch back and forth between the two tasks in blocks of trials, as exemplified by Figure 4. Microstimulation was delivered during both tasks at 46 of 78 stimulation sites, and the order of the two tasks was counterbalanced across experiments. There was no significant effect of block order for either task (t test, p > 0.3), but there was a very weak tendency for effects to be stronger in the first block. Figure 5B summarizes the results. Because microstimulation effects were measured in different units for the two tasks, we normalized the leftward shift between each pair of psychometric functions by the slope of the psychometric function obtained from the nonstimulated trials (see Materials and Methods). Positive values of the normalized shift denote a bias toward the preferred disparity of the neuron, and significant effects are shown as filled bars in the marginal distributions of Figure 5B.

For this subset of 46 stimulation sites, the median normalized effect for the coarse task (0.57) was significantly larger than zero (sign test, p < 0.0001), and 17 of 18 significant effects were consistent with the disparity preference of MU activity at the stimulation site. In contrast, the median normalized effect for the fine task (0.00) was not significantly >0 (sign test, p = 0.88), and 8 of 12 significant effects were consistent with the disparity preference. Examining the paired data from each site, we find that microstimulation effects were significantly larger for the coarse task than the fine task (Wilcoxon signed-rank test, p = 0.0035). Consistent with a previous study (DeAngelis et al., 1998), stimulation effects in the coarse task were modestly, but significantly, correlated with the strength of disparity tuning at the stimulation site (r = 0.32; p = 0.02); in contrast, there was no correlation between stimulation effects and tuning strength for the fine task (r = 0.02; p = 0.91). Thus, results from this subset of interleaved experiments confirm that the contribution of MT to depth perception depends on the demands of the task.

We can exclude the possibility that the lack of microstimulation effects in the fine task results from lack of power to detect shifts in the psychometric function. For each experiment, we determined the 95% confidence interval around the monkey's point of subjective equality (50% preferred decisions) in the nonstimulated condition, and we normalized these confidence intervals by the slope of the psychometric function to allow direct comparison of results for the two tasks. The average normalized confidence interval was 0.88 ± 0.35 SE for the fine task and 0.83 ± 0.44 SE for the coarse task. The difference between these means was not statistically significant (paired t test, p = 0.37). Thus, we could reliably measure a shift of the psychometric function smaller than one threshold unit for either task, which indicates that sensitivity cannot explain the lack of microstimulation effects in the fine task.

Analysis of disparity tuning at microstimulation sites

In the fine task, we placed the surround (pedestal) disparity at the steep slope of the MU tuning curve, and we expected that microstimulation (if it had any effect) would bias decisions toward the preferred disparity of the stimulated neurons (see Discussion). It is therefore critical that the slopes of the tuning curves of the stimulated MT neurons have a consistent sign around the pedestal disparity. If we were to stimulate neurons with a mixture of positively and negatively sloped tuning curves, this might account for the lack of microstimulation effects in the fine task. We performed two set of analyses to address this issue.

First, we examined the disparity tuning of MU activity at the three recording sites (100 μm apart) that bracketed each microstimulation site. Such quantitative measures of disparity tuning were collected in almost all experiments while searching for good microstimulation sites. Supplemental Figure 1 (available at www.jneurosci.org as supplemental material) shows the disparity tuning of MU activity around all of the microstimulation sites from monkey R (except for one experiment in which tuning data were not saved). Normalized MU responses are shown for each of three consecutive recording sites, 100 μm apart, and the vertical line shows the pedestal disparity for each microstimulation experiment. In all 47 cases, the reader can verify that MU tuning curves have a consistent slope around the pedestal disparity. Thus, the slope of MU disparity tuning was consistent within the region around all microstimulation sites. This was also true of the disparity tuning in monkey B (data not shown).

Second, we examined the relationship between the slopes of disparity tuning curves for SU and MU responses, because the above analysis does not rule out the possibility that the MU response includes some neurons with tuning curves of opposite slope. We analyzed data from a large body of previous SU recordings (DeAngelis and Uka, 2003), and we extracted MU responses from raw neural signals that were stored during these recordings (for analysis details, see DeAngelis and Newsome, 1999). We fit the corresponding SU and MU tuning curves with Gabor functions, as described previously (DeAngelis and Uka, 2003), and we computed the slopes of the tuning functions. We determined the disparity at which the MU tuning curve had maximal slope, and we found that the slope of the SU tuning curve had the same sign at 94% of recording sites. Moreover, the SU and MU tuning slopes were highly correlated across experiments (r = 0.82; p ≪ 0.0001), indicating that almost all neurons that contribute to the MU response have tuning curves with a consistent slope around the pedestal disparity.

Together, these analyses argue strongly against the possibility that microstimulation failed to bias judgments in the fine task because of variability in the tuning curve slope among the stimulated neurons.

Analysis of vergence eye movements

To interpret the results from the fine task, it is important to know that the monkey's vergence angle was appropriately maintained near the plane of the display monitor. If the monkey's vergence angle were affected by microstimulation, then the stimuli would no longer be varying around the steep slope of the tuning curve and the stimulated neurons might not be relevant to the task. This could potentially account for negative effects of microstimulation. Thus, we analyzed vergence eye movements obtained with dual eye coils in the fine task.

Figure 6A shows data from a typical experiment for monkey R. For each trial, we computed the time-average vergence angle during the 1.5 s stimulus presentation, and we expressed this on a scale where 0 represents the desired vergence angle corresponding to the viewing distance of 57 cm. Figure 6A shows the vergence angle for each trial as a function of the relative disparity between center and surround stimuli on that trial. Filled circles denote trials in which microstimulation was delivered; unfilled squares indicate trials without microstimulation. The data were analyzed using analysis of covariance (ANCOVA) with microstimulation (on or off) as an ordinal factor and relative disparity as a covariate. The presence of microstimulation had no significant effect on vergence angle (p = 0.56). There was a very weak tendency, which did not reach significance (r = 0.06; p = 0.10), for vergence angle to be positively correlated with center disparity, and the slope of the best linear fit (solid line) was 0.16. If vergence were to track changes in center disparity, the slope would be close to 1. There was also no significant interaction between the effects of microstimulation and center disparity in this experiment (p = 0.21). The overall SD of vergence angle across trials was 0.075° for this experiment, which was quite typical of monkey R (median SD, 0.087°). The median SD of vergence angle was somewhat larger for monkey B (median SD, 0.16°).

Figure 6.

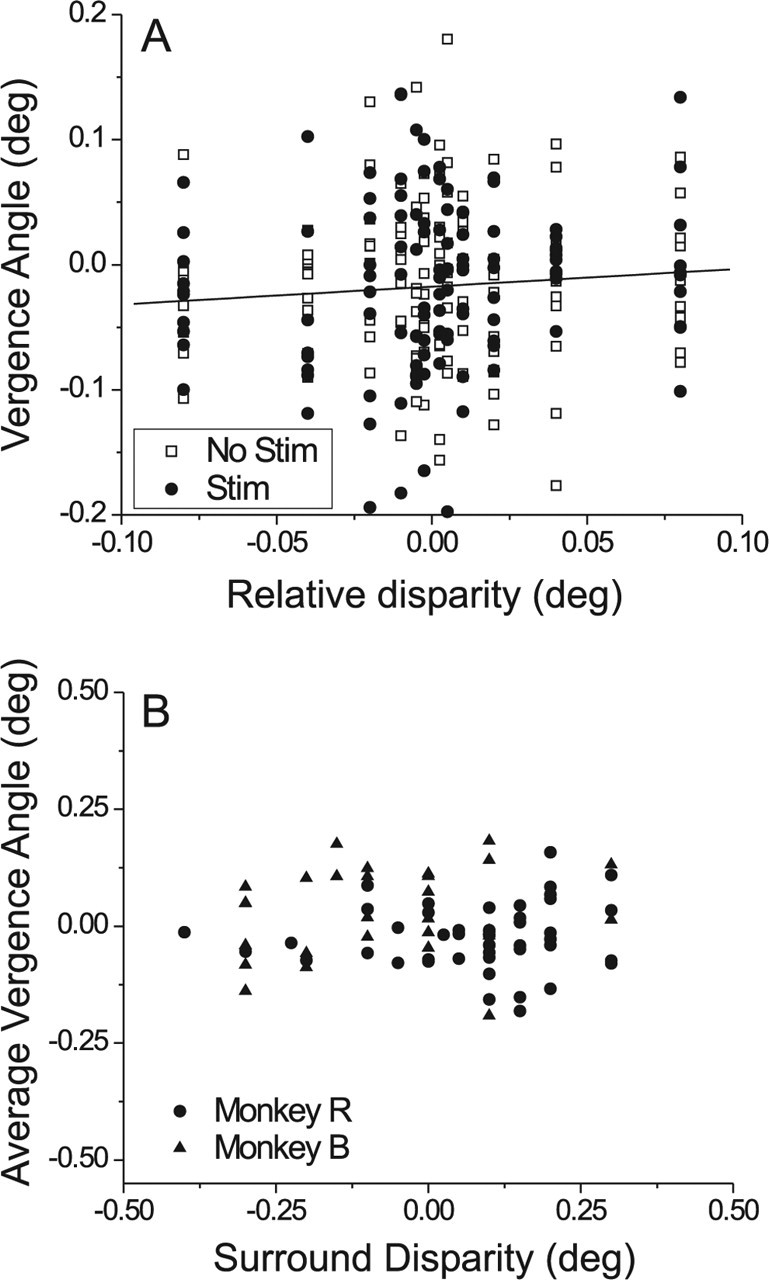
Analysis of vergence eye movements during microstimulation in the fine task. A, Vergence data from an example experiment. The time-averaged vergence angle for each trial is plotted against the relative disparity between center and surround stimuli. Filled circles indicate trials during which microstimulation was delivered; open squares correspond to trials without microstimulation. B, The average vergence angle (across all trials and all center disparities) of the monkey is plotted as a function of the disparity of the surrounding annulus. Each datum represents one experiment, with circles and triangles denoting data from monkeys R and B, respectively.

The results of ANCOVA for the other experiments were generally quite similar to those of Figure 6A. Microstimulation did not have a significant effect on vergence angle in any experiment (0 of 78), and only 2 of 78 sites showed a significant interaction effect. The correlation between vergence angle and relative disparity reached a significance criterion of 0.05 for 22 of 78 experiments. The median slope of the best linear fit between vergence angle and relative disparity was 0.18, similar to that seen in Figure 6A. Thus, although vergence angle did occasionally vary significantly with the center patch disparity, the effect was quite small. Across a typical range of variation of center disparities of 0.16°, vergence angle varied by only 0.028° on average. Moreover, across experiments, the strength of the microstimulation effect in the fine task was not correlated with the slope of the relationship between vergence angle and center disparity (p > 0.2).

Figure 6B plots the average vergence angle (across trials and center disparities) against the surround (pedestal) disparity for all 78 experiments performed in two monkeys. There are two points to be made from this figure. First, the variation in average vergence angle from experiment to experiment is smaller than the variation in pedestal disparity. Second, there is no significant correlation (r = −0.01; p = 0.91) between average vergence angle and pedestal disparity. This indicates that monkeys were not systematically converging their eyes on the surround stimulus.

Overall, these analyses indicate that vergence was well controlled in these experiments, and there is no evidence that microstimulation altered vergence angle.

Do MT neurons signal absolute or relative disparity?

We hypothesized that MT neurons do not contribute to performance of the fine task because MT lacks an explicit representation of relative disparities, which are important for stereoacuity (Westheimer, 1979; Prince et al., 2000). Thus, we asked whether MT neurons signal the absolute disparity that falls within their receptive fields, or the difference in disparity between their receptive field and the surrounding regions. This was tested by presenting bipartite (center/surround) stereograms and varying the horizontal disparity of both the center and surround patches while monkeys simply maintained fixation (Fig. 7A) (Thomas et al., 2002). A typical stimulus set consisted of all combinations of nine center disparities and either three or five surround disparities (see Materials and Methods). If MT neurons signal relative disparity, then the disparity tuning curve for the center patch should shift horizontally with the disparity of the surround patch, as illustrated schematically in Figure 7C. Such a neuron would signal the difference in disparity between the center and surround patches. However, if MT neurons signal absolute disparity, then the disparity-tuning curve for the center patch should not shift with surround disparity (Fig. 7D). Some changes in response gain with surround disparity might be expected, however, because MT neurons can exhibit disparity-selective surround inhibition (Bradley and Andersen, 1998).

Figure 8A shows data from a typical neuron. Response is plotted as a function of the absolute disparity of the center patch, with each curve representing a different surround disparity from −1.0 to +1.0°. If the neuron coded relative disparity, the peaks of the tuning curves would be expected to shift horizontally over a range of 2°. To the contrary, there was little change in preferred center disparity as a function of surround disparity (with perhaps a small rightward shift at +1.0°). Thus, the data from this neuron are consistent with coding of absolute disparity.

We quantified these results by fitting disparity-tuning curves for each pair of surround disparities with Gabor functions (see Materials and Methods). The two Gabor functions were constrained to have the same shape, but were allowed to shift horizontally and vertically and were allowed to scale in amplitude (center-shift model). Figure 8B shows Gabor fits to a pair of tuning curves from Figure 8A (surround disparities 0° and +1.0°). To summarize the effect of surround disparity, we computed a shift ratio, which is defined as the horizontal shift between the two curves divided by the difference in surround disparities (Thomas et al., 2002) (see Materials and Methods). A shift ratio of 1 indicates relative disparity tuning, whereas a shift ratio of 0 indicates absolute disparity tuning. The shift ratio was 0.17 for the pair of curves in Figure 8B (the largest value obtained from this neuron for any pair of surround disparities).

To assess the statistical significance of shift ratios, each pair of tuning curves was also fit with a pair of Gabor functions for which vertical shifts and amplitude scaling were allowed, but horizontal shifts were not (center-shared model). We then tested whether the center-shift model explained significantly more variance than the center-shared model, using a sequential F test (Draper and Smith, 1966; Thomas et al., 2002). For the example data in Figure 8B, the center-shift model provided a significantly better fit (sequential F test, p = 0.003). Thus, the change in surround disparity from 0 to +1.0° produced a small, but significant horizontal shift in the disparity-tuning curve for this neuron. However, for all pairings of surround disparities not including +1.0°, shift ratios were not significant (p > 0.05).

Figure 8C shows the distribution of shift ratios for 201 pairings of surround disparities from 45 MT neurons. A shift ratio was calculated for each unique pair of surround disparities that showed significant tuning when center disparity was varied (ANOVA, p < 0.01). Note that shift ratios are distributed around 0 (median 0.053), with a small, but significant, bias toward positive values (sign test, p < 0.0001). Fifty-two of 201 shifts were significantly different from zero (Fig. 8C, filled bars) (sequential F test, p < 0.05) with the majority being larger than 0 (43 of 52). Despite this bias toward positive values, there are few shift ratios larger than 0.25, and almost none larger than 0.5. Thus, MT neurons, like V1 neurons (Thomas et al., 2002), do not signal the relative disparity between their classical receptive fields and the surrounding regions. Note, however, that this does not preclude the possibility of relative disparity selectivity in a different stimulus geometry (Nguyenkim and DeAngelis, 2003) (see Discussion).

In these experiments, the boundary between the center and surround patches was always near the edge of the classical receptive field. We also tested 17 neurons (10 from monkey R, 7 from monkey B) with a stimulus in which the center patch was one-third to one-half the size of the classical receptive field, thus, placing the disparity boundary squarely within the classical receptive field. Although this stimulus configuration generally produced much larger vertical shifts and scaling effects as surround disparity was varied, the distribution of shift ratios for these neurons (data not shown) was virtually identical to that of Figure 8C. The median shift ratio was 0.06 (n = 56), which was not significantly different from 0 (sign test, p = 0.10). This indicates that MT neurons do not signal relative disparity in a center-surround stimulus geometry, even when the disparity boundary lies within the classical receptive field.

In the data of Figure 8, each cell was tested using stimuli containing motion in the preferred direction. In contrast, Thomas et al. (2002) tested neurons with dynamic random dot stimuli. Thus, as an additional control, we tested 28 neurons (14 from monkey R, 10 from monkey B, and 4 from monkey J) for relative disparity selectivity using dynamic random dots lacking coherent motion (0% motion coherence). The median shift ratio in these control data was 0.11 (n = 146 shifts). This median value was significantly larger than zero (sign test, p < 0.01), but again there were almost no shifts larger than 0.5. Thus, the lack of robust relative disparity sensitivity in MT, as compared with V2 (Thomas et al., 2002) and V4 (Umeda et al., 2004), does not appear to be related to the stimulus parameters that we have used.

Discussion

A detailed account of the neural basis of perception involves understanding how each neural representation of sensory stimuli is specialized to contribute to behavior. We used electrical microstimulation to show that area MT contributes to coarse judgments of absolute disparity but does not contribute to fine judgments of relative disparity. We hypothesized that this pattern of results arose because MT neurons do not carry relative disparity signals that are needed to perform the fine task with high precision (Westheimer, 1979; Prince et al., 2000), and we supported this hypothesis through single-unit recordings. Our findings provide a link between the neural representation of disparity in MT and the functional contributions of MT to depth perception.

Disparity sensitivity in MT versus V1

One potential explanation for our findings is that MT neurons do not have sufficient sensitivity to account for performance of the fine task. However, our single-unit recordings suggest otherwise. Although the average MT neuron is about half as sensitive as the monkey in the fine task, many MT neurons have thresholds comparable with those of the animals (Fig. 3). Thus, monkeys could base their fine disparity judgments on MT responses, but they apparently do not.

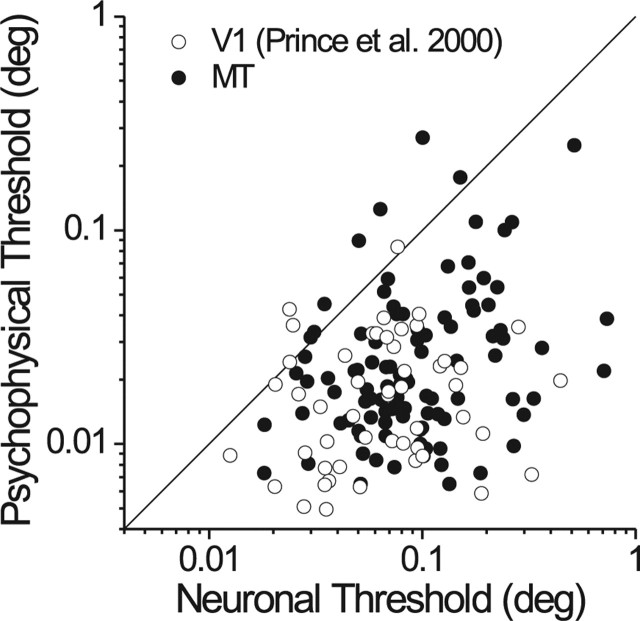
Given that MT neurons have substantially broader disparity tuning than V1 neurons (DeAngelis and Uka, 2003), one might expect V1 neurons to be more sensitive in the fine task. We compared our results to the V1 data of Prince et al. (2000). Because different ideal observer models were used in the two studies, we reanalyzed our MT data using their methods. Figure 9 compares the two datasets, and it is clear that the MT and V1 populations have very similar sensitivity overall. The median neuronal threshold in MT (0.083°) is slightly, but significantly, larger than the median threshold (0.069°) in V1 (Mann–Whitney U test, p < 0.01). Note, however, that Prince et al. (2000) excluded 60% (140 of 232) of their V1 neurons because of weak disparity tuning whereas we excluded only 9% (13 of 147) of our MT neurons for this reason. Given this sampling difference, it seems likely that neuronal sensitivity in MT is no worse than sensitivity in V1; indeed, the most sensitive neurons in both areas have comparable thresholds (Fig. 9). Despite several differences between visual stimuli used in the two studies (contrast, eccentricity, motion coherence, duration), psychophysical thresholds are also similar in the two datasets. Most importantly, the relative sensitivity of neurons to behavior is quite similar in the two studies, indicating that MT and V1 carry disparity signals with comparable precision.

Figure 9.

Comparison of neuronal sensitivity in V1 and MT for the fine task. V1 data (open symbols) are from the study by Prince et al. (2000), and MT data (filled symbols) are from the same sample as in Figure 3. For comparison with V1, the MT data were reanalyzed using the same orthoneuron formulation and fitting procedures used in the V1 study.

In theory, the amount of information that neurons carry about small variations in disparity is given by the local slope of the tuning curve divided by the SD of the response (Seung and Sompolinsky, 1993). Slope can vary either by a horizontal scaling of the width of the tuning curve, or by a vertical scaling of response strength. It appears that the broader tuning of MT neurons (compared with V1) is compensated by their stronger response modulation (DeAngelis and Uka, 2003) such that sensitivity to small disparity variations is comparable with that in V1.

If MT neurons are sensitive to small disparity variations, why doesn't MT contribute to performance of the fine task? It could be that some other visual area has disparity sensitivity far superior to that of either MT or V1, but there is currently no evidence for this. A more likely explanation is that MT lacks explicit relative disparity signals that are needed for fine disparity discrimination (Westheimer, 1979; Prince et al., 2000). Under normal viewing conditions, and especially in the presence of head and eye movements, vergence angle can be fairly unstable (Steinman et al., 1982; Steinman et al., 1985; Collewijn et al., 1991). Neurons that explicitly code relative disparities would be impervious to vergence errors, and would thus allow better discrimination of fine relative disparities.

Although the distinction between absolute and relative disparity processing is likely to be the critical difference between our two tasks, we cannot rule out contributions from other variables. The two tasks also differ in the range of disparities presented (coarse vs fine) and the presence/absence of disparity noise. Nevertheless, our results establish a task-specific contribution of MT to depth discrimination, and provide a highly plausible explanation for this specificity.

Other alternative explanations

Although a lack of relative disparity signals in MT most likely explains our findings, it is important to consider alternatives. First, it is unlikely that our results stem from one stimulus set eliciting more robust activity from MT neurons. Responses to 0% binocular correlation and responses at the steepest slope of the tuning curve both tend to lie near the midpoint of the dynamic range of an MT neuron (DeAngelis and Uka, 2003). Second, it is unlikely that microstimulation fails to bias relative disparity judgments simply because the visual and electrical stimuli activate heavily overlapping populations of neurons. Nichols and Newsome (2002) have shown that microstimulation of MT biases analog direction judgments when visual and electrical stimuli have similar directions. Britten and Van Wezel (1998, 2002) have shown that microstimulation of the medial superior temporal area biases fine discrimination of heading direction, a task with many similarities to our fine task. Third, it is unlikely that different “read-out” strategies explain the difference between our coarse and fine tasks. In the fine task, we placed the reference stimulus at the steepest slope of the tuning curve, under the assumption that neurons operating around this point are most relevant to the task (lower envelope principle, Parker and Newsome, 1998) because they carry the most information (Seung and Sompolinsky, 1993). If a coding strategy such as vector averaging is used (Groh et al., 1997; Nichols and Newsome, 2002), neurons with preferred disparities close to the reference will also contribute to perceptual decisions. Importantly, however, microstimulation would still shift the “hill” of activity in MT toward the preferred disparity of the stimulated neurons; thus, the predicted outcome would be the same if the monkey uses a vector-average strategy instead of a lower-envelope principle (Britten and Van Wezel, 2002). Fourth, it is unlikely that our results are an artifact of eye movements. If microstimulation changes the monkey's vergence angle, then the stimulated neurons may no longer be the ones that provide the critical disparity information. However, our analyses (Fig. 6) show that microstimulation does not alter vergence angle.

There may still be many possible explanations for a negative effect of microstimulation in the fine task. For example, the critical neurons could reside in MT but not be activated appropriately by microstimulation. However, preliminary results of an ongoing study (Chowdhury and DeAngelis, 2005) show that reversible chemical inactivation of MT (using muscimol) does not impair monkeys' ability to perform the fine task. Because microstimulation and inactivation have very different spatial specificities yet both produce compatible results, we gain confidence in our conclusion that MT plays little role in performance of the fine task.

Cortical representation of relative disparity

We suggest that MT microstimulation fails in the fine task because MT lacks an explicit representation of relative disparities that is needed to discriminate fine depth structure in the face of variations in vergence angle (Prince et al., 2000; Thomas et al., 2002). By this logic, neurons that code relative disparities are more likely to mediate fine depth discrimination. Where do these neurons reside? Whereas Cumming and Parker (1999) have shown that V1 neurons only signal absolute disparities, Thomas et al. (2002) have shown that a relatively small fraction of neurons in V2 are tuned for relative disparity. Relative disparity signals could be enhanced further along either the dorsal or ventral streams, because V2 provides input to both pathways (Felleman and Van Essen, 1991). Our MT data show that relative disparity signals are not more prominent at the next stage along the dorsal stream, suggesting that relative-disparity-selective V2 neurons may not project to MT. Rather, our data suggest that relative disparity signals are likely to be more prominent in V4, and preliminary results from Umeda et al. (2004) support this conjecture. Robust relative disparity signals in V4 may supply critical inputs to neurons in the inferotemporal cortex that signal 3D shape defined by disparity gradients (Janssen et al., 1999, 2000a,b).

Thus, a working hypothesis is that absolute disparity signals are emphasized in the dorsal stream to compute the location of objects in 3D space, whereas relative disparity signals are emphasized in the ventral stream to compute 3D shape (Parker, 2004; Neri, 2005). Recent results from human fMRI (Neri et al., 2004) also support this hypothesis, which should be amenable to direct tests in the monkey. However, not all data are consistent with this simple view (see also Neri, 2005). Some MT neurons signal 3D surface tilt independent of absolute disparity (Nguyenkim and DeAngelis, 2003), which suggests that these neurons possess a form of relative disparity selectivity in response to linear gradients of disparity. In contrast, we do not see any clear relative disparity selectivity in MT using center-surround stimuli (Fig. 8). This highlights the point that relative disparity selectivity, in general, may be highly dependent on stimulus configuration. Tilt selectivity in MT was usually seen only at large slants (Nguyenkim and DeAngelis, 2003). Thus, this mechanism may be involved in representing the coarse 3D spatial layout of a scene, but may not be useful for fine depth or shape discrimination. We cannot firmly rule out the possibility, however, that performance of the fine task may depend on the activity of neurons for which the relative disparity boundary falls in the center of the receptive field.

In conclusion, our study addresses the fundamental question of how neural representations of sensory information are specialized for different purposes. By showing that the neural representation of disparity in MT can account for a task-specific contribution of this area to depth discrimination, we have clarified the roles that MT plays in 3D vision.