Modeling and Sensitivity Analysis of Acoustic Release of Doxorubicin from Unstabilized Pluronic P105 using an Artificial Neural Network Model

Abstract

This paper models steady state acoustic release of Doxorubicin (Dox) from Pluronic P105 micelles using Artificial Neural Networks (ANN). Previously collected release data were compiled and used to train, validate, and test an ANN model. Sensitivity analysis was then performed on the following operating conditions: ultrasonic frequency, power density, Pluronic P105 concentration, and temperature. The model showed that drug release was most efficient at lower frequencies. The analysis also demonstrated that release increases as the power density increases. Sensitivity plots of ultrasound intensity revealed a drug release threshold of 0.015 W/cm² and 0.38 W/cm² at 20 and 70 kHz, respectively. The presence of a power density threshold provides strong evidence that cavitation plays an important role in acoustically activated drug release from polymeric micelles. Based on the developed model, Dox release is not a strong function of temperature, suggesting that thermal effects do not play a major role in the physical mechanism involved. Finally, sensitivity plots of P105 concentration indicated that higher release was observed at lower copolymer concentrations.

Introduction

Pluronic P105 copolymer forms dense micelles at a concentration of 4% or above (1). These micelles are capable of encapsulating chemotherapeutic agents and releasing their contents using acoustic energy (2–11). Similarly, we have shown that acoustically activated drug release increases with increasing power densities and decreasing frequencies (4). Our research group has also reported that P105 micelles stabilized with an interpenetrating network of N,N-diethylacrylamide can be acoustically stimulated to release Doxorubicin (Dox) (2). Recently, we have shown that acoustically activated drug release from unstabilized Pluronic P105 micelles is highly correlated to the appearance of a subharmonic peak in acoustic spectra, revealing the important role of cavitation in this release phenomenon (3). In all of our experiments, a custom made ultrasonic exposure chamber with fluorescence detection was used to investigate drug release from micelles. The apparatus was designed to measure real-time release kinetics of Dox from different micellar systems including stabilized and unstabilized Pluronic P105 micelles. Dox exhibits a substantial decrease in fluorescence when transferred from the hydrophobic poly-propylene-oxide (PPO) core of the micelle to the surrounding aqueous solution (2, 6).

Mechanistic models were used to predict the kinetics of release and re-encapsulation in an attempt to optimize the application of ultrasound in future in vivo experiments (6). That study showed that the model with zero-order release and first-order predicted experimental data compared to the three other proposed models. Although this mechanistic model was able to approximate the kinetics of both release and re-encapsulation, the range of data used in that study encompasses limited operating conditions including power density, frequency, Pluronic P105 concentration, and temperature.

The complex nature of this novel drug delivery system prompts the need for a modeling technique that can be used to predict drug release at a wider range of operating conditions. Such models can be utilized to mimic and extrapolate the behavior of drug loaded micelles without the need for further extensive experimentation.

In the research described in this paper, artificial neural network models (ANNs) were used to predict drug release as a function of the four variables mentioned above. Such modeling entails using a large number of experimental data to reconcile model predictions with actual release measurements in order to validate the ANN model. The next section provides a brief background and describes the methodology used in neural network modeling.

Neural Networks Modeling: Background and Methodology

The development of artificial neural networks started in the early middle of the last century to help cognitive scientists in understanding the complexity of the nervous system. These models evolved steadily and were adopted in many areas of science. Basically, ANNs are numerical structures inspired by the learning process of the human brain. They are constructed and used as alternative mathematical tools to solve a diversity of problems in the fields of system identification, forecasting, pattern recognition, classification, control, and many others (12–15). The interest in ANN as a mathematical modeling tool resulted in the consolidation of its theoretical background and the development of its underlying learning and optimization algorithms.

Our area of interest in this paper is the modeling and simulation using Pluronic P105 micelles as drug delivery vehicles and acoustic power as a trigger mechanism. The implementation of empirical correlations for this complex system involves a great deal of mathematical and in many instances lacks the desired accuracy. Neuron-based modeling can be used confidently as a substitute in such situations. This is due to the favorable features entailed in their use, such as simplicity, fault and noise tolerance, plasticity (the ability to retain its prediction efficiency even after the removal or damage of some of its neurons), black box modeling methodology, and robustness (the capability to adapt to process changes).

ANNs can be categorized, in terms of their topology, as single and multi-layer feedforward networks (FFNN), feedback re-encapsulation most closely networks (FBNN), recurrent networks (RNN), and self-organized networks. In addition, they can be further categorized in terms of application, connection type, and learning method. The most commonly used type of networks is the feedforward networks (FFNN) shown in Figure 1. This network topology is composed of one input layer, one output layer, and a minimum of one hidden layer. The term feedforward describes the way in which the output of the FFNN is calculated using its input layer-by-layer throughout the network. No matter how complex the network is, its building block is a simple structure called the neuron. It performs a weighted sum of its inputs and calculates an output using certain predefined activation functions. Activation functions for the hidden units are needed to introduce the nonlinearity into the network. Sigmoidal functions, such as logistic and tanh, and the Gaussian function, are the most common choices of activation functions. The neural system architecture is defined by number of neurons and the way by which the neurons are interconnected. The network is fed with a set of input-output pairs and trained to reproduce the outputs. The training is done by adjusting the neurons weights and biases using an optimization algorithm that attempts to minimize the quadratic error between experimental data and computed outputs. The performance function used in the optimization is usually based on the squared difference between the actual observed output a_i and the network prediction t_i for n sample points (14, 15).

Figure 1.

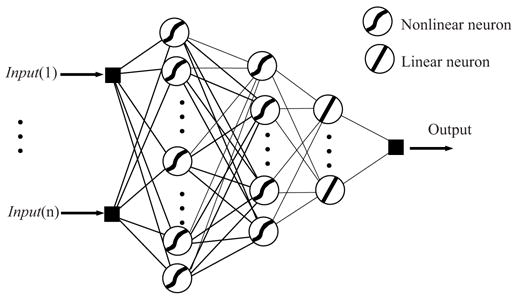
General structure of a three layers feedforward ANN.

$$\text{Performance\hspace{0.28em}Index}=\frac{1}{n}\left[\sum _{i=1}^n{({\mathbf{t}}_{\mathit{i}}-{\mathbf{a}}_{\mathit{i}})}^2|\right]$$ [1]

Input-target training data are usually pretreated in order to improve the numerical condition of the optimization and training process. Thus, the data is normally divided into three subsets:process training, validation, and testing. The training subset is used to accomplish network learning and fit network weights by minimizing an appropriate error function. Backpropagation is the training technique usually used for this purpose. It refers to the method for computing the gradient of the case-wise error function with respect to the weights of the feedforward network. The performance of the network is then independently compared by evaluating the error function using the validation subset. The testing subset data is then used to measure the generalization of the network (i.e., how accurately the network predicts outputs for inputs that are not in the training set). This process is sometimes referred to as hold-out validation.

Selecting the network structure is a crucial step in the overall design of ANNs. The structure must be optimized to reduce computer processing, achieve good performance and avoid overfitting. The selection of the best number of hidden units depends on many factors. The size of the training set, the amount of noise in the targets, the complexity of the sought function to be modeled, the type of activation functions used and the training algorithm all have interacting effects on the sizes of the hidden layers. There is no way to determine the best number of hidden units without training several networks and estimating the generalization error of each. If there are few hidden units, then high training and high generalization errors due to underfitting may occur. On the other hand, if many hidden layers are used, low training error can be achieved, but network generalization degrades (16). A good reference on the feedforward networks and its applications is given by Fine (17).

Materials and Methods

Materials

Pluronic P-105 was provided by BASF Corp. (Mount Olive, NJ); Doxorubicin (Dox) was obtained from the University of Utah Hospital (Salt Lake City, UT) in a 1:5 mixture with lactose and from Pharmacia & Upjohn Company (Kalamazoo, MI); it was dissolved in phosphate buffered saline (PBS) and sterilized by filtration through a 0.2 μm filter (Millipore Billerica, MA). The pH of PBS was 7.4.

Drug Encapsulation in Pluronic Micelles

Stock solutions of Pluronic (BASF, Mount Olive, NJ) were prepared by dissolving P105 in a PBS solution to the desired final concentration. Dox was dissolved into the P105 solutions at room temperature (37 °C) to produce a final Dox concentration of 10 μg/ml. The same drug concentration was also prepared in PBS (pH =7.4).

Measuring Ultrasound-triggered Release of Dox From Pluronic P105 Micelles

The chamber was built to measure the change of fluorescence level with and without the application of ultrasound. Details were described previously (4). Briefly, an argon-ion laser beam at 488 nm was directed to either a cuvette or a tube containing the encapsulated drug. The emissions were collected using a fiber optic collector and filtered to remove the excitation wavelength. Then these emissions were quantified using a photodetector on an oscilloscope and subsequently stored on a computer for further analysis (4).

The decrease in fluorescence of the encapsulated drug solution was assumed to be directly proportional to the amount of drug released relative to a known baseline. The fluorescence of Dox in PBS, in the absence of Pluronic, was measured to simulate 100% release. Then the percent release was calculated as follows:

$$\%\mathrm{\hspace{0.17em} }\text{release}=\frac{I_{P105}-I_{US}}{I_{P105}-I_{\mathit{PBS}}}\times 100\%$$ [2]

where, I_US is the fluorescence intensity upon exposure to ultrasound, I_PBS is the fluorescence intensity in a solution of Dox in PBS, and I_P105 is the intensity recorded when the drug is encapsulated in Pluronic P105 (which corresponds to 0% release or 100% encapsulation).

In these experiments, the fluorescence intensity of the drug in PBS was measured both with and without the application of ultrasound. Ultrasonic power at 67, 80, and 90 kHz was generated using a Sonicor SC-100 ultrasound bath (Sonicor Instr., Copaique, N. Y.). The intensity of ultrasound was controlled by adjusting the input voltage using a variable A.C. transformer (Variac). Ultrasound at 20 kHz was generated using a probe transducer (Sonics and Materials, Newton, CT) inserted into the water bath. While the sonication at 47 kHz was performed in a Cole-Parmer sonication bath (Cole-Parmer, Mount Vernon, IL). The insonation intensity was determined using a calibrated hydrophone (Bruel and Kjaer model 8103, Decatur, GA). The power densities used in data collection fell in the range of 0–0.06 W/cm² at 20 kHz, and 0–2.8 W/cm² at 47, 67, 80, and 90 kHz. Three different temperatures were used in these experiments: 24 °C, 37 °C, and 56 °C. Finally, four polymeric concentrations were used in the modeling: 0.1%, 1%, 5%, and 10%. Further details can be found in (4).

Ultrasonic power at 67, 80, and 90 kHz was generated using a Sonicor SC-100 ultrasound bath (Sonicor Instr., Copaique, N.Y.), which employs two flat piezoelectric transducer mounted on the underside of the stainless steel tank. The waveform can be described as a 67, 80, or 90 kHz signal that is amplitude modulated sinusoidally at about 120 Hz. The geometry of the bath creates standing waves, and the tube or cuvette with the sample was placed in a region of high power density (or intensity), usually directly above one of the transducers. The insonation intensity at the sampling point was determined using a calibrated hydrophone (Bruel and Kjaer model 8103, Decatur, GA). The intensity of ultrasound was controlled by adjusting the input voltage using a variable A.C. transformer (Variac). In other experiments, 20 kHz ultrasound was generated using a probe transducer (Sonics and Materials, Newton, CT) inserted adjacent to the tube or cuvette in the water bath. This instrument produced a continuous sinusoidal waveform, and acoustic waves radiate spherically from the tip of the probe. Reflections in the water bath created standing waves. Again, the intensity at the sampling point was measured with the hydrophone. Further details can be found in (4).

Results and Discussion

ANNs were applied to model acoustically activated drug release from polymeric micelles. The aim is to predict drug release as a function of the following input variables: frequency, power density, polymer concentration, and temperature. The MATLAB neural networks toolbox (18) was used for this analysis.

Drug release experimental data (3, 4) were grouped in five vectors (four inputs and one output) and were sorted and pre-processed to fall in the range [−1, 1] by calculating the minimum and maximum of each vector variable and then scaling the data with respect to these limits. This was achieved using the MATLAB function premnmx. This improves the efficiency of the network training. The data set with 359 data points was subdivided into three subsets namely: training, validation, and testing. The size ratio of these subsets was 2(training):1(validation):1(testing), respectively.

The network structure was selected after running some preliminary simulations to explore the training speed and response time of different structures. To keep the network structure as simple as possible, three layers were used in all networks: one input layer, one hidden layer, and one output layer. The number of neurons in the input and output layers was limited to the number of input and output variables provided. Consequently, four neurons were used in the input layer and one neuron in the output layer. On the other hand, the number of neurons in the hidden layer was selected after testing the performance of different network combinations. It was observed that the least number of neurons in the hidden layer, which converged to a final acceptable solution, was eight neurons. This structure ensures training with reasonable speed for a specific network performance. The constituents of the network layers (i.e., types of neurons used), were taken to be tansigmoidal for the input and hidden layers, whereas linear neurons were used for the output layer. This is a common choice for function approximation neural networks (18).

The optimization algorithm used for network training was the Levenberg-Marquardt. The MATLAB routine trainlm with memory reduction was used for the optimization. Previously, we found that this algorithm attains fast learning speed and high performance relative to other optimization algorithms. The details of this algorithm are given by Hagan (19). The optimization performance target was set to 1 × 10⁻⁵.

Based on this selected network structure, the training process achieved the performance target for maximum training epochs of 3000. The learning rate was chosen to be 0.1. This value ensures stable fast learning. The training took approximately 10 minutes without any violation to the validation error. Figure 2 represents the SIMULINK interface for the ANN drug release model. As mentioned earlier, four input variables are used (frequency, power density, pluronic concentration, and temperature). The output variable is drug release. Figure 3 shows a linear correlation between experimental and network predictions of drug release (R² = 0.957). As can be seen from the figure, the network gave accurate predictions with most predictions within the 95% confidence limit. Figure 4 shows the complete experimental dataset and the corresponding ANN predictions. Additionally, Figure 5 shows neural network training versus the standard square of error. Clearly, the square of error decreases as the number of epochs increases.

Figure 2.

The SIMULINK interface for the ANN drug release model. Four input variables are used (frequency, power density, pluronic concentration, and temperature). The output variable is drug release percent.

Figure 3.

A plot of Neural Network (NN) predictions versus experimental data. The plot shows a linear fit with an R ² = 0.957.

Figure 4.

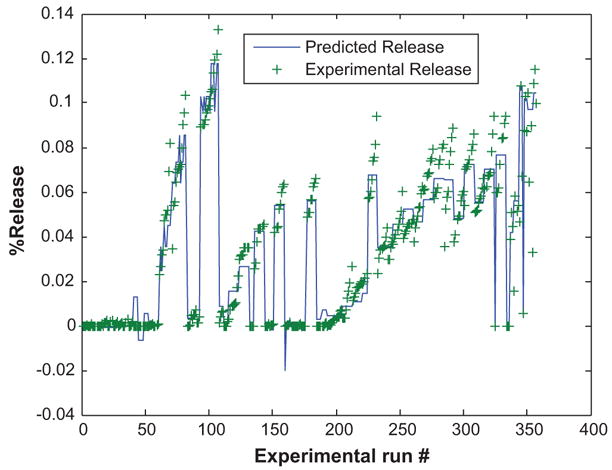
Comparison of NN drug delivery model predictions with experimental data. The plot shows the model simulation output (−) and the experimental data (+).

Figure 5.

Variation of Standard Square of Error with Neural Network training Epochs.

Following the training of the network, post-processing of the output data vector was performed using the same scaling parameters determined in the pre-processing stage. The MATLAB function postmnmx was used for this purpose. A Matlab/Simulink simulation model was built for the trained network. This was achieved by converting the Matlab network structure into a Simulink block and defining the Input/Output ports, data processing, and simulation parameters. The model input was configured in a form of pre-assigned sequences for the four input variables. These sequences allow the user to vary input variables simultaneously or individually in order to characterize the effect of these variables on drug release. As such, different sensitivity profiles were obtained as shown below.

Effect of Ultrasonic Frequency on Drug Release

Figure 6 depicts a sensitivity plot of Dox release versus frequency at several power densities, a constant bath temperature of 37 °C, and a Pluronic P105 concentration of 10%. The plot indicates that drug release from micelles was most efficient at lower frequencies. This is in agreement with all previously published data (4). At higher frequencies, higher power densities are needed to obverse the same amount of Dox release as those measured at lower frequencies. Lower frequencies have more energy capable of perturbing the micelles (either by microstreaming or shock waves during cavitation events), thus allowing Dox to escape out of the micelle and into the surrounding aqueous environment.

Figure 6.

The drug release sensitivity plots of frequency. (Power densities = 0.2, 0.3, 0.4, and 0.5 W/cm², Temp = 37 °C, Concentration = 10%).

Drug Release as a Function of Power Density

Figures 7 and 8 demonstrate that release increases as the power density increases. This behavior is expected because higher ultrasonic intensities are capable of perturbing the micelles more vigorously, which leads to the drug release observed here. Figures 7 and 8 indicate the presence of a release threshold at approximately 0.02 and 0.38 W/cm² for 20 and 70 kHz, respectively. This power density threshold has been related to the emergence of a subharmonic peak in acoustic spectra, which would indicate that cavitation events play an important role in this release phenomenon. It should be noted here that drug release versus the power density is linear at 20 kHz while it shows a non-linear behavior at 70 kHz. This is mainly due to the nature of the fitting function used in ANN that attempts to fit all experimental data collected at this higher frequency.

Figure 7.

The drug release sensitivity plot of power density at 20 kHz. (Temp = 37 °C, Concentration = 10%).

Figure 8.

The drug release sensitivity plot of power density at 70 kHz. (Temp = 37 °C, Concentration = 10 %).

Drug Release as a Function of Temperature

Figure 9 shows a sensitivity plot of Dox release versus temperature at several power densities, a Pluronic Concentration of 10%, and 70 kHz ultrasound. It suggests that hyperthermic effects do not play a major role in the amount of drug released. However, the role of temperature becomes more pronounced at lower power densities. This confirms previous reports that the observed drug release is not attributed to the increase in the local temperature of the sonicated regions, but rather to non-thermal mechanical effects (8).

Figure 9.

The drug release sensitivity plot of temperature. (Power densities = 0.8, 0.9, and 1 W/cm², Concentration = 10%, Frequency = 70 kHz).

Drug Release as a Function of Pluronic Concentration

Figure 10 shows the sensitivity plot of Dox release versus weight percent of Pluronic P105 at a power density of 1 W/cm², a temperature of 37 °C, and two different frequencies. Higher drug release from P105 micelles as the concentration of the copolymer decreases may be attributed to the higher local concentration of the drug in the coploymer’s core. The increase in the hydrophobic/hydrophobic interaction between the PPO core of the micelle and Dox at higher P105 concentration reduces micellar perturbation caused by ultrasound. Thus, less drug molecules are able to diffuse out of the micelle, which in turn minimizes observed release. We speculate that these micellar perturbations are caused by microstreaming or shock waves during cavitation events.

Figure 10.

The drug release sensitivity plots of Pluronic P105 concentration. (Power density = 1 W/cm², Temp = 37 °C, Frequency = 20 kHz and 90 kHz).

Our previous research has shown that drug release is not based on ultrasonic thermal effect. Instead, there are several non-thermal effects caused by ultrasound that include oscillating bubbles, radiation pressure, radiation torque, and acoustic streaming. These effects play an important role in increasing the convection and subsequent transport of the drug. Cavitation occurs when a gas bubble expands and contracts in size in response to the oscillating pressure during sonication. Bubbles with a natural resonance frequency that match the frequency of ultrasonic activation are capable of achieving the highest amplitude of cavitation or oscillation. When the power density increases the size of the bubble approaches the resonance size that causes extreme non-linear bubble oscillations. This results in the destruction of the bubble. The collapse is typically attributed to the increase in the inward-moving water surface so that it overcomes the pressure inside the bubble. This phenomenon is referred to as transient or collapse cavitation. It is capable of creating shock waves, increasing the local pressure by 100 atm, and the local temperature by several thousands of degrees (K). Several reports in literature have shown that shockwaves can cause substantial cell damage and possible cell lysis. Another adverse bioeffect is caused by free radicals generated during bubble collapse. It is important to note here that stable (non-inertial) cavitation, where bubbles are able to cavitate without imploding, is capable of causing some bio-effects (20). As the bubble oscillates, high shear stresses are created near the bubble surface that can create micropores in the cell membrane, thereby making the cell more permeable to other macromolecules present in the vicinity (21, 22).

Subharmonic and higher harmonic emissions are characteristics of cavitation events (both stable and collapse) and are caused by bubbles oscillating at half (f/2), and nf/2 of the driving frequency (f), respectively. In addition to these harmonic emissions, collapse cavitation has been correlated with the intensity of the non-harmonic background noise generated by shock waves as bubbles are destroyed. Figure 8 suggests that the release of Dox from P105 micelles has a threshold of acoustic intensity of approximately 0.38 W/cm² at 70 kHz. Several studies have shown that inertial cavitation has an apparent threshold (this is one of the reasons why cell lysis is usually attributed to inertial cavitation events) (23–25). However, Liu et al. (26) have shown that under certain conditions hemolysis (red blood cell lysis) is caused by stable or non-inertial cavitation. Stable cavitation does not have an intensity threshold because any level of pressure oscillation will cause the bubble to expand and contract in an acoustic field. Again, it is important to keep in mind that biological effects of stable cavitation have a power density threshold; although, substantially lower than that observed for inertial cavitation. The presence of a power density threshold in Figures 7 and 8 suggest that acoustically activated drug release from unstablilized P105 micelles is caused by collapse rather than stable cavitation. The threshold of collapse cavitation increases as the frequency of ultrasound increases. For example, the onset of collapse cavitation at 20 kHz occurs at approximately 0.015 W/cm² while at 70 kHz this threshold increases to 0.38 W/cm².

Although most of our studies were conducted using an isothermal water bath at 37 °C, to simulate physiological conditions, we have investigated the effect of temperature upon release. This was done in an attempt to rule out the possibility that the absorption of ultrasonic energy by the micelle raises the local temperature and activates release by decreasing the local viscosity of the micellar core, thus rendering Dox molecules more mobile. Figure 9 shows that Dox release is not a strong function of temperature, suggesting that thermal effects do not play an important role in the physical mechanism involved with this drug delivery technique.

Finally, it is worth mentioning here that several factors should be considered when measuring the release of chemotherapy drugs in vivo whereby micelles are able to circulate freely in the blood stream. The hydrophobic nature of anti-neoplastic agents will complicate the sequestration process after the drug has been released via ultrasonic stimulus. Other hydrophobic molecules circulating in blood, e.g., albumin, will compete with Pluronic micelles to re-encapsulate acoustically released drug molecules. Additionally, ultrasound has to be carefully focused and controlled to prevent cell lysis in the healthy tissues surrounding the sonicated tumor. Sonolysis (cell lysis observed when tissues are exposed to acoustic energy) is caused by transient cavitation events whereby cavitating bubbles implode near the membrane of sonicated cells causing substantial damage to various cellular compartments and leading subsequently to cell death.

Conclusion

In conclusion, neural network models can be used to model and predict the acoustic release of Dox from Pluronic P105 micelles. ANNs are simple to apply and are capable of providing robust and accurate predictions. This modeling will enable optimizing the operating conditions, which can be used in future in vivo experiments.