The narrow escape problem for diffusion in cellular microdomains

Abstract

The study of the diffusive motion of ions or molecules in confined biological microdomains requires the derivation of the explicit dependence of quantities, such as the decay rate of the population or the forward chemical reaction rate constant on the geometry of the domain. Here, we obtain this explicit dependence for a model of a Brownian particle (ion, molecule, or protein) confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. We call the calculation of the mean escape time the narrow escape problem. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation problem. Here, we present asymptotic formulas for the mean escape time in several cases, including regular domains in two and three dimensions and in some singular domains in two dimensions. The mean escape time comes up in many applications, because it represents the mean time it takes for a molecule to hit a target binding site. We present several applications in cellular biology: calcium decay in dendritic spines, a Markov model of multicomponent chemical reactions in microdomains, dynamics of receptor diffusion on the surface of neurons, and vesicle trafficking inside a cell.

The function of biological microdomains, and specifically neurobiological microstructures, such as dendritic spines, is largely unknown, and much effort has been spent in the last 20 years to unravel the molecular pathways responsible for the maintenance or modulation of cellular functions and, ultimately, to extract fundamental principles (1, 2). The cytoplasm of eukaryotic cells is a complex environment where dynamic organelles, cytoskeletal network, and soluble macromolecules are organized in heterogenous structures and local microdomains (3). These submicrometer domains may contain only a small number of molecules, of the order between just a few and up to hundreds. This is the case in microdomains like endosomes (4), synapses (5), and the sensory compartments of cells, such as the outer segment of photoreceptors, but at such low molecular number, the addition of external chemical binding dye molecules, necessary for experimental purposes, may alter the signaling pathway and thus modify the physiological phenomenology. This circumstance calls for physical and mathematical modeling to separate the interfering effects, and ultimately the physical–mathematical model is expected to be a fundamental tool for both the quantitative and qualitative study of chemical reactions in microdomains.

Because of the small number of molecules involved in chemical reactions occurring in extremely confined domains (such as endoplasmic reticulum, caveolae, and mitochondria, to obtain quantitative information about chemical processes, modeling and simulations seem to be inevitable to reconstruct the microdomain's environment and to obtain precise quantitative information about the molecular dynamics. However, most of the existing models are based on continuum concepts, in which the medium is assumed homogeneous and the number of molecules involved is assumed sufficiently large, which is not the case here.

To derive principles and to guess the role of a microdomain, we have developed various computations to quantify precisely the role of the geometry in molecular diffusion. The narrow escape problem deals with computing the mean time that a Brownian particle takes to diffuse to a small absorbing portion of an otherwise reflecting boundary of a given domain. As the absorbing boundary shrinks to zero, the mean time to absorption diverges to infinity, rendering the narrow escape a singular perturbation problem. Once formulated in terms of boundary value problems for partial differential equations, their singular perturbation analysis yields explicit asymptotic expressions for the mean escape time, depending on the diffusion coefficient, the ambient potential, dimensions, and the local and global geometrical properties of the domain, and its boundary.

The narrow escape or the small hole computation leads to the development of Markov models of chemical reactions and accounts for the small number of molecules involved. After presenting the modeling framework of the narrow escape, we discuss several applications of the present theory to calcium dynamics in dendritic spines, the forward binding rate of chemical reactions, receptor trafficking on the surface membrane of cells, and an application to vesicle trafficking in neuronal growth.

Formulation and Mathematical Results

We assume that biological particles (e.g., an ion, molecule, or receptor) diffuse in a field of force (such as electrical potential) and that their motion can be described by the overdamped Langevin–Smoluchowski (6) equation:

where

γ is the friction coefficient per unit of mass, F(x) the force per unit of mass, T is absolute temperature, m is the mass of the molecule, k_B is Boltzmann's constant, and ẇ is a vector of independent δ-correlated Gaussian white noise, which represent the effect of the thermal motion. The derivation of the Smoluchowski equation (Eq. 1) is given in refs. 7 and 8 for the three-dimensional motion of a molecule in solution, where Einstein's formula (Eq. 2) can be applied. In two dimensions, such as for diffusion of a cylinder in the surface of a membrane, the diffusion coefficient is given by the Saffman–Delbrück formula (9)

where μ is the viscosity of the solution, μ′ is the viscosity of the membrane, h the length of the cylinder, a is its radius, and γ_E is Euler's constant 0.5772. …

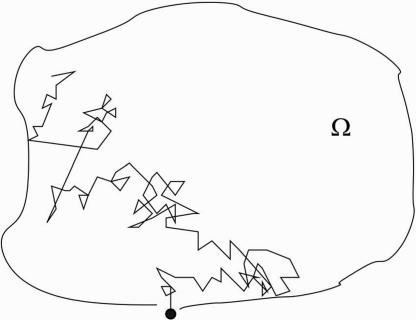
A generic problem in cellular biochemistry is to estimate the mean sojourn time of a Brownian particle in a bounded domain Ω before it escapes through a small absorbing window ∂Ω_a in its boundary ∂Ω. The remaining part of the boundary ∂Ω_r = ∂Ω − ∂Ω_a is assumed reflecting for the particle. The reflection may represent a high potential barrier on the boundary, or an actual physical obstacle. The opening may represent a narrow corridor in the barrier or a defect in the physical obstacle (see Fig. 1).The biological interpretation of the mean sojourn time is discussed below.

Fig. 1.

The escape of a Brownian trajectory through a small window.

The escape time can be estimated asymptotically in the limit

The probability density function (pdf) p_ε (x, t) of the trajectories of Eq. 1 is the probability per unit volume (area) of finding the Brownian particle at the point x at time t prior to its escape. The pdf satisfies the Fokker–Planck equation,

with the initial condition

and the mixed Dirichlet–Neumann boundary conditions t > 0

where ρ₀(x) is the initial pdf [e.g, ρ₀(x) = 1/|Ω| for a uniform distribution or ρ₀(x) = δ(x − y), when the molecule is initially located at position y]. In the later case, the function

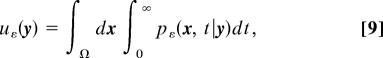where p_ε (x, t| y) is the pdf conditioned on the initial position, represents the mean conditional sojourn time. It is the solution of the boundary value problem (7)

Eq. 12 is the adjoint boundary condition to Eq. 8. The survival probability is

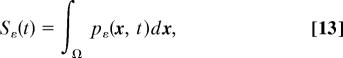where

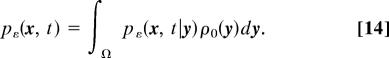The density p_ε(x, t| y) can be computed by expanding in eigenfunctions

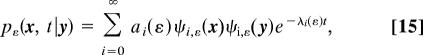where λ_i(ε) (resp. ψ_i,ε) are the eigenvalues (resp. eigenfunctions) of the Fokker–Planck operator in Eqs. 5, 7, and 8 and the coefficients a_i(ε) depend on the initial function ρ₀(y). The mean sojourn time can be expressed using the expansion represented by Eq. 15 (7),

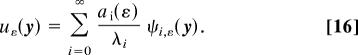When ε > 0, the eigenvalues are strictly positive so that the steady state is

(the Brownian particle escapes in finite time with probability 1) and the mean sojourn time is asymptotically 1/λ₀(ε) when ε ≪ 1. Thus λ₀(ε) → 0 as ε → 0. For free Brownian motion [with F(x) = 0], λ₁(ε) = O(1) in this limit. Approximating the pdf, solution of Eq. 8 by

shows that under the small hole approximation, the survival probability is exponentially distributed,

because

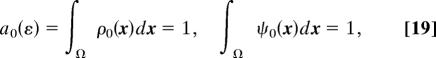due to normalization. If the medium contains initially N₀ independent particles, the population N(t) decays exponentially with rate λ₀(ε),

The asymptotic solution of Eqs. 10–12 depends on the dimension (2 or 3) and the local geometry near the small opening (10–13). When the boundary of the domain is regular, the escape time u_ε(y) is given for ε ≪ 1 (ε is the angle of the absorbing boundary) by

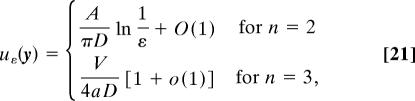where a represents the small radius of a geodesic disk located on the surface of the domain Ω and depending on the dimension, A (resp. V) is the surface (resp. volume) of the domain Ω. The function u_ε(y) does not depend on the initial position y, except for a small boundary layer near ∂Ω_a, due to the asymptotic form found in refs. 10–13.

In dimension 2, the first-order term matters, because, for example, if ε ≈ 10⁻¹, then ln 1/ε ≈ 2.3, so the second term in the expansion (Eq. 21) is comparable to the leading term. The second term can be found when Ω is a circular disk of radius R and the particle starts at the center (12, 13), as

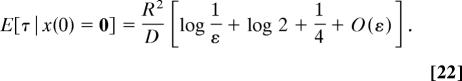The escape time, averaged with respect to a uniform initial distribution in the disk, is given by

The geometry of the small opening can affect the escape time: If the absorbing window is located at a corner of angle α, then

More surprising, near a cusp in a two-dimensional domain, the escape time Eτ grows algebraically, rather than logarithmically: In the domain bounded between two tangent circles, the escape time is

where d > 1 is the ratio of the radii. Finally, when the domain is an annulus, the escape time to a small opening located on the inner circle involve a second parameter, which is β = (R₁/R₂) < 1, the ratio of the inner to the outer radii, the escape time, averaged with respect to a uniform initial distribution, is

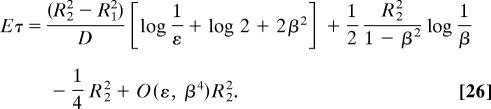Eq. 26 contains two terms of the asymptotic expansion of E_τ, and 2ε is the angle of the absorbing boundary. The case β ≈ 1 remains open, and, for general domains, the asymptotic expansion of the escape time remains an open problem, as does the problem of computing the escape time near a cusp point in three-dimensional domains. For Brownian motion in a field of force F(x) ≠ 0 the gap in the spectrum is not necessarily between the first and the second eigenvalues, depending on the relative size of the small hole and force barriers the particle has to overcome in order to escape. The escape stream is not necessarily Poissonian (14).

Calcium Diffusion in Dendritic Spines

Dendritic spines are small protrusions located on the surface of a neuronal dendrite; they receive most of the excitatory inputs, and their physiological role is still unclear. The number and the shapes of the spines are highly correlated with cortical and synaptic plasticity (15, 16). Moreover, calcium dynamics in dendritic spines is a fundamental signal, which can trigger physiological changes involved in remodeling the synaptic weight (1, 2, 5). The small hole computation of a single Brownian particle can be used to estimate the rate of calcium clearance as a function of the dendritic spine geometry. The present computation improves the approximation of this rate attempted in refs. 17 and 18, which was used in many studies to interpret experimental data (19, 20).

Calcium diffusion involves many pathways (15): It can bind to calcium buffers or calcium binding molecules, enter the endoplasmic reticulum, or be pumped out through exchangers or pumps. The escape time determines much of the time course of calcium dynamics and its dependence on the geometry of a dendritic spine. We approximate the shape of a dendritic spine by a spherical head Ω connected to the rest of the dendritic shaft by a cylindrical neck of length L and radius a. In this approximation, the radius of the neck is small relative to that of the spine head, so the mean time for a diffusing ion (which cannot return to the head once it is in the neck) to escape a dendritic spine by diffusion alone can be decomposed into the mean time to find the small absorbing window (the neck) plus the mean time to escape into the dendritic shaft. The former is approximated by Eq. 21, while the second time is L²/2D, which gives the mean escape time as

According to Eq. 18, the time course of calcium dynamics can be approximated by a single exponential with rate constant λ = 1/τ. For example, in a dendritic spine of length L = 1 μm, volume V = 1 μm³, radius a = 0.1 μm, and diffusion coefficient D = 400 μm²/s, we have (V/4aD) = 6.25 ms, while (L²/2D) = 1.25 ms; thus, the total time is τ ≈ 7.5, which gives an estimate of the diffusion time scale in spine (21). The influence of pumps on calcium dynamics has been investigated in ref. 22. It was shown that they affect the dynamics by shifting the extrusion rate. To compute the shift, consider N pumps with an identical extrusion rate, ξ, uniformly distributed along the neck. Then the total extrusion rate is

It is known that the geometry of the dendritic spines changes depending on variables such as exposure to calcium concentration (15, 19, 21). That is, dendritic spines can regulate dynamically their geometry and possibly the distributions and the number of pumps. Thus they dynamically regulate the fraction of calcium reaching the dendrite. The ratio of pumped ions to arriving ions can be evaluated according to several parameters. We demonstrated in ref. 22 that the distribution of pumps along the spine neck can modulate such a ratio. On the other hand, given a fixed number of pumps, there exists a critical length such that above it the spine head is effectively isolated and below it the spine head conducts calcium (21).

Finally, the radius of the spine neck does not play a significant role in calcium diffusion inside a thin spine neck when it is approximated as a small cylinder, because this parameter enters only in the second exponential in the sum (Eq. 15), while the neck length directly enters the first one. Using the narrow escape computation, it is possible to compute the effect of crowding ions in a dendrite, which modifies the calcium time course by directly changing the expression of the first exponential decay rate.

Markov Model of Chemical Reactions with a Small Number of Molecules

The forward binding rate of a chemical reaction as it was previously computed does not make much sense when only a few molecules are involved. Indeed, the widely used Smoluchowski formula k = 2πRD[X] (6) for the binding rate k of Brownian particles with diffusion coefficient D and concentration [X], improved in refs. 23 and 24, assumes infinite medium and a spherical absorbing or partially absorbing surface of radius R. These assumptions obscure the role of the restricted geometry of microdomains and thus cannot adequately describe chemical reactions in microdomains. As we will see now, our explicit analytical formula (Eq. 21) for the mean time to diffuse to a small absorbing (binding) portion of the boundary of a microdomain determine the explicit dependence of k on the shape of the domain.

In a closed microdomain Ω, a chemical reaction that involves only a few species, such as

can be described in terms of a Markov process. We assume that M molecules (total number is M₀) are diffusing inside a domain Ω and can be bound to a substrate S consisting of a single site S₀ = 1, of small size a, located on the boundary [the general analysis of a chemical reaction of a ligand with a substrate is given in supporting information (SI) Appendix 1. We assume here that the number of M molecules that can be bound to S is not limited. The mean time for a diffusing molecule to unbind is (1/k₋₁) and depends only on the local potential (7, 25). It is given by the Arrhenius law

where C is a constant that depends on the temperature T_e, the electrostatic potential barrier ΔE generated by the binding molecule, and the friction coefficient, while k₁ represents the forward rate, which is given by the small window approximation a ≪ 1 as

The probabilities p_k(t) = Pr{M_b(t) = k} that there are exactly k M_b molecules produced at time t satisfy the master equations (see SI Appendix 1)

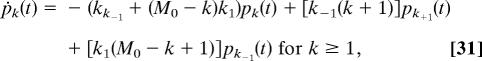while, for k = 0,

and, for k = M₀,

The mean and the variance of p_k are defined, respectively, as

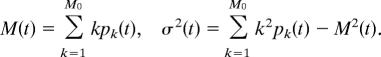For example, the steady-state mean and variance are computed by directly solving the recurrence (Eq. 31) with the normalization condition Σ_k=0^M₀ p_k = 1. The steady-state probabilities are (C _M0^k are the binomial coefficients) p_k = p_k (∞) = C _M0^k /(1 + k₁/k₋₁)^S₀ (k₁/k₋₁)^k, and, after some computations, we get for the moments

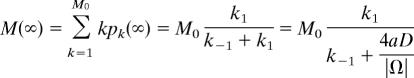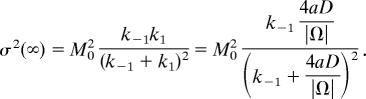This framework is sufficiently general to include the Michaelis– Menten reaction theory and modulation of the reaction due to push–pull reactions. When the microdomain Ω is open and diffusing molecules arrive at random times, the time course of any chemical reaction inside Ω is affected, yet the properties of the moments can be estimated analytically (26).

Receptor Trafficking on a Neuronal Membrane Near a Synapse: Contribution to the Synaptic Weight

The synaptic weight between a pre- and a postsynaptic neurons depends in part on the number of postsynaptic receptors. In general, starting from a presynaptic neuron, the postsynaptic current depends on the type k, the number N_k, the conductance γ_k of the receptors, and the probability p_k(t|f) that channel k opens, conditioned on the firing rate f. The conditional probability p_k(t|f) depends on such diverse biophysical parameters as the presynaptic terminal dynamics and up to the gating properties of the channel, which depend on its molecular structure. The conductivity γ_k controls the flux of ions through a channel of type k, and it depends mainly on the molecular properties of the primary subunit structure. The postsynaptic current is given by

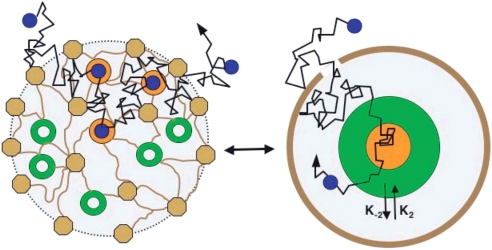
There is experimental evidence that channels are not static, so the number of channels N_k in a given domain is not a constant but rather fluctuates in time. Glutamatergic and GABAergic receptors on the surface of neurons, as well as other receptors, traffic in and out of a fundamental microstructure called the postsynaptic density (PSD) (5, 27, 28). The receptor movement has been approximated so far as mostly Brownian, with measurable sojourn times (confinements) in small subdomains (Fig. 2).When the confining restriction is due to a corral zone around the receptor, the mean escape time, given by Eq. 21, is a good approximation of the measured confinement time (26). Indeed, for a diffusion constant D = 0.004 μm²/s, a corral zone approximated by a disk of radius R = 0.25 μm, a ratio of absorbing to total boundary ε = 10⁻³/(2 · π · 0.25), according to Eq. 21 the time in the corral area is τ ≈ 125 s, which is comparable with the experimental observations given in ref. 27. This result confirms that barrier restriction can be responsible for the long time confinement of Brownian receptors. However, inside the PSD region, receptors can be anchored to the membrane when they bind to scaffolding proteins. Fig. 2 represents a coarse-grained model of the PSD into three compartments, where the free binding sites and the bound sites have been combined into the green annulus and orange disk, respectively; the grey annulus represents the domain of free diffusion of the receptors; and the scaffolding molecules, as well as many other structures, such as transmembrane molecules, submembranous cytoskeleton-constituting obstacles, and fences are grouped into the brown boundary. The total number of scaffolding molecules (orange plus green) is constant, but the proportion of bound and unbound sites depends on the number of receptors in the PSD. The peripheric brown fence is connected to the extrasynaptic region through a small hole that restricts the dynamics of the receptors. A random trajectory of a receptor (blue) has been drawn in both pictures (black broken line). K₁ is the forward binding rate of a receptor to the scaffolding molecules (which depends on the total number of scaffolding molecules and the mean time it takes to enter this domain), K₋₁ is the backward binding rate.

Fig. 2.

Homogenization of the PSD. (Right) Scattered free, bound, and scaffolding molecules and other obstacles and fences in the PSD. (Left) A course-grained model with concentrated free (green), bound (orange), and scaffolding and other molecules (brown) (see text). [Reproduced with permission from ref. 29 (Copyright 2006, Biophysical Society).]

The Markov model, combined with the narrow escape approximation, can account for the interactions of receptors with the scaffolding molecules and can give an estimate of the mean and variance of the number of bound receptors at synapses, as well as of the chemical reactions described in the previous paragraph (29). The computation is based on four assumptions. (i) The stream of receptors entering the synaptic region is Poissonian with rate equal to the inward flux J. (ii) The escape rate of receptors from the PSD is the reciprocal of the escape time τ ∼ (|Ω|/πD) ln(1/ε), given by Eq. 21. This assumption is motivated by the fact that transmembrane molecules, such as the one involved in adhesion or such as those that bind receptors, may act as pickets and that submembranous molecules can create a fence (see Fig. 2) (30). Finally, (iii) a receptor can bind a free scaffolding molecule at rate k₂, according to the standard law of chemical reactions, and (iv) they can dissociate from a scaffolding molecule with a rate k₋₂. Using assumptions i–iv, the steady-state Markov model balances the flux J with the number of escaping receptors. The number of bounded receptors and their mean can be estimated from the model as a function of the flux (see SI Appendix 1) (29). The number of bound receptors R_b is given by

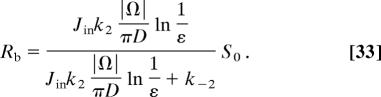Recent experimental findings (D. Choquet and A. Triller, personal communication) have demonstrated that the receptor movement is modulated by neuronal activity and depends on the type of receptors, which results in a modulation of the flux J_in.

Residence Time of a Receptor in the Synapse

The calculation of the mean time a Brownian molecule spends inside a microdomain Ω before it escapes through one of the small holes on the boundary, when it can be caught and released by a scaffolding molecule inside Ω, is a generalization of the narrow escape problem described above. This mean time depends on several parameters, such as the backward binding rate (with the agonist molecules), the mean escape time from the microdomain, and the mean time it takes for the molecule to reach the binding sites (forward binding rate). This mean time is usually called the dwell time, and experimental measurements, such as FRAP (fluorescent recovery after photobleaching), are used for its estimate.

We assume for simplicity that the microdomain Ω can be decomyposed into a part where the receptor is diffusing freely and a part where it is bound to the scaffolding molecule (see SI Appendix 1). Under these assumptions the dwell time can be computed by counting all the possibilities of a Brownian molecule to exit after 0,1,… bindings. Summing the probabilities of all these events, we obtain a geometric series and the dwell time E(τ_D) is calculated to be

〈τ〉 is the mean time to exit when no binding occurs, 〈T 〉 is the mean time to enter the binding site area, m_δ is the probability to bind before exit, given a uniform initial distribution, and k₋₁ is the backward binding rate.

An explicit expression for the dwell time (Eq. 34) is given in SI Appendix 1. The mean, M_b = ((1 − m_δ)/m_δ), and the variance, V_b = ((1 − m_δ)/m_δ²), of the number of bounds made by a single molecule before it exits Ω can be computed in the limit ε ≪ 1 fixed, but for uniform β ≪ 1, (SI Appendix 1),

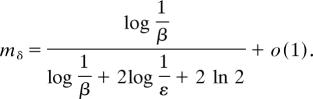The Reaction Rate with Narrow Escape and Thermal Activation

Recently (14), Eq. 10 was solved for a bounded domain, whose boundary contains a small absorbing window, at x₀, but the particle diffuses in a field of force with a single attractor at x_m and the potential φ forms a well inside the domain. In the special case of a small circular window and small noise, the rate is given asymptotically by

where a is the radius of the window, ω_i are the frequencies at x_m, ΔE = φ(x₀) − φ(x_m). Note that ΔE is not the barrier height. The activation rate (Eq. 35) is of Arrhenius form and has two contributions: One is due to an activation over the potential barrier, and the other is due to the geometry of the absorbing window alone. Geometrical properties of the domain, such as its volume, are not included in the leading order asymptotics of the reaction rate. In dimension 2, the formula becomes

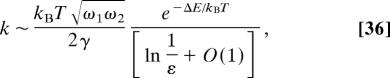where ε is given in Eq. 4.

Vesicle Trafficking in Cells

Neuronal development involves axonal and dendritic growth, attributed to the delivery of trafficking vesicles at a small portion of the cell membrane (30). Vesicle movement can be described by a stochastic equation, which accounts for intermittent switching between a directed motion on microtubules and free diffusion in the bulk. A simple model assumes a constant drift component, obtained by an homogenization procedure. Then the rate of arrival of vesicles to the location where a protrusion is initiated, is given by a formula similar to Eq. 35, but with repulsive, rather than attractive, drift. For a circular model of a cell and uniform velocity along microtubules, the rate of vesicle arrival at the protrusion is

where Ω is the domain of the cell, S is the surface of the external membrane, δ is the radius of the (circular) protrusion, N₀ is the number of steady state vesicles, and V_d is the drift velocity along microtubules. For a cell of radius R = 5 μm, a surface S = 4π R², δ = R/60, a vesicular velocity V_d = 0.083 m/s and N₀ = 6,000, we find a rate per vesicle κ_δ = 0.5, in good agreement with the measured rate given in ref. 31. This rate contributes to the dendritic growth.

Future and Perspectives

The narrow escape problem is ubiquitous in cellular biology, because it concerns the random time between the release of a given particle in a cell and the time it activates a given protein on the cell membrane. The narrow escape problem has many possible extensions. For example, it can be used for the establishment of principles describing viral trafficking in a host cell (32). In these applications, virus transport can be modeled by a stochastic equation with a small absorbing window that represents a small pore located on the surface of the nucleus. Reaching this goal is critical for DNA viruses, before replication can start.

Another problem that can be addressed in the small-hole framework consists in computing the time needed for a transcription factor to find its binding site on a DNA fragment. Indeed, when the search involves three-dimensional dynamics, the narrow escape formula derived for dimension 3 can be used to incorporate the effect of the nucleus geometry on the search time.

Finally, the narrow escape problem may be a powerful tool in nonviral gene delivery. During intracellular trafficking, plasmid DNA has to diffuse through a crowded (33) and hostile (34) environment before escaping into the nucleus. A realistic quantitative description of DNA transport into the cytoplasm that accounts specific and nonspecifics local interactions is still lacking. Being able to account for specifics protein structure should be one of the goals for a future narrow escape theory concerning trafficking at the cell level. In that perspective, the narrow escape theory should become a tool for the study of gene delivery, and we hope that such model will help designing improved synthetic vectors.

Abbreviations

pdf

probability density function

PSD

postsynaptic density.