Computational biology in the study of cardiac ion channels and cell electrophysiology

Abstract

The cardiac cell is a complex biological system where various processes interact to generate electrical excitation (the action potential, AP) and contraction. During AP generation, membrane ion channels interact nonlinearly with dynamically changing ionic concentrations and varying transmembrane voltage, and are subject to regulatory processes. In recent years, a large body of knowledge has accumulated on the molecular structure of cardiac ion channels, their function, and their modification by genetic mutations that are associated with cardiac arrhythmias and sudden death. However, ion channels are typically studied in isolation (in expression systems or isolated membrane patches), away from the physiological environment of the cell where they interact to generate the AP. A major challenge remains the integration of ion-channel properties into the functioning, complex and highly interactive cell system, with the objective to relate molecular-level processes and their modification by disease to whole-cell function and clinical phenotype. In this article we describe how computational biology can be used to achieve such integration. We explain how mathematical (Markov) models of ion-channel kinetics are incorporated into integrated models of cardiac cells to compute the AP. We provide examples of mathematical (computer) simulations of physiological and pathological phenomena, including AP adaptation to changes in heart rate, genetic mutations in SCN5A and HERG genes that are associated with fatal cardiac arrhythmias, and effects of the CaMKII regulatory pathway and β-adrenergic cascade on the cell electrophysiological function.

1. Prologue

‘Things should be made as simple as possible, but not any simpler.’

Albert Einstein

Cardiac muscle can generate propagating electrical impulses (action potentials), a property that classifies it as an excitable tissue similar to skeletal muscle and nerve. At the single-cell level, the electrical action potential (AP) triggers mechanical contraction by inducing a transient rise of intracellular calcium which, in turn, carries the contraction message to the contractile proteins of the cell. This process that couples electrical excitation to mechanical function is termed excitation-contraction coupling. APs are generated by individual cells and are conducted from cell to cell through intercellular gap junctions, forming waves of excitation that activate and synchronize the blood pumping action of the heart. Similar to nerve and skeletal muscle, AP initiation and conduction in cardiac ventricular tissue rely mostly on a single membrane process, namely the flow of sodium ions through sodium-specific ion channels. However, unlike the short-duration APs of skeletal muscle and nerve, the cardiac ventricular AP is characterized by long plateau and repolarization phases that prevent premature arrhythmogenic excitation and provide control of mechanical contraction. In contrast to the ‘single-current mechanism’ of AP initiation, the plateau and repolarization phases rely on multiple ionic processes that provide precise control of the AP time-course and duration. In the cell, membrane ion channels interact with dynamically changing ionic concentrations and varying transmembrane voltage, and are subject to various regulatory processes. These interactions are nonlinear, making the single cardiac cell a complex interactive system where a high degree of synthesis and integration occurs. Because our intuition is mostly ‘linear’, our ability to predict the outcome of these multiple nonlinear processes and to elucidate the underlying mechanisms is very limited. Analysis and synthesis of such complex nonlinear systems require mathematical approaches similar to those applied in other fields of science, notably physics and engineering.

In the last decade major advances were made in our ability to identify genetic mutations and link them to clinical disease phenotypes. A large body of knowledge has accumulated on the molecular structure of cardiac ion channels, their kinetic properties as related to this structure, and the modification of the structure/function by genetic defects that are associated with cardiac arrhythmias (Schwartz et al. 1995; Keating & Sanguinetti, 1996; Brugada et al. 1998; Priori et al. 1999a, b; Clancy & Kass, 2005; Nerbonne & Kass, 2005). Most of these data were obtained in expression systems (e.g. Xenopus oocyte, HEK cells) and isolated membrane patches, away from the physiological environment of the cardiac cell where the ion channels interact to generate the AP. A major challenge for the next decade and beyond is the integration of this information into the functioning cardiac cell and tissue in order to relate molecular-level processes and their modification by disease to whole-cell function and cardiac excitation.

In this review, we describe how computational biology approaches can be used to achieve this goal. Specifically, we use mathematical models of cardiac ion channels and cells to link molecular processes that underlie ion-channel function to the electrical activity of the whole cell. Simulations include normal functioning of cardiac cells in response to changes in heart rate (AP rate-adaptation) and altered cellular phenotypes due to ion-channel mutations. Simulating mutations and molecular interactions requires the formulation of single-channel models that represent specific channel states (e.g. open, closed, inactivated) and their interdependencies, and incorporation of these models into the model of the whole cell. This single-channel-based approach constitutes a major departure from the Hodgkin–Huxley scheme developed for the squid axon (Hodgkin & Huxley, 1952) and adopted in many cardiac cell models, where the starting point for computing the AP is macroscopic ionic currents through large ensembles of ion channels. Finally, two recent examples are described, demonstrating how regulatory pathways (the CaMKII pathway and the β-adrenergic cascade) can be incorporated into integrative mathematical models of the whole cell.

2. The Hodgkin–Huxley formalism for computing the action potential

2.1 The axon action potential model

The first computational model of the AP was formulated by Hodgkin and Huxley for the axon. Their circuit model of the cell membrane remains the basis for many modern neuronal and cardiac AP models, so we begin with a brief description of their work. In collaboration with Katz, Hodgkin and Huxley made a fundamental stride in characterizing voltage-dependent conductance changes in excitable cells by applying the voltage-clamp technique to the nerve axon (Hodgkin et al. 1952). These experiments suggested that inward movement of Na⁺ is responsible for the strong positive deflection observed in intracellular recordings of the membrane potential, V_m, upon depolarization (Hodgkin & Huxley, 1939), while outward flow of K⁺ causes repolarization to the resting, hyperpolarized state. Intrigued by these results, Hodgkin and Huxley constructed a mathematical model to test whether these fluxes could generate the AP morphology that they had recorded (Hodgkin & Huxley, 1952).

The framework for this model is described by the circuit diagram in Fig. 1a. Represented by the circuit are Na⁺, K⁺ and leakage currents as well as the capacitive effect of the membrane, which is a result of its hydrophobic nature that makes it impermeable to charged ions. This capacitance provides charge separation so that changes in V_m are due to charge displacement caused by the ionic currents and can be described by the following equation:

Fig. 1.

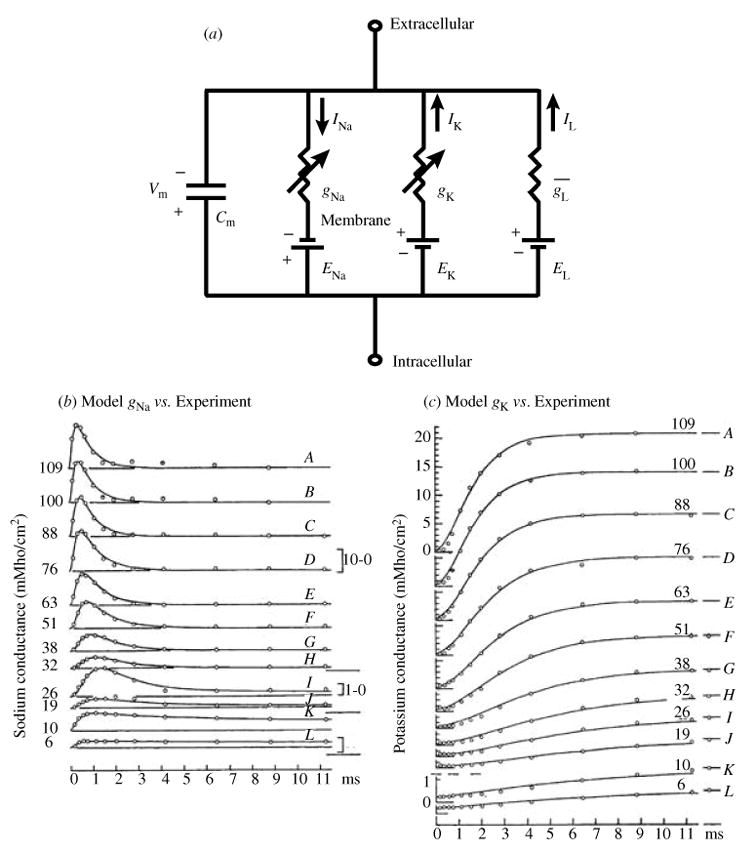
(a) Circuit diagram of the Hodgkin–Huxley membrane model. Two voltage-dependent conductances (g_Na, sodium and g_K, potassium) and one voltage-independent conductance ( $\overline{g_{\text{L}}}$) in parallel with a capacitor describe the electrical properties of the membrane. The driving force for each current is the difference between the transmembrane potential, V_m, and the equilibrium potential, E, for the charge-carrying ion, for example, the driving force for I_Na is (V_m − E_Na). The equilibrium potential is calculated with the Nernst equation. (b, c). Voltage and time dependence of ionic conductances; comparison of the Hodgkin–Huxley model with experiment. (b) Model-simulated sodium conductance, g_Na (solid line) is superimposed on experimental data (open circles). V_m values (mV) are indicated by numbers on each trace; conductance scales (mMho/cm²) are provided on the right. (c) Same as (b) for potassium conductance, g_K. V_m values (mV) are indicated by numbers above tracings and conductance scales (mMho/cm²) are on the left. (From Hodgkin & Huxley, 1952, with permission.)

$$\frac{\text{d}{V}_{\text{m}}}{\text{d}t}=-\frac{1}{C_{\text{m}}}\cdot I_{\text{ion},}$$

where C_m is the membrane capacitance (μF/cm²) and I_ion is the total transmembrane ionic current (μA/cm²).

This equation assumes space-clamp conditions and absence of external stimulus. Cell capacitance per unit area of membrane and current densities are typically used to calculate V_m, to normalize for variability in cell size.

For the axon model I_ion is the sum of three currents: I_Na, which represents the depolarizing sodium current, I_K that accounts for the repolarizing K⁺ current and I_L, a leakage current. The driving force for I_Na and I_K is generated by transmembrane Na⁺ and K⁺ concentration gradients, and its magnitude is the difference between V_m and the equilibrium potential, which is computed using the Nernst equation (Plonsey & Barr, 2000). For example, the Na⁺ equilibrium potential, E_Na, is found with the following Nernst equation:

$$E_{\text{Na}}=\frac{R\cdot T}{F}\cdot ln\left(\frac{{[{\text{Na}}^{+}]}_{\text{o}}}{{[{\text{Na}}^{+}]}_{\text{i}}}\right),$$

where E_Na is the equilibrium potential for Na⁺ (mV), R is the gas constant [J · (kmol · K)⁻¹], T is the temperature (K), F is Faraday’s constant (C · mol⁻¹), and [Na⁺]_i and [Na⁺]_o are the intracellular and extracellular Na⁺ concentrations (mM).

Once the driving force is known, the current is calculated using Ohm’s law. For example, the equation for I_Na is

$$I_{\text{Na}}=g_{\text{Na}}\cdot (V_m-E_{\text{Na}}),$$

where I_Na is the transmembrane Na⁺ current (μA/cm²) and g_Na is the Na⁺ conductance (mS/cm²).

Hodgkin and Huxley computed the conductance for each current as a function of the open probability of a series of hypothetical gates and the maximum conductance of the membrane for each ion species. The gates provide the voltage and time dependence of the conductance, and the maximum conductance is simply the conductance when all gates are open. Each gate can go through a first-order voltage-dependent transition from a closed to an open position or from an open to a closed position at a rate that is independent of the positions of all other gates. An ion can pass through the gate only in its open position.

Na⁺ current activation (increasing conductance) is accurately modeled by three identical activation gates that move from closed to open positions at depolarized V_m. The open probability of the activation gate is typically assigned the variable m that ranges from 0 (all gates closed) to 1 (all gates open), and the time-dependent change in m is described by the following first-order differential equation:

$$\frac{\text{d}m}{\text{d}t}=\alpha \cdot (1-m)-\beta \cdot m,$$

where m and (1−m) are the gate open and closed probabilities, t is time (ms), and α and β are V_m-dependent opening and closing transition rates (ms⁻¹).

Since the transitions are assumed to be independent, the probability that all three gates are open is m³. At positive V_m all three gates transition rapidly (within milliseconds even at 6–7 °C, Fig. 1b) to the open state, providing the depolarizing current necessary for the AP upstroke.

The voltage-clamp recordings (Fig. 1b) also show a decrease in current shortly after activation. This process was termed inactivation, and was modeled by using a single first-order inactivation gate with open probability h. At hyperpolarized potentials, h is fully open. When the membrane is depolarized, the inactivation gate closes to cause the monoexponential decrease observed in I_Na. Since h operates independently of m, the open probability for the Na⁺ gates is m³ · h, and the conductance is

$$g_{\text{Na}}=\overline{g_{\text{Na}}}\cdot m^3\cdot h,$$

where $\overline{g_{\text{Na}}}$ is the maximum conductance (mS/μF).

The equations that describe I_K are similar, with the driving force dependent on the transmembrane K⁺ gradient, which causes the current to be outward. The other significant difference is in the gating; no inactivation is observed and activation is more sigmoidal (Fig. 1c). Fitting this behavior requires four identical independent gates, n, and the open probability is n⁴:

$$I_{\text{K}}=\hspace{0.17em}\overline{g_{\text{K}}}\cdot n^4\cdot (V_{\text{m}}-E_{\text{K}}),$$

where I_K is current (μA/cm²), $\overline{g_{\text{K}}}$ is the maximum K⁺ conductance (mS/cm²), and E_K = (R · T/F ) · ln ([K⁺]_o/[K⁺]_i).

For completeness, there is also a leakage conductance, which was incorporated to account for current not carried by I_Na or I_K. This conductance is assumed constant and does not vary with time or V_m. The leakage current, I_L, has the following formulation:

$$I_{\text{L}}=\overline{g_{\text{L}}}.(V_{\text{m}}-E_{\text{L}}),$$

where $\overline{g_{\text{L}}}$ is its constant conductance and E_L its equilibrium potential.

Hodgkin and Huxley were successful in reproducing the axonal AP morphology under a variety of conditions with this surprisingly simple and elegant model. However, the actual mechanism that produced the voltage- and time-dependent gating in the axon still remained undiscovered. Over the following decades, the ion channel was established as the protein structure that provides the pathway for ion flow across the membrane, and detailed genetic, structural and electrophysiological description of ion channels has been published (for review see Hille, 2001).

2.2 Cardiac action potential models

The first cardiac AP models were formulated by McAllister et al. (1975), of the Purkinje fiber, and Beeler & Reuter (1977), of the ventricular myocyte. These models relied on the Hodgkin–Huxley formalism to describe the ionic currents, and similar to the Hodgkin–Huxley model assumed that intracellular ion concentrations ([Na⁺]_i, [K⁺]_i) remain constant during the AP. However, in cardiac myocytes, entry of Ca²⁺ through I_Ca(L), the L-type calcium channel, causes a dramatic change in its intracellular concentration, mostly by triggering Ca²⁺ release from the sarcoplasmic reticulum (SR) via the calcium-induced calcium-release (CICR) process (Fabiato, 1992). Incorporation of dynamic changes in [Ca²⁺]_i was necessary to reproduce AP morphology even in the earliest ventricular cell models (e.g. the Beeler–Reuter model) (Beeler & Reuter, 1977).

Changes in [Na⁺]_i and [K⁺]_i can also influence AP morphology over time if cells are paced at fast rate. The first model to incorporate detailed information regarding dynamic concentration changes of these ions during the AP was the DiFrancesco–Noble model of the Purkinje fiber AP (DiFrancesco & Noble, 1985). Rasmusson et al. (1990) developed a similar model for a bullfrog atrial cell. The Luo–Rudy dynamic (LRd) model of the guinea pig ventricular AP formulated these processes for the ventricular myocyte (Luo & Rudy, 1994a) (Fig. 2a). These models were founding members in a new class of ‘second-generation’ models that account for dynamic ion concentration changes. Several such models of the ventricular and atrial AP in different species have been published since that time (Rasmusson et al. 1990; Courtemanche et al. 1998; Noble et al. 1998; Priebe & Beuckelmann, 1998; Nygren et al. 1998; Ramirez et al. 2000; Rice et al. 2000; Puglisi & Bers, 2001; Fox et al. 2002; Matsuoka et al. 2003; Pandit et al. 2003; Bondarenko et al. 2004; Hund & Rudy, 2004; Iyer et al. 2004; Shannon et al. 2004).

Fig. 2.

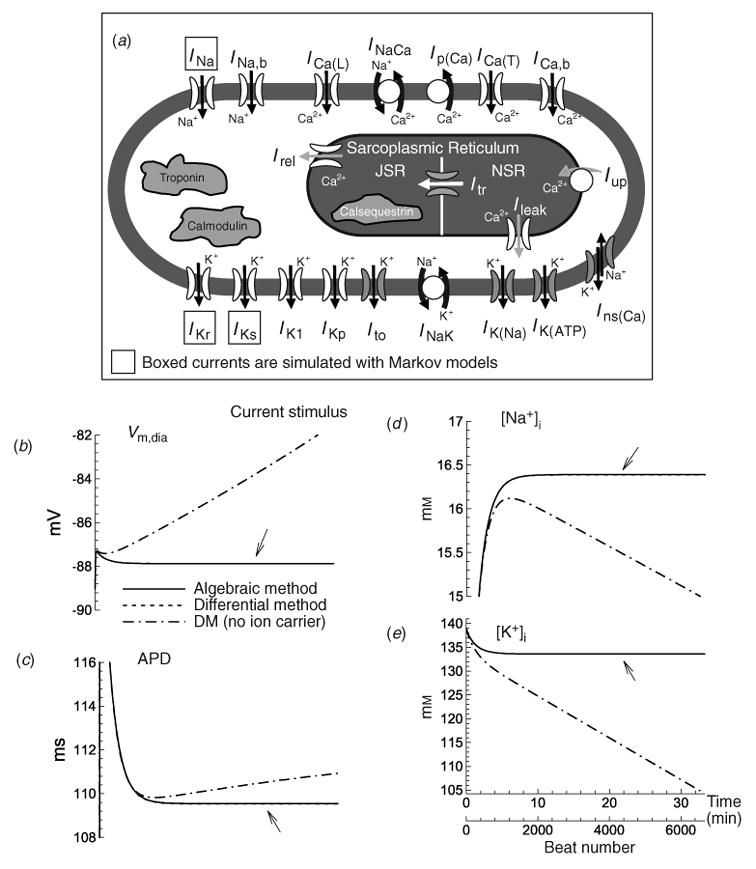
A schematic of the Luo–Rudy dynamic (LRd) ventricular cell model. The model is based mostly on data from the guinea pig. Dynamics of intracellular Na⁺, K⁺, and Ca²⁺ are accounted for in the model. Dynamic changes of intracellular Ca²⁺ are determined by transmembrane fluxes, release and uptake by a two compartment sarcoplasmic reticulum (SR), and Ca²⁺ interactions with buffers. Boxed ionic currents are simulated with recently published Markov formulations (other currents follow the Hodgkin–Huxley formulation). Definitions: I_Na, fast sodium current; I_Ca(L), calcium current through L-type calcium channels; I_Ca(T), calcium current through T-type calcium channels (Droogmans & Nilius, 1989; Balke et al. 1992; Vassort & Alvarez, 1994); I_Kr, rapid delayed rectifier potassium current (Clancy & Rudy, 2001; Silva & Rudy, 2005); I_Ks, slow delayed rectifier potassium current (Silva & Rudy, 2005); I_K¹, inward rectifier potassium current (Kurachi, 1985); I_Kp, plateau potassium current (Yue & Marban, 1988; Backx & Marban, 1993); I_Na,b, sodium background current; I_Ca,b, calcium background current; I_NaK, sodium–potassium pump current; I_NaCa, sodium–calcium exchange current; I_p(Ca) calcium pump in the sarcolemma (Caroni et al. 1983); I_up, calcium uptake from the myoplasm to network sarcoplasmic reticulum (NSR) (Tada et al. 1989); I_rel, calcium release from junctional sarcoplasmic reticulum ( JSR) (Meissner, 1995); I_leak, calcium leakage from NSR to myoplasm; I_tr, calcium translocation from NSR to JSR (Yue et al. 1985). The following currents (shaded in the figure) are included under pathological conditions: I_K(ATP), ATP-sensitive potassium current, activated under conditions of ATP depletion (ischemia) (Kakei et al. 1985; Nichols et al. 1991; Noma, 1983; Shaw & Rudy, 1997a); I_K(Na), sodium-activated potassium current, activated under conditions of sodium overload (Kameyama et al. 1984; Luk & Carmeliet, 1990; Wang et al. 1991; Faber & Rudy, 2000); I_ns(Ca), non-specific calcium-activated current, activated under conditions of calcium overload (Ehara et al. 1988; Luo & Rudy, 1994b); Calmodulin and troponin represent calcium buffers in the myoplasm. Calsequestrin is a calcium buffer in the JSR. I_to the transient outward current is not present in guinea pig ventricular myocytes; it is included in certain simulations that examine its possible effects on the AP (Dumaine et al. 1999). Details of the LRd model can be found in the literature (Luo & Rudy, 1991; Luo & Rudy, 1994a; Zeng et al. 1995; Shaw & Rudy, 1997b; Viswanathan & Rudy, 1999; Viswanathan et al. 1999; Faber & Rudy, 2000; Hund et al. 2001; Rudy, 2002) and at http://rudylab.wustl.edu where the model code is also provided. (b)–(e). Stability of dynamic cell models (‘second-generation models’); effect of stimulus charge carrier. (b) V_m during the diastolic interval (V_m,dia); (c) action potential duration (APD); (d) [Na⁺]_i, and (e) [K⁺]_i as a function of time during pacing with a current stimulus at a cycle length (CL) of 300 ms using the algebraic method (solid line) and the differential method (dashed line indicated with arrow); note that the two are indistinguishable. In both cases, the stimulus current carries K⁺ ions into the cell and contributes directly to computed changes in intracellular ion concentrations. Note the stability (lack of drift) and identical results for both methods. An additional simulation is shown using the differential method and a current stimulus formulation that does not account for the charge carrying ion species (dash-dot line). Notice that computed parameters drift if ions carried by the stimulus current are not taken into account in the computation of ion concentration changes, which violates conservation laws. (From Hund et al. 2001, with permission.)

Simulation of changes in intracellular ion concentrations requires incorporation of the pumps and exchangers that maintain resting levels (Fig. 2a). The primary pump is the Na⁺/K⁺ ATPase (NaK) that converts energy produced by the metabolic system into potential energy (in the form of transmembrane ion concentration gradients) that is used to generate the AP. Extrusion of Na⁺ and accumulation of intracellular K⁺ by NaK generates a high [K⁺]_i and maintains a low [Na⁺]_i relative to the extracellular space. The Na⁺/Ca²⁺ exchanger, NCX, uses the sodium gradient created by NaK to extrude Ca²⁺ and together with uptake into the SR, maintain a very low resting intracellular concentration [Ca²⁺]_i. Under certain pathological conditions (e.g. reduced NaK capacity), during continual fast pacing, these gradients can become depleted, because the cumulative amount of ions carried by transmembrane current during repetitive APs surpasses the ability of pumps and exchangers to maintain resting concentrations. These changes can have important physiological consequences. Under pathological conditions of [Na⁺]_i overload, for example, depolarization slows, the AP duration (APD) shortens, and the inducibility of arrhythmia increases (Faber & Rudy, 2000).

Recently, there have been reports that the values of intracellular ion concentrations in second-generation AP models that account for dynamic concentration changes do not reach a steady state when paced over a long period of time, but drift until their values leave the physiological range (Guan et al. 1997; Yehia et al. 1999; Endresen et al. 2000; Krogh-Madsen et al. 2005). In the LRd model, drift is only observed when ions (usually K⁺) that carry the stimulus current are not accounted for. If the stimulus is properly implemented and the ions that it carries are included in computing concentrations, no drift is observed even at fast pacing for long intervals [Fig. 2(b)–(e)] (Hund et al. 2001).

Figure 2 also shows a comparison between two methods solving the equation that describes transmembrane voltage, V_m, in the LRd model. The first ‘differential’ method, which has traditionally been used, describes changes in V_m as a function of the transmembrane ionic current using the differential equation:

$$\frac{\text{d}{V}_{\text{m}}}{\text{d}t}=-\frac{1}{C_{\text{m}}}\cdot I_{\text{ion}}.$$

When dynamic intracellular ion concentrations are accounted for, V_m can also be computed directly from the concentrations by integrating the differential equation for voltage (see Varghese & Sell, 1997; Endresen et al. 2000; Dokos & Lovell, 2001; Hund et al. 2001 for details) to formulate the ‘algebraic’ method:

$$V_{\text{m}}=\frac{V_{\text{myo}}F}{A_{\text{cap}}{C}_{\text{m}}}\left(\underset{\text{X}}{\Sigma }(z_{\text{x}}\cdot {[\text{X}]}_i)+\frac{2\cdot V_{\text{JSR}}}{V_{\text{myo}}}\cdot {[{\text{Ca}}^{2+}]}_{\text{JSR}}+\frac{2\cdot V_{\text{NSR}}}{V_{\text{myo}}}\cdot {[{\text{Ca}}^{2+}]}_{\text{NSR}}-C_0\right),$$

V_myo is the volume of the myoplasm (μL); F is Faraday’s constant (C/mol); V_JSR and V_NSR are volumes of the junctional and network SR compartments; A_cap and C_m are the capacitive area (cm²) and capacitance (μF/cm²) of the membrane; [X]_i and z_x are the myoplasmic concentration and valence of each ion; [Ca²⁺]_JSR and [Ca²⁺]_NSR are Ca²⁺ concentrations in JSR and NSR; C₀ is a constant of integration.

The algebraic equation is based on a charge conservation principle and the charge–voltage relationship of a capacitor, V = q/C (where q is the charge, C the capacitance and V the voltage).

The constant C₀ is determined by substituting the initial values of the ion concentrations into the algebraic equation. With this choice, C₀ is consistent with the initial conditions used for simulations using the differential formulation. A comparison between simulations using the differential or algebraic formulation [Fig. 2(b)–(e)] demonstrates that when C₀ is chosen accordingly, both methods produce identical results (Hund et al. 2001; Kurata et al. 2005).

3. Ion-channel-based formulation of the action potential

3.1 Ion-channel structure

Ion channels are typically composed of one or more α-subunits that can be modulated by accessory subunits. In heart, the sodium channel is formed by a single α-subunit that has four domains (DI–DIV) (Fig. 3a). Each domain is composed of six transmembrane spanning segments (S1–S6) that have been identified based on the hydrophobicity of their amino acids. Differently from the Na⁺ channel, cardiac K⁺ channels are tetrameric with four identical α-subunits, each with six transmembrane-spanning segments (Fig. 3b).

Fig. 3.

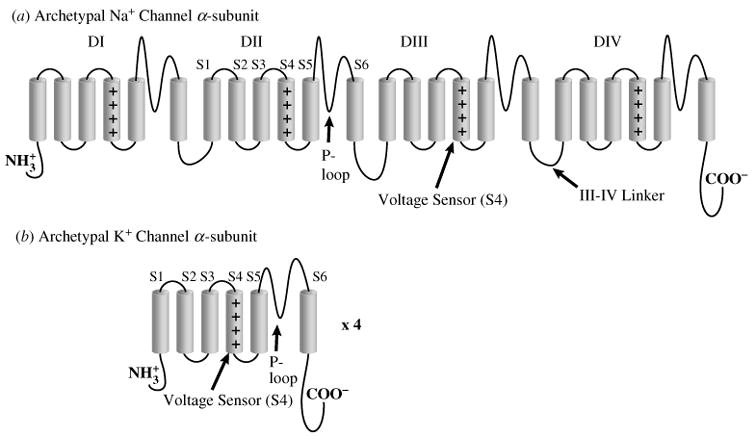
Archetypal Na⁺ and K⁺ channel subunits. (a) The homomeric Na⁺ channel is typically composed of a single four-domain α-subunit. Each domain consists of six transmembrane spanning segments (S1–S6). The fourth segment (S4) contains positively charged amino acids that confer voltage sensitivity on the channel. The S5–S6 linker forms a hairpin that enters the membrane to partially form the channel pore (P-loop), and determines ion selectivity. Several amino acids in the III–IV linker (labeled) have been linked to sodium channel fast inactivation. (b) Homomeric K⁺ channels are typically composed of four identical α-subunits. Each subunit bears some functional resemblance to the domains of the Na⁺ channel.

The domains in the Na⁺-channel α-subunit and the K⁺-channel α-subunits have similar structures that confer voltage dependence and ion selectivity. The S5–S6 linker, or P-loop, enters the membrane as a hairpin to form the pore through which the ion enters or leaves. A stretch of amino acids within the P-loop determines channel selectivity. Voltage-dependent activation is caused by movement of the voltage sensor, S4, which contains positive charges that cause the segment to shift when V_m changes. This shift changes the channel conformation to an open configuration that allows the passage of ions.

One astounding aspect of the Hodgkin–Huxley K⁺ channel model is the correspondence between the four hypothetical activation gates, n, and the four α-subunits that form the tetrameric channel. Each subunit contains a voltage sensor, and all four sensors must be in the activated position for the channel to open. Therefore, each activation gate can be thought of as simulating the activation of an individual subunit. Of course, the channel structure and the correspondence between abstract model ‘gates’ and movement of voltage sensors of the channel protein were completely unknown to Hodgkin and Huxley when they constructed their model.

3.2 Markov models of ion-channel kinetics

As more information about ion-channel gating has been obtained, it has become clear that models with explicit representation of single ion-channel states are required. In the Hodgkin–Huxley formulation, the gating parameters (e.g. n, m, h) do not represent specific kinetic states of ion channels. It has also become apparent that the Hodgkin–Huxley formulation is not sufficient to describe various aspects of channel behavior. One such aspect is the inactivation of the Na⁺ channel, which has a greater probability of occurring when the channel is open (Armstrong & Bezanilla, 1977; Bezanilla & Armstrong, 1977). If this is the case, then inactivation depends on activation and the assumption of independent gating that allows us to multiply m³ and h to compute conductance no longer holds. What we require is a class of models that can accurately represent the dependence of a given transition on the occupancy of different states of the channel. For sodium channel inactivation, the model must account for the dependence of the inactivation transition on the probability that the channel occupies the open state. Markov-type models fit this profile, and are based on the assumption that transitions between channel states depend on the present conformation of the channel, but not on previous behavior. Because the molecular interactions of channels are often state dependent, Markov model transitions typically represent specific channel movements that have been characterized experimentally. This section describes the application of Markov-type models to simulate such interactions.

We begin by describing a simple hypothetical channel with a single open (O) and a single closed (C) state (Fig. 4a). The following first-order equations describe the rate of change of occupancy in the closed and open states:

Fig. 4.

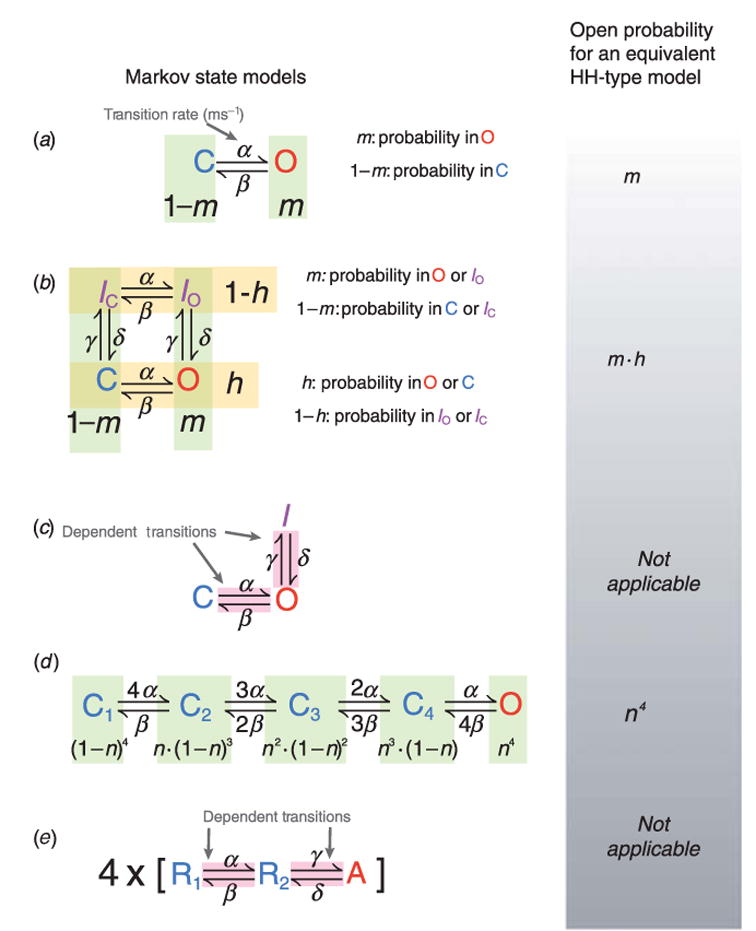
Examples of Markov and equivalent Hodgkin–Huxley (HH) models of ionic currents. (a) A two-state closed (C) – open (O) model with α and β as forward and reverse transition rates. In the equivalent HH-type formulation, current activation is described by a single gating variable, such as m. (b) A four-state model with two independent transitions. C, Closed; O, open; I_C, closed-inactivated I_O, open-inactivated. The transition rates α, β between I_C and I_O and between C and O are identical, as are transition rates γ, δ between C and I_C and between O and I_O. Thus activation and inactivation transitions are independent in this model. Independent transitions are readily modeled using the HH formulation. The probability for current activation is m and the probability that it is not inactivated is h; the open probability is m · h. (c) A three-state model with dependent transitions from C to O and O to I. There is no HH equivalent because of the dependent transitions. (d) K⁺ channels have four identical subunits, suggesting four independent identical transitions to the activated state. When all subunits are activated, the channel is open. Assigning an activation gate n, the probability of all four subunits being in the activated position, and thus the probability of the channel being open, is n⁴. (e) Biophysical analysis has shown that each of the four voltage sensors in certain K⁺ channels undergoes two transitions before channel opening. A model describing this gating property is shown; R₁ is the rest state, R₂ is an intermediate state, and A is the activated state. The channel is open when all four sensors are in the activated (A) position. Because transitions from R₂ to A depend on transitions from R₁ to R₂, a HH analog of the Markov model does not exist.

$$\begin{array}{l}\frac{\text{d}C}{\text{d}t}=-\alpha \cdot \text{C}+\beta \cdot \text{O},\\ \frac{\text{dO}}{\text{d}t}=\alpha \cdot \text{C}-\beta \cdot \text{O},\end{array}$$

where O and C are the probabilities that the channel resides in the open or closed state; α and β are voltage dependent transition rates (ms⁻¹) between these states.

In addition to activation, many channels undergo inactivation. A hypothetical four-state model (closed, open, and two inactivated states) with two sets of forward and reverse transition rates is shown in Fig. 4b. One set of rates, α and β, describes movement between states where the channel is open (O) or closed (C) (states that are not inactivated), and between the two inactivated states I_O and I_C. In the Markov scheme of Fig. 4b, these are horizontal transitions. The second set, γ and δ, describes vertical transitions to and from the inactivated states. Channels are only open when the channel is both activated and not inactivated, in state O. If differential equations are used to compute the occupancy of each state they take the following form:

$$\begin{array}{l}\frac{\text{dC}}{\text{d}t}=\beta \cdot \text{O}+\delta \cdot I_{\text{C}}-(\alpha +\gamma )\cdot \text{C},\\ \frac{\text{dO}}{\text{d}t}=\alpha \cdot \text{C}+\delta \cdot I_{\text{O}}-(\beta +\gamma )\cdot \text{O},\\ \frac{\text{d}{I}_{\text{C}}}{\text{d}t}=\beta \cdot I_{\text{O}}+\gamma \cdot \text{C}-(\alpha +\delta )\cdot I_{\text{C}},\\ \frac{\text{d}{I}_{\text{O}}}{\text{d}t}=\alpha \cdot I_{\text{C}}+\gamma \cdot \text{O}-(\beta +\delta )\cdot I_{\text{O}},\end{array}$$

where α, β, γ, and δ are transition rates, as shown in Figure 4b.

Because each state represents a channel conformation, calculating the occupancies of these states can provide mechanistic insight into how transitions within the channel itself govern its behavior and participation in the AP. For example, channels that move during depolarization from C to I_C to I_O are not available to conduct current and do not participate in the AP. In contrast, channels that arrive at I_O through O are available to conduct current while occupying the open state and have an effect on the AP. Thus, the Markov formulation can be used to relate AP morphology and properties to specific kinetic states of ion channels and the transitions between them during the different AP phases.

When using Hodgkin–Huxley type formulations, the occupancy for each state is not explicitly calculated. Instead, these models assume independent gating, an assumption that improves computational efficiency, which was certainly necessary in 1952 when the Hodgkin–Huxley model was published. In the Markov model of Fig. 4b the vertical transitions (C to I_C and O to I_O) have identical transition rates (α, β). This implies that channel inactivation can be represented by a single gate. Similarly, the horizontal transition rates between I_C and I_O are identical to the transition rates between C and O, and can be represented by a single gate. Horizontal movement from [C, I_C] to [O, I_O] represents channel activation; we can assign an activation gate m to describe these transitions. Similarly, we assign a second gate, h, to the inactivation process. Because the rates of inactivation transitions from C or O are identical, inactivation does not depend on the position of the activation gate (i.e. whether it is in the C or O position). The probability that the channel is in C or in O is h, and the probability that the channel is in O or in I_O is m. Because the gates are independent, the open probability (O) is calculated as their product (m · h). This expression is the same as would have been derived for the Hodgkin–Huxley formulation. Thus, under the assumption of independent gating the Markov formalism and the Hodgkin–Huxley formalism are interchangeable.

However, experiments have shown that typically channel activation and inactivation processes are not independent, but coupled. A simple version of activation and inactivation coupling, in a hypothetical channel, is shown in Fig. 4c. In this scheme, channel inactivation can only occur from the open state, and channel activation and inactivation do not involve independent transitions (such as the independent movement of several voltage sensors, see example in Fig. 4d and related discussion). Therefore, the state-to-state transitions are dependent, the assumption of independent gating is no longer valid, and the Hodgkin–Huxley formalism in terms of gating variables can not be applied; each state must be described individually by a differential equation:

$$\begin{array}{l}\frac{\text{dC}}{\text{d}t}=\alpha \cdot \text{C}-\beta \cdot \text{O},\\ \frac{\text{dO}}{\text{d}t}=\alpha \cdot \text{C}+\delta \cdot I-(\beta +\gamma )\cdot \text{O},\\ \frac{\text{d}I}{\text{d}t}=\gamma \cdot \text{O}-\delta \cdot I,\end{array}$$

where α, β, γ, and δ are transition rates, as shown in Fig. 4c.

So far, we have only described activation that involves a single transition. However, since most channels are tetrameric and the voltage sensor in each subunit must activate, more than one transition is normally needed to describe activation. A state diagram for a Markov model that represents each of the voltage sensor transitions in a tetrameric channel with identical subunits is shown in Fig. 4d. Each closed state represents a permutation of the positions of the voltage sensors. For example, the first closed state is the permutation where all four sensors are in the resting position, the second where one voltage sensor is activated and the other three are resting. The final state, open, is where all four subunits have a voltage sensor in the activated conformation. The transition rates reflect these permutations, e.g. the rate from C₁ to C₂ is 4 · α, because all of the four voltage sensors are in the resting position and can move independently to the activated position. Analogously, the rate from C₂ to C₁ is β because only a single voltage sensor has yet to return to the resting state. The occupancy of each state can be computed with a differential equation as for the above models.

Since each subunit in Fig. 4d activates independently, channel activation can be represented with a gate assigned to each subunit, to form an analogous Hodgkin–Huxley-type model. All subunits in this channel are identical, so they can be represented by identical gates, to which we assign the gating variable n. Because the four gates are independent, the open probability of the channel is n⁴.

Just as channel activation and inactivation are not typically independent, channel activation itself may also contain dependent transitions. A model containing such dependent transitions has been proposed for Shaker K⁺ channel activation to account for a delay observed before activation (Zagotta et al. 1994a, b). This model represents four subunits with identical activation rates, but supposes that each of those subunits goes through two conformational transitions, R1 and R2, before reaching the activated state, A. A state diagram for one of the four subunits is shown in Fig. 4e. As can be seen from the state diagram, no subunit can reach the activated state without first traversing an intermediate state (R₂).

Until recently these two transitions were hypothetical voltage sensor conformations that were needed to account for the macroscopic channel behavior of delayed activation. Silverman and colleagues have published experimental evidence in Shaker K⁺ channels that arginine residues in the voltage sensor (S4) interact with acidic residues in S2 sequentially (Silverman et al. 2003), providing a mechanism for two-stage voltage sensor activation, as suggested by Zagotta et al. (1994b) (Fig. 5a). These experiments suggest the model shown in Fig. 5a (upper panel), which has resting (R₁), intermediate (R₂) and activated (A) positions. The amino acids involved in this interaction are conserved in many K⁺ channels, suggesting that this activation mechanism is also likely to be operational in cardiac K⁺ channels.

Fig. 5.

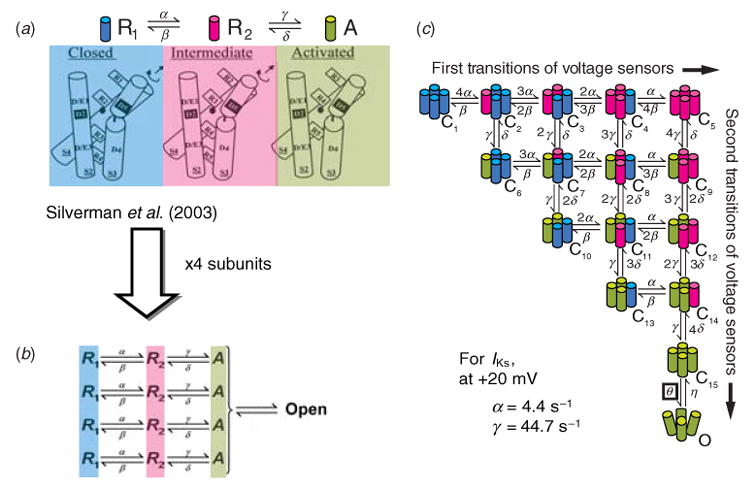
Conformational changes of K⁺ channels during activation. (a) Structural basis for two voltage-sensor transitions before channel opening (modified from Silverman et al. 2003, with permission). (b) Kinetic representation of the two voltage-sensor transitions in panel (a); all four α-subunits that form the channel undergo a first transition from a resting state (R₁) to an intermediate state (R₂) and a second transition from R₂ to an activated state (A). Once all voltage sensors are in the activated state, the channel can open. (c) Total number of combinations of voltage-sensor positions in the four subunits is 15 and can be represented by 15 closed states before channel opening. Blue, red, green indicate a voltage sensor in position R₁, R₂ or A, respectively. (From Rudy, 2006, with permission.) Panel (a) is based on data from ether-à-go-go (eag) and Shaker K⁺ channels and is adapted from Silverman et al. 2003, with permission.

The voltage-sensor activation model can be extended to represent each of the channel’s four subunits (Fig. 5b), with a final cooperative transition to the open state. The corresponding Markov state diagram is shown in Fig. 5c. Each left–right transition represents movement of one voltage sensor from R₁ to its intermediate position R₂; such transitions are slow (α = 4 · 4 s⁻¹ for cardiac slow delayed rectifier, I_Ks). Each top-down transition represents movement of a voltage sensor from R₂ to its activated position, A; such transitions are typically fast (for I_Ks, γ = 44 · 7 s⁻¹). Thus, each closed state corresponds to an experimentally indicated conformation of the channel with a unique combination of voltage-sensor positions (e.g. C₃ has two sensors in R₁ and 2 in R₂; C₇ has two sensors in R₁, one in R2 and one in A; C₁₀ has two in R₁ and two in A, etc.). The 15 closed states represent all such possible combinations. When all voltage sensors are activated (C₁₅), a cooperative transition can occur to the open state O. For I_Ks, this last transition is voltage independent (Loussouarn et al. 2003; Silva & Rudy, 2005).

The Markov models compute occupancy of the channel in its various kinetic states as a function of voltage and time (and possibly other factors such as ligand binding). The channel conducts ions when it occupies its open state (or, in some cases, multiple open states). Therefore, the macroscopic current density through an ensemble of such channels is described by the following equation:

$$I_{\text{X}}=\overline{g_{\text{sc},\text{x}}}\cdot n\cdot \text{O}\cdot (V_{\text{m}}-E_{\text{X}}),$$

where for an arbitrary channel X, $\overline{g_{\text{sc},\hspace{0.17em}\text{x}}}$ is the single channel conductance, n is the number of channels per unit membrane area, O is the probability that a channel occupies the open state, and (V_m − E_X) is the driving force.

This equation specifically accounts for the fact that current is generated by a population of ion channels that reside in the open state with a probability that depends on time and voltage.

This single-channel based formulation of the current density can be incorporated into a model of the AP. Because in this scheme discrete channel states (i.e. open, closed, inactivated) are represented explicitly, the model can be used to describe not only the macroscopic current during the AP, but also the occupancies and transitions of channel states. This approach provides a mechanistic link between the whole-cell AP and the structure/function of ion channels. An example of such an approach, describing state occupancies and transitions of selected ion channels during the AP at slow and fast pacing, is provided in the next section.

3.3 Role of selected ion channels in rate dependence of the cardiac action potential

Increased heart rate and elevated force of contraction are essential for increasing cardiac output. However, if APD does not shorten at fast rates ventricular relaxation during the diastolic interval (DI) cannot take place, resulting in reduced filling and decreased cardiac function. In response to rate increase, myocytes have the intrinsic ability to adapt, shortening APD to allow a sufficient DI for filling. This rate-dependent adaptation relies on complex interdependence between the ion channels that determine the AP, and on the molecular interactions that determine channel opening, closing and inactivation. By inserting detailed Markov models of the main depolarizing (I_Na) (Clancy & Rudy, 1999, 2002) and repolarizing [I_Kr (Clancy & Rudy, 2001) and I_Ks (Silva & Rudy, 2005)] currents into an AP model (Fig. 2a), the cellular-level effects can be studied. Because molecular interactions are usually dependent on the conformation of the channel, Markov-type models have been helpful in simulating this behavior (in the LRd model, Hodgkin–Huxley or Markov representations of currents can be used interchangeably).

I_Na, the fast inward Na⁺ current, does not seem a likely candidate to play a major role in AP changes with rate, primarily because of its very large density that is necessary to ensure AP generation and conduction with a large margin of safety (Shaw & Rudy, 1997b). However, at fast rate channels can accumulate in an inactivated state that has a slow exit rate. This accumulation inhibits a sufficient number of channels to reduce I_Na, the maximum V_m and the maximum rate of depolarization, dV_m/dt_max. This effect was accounted for in earlier AP models using the Hodgkin–Huxley formalism [Beeler–Reuter (Beeler & Reuter, 1977), LR1 (Luo & Rudy, 1991)] and was studied in detail. However, it was not until recently that specific molecular level interactions have been identified as candidates for this and other regulatory processes of I_Na.

In the heart, I_Na is generated primarily by channels formed with the α-subunit Na_v1.5, which is genetically encoded by SCN5A (George et al. 1995). Additionally, expression of multiple modulatory β-subunits (β₁ –β₄) is detected. Na_v1.5 (Fig. 3a) has four homologous domains (DI–DIV), each with six transmembrane-spanning segments (S1–S6) and a pore-forming P-loop between S5 and S6. Positively charged residues in S4 of each domain link channel activation to changes in V_m (Grant, 2001). A conserved phenylalanine residue in the III–IV linker of heart and brain I_Na channels has been linked to fast inactivation (Hartmann et al. 1994; Moorman et al. 1990), and is part of three hydrophobic amino acids [isoleucine-phenylalanine-methionine (IFM)] that have been shown to block the open pore (McPhee et al. 1994, 1995, 1998). Docking sites for this inactivation gate have been identified on the S4–S5 linkers in domains III and IV (Balser, 1999). Recently, the C-terminus has been shown to participate in fast inactivation by interacting with the III–IV linker and stabilizing the inactivated state (Motoike et al. 2004).

Each of these processes has been accounted for in the Markov model shown in Fig. 6a (Clancy & Rudy, 2002). Since I_Na activation is a cooperative process (Chanda et al. 2004) (activation of a voltage sensor in one domain influences activation in the other domains), three closed states, each representing a putative channel conformation are used, rather than modeling the activation of voltage sensors in each domain separately. Fast inactivation takes place preferentially from the open state reflecting its dependence on channel activation (Armstrong & Bezanilla, 1977; Bezanilla & Armstrong, 1977). Inactivation can then be stabilized by a transition from IF to an intermediate inactivated state IM₁, which reflects participation of the C-terminus (Veldkamp et al. 2000), and channels that are slowly inactivated reside in IM₂. Finally, closed-state inactivation has been included by movement from C₃ and C₂ into the inactivated tier (IC₃ and IC₂) to correctly simulate channel availability (Clancy & Rudy, 2002).

Fig. 6.

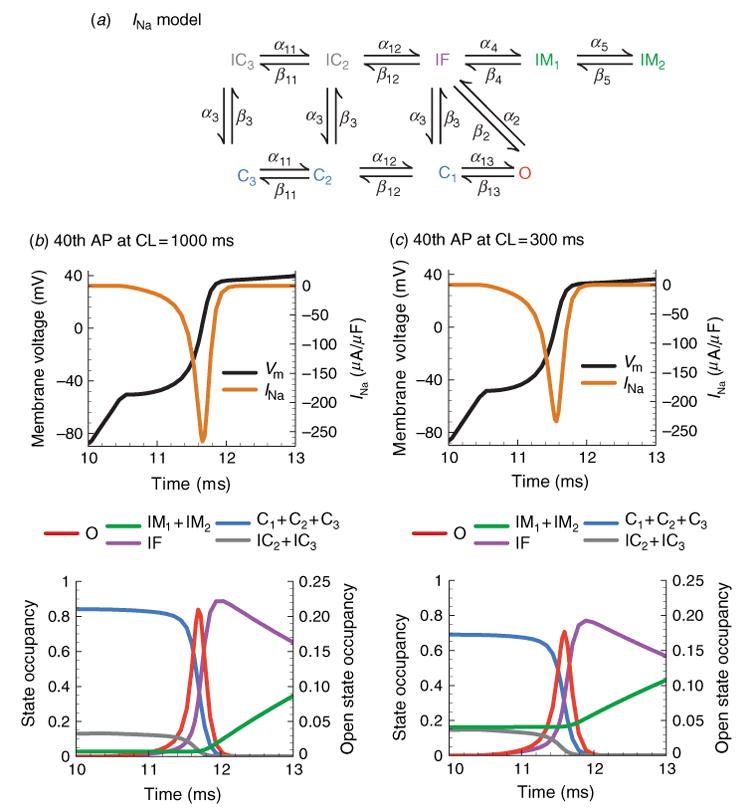
Kinetic transitions of Na⁺ channels during the AP at slow and fast rate. (a) Markov model of the Na⁺ channel (Clancy & Rudy, 2002). States are color coded according to their type: closed-inactivated (gray), fast-inactivated (purple), slow inactivated (green), closed (blue), open (red). (b) I_Na, V_m and channel state occupancies during first 3 ms of the 40th AP at slow rate, CL = 1000 ms. The channel state occupancies during the same time period (bottom panel) show a rapid transition out of the closed states into the open state. The time required for inactivation after channel opening determines peak I_Na = –270 μA/μF. While V_m remains at depolarized potentials, channels enter the slow inactivated states. At slow rate, few channels are inactivated at the initiation of the AP. (c) I_Na, V_m and channel state occupancies during first 3 ms of the 40th AP at fast rate, CL = 300 ms. Accumulation of channels in the slow inactivated states (green) at fast rate results in reduction of I_Na during the upstroke and consequently a slower dV_m/dt_max.

While I_Na participates only in the first few ms of the AP, its rate-dependence is highly dependent on APD and DI. During the initial AP upstroke I_Na can generate as much as 300 μA/μF of inward current (Fig. 6b). This current is generated by rapid closed to open transitions followed by fast inactivation. Throughout the rest of the AP, channels continue to transition to stable inactivated states IM₁ and IM₂. The number of channels that remain in these states between beats determines channel availability for the subsequent AP. At slow rates, there is practically no accumulation of channels in IM₁ and IM₂ (Fig. 6b). Because V_m is depolarized for a higher percentage of time at fast rate, more channels transition to IM₁ and IM₂ with less time to recover. At cycle length (CL) = 300 ms 20% of channels remain in these unavailable states between beats, and I_Na magnitude is noticeably reduced (Fig. 6c). This reduced depolarizing current results in a lower peak V_m, which affects the activation of other channels that are important determinants of APD, such as I_Kr, I_Ks, and I_Ca(L).

Like I_Na, guinea-pig I_Kr activation and onset of fast inactivation are relatively rapid. Activation dependence on V_m is also a result of displacement of positive charges in S4. However, instead of four domains in a single α-subunit, I_Kr is a tetrameric channel formed by four identical subunits that are genetically encoded by HERG. Several different auxiliary β-subunits have been shown to interact with the homomeric HERG channel including the MinK-related peptide (MiRP1, aka KCNE2) (Abbott et al. 1999) and MinK (aka KCNE1) (Yang et al. 1995; Ohyama et al. 2001). Voltage-dependent inactivation is caused by conformational changes in the outer mouth of the channel that mechanistically resembles C-type inactivation in Shaker (Smith et al. 1996). While it is plausible that charges in S4 could determine voltage dependence, mutation of these charges does not affect the amount of gating charge transfer during inactivation (Zhang et al. 2004). An alternate possibility is that voltage-dependence is conferred by the P-helix (positions 614–621 of the NH₂ -terminal half of the P-loop) (Zhang et al. 2004), however, this hypothesis has not been tested.

As with I_Na, I_Kr activation is modeled using cooperative transitions (Clancy & Rudy, 2001), and inactivation occurs preferentially from the open state (Fig. 7a) (Clancy & Rudy, 2001; Silva & Rudy, 2005). Some inactivation can also occur from the closed state nearest to the open state (C₁) as demonstrated by single-channel recordings (Kiehn et al. 1999). During most of the AP, the balance between I_Kr activation and inactivation favors inactivation (Fig. 7b, c), preventing the development of a large current. As V_m repolarizes and reaches levels where significant channel recovery from inactivation occurs, open-state occupancy rises to a maximum and I_Kr intensifies, reaching a peak late during the AP (Fig. 7b, c). Consequently, I_Kr participates mostly late during the AP, where it can influence repolarization significantly due to the delicate balance between inward and outward currents at this stage. Because voltage dependence of recovery is much stronger than time dependence during the AP, peak I_Kr is similar at slow and fast rates (cf. Fig. 7b, c), making I_Kr secondary to I_Ks in underlying rate-dependent adaptation of APD in guinea pig ventricular myocytes.

Fig. 7.

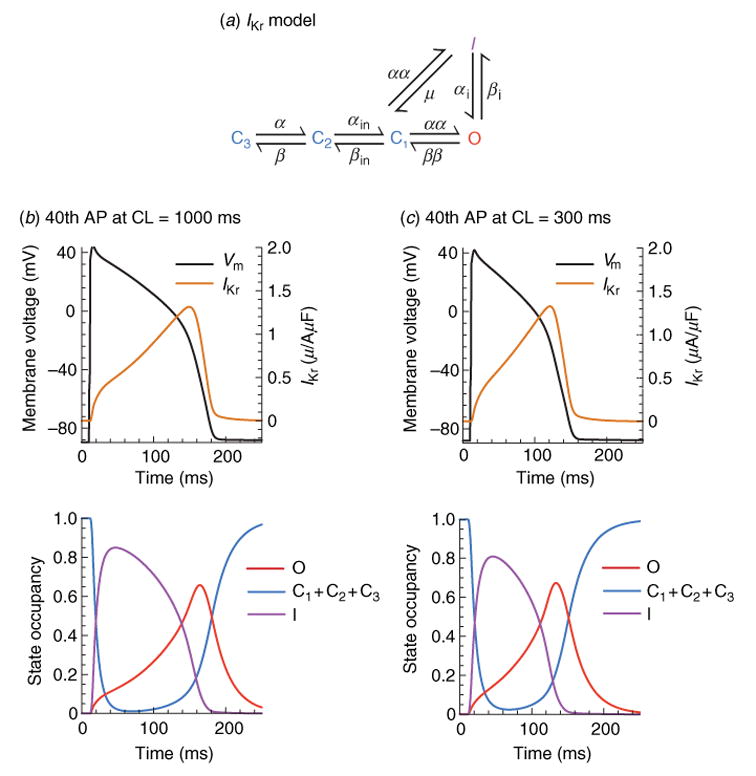
Kinetic transitions of I_Kr channels during the AP at slow and fast rate. (a) Markov model of the I_Kr channel (Clancy & Rudy, 2001; Silva & Rudy, 2005). States are color coded according to their type: closed (blue), inactivated (purple), open (red). (b) I_Kr, V_m, and channel state occupancies during the 40th AP at slow rate, CL = 1000 ms. Even though I_Kr activates nearly instantaneously, few channels move into the open state because of rapid inactivation. Then, as V_m decreases, channels begin to recover from inactivation generating a pronounced peak of open-state occupancy and peak current during the late phase of the AP. (c) I_Kr, V_m, and channel state occupancies during the 40th AP at fast rate, CL = 300 ms. Surprisingly, peak I_Kr is not changed significantly at fast rate. Examination of the state occupancies (bottom panel) reveals that conditions at AP initiation are identical at fast and slow rates, preventing any current accumulation. However, faster increase of I_Kr at fast rate during the AP contributes to APD shortening.

The primary repolarizing current in guinea pig is I_Ks, and it is composed of four KCNQ1 α-subunits as well as a modulatory β-subunit, KCNE1. While the ratio of KCNE1 to KCNQ1 in native channels has been probed using several different methods (Cui et al. 1994; Sesti & Goldstein, 1998; Wang et al. 1998; Chen et al. 2003), a consensus remains elusive. A recent study (Chen et al. 2003) concluded that each I_Ks channel contains four KCNQ1 subunits and two KCNE1 subunits and that other subunit stoichiometries are not naturally assembled. Noise variance analysis has shown that KCNE1 increases single-channel I_Ks conductance as well as channel expression relative to KCNQ1 alone (Pusch, 1998; Sesti & Goldstein, 1998; Yang & Sigworth, 1998). It also removes inactivation and slows channel activation kinetics (Tristani-Firouzi & Sanguinetti, 1998), creating a significant delay before activation. Biophysical analysis of the delay in Shaker channels suggests that two-stage voltage sensor activation, as described in Section 3 · 2 above, is necessary to reproduce the activation kinetics (Zagotta et al. 1994b). We used a similar model, where each closed state represents a possible combination of voltage sensor positions (see Fig. 5) to represent I_Ks (Fig. 8a) (Silva & Rudy, 2005). We added a cooperative, voltage-independent transition before opening, to reproduce steady-state activation measurements (Lu et al. 2001). Application of phosphatidylinositol- 4,5-bisphosphate (PIP₂) to excised patches containing I_Ks channels strongly affects their open probability, but does not change the voltage-dependent properties of the channel (Loussouarn et al. 2003) indicating that PIP₂ interaction is with this voltage-independent transition [observed in Shaker K⁺ channels as well (Koren et al. 1990)]. A second open state, also included in the model, is evident when the channel is probed with rubidium and is responsible for two exponential components of deactivation observed experimentally (Pusch et al. 2000). The complete I_Ks model is shown in Fig. 8a (details can be found in Silva & Rudy, 2005).

Fig. 8.

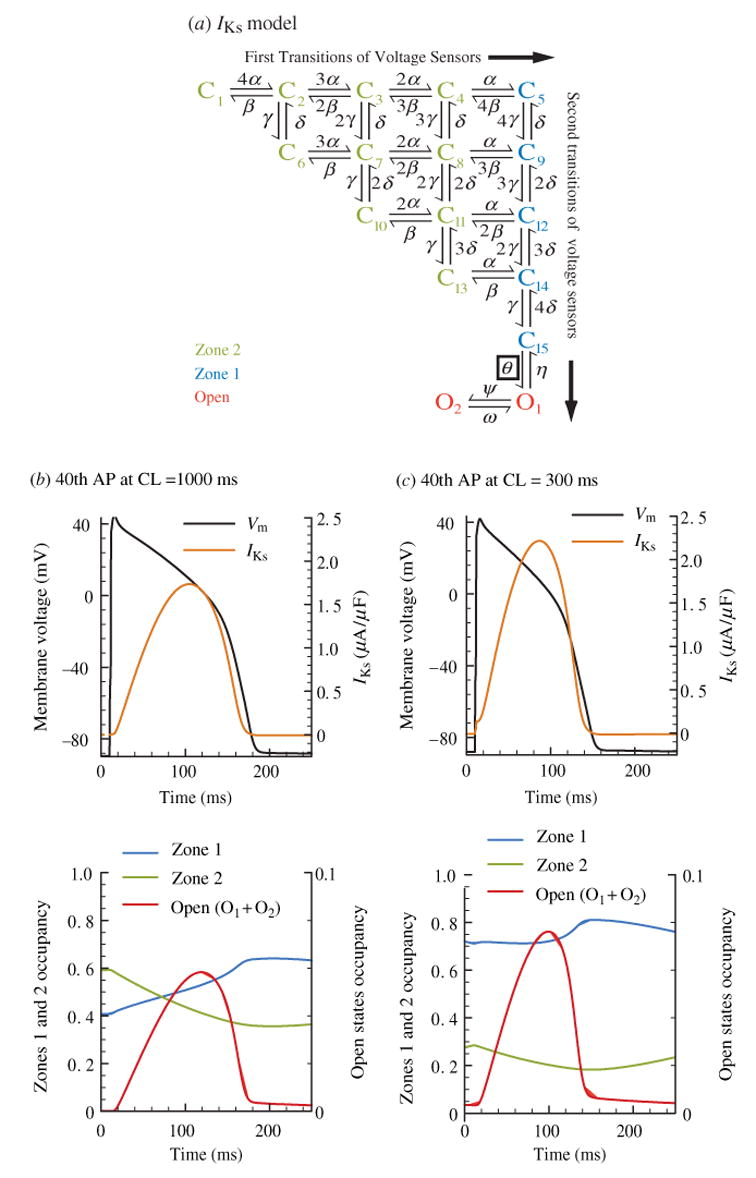
Kinetic transitions of I_Ks channels during the AP at slow and fast rate. (a) Markov model of the I_Ks channel (Silva & Rudy, 2005). States are color coded according to their type: zone 2, closed states for which not all voltage sensors have completed the first transition (light green). zone 1, closed states for which all four voltage sensors have completed the first transition (blue). Open (red). (b) I_Ks, V_m and channel state occupancies during the 40th AP at slow rate, CL = 1000 ms. I_Ks rises slowly, resulting in peak current at the end of the AP where it most efficiently contributes to repolarization. Only 40% of channels reside in zone 1 at AP onset and can activate rapidly. While V_m remains depolarized, channels continue to transition from zone 2 to zone 1. (c) I_Ks, V_m, and channel state occupancies during the 40th AP at fast rate, CL = 300 ms. Since the diastolic interval is shorter at CL = 300 ms, V_m stays at depolarized potentials for a larger percentage of time, which causes accumulation in zone 1 of closed states. At AP onset 75% of channels reside in zone 1, facilitating rapid transitions to the open state. This results in increased I_Ks late during the AP and APD shortening. Note that the mechanism for I_Ks increase is accumulation in closed states near the open state (zone 1) as opposed to open-state accumulation. The accumulation in zone 1 creates a reserve of channels that are ready to open rapidly, ‘on demand’ to generate a greater repolarizing current; we call this pool of channels ‘available reserve’.

Closed states in the model are divided into two zones, zone 2 (green) contains channels where at least one subunit still has to make a first transition to the intermediate state R₂ (see Fig. 5a), zone 1 (blue) contains channels with voltage sensors that only need to make more rapid second transitions into the activated state A. As shown in Fig. 8b, at the slow rate (CL = 1000 ms) 60% of I_Ks channels reside in zone 2 before AP depolarization and must make a slow transition into zone 1 before opening. At this rate, only 40% of channels reside in zone 1 before AP onset. In contrast, at the fast rate (CL = 300 ms) nearly 75% of channels accumulate in zone 1 before AP onset, leading to a rapid rise in current during the AP (Fig. 8c). At this rate, there is not sufficient time between beats for channels to transition back to zone 2 before the next AP. Note that there is minimal open-state accumulation, rather, accumulation takes place in zone 1 of closed states that are near the open state. This result, a consequence of two-stage voltage-sensor activation, is confirmed by AP-clamp experiments showing a rapid increase in I_Ks at fast rate, but no instantaneous current at AP initiation (Rocchetti et al. 2001) that would have been indicative of open-state accumulation. Thus, at fast rate there is a build-up of channels in zone 1 of closed states. These channels can open quickly ‘on demand’ to cause fast I_Ks increase towards the repolarization phase of the AP, when the current can effectively shorten the APD. We termed the channels that accumulate in zone 1 ‘available reserve’ (AR). This novel mechanism of APD shortening at fast rate differs from the accepted mechanism which relies on channel accumulation in the open state to generate instantaneous current upon AP depolarization.

3.4 Physiological implications of I_Ks subunit interaction

As noted above, KCNE1 interaction with KCNQ1 to form I_Ks increases channel conductance and expression, and removes inactivation. It also acts to decrease activation rate and accelerate deactivation. These effects clearly oppose each other; the conductance increase and removal of inactivation augment the current, while the activation/deactivation kinetic changes reduce the current. Moreover, in human myocytes slowing of activation and increased rate of deactivation are much more pronounced than in other species (Virag et al. 2001). The co-existence of opposing effects would seem to prohibit I_Ks participation in AP repolarization and in determining APD. In particular, fast deactivation prevents channel accumulation in the open state at fast rate, a property that has been considered necessary for participation in rate-adaptation of APD. However, mutations to both KCNQ1 (Wang et al. 1996) and KCNE1 (Splawski et al. 1997) (LQT1 and LQT5 mutations respectively) can prolong the QT interval and predispose patients to cardiac arrhythmias and sudden death. Adenosine 3′,5′-monophosphate (cAMP)-dependent protein kinase A (PKA) and protein phosphatase 1 (PP1) co-immunoprecipitate with human KCNQ1, implying an I_Ks role in APD modulation during β-adrenergic stimulation (Terrenoire et al. 2005). Heterogeneity in I_Ks channel density, in particular its low density in mid-myocardial cells (M-cells) is responsible for differences in APD across the ventricular wall in many species (Liu & Antzelevitch, 1995; Antzelevitch & Fish, 2001; Antzelevitch & Dumaine, 2002). It has also been suggested that I_Ks serves as a repolarization reserve (RR) that can compensate for reductions in I_Kr by mutations or drugs (Roden, 2004). These observations suggest that I_Ks does play an important role in AP repolarization in human heart.

To explore the KCNQ1–KCNE1 subunit interaction in the context of AP repolarization, we constructed two Markov-type models, the first of the homomeric human KCNQ1 channel and the second of the human heteromeric I_Ks channel (KCNQ1 with KCNE1) (Kupershmidt et al. 2002). The KCNQ1 model (not shown) has a similar 15 closed-state structure to that of I_Ks (Fig. 8a) but differs in several significant aspects (Silva & Rudy, 2005). It includes an inactivation process, detected as a hook in the tail current (Tristani-Firouzi & Sanguinetti, 1998); the hook is only observed after a delay, implying multiple open states (five in the model) (Pusch et al. 2001). Deactivation is slower and activation transitions are more rapid resulting in more channels residing in closed states near the open state even at slow rates (Silva & Rudy, 2005). Two-stage voltage-sensor activation is still used to model channel opening because of an experimentally observed delay of several ms before KCNQ1 activation (Tristani-Firouzi & Sanguinetti, 1998).

Each model is inserted into the LRd model of the guinea pig ventricular myocyte to create a virtual chimeric myocyte. This environment is interesting because, as discussed above, the guinea pig relies heavily on I_Ks for repolarization, while minimizing the role of I_Kr during the AP plateau. Such conditions are observed in human ventricular myocytes when I_Kr is reduced, and are suitable for testing the ability of I_Ks to participate in the RR when I_Kr is compromised by mutations or drugs.

Figure 9 shows APs at fast and slow rates, with I_Ks [panels (a) and (c)] and with KCNQ1 [panels (b) and (d )]. Densities were adjusted to produce similar APDs for both channels, with duration of ~200 ms at CL = 1000 ms. APs with I_Ks shorten substantially more at the fast rate (CL = 250 ms) than those with KCNQ1 (Fig. 9a, b). The KCNQ1 and I_Ks currents underlying V_m are plotted below the respective APs. At fast rates, KCNQ1 generates a large instantaneous current at the AP onset (Fig. 9d, arrow), which does not increase any further during the AP. The instantaneous current is generated by channel accumulation in the open state between beats. In contrast, at the fast rate little open state accumulation is observed for I_Ks (Fig. 9c, arrow), but the current rises more rapidly by relying on the fast opening of channels that accumulate in zone 1 to build up an ‘AR’. Minimizing the current at the beginning of the AP conserves current and allows I_Ks to peak at the end of the AP, where it is most efficient in causing repolarization.

Fig. 9.

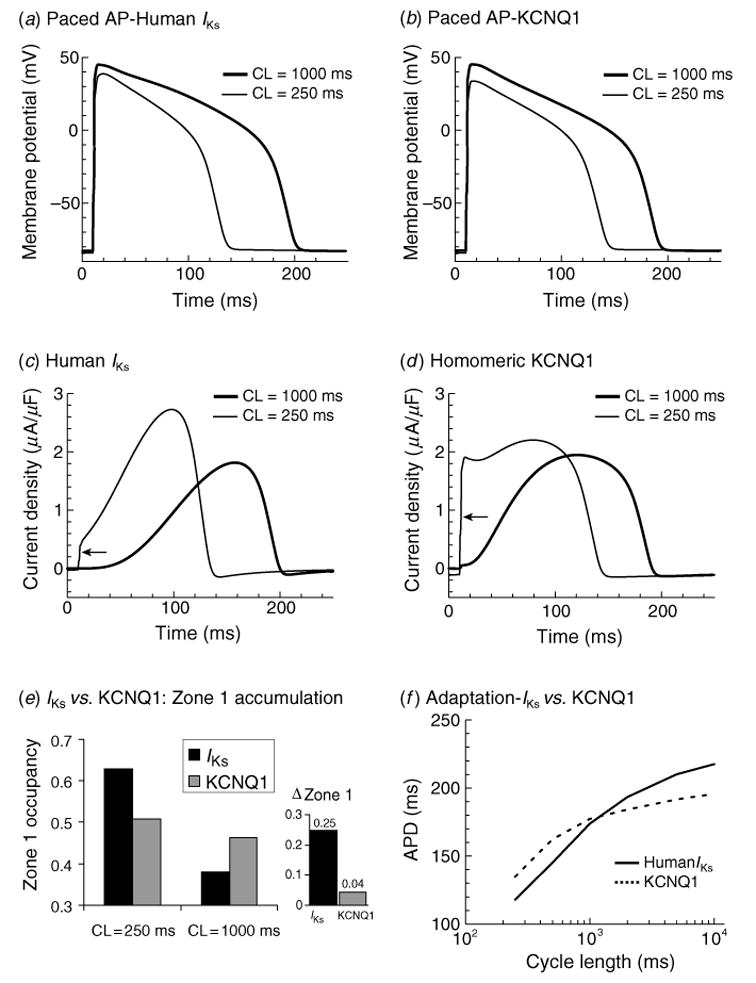
APD rate-rdaptation with human I_Ks vs. human KCNQ1. (a) 40th AP computed with human I_Ks in the cell model at CL = 250 ms (thin line) and CL = 1000 ms (thick line). (b) Same as panel (a) with KCNQ1 replacing I_Ks in the model. (c) Human I_Ks during the AP at fast and slow rates. Some open-state accumulation at fast rate causes a small instantaneous current upon depolarization (arrow), while closed-state accumulation in zone 1 [see panel (e) and Fig. 10c] creates a reserve that allows the current to increase to a late peak that shortens APD effectively. (d ) KCNQ1 during the AP at fast and slow rate. Slow kinetics of deactivation cause large open- state accumulation at fast rate and large instantaneous current upon depolarization (arrow). Note that in the absence of zone 1 reserve [see panel (e)], the current stays constant during the AP, lacking the late, repolarizing peak of I_Ks. (e) Human I_Ks (black) and KCNQ1 (gray) zone 1 occupancy at CL = 250 ms and 1000 ms. Accumulation in zone 1 at fast rate allows I_Ks to participate in adaptation. In contrast, little accumulation is seen in zone 1 for KCNQ1. ΔZone 1 is increase in zone 1 occupancy between CL = 1000 ms and 250 ms. (f) APD adaptation curves for an AP with human I_Ks (solid line) and KCNQ1 (dashed line). Lack of accumulation in zone 1 results in less APD shortening at fast rates with KCNQ1 compared to I_Ks. (From Silva & Rudy, 2005, with permission.)

The difference observed between KCNQ1 and I_Ks participation in the AP is a result of different levels of channel accumulation in zone 1. I_Ks channels increase zone 1 occupancy by 25% as rate changes from slow to fast (Fig. 9e). In contrast, KCNQ1 occupancy in zone 1 remains practically constant (only 4% increase) regardless of rate (Fig. 9e). This enhanced capacity to build an AR, a consequence of the kinetic changes conferred by the interaction with KCNE1, results in superior ability of I_Ks to cause rate adaptation of APD in comparison to KCNQ1 (steeper adaptation curve in Fig. 9f ). We conclude that the kinetic changes conferred by KCNE1 complement its effect of increasing channel conductance by enabling I_Ks channels to participate in repolarization late during the AP when they are most effective.

3.5 Mechanism of cardiac action potential rate-adaptation is species dependent

While the mechanisms that regulate APD adaptation to changes in rate are similar across mammalian species, the degree of participation of a given channel varies widely. Moreover, because of differences in channel kinetics and expression levels, AP morphology is also species specific. For example, canine ventricular epicardial APs display a notch during the early plateau phase (Fig. 10a, left) that is caused by the transient outward K⁺ current, I_to,1 (Liu et al. 1993; Hund & Rudy, 2004). This notch is absent in guinea pig APs (Fig. 10a, right), as I_to,₁ is not detected in guinea pig ventricular myocytes.

Fig. 10.

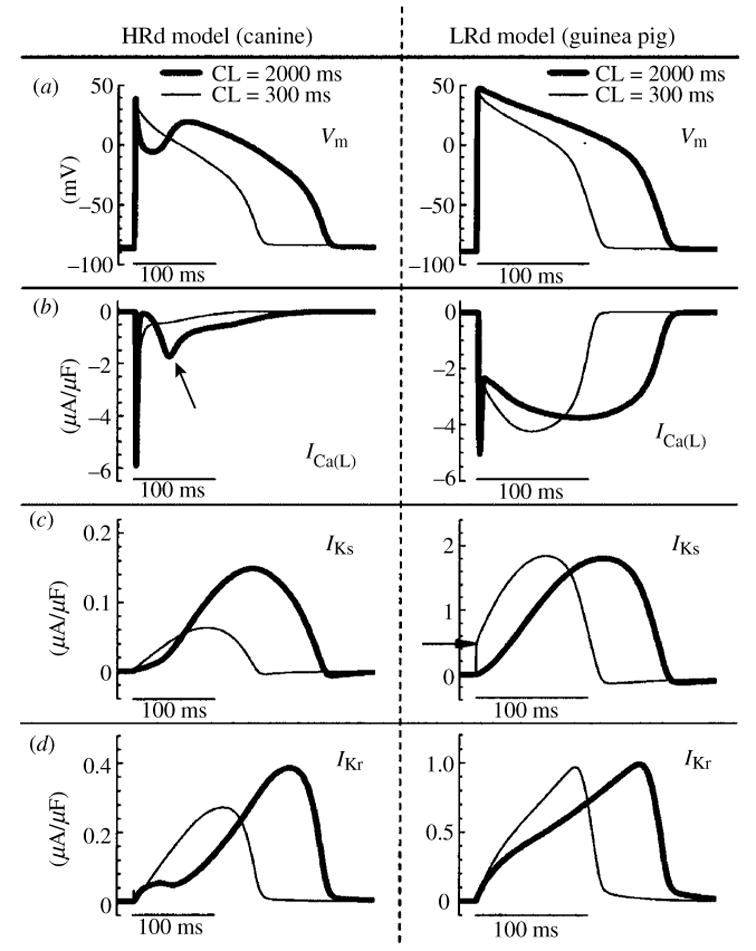
Role of selected ion-currents in APD rate-adaptation in the canine and the guinea pig. Simulations conducted with HRd canine (Hund & Rudy, 2004) (left panels) and LRd guinea pig (Luo & Rudy, 1994a) (right panels) cell models. Steady-state values are shown at fast rate (CL = 300 ms, thin line) and slow rate (CL = 2000 ms, thick line). (a) AP; (b), I_Ca(L); (c), I_Ks (arrow indicates I_Ks accumulation); (d ), I_Kr. Schematic of the HRd model is provided in Fig. 31. (From Hund & Rudy, 2004, with permission.)

The presence of I_to,1 in canine epicardial myocytes indirectly influences, through its effects on other currents, rate-dependent AP changes and APD adaptation. At slow rate, a large I_{to, 1} creates a deep notch in V_m (Fig. 10a, left) that is greatly reduced or absent at fast rate because of reduced I_{to, 1} (a consequence of its slow recovery from inactivation). The reduction in V_m due to the notch at slow rate increases the driving force for I_Ca(L) and enhances its voltage-dependent activation during the AP plateau (Fig. 10b, left, arrow). The increase of plateau I_Ca(L) leads to APD prolongation and formation of the prominent dome that characterizes the canine ventricular epicardial AP (Liu et al. 1993). The transient reduction of V_m also inhibits the reverse mode of I_NaCa (not shown). In this mode, I_NaCa brings Ca²⁺ into the cell and extrudes Na⁺ with a 1:3 stoichiometry, generating a net outward (repolarizing) current. Inhibition of this current by the notch contributes to APD prolongation. Finally, the magnitude of I_Kr during the AP is determined primarily by the fraction of channels that recover from inactivation (see Fig. 7). At lower V_m, fewer channels activate and inactivate, reducing the number of channels that are available to recover from inactivation during the AP. The resulting reduction of I_Kr also contributes to APD prolongation.

Figure 10 provides a comparison of rate-dependent AP changes and APD adaptation in the canine (left panels) and the guinea pig (right panels). Reduced plateau I_Ca(L) (Fig. 10b, left) is the primary mechanism of canine AP shortening at fast rate (elimination of the I_Ca(L) effect in the model reduces adaptation by 71% for a CL range of 8000 ms to 300 ms) (Hund & Rudy, 2004). In contrast, I_Ca(L) in the guinea pig shows only minimal dependence on rate (Fig. 10b, right). The major determinant of APD adaptation in the guinea pig is I_Ks. In this species, I_Ks is a relatively large current which is slow to deactivate. At fast rate, slow deactivation results in some I_Ks accumulation between beats (Fig. 10c, right, arrow) and there is faster increase of current during the AP plateau, resulting in APD shortening. Faster increase of I_Kr at fast rate also contributes to APD adaptation in the guinea pig (Fig. 10d, right). In the canine, I_Ks and I_Kr are much smaller than in the guinea pig and I_Ks accumulation does not occur between beats due to its faster deactivation (Fig. 10c, left). However, as discussed in Section 3.4, I_Ks is able to develop an AR of deactivated channels at fast rate, and its role in repolarization is augmented under conditions of β-adrenergic stimulation (Marx et al. 2002; Stengl et al. 2003; Volders et al. 2003). I_Kr in the canine decreases at fast rates, an effect that actually opposes APD shortening. The decrease of I_Kr is a result of two opposing effects : (1) reduced I_{to, 1} acting to increase V_m (reduced notch) and increase I_Kr; (2) reduced plateau I_Ca(L) acting to decrease V_m and reduce I_Kr. The net result is I_Kr reduction at fast rate (Fig. 10d, left).

The simulations in this section serve to underscore an important property of the cardiac AP. Under most conditions, the AP upstroke is generated by a very large I_Na with a large margin of safety (major reduction of I_Na is required to affect the upstroke). The dependence on a single, large current is consistent with the requirement that AP generation should be a robust ‘all or none’ process. In contrast, the AP plateau and repolarization phases are controlled by a delicate balance between much smaller inward and outward currents, and by their interplay via the membrane potential. Such delicate balance between multiple currents provides multiple ‘control points’ for precise control of APD and its rate dependence. The need to accommodate more APs per unit time when rate increases dictates such ‘system design’. Unfortunately, this delicate balance can be easily perturbed by undesired changes in the properties of any of the component currents. Such changes can be caused by genetic mutations of ion-channel proteins, by pathology-induced remodeling, or by drugs. In the next section, we provide examples of simulations that examine the cellular electrophysiological consequences of ion-channel mutations.

4. Simulating ion-channel mutations and their electrophysiological consequences

Abnormal repolarization of the AP provides a substrate for life-threatening cardiac arrhythmias. As stated in the conclusion of the previous section, the dependence of repolarization on a delicate balance between various currents makes it vulnerable to perturbation by disease or drugs. Mutations in genes that encode cardiac ion channels can lead to abnormal channel function (‘channelopathy’) which perturbs the AP to cause arrhythmias (Keating & Sanguinetti, 1996; Priori et al. 1999a, b). Mutation-induced alterations in ion channel function are studied in expression systems (e.g. Xenopus oocyte) in isolation from the physiological environment of the cardiac cell where the channels interact to generate the AP. In this section we demonstrate how computational biology can be used to integrate this information into the functioning cardiac cell in order to relate these molecular-level findings to whole-cell function and to the clinical phenotype. We provide examples from the hereditary Long QT syndrome (LQT) that presents clinically as prolongation of the QT interval on the electrocardiogram and the occurrence of life-threatening arrhythmias and sudden cardiac death. Specifically, we simulate LQT type 3 (LQT3) and LQT type 2 (LQT2) that are associated with mutations in SCN5A (the gene that encodes I_Na) and in HERG (I_Kr), respectively. We also simulate the Brugada syndrome (Brugada et al. 1998) that presents clinically as ST segment elevation in the right precordial leads of the electrocardiogram and is also associated with severe arrhythmias and sudden death. Because mutations affect specific structural elements and kinetic states of the model and their interdependencies, single-channel-based Markov models are required to conduct these simulations. We also show how the molecular structure of an ion channel (I_Ks) underlies its ability to compensate for reduced repolarizing current when I_Kr is compromised by mutation (LQT2) or drugs (‘acquired LQT’), a property that identifies the role of I_Ks as repolarization reserve (RR) under pathological conditions.

4.1 Mutations in SCN5A, the gene that encodes the cardiac sodium channel

4.1.1 The ΔKPQ mutation and LQT3

ΔKPQ is a mutation in the SCN5A gene that encodes I_Na. It causes a deletion of three amino acids from a highly conserved region of the III–IV linker, a portion of the I_Na channel protein that is involved in fast inactivation (Fig. 11, inset). It was observed experimentally in expression systems that this structural defect leads to two modifications of channel function: (1) faster activation and recovery from inactivation, and (2) transient complete failure of inactivation in some of the channels (Bennett et al. 1995; Dumaine et al. 1996; Chandra et al. 1998; Nuyens et al. 2001).

Fig. 11.

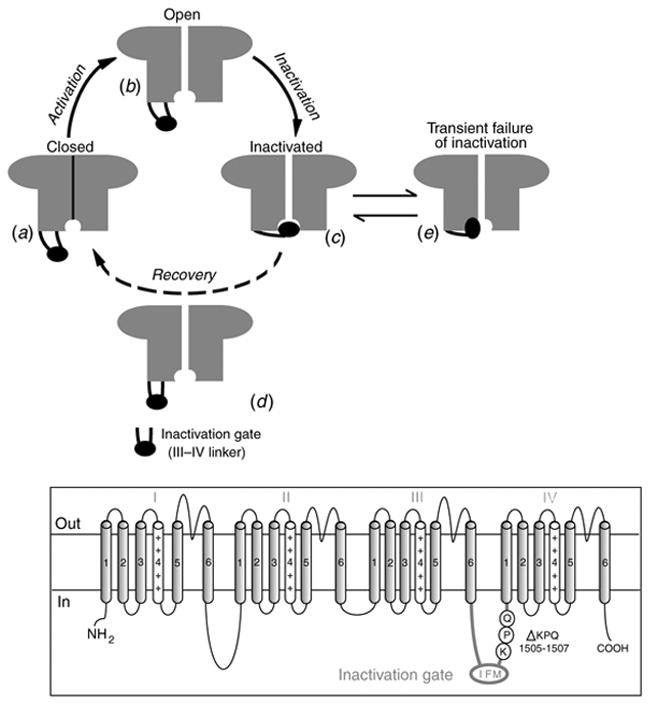
The excitatory cycle of an ion channel and its alteration by the ΔKPQ deletion mutation of the Na⁺ channel. (a)–(e) Schematic description of ion-channel transitions during the action potential. Because of the ΔKPQ structural defect in the III–IV linker, the ‘hinged-lid’ mechanism of inactivation fails to plug the channel pore in some channels, some of the time. Thus, ΔKPQ mutant channels experience a transient failure of inactivation [panel (e)]. The boxed panel shows the mutant channel, where three amino acids, Lys1505 (K), Pro1506 (P) and Gln1507 (Q) are deleted from the III–IV linker which participates in fast inactivation.

During its excitatory cycle (Fig. 11) an ion channel awaits excitation in a closed configuration (a). Upon excitation, it permits the passage of ions through the channel pore (b). Based on the ‘hinged-lid’ model of inactivation (West et al. 1992), the open configuration of the channel allows a portion of the protein (in the III–IV linker) to plug the channel pore, a process termed inactivation (c). To complete the cycle, the hinged-lid structure leaves the channel pore allowing the channel to close (a process termed recovery) and return to its rest state (a), ready for the next excitatory cycle. Because of the structural defect in the inactivation gate, ΔKPQ mutant channels experience a transient failure of inactivation as shown schematically in (e), where the hinged-lid structure fails to plug the channel pore. As stated above, ΔKPQ channels that do inactivate recover from inactivation faster than wild-type (WT) normal channels.

The modifications of channel gating by the ΔKPQ mutation were simulated in the Markov model of I_Na shown in Fig. 12a (Clancy & Rudy, 1999). The WT channel model includes three closed states (C3, C2, C1), an open state (O) which is the only conducting state of the channel, and fast (IF) and slow (IS) inactivation states. The mutant channel contains two modes of gating, the upper ‘background mode’ and the lower ‘burst mode’. The background mode is similar in structure to the WT model, except for altered voltage dependence of activation, inactivation, and recovery from inactivation that results in faster transitions between these states, reflecting the experimentally observed kinetic changes. The burst mode does not include an inactivation state, simulating the transient failure of inactivation of ΔKPQ channels.

Fig. 12.

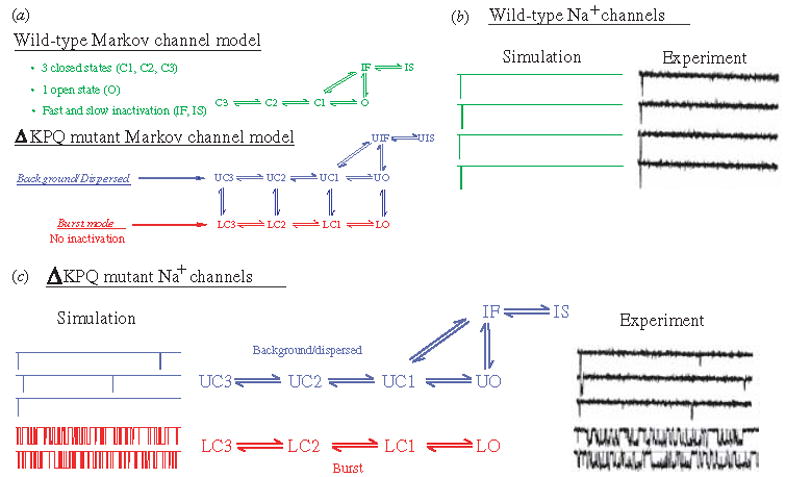
(a) Markov models of the wild-type (WT) and ΔKPQ mutant Na⁺ channels. The WT channel (top, green) contains three closed states, an open (conducting) state, and fast and slow inactivated states. The ΔKPQ channel has two modes of gating : the background (or dispersed) mode (blue) that is similar in structure to WT, and a burst mode (red) in which channels fail to inactivate. The U and L prefixes to ΔKPQ states indicate upper mode and lower mode, respectively. (Modified from Clancy & Rudy, 1999, with permission.) (b, c) WT and ΔKPQ single-channel gating. (b) Simulated WT channels (left) show only single openings in response to depolarization, as observed experimentally by Chandra et al (right). (c) Simulated ΔKPQ channels in the background mode (left, blue) show secondary reopenings beyond the first opening. In the burst mode (red), channels do not inactivate and fluctuate between open and closed states. Similar behavior is observed experimentally. (Modified from Clancy & Rudy, 1999; experimental data are reproduced from Chandra et al. 1998, with permission.)

Figure 12(b,c) compares single-channel gating of WT [panel (b)] and ΔKPQ [panel (c)] as recorded experimentally (right tracings) or simulated by the model of panel (a) (left tracings). In both experiments and simulations, WT channels open and inactivate in response to a depolarizing pulse, showing only a single opening event on each tracing (Fig. 12b). ΔKPQ channels in the background mode open and recover from inactivation faster than WT. Because of the strong coupling between states O and IF, faster opening results in an increased population of channels in the IF state. Faster recovery of these channels from IF into the open state increases the probability of channel reopenings after the first opening during a depolarizing pulse. Such secondary openings are clearly evident in the recorded and simulated three top traces of Fig. 12c. Most mutant channels (>99%) reside in the background mode. However, there is a small, but finite, probability of channel entry into the burst mode, where channels are ‘trapped’ because of even smaller probability of return to the background mode. The burst-mode model does not include the inactivation states IF and IS, representing the transient failure of channels to inactivate. In this mode, channels fluctuate between closed and open states and display frequent opening events (‘bursting’) as seen in the simulated and recorded bottom two traces of Fig. 12c.

The observation that ΔKPQ channels reopen and burst at depolarized potentials leads to the hypothesis that together these modes generate a significant late I_Na current during the AP plateau and that this current is sufficient to delay AP repolarization and prolong the APD. The prolonged APD is reflected as QT interval prolongation on the ECG, the Long QT syndrome phenotype. To examine this possibility, the Markov models of Fig. 12 were introduced into the LRd ventricular cell model (Fig. 2a) paced at various rates (Clancy & Rudy, 1999). Figure 13 shows simulated APs (top) and corresponding macroscopic transmembrane I_Na through an ensemble of Na channels for : (I) WT paced at CL of 400 ms; (II) ΔKPQ at the same CL; and (III) ΔKPQ at a slower rate (CL = 600 ms). ΔKPQ experimental data are included for comparison in (IV), showing close resemblance of the measured I_Na trace with that simulated in (II). During a WT AP, I_Na displays an early large peak (‘spike’) that generates the AP upstroke; it decays quickly, reflecting the absence of late openings at the single-channel level. In contrast, the additive effects of channel reopenings in the background mode and bursting in the burst mode of ΔKPQ result in a late component of macroscopic current during the AP plateau. Despite its small magnitude (3·0 μA/μF; only 1% of the early peak I_Na), this current is sufficient to shift the delicate balance between inward and outward currents in the inward (depolarizing) direction and prolong the APD. In the simulation presented here APD of the mutant cell is markedly prolonged, by 62·3 ms, relative to WT at CL = 400 ms. With slowing of the pacing rate to CL = 600 ms, a secondary depolarization develops during the late plateau phase of the AP. This after-depolarization is classified as early after-depolarization (EAD) because it occurs during the AP, before complete AP repolarization. In the context of arrhythmogenesis, regional delays of the repolarization process by AP prolongation and/or EADs can create spatial non-uniformities of excitability (‘dispersion of repolarization’) that provide a substrate for the development of unidirectional block and re-entry. Moreover, under certain conditions EADs can elicit an excitatory response that provides the trigger for arrhythmic activity. Note that in the simulation of Fig. 13, EADs develop at a relatively short CL (600 ms). In the congenital LQT3, arrhythmias occur at slow heart rates (bradycardia), usually during sleep or relaxation (Schwartz et al. 1995). The simulation assumes that all (100%) Na channels in the cell are ΔKPQ mutant channels. Typically, affected individuals are heterozygous for the mutation, so that only 50% of channels are ΔKPQ. Repeating the simulation with 50% WT and 50% ΔKPQ Na channels (Fig. 14), slowing the rate to CL of 1200 ms (a typical heart rate of clinical bradycardia) is required for EAD generation.

Fig. 13.

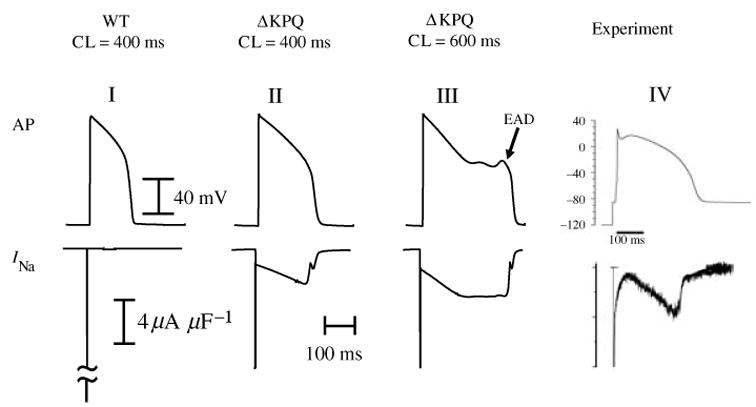
Effect of ΔKPQ mutation on the whole-cell AP. Simulated AP is shown on top and corresponding I_Na on the bottom. ΔKPQ I_Na generates a persistent current during the AP plateau that prolongs APD (II) relative to WT (I). As pacing rate is decreased, persistent I_Na increases causing greater prolongation of APD and generation of EADs (III). Panel IV shows experimental AP-clamp mutant data from Wang et al. (1997); note the similar morphology of persistent I_Na to that simulated in panel II. (From Clancy & Rudy, 1999; experimental data are reproduced from Wang et al. 1997, with permission.)

Fig. 14.

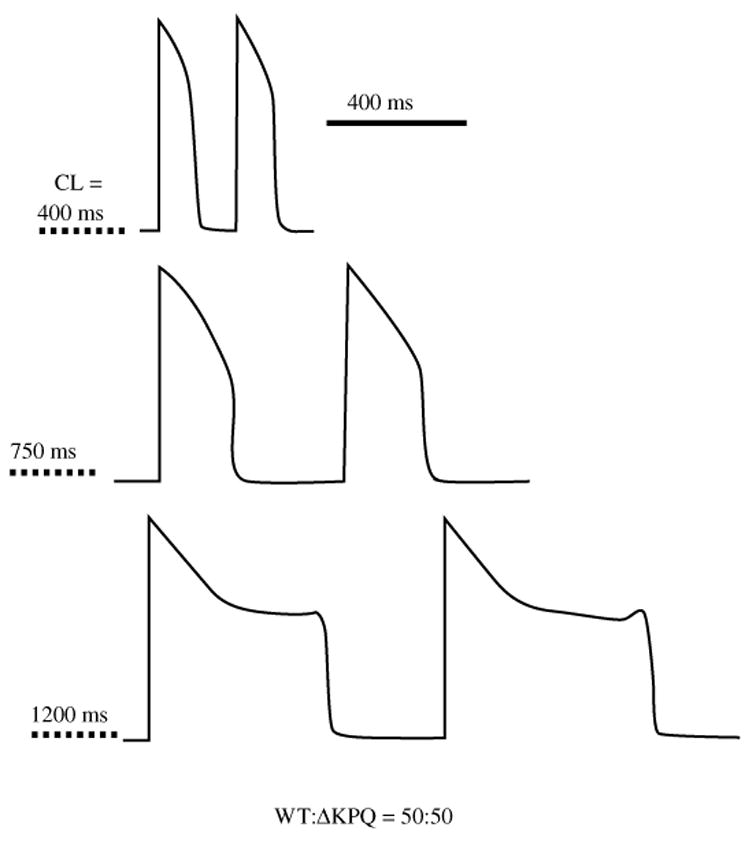
Effect of ΔKPQ at various pacing cycle lengths (CL). The cell contains equal densities of WT and mutant channels (50%/50%). As pacing rate decreases, APD prolongation becomes more pronounced. At a bradycardia CL of 1200 ms, EADs develop. (From Clancy & Rudy, 1999, with permission.)

The late (sustained) component of ΔKPQ I_Na arises mostly from bursting channels caught in the burst mode of gating. These channels experience a transient failure of inactivation. A different kinetic mechanism has been suggested by computer simulations to underlie LQT3 associated with the SCN5A I1768V mutation (Clancy et al. 2003). For this mutation, I_Na mutant channels recover from inactivation at a faster rate than WT and reopen during the repolarization phase of the AP, when the membrane voltage is decreasing (non-equilibrium conditions). The I_Na current generated by channel reopenings tilts the balance of currents during repolarization in the depolarizing direction, thus prolonging repolarization and APD, and leading to formation of EADs.

The EAD in Fig. 13 (III) depolarizes from plateau potentials and is therefore termed a plateau EAD. The simulation of Fig. 15 provides insight into the ionic mechanism that underlies depolarization of such EADs (January et al. 1988; January & Riddle, 1989; Rosen, 1990; Luo & Rudy, 1994b; Zeng & Rudy, 1995; Viswanathan & Rudy, 2000). APs (Fig. 15a) and corresponding I_Ca(L) (Fig. 15b) are shown for the last paced beat of a train of 40 beats (CL = 500 ms) and for an additional beat that follows a 1500 ms pause (onset of clinical arrhythmias in LQT syndrome often follows a pause). We overlay the pre-pause and post-pause data in Fig. 15 to facilitate comparison. Three EADs are generated during the post-pause AP plateau. Inspection of the I_Ca(L) tracing shows that the upstroke of each EAD corresponds to an increase of inward I_Ca(L). In contrast, in the pre-pause AP, I_Ca(L) decreases monotonically to the baseline and EADs are not generated. If I_Ca(L) during the post-pause AP is clamped to follow the monotonic decline that it traces during the pre-pause AP, the EADs are abolished (not shown). These simulations identify I_Ca(L) as the depolarizing charge carrier that generates the EAD upstroke. Thus, I_Ca(L) provides the primary ionic mechanism of plateau EAD generation. In the different types of the LQT syndrome, mutations in different ion channels lead to APD prolongation. In LQT3 the mutations are in SCN5A, leading to a late I_Na current that prolongs the APD, as shown for the ΔKPQ mutation in Fig. 13. The prolonged plateau provides sufficient time at the appropriate potential range for I_Ca(L) recovery from inactivation and reactivation. The inward I_Ca(L) current generated by reactivation carries a depolarizing charge that depolarizes the membrane to form the EAD. It is important to recognize that in the LQT3 example of Fig. 13, the defective mutant channels do not generate the arrhythmogenic EAD. By prolonging the plateau phase of the AP they provide conditions for I_Ca(L) recovery and reactivation, setting the stage for EAD generation by L-type Ca channels that are ‘innocent bystanders’, completely normal and unaffected by the mutation. This illustrates an important principle regarding the electrophysiological responses of the cell; being a highly interactive nonlinear system, the cellular response to a particular perturbation (e.g. altered I_Na) is determined by complex interactions between the various components of the cell. Considering that human intuition is mostly linear, computational biology provides a useful tool for elucidating mechanisms and predicting cellular responses, as demonstrated by the simulations presented here.

Fig. 15.

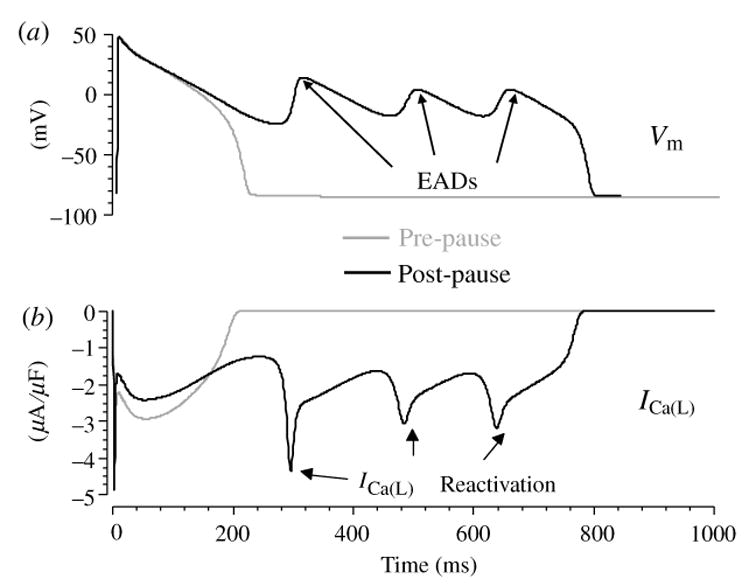
Ionic mechanism of plateau EADs. (a) Pre-pause (gray) and post-pause (black) APs. (b) The corresponding I_Ca(L) during the AP. Reactivation of I_Ca(L) [(b), arrows] depolarizes the membrane to generate the EADs [(a), arrows]. (Modified from Viswanathan & Rudy, 1999, with permission.)

4.1.2 SCN5A mutation that underlies a dual phenotype

1795insD is a mutation that involves insertion of an aspartic acid in the C terminus of the cardiac Na channel (Fig. 16a). This single mutation causes two distinct clinical syndromes in affected individuals; LQT at slow heart rate and Brugada syndrome at fast heart rate, that can lead to life-threatening cardiac arrhythmias and sudden death (Bezzina et al. 1999; Veldkamp et al. 2000). LQT is reflected in the ECG as prolongation of the QT interval; Brugada manifests as ST segment elevation in the right precordial leads (Fig. 17). Coexistence of these syndromes in the same individual is seemingly paradoxical because LQT is associated with enhanced I_Na (generation of a late component of current, as shown in the previous section), whereas Brugada is associated with reduced I_Na. Using computational biology, we attempted to explain how a single Na-channel mutation can cause these two distinct ECG phenotypes.

Fig. 16.

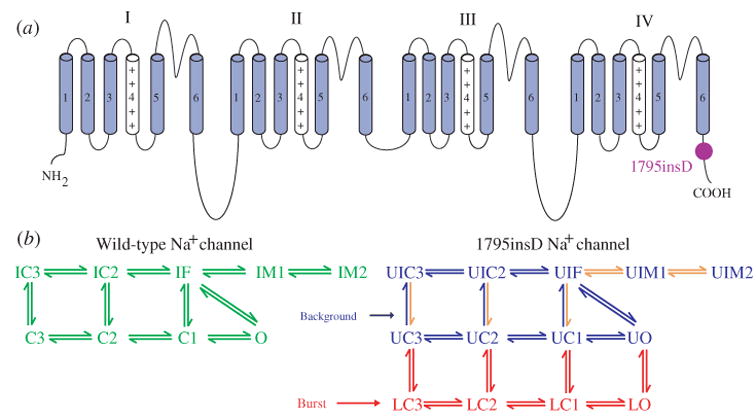
Markov models of WT and 1795insD mutant Na⁺ channels. (a) Location of the aspartic acid insertion in the C terminus of the 1795insD mutant channel protein. (b) The WT Markov model (left, green) and the 1795insD Markov model (right) with its background mode (blue) and burst mode (red). Orange arrows indicate transitions with rate modified by the mutation (e.g. slower recovery from IC3 to C3; see text). IM1 and IM2 are intermediate inactivation states. (Modified from Clancy & Rudy, 2002, with permission.)

Fig. 17.

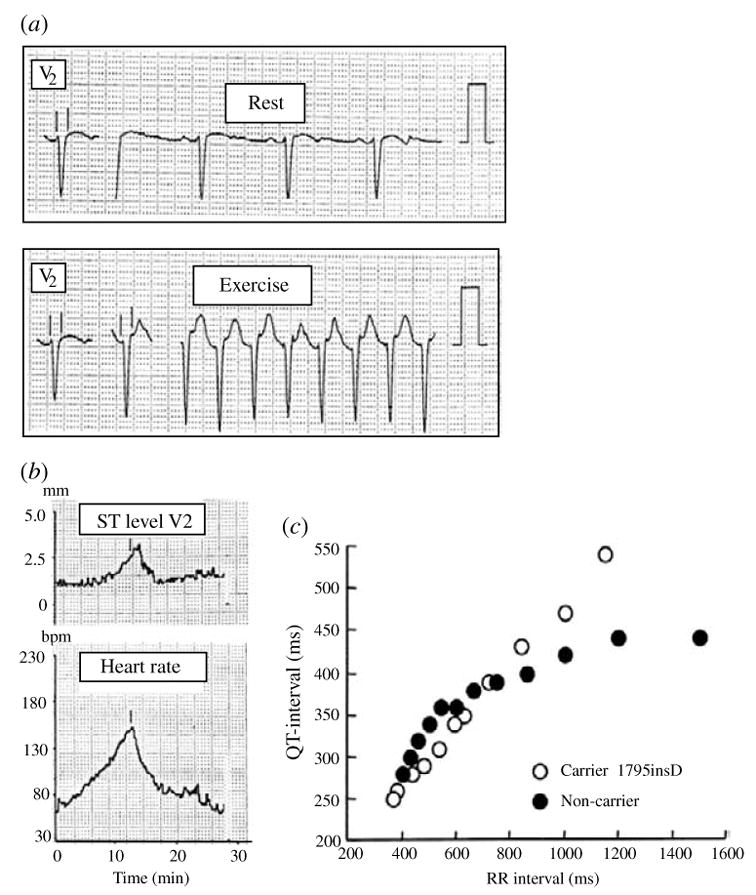
Clinical data from patients with the 1795insD mutation. (a) ST-segment elevation at fast heart rate (Exercise, bottom) compared to control (Rest, top) in lead V₂ of the ECG. (b) Indicates that the ST-segment elevation (top) increases with heart rate (bottom). (c) Indicates much greater QT prolongation in mutation carriers (○) compared to non-carriers (●) as heart rate decreases. (From Veldkamp et al. 2000, with permission.)

Similar to the ΔKPQ simulations of the previous section, our starting point is the development of Markov models for WT and 1795insD Na channels (Fig. 16b) (Clancy & Rudy, 2002). To account for all experimental observations, two intermediate inactivation states IM1 and IM2 (with slower kinetics than IF) and closed-inactivation states IC2 and IC3 (accounting for channel inactivation directly from the closed states) are included in the model (Veldkamp et al. 2000; Wang et al. 2000; Wehrens et al. 2000; Abriel et al. 2001). The mutant channel displays bursting kinetics, represented in the model as a burst mode. Transitions into the burst mode can occur from the closed and open states of the model, but not from the inactivated states. In mutant channels, transitions into IM1 and IM2 are faster than in WT, whereas recovery from these inactivation states is slower, making these states more ‘absorbing’. Similarly, transition out of IC2 and IC3 are also slower than WT, increasing the absorbency of these states. As shown in Fig. 18, the greater absorbency reduces channel availability (leftward shift of the availability curve, middle column) and, importantly, slows significantly its recovery from inactivation (left column). A plot on a logarithmic timescale (left column, insets) reveals that mutant channels may require more than 100 ms to recover from inactivation, a time that is of the order of the AP duration. As a result, there is loss of I_Na current that is cumulative between beats at fast rates of pacing (Fig. 19).

Fig. 18.

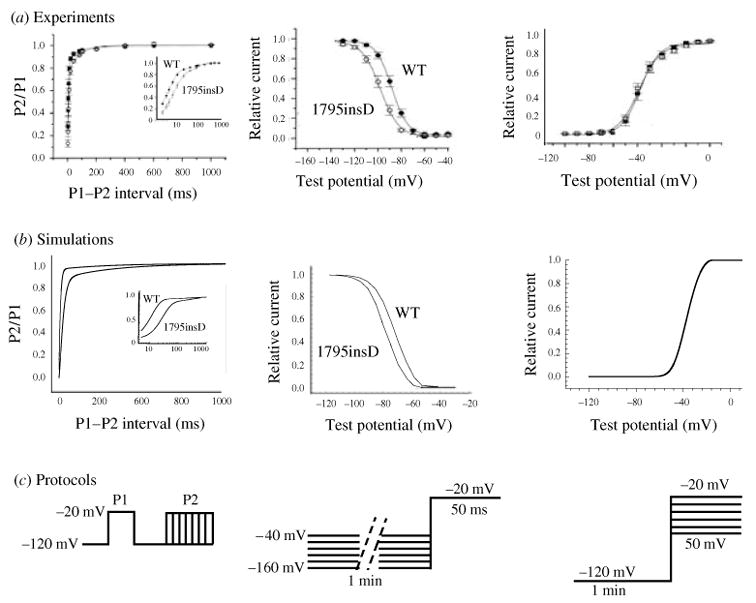
Properties of WT and 1795insD mutant I_Na current. (a) Experimental data from Veldkamp et al. (2000). (b) Simulations of the experimental protocols. (c) Diagrams illustrating the protocols. Voltage dependence of activation (right) is indistinguishable between WT and mutant. Channel availability curve (middle) is shifted to the left by the mutation because of increased absorbency of inactivation states; thus, at any given voltage, channel availability is reduced. Mutant channels recover slower from inactivation (left); on an expanded log scale (inset) it is evident that recovery time could be as long as 100 ms, which is on a timescale of the AP duration. (From Clancy & Rudy, 2002; experimental data are reproduced from Veldkamp et al. 2000, with permission.)

Fig. 19.

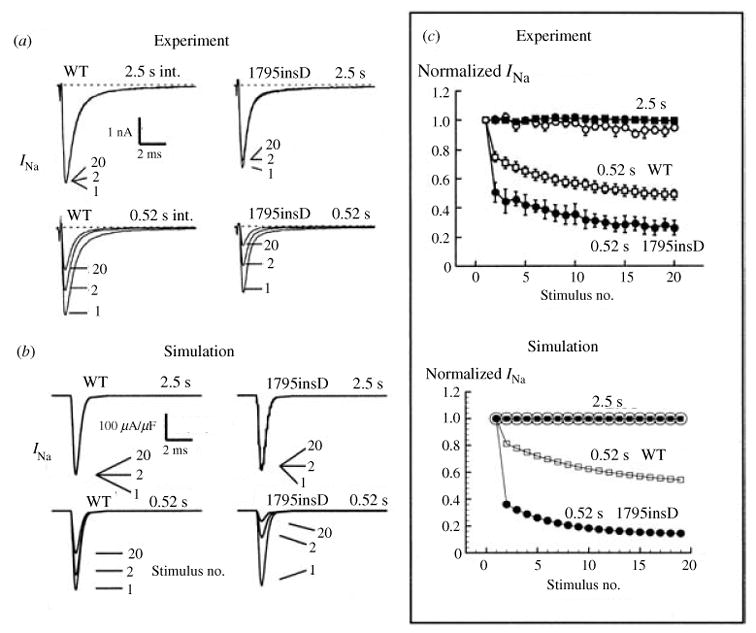
The 1795insD mutation causes rate-dependent reduction of I_Na. A train of 500 ms depolarizing pulses are applied at slow (2·5 s interval) or fast (0·52 s interval) rate. (a) I_Na for WT (left) and mutant (right) channels at these slow (top) and fast (bottom) rates. At fast rate there is progressive (cumulative) loss of I_Na from stimulus 1 to stimulus 2 to stimulus 20. (b) Results of the corresponding simulation. (c) Summary of the results of panels (a) and (b) indicating normalized peak I_Na for 20 stimuli during the same protocol. At slow rate (2·5 s), there is no loss of current. At fast rate (0·25 s) the mutant loss is greater than WT. Experiment (top) and simulation (bottom) show similar behavior. (From Clancy & Rudy, 2002; experimental data are reproduced from Veldkamp et al. 2000.)

To examine how this single mutation can cause the two distinct ECG abnormalities associated with LQT and Brugada, we simulated its effects on the AP of different myocardial cell types from the epicardium (epicardial cells) and from the mid-myocardium (M cells) (Clancy & Rudy, 2002). Epicardial cells, especially from the right ventricular outflow tract (RVOT) are characterized by high levels of I_to (the transient outward current) and I_Ks expression (Antzelevitch et al. 1999; Dumaine et al. 1999; Yan & Antzelevitch, 1999). The AP of such cells has a characteristic ‘spike and dome’ morphology (Fig. 20) with an early spike (formed by I_Na-supported depolarization) and a plateau-phase dome (formed by I_Ca(L)-supported depolarization) separated by an early plateau notch (formed by I_to-supported repolarization). When mutant RVOT epicardial cells are paced at fast rate of CL = 300 ms (Fig. 21), AP alternates between two morphologies : ‘coved dome’ with a marked and greatly prolonged notch, and ‘loss of dome’ due to premature repolarization from the notch without formation of the dome. These morphology changes occur only in epicardial cells at fast rate; they do not occur at slow rate in any cell type and, importantly, they do not occur in endocardial or M cells even at fast rate. As a result, at fast rate a transmural gradient in transmembrane potential is established during the AP plateau and repolarization phases. As will be shown below, this gradient is reflected in ST segment changes on the ECG.

Fig. 20.

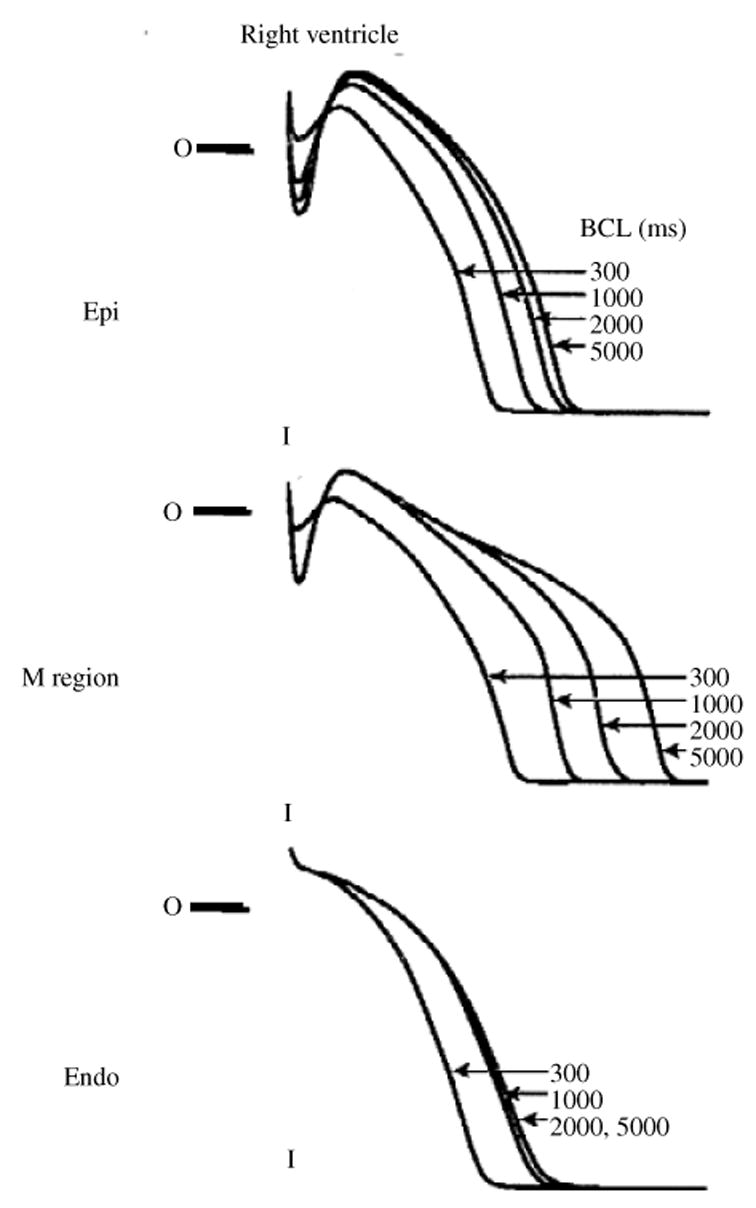
AP of different right ventricular cell types. Epicardial cells (top) show a distinct ‘spike and dome’ morphology of the AP, with a deep notch separating spike from dome. M cells from the mid-myocardium (middle) typically have a more shallow notch; their I_to and I_Ks densities are lower than those of epicardial cells and as a result their AP repolarization phase is easily perturbed by mutations or drugs, or by changes of pacing rate (shown in the figure). Endocardial cells (bottom) do not express I_to and their AP does not display a notch. (From Sicouri & Antzelevitch, 1991, with permission.)

Fig. 21.

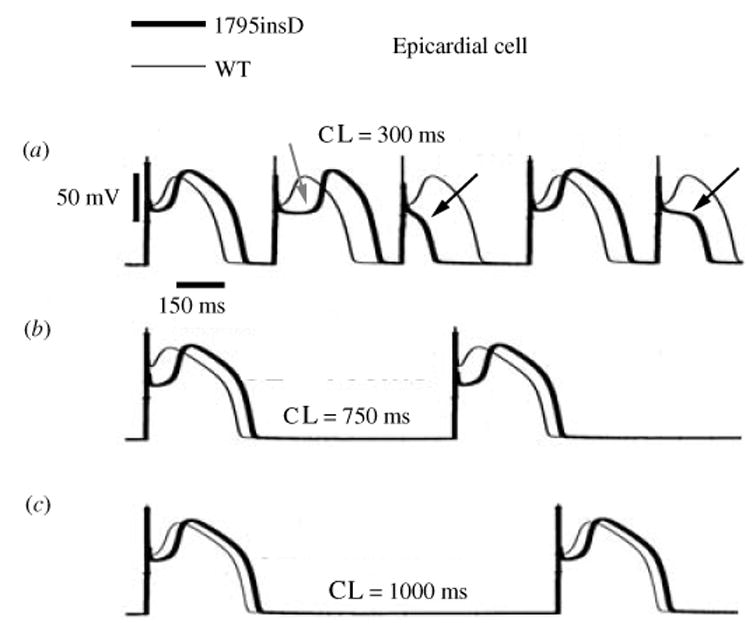
Rate-dependent effect of 1795insD on epicardial cell AP. At fast pacing (a) the AP morphology alternates between ‘loss of dome’ (black arrows) and a prolonged notch (‘coved dome’, gray arrow). At intermediate rate (b) the AP has a coved-dome morphology on every beat. At slow rate (c ) WT and mutant AP morphologies are similar. (From Clancy & Rudy, 2002, with permission.)

The mechanism underlying the AP morphology changes of RVOT epicardial cells at fast rate is as follows (Fig. 22) : mutant peak I_Na is reduced because of incomplete recovery between beats as a consequence of the high absorbency of inactivation states of mutant channels. On the background of large outward I_to and I_Ks in these cells, the reduction of I_Na tilts the balance of currents in the outward direction, causing premature repolarization before significant activation of plateau I_Ca(L) and loss of the AP dome. On alternate beats, I_Na may recover more completely during the prolonged recovery time (diastolic interval) that follows the short ‘loss of dome’ AP. For such beats I_Na may be sufficient to overcome the large I_to, I_Ca(L) activation does occur and the dome is generated following a prolonged notch (‘coved-dome’ AP). In M cells I_to and I_Ks are smaller than in epicardial cells, and in endocardial cells I_to is absent. Consequently, the suppressed mutant I_Na is capable of maintaining a balance of currents that is sufficiently depolarizing, and loss of the dome or a very prolonged notch do not occur in these cells.

Fig. 22.

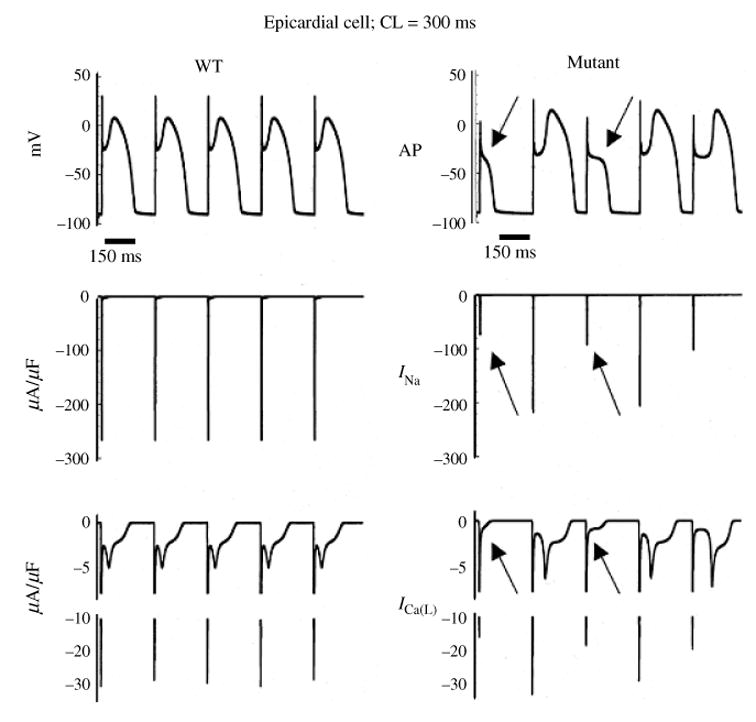
Mechanism of 1795insD effect on AP of epicardial cell during fast pacing. APs are shown on top, with corresponding I_Na and I_Ca(L) in middle and bottom panels, respectively. For WT channels ( left) I_Na is fully recovered between beats. I_Ca(L) develops its plateau phase, and the AP is normal on every beat. For mutant channels (right) cumulative loss of I_Na (arrows in middle panel) causes premature repolarization, loss of plateau I_Ca(L) (arrows in bottom panel) and loss of the AP dome (arrows in top panel). For some beats (e.g. last AP shown) the I_Na loss is not sufficient to cause a complete loss of the dome and the notch is greatly prolonged. (From Clancy & Rudy, 2002, with permission.)

The AP changes described above occur only at fast pacing rates. At slow rates, mutant channels have sufficient recovery time between beats and severe cumulative suppression of I_Na does not occur. Consequently, the effect of the mutation on epicardial AP at slow rate is minimal (Fig. 21). In contrast, as shown in Fig. 23, the mutation affects the M-cell AP preferentially at slow rate. During the long diastolic interval, channels recover from the absorbing inactivated states and populate the closed states (see Markov I_Na model in Fig. 16b), from which they can enter the burst mode. Similar to the ΔKPQ mutation, the burst mode generates a late I_Na current during the AP plateau that prolongs the APD (Fig. 24). In M cells, I_Ks is smaller than in the other cell types and the late I_Na is opposed by a smaller repolarizing current. Therefore, the mutation causes preferential prolongation of M-cell APD at slow rate. In the simulation of Fig. 23, M-cell APD is unaffected at CL = 300 ms; it is prolonged by ~60 ms at CL = 850 ms, and at CL = 1000 ms APD is markedly prolonged and EADs develop.

Fig. 23.

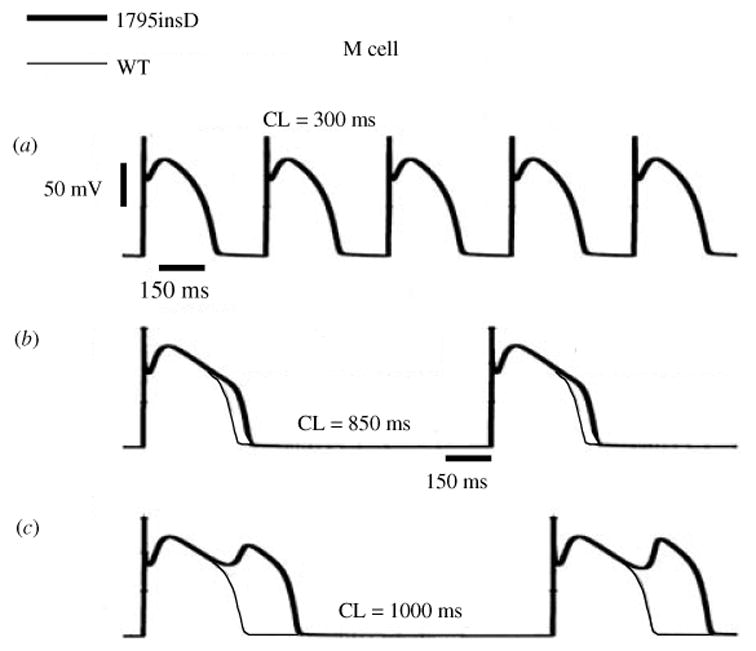
Rate-dependent effect of 1795insD on M cell AP. At fast rate (a) the WT and mutant APs are indistinguishable. At a rate of CL = 850 ms (b) mutant AP is prolonged relative to WT. At slow rate (c) of CL = 1000 ms, mutant APD is greatly prolonged and arrhythmogenic EADs develop. (From Clancy & Rudy, 2002, with permission.)

Fig. 24.

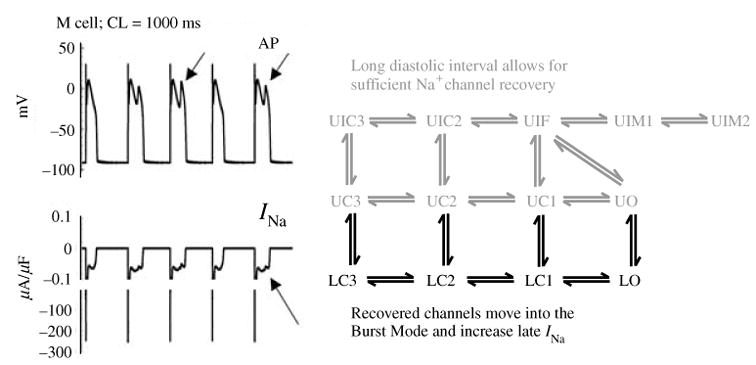
Mechanism of 1795insD effect on AP of M cell during slow pacing. Left: mutant APs are shown on top, with corresponding I_Na on bottom. Mutant I_Na generates current during the AP plateau (bottom arrow) that prolongs the APD and results in EAD formation (top arrows). Right: the I_Na Markov model identifies the processes that lead to late I_Na during the AP plateau. At slow rate, there is sufficient time between beats for channels to recover from inactivation into the closed and open states of the background mode (gray). From these states, they can transition into the burst mode (black) to generate late I_Na. (From Clancy & Rudy, 2002, with permission.)

The longest myocardial APD determines the QT interval on the ECG. Therefore, prolongation of the M-cell APD at slow rate explains the QT interval prolongation and LQT ECG phenotype of patients with the 1795insD mutation at slow rate (Fig. 25). At fast rate, the preferential suppression of RVOT epicardial plateau potentials creates a potential gradient ▽V_m from the epicardial to the M region during the AP plateau (the phase that corresponds to the ST segment of the ECG; Fig. 25). Because ECG potentials are proportional to −▽V_m, this gradient generates ST segment elevation on the ECG, the Brugada phenotype. The ST-segment elevation is prominent in the right precordial leads because of their proximity to the RVOT, the location of epicardial cells with a large I_to that lose the dome or experience a prolonged notch. Figure 26 shows simulated ECG waveforms in a multicellular model that contains the epicardial/M/endocardial heterogeneity (Gima & Rudy, 2002). Incorporation of late I_Na prolongs the QT interval and broadens the T wave, as observed clinically in LQT3 patients. Reduction of I_Na through increased inactivation generates ST-segment elevation in the computed ECG waveforms with morphological changes that reflect the severity of I_Na suppression, in agreement with clinical observations in Brugada patients (Antzelevitch, 2001).

Fig. 25.

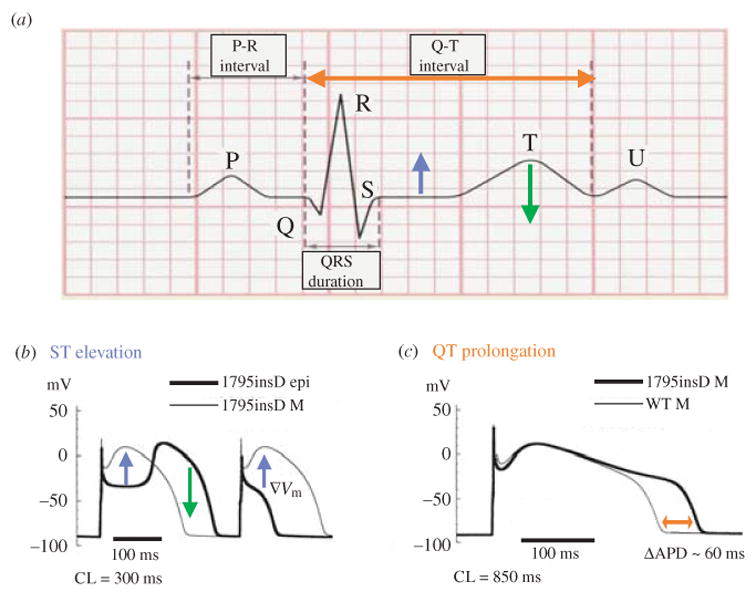
Mechanisms of ECG changes caused by the 1795insD mutation. (a) Stylized ECG defining the different deflections, waves and intervals. (b) Cellular mechanism of ST elevation and T-wave inversion. At fast rate, loss of dome or coved dome in epicardial cells creates a voltage gradient (▽V_m, blue arrows) between these cells (bold line) and M cells (thin line) during the AP plateau, leading to ST-segment elevation on the ECG [blue arrow in (a)]. Greatly prolonged notch in a coved-dome epicardial AP could delay its repolarization beyond that of M cell, thus reversing the normal gradient (normally, M cells have the longest APD and repolarize last) as indicated by the green arrow in (b), possibly leading to T-wave inversion [green arrow in (a)]. (c) Cellular mechanism of QT prolongation. At slow rate M-cell APD is prolonged by the mutation (red arrow). The delayed repolarization is reflected as QT prolongation on the ECG [red arrow in (a)]. [Simulation data in (b) and (c) are reproduced from Clancy & Rudy, 2002, with permission.]

Fig. 26.

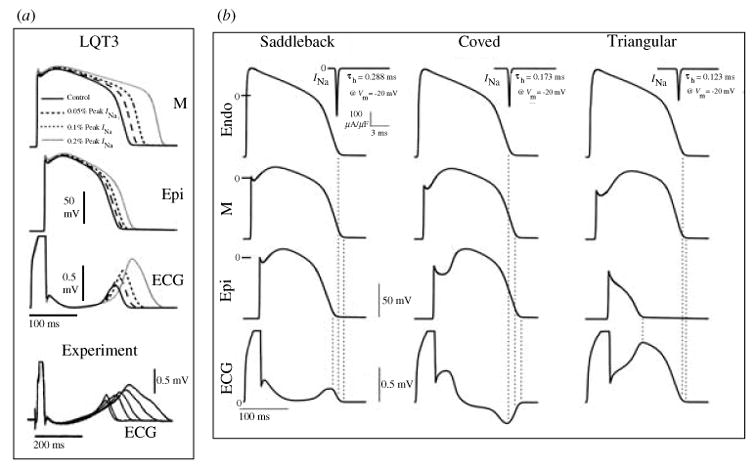
Simulations of ECG changes in LQT3 and Brugada syndromes. The simulations were conducted in a 1-dimensional fiber containing regions of epicardial (Epi), endocardial (Endo) and M cells. The different cell types AP and ECG are shown. (a) LQT3 is simulated, with increasing severity, by incorporating a late I_Na component with magnitude of 0.05%, 0.1%, and 0.2% of peak I_Na. APD prolongation increases with increasing severity and M cell APD prolongs more than epicardial APD, increasing dispersion of repolarization. These AP changes are reflected as QT prolongation and T-wave widening in the ECG. These simulation results are consistent with experimental data of Shimizu & Antzelevitch, 1997 recorded in a transmural wedge preparation (shown in the bottom panel). (b) Brugada syndrome at increasing severity is simulated by accelerating fast inactivation of I_Na (progressively decreasing its time constant, τ_h, from left to right). For all degrees of severity, ST-segment elevation is observed on the ECG, with typical ‘saddleback’, ‘coved’, and ‘ triangular ’ morphologies as severity increases. (From Gima & Rudy, 2002; experimental data in panel (a) are reproduced from Shimizu & Antzelevitch, 1997, with permission.)

The 1795insD simulations demonstrate an important principle, namely that even a simple mutation (an insertion of a single amino acid) can cause multiple different (and even opposite) phenotypes with different pathological and clinical manifestations. This ability stems from the fact that the mutation interacts with a heterogeneous substrate, in this case the heterogeneous myocardium that contains different cell types with different electrophysiological properties. Through rate-dependent processes, the I_Na mutation affects differently epicardial, endocardial, and M cells in a rate-dependent fashion to produce multiple clinical phenotypes. The observation that the phenotypes are determined by complex interactions between the mutant channel and its physiological environment highlights the need for integrative computational models for establishing a mechanistic link between abnormal channel function and its arrhythmogenic consequences.

4.2 Mutations in HERG, the gene that encodes I_Kr : re-examination of the ‘gain of function/loss of function’ concept

Various mutations in HERG, the major subunit of I_Kr, underlie type 2 of the congenital long-QT syndrome, LQT2 (Roden & Balser, 1999). Many of these mutations cause trafficking abnormalities that prevent transport of the channel protein to the cell membrane (Zhou et al. 1998). The resulting complete absence of I_Kr constitutes a total ‘loss of function’ of this current. The reduction of total repolarizing current due to loss of I_Kr, causes AP prolongation which is reflected on the ECG as prolongation of the QT interval (the LQT phenotype). Other mutations do not cause complete loss of I_Kr current, but alter the channel kinetic properties. The mechanisms through which such mutations cause AP prolongation are not so obvious and require careful investigation. As with the SCN5A mutations of the previous sections, we use computational biology to study the effects of selected HERG mutations on the AP (Clancy & Rudy, 2001).

Three mutations are selected as examples (Fig. 27). The T474I point mutation in the S2–S3 linker shifts the activation curve to more negative potentials (as determined experimentally, mutant V_½ is shifted by −27.3 mV relative to WT) (Zhou et al. 1998). Such shift causes earlier activation during the AP, a property that constitutes ‘gain of function’. However, experiments also show reduction of macroscopic current density (Nakajima et al. 1998; Zhou et al. 1998). To simulate the negative shift of activation, we alter the voltage dependence of activation transition rates (from C3 to C2 and C1 to O; see Markov model of I_Kr, Fig. 7a). The observed reduction in macroscopic current is simulated by reducing G_Kr, the maximum membrane conductance for I_Kr, by 35%.

Fig. 27.

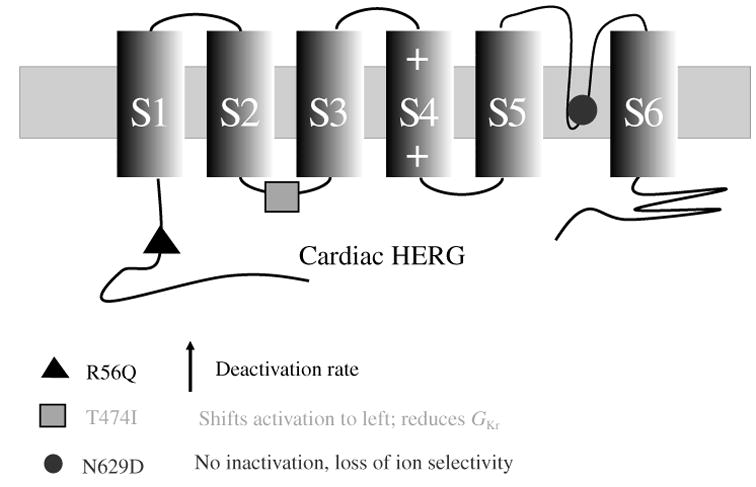
HERG mutations. Structure of cardiac HERG showing locations of mutations simulated in this study. Kinetic changes caused by the mutations are summarized below the diagram. For Markov model of I_Kr see Fig. 7a (Clancy & Rudy, 2001; Silva & Rudy, 2005).

R56Q is a point mutation in the Per–Arnt–Sim (PAS) domain in the N-terminus of HERG, which in the WT interacts with the channel to reduce its deactivation rate (Chen et al. 1999). Mutations in this region appear to alter the interaction of the N-terminus with the channel, thereby accelerating channel deactivation. In the Markov model of I_Kr, this effect is simulated by increasing the rate of transition from the open state to the closest closed state (O to C1; the process of deactivation) and into deeper closed states (from C2 to C3). With faster deactivation,the channel resides for a shorter time in its open, conducting state. This constitutes ‘ loss of channel function ’ and results in reduced I_Kr current.

The N629D mutation results in two alterations of channel properties : (1) loss of C-type inactivation, and (2) loss of K⁺ selectivity (mutant channels can conduct other monovalent cations) (Lees-Miller et al. 2000). These changes constitute ‘ gain of function’ because the channel does not inactivate and can rely on Na⁺, in addition to K⁺, as charge carrier. Based on the ‘ loss of function/gain of function’ classification, a gain of I_Kr function is expected to generate a greater repolarizing current and shorten the AP. Yet, this mutation is associated with LQT, a seemingly paradoxical observation. We simulate the changes in I_Kr function by eliminating inactivation (O to I transition rate is set to zero) and by permitting Na⁺ to be conducted through the channel with relative selectivity P_Na/P_K=0.65.

The effect of the above three mutations on the cellular AP are simulated by inserting the mutant I_Kr channels into the LRd model cell. A comparison of APs from the mutations and from WT is shown in Fig. 28. I_Kr current and occupancies of channel states during the AP are also shown. For WT (left column) upon AP depolarization channels move from C3 to C2 to C1 (see Fig. 27b for Markov I_Kr model) from which they can open to O or inactivate to I. Channels that open, inactivate rapidly from O to I. The balance between inactivation from the open state (O to I) and recovery from inactivation to the open state (I to O) shifts progressively to favor recovery during AP plateau repolarization. Consequently, a pronounced peak of occupancy in the open state (O) is generated late during the plateau (Fig. 28f, arrow) causing I_Kr to peak at this time (Fig. 28b), when it is most effective in influencing repolarization and APD (at this phase, a very delicate balance between inward and outward currents determines the AP time-course which is easily modulated) (Clancy & Rudy, 2001).

Fig. 28.

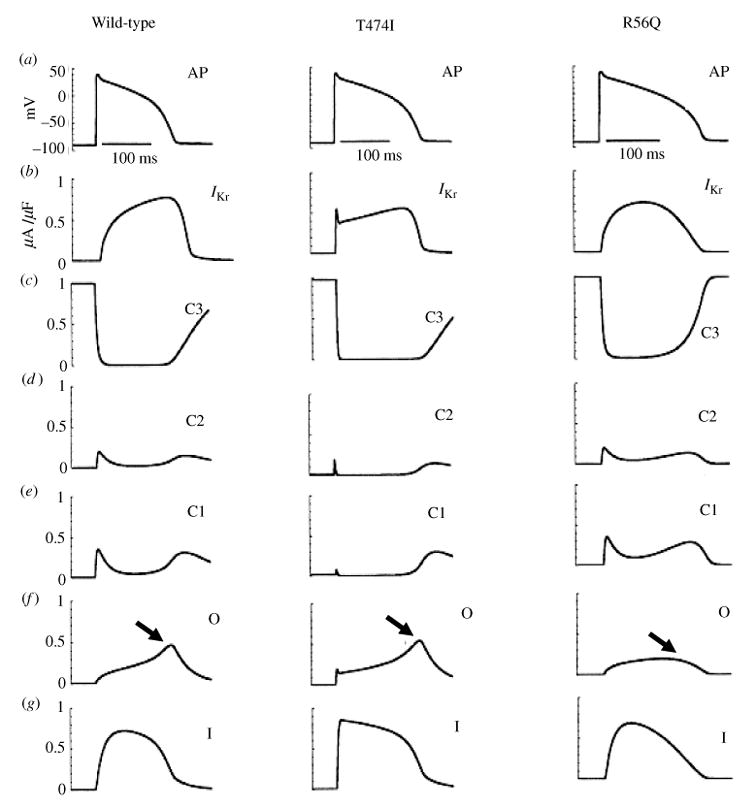
Effects of HERG mutations on the AP. (a) The AP (1000th paced beat) at a cycle length (CL)=750 ms. (b) Denotes I_Kr during the AP. (c)–(g) The probabilities of residence in the indicated channel states over the course of the AP. Left column: wild-type; middle column: T474I mutation; right column: R56Q mutation. (From Clancy & Rudy, 2001, with permission.)

For the T474I mutant, there is only minor prolongation of APD relative to WT, caused by the G_Kr reduction. The kinetic alteration caused by the mutation (negative shift of activation) accelerates activation and influences I_Kr early during the AP (Fig. 28b), when it has minimal effect on AP repolarization and APD. Note that the late peak of open-state occupancy is preserved in mutant channels (Fig. 28f ), ensuring that mutant I_Kr reaches its peak late in the AP (similar to WT) when it has a strong influence on AP repolarization and APD.

The R56Q mutation causes a large prolongation of APD (at pacing CL of 750 ms, APD is prolonged by 33 ms relative to WT). In contrast to the T474I mutation that alters I_Kr early during the AP, R56Q exerts its effect during the late AP plateau and repolarization phase. The mutation accelerates deactivation (transitions from O to C1), which removes the late peak of open-state occupancy (Fig. 28f, arrow) and of I_Kr (Fig. 28b). The resulting reduction of I_Kr current late in the AP, when I_Kr normally plays a major role in repolarization, causes major prolongation of APD.

As stated earlier, N629D is a ‘ gain of function’ mutation; its effects on the AP of epicardial and M cells are shown in Fig. 29. The mutation-induced alteration of ion selectivity elevates the reversal potential of I_Kr to −13 mV, in the range of the AP plateau potentials. Consequently, I_Kr reverses direction during the AP plateau and becomes an inward current when the membrane repolarizes below −13 mV. This late depolarizing current (Fig. 29, arrows), carried by Na⁺ ions, causes major prolongation of epicardial APD (by 80 ms). In the M cell, on the background of the smaller I_Ks in such cells, the inward I_Kr current is sufficient to cause the generation of EADs. Interestingly, the mechanism of APD prolongation is a late inward current carried by Na⁺ ions. In this aspect, it resembles the mechanism of APD prolongation associated with the SCN5A mutations described in Sections 5.1. and 5.2. above, where a late Na⁺ current is carried by the mutant I_Na channels.

Fig. 29.

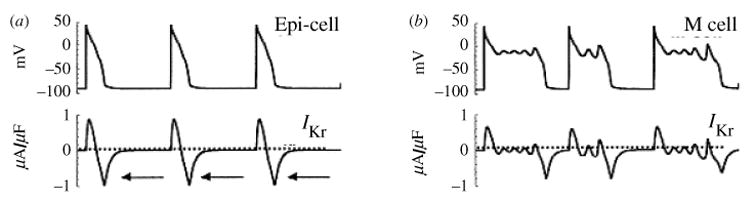
Simulation of HERG N629D mutation. AP and I_Kr during the AP are shown for (a) epicardial cell and (b) M cell. (Adapted from Clancy & Rudy, 2001, with permission.)

The HERG simulations in this section demonstrate an important principle: the consequence of a mutation that alters channel kinetics depends on the details of the kinetic change and when during the AP it exerts its effect. In the examples of this section, accelerated activation (T474I) had only minor effect on repolarization because its effect was early during the AP. In contrast, accelerated deactivation (R56Q) had a large effect on APD because it had an effect during the late AP plateau. Moreover, a ‘ gain of function ’ mutation (N629D) in HERG, normally a repolarizing channel, caused APD prolongation. These observations challenge the widely accepted concept that the effect of an ion-channel alteration on the APD can be simply classified in terms of ‘ loss or gain of function’; that is, gain (loss) of a depolarizing channel function causes prolongation (shortening) of APD respectively, and gain (loss) of a repolarizing channel function causes shortening (prolongation) of APD respectively. In general, such classification is too simplistic and, as demonstrated here, could lead to erroneous predictions of effects on the AP and of the resulting cellular electrophysiological phenotype.

4.3 Role of I_Ks as 'repolarization reserve'

In Sections 3.3 and 3.4, the role of I_Ks in rate-dependent repolarization and APD adaptation was discussed. Mutations in the α-subunit of I_Ks lead to type 1 long QT syndrome (LQT1) which is the most common of the LQT types and generates cardiac arrhythmias at high levels of β-adrenergic tone (during exercise or stress) (Duggal et al. 1998; Schwarz et al. 1977). The effects of reduced I_Ks on the AP have been simulated for different cell types (epicardial, M, and endocardial) and at different rates (Viswanathan & Rudy, 2000). A simulation of a mutation that interrupts β-adrenergic regulation of I_Ks (KCNQ1-G589D) has predicted APD prolongation and transient after-depolarizations during β-adrenergic stimulation (Saucerman et al. 2004). This mutation has been linked to LQT syndrome in Finnish patients and associated with exercise induced arrhythmias (Piippo et al. 2001; Fodstad et al. 2004).

Here, we examine the role played by I_Ks when I_Kr is reduced. I_Kr can be compromised by mutations that cause the congenital LQT2 (Section 4.2) More common is I_Kr blockade by drugs, including certain antibiotics and antipsychotic agents, that leads to the acquired form of LQT (Roden, 2004). It has been hypothesized that I_Ks can supply a RR current that can compensate for the reduction in I_Kr under such conditions (Roden, 2004). This possibility is examined in the simulations of Fig. 30.

Fig. 30.

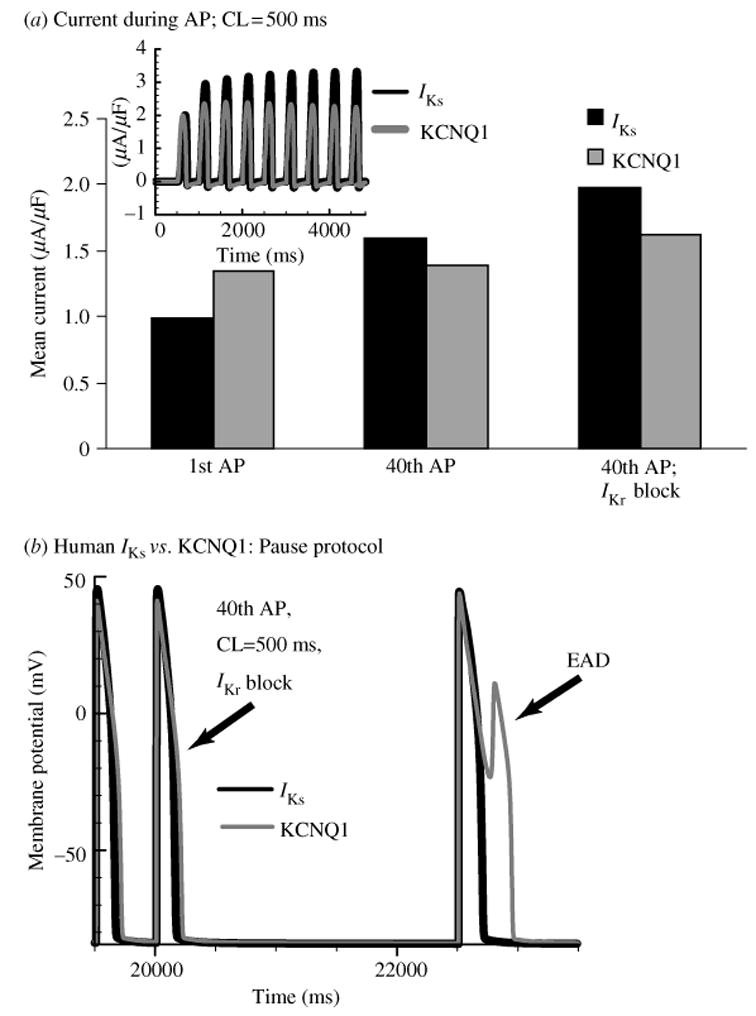
I_Ks as repolarization reserve. (a) Mean I_Ks during the AP (black) accumulates during pacing, showing significant increase over 40 paced APs. In contrast, KCNQ1 shows only a small increase. When I_Kr is blocked (right bars) I_Ks increases further, providing a compensating repolarizing current. (b) When I_Kr is blocked, a post-pause AP develops an EAD with KCNQ1 (gray) but not with I_Ks (black). (From Silva & Rudy, 2005, with permission.)

Figure 30a shows mean I_Ks (black) and mean KCNQ1 current (gray) during the first and 40th AP for pacing at CL of 500 ms. Comparison of the two beats shows that I_Ks increased by~50% during the period of pacing, while KCNQ1 remained almost unchanged. In the presence of I_Kr blockade, the increase of I_Ks from beat 1 to beat 40 is even greater, while KCNQ1 shows only a limited change. The ability of I_Ks to supply a greater current when I_Kr is blockaded results from its build up of an AR in zone 1 of closed states (Sections 3.3 and 3.4). In the presence of I_Kr blockade, the AP plateau is maintained at a higher potential and for a longer time. This facilitates transitions of I_Ks channels into zone 1 that constitutes the AR. In contrast, KCNQ1 channels accumulate in the open state between beats (Sections 3.3 and 3.4) and open on every beat, preventing significant build up of AR. In this respect, KCNQ1 is a ‘wasteful ’ channel.

It is important to evaluate whether I_Ks can provide the RR needed to prevent development of EADs when I_Kr is compromised. Many clinical arrhythmias due to reduced I_Kr occur following a pause (Kay et al. 1983; Viswanathan & Rudy, 1999). A pause protocol in presence of I_Kr block is simulated in Fig. 30b, with a pause inserted after 40 beats. The post-pause AP with KCNQ1 (gray) develops an EAD as a consequence of insufficient KCNQ1 current during the late AP. In contrast, the AP with I_Ks (black) repolarizes normally because I_Ks provides current late during the AP plateau, where it can affect repolarization significantly and prevent formation of the EAD.

Thus, I_Ks can provide RR and prevent arrhythmogenic EADs when I_Kr is compromised by disease or drugs. Its ability to do so results from its kinetic properties that maximize the current late, rather than early, during the AP. These kinetic properties are conferred by the interaction between the molecular subunits of the channel, KCNQ1 and KCNE1.

5. Modeling cell signaling in electrophysiology

Traditionally, cellular models have focused on simulating electrical activity under control conditions, where adrenergic and other cell stimuli are at basal levels. Various regulatory pathways have a strong modulatory effect on cell electrophysiology. This effect can be achieved through direct interaction with ion channel proteins [e.g. β-adrenergic modulation of I_Ks (Marx et al. 2002)] or indirectly by modifying cellular Ca²⁺ cycling and the Ca²⁺ transient which, in turn, interacts with various electrogenic processes (e.g. Na⁺–Ca²⁺ exchange) to modulate the AP. The participation of regulatory processes in cell electrophysiology is essential for normal cardiac function. However, such processes can also tilt the delicate electrophysiological balance in the direction of arrhythmogenesis, as observed in LQT1 patients (Priori et al. 2003) or in patients with catecholaminergic polymorphic ventricular arrhythmias due to abnormal Ca²⁺ cycling (Lahat et al. 2003; Francis et al. 2005), where arrhythmias are triggered under high β-adrenergic tone.

The dynamic interactions between regulatory pathways, cellular Ca²⁺ cycling, and cell electrophysiology add a high level of complexity to cell behavior. Without the guidance of mathematical models, it is impossible to predict the cellular responses to modification of any of the cell components (by disease, drugs or other interventions) or to identify the underlying mechanism with any degree of certainty. In this section we provide examples of models that integrate the effects of cell signaling and regulatory pathways into the electrophysiological behavior of cardiac cells.

5.1 CaMKII regulation of the Ca²⁺ transient

The heart enhances its output in response to elevated cardiovascular demand by increasing its rate which is concurrent with a greater force of contraction. This force-frequency dependence arises even in the absence of β-adrenergic stimulation, as evidenced by the observation that in isolated myocytes fast pacing leads to a greater calcium transient (CaT) amplitude and increased force of contraction (Wang et al. 1988). The CaMKII signaling cascade is likely to be involved in this process, because it has been shown to interact with the cell machinery that generates the CaT (Maier & Bers, 2002; Hund & Rudy, 2004, 2006; Zhang et al. 2005). Specifically, CaMKII substrates include I_Ca(L), the ryanodine receptor (RyR), the SR Ca²⁺-uptake pump (SERCA2a) and phospholamban (PLB) (Le Peuch et al. 1979; Wegener et al. 1989; Witcher et al. 1991; Toyofuku et al. 1994; Yuan & Bers, 1994; Odermatt et al. 1996; Hagemann et al. 2000). CaMKII also phosphorylates neighboring CaMKII subunits (autophosphorylation) (Hanson et al. 1994), enabling it to detect Ca²⁺ spike frequency, which links its effects to the rate of pacing and of AP generation (Fig. 31).

Fig. 31.

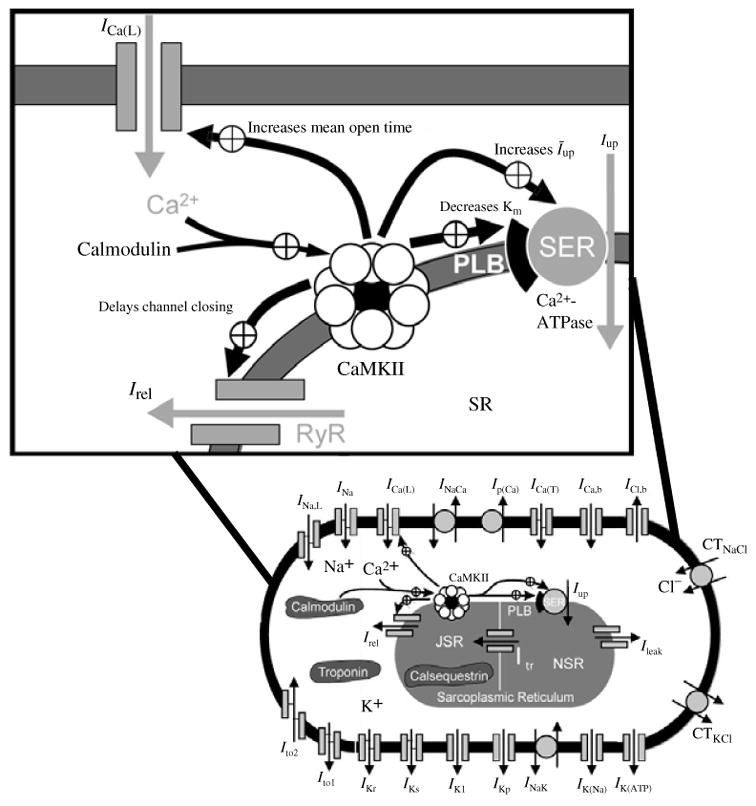
CaMKII pathway incorporated into a canine ventricular cell model. Bottom: cell model containing the CaMKII pathway. Top: a detailed view of the CaMKII pathway and substrates. Upon Ca₂₊ binding, CaMKII phosphorylates I_Ca(L), I_rel (the ryanodine receptor, RyR), SERCA2a (SR Ca²⁺-ATPase; SER in the figure), and phospholamban (PLB). PLB phosphorylation relieves inhibition of SERCA2a Ca²⁺ uptake. Autophosphorylation of CaMKII is also represented in the model, a property which enables detection of Ca²⁺ spike frequency. The model includes a calcium subspace where I_Ca(L) and I_rel interact. It also includes I_to,2, an inward chloride current, and intracellular Cl⁻ regulation by the Na⁺-dependent Cl⁻ co-transporter CT_NaCl and the K⁺-Cl⁻ co-transporter CT_KCl. (Modified from Hund & Rudy, 2004, with permission.)

The rate-dependent activity of CaMKII and its effects on the above substrates were simulated in a model of the canine ventricular cell (Hund & Rudy, 2004). Model comparison to experiment at different rates (Fig. 32a) shows accurate reproduction of the increase in CaT at fast rates (a ‘ positive force-frequency ’ relationship) and more rapid rate of relaxation (enhanced lusitropy). The magnitude of the simulated transient at various rates is compared to experiment (Sipido et al. 2000) and shows close correlation (Fig. 32b). Underlying the increase in CaT magnitude at faster rates is increased CaMKII activity that enhances SR Ca²⁺ uptake by PLB phosphorylation (Fig. 32d), resulting in increased Ca²⁺ loading. CaMKII also increases peak I_Ca(L), the trigger for SR release, and enhances Ca²⁺ release via RyR. The result is an increased excitation-contraction coupling (ECC) gain at fast rate (Fig. 32c) and a greater CaT. When CaMKII is inhibited in the model, the rate dependence of CaT becomes negative (‘negative force-frequency’) for pacing rates >1 Hz (Fig. 32b), because increased ECC gain (Fig. 32c) mediated by CaMKII, no longer occurs.

Fig. 32.

CaMKII regulation of the Ca²⁺-transient rate-dependence. (a) Simulated (bottom) and measured (top) steady-state Ca²⁺ transient (CaT) for 0.25, 0.5, 1, and 2 Hz pacing. (Experimental tracings are adapted from Sipido et al. 2000, with permission.) (b) CaT-frequency relation for experiment (circles), model under control conditions (line), and in presence of CaMKII inhibition (dashed line). (c) Minimal diastolic CaMKII activity (thick line, normalized to 3.3 Hz) and excitation-contraction coupling (ECC) gain. ECC gain=∫_A F_reldt/∫_A F_Ca(L)dt, where F_rel and F_Ca(L) are fluxes through RyR and I_Ca(L), respectively, and the integration interval, A, is over one cycle. Gain is shown for control model (thin line) and in presence of CaMKII inhibition (dashed line). (d ) PLB phosphorylation vs. pacing frequency compared with experimental data (Hagemann et al. 2000). (From Hund & Rudy, 2004, with permission.)

This result implies that existence of the positive force-frequency relationship is dependent on the CaMKII signaling cascade, and enforces the notion that cell signaling plays an integral role in cell excitation and contraction.

5.2 The β-adrenergic signaling cascade

β-adrenergic stimulation directly increases the force of contraction in isolated ventricular myocytes by increasing Ca²⁺ influx through I_Ca(L), which results in elevated [Ca²⁺]_i that signals stronger contraction. This increase in a depolarizing current can also lead to prolonged APs that are susceptible to arrythmogenic EADs (Priori & Corr, 1990; Zeng & Rudy, 1995). One way in which the myocyte stabilizes the AP to counter EAD formation is increasing repolarizing current, primarily I_Ks, in response to β-adrenergic stimulus (Walsh & Kass, 1988). However, if I_Ks availability were reduced by mutation (LQT1), or if it were unable to respond to β-adrenergic stimulation, this important anti-arrhythmic mechanism (termed ‘RR’) would be compromised and cells would be more susceptible to EAD generation and triggered activity. In support of this hypothesis, patients with I_Ks mutations and the LQT1 syndrome are prone to arrhythmias and sudden cardiac death in situations where β-adrenergic tone is elevated (Priori et al. 2003).

The interaction between β-adrenergic stimulation and I_Ks was recently shown to involve association of cAMP-dependent PKA and PP1 with the C-terminal domain of KCNQ1 (the α-subunit of I_Ks) (Marx et al. 2002). This finding shows that the β-adrenergic signaling cascade is actually a part of the I_Ks channel complex, directly participating in the generation of the AP. Additional experiments with accompanying simulations have shown that this interaction enhances I_Ks participation in the AP by increasing the rate of I_Ks activation and slowing the rate of deactivation, resulting in I_Ks accumulation and more open channels throughout the course of the AP (Terrenoire et al. 2005).

The effects described above reflect the steady-state consequences of β-adrenergic stimulation, however the time-dependence of substrate phosphorylation may also affect the cellular phenotype. A β-adrenergic model that accounts for time-dependence of substrate phosphorylation (for timescales that are faster than 10 min and slower than 0.1 s) has been formulated based on data primarily from the rat (Saucerman et al. 2003) (schematic shown in Fig. 33a). This model simulates agonist stimulation of the β₁-adrenergic receptor ( β₁AR) (Post et al. 1995) and subsequent activation of the stimulatory G protein subunit (G_s) (Brandt & Ross, 1986; Frace et al. 1993), which increases adenylyl cyclase (AC) activity (Dessauer et al. 1997). In the model, the β₁AR can be inhibited by β-adrenergic receptor kinase ( βARK) (Freedman et al. 1995) and by the catalytic subunit of PKA (Fishman et al. 1991; Freedman et al. 1995). Dissociation of the PKA catalytic subunit from the holoenzyme (Smith et al. 1981), which consists of two regulatory and two catalytic subunits, occurs when cAMP (synthesized by AC) binds to the regulatory subunits (Beavo et al. 1974; Hofmann et al. 1975). The concentration of free cAMP is determined by the rate of synthesis by AC (Dessauer et al. 1997), degradation by phosphodiesterase (Reeves et al. 1987), and by sequestration due to its binding to the PKA regulatory subunits (Beavo et al. 1974; Hofmann et al. 1975). Two types of PKA have been identified in myocytes and were included in the model: type I, which is predominant in rat ventricular myocytes and diffuses through the cytosol (Corbin et al. 1977; Taylor et al. 1990), and type II, which is typically anchored to the membrane by an A kinase-anchoring protein (AKAP) (Bers, 2001). Both types I and II PKA catalytic subunits can be inhibited by the heat-stable protein kinase inhibitor (PKI) (Walsh et al. 1990; Johnson et al. 2001). PKA type I phosphorylation targets include PLB (inhibitory effect) (Gibson & Taylor, 1997) and protein phosphatase inhibitor-1 (I1) (stimulatory effect) (Cohen et al. 1977), while PKA type II is responsible for I_Ca(L) channel phosphorylation (increased current) (Bers, 2001). PLB inhibits uptake of Ca²⁺ into the SR by SERCA2a, therefore inhibiting PLB activity via PKA phosphorylation results in increased uptake. Stimulation of I1, which is itself inhibited by protein phosphatase-2A (PP2A) (Takai et al. 2000), has similar consequences (increased Ca²⁺ uptake by SERCA2a) because it inhibits a PLB agonist, protein phosphatase-1 (PP1) (Takai et al. 2000). PP1 and PP2A can also be co-localized to the membrane where they serve as I_Ca(L) inhibitors (Bers, 2001).

Fig. 33.

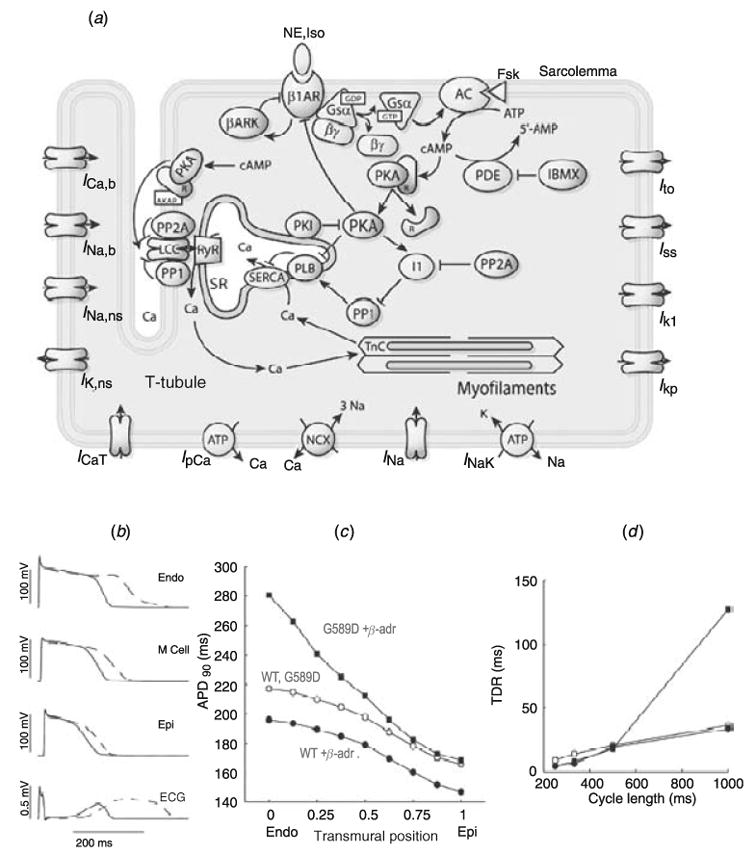
(a) Schematic of the β-adrenergic network and signaling mechanisms in the model of Saucerman et al. (2003). Schematic of integrated model components, including the β₁-adrenergic network, calcium handling, and electrophysiology; β-adrenergic model is based on data from rat, while electrophysiology data are from rabbit. NE, norepinephrine; Iso, isoproterenol; β₁AR, β₁-adrenergic receptor; βARK, β-adrenergic receptor kinase; AC, adenylyl cyclase; Fsk, forskolin; PDE, phosphodiesterase; PKA, protein kinase A; PKI, heat-stable protein kinase inhibitor; PP1, protein phosphatase-1; PP2A, protein phosphatase-2A; I1, protein phosphatase inhibitor-1; PLB, phospholamban; LCC, L-type calcium channel; SERCA, sarcoplasmic reticulum Ca²⁺-ATPase; RyR, ryanodine receptor. (Modified from Saucerman et al. 2003, with permission.) (b)–(d ). Simulated effects of G589D mutation and β-adrenergic signaling on action potential in a transmural ventricular tissue model. (b) In presence of β-adrenergic stimulation, action potentials prolong in G589D mutants (dashed line) compared with WT (solid line) preferentially in endocardial cells, forming a broad T-wave and prolonged QT interval on the simulated ECG. (c) Transmural heterogeneity of APD₉₀ in absence (empty markers) and presence of β-adrenergic stimulation (filled markers) for WT (circles) and G589D mutant (squares) tissue models. (d ) Transmural dispersion of repolarization (TDR) is particularly elevated in sympathetic-stimulated G589D mutant models (filled squares) at long cycle lengths. (Modified from Saucerman et al. 2004, with permission.)

To study the cellular level electrophysiological effects of the β-adrenergic signaling cascade, this model was expanded to include PKA phosphorylation of the L-type calcium channel, PLB, I1, RyR, troponin I (Saucerman & McCulloch, 2004) and KCNQ1 (Saucerman et al. 2004), and was incorporated into a model of the rabbit ventricular AP (Puglisi & Bers, 2001). Since the model was formulated to reproduce data from the rat, protein expression levels of the β₁AR, PDE, PKA and PLB were adjusted to reproduce cAMP and PKA dependence on time and isoproterenol in the rabbit (Saucerman et al. 2004).

Using this model to simulate control conditions in normal cells, β-adrenergic stimulation resulted in AP shortening (Saucerman et al. 2004). However, in the presence of a simulated KCNQ1-G589D mutation, which prevents PKA-mediated I_Ks increase (Kass & Moss, 2003), APD prolonged significantly. Incorporation of the mutant cell model into a transmural rabbit ventricular tissue model that included endocardial, mid-myocardial and epicardial cell types, resulted in β-adrenergic-mediated repolarization abnormalities and APD prolongation that was most significant in the endocardial layer (Fig. 33b, c). Since APD prolongation was spatially nonuniform in the tissue, it resulted in increased transmural dispersion of repolarization (TDR), a substrate that is prone to the development of re-entrant arrhythmias (Verrier & Antzelevitch, 2004) (Fig. 33d). These results indicate that interruption of β-adrenergic effects on I_Ks is likely to generate arrhythmic behavior via repolarization abnormalities and increased spatial dispersion of repolarization.

The CaMKII and β-adrenergic simulations presented above underscore the importance of accounting for cell signaling effects in models of cardiac cell electrophysiology and calcium cycling. These models are first examples of this integrated modeling approach, and reflect our current (but still evolving) understanding of the signaling pathways. As experiments provide better characterization of substrates and help resolve existing controversies, these models will have to be revisited and refined.

6. Epilogue

‘The earth is like a single cell. ’ Lewis Thomas, The Lives of the Cell

Mechanistic understanding of the cardiac excitatory process is a prerequisite for correct diagnosis and effective treatment of cardiac arrhythmias. Such understanding requires integration of processes at various levels, from the ion channel, to the whole cell, to the multicellular tissue, to the heart as a whole organ. Traditionally, the reductionist approach has been applied to cardiac research, collecting data from isolated building blocks of the highly integrated cardiac system. Such data are usually acquired under conditions that do not mimic the physiological (or pathophysiological) environment. In this review we describe and provide examples of the use of computational biology (mathematical modeling) in the integration of individual components into the physiologically functioning system of the cardiac cell. As demonstrated here, even the single cell is a highly complex, nonlinear and interactive system. In this system, ion channels interact with a dynamic ionic environment, with the membrane voltage, and with a variety of regulatory molecules to generate and modulate the cardiac AP; the outcome of these interactions usually defies intuition.

This article focuses on integration from the molecular properties of ion channels to the whole-cell electrophysiological function, thus defining the single cardiac cell as the complex system of interest [simulations of the interactions between ion channels and the multicellular tissue during AP propagation were described in a recent review article (Kleber & Rudy, 2004)]. The simulations presented here demonstrate that the role of ion channels in shaping and controlling the cardiac AP is defined by their molecular properties and transitions between kinetic states during the AP time-course. Similarly, the effect of an ion-channel mutation depends on the mutation-induced changes in channel kinetics and, in particular, when during the AP the mutation exerts its effect. Thus, the ‘ gain of function/loss of function ’ rule is not always sufficient to predict the effect of a given mutation on the cardiac AP. The fact that cardiac cells are heterogeneous adds another level of complexity because, as demonstrated by the dual phenotype simulations of the SCN5A 1795insD mutation, the electrophysiological consequences of ion-channel abnormality depend on the ionic profile of the cell. This profile is not only heterogeneous but also dynamic, as ion-channel expression levels change due to remodeling processes induced by pathology and aging. At a higher level of complexity yet, these processes are modulated by interactions with regulatory pathways and the calcium subsystem of the cell.

Computational biology is a powerful approach that can help identify and elucidate mechanistic interactions between various components of the cell and predict their effect on the whole-cell behavior. Given the explosion of genetic and molecular data, we believe that this approach will continue to evolve and provide a framework for interpretation and integration of experimental information not only in the cardiac system, but in other systems as well.