Abstract
Bubble-based acoustic radiation force can measure local viscoelastic properties of tissue. High intensity acoustic waves applied to laser-generated bubbles induce displacements inversely proportional to local Young’s modulus. In certain instances, long pulse durations are desirable but are susceptible to standing wave artifacts, which corrupt displacement measurements. Chirp pulse acoustic radiation force was investigated as a method to reduce standing wave artifacts. Chirp pulses with linear frequency sweep magnitudes of 100, 200, and 300 kHz centered around 1.5 MHz were applied to glass beads within gelatin phantoms and laser-generated bubbles within porcine lenses. The ultrasound transducer was translated axially to vary standing wave conditions, while comparing displacements using chirp pulses and 1.5 MHz tone burst pulses of the same duration and peak rarefactional pressure. Results demonstrated significant reduction in standing wave effects using chirp pulses, with displacement proportional to acoustic intensity and bubble size.
Keywords: Acoustic radiation force, laser-induced optical breakdown, microbubble, chirp, standing waves
INTRODUCTION
Acoustic radiation force has broadened the scope of traditional ultrasound elasticity imaging. High intensity acoustic waves generate small tissue displacements dependent on local stiffness and absorption, while the temporal response provides information about local viscosity. Displacements are typically tracked using ultrasound imaging with speckle tracking algorithms. Acoustic radiation force allows palpation of underlying tissue structures not accessible with external compression. Applications of acoustic radiation force elasticity imaging are varied, including mechanical evaluation of the breast, vitreous, thrombosis development, arteries, and other soft tissues (Nightingale et al. 2002; Sarvazyan et al. 1998; Trahey et al. 2004; Viola et al. 2004; Walker 1999).
Bubble-based acoustic radiation force was recently introduced as a technique to measure highly localized viscoelastic properties of tissue (Erpelding et al. 2005a). Bubbles serve as effective targets for acoustic radiation force for a number of reasons. The acoustic radiation force generated by reflection off the bubble surface is greater than in absorption-based techniques since bubbles approximate perfect reflectors. Also, bubble size is a primary factor determining measurement localization, allowing for spatial accuracy better than 100 μm (Erpelding et al. 2005b). In addition, bubbles provide tracking targets in anechoic tissues. Previous research has shown that bubble displacements are proportional to the acoustic intensity and bubble radius and inversely proportional to the material Young’s modulus (Erpelding et al. 2005a; 2005b). Target bubbles for acoustic radiation force measurements are generated by laser-induced optical breakdown (LIOB). LIOB involves nonlinear absorption of laser energy above a threshold fluence, resulting in plasma formation, shock wave emission, and cavitation bubble creation at the breakdown site.
A promising application of bubble-based acoustic radiation force is measuring intraocular lens elasticity. An in vivo technique capable of measuring lens elastic properties with high spatial resolution and minimal disruption of lens structures would represent a significant advance over previous techniques and provide insight into the development of presbyopia. Initial results mapping the elastic properties in explanted porcine lenses with bubble-based acoustic radiation force were promising (Erpelding et al. 2005b). Results showed a stiffer lens nucleus than lens cortex, consistent with other recent findings (Beers and van der Heijde 1994, Heys et al. 2004; Pau and Kranz 1994). The temporal response of bubble displacement suggested a time constant on the order of a few milliseconds. This is consistent with other acoustic radiation force techniques that report soft tissue displacement recovery times of less than 5 ms (Nightingale et al. 2003).
Maximum bubble displacements are needed to evaluate a wide range of tissue elastic properties with acoustic radiation force. Maximum displacements are generated using radiation force pulse durations longer than the bubble response time constant. However, standing waves can develop with pulses longer than the round trip propagation time between the transducer and a highly reflecting surface, like the bottom of a water tank. Standing waves occur when significant reflected sound from the tank bottom is redirected off the transducer surface, establishing a series of acoustic pressure nodes and antinodes caused by the interference of the transmitted and reflected waves. In an ideal standing wave, antinodes occur at positions of constructive interference where the pressure amplitude doubles, while nodes occur at positions of destructive interference where the pressure amplitude is zero. The distance between adjacent pressure nodes, or antinodes, is equal to half a wavelength of the excitation frequency.
Ultrasound standing waves have been exploited for bubble-enhanced cell membrane sonoporation (Khanna et al. 2003, 2006) and for particle sorting (Hawkes and Coakley 2001). For acoustic radiation force elasticity measurements, standing waves represent a displacement artifact since the force on the bubble is highly dependent on its position in the pressure field. Traveling wave conditions ensure bubble displacements from acoustic radiation force are indicative of local tissue elasticity and that radiation force is directed along the propagation direction.
The purpose of the current investigation is to minimize standing wave artifacts by applying acoustic radiation force with a chirp rather than a tone burst. A linear frequency sweep over the pulse duration may prevent significant standing wave generation. A similar approach was used by Mitri et al. (2005) to remove the standing wave artifact in acoustic emission from continuous wave vibro-acoustography.
MATERIALS AND METHODS
Bead Experiments
Several experiments compared acoustic radiation force generation via chirp and tone burst excitation. In the first, 500 μm diameter glass beads were embedded within a 5% gelatin phantom (Type-A, Sigma-Aldrich, St. Louis, MO) and used as targets for acoustic radiation force from the 1.5 MHz outer element (f/1.6) of a two-element confocal ultrasound transducer. Glass beads were stable targets used to verify the expected reduction in standing wave effects through chirp excitation. With a single bead at the transducer focus (50 mm), the transducer was moved axially in 100 μm steps over 2mm to change standing wave conditions and measure bead displacement. Chirp waveforms with 100 kHz, 200 kHz, and 300 kHz linear frequency sweeps centered about 1.5 MHz were produced by an HP 3314A function generator (Agilent Technologies, Palo Alto, CA). Tone bursts at 1.5 MHz were generated by an Agilent 33250A arbitrary waveform generator (Agilent Technologies, Palo Alto, CA). Both chirp and tone bursts were 6.5 ms in duration and amplified with a 50 dB RF power amplifier (ENI model 240L, MKS Instruments, Wilmington, MA).
The transducer acoustic output using tone burst excitation was measured by a calibrated membrane hydrophone (GEC-Marconi, Chelmsford, UK). Both chirp and tone bursts were excited by the same drive voltage, resulting in peak rarefactional pressures of 2.1 MPa (non-derated, MI = 1.7). Spatial-peak pulse-average intensities (ISPPA) for all excitation types are given in Table 1, showing decreased chirp pulse intensities. The −6 dB bandwidth of the outer transducer element was 180 kHz, resulting in reduced chirp pulse intensities as energy shifts away from the 1.5 MHz resonance frequency. Chirp pulse intensities were measured relative to the calibrated tone burst output by averaging force balance measurements over a range of axial depths.
Table 1.
Spatial peak, pulse average intensities for acoustic pulses producing radiation force on 500 μm glass beads embedded within gelatin phantoms.
| Acoustic Pulse | ISPPA (W/cm2) |
|---|---|
| Tone Burst | 173 |
| 100 kHz Chirp | 142 |
| 200 kHz Chirp | 125 |
| 300 kHz Chirp | 108 |
Bead position was tracked using pulse-echoes from the 7.44 MHz inner element (f/3.9) generated with a commercial pulser-receiver (Panametric NDT, Waltham, MA) at a 4.88 kHz repetition frequency and recorded for a total of 20.5 ms using a digital acquisition board (CS 8500, Gage Applied Technologies, Montreal, Canada). Bead displacements were measured assuming a sound speed of 1500 m/s using a phase sensitive cross-correlation method referenced to the final bead position 14 ms after acoustic radiation force ends. All quoted bubble displacements represent the maximum displacements, measured by the ultrasound pulse-echo directly following acoustic radiation force. All experiments were performed in a tank filled with deionized water at room temperature.
Bubble Experiments
Subsequent experiments compared chirp and tone burst excitation on LIOB bubbles in a porcine lens. Fresh porcine eyes from young pigs (approximately 6–9 months old) were obtained from a local slaughterhouse and transported to the laboratory on ice. Lenses were immediately explanted into a 5% gelatin phantom upon arrival and experiments were performed within 24 hours. An integrated acoustical-optical setup enabled radiation force measurements directly following bubble creation within porcine lenses using laser illumination directed from below the sample and ultrasound insonation from above. As shown in Fig. 1, porcine lenses were placed at the bottom of the tank, directly above a glass coverslip (160–190 μm thick, Fisher Scientific, Hampton, NH). An ultrafast Nd:glass laser, described previously (Erpelding et al. 2005a), used 800 fs, 1053 nm pulses focused along the lens equatorial plane to create target microbubbles. A mechanical shutter controlled the number of laser pulses delivered, while a neutral density filter controlled the laser pulse energy. Laser pulses were directed through an f/2 lens at a 1.5 kHz repetition rate and pulse energy of 13 μJ (11.5 J/cm2). Acoustic radiation force was generated using 200 kHz chirp and tone bursts centered at 1.5 MHz, while axially translating the transducer in 100 μm steps, as described above. The lens sound speed was assumed to be 1641 m/s (Jansson and Kock 1962) for bubble displacement measurements.
Fig. 1.
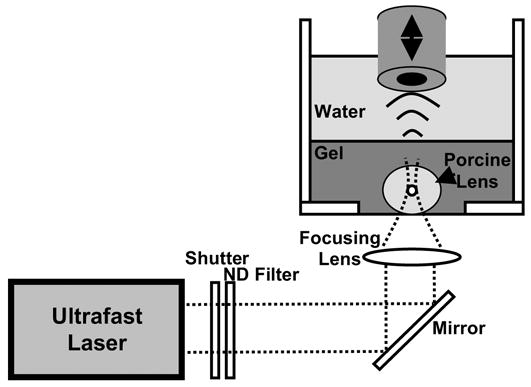
Experimental setup for simultaneous optical breakdown and acoustic radiation force experiments with an explanted porcine lens. The ultrasound transducer has a focal length of 50 mm, while the optical focusing lens has a focal length of 30 mm. LIOB bubbles are created along the porcine lens equatorial plane, approximately 3–5 mm above the glass coverslip at the tank bottom. The tank has a 127 mm square base and 100 mm height.
In addition, fundamental relationships between bubble displacements, acoustic intensity, and bubble size using chirp pulses were investigated. Bubble displacements in a porcine lens were measured with the transducer at a fixed position using 200 kHz chirp intensities (ISPPA) ranging from 18 – 155 W/cm2. This experiment was used to verify the linear relationship between acoustic intensity and bubble displacement. Finally, the linear relationship between bubble displacement and size was verified by applying a series of 200 kHz chirp pulses to a shrinking bubble in a porcine lens at an ISPPA of 125 W/cm2.
RESULTS
Bead Displacements
Bead displacements induced by tone burst and chirp excitations are plotted versus the bead axial position in Fig. 2. Tone burst excitation clearly demonstrates standing wave effects, as the induced displacement is highly dependent on bead axial position. As the axial position changes, the resulting force varies according to the superposition of the transmitted and reflected pressure waves. At certain depths, displacements opposite to the acoustic wave propagation direction (i.e. negative displacements) are observed. Tone burst bead displacements have local maxima spaced by approximately 500 μm, equal to half the wavelength for 1.5 MHz insonation. This is consistent with a standing wave artifact since pressure nodes and antinodes are spaced by half a wavelength of the excitation frequency.
Fig. 2.
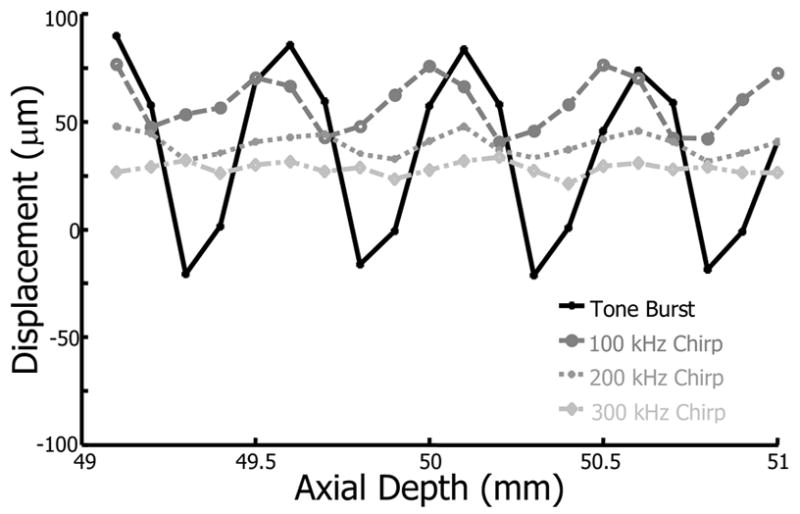
Bead displacement within a 5% gelatin phantom as a function of axial position for tone burst (solid), 100 kHz chirp (dashed), 200 kHz chirp (dotted), and 300 kHz chirp (dash-dot) excitation.
Chirp excitation produces a reduced standing wave effect, as indicated by smaller displacement variation. As the frequency sweep of the chirp increases from 100 kHz to 300 kHz, displacement mean and variance decrease. Decreased variance is due to a greater sweep rate that eliminates nearly all standing wave effects. The decrease in mean displacement results from lower pulse average intensities with greater frequency sweeps, as shown in Table 1. Lower intensities are generated as pulse energy shifts away from the 1.5 MHz resonant frequency of the narrowband transducer.
To quantify differences between tone and chirp bursts, the standing wave ratio (SWR) is defined as follows,
| (1) |
where σDisp and μDisp are the displacement standard deviation and mean, respectively. A similar metric was used in evaluating standing wave reduction by Mitri et al. (2005). Larger SWRs signify greater standing wave influence on displacement. The SWRs for the data in Fig. 2 are presented graphically in Fig. 3. Figure 3 indicates lower SWRs for chirp pulses than for tone burst excitation and SWRs decrease as the frequency sweep magnitude is increased. For instance, a 200 kHz chirp produced an 18.6 dB reduction in the SWR versus tone burst excitation, while a 300 kHz chirp improved the SWR reduction to 20.6 dB but with smaller mean displacement. Accordingly, 200 kHz was used in the remainder of the experiments since it produces significant reduction in the standing wave effect while still generating sufficient displacement.
Fig. 3.
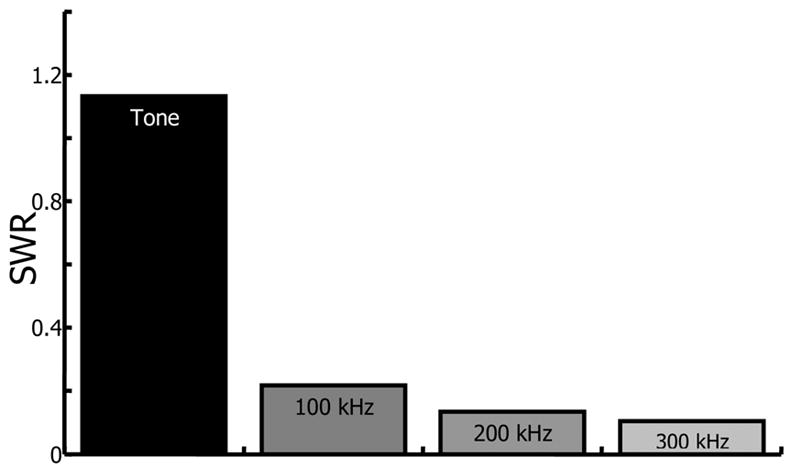
Standing wave ratio (SWR) for bead displacement in a 5% gelatin phantom from tone, 100 kHz chirp, 200 kHz chirp, and 300 kHz chirp excitation. SWR is defined as the displacement standard deviation divided by the mean displacement.
Bubble Displacements
The results for bubble displacement within a porcine lens are presented in Fig. 4. In this experiment, a single bubble was created via LIOB at the lens center along the equatorial plane. Tone burst and 200 kHz chirp excitations were applied to a single bubble while axially translating the transducer in 100 μm steps. As with the bead results, single frequency tone bursts generate significant standing waves with a displacement highly dependent on bubble axial position. Tone burst bubble displacements have local maxima spaced by half a wavelength of the excitation wavelength. Displacements induced by the 200 kHz chirp, however, are much less dependent on axial position. As expected, 200 kHz chirp excitation reduced standing wave effects and reduced the SWR by 17.2 dB.
Fig. 4.
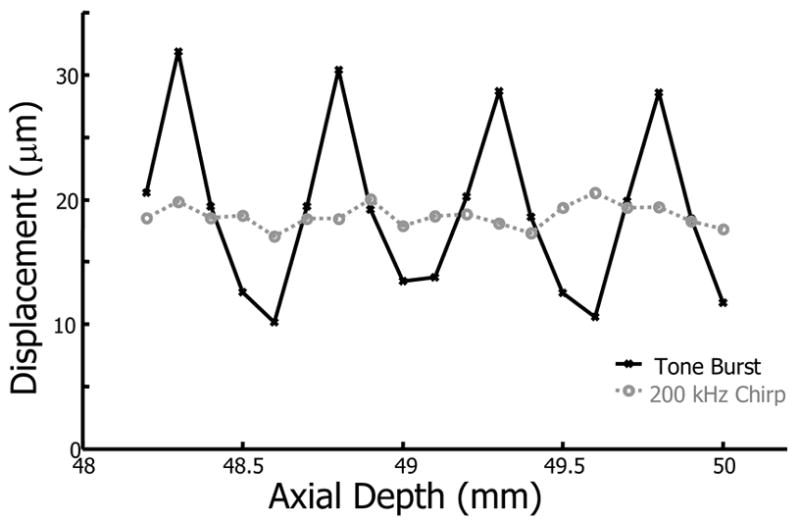
Bubble displacement as a function of axial position at the center of a porcine lens from tone burst (solid line) and 200 kHz chirp (dashed line) excitation.
Effect of Acoustic Intensity
Experiments were performed to verify the linear dependence of acoustic intensity on bubble displacement. A series of 200 kHz chirp pushes were applied to a single bubble within a porcine lens at a fixed axial position with intensities from ISPPA = 20 W/cm2 to ISPPA = 171 W/cm2. The bubble was created 2 mm away from the lens center along the equatorial plane. The results are given in Fig. 5. The dashed curve is a linear fit to the measured bubble displacements and demonstrates that larger bubble displacements result from higher acoustic intensities. The expected linear relationship between acoustic intensity and displacement was verified.
Fig. 5.
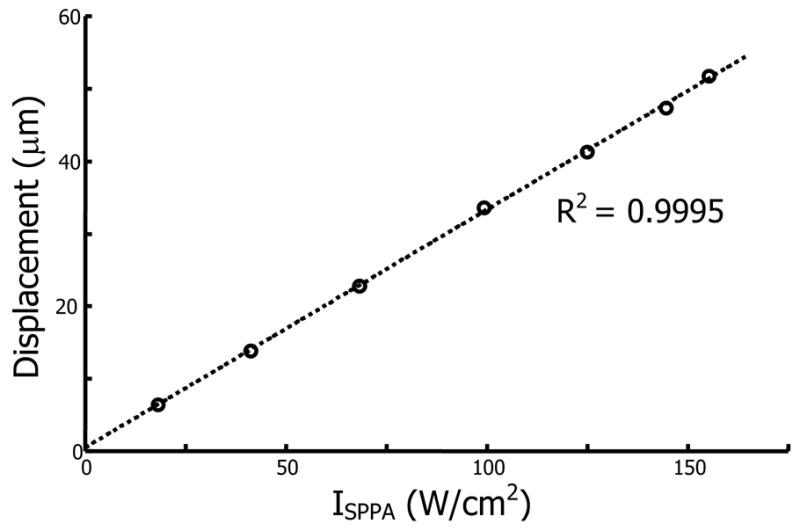
Bubble displacement versus spatial-peak, pulse average intensity for a single bubble within a porcine lens using 200 kHz chirp insonation. The dashed line is a linear fit to the measured displacements.
Effect of Bubble Size
LIOB bubbles have finite lifetimes that depend on the number of laser pulses applied, laser pulse fluence, and surrounding material properties (Tse et al. 2005). LIOB bubble lifetimes within porcine lenses range from less than a minute to greater than 10 minutes, according to the laser exposure and bubble location within the lens (Erpelding et al. 2005b). The effect of bubble size on acoustic radiation force was investigated by applying eight 200 kHz chirp pulses to a single bubble placed 3 mm from the lens center along the equatorial plane. Chirp pulses were applied approximately every 15 seconds prior to the bubble collapse 2.5 minutes after LIOB. The results from this experiment are presented in Fig. 6, with the dashed line representing a linear fit to the measured displacements. As the bubble slowly shrinks prior to its ultimate collapse, smaller displacements were induced as the radiation force decreased with the bubble cross-sectional area. In Fig. 6, bubble radius is measured by the square root of the integrated backscatter from the bubble echo. The final two bubble displacements deviate slightly from the linearly decreasing trend since just prior to collapse, bubbles approached resonant size and are susceptible to dynamic, unstable acoustic radiation force effects. However, the linear relationship between bubble radius and displacement is in good agreement for bubbles acoustically driven far from their resonant frequency.
Fig. 6.
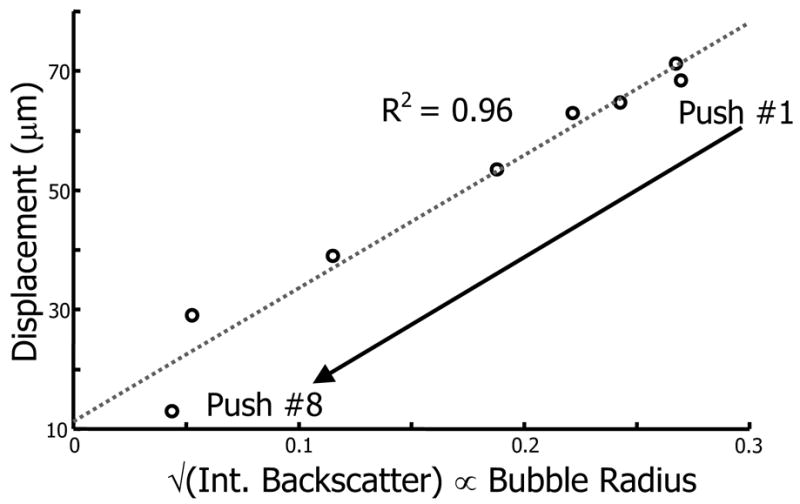
Single bubble displacement plotted versus the square root of the bubble integrated backscatter within a porcine lens using a 200 kHz chirp pulse. Integrated backscatter is proportional to the bubble cross-sectional area, so the square root of integrated backscatter is proportional to bubble radius. The dashed line is a linear fit to the measured displacement. As the bubble shrinks prior to its ultimate collapse, smaller displacements are observed.
DISCUSSION AND CONCLUSIONS
Previous researchers have investigated acoustic radiation force on spherical targets. Theoretical expressions for the radiation force on a rigid sphere due to a plane standing wave were derived by King (1934). Further developments extended the theory to include compressible spheres (Yosioka and Kawasima 1955) and arbitrary pressure fields (Gorkov 1962). The direction of radiation force in a standing wave depends on the relative density of the sphere compared to the surrounding material. Denser objects are directed to pressure nodes, while less dense objects are directed to pressure antinodes. The specific case of radiation force on a bubble target due to a standing wave in liquids has also been considered, primarily with regard to acoustic levitation (Asaki and Marston 1994, Blake 1949, Crum and Eller 1970, Crum 1975, Eller 1968, Lee and Wang 1993, Leighton 1994, Miller 1977, Wu and Du 1990). In a liquid, the radiation force on a bubble small compared to an acoustic wavelength is given by the time average product of the bubble volume and pressure gradient (Eller 1968). Therefore, ideally the net radiation force at standing wave pressure nodes and antinodes is zero and bubbles are driven towards these positions depending on their size relative to the excitation frequency. Bubbles driven above resonance are directed to pressure nodes, while bubbles driven below resonance are directed to pressure antinodes.
Although the present study considers standing waves primarily in viscoelastic solids, previous research gives insights into the expected behavior. The distance between the pressure nodes and antinodes is given by half a wavelength of the excitation frequency, which implies that bubble displacements corrupted by standing wave artifacts should have a spatial periodicity equal to half a wavelength. Glass bead displacements in a gel phantom (Fig. 2) and bubble displacements in a porcine lens (Fig. 4) from tone burst excitation both demonstrate a spatial periodicity equal to half a wavelength. Also, the range of bubble sizes and excitation frequencies used in the present study correspond to bubbles driven above their resonance frequency. Accordingly, in the presence of standing waves, bubbles should be directed toward pressure nodes.
Bead displacements in response to tone burst excitation (Fig. 2) demonstrate negative displacements (i.e. towards the transducer). Radiation force directs glass beads towards pressure nodes in a standing wave since beads are denser than the surrounding gel. Depending on the position of the bead relative to the nearest pressure node, the bead will either displace away from or towards the transducer. Positive bead displacements from tone burst excitation are larger in magnitude than negative displacements (Fig. 2), which may result from imperfect standing wave conditions. No negative bead displacements were observed using chirp pulses, suggesting a unidirectional force away from the transducer and a reduced standing wave.
The results from this study illustrate that chirp acoustic radiation force effectively reduces standing wave artifacts. Bubble-based acoustic radiation force methods seek a bubble displacement directly related to the local Young’s modulus. Standing wave artifacts are troublesome since bubble displacement can be greatly affected by its axial position in the standing wave pressure field. The simplest solution would be to decrease the pulse duration sufficiently so that standing waves are not a factor; however this is not always a viable option. Tissues with long displacement time constants (several milliseconds) require long acoustic radiation force pulse durations. Under these conditions, chirp pulses are the best option to reduce standing wave artifacts.
Bubble displacements induced by chirp acoustic radiation force are proportional to acoustic intensity and bubble size. Chirp acoustic radiation force can be used to evaluate the mechanical properties of tissue since the acoustic intensity is known and bubble size can be accounted for using integrated backscatter. Therefore, displacement measurements made with minimal standing wave artifacts will directly measure the local elastic properties. Ultrasound frequency and LIOB parameters should be selected to ensure that bubbles are excited off resonance, so that bubble displacements are indicative of the local Young’s modulus and not resonant phenomena.
Potential in vivo applications of bubble-based acoustic radiation force in the lens will likely benefit from chirp excitation, as well. In the current experimental procedure much of the reflected sound responsible for standing waves came from the glass coverslip at the water tank bottom. The complex reflection and scattering of sound in vivo from the front and back lens surfaces and the bubble itself are likely to generate temporary standing waves with a single frequency pulse. Chirp pulses may provide a way to avoid standing wave artifacts otherwise induced in vivo and will undergo further study as a clinical technique is developed.
In an ongoing study, chirp excitation has been used to investigate age-related changes in the elastic properties of porcine lenses. The displacement time constants in porcine lenses were several milliseconds, requiring sufficiently long pulse durations to measure displacement differences spatially throughout the lens. Chirp pulses allowed for long pulse durations (6.5 ms) with significantly reduced standing wave artifacts.
Acknowledgments
We gratefully acknowledge the Intralase Corporation for use of the Nd:glass ultrafast laser and support from NIH grant EY 015876 and the Whitaker Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Asaki TJ, Marston PL. Acoustic radiation force on a bubble driven above resonance. J Acoust Soc Am. 1994;96(5):3096–3099. [Google Scholar]
- Beers AP, van der Heijde GL. In vivo determination of the biomedical properties of the component elements of the accommodation mechanism. Vision Res. 1994;34(21):2897–2905. doi: 10.1016/0042-6989(94)90058-2. [DOI] [PubMed] [Google Scholar]
- Blake FG. Bjerknes forces in stationary sound fields. J Acoust Soc Am. 1949;21(5):551. [Google Scholar]
- Crum LA, Eller AI. Motion of bubbles in a stationary sound field. J Acoust Soc Am. 1970;48(1):181–189. [Google Scholar]
- Crum LA. Bjerknes forces on bubbles in a stationary sound field. J Acoust Soc Am. 1975;57(6):1363–1370. [Google Scholar]
- Eller A. Force on a bubble in a standing acoustic wave. J Acoust Soc Am. 1968;43(1):170–171. [Google Scholar]
- Erpelding TN, Hollman KW, O’Donnell M. Bubble-based acoustic radiation force elasticity imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2005a;52(6):971–979. doi: 10.1109/tuffc.2005.1504019. [DOI] [PubMed] [Google Scholar]
- Erpelding TN, Hollman KW, O’Donnell M. Spatially mapping the elastic properties of the lens using bubble-based acoustic radiation force. Proc IEEE Ultrason Symp. 2005b;1:613–617. [Google Scholar]
- Gorkov LP. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov Phys Dokl. 1962;6(9):773–775. [Google Scholar]
- Hawkes JJ, Coakley WT. Force field particle filter, combining ultrasound standing waves and laminar flow. Sensor Actuat B-Chem. 2001;75:213–222. [Google Scholar]
- Heys KR, Cram SL, Truscott RJW. Massive increase in the stiffness of the human lens nucleus with age: the basis for presbyopia? Mol Vision. 2004;10:956–963. [PubMed] [Google Scholar]
- Jansson F, Kock E. Determination of the velocity of ultrasound in the human lens and vitreous. Acta Ophthalmol. 1962;40:420–433. doi: 10.1111/j.1755-3768.1962.tb02390.x. [DOI] [PubMed] [Google Scholar]
- Khanna S, Amso NN, Paynter SJ, Coakley WT. Contrast agent bubble and erythrocyte behavior in a 1.5-MHz standing ultrasound wave. Ultrasound Med Biol. 2003;29(10):1463–1470. doi: 10.1016/s0301-5629(03)01017-2. [DOI] [PubMed] [Google Scholar]
- Khanna S, Hudson B, Pepper CJ, Amso NN, Coakley WT. Fluorescin isothiocyanate-dextran uptake by chinese hamster ovary cells in a 1.5 MHz ultrasonic standing wave in the presence of contrast agent. Ultrasound Med Biol. 2006;32(2):289–295. doi: 10.1016/j.ultrasmedbio.2005.11.002. [DOI] [PubMed] [Google Scholar]
- King LV. On the acoustic radiation pressure on spheres. Proc R Soc London, Ser A. 1934;147:212–240. [Google Scholar]
- Lee CP, Wang TG. Acoustic radiation force on a bubble. J Acoust Soc Am. 1993;93(3):1637–1640. [Google Scholar]
- Leighton TG. The acoustic bubble. San Diego, CA: Academic Press; 1994. [Google Scholar]
- Miller DL. Stable arrays of resonant bubbles in a 1 MHz standing wave acoustic field. J Acoust Soc Am. 1977;62(1):12–19. [Google Scholar]
- Mitri FG, Greenleaf JF, Fatemi M. Chirp imaging vibro-acoustography for removing the ultrasound standing wave artifact. IEEE Trans Med Imaging. 2005;24(10):1249–1255. doi: 10.1109/TMI.2005.854518. [DOI] [PubMed] [Google Scholar]
- Nightingale K, Palmeri M, Bouchard R, Trahey G. Acoustic radiation force impulse imaging: a parametric analysis of factors affecting image quality. Proc IEEE Ultrason Symp. 2003;1:548–553. [Google Scholar]
- Nightingale K, Scott Soo M, Nightingale R, Trahey G. Acoustic radiation force impulse imaging: in vivo demonstration of clinical feasibility. Ultrasound Med Biol. 2002;28(2):227–235. doi: 10.1016/s0301-5629(01)00499-9. [DOI] [PubMed] [Google Scholar]
- Pau H, Kranz J. The increasing sclerosis of the human lens with age and its relevance to accommodation and presbyopia. Graefe’s Arch Clin Exp Opthlalmol. 1991;229(3):294–296. doi: 10.1007/BF00167888. [DOI] [PubMed] [Google Scholar]
- Sarvazyan AP, Rudenko OV, Swanson SD, Fowlkes JB, Emelianov SY. Shear wave elasticity imaging: a new ultrasonic technology of medical diagnostics. Ultrasound Med Biol. 1998;24(9):1419–1435. doi: 10.1016/s0301-5629(98)00110-0. [DOI] [PubMed] [Google Scholar]
- Trahey GE, Palmeri ML, Bentley RC, Nightingale KR. Acoustic radiation force impulse imaging of the mechanical properties of arteries: in vivo and ex vivo results. Ultrasound Med Biol. 2004;30(9):1163–1171. doi: 10.1016/j.ultrasmedbio.2004.07.022. [DOI] [PubMed] [Google Scholar]
- Tse C, Zohdy MJ, Ye JY, Norris TB, Balogh LP, Hollman KW, O’Donnell M. Acoustic detection of controlled laser-induced microbubble creation in gelatin. IEEE Trans Ultrason Ferroelectr Freq Control. 2005;52(11):1962–1969. doi: 10.1109/tuffc.2005.1561665. [DOI] [PubMed] [Google Scholar]
- Viola F, Kramer MD, Lawrence MB, Oberhauser JP, Walker WF. Sonorheometry: a noncontact method for the dynamic assessment of thrombosis. Ann Biomed Eng. 2004;32(5):696–705. doi: 10.1023/b:abme.0000030235.72255.df. [DOI] [PubMed] [Google Scholar]
- Walker WF. Internal deformation of a uniform elastic solid by acoustic radiation force. J Acoust Soc Am. 1999;105(4):2508–2518. doi: 10.1121/1.426854. [DOI] [PubMed] [Google Scholar]
- Wu J, Du G. Acoustic radiation force on a small compressible sphere in a focused beam. J Acoust Soc Am. 1990;87(3):997–1003. [Google Scholar]
- Yosioka K, Kawasima Y. Acoustic radiation pressure on a compressible sphere. Acustica. 1955;5:167–173. [Google Scholar]


