Spatial Reference Frames of Visual, Vestibular, and Multimodal Heading Signals in the Dorsal Subdivision of the Medial Superior Temporal Area

Abstract

Heading perception is a complex task that generally requires the integration of visual and vestibular cues. This sensory integration is complicated by the fact that these two modalities encode motion in distinct spatial reference frames (visual, eye-centered; vestibular, head-centered). Visual and vestibular heading signals converge in the primate dorsal subdivision of the medial superior temporal area (MSTd), a region thought to contribute to heading perception, but the reference frames of these signals remain unknown. We measured the heading tuning of MSTd neurons by presenting optic flow (visual condition), inertial motion (vestibular condition), or a congruent combination of both cues (combined condition). Static eye position was varied from trial to trial to determine the reference frame of tuning (eye-centered, head-centered, or intermediate). We found that tuning for optic flow was predominantly eye-centered, whereas tuning for inertial motion was intermediate but closer to head-centered. Reference frames in the two unimodal conditions were rarely matched in single neurons and uncorrelated across the population. Notably, reference frames in the combined condition varied as a function of the relative strength and spatial congruency of visual and vestibular tuning. This represents the first investigation of spatial reference frames in a naturalistic, multimodal condition in which cues may be integrated to improve perceptual performance. Our results compare favorably with the predictions of a recent neural network model that uses a recurrent architecture to perform optimal cue integration, suggesting that the brain could use a similar computational strategy to integrate sensory signals expressed in distinct frames of reference.

Introduction

To navigate effectively through a complex, three-dimensional (3D) environment, we must accurately estimate our direction of self-motion, or heading. The perception of heading is an especially challenging problem for the nervous system because it requires the integration of multiple sensory cues. Visual information such as optic flow can be used to judge heading under certain conditions (Gibson, 1950; Warren, 2003). However, vision alone is often insufficient because the retinal image is confounded by changes in gaze or by motion of objects in the visual field (Royden et al., 1992, 1994; Royden, 1994; Warren and Saunders, 1995; Banks et al., 1996; Royden and Hildreth, 1996; Crowell et al., 1998). A possible solution may be to combine visual information with inertial signals that specify the motion of the head in space, such as from the vestibular otolith organs (Fernandez and Goldberg, 1976). Indeed, behavioral evidence suggests that humans and monkeys can combine visual and vestibular cues to improve self-motion perception (Telford et al., 1995; Ohmi, 1996; Harris et al., 2000; Bertin and Berthoz, 2004; Gu et al., 2006b), but it remains unclear exactly where and how the brain carries out this sensory integration.

The dorsal subdivision of the medial superior temporal area (MSTd) is a strong candidate to mediate the integration of visual and vestibular signals for heading perception. Neurons in MSTd have large visual receptive fields and are selective for optic flow patterns similar to those seen during self-motion (Tanaka et al., 1986, 1989; Duffy and Wurtz, 1991, 1995). Electrical microstimulation in MSTd can bias monkeys' judgments of heading from optic flow (Britten and van Wezel, 1998, 2002), suggesting a causal role for this region in heading perception. MSTd neurons are also selective for motion of the animal in darkness, which suggests that they receive vestibular inputs (Duffy, 1998; Bremmer et al., 1999; Page and Duffy, 2003). We recently extended these findings by measuring the 3D heading tuning of MSTd neurons using a virtual reality system that can independently control visual and vestibular cues (Gu et al., 2006a). However, our previous study left an important question unanswered: in what spatial reference frame(s) are heading signals represented in MSTd? Vestibular afferents signal motion of the head in space (i.e., a head-centered reference frame), whereas the early visual system encodes motion relative to the retina (i.e., an eye-centered frame). To resolve this discrepancy, it is commonly thought that multisensory neural populations should represent visual and nonvisual signals in a common reference frame (Stein and Meredith, 1993; Cohen and Andersen, 2002), but it is not known whether this occurs for signals related to self-motion. In addition, reference frames have not been measured during the more natural case of multimodal stimulation.

We measured the tuning of single neurons for heading defined by visual cues, vestibular cues, or a combined visual-vestibular stimulus. The position of the eyes was varied to dissociate eye and head coordinates. We found that visual and vestibular heading signals do not share a common reference frame at the level of the MSTd. Reference frames in the combined condition were dependent on the relative strength of visual and vestibular tuning, and on whether unimodal tuning was congruent or opposite. Our results are broadly consistent with recent network models that can integrate signals expressed in distinct reference frames (Deneve et al., 2001; Pouget et al., 2002; Avillac et al., 2005).

Materials and Methods

Animal preparation.

Subjects were three male rhesus monkeys (Macaca mulata) weighing 4–7 kg. Under sterile conditions, monkeys were chronically implanted with a circular delrin cap for head stabilization as described previously (Gu et al., 2006a), as well as one or two scleral search coils for measuring eye position (Robinson, 1963; Judge et al., 1980). After surgical recovery, monkeys were trained to fixate visual targets for juice rewards using standard operant conditioning techniques. Before recording experiments, a plastic grid (2 × 4 × 0.5 cm) containing staggered rows of holes (0.8 mm spacing) was stereotaxically secured to the inside of the head cap using dental acrylic. The grid was positioned in the horizontal plane and extended from the midline to the area overlying the MSTd bilaterally. Vertical microelectrode penetrations were made via transdural guide tubes inserted in the grid holes. All procedures were approved by the Institutional Animal Care and Use Committee at Washington University and were in accordance with National Institutes of Health guidelines.

Heading stimuli.

During experiments, monkeys were seated comfortably in a primate chair with their head restrained. The chair was secured to a 6-degrees-of-freedom motion platform (MOOG 6DOF2000E; Moog, East Aurora, NY) (see Fig. 1 A) that allowed physical translation along any axis in 3D (Gu et al., 2006a). Visual stimuli and fixation targets were back-projected (Christie Digital Mirage 2000; Christie, Cyrus, CA) onto a tangent screen positioned 30 cm in front of the monkey and subtending 90° × 90° of visual angle. Optic flow was generated using the OpenGL graphics library, allowing the accurate simulation of speed, size, and motion parallax cues experienced during real self-motion. The stimuli depicted movement of the observer through a random cloud of dots plotted in a virtual workspace 100 cm wide, 100 cm tall, and 40 cm deep. Stimuli were viewed binocularly with no disparities added to the display (i.e., no stereo cues were present). The projector, screen, and field coil frame were mounted on the platform and moved along with the animal, and the field coil frame was enclosed such that the animal experienced no visual motion other than the optic flow presented on the screen.

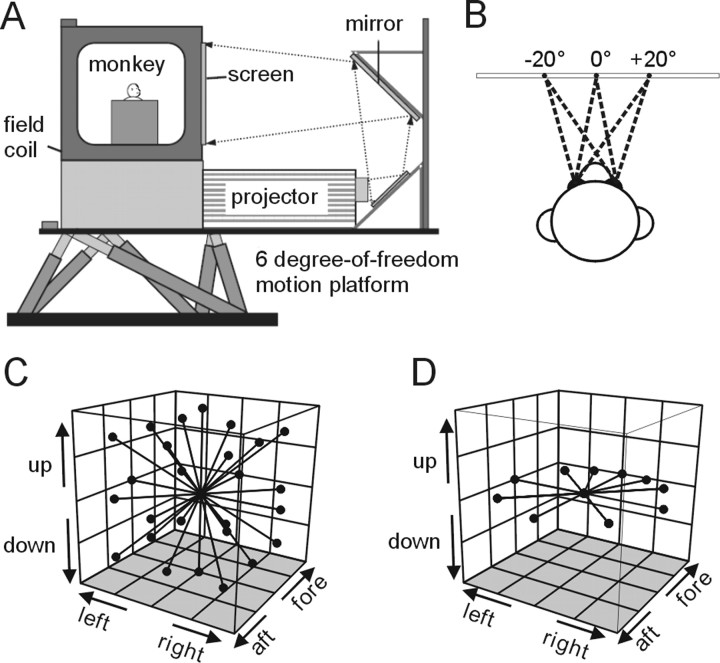
Figure 1.

Experimental setup and heading trajectories. A, Schematic illustration of the virtual reality apparatus. The monkey, field coil, projector, and screen were mounted on a motion platform that can translate in any direction in 3D. B, On each trial, the monkey was required to fixate one of three possible targets along the horizontal meridian, separated by 20, 22.5, or 25° of visual angle. C, Illustration of the 26 movement trajectories used to measure heading tuning in the 3D experiments. All movements originated from the center position and had a Gaussian velocity profile (total displacement, 13 cm; duration, 2 s). D, Illustration of the 10 trajectories tested in the 2D (horizontal plane) experiments.

At the onset of each trial, the monkey was presented with a fixation point at one of three locations (randomly interleaved): straight ahead (0°), right of center, or left of center (±20, ±22.5, or ±25°, consistent within each experimental session) (see Fig. 1 B). After fixation was acquired within a 2° × 2° window, a heading stimulus was presented either by translating the platform (vestibular condition), simulating translation via optic flow (visual condition), or by a congruent combination of the two cues (combined condition). The only task required of the animals was to maintain fixation throughout the 2 s stimulus period and they were given a juice reward after each successful trial. It should be noted that the response properties of MSTd neurons can depend on the attentional demands of the task (Treue and Maunsell, 1999; Recanzone and Wurtz, 2000) and, thus, we cannot rule out the possibility that our results could have been different if the animals were performing an active task rather than passive fixation.

Stimuli in the combined condition were synchronized to within 1 ms by using a transfer function to predict platform motion from the command signal given by the stimulus control computer (for details, see Gu et al., 2006a). All stimuli had a Gaussian velocity profile with the following parameters: duration, 2 s; amplitude, 13 cm (total displacement); peak acceleration, 0.09 G (0.87 m/s²); peak velocity, 0.27 cm/s. In one set of experiments, the possible motion directions were evenly distributed throughout 3D space in increments of 45° (26 total directions) (see Fig. 1 C) (3D experiments), and typically only one stimulus condition (visual or vestibular) was tested for each neuron because of time constraints. In other experiments, heading directions were limited to the horizontal plane (see Fig. 1 D) (2D experiments), and all three stimulus conditions (visual, vestibular, and combined) were interleaved in a single block of trials. Ten heading directions were tested in the 2D experiments: the eight directions separated by 45°, plus two additional directions 22.5° to the left and right of straight ahead (see Fig. 1 D).

Neural recordings.

Single-unit activity in area MSTd was recorded using tungsten microelectrodes (FHC, Bowdoinham, ME) and standard techniques. MSTd was initially localized via structural MRI scans as described previously (Gu et al., 2006a). Briefly, the scans were used to determine the position of several reference penetrations within the recording grid relative to expected boundaries between cortical areas. These boundaries were derived from the segmentation and morphing of the structural MRI images to a standard macaque atlas using CARET software (Van Essen et al., 2001). This procedure identified the subset of grid holes that were most likely to provide access to MSTd in each hemisphere of each monkey. Electrode penetrations were then guided by the pattern of white and gray matter apparent in the background activity, as well as the response properties of each neuron encountered (for details, see Gu et al.). Receptive fields were hand mapped using in-house software that controlled the position, size, and velocity of random dot patches. This was not performed for every neuron in our sample, but detailed mapping was performed extensively at all electrode depths whenever a new recording hole was used, and periodically thereafter. Putative MSTd neurons had large receptive fields (30–70° in diameter) that often contained the fovea and portions of the ipsilateral visual field, were selective for full-field optic flow stimuli, and usually did not respond well to small (<10°) moving dot patches (Komatsu and Wurtz, 1988a,b; Tanaka et al., 1993). We attempted to record from any MSTd neuron that could be isolated and was spontaneously active or responded to flickering and/or drifting dot patches. However, because only ∼64% of MSTd neurons show significant tuning for our inertial motion stimuli (Gu et al., 2006a), it was sometimes necessary to bypass cells that did not show a clear response in the vestibular condition. Other than the need to test neurons with significant vestibular tuning, there was no overt bias in the selection of neurons for this study.

Data analysis.

Analyses were done using custom scripts in Matlab (Mathworks, Natick, MA), and statistical tests were performed in Matlab or InStat (GraphPad Software, San Diego, CA). All neurons with significant heading tuning (p < 0.05 by one-way ANOVA) for at least two eye positions in either the visual or vestibular condition were included in the reference frame analysis (displacement index) (see below). This criterion was used because our primary goal was to determine the shift of the tuning function between eye positions. For all analyses, cells were required to have at least three repetitions of each heading direction, eye position, and stimulus condition. For the majority of neurons (65%), five or more repetitions were collected. One repetition consisted of 81 trials for the 3D experiments (26 heading directions by three eye positions by one stimulus condition plus three null conditions to measure spontaneous firing rate at each eye position), and 93 trials for the 2D experiments (three stimulus conditions by 10 heading directions by three eye positions plus three null conditions).

Tuning profiles were constructed by plotting the mean firing rate as a function of azimuth and elevation of the heading direction (or azimuth only for the 2D experiments). To plot the 3D data on Cartesian axes (see Fig. 2), spherical tuning functions were transformed using the Lambert cylindrical equal-area projection (Snyder, 1987). In this projection, the abscissa represents azimuth angle, and the ordinate represents a cosine-transformed version of elevation angle. Firing rate was computed over the central 1 s of the stimulus duration, as most of the velocity variation occurred in this interval. Repeating the analyses using the full 2 s duration did not change the overall results.

Figure 2.

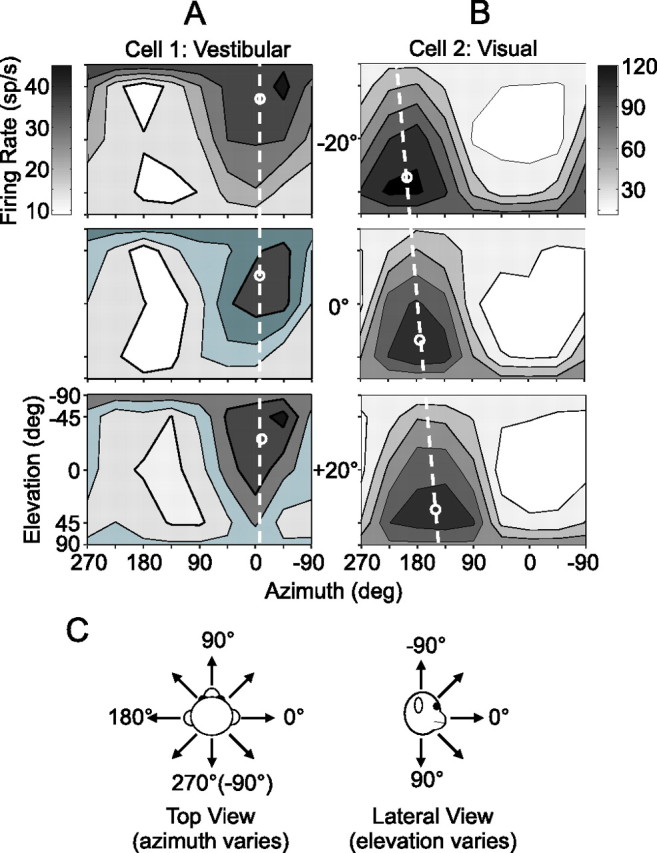
3D heading tuning functions of two example MSTd neurons. A, B, Cell 1 was tested in the vestibular condition (A) and cell 2 in the visual condition (B). Tuning was measured at three different eye positions: −20° (top), 0° (middle), and +20° (bottom). Mean firing rate (grayscale) is plotted as a function of the heading trajectory in spherical coordinates, with the azimuth and elevation of the heading vector represented on the abscissa and ordinate, respectively. For illustration purposes, small white circles are positioned at the preferred heading for each tuning function, computed as a vector sum of responses around the sphere. C, Conventions for defining the real (vestibular) or simulated (visual) motion directions of 3D heading stimuli.

The spatial reference frame of heading tuning was assessed for each neuron and stimulus condition via a cross-covariance technique (Avillac et al., 2005). Briefly, tuning functions for each eye position were linearly interpolated to 1° resolution (using the Matlab function interp1) and systematically displaced relative to one another. Because our stimulus space is spherical (3D experiments) or circular (2D experiments), this displacement was equivalent to a rotation of the tuning function in azimuth (i.e., about the vertical axis). For each pair of eye positions, we determined the amount of displacement that resulted in the greatest covariance between the two interpolated tuning functions, and then normalized this value by the change in eye position to give a displacement index (DI):

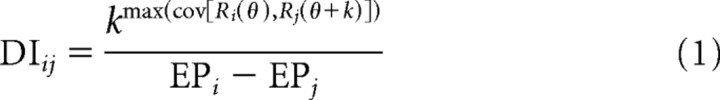Here, k (in degrees) is the relative displacement of the tuning functions (denoted R_i and R_j), and the superscript above k refers to the maximum covariance between the tuning curves as a function of k (ranging from −180° to +180°). The denominator represents the difference between the eye positions (EP_i and EP_j) at which the tuning functions were measured. If a tuning curve shifts by an amount equal to the change in eye position, the DI will equal 1 (eye-centered tuning). If no shift of the tuning curve occurs at different eye positions, the DI will equal 0 (head-centered tuning). Ninety-three percent of neurons in our sample had significant visual and/or vestibular tuning at all three eye positions (ANOVA, p < 0.05) and, thus, yielded three DI values (one for each pair of tuning curves); these were averaged to give a single DI for each cell in each stimulus condition. For the remaining cells, we used only the single DI value computed from the two significant tuning curves. Confidence intervals were computed for each DI using a bootstrap method: bootstrapped tuning functions were generated by resampling (with replacement) the data for each heading direction and then a DI was computed using the bootstrapped data. This was repeated 200 times to produce a distribution of DIs from which a 95% confidence interval was derived (percentile method). A DI was considered significantly greater or less than a particular value (e.g., 0 or 1) if its 95% confidence interval did not include that value.

Because the DI distributions were broad and partially overlapping (see Fig. 3), we used a curve-fitting analysis to determine whether each neuron was more consistent with an eye-centered or a head-centered representation of heading. For this analysis, only data from heading directions in the horizontal plane were included, such that data from the 3D and 2D experiments could be pooled into a single population summary. Tuning curves were fit with a modified wrapped Gaussian function of the following form:

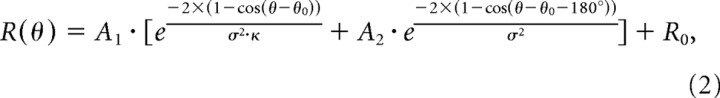where θ₀ is the location of the peak, σ is the tuning width, A ₁ is the overall amplitude, and R ₀ is the baseline. The second exponential term in the equation can produce a second peak 180° out of phase with the first, but only if the parameter A ₂ is sufficiently large. The relative widths of the two peaks are determined by the parameter κ. Tuning curves with multiple peaks were fairly uncommon in our sample, but this extra term was necessary to fit a subset of neurons in all stimulus conditions.

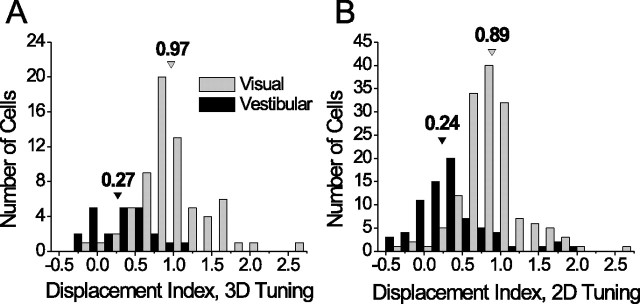
Figure 3.

Distributions of DI values. Black bars represent the vestibular condition and gray bars the visual condition. Arrowheads indicate the median DI for each stimulus condition. A, DI distributions for the 3D experiments only (vestibular, n = 23; visual, n = 69). B, DI distributions for the complete pooled sample (3D and 2D experiments; vestibular, n = 74; visual, n = 150).

Data from all three eye positions were fit simultaneously (using the Matlab function fmincon), such that the total number of data points included in each fit was at least 72 for the 3D experiments [eight heading directions in the horizontal plane by three eye positions by three repetitions (minimum) of each stimulus] and 90 for the 2D experiments (10 heading directions by three eye positions by three repetitions). Five of the six parameters in Equation 2 were free to vary across eye positions, with the exception of the peak parameter θ₀ (thus, the total number of free parameters for each fitting operation was 16). The peak parameter was constrained either to shift by exactly the amount of the change in eye position (“eye-centered model”) or to be constant across eye positions (“head-centered model”). For each model, the best-fitting function was compared with the data to determine the goodness-of-fit. To remove the influence of correlations between the two models themselves, we computed partial correlation coefficients using the following formulas:

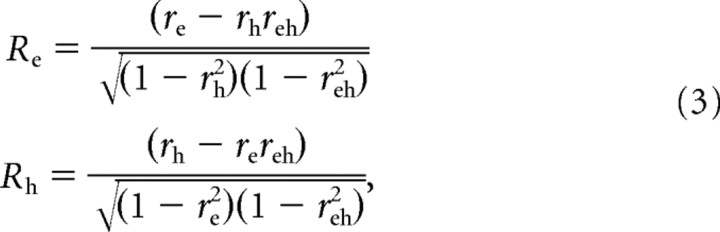where r _e and r _h are the simple correlation coefficients between the data and the eye- and head-centered models, respectively, and r _eh is the correlation between the two models. Partial correlation coefficients R _e and R _h were normalized using Fisher's r-to-Z transform so that meaningful comparisons could be made based on the difference between Z scores, independent of the number of data points (Angelaki et al., 2004; Smith et al., 2005). Using this analysis, a scatter plot of eye-centered versus head-centered Z scores can be separated into regions indicating a significantly better fit of one model over the other (see Fig. 4 C). For example, a cell was considered significantly eye-centered if the Z score for the eye-centered model was >1.645 and exceeded the head-centered Z score by at least that amount (equivalent to a p value of <0.05).

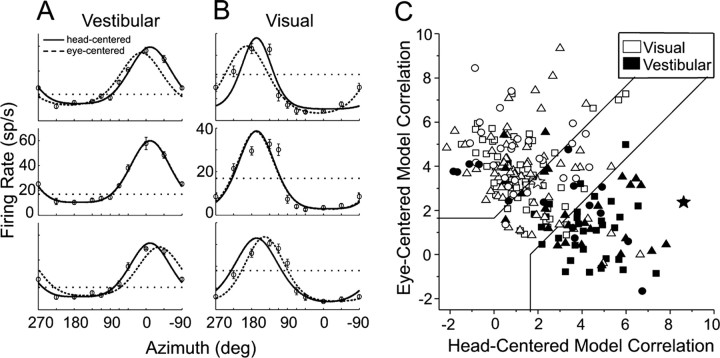
Figure 4.

2D heading tuning functions of an example MSTd neuron, with the best-fitting eye- and head-centered models. In each tuning curve, the firing rate is plotted as a function of heading direction (azimuth), and the panels from top to bottom represent tuning measured at eye positions of −22.5°, 0°, and +22.5°. The horizontal dotted line indicates spontaneous firing rate, and error bars represent SEM. A, Tuning in the vestibular condition. Superimposed dashed and solid curves depict the best-fitting eye-centered and head-centered models, respectively (see Materials and Methods). B, Tuning of the same neuron in the visual condition. C, Eye- and head-centered model correlation coefficients (Z-transformed), separated by stimulus condition (vestibular, filled symbols, n = 74; visual, open symbols, n = 150) and including all cells in the 2D and 3D experiments. Shapes denote different animals: triangles, monkey Z; circles, monkey A; squares, monkey Q. Significance regions are based on the difference between eye- and head-centered Z scores corresponding to p < 0.05 (top left, eye centered; bottom right, head centered; central diagonal region, unclassified). The two large star-shaped symbols, one filled and one open, represent the example cell in Figure 4, A and B, respectively.

To plot the average time course of responses in each stimulus condition, we computed mean firing rate in 20 ms bins throughout the 2 s stimulus period using only data from the heading direction that gave the largest response for each neuron. Individual neuron response time courses were normalized by dividing by the maximum bin, then averaged across all cells to give the mean response time course (see Fig. 8 A). For the associated DI time courses (see Fig. 8 B), complete tuning functions were generated using mean firing rate computed within a sliding 100 ms window that was moved in increments of 50 ms, and DI was computed from these tuning functions as described above.

Figure 8.

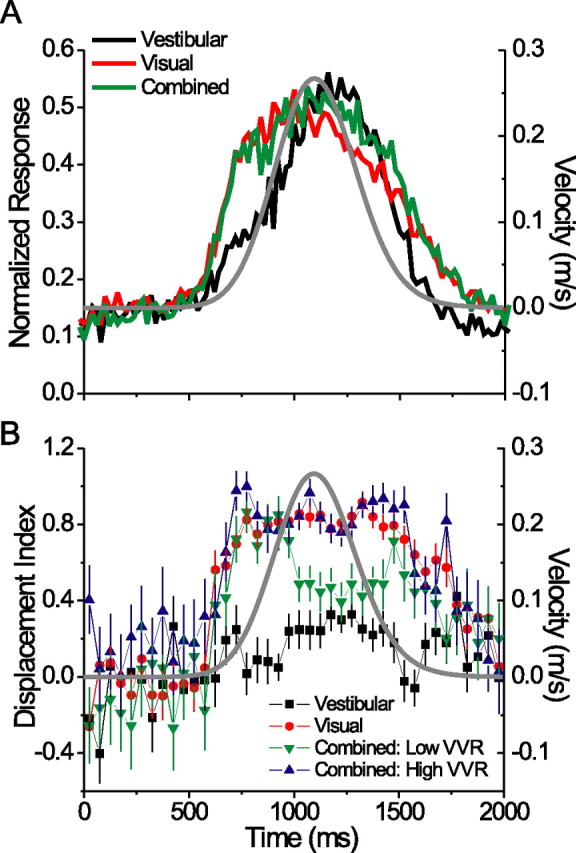
Average response time course and evolution of reference frames over time. A, Normalized mean response time course (PSTH) for the preferred heading direction in the three stimulus conditions, in 20 ms bins. Gray Gaussian curve indicates the stimulus velocity profile. B, Mean DI time courses (100 ms bins, sliding every 50 ms). Error bars indicate SEM. Combined condition data are separated into high- (>2.0) and low-VVR (<2.0) groups (see text).

Neural network model.

To explore the computational implications of the observed spatial tuning properties in MSTd, we constructed a recurrent neural network model similar to that of Pouget and colleagues (Deneve et al., 2001; Pouget et al., 2002; Avillac et al., 2005). We chose this type of model because it has been shown previously to produce spatially accurate estimates from multiple sensory cues without requiring them to be encoded in the same reference frame (Avillac et al., 2005). Several other groups have successfully modeled the integration of optic flow signals with extraretinal eye velocity information that is typically required for accurate heading perception during smooth pursuit eye movements (Lappe et al., 1996; van den Berg and Beintema, 1997, 2000; Beintema and van den Berg, 1998; Lappe, 1998; Grossberg et al., 1999). However, to better simulate our experimental conditions, we instead sought to model the integration of eye-centered (visual) and head-centered (vestibular) signals during static fixation, a task for which the recurrent basis function approach is well suited (Avillac et al., 2005). This approach should not be confused with that of another previous study (Ben Hamed et al., 2003) in which MSTd neurons were found to combine multiple variables (eye position, pursuit direction, and the head-centered position of the focus of expansion) in a nonlinear manner, similar to basis functions. Also note that this model is fundamentally different from our previous network that used a feedforward architecture (Gu et al., 2006a). In that model, visual and vestibular signals remained in purely eye and head coordinates, respectively, and an eye position signal was used to transform visual signals into a head-centered frame in the output layer. In contrast, the recurrent network discussed here generally uses units with intermediate reference frames to perform statistically optimal cue integration in the presence of noise (Deneve et al., 2001; Deneve and Pouget, 2004).

The network contains three input layers: (1) a vestibular layer encoding heading relative to the head (X _h), (2) a visual layer encoding heading relative to the retina (X _r), and (3) a layer encoding the position of the eyes in the orbits (X _e). These layers are termed “input” for convenience, although they also constitute the network output. The input layers make recurrent connections with an intermediate layer (known as a basis function layer), which pools the input activity using a set of predetermined connection weights. The weights are designed to implement a simple linear relationship between the three input variables: X _h = X _r + X _e (Deneve et al., 2001; Pouget et al., 2002). Feedback from the basis function layer modulates the activity of the input units, which is then averaged over several iterations to compute the output.

We used the same network equations and parameters as Avillac et al. (2005), with the following exceptions. Tuning curves for the visual and vestibular input units (n = 40 each) were specified by Equation 2, using identical parameters for the two layers. To obtain the parameter values to be used in the model, we performed a least-squares fit to the visual and vestibular data for each MSTd neuron in our sample (without the “head-centered” or “eye-centered” restriction used in the curve-fitting analysis), then took the mean of each parameter from these curve fits (with the exception of the peak parameter, θ₀, which was varied uniformly throughout the 360° stimulus space). The best fitting parameter values were as follows: A ₁ = 41.04, σ = 2.69 radians, A ₂ = 0.15, κ = 0.58, and R ₀ = 7.48. The eye position units were given standard circular Gaussian tuning curves of width σ = 0.4 radians (Deneve et al., 2001) and amplitude equal to that of the visual and vestibular input units. Varying the width of the eye position units between 0.2 and 0.8 radians had very little effect on the outcome (supplemental Fig. 1, available at www.jneurosci.org as supplemental material).

Our primary goal was to determine the pattern of inputs that provided the best match between the model and our physiological results. To this end, we varied the network connectivity by applying a scaling factor to the weights from the visual and eye position layers. The weights from the vestibular layer were arbitrarily chosen to remain constant. This scaling was parameterized by a visual-vestibular ratio (VVR), measuring the strength of the visual inputs relative to the vestibular inputs [identical to visual-tactile ratio by Avillac et al. (2005) and analogous to the VVR computed for our neuronal data] (see Results) (Eq. 4), and an eye position ratio (EPR), measuring the relative strength of the eye position inputs. We then simulated the three stimulus conditions used in our recording experiments by providing noisy inputs from the visual layer, vestibular layer, or both (eye position inputs were always present). For each condition, we computed the mean displacement index of the basis function units across a broad range of VVR and EPR (from 0.1–2 in increments of 0.1) (see Fig. 9 B). These averaged model DI values were compared with the individual neuronal DI values by computing a mean-squared difference: 1/n × Σ_i(DI_avg(model) − DI_i(neuronal))² across all tested values of VVR and EPR (see Fig. 9 C).

Figure 9.

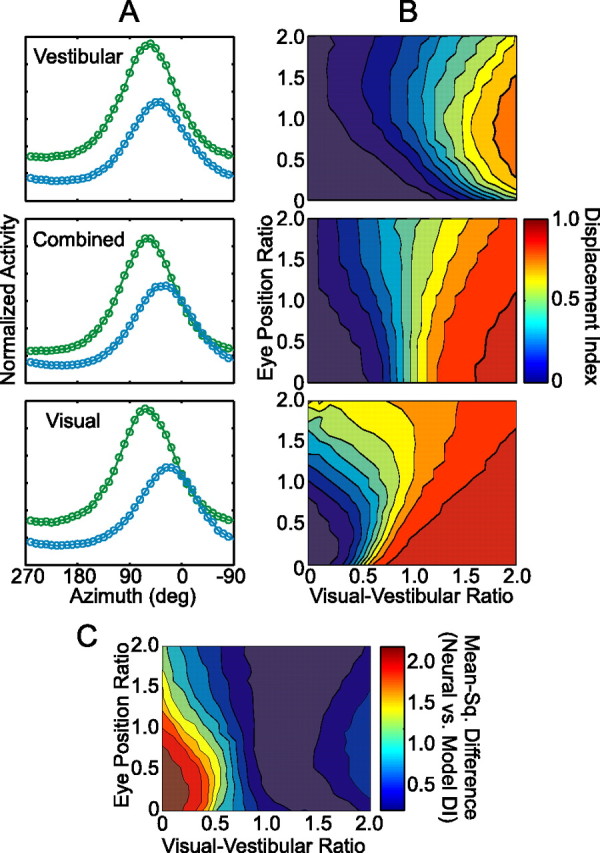
Neural network properties and comparison with MSTd data. A, Example tuning curves for a single basis function unit in the network, measured at two eye positions, −27° (green curves) and +27° (blue curves). The network was run under three simulated stimulus conditions (from top to bottom): vestibular, combined, and visual. VVR and EPR were both 1.0 for this unit. B, Mean DI (color coded) of the basis function units for each condition, plotted as a function of VVR and EPR. Panels from top to bottom (as in A): vestibular, combined, and visual. C, Mean-squared difference (color coded) between the neural and model DI distributions [1/n × Σ_i(DI_avg(model) − DI_i(neuronal))²] as a function of VVR and EPR. Included in this analysis were the visual, vestibular, and combined DI results from only those neurons with significant tuning in all three conditions (n = 54) (Fig. 6 A,B).

To facilitate a direct comparison between the predicted DI from the model and our MSTd results, we constructed a version of the network in which the VVR of each intermediate unit was randomly drawn, with replacement, from the distribution of neuronal VVR values computed from our MSTd sample (including only cells with significant tuning in the visual and vestibular conditions; n = 66). With no data to constrain EPR, we allowed it to vary uniformly between 0.1 and 2.0. Simulated visual and vestibular DI distributions were then computed from this network, and the entire procedure was repeated 50 times to generate a mean and SD for each bin in the DI histograms. These are plotted in Figure 10 along with the corresponding neuronal DI distributions for comparison.

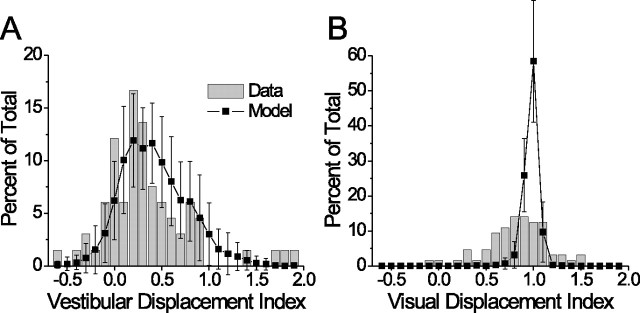
Figure 10.

Predicted and actual DI distributions, given the pattern of VVRs observed in the MSTd. All cells with significant visual and vestibular tuning were included (n = 66). A, Vestibular condition. B, Visual condition. Gray bars show the neural data, black squares show the model results (mean ± SD; n = 50 repetitions).

Results

Single-unit activity was recorded from 162 MSTd neurons (73 from monkey Q, 62 from monkey Z, and 27 from monkey A) during fixation at three different horizontal eye positions separated by 20, 22.5, or 25° (Fig. 1 B). Heading stimuli were delivered by means of a virtual reality apparatus (Fig. 1 A) that allowed independent control of visual and inertial self-motion cues (Gu et al., 2006a) (see Materials and Methods). We presented either translational inertial motion in the absence of visual motion (vestibular condition), optic flow simulating translational motion (visual condition), or a congruent combination of both cues (combined condition). For each neuron and each stimulus condition tested, we assessed the spatial reference frame of heading tuning by comparing tuning functions measured at different eye positions. The monkey's head was fixed with respect to the chair and motion platform, thus, we made a direct comparison between eye and head coordinates (the latter of which cannot be distinguished from body or world coordinates based on our experiments).

Reference frames of 3D heading tuning

In a first set of experiments, heading stimuli were presented along 26 possible trajectories distributed throughout 3D space in increments of 45° (Fig. 1 C) and, typically, only one condition (visual or vestibular) was tested for a given neuron. Figure 2, A and B, shows two example neurons tested in the vestibular and visual conditions, respectively. The three contour maps from top to bottom represent the heading tuning functions measured at three eye positions: −20° (leftward), 0° (straight ahead), and +20° (rightward). In each contour map, mean firing rate (grayscale) is plotted as a function of the azimuth (abscissa) and elevation (ordinate) of the heading direction as defined in Figure 2 C. For all stimulus conditions, heading directions are referenced to physical body motion (i.e., “heading direction” refers both to the direction of actual motion in the vestibular condition and the direction of simulated motion in the visual condition). Tuning functions are plotted in head coordinates; thus, a head-centered neuron will have very similar spatial tuning across eye positions, whereas the tuning of an eye-centered neuron will shift laterally with eye position. The small white circles indicate the preferred heading, computed as the direction of the vector sum of all responses around the sphere. The white dashed line connects the preferred headings at each eye position to better illustrate the shift (or lack thereof).

To quantify the spatial shift of the tuning functions, we computed a DI for each cell and each stimulus condition using a cross-covariance technique (Duhamel et al., 1997; Avillac et al., 2005) (see Materials and Methods) (Eq. 1). A DI of 1 indicates a shift of the tuning function equal to the shift in eye position (i.e., an eye-centered reference frame), whereas a DI of 0 indicates no shift of the tuning function (consistent with a head-centered frame). The neuron in Figure 2 A (vestibular condition) had a DI of −0.01, which was not significantly different from zero by a bootstrap test (p > 0.05). In contrast, the cell in Figure 2 B (visual condition) showed a systematic displacement of its tuning function from left to right as eye position changed from −20° to +20°. The tuning of this neuron was very close to eye-centered, with a DI of 0.98 (not significantly different from 1 by bootstrap test, p > 0.05).

A histogram of DI values from the 3D experiments is shown in Figure 3 A, separated by stimulus condition. The median DI for the vestibular condition was 0.27, which was significantly >0 (p = 0.003) and significantly <1 (p < 0.0001, one-sample Wilcoxon signed rank test). This indicates a reference frame for vestibular signals that is closer to head-centered, but shifted slightly toward eye-centered. In contrast, the median visual DI was 0.97 (not significantly different from 1 by signed rank test, p = 0.94). Several neurons exhibited shifts in their tuning functions that exceeded the shift in eye position by 50% or more. The utility of such neurons is unclear, but in 14 of 69 cells in this sample (20%), the visual DI was significantly >1 (bootstrap, p < 0.05; range = 1.15–2.64) and therefore not likely attributable to neuronal noise.

We chose the cross-covariance method because it takes into account the entire tuning function rather than just one parameter such as the peak or vector sum. This technique is robust to changes in the gain or width of tuning curves and can tolerate a wide variety of tuning shapes (Duhamel et al., 1997; Avillac et al., 2005). Nevertheless, we also computed a standard “shift ratio” metric based on the difference in preferred azimuth between each pair of eye positions. This technique produced similar results: the median shift ratio was 0.14 for the vestibular condition (significantly >0, p = 0.03) and 0.97 for the visual condition (not significantly different from 1, p = 0.73). In neither condition were the shift ratios significantly different from the corresponding DI values (Wilcoxon matched pairs test, p = 0.43 and 0.67 for the two conditions, respectively).

Reference frames of 2D heading tuning

In general, the large number of trials required to present all 26 heading directions in the 3D experiments did not permit testing of more than one stimulus condition for a given cell. Thus, we performed a second set of experiments in which heading direction varied only in azimuth (Fig. 1 D). This simplified version of the experiment allowed us to examine whether visual and vestibular reference frames were matched for individual neurons, and to compare the single-cue conditions with the combined condition. Data from an example neuron are shown in Figure 4, A and B (combined condition results are considered in a separate section below). As in Figure 2, the tuning curves from top to bottom represent the tuning measured at leftward, central, and rightward fixation. Displacement index was computed in the same manner as in the 3D experiments; for this example cell, the vestibular DI was 0.16 (Fig. 4 A) and the visual DI was 0.82 (Fig. 4 B).

Before analyzing the reference frames of individual neurons, we wanted to verify that our DI measurements in the horizontal plane were a good approximation of the DI computed from the full 3D tuning functions. Using the data from the 3D experiments, we derived 2D tuning curves by including only heading directions with elevation = 0° (i.e., taking a cross section through the horizontal plane). We then compared DI values computed from the derived 2D tuning curves to their corresponding 3D DI values, and found that they were very similar (paired t test, p = 0.48). Hence, we retained these horizontal plane cross sections and pooled the data from the 2D and 3D experiments. Some neurons tested in the 3D protocol (n = 16 in the visual condition and 12 in the vestibular condition) were poorly tuned in the horizontal plane (p > 0.05 by one-way ANOVA) and, thus, were excluded from the final pooled sample of 2D data (vestibular, n = 74; visual, n = 150). The DI distributions for the pooled 2D data are shown in Figure 3 B. Note that with this larger sample, the median visual DI (0.89) was significantly <1 (p < 0.001), but the basic pattern of results remains unchanged.

Classification of individual neurons

The population data of Figure 3 suggest that visual and vestibular heading signals in MSTd remain in distinct spatial reference frames, on average. However, these distributions overlap partially, and it is important to characterize the behavior of individual cells. To classify the neurons in our sample, we performed a curve-fitting analysis that assessed whether the tuning of each cell was better explained by an eye-centered or head-centered model. This analysis involved fitting a wrapped Gaussian function (see Materials and Methods) (Eq. 2) to the data at all three eye positions simultaneously, and constraining the function to either shift laterally by the amount of the change in eye position (eye-centered model) or to remain head-fixed (head-centered model). Figure 4 A shows the best-fitting head-centered (solid line) and eye-centered curves (dashed line) overlaid with the vestibular data from the example neuron. The head-centered model clearly fits better than the eye-centered model at both leftward and rightward eye positions (Fig. 4 A, top and bottom plots). We quantified the goodness-of-fit of each model using a partial correlation analysis (Angelaki et al., 2004; Smith et al., 2005) (see Materials and Methods) (Eq. 3). For the vestibular condition (Fig. 4 A), the example neuron had a partial correlation coefficient of 0.93 for the head-centered model and 0.43 for the eye-centered model. Figure 4 B shows the model fits for the same neuron in the visual condition. Here, the eye-centered model was better correlated than the head-centered model (partial correlation coefficient of 0.56 vs 0.37).

To simplify the plotting and interpretation of the model correlation coefficients, we normalized their variance using Fisher's r-to-Z transform (Angelaki et al., 2004; Smith et al., 2005). Figure 4 C plots the Z-transformed partial correlation coefficients of the eye-centered model against those of the head-centered model, for both the visual condition (open symbols, n = 150) and the vestibular condition (filled symbols, n = 74). The neuron in Figure 4, A and B, is represented by the large filled and open stars, respectively. The plot is separated into significance regions based on the difference between eye-centered and head-centered Z scores. Cells in the upper-left region were significantly better fit by the eye-centered model than the head-centered model (p < 0.05), and vice versa for the lower-right region. Cells in the central diagonal region remain unclassified by this analysis. Using these criteria, 67% (101/150) of neurons in the visual condition were classified as eye-centered, 5% (7/150) were head-centered, and 28% (42/150) were unclassified. Results in the vestibular condition were very different: 14% (10/74) of these cells were classified as eye-centered, 65% (48/74) were head-centered, and 22% (16/74) were unclassified.

Given the significant proportion of unclassified neurons in both conditions, we examined these cells in more detail to determine how many could legitimately be considered intermediate between eye- and head-centered coordinates. Using a bootstrap test (see Materials and Methods), we found that 22 of the 42 unclassified cells in the visual condition (52%) and 6 of 16 unclassified cells in the vestibular condition (38%) had DI values significantly >0 and <1, indicating a true “partial shift” or intermediate reference frame. Together with the data of Figure 3, these results show that visual and vestibular heading signals remain in their native reference frame for about two-thirds of cells in MSTd, with several neurons in both conditions showing intermediate frames.

Comparison of reference frames across conditions

The distributions depicted in Figures 3 and 4 C are fairly broad, raising the question of whether reference frames in the two conditions are correlated across the population. Figure 5 A plots visual versus vestibular DI for all cells with significant tuning in both conditions (n = 66). The great majority of data points lie above the unity slope line, confirming that visual DIs were typically greater than vestibular DIs. We found no significant correlation between DI values in the two conditions (Spearman rank correlation, r = 0.20; p = 0.10), despite a handful of outliers with high vestibular and visual DIs.

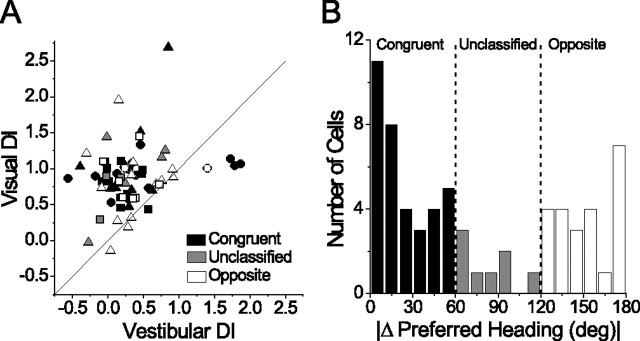
Figure 5.

Comparison between visual and vestibular DI measured in the same neurons. A, Visual DI plotted against vestibular DI for all neurons with significant tuning in both conditions (n = 66). Shapes are as in Figure 4 C, and the diagonal is the unity slope line through (0,0). B, Histogram of the difference between the preferred heading in the visual and vestibular conditions. Cells with visual and vestibular heading preferences within 60° of each other were classified as congruent (A, filled black symbols; n = 35), cells with a difference >120° were classified as opposite (open symbols; n = 23), and the remainder were unclassified (filled gray symbols; n = 8).

Previous studies (Duffy, 1998; Gu et al., 2006a) have shown that visual and vestibular heading preferences of individual MSTd neurons can be congruent, but are just as often incongruent or opposite (Fig. 4, compare A, B). Thus, we asked whether visual and vestibular DI values, and the correlation between them, were dependent on the congruency of tuning. To make this comparison, we classified cells based on the angular difference between the preferred heading directions in the visual and vestibular conditions. Figure 5 B shows the distribution of this difference in heading preference, which is clearly bimodal (Silverman's test for multimodality, p < 0.0001). Cells with a difference in preferred heading of <60° were classified as congruent (Fig. 5 A, filled black symbols), those with a difference >120° were classified as opposite (open symbols), and all others were unclassified (filled gray symbols). We found no significant difference between the median DI of congruent versus opposite cells (Mann–Whitney U test, p = 0.38 for vestibular and 0.55 for visual). Moreover, there was no significant correlation between visual and vestibular DIs when considering congruent and opposite cells separately (congruent cells, r = 0.20, p = 0.25; opposite cells, r = 0.11, p = 0.63). Thus, reference frames in the single-cue conditions do not depend on the congruency of visual and vestibular tuning.

Multimodal reference frames: effects of congruency and relative unimodal tuning strength

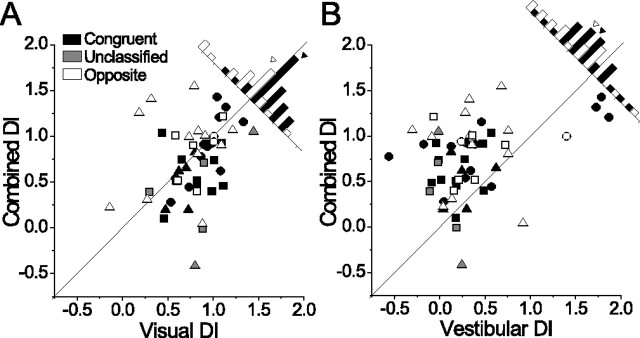
We next compared DI values in the combined condition with each single-cue condition for all neurons showing significant tuning in all three conditions (n = 54). On average, reference frames in the combined condition were quite similar to the visual condition (median DI for this sample, visual, 0.83; combined, 0.79; Wilcoxon matched-pairs test, p = 0.12) (Fig. 6 A), but very different from the vestibular condition (median DI, 0.26; p < 0.0001) (Fig. 6 B). Combined DI showed a significant positive correlation with visual DI (r = 0.40; p = 0.003) (Fig. 6 A) and a weaker correlation with vestibular DI (r = 0.27; p = 0.047) (Fig. 6 B).

Figure 6.

Comparison of single-cue and combined conditions. A, B, Combined DI plotted against visual DI (A) and vestibular DI (B) for all neurons with significant heading tuning in all three conditions (n = 54; 12 cells from Fig. 5 are omitted: 8 were not tested in the combined condition and 4 did not show significant combined tuning). Diagonal lines are unity slope lines, and congruency classification is indicated by grayscale as in Figure 5 A. Histograms show the distribution of data points relative to the diagonal (unclassified cells are excluded for clarity), with filled and open arrowheads indicating the means of the congruent and opposite distributions, respectively.

Interestingly, the relationship between the visual and combined DI was dependent on the congruency of visual and vestibular tuning. For congruent cells, the combined DI was often lower than the corresponding visual DI (Fig. 6 A) (majority of filled black symbols are below the unity slope line; see diagonal histograms), whereas for opposite cells the combined DI was typically equal to or greater than the visual DI (more open symbols are along or above the diagonal). On average, the combined DI was 0.12 less than the visual DI for congruent cells, and 0.14 greater than the visual DI for opposite cells [t test on the difference, (DI_combined − DI_visual), comparing congruent and opposite cells; p = 0.02]. This suggests that vestibular signals influence the combined tuning of congruent cells such that they show a more intermediate reference frame, whereas opposite cells tend to remain closer to eye-centered.

Another important attribute of cells in the MSTd is the relative strength of visual and vestibular tuning. Although the majority of MSTd neurons show stronger heading tuning in the visual condition than in the vestibular condition (Gu et al., 2006a), this can vary considerably from cell to cell. We therefore asked whether the DI in each condition was correlated with relative tuning strength, quantified as a VVR:

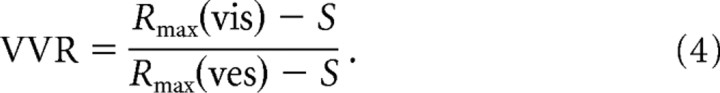R _max(vis) and R _max(ves) are the maximum mean responses in the visual and vestibular conditions, respectively, and S is the spontaneous firing rate. To control for the presence of gain fields (see below), the numerator and denominator of this ratio were each taken at the eye position yielding the maximum value. This was not always the same eye position for the two conditions, but repeating the analysis using only the data from central fixation produced similar results. We also saw no differences in the pattern of results when using the minimum response (R _min) in place of S in Equation 4. These two versions of the VVR metric were highly correlated with each other (r = 0.88) and not significantly different by a Wilcoxon matched-pairs test (p = 0.064). For all neurons in which both single-cue conditions were tested (n = 103), VVR ranged from 0.13 (vestibular dominance) to 20.99 (visual dominance) with a median of 1.86 (significantly >1; Wilcoxon signed rank test, p < 0.0001). This result confirms that visual responsiveness in the MSTd is greater than vestibular responsiveness for our heading stimuli (Gu et al., 2006a).

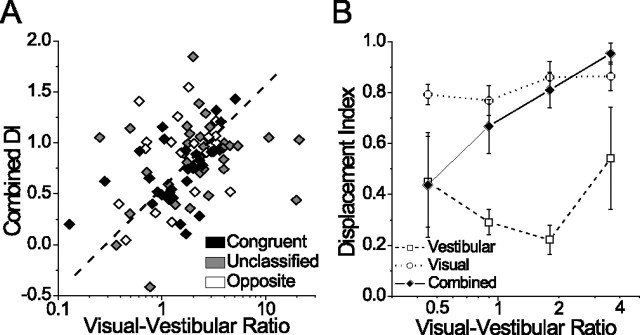
We hypothesized that DI would be positively correlated with VVR [i.e., that heading tuning would become more eye-centered (DI approaching 1) as the relative strength of the visual input increased] (Avillac et al., 2005). We found this to be the case for the combined condition (Spearman r = 0.37; p < 0.001) (Fig. 7 A), but not for the visual (r = 0.15; p = 0.12) or vestibular conditions (r = 0.10; p = 0.41) (Fig. 7 B). Note that the correlation in the combined condition was strongest for congruent cells (Fig. 7 A, filled black symbols) (r = 0.61; p < 0.001), consistent with the general effect of congruency on combined DI (Fig. 6 A). Figure 7 B summarizes the relationship between the VVR and DI for all three conditions using logarithmically spaced bins and excluding outliers (VVR values <0.3, n = 3 and >5.5, n = 3) for display purposes. The clear trend is that DI in the combined condition increases with VVR, whereas in the single-cue conditions it does not. We repeated this analysis using a different metric of tuning strength that measures the peak-to-trough modulation relative to response variability (a discrimination index) (Prince et al., 2002; DeAngelis and Uka, 2003). This metric produced the same pattern of results (data not shown), supporting the conclusion that the reference frame of multimodal heading tuning in MSTd is influenced by the relative strength of visual and vestibular tuning.

Figure 7.

Relationship between the DI and VVR. A, Combined DI plotted against VVR for all cells with significant tuning in the combined condition (n = 103). Here, the dashed diagonal line is a best-fit line (linear regression with two dependent variables: combined DI and log-transformed VVR). B, Summary of DI vs VVR for the three stimulus conditions, using log-spaced binned averages. Error bars indicate SEM. Extreme values of VVR >5.5 (n = 3) and <0.3 (n = 3) were excluded from the graph for clarity.

Time course of reference frames

For all preceding analyses, we computed firing rate over the middle 1 s of the stimulus period, based on the fact that most of the velocity variation in the stimulus occurred during this interval. However, meaningful changes in tuning properties can occur on much shorter time scales (Ringach et al., 1997; Cottaris and De Valois, 1998; Menz and Freeman, 2004), prompting us to examine the evolution of spatial reference frames over time. For each neuron, we computed DI within a 100 ms window that was stepped through the 2 s stimulus period in increments of 50 ms. We then plotted the mean DI (±SEM) across neurons for each time point, separated by stimulus condition (Fig. 8 B). For comparison, we also plotted the average response time course [peristimulus time histogram (PSTH)] for the preferred heading direction (Fig. 8 A), and overlaid the stimulus velocity profile on both plots (gray Gaussian curve). Given the relationship between the VVR and combined DI (Fig. 7), we separated the combined condition data into two groups of equal size: “low-VVR” cells (VVR <2; n = 43) and “high-VVR” cells (VVR >2; n = 43).

The first observation from this figure is that the separation between visual and vestibular reference frames occurs rapidly, as soon as the cells begin to respond (∼600 ms into the trial). The combined DI in both the high- and low-VVR groups also rises sharply, along with the visual DI. However, the combined DI of low-VVR cells begins to decrease ∼950 ms into the stimulus period and remains intermediate (DI between 0.4 and 0.5) for much of the remainder of the trial (Fig. 8 B, green symbols). This delayed transition in combined reference frames from eye-centered to intermediate parallels the delay in the average vestibular response relative to the average visual response (Fig. 8 A). We suggest that this slow development of intermediate reference frames might reflect the temporal dynamics of visual-vestibular integration in MSTd.

Eye position gain fields

Up to this point, we have described the spatial shift in heading tuning of MSTd neurons with changes in eye position. Independent of such tuning shifts, another potentially important feature of many extrastriate and posterior parietal neurons is a modulation of response gain as a function of eye position, known as a “gain field” (Andersen et al., 1985, 1990; Bremmer et al., 1997). For the present study, a gain field was defined as a significant difference (by one-way ANOVA) in the maximum evoked response (R _max − S) measured at different eye positions. We chose to use the maximum evoked response for consistency with previous work; an alternative definition of gain fields using peak-to-trough modulation (R _max − R _min) yielded similar results (data not shown).

We found that 14% (10/74) of neurons showed significant gain fields in the vestibular condition, as compared with 31% (47/150) of neurons in the visual condition and 24% (23/94) in the combined condition. It was not possible to determine the exact shape of gain fields because of the small number of eye positions tested, but we were able to classify them as either monotonic or nonmonotonic based on the following criterion. If the maximum evoked response at central fixation was significantly greater or less than the maximum response at both eccentric eye positions, the cell was considered to have a nonmonotonic (peaked or troughed) gain field. Otherwise, the gain field was considered monotonic. By this criterion, 90% (9/10) of significant gain fields in the vestibular condition were monotonic, whereas 77% (36/47) of visual gain fields and 61% (14/23) of combined gain fields were monotonic. To estimate the slope of gain fields, the maximum evoked response was plotted as a function of eye position, and a linear least-squares fit was applied to the data. Visual gain field slopes ranged from 0.03–1.58 (spikes/s)/deg with a median of 0.19. Vestibular gain fields were generally weaker, with slopes ranging from 0.04 to 0.57 (median, 0.09; significantly less than median visual gain field slope, p < 0.0001).

Our estimates of the prevalence and slope of visual gain fields are substantially less than reported previously in the MST (Bremmer et al., 1997) (but see Squatrito and Maioli, 1997). Three main factors may account for this difference. First, our experimental paradigm differed fundamentally from that of Bremmer et al. (1997), who measured visual responses to planar motion stimuli that were always presented at the optimal speed, size, and retinal location for each neuron. We, however, measured heading tuning using a set of 3D optic flow stimuli that was identical for all neurons. Second, we did not vary eye position vertically, so gain fields that vary only along this dimension would have been missed in our experiments. Last, our stimuli always fully occupied a 90° × 90° head-fixed screen and, thus, subtended a different portion of the visual field at different eye positions. Larger or more peripheral receptive fields in our sample may have extended off the screen and not been fully stimulated by the optic flow when the animal fixated eccentric targets (assuming most MSTd receptive fields are anchored to the retina) (Bremmer et al., 1997; Squatrito and Maioli, 1997). Because of this limitation, our gain field results in the visual and combined (but not the vestibular) conditions must be interpreted with caution.

Neural network simulations

Given the lack of a common reference frame for visual and vestibular signals in the MSTd, we were interested in whether such a population could still successfully integrate the two cues and produce accurate estimates of heading. To approach this question, we modeled the MSTd using an architecture known as a recurrent basis function network (Deneve et al., 2001; Pouget et al., 2002; Avillac et al., 2005). In this model, a multisensory layer (known as a basis function layer) is reciprocally connected with three input layers: a head-centered (vestibular) layer, an eye-centered (visual) layer, and a layer encoding eye position (for details, see Materials and Methods). The state of the network begins with a noisy hill of activity in each of the three input layers, corresponding to a particular heading direction and eye position. Through an iterative process, the basis function layer mediates the integration of the head-centered and eye-centered inputs, resulting in units that exhibit gain fields and intermediate reference frames. Previous studies have demonstrated the ability of this model to perform nearly optimal sensory integration in the presence of noise (Deneve et al., 2001; Deneve and Pouget, 2004) and to predict the reference frames of visual and tactile signals in ventral intraparietal areas (VIPs) (Avillac et al., 2005). As described below, we have developed this model further by including simulations of our combined stimulus condition, as well as making more direct predictions of spatial reference frames based on the relative strength of visual and vestibular signals in the MSTd.

A main conclusion of previous work (Deneve et al., 2001; Avillac et al., 2005) is that the reference frame of the model units depends heavily on the relative strength of their inputs. Thus, our first goal was to map in detail the pattern of reference frames predicted by the model for a variety of input-weighting schemes. We varied the weights by manipulating two independent parameters: the VVR and EPR, corresponding to the strength of the visual and eye position inputs, respectively, relative to the vestibular inputs (see Materials and Methods). To simulate the three stimulus conditions used in our recording experiments, we restricted the initial sensory input to come from only the visual layer, only the vestibular layer, or both (eye position inputs were always present). For each simulated condition, we varied the VVR and EPR and computed the displacement index of the basis function units for each pair of ratio values.

Figure 9 A shows example tuning curves for a single basis function unit with VVR = EPR = 1.0. Each panel shows the tuning at two simulated eye positions: −27° (green curves) and +27° (blue curves). DI values for this example unit were as follows: visual, 0.7; combined, 0.5; vestibular, 0.3. There is also a clear gain field in all three conditions, as was the case for most model units. Because of the uncertainty in our neuronal gain-field measurements for the visual and combined conditions (see above), we did not perform a detailed comparison between the neuronal and model gain field properties. In Figure 9 B, mean DI of the basis function units (color-coded) is plotted as a function of VVR and EPR. The primary trend in all three conditions is a positive monotonic relationship between VVR and DI for a given value of eye position ratio, as shown previously [Avillac et al. (2005), their Fig. 8 b]. Additionally, we report here that the relative strength of the eye position inputs (EPR) has a complex influence on the relationship between the VVR and DI, and that this effect depends greatly on which input layers are active (i.e., which stimulus condition is being simulated). Because we lack a clear way to link EPR with physiological measurements, this result does not have a straightforward interpretation and we will not pursue it further here.

A striking similarity with our MSTd data emerges when examining the simulated combined condition. Combined DI in the model is generally intermediate between visual and vestibular DI, but approaches visual DI at higher values of VVR (Fig. 9 B, center and bottom). This trend is roughly consistent with our neuronal results: when VVR = 1.0, the average combined DI of the basis function units is 0.5, which is similar to the corresponding position of the regression line in Figure 7 A. Given that VVR was >1.0 for the majority of MSTd neurons (Fig. 7 A), the model correctly predicts an average combined DI that is closer to eye-centered (median, 0.79). However, unlike the model, reference frames of MSTd neurons in the visual and vestibular conditions remained roughly constant across a wide range of VVR values (Fig. 7 B).

To determine the network parameters that best matched the neuronal data as a whole, we computed the mean-squared difference between the model and neuronal DI distributions at different values of VVR and EPR (Fig. 9 C). We found that the network best matched our MSTd results when VVR and EPR were set to 1.2 and 1.1, respectively. Note, however, that the error between the model and MSTd neurons is near minimal over a range of VVR values from ∼1.0–1.5. This indicates that the reference frame properties observed in MSTd are most consistent with a network in which the visual inputs are moderately stronger on average than the vestibular inputs. Again, we must emphasize that we did not constrain the model based on our gain-field data because of the experimental limitations mentioned above. This explains the relative invariance of the mean-squared difference in DI as a function of EPR (Fig. 9 C, vertical dimension). Nevertheless, the fact that the model predicts a VVR >1.0 is qualitatively consistent with the visual dominance we observed in MSTd. The median neuronal VVR (1.86) was somewhat greater than the range expected from the model, but this value includes cells without significant vestibular tuning. Because all basis function units in the model received projections from the vestibular input layer, a more reasonable comparison is to include only those cells with significant tuning in both the visual and vestibular conditions (n = 66). For this sample, the median VVR for MSTd neurons was 1.42, which lies within the range where the model matches the data well.

Last, to make a more direct comparison between the model predictions and our neuronal data, we constructed a version of the network in which VVR for each unit was drawn from the actual distribution of VVR values found in MSTd. The resulting model DI distributions are plotted in Figure 10, showing reasonable agreement with the neural data. Unlike the similar analysis performed by Avillac et al. (2005; their Fig. 2 d,f), this procedure involved no optimization of the network whatsoever, but instead represents a direct prediction of DI based solely on the measured neuronal VVR. This parameter-free prediction matches the distribution of vestibular DI quite well, and only slightly overestimates the visual DIs.

It is important to note that the network output remains accurate across a broad range of VVR and EPR, including the values that best matched our MSTd data (Avillac et al., 2005). Thus, our simulations suggest that a neuronal population with MSTd-like tuning curves and reference frame properties could perform spatially accurate multisensory integration. Note that this does not exclude the possibility that visual and vestibular heading signals are brought into a common frame elsewhere in the brain, nor does it rule out the potential applicability of other candidate models of sensory integration. However, the simulations do support the hypothesis that robust heading perception can be derived by combining visual and vestibular signals that do not reside in the same reference frame.

Discussion

Despite the conventional wisdom that multiple sensory signals should be expressed in a common frame of reference for integration to occur, we found that the reference frames of visual and vestibular heading signals in the MSTd remain distinct. Tuning in the visual condition was predominantly eye-centered, whereas vestibular tuning was typically closer to head-centered. Several neurons in both conditions showed partial shifts with eye position and could thus be considered to represent heading in an intermediate frame. In the combined condition, reference frames varied as a function of the relative strength and congruency of visual and vestibular tuning. This result suggests that when both cues are present (a condition most similar to real self-motion), the MSTd contains a flexible representation in which the frame of reference depends on the specific relationship between the unimodal tuning properties for a given cell. To our knowledge, this is the first study to measure reference frames of spatial tuning in a multimodal stimulus condition.

Reference frame of optic flow signals: relationship to previous work

Psychophysical studies indicate that human observers can accurately judge heading from optic flow, even while making smooth pursuit eye movements that distort the flow field (Warren and Hannon, 1988, 1990; Royden et al., 1992; Banks et al., 1996). This ability implies that the neural processing of optic flow must somehow take into account the rotation of the eyes. Indeed, several authors have shown that the heading tuning of some neurons in areas MST (Bradley et al., 1996; Page and Duffy, 1999; Shenoy et al., 1999, 2002; Ilg et al., 2004) and VIP (Zhang et al., 2004) compensates for smooth pursuit eye movements. It has been argued that pursuit compensation is equivalent to a transformation of visual signals into a head-, body-, or even world-centered reference frame (Bradley et al., 1996; Ilg et al., 2004; Zhang et al., 2004). The present results suggest otherwise: although some neurons may compensate for eye velocity, we found very little compensation for eye position, meaning that the MSTd does not transform visual information into a head-centered frame during static fixation. In fact, it appears that the opposite may be happening: vestibular signals in the MSTd, on average, are partially transformed toward an eye-centered frame, a result that is recapitulated by the neural network model (Fig. 9 B, top).

Implications for multisensory integration

Integration of multiple sensory cues is important in many behavioral contexts, but it is unclear how the brain performs this integration given that visual and nonvisual signals originate in distinct spatial reference frames. An intuitive solution may be to transform signals into a common frame (Stein and Meredith, 1993; Cohen and Andersen, 2002). This would enable a neuron to encode a particular location in space (or in our case, a particular direction of self-motion) regardless of the sensory modality or the position of the eyes in the orbits. In the superior colliculus, for example, spatial alignment of response fields is required for multimodal response enhancement (Meredith and Stein, 1996), which is thought to contribute to the behavioral improvement during multisensory spatial tasks (Stein et al., 1988, 1989; Frens et al., 1995). If neurons do not use a common reference frame to encode visual and nonvisual signals, the alignment of spatial tuning will be disrupted by a change in eye-in-head position.

Our results are not consistent with the hypothesis that MSTd uses a common reference frame to encode visual and vestibular signals, but they do share several features with recent neurophysiological studies in the intraparietal sulcus (Mullette-Gillman et al., 2005; Schlack et al., 2005). These studies found that visual and auditory receptive fields in the lateral, medial, and ventral intraparietal areas exhibited a range of dependencies on eye position, revealing a continuum of reference frames from head centered to eye centered. Moreover, the correspondence between visual and auditory reference frames for individual neurons was weak at best, similar to our MSTd results. Another recent study (Avillac et al., 2005) showed that, unlike visual receptive fields, tactile receptive fields in area VIP are purely head-centered. These results imply that the visual, auditory, and tactile receptive fields of most parietal neurons cannot remain in spatial alignment for all eye positions.

The basis function modeling approach

How do we interpret the lack of a common reference frame and the prevalence of intermediate frames in multisensory cortex? It has been suggested that intermediate frames may represent a middle stage in the process of transforming signals between eye and head coordinates (Jay and Sparks, 1987; Stricanne et al., 1996; Andersen et al., 1997). If this is true, one should expect areas downstream of MSTd to encode visual and vestibular heading signals in a single frame, be it eye or head centered. Possible areas that warrant investigation include VIP (Schaafsma and Duysens, 1996; Bremmer et al., 2002), 7a (Kawano et al., 1984; Siegel and Read, 1997), and putative “vestibular” cortical areas PIVC (Grusser et al., 1990a,b) and 2v (Buttner and Buettner, 1978).

An alternative hypothesis is that broadly distributed and/or intermediate reference frames may be computationally useful. According to this view, intermediate frames may arise naturally when a multimodal brain area makes recurrent connections with unimodal areas that encode space in their native reference frame (Pouget et al., 2002). Using their modeling framework, Pouget and colleagues (Deneve et al., 2001; Deneve and Pouget, 2004) have shown that a multisensory layer expressing multiple reference frames, combined with an eye position signal, can optimally mediate the interaction between visual and nonvisual signals in the presence of noise. We examined the compatibility of this framework with our MSTd data by building a similar model consisting of three input layers (visual, vestibular, and eye position) feeding onto a multisensory layer that represents an area such as MSTd. Under conditions that mimicked the spatial tuning and reference frame properties of MSTd neurons, the network accurately performed the necessary coordinate transformations to estimate heading from visual and/or vestibular cues. Notably, when we constrained the relative input weights to follow the distribution of VVRs measured in MSTd, the resulting DI distributions were roughly consistent with the neural data (Fig. 10). This result supports the proposed connection between the relative strength of visual and nonvisual signals in a particular brain area and the spatial reference frames in which they are coded (Avillac et al., 2005).

Reference frames for multimodal stimuli

In previous studies, conclusions about the role of neuronal populations in multisensory integration have been made primarily from testing each modality in isolation (Jay and Sparks, 1987; Avillac et al. 2005; Mullette-Gillman et al. 2005; Schlack et al. 2005). However, it is important to consider that integration is only possible when stimuli are truly multimodal, as in our combined condition. Across all neurons, we found that combined DI was generally similar to visual DI, and only weakly correlated with vestibular DI. This result is consistent with our previous finding that the spatial tuning of MSTd neurons for our combined stimuli is usually dominated by the visual signals and poorly matched with vestibular tuning (Gu et al., 2006a). However, we also found that combined DI was correlated with the relative strength of the single-cue responses (VVR) (Fig. 7 A). Cells with stronger visual tuning tended to be more eye centered in the combined condition, whereas cells with stronger vestibular tuning were more intermediate or head centered. This trend was also apparent in the DI time courses (Fig. 8 B), which showed a clear drop in combined DI for low-VVR cells about halfway into the stimulus period. We speculate that this evolution of multimodal reference frames over time occurs as computations take place to combine visual and vestibular signals.

We chose to present a naturalistic combination of cues in which the visual and vestibular information specified a congruent self-motion trajectory. If instead we manipulated the stimulus parameters to equate the average single-cue response strengths (e.g., by reducing the motion coherence or intensity of the random dots), we may have seen more neurons with intermediate reference frames under the combined condition. In fact, this is precisely what the model predicts: when visual and vestibular inputs are weighted equally (VVR = 1.0), the combined DI of the basis function units is halfway between the visual and vestibular DI (Fig. 9 B). As VVR increases, combined tuning becomes more eye centered, approaching the reference frame of visual tuning. This trend was observed in our physiological results (Fig. 7 A,B). However, the model also predicts a positive correlation between DI and VVR in the visual and vestibular conditions, which we did not observe in MSTd. Thus, it appears that the reference frame of heading tuning is only influenced by relative unimodal tuning strength when both cues are present.

Combined DI was also affected by the congruency of tuning in the single-cue conditions. For congruent cells (but not opposite cells), the combined DI was typically less than the corresponding visual DI (Fig. 6 A). Furthermore, the correlation between VVR and combined DI was strongest for congruent cells (Fig. 7 A, filled black symbols). These observations are notable in light of recent preliminary evidence from our laboratory suggesting that congruent cells in MSTd represent a distinct functional class of neurons. In congruent cells, but not opposite cells, neuronal sensitivity during a heading discrimination task was greater for combined stimuli as compared with either single-cue condition, similar to behavioral performance (Gu et al., 2006b). There was also a significant positive correlation between responses to ambiguous stimuli and the monkey's choices (choice probabilities >0.5), but only for congruent cells (DeAngelis et al., 2006). Therefore, the subpopulation of MSTd neurons that contributes most to the improved behavioral performance under cue combination also exhibits more intermediate reference frames that depend strongly on relative input strength. This highlights the potential computational importance of intermediate reference frames, and suggests that a common reference frame for two modalities tested in isolation is not a prerequisite for a neural population to contribute to behavioral multisensory integration.