Health decline, aging and mortality: how are they related?

Abstract

The deterioration of human health with age is manifested in changes of thousands of physiological and biological variables. The contribution of some of such changes to the mortality risk may be small and cannot be reliably detected by existing statistical methods. A cumulative index of health/well-being disorders, which counts changes in observed variables on the way of losing health, may be an appropriate way to take the effects of such variables into account. In this paper we investigate regularities of the aging-related changes in human health/well-being/survival status described by such an index using the new version of the quadratic hazard model of human aging and mortality. We found that the shape and the location of the mortality risk, considered as a function of the introduced health-related index, changes with age reflecting the decline in stress resistance and the age-dependence of the “optimal” health/well-being status. Comparison of these results with findings from early studies using the Cox’s-like model of risk function indicates that the results are likely to describe regularities of deterioration in human health during the aging process.

Introduction

The age pattern of human mortality curve for the adult, old, and oldest old ages often serves as the demographic characteristic of the aging process. Such characterization which is partly justified by the absence of other data on aging-related changes in a human organism must be used with care. The limitations of such interpretation are discussed by Yashin et al. (2002). The presence of additional data (observed covariates) creates a potential for a more detailed characterization of forces involved in the aging-related changes, for example, by evaluating contribution of each covariate to the mortality risk using the Cox’s regression model. Such an approach is efficient when the sample size of the data is large enough to reliably estimate a high dimensional vector of regression coefficients directly relating measured variables to the risks of disease, or death, and when the hypothesis on proportionality of respective hazards is realistic. However, when contribution of each measured variable to the mortality risk is small and the sample size of the data is not large enough, it is not possible to reliably evaluate the effects of each covariate. In such cases the cumulative indices of health/well-being disorders (DIs) (also known as “frailty indices, FI”) represent a reasonable alternative. Statistical properties of such indices have been recently investigated using different survey data (Goggins et al. 2005; Kulminski et al. 2006a, b; Mitnitski and Rockwood 2006; Mitnitski et al. 2005). The results of these analyses suggest that the DIs can describe the aging-related changes in health/well-being/survival status in humans. In particular, the analyses show an accelerated increase in the average value of the DIs with age. The DIs are good predictors of death in different settings (Goggins et al. 2005; Kulminski et al. 2006a; Mitnitski et al. 2002; Mitnitski et al. 2005; Rockwood et al. 2006). It is shown (Woo et al. 2006) that the DIs can characterize the health status. The DIs are good predictors of institutionalization (Rockwood et al. 2006). It is also found that the properties of the DIs depend to a large extent on how many deficits are accumulated and to much less extent on specificity of the deficits included in their construction (Mitnitski et al. 2005; Rockwood et al. 2006).

Yashin et al. (2006) investigated properties of the DI using the modified Cox’s regression model to capture possible non-proportionality of hazard rate. The results indicate that the mortality risk may be described by the non-symmetric U-function of the DI. A surprising finding was the non-zero value of the “optimal” DI, corresponding to the minimal value of risk, as well as the age dependence of this optimal value. It was also found that the shape of the U-function of the mortality risk changed with age showing the “narrowing” pattern for the absolute mortality risk. Such age-dynamics was associated with the decline in the resistance to stress with age. In contrast, the opposite, “widening” pattern of the age dynamics was observed for the relative risk. This effect was interpreted as an increase in relative contribution of (unobserved) factors and processes associated with senescence compared to the observed DI. It would be useful to check whether these findings are the artifacts of the model used, or they reflect the properties of the processes involved in deterioration of health/well-being/survival status in humans. In this paper we apply the extended version of the quadratic hazard model (QHM) of human mortality and aging to investigate the dynamic properties of the DI constructed from the NLTCS data and evaluate its effect on the mortality risk. The results are compared with those obtained earlier using an extended version of the Cox’s regression model (Yashin et al. 2006).

Data and methods

Data: the cumulative index of health/well-being disorders (DI)

To make the results of this study comparable with those obtained using the modified Cox’s regression model (Yashin et al. 2006), we constructed the DI using the same subset of disorders (32 questions from the NLTCS detailed questionnaires). This subset is mostly similar to those assessed from the Canadian Study of Health and Aging (Mitnitski et al. 2001) including: difficulty with eating, dressing, walk around, getting in/out bed, getting bath, toileting, using telephone, going out, shopping, cooking, light house work, taking medicine, managing money, arthritis, Parkinson’s disease, glaucoma, diabetes, stomach problem, history of heart attack, hypertension, history of stroke, flu, broken hip, broken bones, trouble with bladder/bowels, dementia, self-rated health, as well as problems with vision, hearing, ear, teeth, and feet. All these disorders (called deficits) are assessed in five NLTCS waves. Following Mitnitski et al. (2001), we define the DI as an unweighted count of the number of such deficits divided by the total number of all potential deficits considered for a given person. For instance, if an individual has been administered 32 questions and responded positively (there is a deficit) to 6 and negatively (no deficit) to 24 of them, then the DI for this person will be 0.2. In this way, we avoid the problem of missing answers counting only those questions explicitly answered in a survey.

Methods

We use the same notations as in Yashin et al. (2006) for the DI and its dynamics, and use the non-symmetric quadratic hazard instead of modified Cox’s proportional hazard. We describe the individual trajectories of the DI using stochastic process Y_t, satisfying stochastic differential equation with two components describing regular and stochastic changes of this index with age (see the Appendix). In constructing the hazard rate, we took into account the evidences that the risks of death considered as functions of covariates are usually U- or J-shaped (Witteman et al. 1994). An important concern is that the U-shaped risk function may be non-symmetric. To reflect this possibility, we introduced a function f_t (see (1)) which characterizes the “optimal” trajectory of an age-dependent covariate (i.e., the DI), i.e., the trajectory for which the mortality risk is minimal. It seems at the first glance that there is no need to introduce such a function for the DI, since its “optimal” value is always likely to be zero. However, the application of the modified Cox’s regression model revealed that f_t differs from zero for both males and females, so we consider a general case to statistically verify this finding using the same data but a different model. Then, the quadratic hazard model constructed in such a way will reflect the probability of death at the age interval [t_k,t_k+1) conditionally on measurements of Y_t and survival up to age t_k. Assume that this probability, Q(_tk, Y_tk), depends only on values of Y_tk, Q(t_k, Y_tk) = 1 − e ^{− μ(t_k Y_tk)(t_k+1−t_k)}, where

$$\begin{array}{l}\mu (t_k,Y_{t_k})={\mu }_{t_k}^0+{(f_{t_k}-Y_{t_k})}^2{\mu }_{t_k}^{11}I(Y_{t_k}\le f_{t_k})\\ +{(f_{t_k}-Y_{t_k})}^2{\mu }_{t_k}^{12}I(Y_{t_k}>f_{t_k}).\end{array}$$ (1)

The possible asymmetry of the risk function is captured by the different terms which measure the contribution of the covariates’ deviations to the one or the other side from the optimal trajectory $f_t({\mu }_t^{11}\hspace{0.17em}\text{and\hspace{0.17em}}{\mu }_t^{12})$.

We also hypothesize that not only the minimum value but also the shape of this U-function may change when individuals get older. For example, one or both branches of the U-risk function may become steeper or flatter with age and this change should be unnecessarily the same for both branches. This feature is captured by the age-dependence of the introduced ${\mu }_t^{11}$ and ${\mu }_t^{12}$ functions.

The baseline hazard ${\mu }_t^0$ was estimated as a Gompertz or a logistic function. We compared 22 different models each based on different assumptions about age dynamics of the covariate Y_t and the structure of functions $f_t^1$ and f_t. The details of respective models are described in the Appendix.

Results

Potential gain in life expectancy

Similarly to the modified Cox’s model (Yashin et al. 2006), the QHM has an advantage of being consistent with the traditional mortality models used by demographers and epidemiologists. Specifically, averaging the QHM with respect to the DI, we will have the age pattern of the total mortality for the elderly described by standard demographic life tables (models QH0 or QH100, see Appendix). Estimating the QHM conditional on the DI, we will evaluate contribution of the DI into the risk of death. The important property of the QHM is that its best estimate conditional on the DI, selected as a result of comparison with other similar models, will allow also for estimation of the age pattern of the baseline mortality ${\mu }_t^0$ when Y_t = f_t, i.e., when individuals will follow an optimal trajectory. This can be achieved by eliminating the harmful effects associated with the DI due to preventive measures or by compensating interventions.

Our analysis shows that in all cases the logistic-function based models provided better estimates than the Gompertz models. The total mortality rates (1) evaluated from the NLTCS data approximated by the logistic function as well as the baseline hazard ${\mu }_t^0$ (for males and females) are shown in the upper left panel of Fig. 1.

Fig. 1.

Estimated trajectories for the quadratic hazard model (QH103) applied to the NLTCS data on cumulative indices of health/well-being disorders (DIs) for females and males. Upper left panel: baseline mortality rates (t is age) in model QH103 (denoted by “QH”) and total mortality rates in the logistic model (QH100, denoted by “logist.”) for females (F) and males (M); upper right panel: age trajectories of the DI, $f_t^1$; middle left panel: the term in the left-hand branch of the U-function, ${\mu }_t^{11}$; middle right panel: the term in the right-hand branch of the U-function, ${\mu }_t^{12}$; bottom left panel: the “optimal” age-trajectory of the DI, f_t; bottom right panel: the initial distribution of Y_t, p(Y_t1)

One can see that controlling for the DI would result in substantial reduction in the mortality rates for both sexes after age 65. This reduction gives rise to an increase in residual life expectancies after age 65 up to 23.0, and 19.2 years for females and males, respectively, compared to 15.4 and 10.5 years without such a control. That is, controlling for the DI after age 65 results in additional 7.6 and 8.7 years of life gained by females and males, respectively.

Features of homeostatic regulation

The analysis shows that the quadratic function $f_t^1$ from equation (A1) fits the data better than the linear one for both sexes that is in agreement with empirical estimates of the DI mean age patterns in the NLTCS (Kulminski et al. 2006a) and the results of the modified Cox’s regression analyses (Yashin et al. 2006). These functions estimated for males and females are shown in the upper right panel of Fig. 1. It is seen that after age 67 the female function is higher than the male one, although not substantially, that agrees with the empirical analyses of the NLTCS data (Kulminski et al. 2006a). The estimate of the initial distribution of Y_t is shown in the bottom right panel of Fig. 1. Our analysis show that the estimates of $f_t^1$ and p(Y_t1) are model insensitive, i.e., they are the same in the QHM and the modified Cox’s regression model (see Yashin et al. 2006).

The “optimal” trajectory of the DI

Surprisingly, the results of early analyses of data on the risk of death considered as a function of the DI at different ages suggested the possibility that the minimum of function f_t can be reached at non-zero trajectory of the DI. Application of the modified Cox’s regression model (Yashin et al. 2006) revealed that the best fitting linear trajectory of f_t significantly differs from zero for females and non-significantly for males. Application of the QHM to the same data resulted in zero estimates of f_t for males and non-zero f_t for females (see Tables 1 and 2). The likelihood ratio test shows that models QH103 (non-zero linearf_t) and QH106 (zerof_t) do not differ significantly for females (P = 0.19, Table 1) and are identical for males (Table 2).

Table 1.

Estimates of parameters for the quadratic hazard models QH0–QH10, QH100–QH110 applied to the NLTCS data on the DI for females

Model	Parameters															ln La	P-valuesb
	aμ0	bμ0	σ2	aμ11	bμ11	aμ12	bμ12	aY	σ0	σ1	af1	bf1 · 102	cf1 · 104	af	bf · 102
QH0	0.032	0.054														−5370.257	<0.0001
QH1	0.008	0.078		3.745	−0.06	0.645	0.008	0.383	0.146	0.121	0.195	0.447		0.033	0.109	5240.845	0.0045
QH2	0.016	0.069		0	0	1.78	0.044	0.382	0.146	0.121	0.195	0.443		0.195	0.443	5201.371	<0.0001
QH3	0.008	0.078		3.734	−0.06	0.645	0.008	0.383	0.146	0.121	0.204	0.282	0.561	0.033	0.109	5246.164	0.6748
QH4	0.01	0.077		0	0	0.724	0.016	0.383	0.146	0.121	0.195	0.447		0.052	0.316	5238.919	0.0054
QH5	0.015	0.071		0	0	1.743	0.035	0.383	0.146	0.121	0.195	0.447				5201.499	<0.0001
QH6	0.006	0.082		–	–	0.541	0.006	0.383	0.146	0.121	0.204	0.282	0.561	0	0	5244.475	0.3138
QH7	0.008	0.078		3.719	−0.06	0.645	0.008	0.37	0.145	0.122				0.033	0.109	5232.679	<0.0001
QH8	0.01	0.077		0	0	0.724	0.016	0.008	0.208	0.131	0.052	0.316		0.052	0.316	1161.610	<0.0001
QH9	0.01	0.077		0	0	0.724	0.016	0.37	0.145	0.122				0.052	0.316	5230.753	<0.0001
QH10	0.015	0.071		0	0	1.743	0.035	0.37	0.145	0.122						5193.333	<0.0001
QH100	0.032	0.054	0													−5370.257	<0.0001
QH101	0.008	0.082	0.203	4.053	−0.065	0.64	0.009	0.383	0.146	0.121	0.195	0.447		0.028	0.136	5240.933	0.0011
QH102	0.016	0.069	0	0	0	1.78	0.044	0.382	0.146	0.121	0.195	0.443		0.195	0.443	5201.371	<0.0001
QH103	0.008	0.082	0.203	4.067	−0.065	0.64	0.009	0.383	0.146	0.121	0.204	0.282	0.561	0.028	0.136	5246.252	–
QH104	0.01	0.08	0.179	0	0	0.731	0.016	0.383	0.146	0.121	0.195	0.447		0.052	0.316	5239.010	0.0023
QH105	0.015	0.071	0	0	0	1.743	0.035	0.383	0.146	0.121	0.195	0.447				5201.499	<0.0001
QH106	0.006	0.087	0.236	–	–	0.55	0.005	0.383	0.146	0.121	0.204	0.282	0.561	0	0	5244.607	0.193
QH107	0.008	0.082	0.203	4.056	−0.065	0.64	0.009	0.37	0.145	0.122				0.028	0.136	5232.767	<0.0001
QH108	0.01	0.08	0.179	0	0	0.731	0.016	0.008	0.208	0.131	0.052	0.316		0.052	0.316	1161.701	<0.0001
QH109	0.01	0.08	0.179	0	0	0.731	0.016	0.37	0.145	0.122				0.052	0.316	5230.844	<0.0001
QH110	0.015	0.071	0.022	0	0	1.743	0.035	0.37	0.145	0.122						5193.333	<0.0001

^aln L—logarithm of the likelihood function for respective models

^bP-values—P-values (the likelihood ratio test) for the null hypothesis in favor of models QHn compared to the model with the maximal likelihood (QH103)

Table 2.

Estimates of parameters for the quadratic hazard models QH0-QH10, QH100-QH110 applied to the NLTCS data on the DI for males

Model	Parameters															ln La	P-valuesb
	aμ0	bμ0	σ2	aμ11	bμ11	aμ12	bμ12	aY	σ0	σ1	af1	bf1 · 102	cf1 · 104	af	bf · 102
QH0	0.061	0.049														−3878.890	<0.0001
QH1	0.021	0.058		–	–	0.7	0.022	0.352	0.156	0.123	0.198	0.347		0	0	1240.382	0.0155
QH2	0.038	0.054		0	0	1.614	0.128	0.352	0.156	0.123	0.198	0.343		0.198	0.343	1206.117	<0.0001
QH3	0.021	0.058		–	–	0.7	0.022	0.352	0.156	0.123	0.208	0.124	0.839	0	0	1244.385	0.568
QH4	0.027	0.059		0	0	0.819	0.043	0.352	0.156	0.123	0.198	0.347		0.047	0.261	1235.077	0.0008
QH5	0.037	0.056		0	0	1.627	0.109	0.352	0.156	0.123	0.198	0.347				1205.951	<0.0001
QH6	0.021	0.058		–	–	0.7	0.022	0.352	0.156	0.123	0.208	0.124	0.839	0	0	1244.385	0.9551
QH7	0.021	0.058		–	–	0.7	0.022	0.342	0.156	0.124				0	0	1234.736	0.0006
QH8	0.027	0.059		0	0	0.819	0.043	0.023	0.217	0.133	0.047	0.261		0.047	0.261	−855.165	<0.0001
QH9	0.027	0.059		0	0	0.819	0.043	0.342	0.156	0.124				0.047	0.261	1229.431	<0.0001
QH10	0.037	0.056		0	0	1.627	0.109	0.342	0.156	0.124						1200.305	<0.0001
QH100	0.061	0.049	0													−3878.890	<0.0001
QH101	0.019	0.074	0.51	–	–	0.711	0.021	0.352	0.156	0.123	0.198	0.347		0	0	1240.545	0.0047
QH102	0.038	0.055	0.101	0	0	1.616	0.127	0.352	0.156	0.123	0.198	0.343		0.198	0.343	1206.118	<0.0001
QH103	0.019	0.074	0.51	–	–	0.711	0.021	0.352	0.156	0.123	0.208	0.124	0.839	0	0	1244.548	–
QH104	0.025	0.07	0.368	0	0	0.83	0.042	0.352	0.156	0.123	0.198	0.347		0.047	0.261	1235.202	0.0003
QH105	0.037	0.056	0	0	0	1.627	0.109	0.352	0.156	0.123	0.198	0.347				1205.951	<0.0001
QH106	0.019	0.074	0.51	–	–	0.711	0.021	0.352	0.156	0.123	0.208	0.124	0.839	0	0	1244.548	1
QH107	0.019	0.074	0.51	–	–	0.711	0.021	0.342	0.156	0.124				0	0	1234.899	0.0002
QH108	0.025	0.07	0.368	0	0	0.83	0.042	0.023	0.217	0.133	0.047	0.261		0.047	0.261	−855.040	<0.0001
QH109	0.025	0.07	0.368	0	0	0.83	0.042	0.342	0.156	0.124				0.047	0.261	1229.556	<0.0001
QH110	0.037	0.056	0	0	0	1.627	0.109	0.342	0.156	0.124						1200.305	<0.0001

^aln L—logarithm of the likelihood function for respective models

^bP–values—P-values (the likelihood ratio test) for the null hypothesis in favor of models QHn compared to the model with the maximal likelihood (QH103)

The estimates of these functions for model QH103 are shown in the lower left panel of Fig. 1. Therefore, the conclusion about non-zero optimal trajectories for females must be interpreted with caution because it might be an artifact of the model specification (the significant difference from zero in the Cox’s model becomes non-significant in the QHM). Nevertheless, both the QHM and the modified Cox’s regression model show that, at each age, there is an interval of the DI values for which there is not substantial relative increase in the mortality rate which constitutes the left branch of the U-shaped hazard function and that the range of the respective DI values increases with age. Zero estimates of f_t in the case of the QHM along with non-significant difference of f_t from zero in the case of the modified Cox’s regression model (Yashin et al. 2006), suggests that males may have different relationship between the DI and the mortality risk than females and, contrary to females, the minimum risk may be reached at zero values of DI. Statistical testing does not confirm the null-hypothesis about similarity of $f_t^1$ and f_t. This indicates that mechanisms involved in regulating processes associated with accumulation of deficits do not tend to follow the optimal trajectory f_t.

The shape of the risk function and its changes with age

Our analysis shows that the risks of death evaluated as functions of the DI are U-shaped for females and that the U-shape is non-symmetric experiencing age-related changes. Since the minimum of risk is estimated at zero DIs for males, there is only the right branch in the U-shape for males (i.e., the risk function for males is actually J-shaped). The function ${\mu }_t^{11}$ in the QHM describes how the left branch of the U-function of risk changes with age (see the middle left panel of Fig. 1). Note that since f_t = 0 for males, the function ${\mu }_t^{11}$ is shown only for females. One can see that the trajectory of ${\mu }_t^{11}$ declines with age. This means that the left branch of the U-shape of the risk function becomes flatter with age. Similarly, the function ${\mu }_t^{12}$ shows how the right branch of the U-function changes with age (see the middle right panel of Fig. 1). One can see that the trajectories of ${\mu }_t^{12}$ increase with age for both females and males. This corresponds to a narrowing of the right branch of the U-shape with age for both sexes. The trajectory of ${\mu }_t^{12}$ increases faster in males that results in a faster narrowing of the U-shape in males as compared to females.

Figure 2 shows the shaded contour maps of the estimated total mortality μ (t,Y_t) and the relative risk RR(t,Y_t) for the best fitting model (QH103, see the Appendix) applied to the NLTCS data on the DI.

Fig. 2.

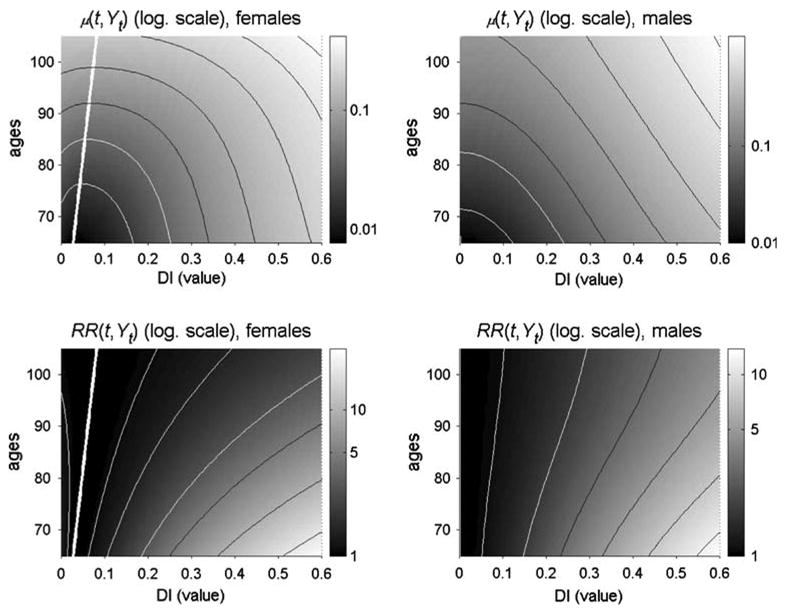
Estimated mortality rate (μ (t,Y_t)) and relative risk (RR(t,Y_t)) for the quadratic hazard model (QH103) applied to the NLTCS data on the DI. Thick white lines denote the “optimal” trajectory of the DI (f_t) (note that for males f_t = 0). Thin black and white lines correspond to different levels of μ(t,Y_t)and RR(t,Y_t)

This figure illustrates the dynamics of the total mortality and the relative risk in the QHM that is similar to that observed in the modified Cox’s regression model (see Yashin et al. 2006): the relative risks show the clear tendency to decline with age for the right branch of the risk function (and also for the left branch for females), whereas the total risk of death shows the opposite tendency and the width of the U-function of risk is getting narrower with age.

Discussion

The quadratic hazard model given by (1) has a completely different structure of the hazard rate than the extended Cox’s like model used in Yashin et al. (2006) for the analysis of the same index (see (A8) in the Appendix). In the Cox’s like model, the observed covariate Y_t and unobserved factors (represented by the baseline hazard) produce the multiplicative effect on the mortality risk. In contrast, the effects of these two groups of factors are additive in the quadratic hazard model. Despite the substantial difference in the model structure, the results of the two analyses show remarkable similarity. Both analyses show that the control for the deficits used in our study could save about 9 and 8 years of life expectancy after age 65 for males and females, respectively. Note that the constructed DI does not include all the deficits developing in an aging human organism. That is why the evaluated years to the average life expectancy may well be an underestimation of what is biologically possible.

Both studies confirm an accelerated increase in functions $f_t^1$ estimated for both sexes, which is also consistent with empirical estimates of the average age trajectory of the DI from other data (Mitnitski et al. 2005) and from the NLTCS data (Kulminski et al. 2006a). The question on interpretation of the regular component which includes the function $f_t^1$ in the stochastic differential equation for Y_t deserves a special attention. One reason is that the deficits not included in the list or deficits, which were not yet measured, may provide an important contribution to the mortality risk. Since the deficits selected to construct the DI may miss some biologically important component, the biological interpretation of changes in the DI with age requires a further study.

The properties of an index constructed as an unweighted count of measured deficits were investigated by Rockwood et al. (2006), Rockwood and Mitnitski (2006) and Kulminski et al. (2006b). It was found that the properties of the DIs depend to a large extent on how many deficits are accumulated and to much less extent on specificity of the deficits included in their construction. The underlying paradigm of the DI is that it can capture systemic effects of health deterioration by measuring a wide set of health disorders, which could reflect aging-associated physiological changes in an individual. In other words, a frail person will suffer from more distinct health problems (of any type!) than a non-frail counterpart. Then, the nature of each specific deficiency appears to be considerably less important than their aggregate ability to reflect vulnerability of a whole organism. The validity of such concept is confirmed by a number of studies in different settings (Australian, Canadian, Chinese, American) using different types and numbers of deficits to define the DI.

Finding such important properties of a simple index, however, does not exclude other approaches to study dynamic aspects of health deterioration. For example, the weighted counts of selected deficits could be more relevant when certain health events (e.g., stroke or heart attack) can make a substantial contribution to the mortality risk. Weighting may also be useful in explaining male–female difference in f_t in both models. The profiles of deficit about, for example, shopping, cooking and self-rated health can be different in males and females. Fitting a regression model to assign weights could be a good idea when the data allow for reliable evaluation of all regression coefficients. This, however, is not always the case in respective studies. One more approach could deal with introducing several indices of cumulative deficits describing disability, co-morbidity, cognitive impairment, etc.

Both analyses show that the increments of the absolute mortality risk associated with the same deviation of the DI from its “optimal” value tend to increase with age. This means that the width of respective U-function of risk gets narrower with age, indicating the aging-related decline in resistance to stress. This finding is in line with the results obtained in animal aging studies, which show a strong connection between the stress resistance and longevity, as well as the decline with age in resistance to many stresses (Semenchenko et al. 2004). These findings support the idea that resistance of human organisms to stresses induced by the increments in the DI declines with age.

Both studies capture the opposite behavior of the absolute and relative risks with increasing age. An increasing role of unobserved factors included in a baseline hazard is confirmed by the widening of the U–function of relative risk with age. It is most likely that such behavior of the age trajectories of relative risks manifests the increasing role of senescence in the total mortality compared to selected risk factors, when individuals get older. It also means that the use of constructed index does not cover all effects of senescence-related factors.

Our analysis also confirms the surprising finding (Yashin et al. 2006) that the optimal trajectory, f_t, of the DI differs from zero for females, although in the case of the QHM the difference is not significant. Nevertheless, the analysis confirms the previous observation, that there is an interval of the DI values forming the left branch of the U-shaped hazard for which there is not substantial relative increase in the mortality rate, and that the range of such DI values increases with age. The presence of this range of the index values means that the adaptation (hormesis) effects may take place: to reach the minimum of the mortality risk, organisms may need to have a non-zero value of the DI. The fact that this effect is more pronounced in females than in males (for whom it is non-significant in the case of the Cox’s model and absent in the case of the QHM) is in agreement with other observations of male/female differences, which show that females have a lower total mortality but have a higher morbidity rate than males. The causes responsible for the non-zero optimal trajectories of the DI deserve a special attention. One reason could be unobserved behavioral factors characterizing health status and affecting dynamics of the DI. For instance, the fact that a person has broken his/her bones may indicate that he/she is more physically active, is in a good physical shape, and has a relatively good potential for a long life. The person can also modify his/her behavior after acquiring a certain number of deficits, thereby reducing the mortality risk. The presence of unobserved deficits may also contribute to this effect.

In sum, the two studies performed with a simple cumulative index using different models confirm the earlier finding that this index is useful for studying dynamic aspects of the aging-related changes in a human organism. The new findings confirmed in both analyses include a non-zero optimal age trajectory of the DI, the age-related decline in resistance to stresses associated with the DI variability, sex difference in all evaluated patterns, and the fact that adaptive mechanisms responsible for the dynamics of DI do not tend to keep the DI around its optimal trajectory corresponding to the minimum of mortality risk. The similarity in the results of analyses obtained using two different models indicates that the evaluated effects are likely to be not the artifacts of particular models but reflect natural regularities of the aging-related deterioration of health/well-being/survival status in humans. These findings require further development of biological background, explaining regularities of deficits accumulation in aging human organism, and connection between observed and unobserved components of this process.

Abbreviations

DI

Cumulative index of health/well-being disorders

NLTCS

The National Long Term Care Survey

QHM

Quadratic hazard model

Appendix

General model

Let X_t, Y_t be two stochastic processes describing the life history of an individual. The process X_tk is equal to zero if an individual died in the age interval [t_k,t_k+1), and it is equal to one if he/she survived until age t_k+1. The process Y_t is a discrete time stochastic process describing observations of a health-related index (covariate). Assume that this process satisfies the following equation:

$$\begin{array}{l}{Y}_{t_{k+1}}=Y_{t_k}+a_{t_k}\left(f_{t_k}^1-Y_{t_k}\right)(t_{k+1}-t_k)\\ +{\sigma }_1\sqrt{t_{k+1}-t_k}{\epsilon }_{t_k},k>1,Y_{t_1},\end{array}$$ (A1)

where ε_tk ∼ N(0,1), $Y_{t_1}\sim N({\stackrel{\sim }{f}}_{t_1}^1,{\sigma }_0^2)$. Let ${\stackrel{\sim }{Y}}_{t_1}^{t_k}=Y_{t_1},\dots ,Y_{t_k}$, k = 1… n be a random vector of observations of the process Y_t at ages t₁,…, t_k. Denote by $Q(t_k,{\stackrel{\sim }{Y}}_{t_1}^{t_k})$ the conditional probability of death at the interval [t_k,t_k+1) of an individual given an observed trajectory ${\stackrel{\sim }{Y}}_{t_1}^{t_k}$, i.e., $Q(t_k,{\stackrel{\sim }{Y}}_{t_1}^{t_k})=P(X_{t_k}=0\mid {\stackrel{\sim }{Y}}_{t_1}^{t_k},X_{t_{k-1}}=1)$. Assume that this probability depends only on values of Y_tk as follows:

$$Q(t_k,{\stackrel{\sim }{Y}}_{t_1}^{t_k})=1-e^{-\mu (t_k,Y_{t_k})(t_{k+1}-t_k)},$$ (A2)

with μ (t_k, Y_tk) given by (A1). For the likelihood function we need conditional distributions of Y_tk given the observations ${\stackrel{\sim }{Y}}_{t_1}^{t_{k-1}}$. From (A1),

$$p\left(Y_{t_k}\mid {\stackrel{\sim }{Y}}_{t_1}^{t_{k-1}}\right)=\frac{1}{\sqrt{2\pi (t_k-t_{k-1})}{\sigma }_1}{e}^{-\frac{{\left(Y_{t_k}-{\overline{Y}}_{t_{k-1}}\right)}^2}{2(t_k-t_{k-1}){\sigma }_1^2}},$$ (A3)

where

$${\overline{Y}}_{t_{k-1}}=Y_{t_{k-1}}+a_{t_{k-1}}\left(f_{t_{k-1}}^1-Y_{t_{k-1}}\right)(t_k-t_{k-1}),$$ (A4)

for k > 2, and

$$p(Y_{t_1})=\frac{1}{\sqrt{2\pi }{\sigma }_0}{e}^{-\frac{{\left(Y_{t_1}-f_{t_1}^1\right)}^2}{2{\sigma }_0^2}}.$$ (A5)

Consider N independent observations of individuals in the above described scheme. Denote by ${\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i}$ the observed trajectories of the process Y_t for i^th individual, where n_i is the number of observations of the process Y_t for i^th individual. Let δ_i = 1 if i^th individual died in the interval $(t_{n_i}^i,t_{n_i+1}^i)$, δ_i = 0 if he/she survived until age $t_{n_i+1}^i$ and δ_i = 2 if an individual is lost to follow up at the last observation (censored at age t_niⁱ). The contribution of i^th individual into the likelihood function is

$$\begin{array}{ll}{L}_i\left({\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i},{\stackrel{\sim }{X}}_{t_1^i}^{t_{n_i}^i},{\delta }_i\right)=& P\left({\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i},{\stackrel{\sim }{X}}_{t_1^i}^{t_{n_i}^i},{\delta }_i\right)\\ & =p\left({\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i}\right)P\left({\stackrel{\sim }{X}}_{t_1^i}^{t_{n_i}^i}\mid {\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i},{\delta }_i\right)\\ & =p\left(Y_{t_1^i}\right)\prod _{k=2}^{n_i}p\left(Y_{t_k^i}\mid {\stackrel{\sim }{Y}}_{t_1^i}^{t_{k-1}^i}\right)\\ & \prod _{k=1}^{n_i-1}\left(1-Q\left(t_k^i,{\stackrel{\sim }{Y}}_{t_1^i}^{t_k^i}\right)\right)\\ & {\left(1-Q\left(t_{n_i}^i,{\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i}\right)\right)}^{I({\delta }_i=0)}\\ & Q{\left(t_{n_i}^i,{\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i}\right)}^{I({\delta }_i=1)},\end{array}$$ (A6)

where the respective probabilities are given by (A2)–(A5). The likelihood function is a product of $L_i\left({\stackrel{\sim }{Y}}_{t_1^i}^{t_{n_i}^i},{\stackrel{\sim }{X}}_{t_1^i}^{t_{n_i}^i},{\delta }_i\right)$, i = 1… N.

Application to the NLTCS data on the cumulative indices of deficits (DIs)

We applied different variants of the general model to the DIs calculated from the NLTCS data for males and females. In all models, we assumed that a_tk = a_Y and ${\mu }_t^{1j}=a_{{\mu }^{1j}}+b_{{\mu }^{1j}}(t-t_{min})$, j = 1, 2, t_min = 65. We calculated the models for one- and 2-year follow-up (the results are shown for the 1-year follow-up). That is, the observed value of the DI is assumed to be constant during the respective interval after the observation. Note also that this model assumes that we consider the fact of death only during the respective (1- or 2-year) time interval after the observation (i.e., if an individual dies within the specified time interval then he/she is considered to be dead, otherwise the individual is considered to be censored). The following models denoted as QH0-QH10, QH100-QH110 use different specifications of functions $f_t^1$ and f_t.

Model QH0

This is the model with the Gompertz mortality ${\mu }_t^0=a_{{\mu }^0}{e}^{b_{{\mu }^0}(t-t_{min})}$ without the quadratic hazard term and observations of the DI. Parameters to be estimated are: a_μ⁰ and b_μ⁰.

Model QH1

$f_t^1$ and f_t are linear functions of age, $f_t^1=a_{f^1}+b_{f^1}(t-t_{min})$ f_t = a_f + b_f(t − t_min). In all models QH1-10, we use the Gompertz mortality ${\mu }_t^0=a_{{\mu }^0}{e}^{b_{{\mu }^0}(t-t_{min})}$. In models QH1-10 and QH101-110, we estimated parameters a_μ⁰, b_μ⁰, a_μ¹¹, b_μ¹¹, a_μ¹², b_μ¹², a_Y, σ₀, and σ₁. The QH1 model-specific parameters are: a_f¹, b_f¹, a_f and b_f.

Model QH2

The same as QH1, but with equal $f_t^1$ and f_t: $f_t^1=f_t=a_f+b_f(t-t_{min})$. The QH2 model-specific parameters are: a_f and b_f.

Model QH3

$f_t^1$ is a quadratic and f_t is a linear function of age, $f_t^1=a_{f^1}+b_{f^1}(t-t_{min})+c_{f^1}{(t-t_{min})}^2$, f_t = a_f + b_f(t − tmin). The QH3 model-specific parameters are: a_f¹, b_f¹, c_f¹, a_f, and b_f.

Model QH4

The same as QH1, but with fixed f_t: $f_t=a_f^{\ast }+b_f^{\ast }(t-t_{min})$, where the parameters $a_f^{\ast }$ and $b_f^{\ast }$ were empirically estimated from the data on mortality. The QH4 model-specific parameters are: a_f¹ and b_f¹.

Model QH5

$f_t^1$ is a linear function of age, $f_t^1=a_{f^1}+b_{f^1}(t-t_{min})$, and f_t = Ŷ_t, where Ŷ_t is the trajectory of mean values of Y at ages t estimated from the data and smoothed using the moving average method with window 7. The QH5 model-specific parameters are: a_f¹ and b_f¹.

Model QH6

The same as QH3, but with fixed zero f_t. The QH6 model-specific parameters are: a_f¹, b_f¹ and c_f¹.

Model QH7

f_t is a linear function of age, ft = a_f + b_f (t − tmin), and $f_t^1={\widehat{Y}}_t$, where Ŷ_t is the trajectory of mean values of Y at ages t estimated from the data and smoothed using the moving average method with window 7. The QH7 model-specific parameters are: a_f and b_f.

Model QH8

$f_t^1$ and f_t are fixed: $f_t^1=f_t=a_f^{\ast }+b_f^{\ast }(t-t_{min})$, where the parameters $a_f^{\ast }$ and $b_f^{\ast }$ were estimated from the data on mortality.

Model QH9

$f_t^1$ and f_t are fixed: $f_t=a_f^{\ast }+b_f^{\ast }(t-t_{min})$, where the parameters $a_f^{\ast }$ and $b_f^{\ast }$ were estimated from the data on mortality, and $f_t^1={\widehat{Y}}_t$, where Ŷ_t, is the trajectory of mean values of Y at ages t estimated from the data and smoothed using the moving average method with window 7.

Model QH10

$f_t^1$ and f_t are fixed: $f_t^1=f_t={\widehat{Y}}_t$, where Ŷ_t is the trajectory of mean values of Y at ages t estimated from the data and smoothed using the moving average method with window 7.

Model QH100–110

Similar to QH0-QH10 but use the logistic baseline mortality rate

$${\mu }_t^0=a_{{\mu }^0}{e}^{b_{{\mu }^0}(t-t_{min})}/\left(1+{\sigma }_2^2\frac{a_{{\mu }^0}}{b_{{\mu }^0}}\left(e^{b_{{\mu }^0}(t-t_{min})}-1\right)\right)$$ (A7)

in place of the Gompertz mortality rate ${\mu }_t^0=a_{{\mu }^0}{e}^{b_{{\mu }^0}(t-t_{min})}$. Here σ₂ is an additional parameter to be estimated.

Extended Cox’s model

Here we briefly describe the extended Cox’s model analyzed in Yashin et al. (2006) and cited in this paper. Generally, this is the model given by (A1)–(A6) with the Cox-like proportional hazards instead of (1):

$$\mu (t,Y_t)={\mu }_0(t)e^{({\beta }_2+{\beta }_{4}t)(Y_t-f_t)I(Y_t\ge f_t)+({\beta }_3+{\beta }_{5}t)(f_t-Y_t)I(Y_t<f_t)}.$$ (A8)

Here the notations for Y_t and f_t are the same as above, I(·) is an indicator function, which equals 1, if the inequality in the parentheses is true, and 0 otherwise, β₂, β₃, β₄, and β₅ are regression coefficients. Possible asymmetry of the risk function is captured by the different regression coefficients β₂ andβ₃, which measure the contribution of the covariates’ deviations to the one or the other side from the optimal trajectory f_t. The linear dependence of regression coefficients on age allows for capturing age-related changes in the shape of the risk function.

In Yashin et al. (2006), we analyzed models Cox0–Cox10 and Cox100–Cox110, which are the respective analogues of QH0–QH10 and QH100–QH110, i.e., the models with similar specifications of $f_t^1$, f_t, a_t, and mortality rates (A8) with the Gompertz baseline hazards μ₀(t) = μ₀e^β₁t for Cox0–Cox10 and the logistic baseline hazards ${\mu }_0(t)={\mu }_0{e}^{{\beta }_{1}t}/(1+{\sigma }_2^2{\mu }_0(e^{{\beta }_{1}t}-e^{{\beta }_1{t}_{min}})/{\beta }_1)$ for Cox100–Cox110.