Cell Segmentation Using Coupled Level Sets and Graph-Vertex Coloring

Abstract

Current level-set based approaches for segmenting a large number of objects are computationally expensive since they require a unique level set per object (the N-level set paradigm), or ⌈log₂N⌉ level sets when using a multiphase interface tracking formulation. Incorporating energy-based coupling constraints to control the topological interactions between level sets further increases the computational cost to O(N²). We propose a new approach, with dramatic computational savings, that requires only four, or fewer, level sets for an arbitrary number of similar objects (like cells) using the Delaunay graph to capture spatial relationships. Even more significantly, the coupling constraints (energy-based and topological) are incorporated using just constant O(1) complexity. The explicit topological coupling constraint, based on predicting contour collisions between adjacent level sets, is developed to further prevent false merging or absorption of neighboring cells, and also reduce fragmentation during level set evolution. The proposed four-color level set algorithm is used to efficiently and accurately segment hundreds of individual epithelial cells within a moving monolayer sheet from time-lapse images of in vitro wound healing without any false merging of cells.

1 Introduction

High-throughput content screening using cell image-based assays offers a powerful new tool for understanding the chemical biology of complex cellular processes and offers opportunities for identifying new targets in drug discovery [1]. Image-based live-cell assay experiments need to image and analyze hundreds of thousands of images collected over a short period of time using automated high speed microscopy data acquisition [2]. Since tens of thousands of cells typically need to be screened, highly reliable image analysis algorithms are of critical importance. One fundamental task of automated screening systems is accurate cell segmentation that often precedes other analyses such as cell morphology, tracking and behavior. Since cells undergo complex changes during the cell division process, identifying and segmenting hundreds of closely interacting cells per frame is a challenging task. Cells are also densely clustered due to spatiotemporal sampling and instrumentation cost trade-offs. The accurate, scalable, and computationally efficient segmentation of closely grouped cells, without distinct edges, that approach, touch or overlap each other and whose nuclei become more indistinct at the start of mitosis is the focus of this paper.

Level set based image segmentation techniques [3], in comparison to other algorithms, are well suited to segment a large (unknown) number of deformable but characteristically similar objects (in terms of intensity variation), like cells. Level set methods, adapted to image sequences, are versatile and able to readily adapt to indistinct cell boundaries, appearing or disappearing cells, complex cell shape changes over time, global illumination or focus changes, background motion and non-stationary noise processes.

The two-phase Chan and Vese level set algorithm which segments an image into two sets of possibly disjoint regions, by minimizing a simplified Mumford-Shah functional [4], is ideal for the segmentation of cell image sequences or other sequences in which the intensities or textures of all foreground objects in the images are nearly the same [5]. However, if multiple cells are overlapping, touching or in close proximity to each other, level set methods will tend to merge adjacent contours into a single object (as shown in Fig. 1), which leads to difficulties when tracking individual cells. In order to prevent the merging of cells during tracking, an implicit pair-wise region-based coupling constraint was introduced within the level set and parametric snake-based segmentation frameworks by Zhang et al., [6], Dufour et al., [7] and Zimmer and Olivo-Marin [8]. The critical a priori assumption that cells do not merge (which is mostly accurate) is used to guide the curve evolution process during segmentation. Without this coupling constraint, cells that are properly segmented in previous frames may get merged with other cells in subsequent frames. The proposed graph vertex coloring (four-color) level set method uses implicit active contours, so we focus our comparison to the coupled geometric level set approach [6].

Fig. 1.

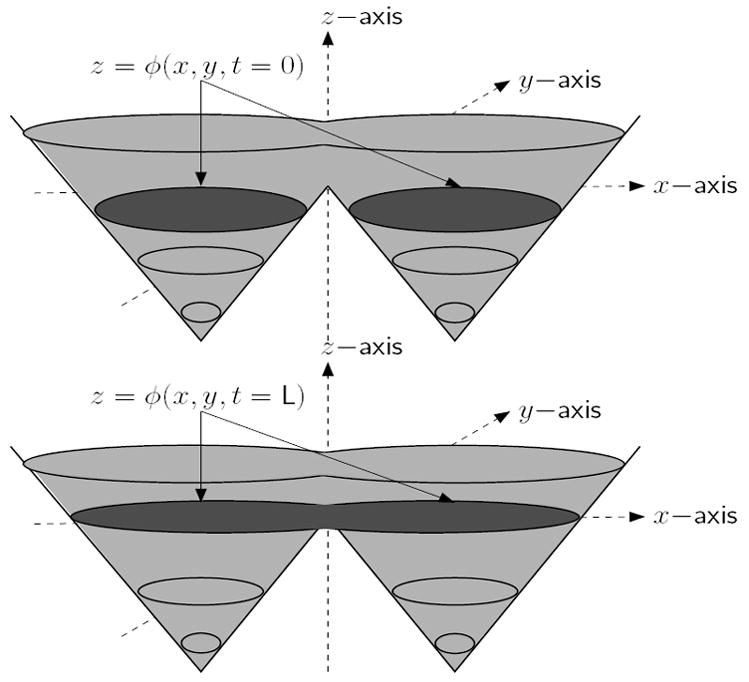
Neighboring regions get merged with a single level set

In [6], the first frame of the image sequence is segmented into N–connected components. Each object (cell) is then assigned a unique level set leading to an N–level set paradigm. These level sets are subsequently used to track the cells throughout the image sequence. The energy functional, E_nls(c_in, c_out, Φ), used to evolve N – coupled level sets, with η = 0, is shown below [6]:

$$\begin{array}{l}{E}_{\mathit{nls}}({\mathit{c}}_{\mathit{i}\mathit{n}},c_{\mathit{out}},\mathbf{\Phi })={\mu }_{in}\sum _{i=1}^N{\int }_{\mathrm{\Omega }}{(I-c_{in}^i)}^{2}H({\phi }_i)d\mathit{y}\\ +{\mu }_{\mathit{out}}{\int }_{\mathrm{\Omega }}{(I-c_{\mathit{out}})}^2\prod _{i=1}^N\left(1-H({\phi }_i)\right)d\mathit{y}+\nu \sum _{i=1}^N{\int }_{\mathrm{\Omega }}\mid \nabla H({\phi }_i)\mid d\mathit{y}\\ +\gamma \sum _{i=1}^N\sum _{j=i+1}^N{\int }_{\mathrm{\Omega }}H({\phi }_i)H({\phi }_j)d\mathit{y}+\eta \left\{\sum _{i=1}^N{\int }_{\mathrm{\Omega }}\frac{1}{2}{(\mid \nabla {\phi }_i\mid -1)}^{2}d\mathit{y}\right\}\end{array}$$ (1)

Here, Φ = { φ₁, φ₂, …, φ_N } represents N –level sets associated with N cells in the image; c_in represents the average intensities of cells for φ_i ≥ 0 while c_out is the average intensity of the background¹. The first and second terms are homogeneity measures of the foregrounds and background of all level sets. The third term controls the lengths of interfaces φ_i = 0, and minimizes the length of all level sets. The fourth term of the functional penalizes pair-wise couplings or overlaps between level sets, while the last term enforces the constraint of | ∇φ_i| = 1, thus helping us avoid explicit redistancing of level sets during the evolution process [9]. The constants μ_in, μ_out, ν, ɣ and η are weights associated with each of the terms.

However, the coupled level set algorithm of Zhang et al., is computationally expensive and scales as the square of the number of objects (cells) in the frame. Since each frame may have hundreds to thousands of cells, speed of the algorithm for high-throughput screening studies is extremely important. Trying to evolve thousands of level sets by solving thousands of separate partial differential equations with millions of coupling interaction terms is currently impractical or too expensive even using specialized hardware or parallel processing computing clusters. The number of level sets can be reduced from N to ⌈log₂N⌉ using a multiphase Vese and Chan level set segmentation algorithm, as described in [10]. However, there appears to be no mechanism to define spatial coupling constraints between the multiple phases. Each phase segments a set of objects with similar gray-level intensities. So, if two cells touch or overlap each other they will be associated with the same phase, and hence would get merged.

2 Four-Color Level Set Algorithm with Coupling Constraints

In order to improve computational efficiency, we want to take advantage of the fact that objects of interest (i.e., cell nuclei) have similar intensity characteristics. In addition, each object has only a limited number of neighbors compared to the total number of objects in the frame. We want to divide the N objects into k independent sets (or k-colors ) such that objects within each set are not neighbors, and for a given object its clique of neighbors do not share the color of the given object (i.e., are in different independent sets). Hence, in order to prevent cell merges, the first task is to assign cells into a small number of independent sets (i.e., separate colors or level sets). In this scenario:

What is the minimum number of “colors”, k, that need to be assigned, so that no two neighboring cells have the same “color”?

Representing a segmentation as a graph in which cells are vertices, and the adjacency relationships are edges, the problem can be computationally solved using graph-vertex coloring (i.e., graph chromaticity or k-coloring). For general graphs finding the minimum value of k is an NP-complete problem. However, for planar graphs, the famous “Four-Color Theorem” states that at most k = 4; any planar graph can be colored with at most four colors such that no two neighboring vertices are assigned the same color [11,12,13]. Although for some graphs k = 2, or 3, for most applications including biological cell segmentation typically k = 4. Since four level sets are sufficient for 2D cell imaging studies, we set k = 4 and do not search for a graph’s chromatic number.

Hence, we can now use Eq. 1, with N = 4 and make the coupled level set functional independent of, N, the number of objects (i.e., cells) in the image. This reduces the number of coupling terms from O(N ²) to O(1) (i.e., a constant number of six coupling terms, per level set, in the energy functional shown in Eq. 1).

Using the realistic a priori assumption that all cells in the image have very similar characteristics, enables us to assign a single average intensity c_in to all of them (i.e., ∀i, $c_{in}^i=c_{in}$). This is identical to the two-phase Chan and Vese level set algorithm with just one foreground [4], and more efficient than [6] which requires computing N average intensities.

The four Euler-Lagrange evolution equations associated with the minimization of Eq. 1 are as follows (i = 1, 2, 3, 4):

$$\begin{array}{l}\frac{\partial {\phi }_i}{\partial t}=-\delta ({\phi }_i)\{{\mu }_{in}{(I-c_{in}^i)}^2-{\mu }_{\mathit{out}}{(I-c_{\mathit{out}})}^2\prod _{j=1,j\ne \mathrm{i}}^4\left(1-H({\phi }_j)\right)\\ -\nu \hspace{0.17em}\text{div}\left(\frac{\nabla {\phi }_i}{\mid \nabla {\phi }_i\mid }\right)+\gamma \sum _{j=i+1}^{4}H({\phi }_j)\}+\eta \left\{\mathrm{\Delta }{\phi }_i-\text{div}\left(\frac{\nabla {\phi }_i}{\mid \nabla {\phi }_i\mid }\right)\right\}\end{array}$$ (2)

where, Δ is the Laplacian operator. In our implementation of the energy functional shown in Eq. 1, we use regularized Heaviside and Dirac-delta functions [4].

Computing a single average c_in for all objects helps us in randomly associating cells with different level set functions, subject to the four-color criterion being satisfied. Thus, cells associated with a “red” level set in a previous frame, can be associated with a “blue” level set in a subsequent frame. It is necessary to “re-color” the cells at the beginning of the iteration process, as positions of cells may change during the evolution process.

In addition to the energy-based coupling term of Eq. 1 to penalize overlaps between level sets, we also use an explicit topological technique to penalize such overlaps. First, we compute δ(φ_i); i ∈ [1,4]. As we use a narrow-band approach (i.e., δ(φ_i) > s_thresh ) to update the level set curves, we check the saliency of δ(φ_i) i.e., δ(φ_i) > δ(φ_j); j ≠ i to identify pixels on the front of the current level set that overlaps the narrow-band fronts of other level sets. A pixel on the front of a current level set is updated only if its saliency is highest. Topological “collisions” between adjacent cells are detected in this manner and the evolution of the associated level sets near the colliding fronts are stopped (see Fig. 3).

Fig. 3.

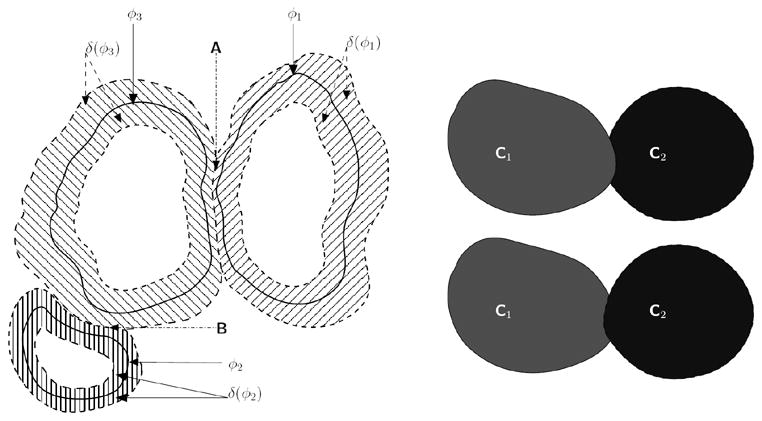
[Left]Narrow-band fronts of cells belonging to three different “colors”. The corresponding zero level set curves are given by φ₁ (“red”), φ₂ (“green”), and φ₃ (“blue”), with the narrow bands given by the region where δ(φ_i) > s_thresh. At region A, the narrow band of the “red-colored” cell intersects with the narrow band of the “blue-colored” cell. We enforce an explicit rule that the narrow band of a cell, φ_i that is currently being updated cannot overlap with a different colored cell (i.e., (φ_j)). Hence, in region A, the narrow-band of the “red-colored” cell (i.e., δ(φ₁) > s_thresh does not include those areas for which φ₃ ≥ 0. A similar rule is applied when updating the “blue-colored” cell, at region B. [Right] If a “collision” occurs between cells (i.e., δ(φ_i) = δ(φ_j), i ≠ j), then depending on which order the level sets are updated, we may get either C₁ protruding into C₂ or vice-versa.

The four-color level set segmentation algorithm is given below:

1. Initialize the segmentation process using level lines [14], and applied to the starting image. Isolate cells that may be touching or very close to each other to produce the segmentation mask (used in step 4).

2. Apply steps 3 to 8 for each frame f = 1…N

3. To speed up convergence project the segmentation mask (i.e., converged level set) from the previous frame as an initial estimate (c.f. [14, 15]).

4. Use the binary segmentation mask to extract connected components, their centroids, and associated (planar) adjacency or neighborhood graph such as the Delaunay triangulation (c.f. [16]). Apply a graph-vertex coloring algorithm (c.f. [17]) to partition the cells into four independent sets and produce a colored segmentation mask.

5. Associate one level set function with each mask color, and calculate the signed distance functions for each of the four initial zero level sets (i.e., ${\phi }_i^0$ at evolution time t = 0).

6. For each frame apply K iterations, and

   1. Update c_in and c_out;

   2. Evolve the level set within the narrow band of a cell using Euler-Lagrange equations;

   3. Enforce an explicit coupling rule that the narrow band of a cell, φ_i cannot overlap with the level set of any of its neighbors.

7. Generate a binary mask from the four-color segmentation and apply morphological filtering to remove spurious fragments.

8. Apply a spatially-adaptive level line-based coarse segmentation to the background (i.e., complement of the dilated colored segmentation mask), in order to detect objects not present in the previous frame (i.e., new objects entering the current frame).

3 Results and Analysis

The proposed algorithm was tested on a wound healing image sequence consisting 136 frames, with dimensions of 300×300 pixels (40μm×40μm). The sequence used in our simulations was obtained using a monolayer of cultured porcine epithelial cells, as described by Salaycik et al., in [18]. Images were sampled uniformly over a 9:00:48 hour period and acquired using phase contrast microscopy with a 10× objective lens, at a resolution of approximately 0.13μm per pixel. We provide two sets of results for our four-color level set algorithm with μ_in = 1, μ_out = 1, ν = 0.004, γ = 1.0, η = 0.1, while the number of iterations K is set to 10 for each frame. A qualitative comparison in Fig. 4 shows the benefit of an explicit topological coupling constraint on two representative frames (113 and 124) where cell merges are correctly prevented. A quantitative comparison in Table 1 shows the benefit of using the (energy-based and explicit) coupling constraints in preventing 46 manually verified cell merge events. Splits, merges, appearances (App.) and disappearances (Disapp.) in Table 1 were confirmed manually, since complete ground truth for such a complex sequence is difficult and time consuming to construct. Appearances and disappearances indicate cells that are not associated with cells in the previous or next frame, respectively (i.e., cells entering or leaving the frame, or cell apoptosis). Splits and merges are cells that can be associated with multiple parents or children in the trajectory, respectively (i.e., cell mitosis or cell clumping). However, segmentation artifacts or tracking mis-associations can produce any of these events. Cell splits, merges, appearances or disappearances can be due to biological events, or segmentation and tracking errors [5]. A split-merge-split cycle which is indicative of fragmentation during segmentation leads to a high score for split and merge events. The results shown in Table 1, confirm the advantage of using coupling in our four-color level set algorithm.

Fig. 4.

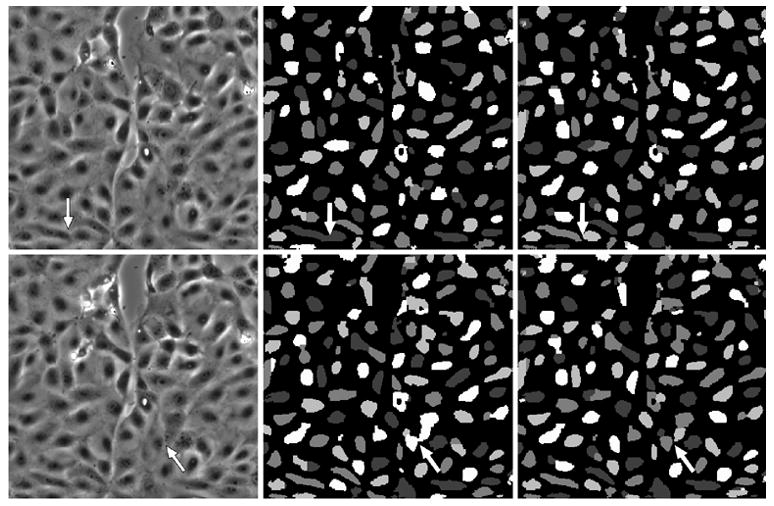
The left column indicates frame numbers 113 and 124 from the wound healing image sequence. The central column depicts segmentation results when our four level-set functional, without any explicit control on the evolution of level set functions. The right column indicates segmentation results when using our four level-set algorithm, with explicit coupling. The “color” masks are different in each frame due to a “re-coloring” process applied at the beginning of the iteration process. Images have been scaled for display purposes. The arrows in the central and right columns show where cell merge events occur.

Table 1.

Tracking results, when using the four-color level set algorithm, with and without coupling. With coupling indicates both energy-based (γ = 1.0) and explicit coupling constraints. Without coupling indicates (γ = 0) as well as no explicit coupling.

	Objects	Splits	Merges	App.	Disapp.
Uncoupled	13986	73	46	24	35
Coupled	14570	34	0	21	30

4 Conclusions

A novel four-color level set algorithm for segmenting N cells (objects) based on graph-vertex coloring was presented, using the “active contour without edges” level set coupled energy functional, combined with a new explicit topological object to object coupling constraint. The four color level set algorithm dramatically reduces the computational cost of incorporating coupling constraints to prevent cells (objects) from merging, from O(N ) level sets and O(N²) coupling constraints to O(1) level sets and O(1) coupling constraints for N objects. The reduction in the number of level sets (N to 4) and energy-based coupling constraints in the Euler-Lagrange equations (N² – N to 12), with 12 explicit topological checks per pixel makes the proposed algorithm highly scalable, and computationally resource efficient for segmenting a large number of complex shaped objects.

Fig. 2.

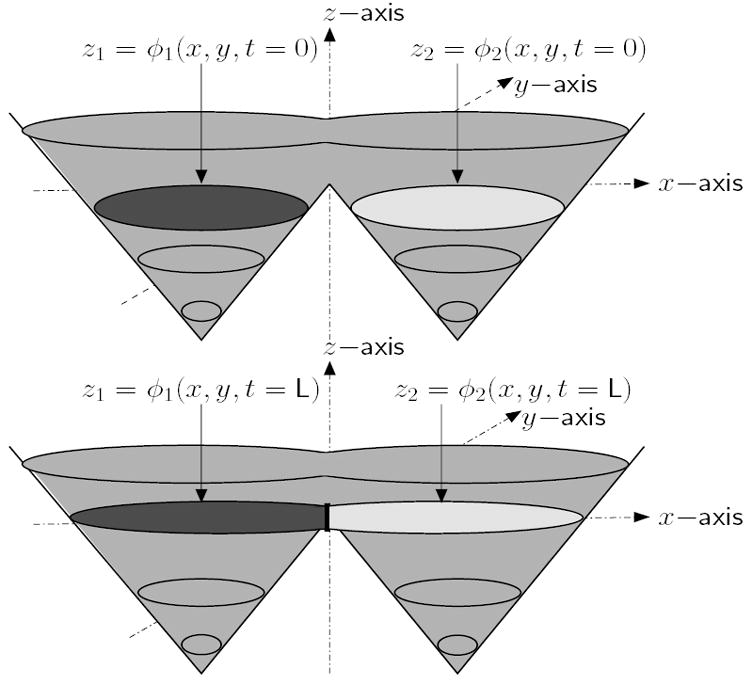
Topology of neighboring regions preserved with two coupled level sets