Evaluation of the Threshold for Lung Hemorrhage by Diagnostic Ultrasound and a Proposed New Safety Index

Abstract

In a recent report (O’Brien W.D Jr, et al. “Superthreshold Behavior of…”, J Ultrasound Med 2006; 25:873–882) it was suggested that the current expression for the mechanical index (MI) was not well suited to its function of quantifying the likelihood of an adverse biological effect following exposure of the gas-filled lung to diagnostic ultrasound. The purpose of this study was to analyze the relatively large database of experimental thresholds for the induction of lung hemorrhage to: i) determine which variable(s) best describe the data, and ii) use the resulting equation to obtain a new formulation for the MI for lung exposures. Data from fourteen studies of lung hemorrhage in four common laboratory animals (mouse, rat, rabbit, pig) were tabulated with regard to five common acoustic variables: center frequency (f_c), pulse repetition frequency (PRF), pulse duration (PD), exposure duration (ED), and the threshold in situ peak rarefactional pressure (p_r). The thirty-four threshold data points were fit by linear regression to: i) a multiplicative model of the other variables, p_r = Af_c^BPRF^CPD^DED^E, where A is a constant, ii) 14 “reduced” models in which one or more variables were not included in the analysis, iii) 4 models in which a multiplicative combination of variables has a common name e.g., duty factor, and iv) the general form of the current expression for the MI. The MI was shown to provide a poor fit to the threshold data (r² = 0.382), as were three of the four named models. The best fits were found for the complete model and for three reduced models, all of which contain the exposure duration. Because the implementation of a time-dependent safety parameter would present significant practical difficulties, a different model, p_r = Af_c^BPRF^CPD^D, was chosen as the basis for the new MI. Thus the expression for the lung-specific mechanical index, MI_Lung, includes several, rather than only one, of the relevant acoustic variables. This is the first potential safety index developed as a direct result of experimental measurements rather than theoretical analysis.

Introduction

Because of its delicate structure and its substantial number of air interfaces, which tend to intensify the interactions between ultrasound and the tissues through which it passes, lung is considered the organ having the greatest potential vulnerability for nonthermal damage by diagnostic ultrasound. This was demonstrated in the initial studies of biological effects on the lung of the mouse (Child et al. 1990). Owing to the low threshold for hemorrhage determined for the lung in that study and the need to determine the responsible mechanism, the lung has become perhaps the most researched of all organ systems. Investigations have been conducted by several different laboratories using a variety of experimental animals ranging in size from newborn mice to 60-kg pigs. Studies included monkeys (Tarantal and Canfield, 1994), mice (Child et al., 1990; Penney et al. 1993; Raeman et al. 1993, 1996; Zachary and O’Brien 1995; Dalecki et al. 1997a; O’Brien et al. 2001a), rats (Holland et al. 1996; Kramer et al. 2001; Zachary et al. 2001; O’Brien et al. 2000, 2001a, 2001b, 2002, 2003a, 2004, 2005; Frizzell et al. 2003), rabbits (Zachary and O’Brien 1995; O’Brien et al. 2006a) and pigs (Baggs et al. 1996; Dalecki et al. 1997b; O’Brien et al. 2003b).

Although some of these studies used commercial diagnostic scanners and relatively limited exposimetry, the fourteen papers analyzed in this report (see Table 1) employed standard laboratory equipment, focused transducers and reliable calibration techniques. These studies have supplied valuable information on the rate of induction of hemorrhage on the lung surface as well as on the surface area and depth of the lesions observed. In addition, most of these reports also provided estimates of the threshold for hemorrhage induction in terms of the in situ peak rarefactional pressure. Some studies have also reported a relationship between the threshold pressure and the other parameters characterizing the acoustic field, e.g., pulse duration (PD) (O’Brien et al. 2003a), or pulse repetition frequency (PRF) and exposure duration (ED) (O’Brien et al. 2005). A recent study by O’Brien et al. (2006b) has also investigated the effect of PRF and ED on the superthreshold behavior of lung hemorrhage in rats. This report is significant because the authors suggest, “a function that considers PRF, PD, and ED might yield a sensitive indicator for consideration of a modified mechanical index (MI), at least for the lung.”

Table 1.

Lung Hemorrhage Threshold Results.

Nature of Study	Animal	Frequency (MHz)	PRF (kHz)	Pulse Duration (μs)	Duty Factor (non)	Exposure Duration (s)	Total On Time (ms)	pr, in situ (MPa)
Threshold1	Mouse	2.8	1.0	1.4	0.0014	10	14	3.6
	Mouse	5.6	1.0	1.2	0.0012	10	12	3.0
	Rat	2.8	1.0	1.4	0.0014	10	14	2.3
	Rat	5.6	1.0	1.2	0.0012	10	12	2.8
Beamwidth2	Rat	2.8	1.0	1.1	0.0011	10	11	3.6
	Rat	2.8	1.0	1.1	0.0011	10	11	3.5
	Rat	5.6	1.0	1.1	0.0011	10	11	3.5
	Rat	5.6	1.0	1.1	0.0011	10	11	3.4
Age-dependence3	Pig, 5d	3.1	1.0	1.2	0.0012	10	12	3.6
	Pig, 39d	3.1	1.0	1.2	0.0012	10	12	5.8
	Pig, 58d	3.1	1.0	1.2	0.0012	10	12	2.9
Threshold4	Rabbit	5.6	1.0	1.1	0.0011	10	11	3.5
Frequency5	Mouse	3.7	0.1	1.0	0.0001	180	18	1.4
Threshold6	Rat	4.0	1.25	1.0	0.00125	90	112.5	2.0
	Rat	4.0	0.4	1.0	0.0004	90	36	2.5
Pulse Length7	Rat	2.8	1.0	1.3	0.0013	10	13	3.1
	Rat	2.8	1.0	4.4	0.0044	10	44	2.8
	Rat	2.8	1.0	8.2	0.0082	10	82	2.3
	Rat	2.8	1.0	11.7	0.0117	10	117	2.0
Frequency8	Mouse	1.1u	0.1	10.0	0.001	180	180	0.4
	Mouse	1.2	0.1	10.0	0.001	180	180	0.7
	Mouse	2.3u	0.1	10.0	0.001	180	180	0.6
	Mouse	3.5u	0.1	10.0	0.001	180	180	1.3
	Mouse	3.7	0.1	10.0	0.001	180	180	1.0
On-Time9	Mouse	1.2	0.017	10.0	0.00017	180	30.6	1.1
Threshold10	Mouse	1.0	0.1	10.0	0.001	180	180	0.4
	Mouse	1.0	1.0	10.0	0.01	2.4	24	1.5
Exposure Duration11	Mouse	2.3u	0.1	10.0	0.001	180	180	0.7
	Mouse	2.3u	0.1	10.0	0.001	20	20	0.8
Threshold12	Pig	2.3	0.1	10.0	0.001	120	120	0.9
Threshold13	Pig	2.3	0.1	10.0	0.001	120	120	0.7
Age-dependence14	Mouse, n	1.15	0.1	10.0	0.001	180	180	0.6
	Mouse, j	1.15	0.1	10.0	0.001	180	180	0.9
	Mouse, a	1.15	0.1	10.0	0.001	180	180	0.7

u = unfocused transducer; n = neonate; j = juvenile; a = adult; d = days of age;

¹Zachary et al. (2001a);

²O’Brien et al. (2001b);

³O’Brien et al. (2003b);

⁴O’Brien et al. (2006);

⁵Child et al. (1990);

⁶Holland et al. (1996);

⁷O’Brien et al. (2003a);

⁸Child et al. (1990);

⁹Raeman et al. (1993);

¹⁰Frizzell et al. (1994);

¹¹Raeman et al. (1996);

¹²Baggs et al. (1996);

¹³Dalecki et al. (1997b);

¹⁴Dalecki et al. (1997a).

The relationship of the threshold peak rarefactional pressure in situ to the other parameters characterizing the acoustic field is of interest because these threshold pressure values may be related directly to the mechanical index, one of the safety indices displayed on the screens of modern diagnostic ultrasound machines, and thus serve as a test of the index. The MI is defined as p_r.3/√f_c, the ratio of the derated peak rarefactional pressure (in MPa) to the square root of the center frequency of the acoustic wave (in MHz) (AIUM/NEMA 1992, 1998, 2004; IEC 2004); the value of the derated pressure, p_r.3, is estimated using a specific analytical model, homogeneous tissue model H.3, which assumes that attenuation coefficient has a constant value of 0.3 dB/cm-MHz (AIUM/NEMA 1992, 1998, 2004; NCRP 1992). The expression for the MI was originally developed from a theoretical formulation for the thresholds for inertial cavitation in water and blood, but it was later extended to attempt to account for all possible nonthermal mechanisms for the induction of adverse biological effects in tissue. The MI did not derive from a theoretical analysis of cavitation or other damage mechanisms in tissue, and it was not substantiated by experimental results before implementation. It is the purpose of this report to make use of the substantial database of thresholds for lung hemorrhage in laboratory animals to follow up on the suggestion of O’Brien et al. (2006b), viz., that the expression for the MI relative to lung hemorrhage might be improved by the incorporation of additional acoustic parameters. In this way, the validity of the current formulation of the MI as a predictor of the likelihood of the induction of an adverse bioeffect in patients whose lungs may be exposed to diagnostic ultrasound is evaluated, and improvements to that formulation are proposed.

Materials and Methods

Data

All of the threshold data analyzed here were taken from 14 reports on lung hemorrhage in laboratory animals published between 1990 and 2006, see Table 1. As shown in the table under “Nature of Study”, many of the studies were motivated by the desire to investigate one of several factors thought potentially to affect the threshold, e.g., the age of the animal or the acoustic beam width at the lung surface. Four laboratory animals are represented, mouse, rat, rabbit and pig. The acoustic parameters of interest and their ranges are: frequency (f_c) – 1.0–5.6 MHz; pulse repetition frequency (PRF) – 0.017–1.25 kHz; pulse duration (PD) – 1.0–11.7 μs; exposure duration (ED) – 2.4–180 s. The values of these parameters for each study used in the present analysis are listed in Table 1 and are as reported by the authors of the respective reports. It should be noted that in some cases the true value for a parameter may reasonably be expected to differ from that listed in the table (e.g., the ED for Baggs et al. 1996 and Dalecki et al. 1997b, see the discussion in O’Brien et al. 2003b), but for the purposes of the present work, we choose to accept the reported values as given by the authors. The values for the threshold peak rarefactional pressure for lung hemorrhage (p_r) are either taken directly from the studies as reported therein or represent our best estimates based on information provided in the respective studies. The criteria used by the respective researchers to determine the thresholds are similar among the studies, although they are not identical. In some cases, the ED₀₅ was used, i.e., the “effective dose” at which 5% of the exposures would induce a lesion as determined by logistic regression analysis of the experimental data (Zachary et al. 2001; O’Brien et al. 2003a). In other studies, the data were fit to a three-parameter, linear-plateau model in which the threshold is one of the parameters (Baggs et al. 1996; Dalecki et al. 1997a,b,c).

Analysis

The peak rarefactional pressure threshold values for the induction of lung hemorrhage shown in Table 1 were modeled by the following equation:

$$p_r=A{f}_c^B{\text{PRF}}^C{\text{PD}}^D{\text{ED}}^E,$$ (1)

where A is a constant, B is the exponent on the center frequency (f_c), C is the exponent on the pulse repetition frequency (PRF), D is the exponent on the pulse duration (PD), and E is the exponent on the exposure duration (ED). It is hypothesized that p_r is proportional to each of these five variables, as indicated by previous reports (O’Brien et al. 2003a, 2005, 2006b) and reviewed above. The multiplicative model for p_r in eqn (1) implies a linear regression model for the logarithm of p_r. Expressed as logarithms (to base 10) and including a term to account for random error e_random, eqn (1) becomes:

$$log{p}_r=log(A)+Blog(f_c)+Clog(\text{PRF})+Dlog(\text{PD})+Elog(\text{ED})+e_{\mathit{random}}.$$ (2)

The parameters log(A), B, C, D and E were estimated by the method of least squares using MATLAB v6.5 (The MathWorks, Natick, MA) running “mregress.m” (Reina 1998). In addition, all possible forms of eqn (2) that may be obtained by omitting any combination of one, two or three of the acoustic variables were also evaluated. For completeness, the form of the MI equivalent to eqn (2) was also evaluated, i.e.:

$$log{p}_r=log(A)+0.5log(f_c)+e_{\mathit{random}}.$$ (3)

Because program mregress.m cannot treat variable B as a fixed constant, this expression was evaluated with the user-function feature of TableCurve 2D (SPSS Inc., Chicago, IL). Evaluations were performed on dimensionless variables obtained by multiplying the values in Table 1 by constants equal to 1/(1 unit). For example, frequency data were made nondimensional by multiplying by 1/(1 MHz) such that the first entry in Table 1, 2.8 MHz, became 2.8, etc. The goodness-of-fit of each of these models was initially assessed from the values of the square of the correlation coefficient (r²), the standard error of the fit and the F-statistic.

To discriminate among the best fits found during the initial analysis, additional criteria were applied. These were the root-mean-squared (rms) errors determined on both linear and logarithmic scales:

$$\text{RMSE}(p_r)=\sqrt{\frac{1}{n}\underset{i=1}{\overset{n}{\Sigma }}{\left[{\widehat{p}}_r-p_r\right]}^2},$$ (4)

and

$$\text{RMSE}[log(p_r)]=\sqrt{\frac{1}{n}\underset{i=1}{\overset{n}{\Sigma }}log{\left[\frac{{\widehat{p}}_r}{p_r}\right]}^2},$$ (5)

respectively, where p̂_r represents the value predicted by the model.

Results

Threshold Modeling

The values of the goodness-of-fit parameters are shown in Table 2 for each of the 15 models resulting from eqn (2). In addition, the results for four named, multiplicative combinations of the four variables are included in the table, as are those for the MI. The variables used in each evaluation are given in the first column of the table, followed by the values for r², the standard error (s.e.) and the F-statistic. Also shown in column one are the names of the MI and the four linear combinations of the variables.

Table 2.

Goodness-of-fit Statistics for All Models and the MI.

Variable(s) Evaluated	(Name)	r2	s.e.	F-statistic
√fc	(MI)	0.3815	0.2556	20.352
fc		0.5030	0.2327	32.388
PRF		0.7184	0.1752	81.623
PD		0.6751	0.1881	66.488
ED		0.6422	0.1974	57.437
PRF × PD	(Duty factor)	0.0356	0.3241	1.183
PRF × ED	(Number of pulses)	0.0226	0.3263	0.741
PRF × PD × ED	(Total on time)	0.6765	0.1877	66.911
fc × PRF × PD × ED	(Number of cycles)	0.3656	0.2629	18.441
fc, PRF		0.7888	0.1541	57.906
fc, PD		0.7072	0.1815	37.429
fc, ED		0.8010	0.1496	62.378
PRF, PD		0.8160	0.1438	68.737
PRF, ED		0.7333	0.1732	42.624
PD, ED		0.8522	0.1289	89.384
fc, PRF, PD		0.8307	0.1402	49.065
fc, PRF, ED		0.8191	0.1450	45.268
fc, PD, ED		0.8729	0.1215	68.653
PRF, PD, ED		0.8546	0.1300	58.759
fc, PRF, PD, ED		0.8736	0.1233	50.085

Comparison of the values in Table 2 leads to the somewhat surprising conclusion that the current definition of the MI is a very poor model to use when attempting to predict the likelihood of an adverse effect from diagnostic ultrasound. Treating the exponent on f_c as a variable yields B = 0.98. This improves the fit to the combined data somewhat, but frequency is still the worst of the four single-variable models tested. The PRF provides the best fit to the data. This too is surprising in light of previous results indicating that the PRF has a low correlation to both threshold and superthreshold damage (Child et al. 1990; O’Brien et al. 2005).

In general, none of the four multiplicative named combinations of variables provide particularly good fits to the threshold data. This finding is contrary to previous results showing that both “Duty factor” and “Number of pulses” are correlated with both the threshold and the extent of damage for lung hemorrhage (O’Brien et al. 2006b). The “Total on time”, PRF × PD × ED, may be considered an exception to this statement, but the fit for this combination of variables is only equal to that of one its constituent parts, PD, and somewhat less than for another of its factors, PRF. Thus none of the named combinations of variables provides a sufficiently good fit to the data to be considered as a model to replace the MI.

The results for the six two-variable models investigated show that the addition of any additional variable to any of the single-variable models increases its predictive power, i.e., it’s ability to fit the threshold data. As expected based on previous results (O’Brien et al. 2006b), the combination of the PRF and the PD provides a good fit to the data. The best fit is found for the combination of PD and ED, two variables that have been shown to be significantly correlated with the occurrence of lesions on the lung surface (O’Brien et al. 2001a; 2003a).

The results for the four three-variable models show that adding a third acoustic parameter generally improves the fits still further, although the improvement is less than seen in the transition from one to two variables. The best fits are obtained by adding either f_c or PRF to the combination of PD and ED, with f_c-PRF-PD being the better of the two. In fact, the combination of f_c, PD and ED yields the smallest standard error for any model tested. In contrast, the combination of PRF, PD and ED, or total on time, shows only marginal improvement over the two-variable model of PD and ED in terms of r², and it is actually somewhat worse than PD-ED with regard to standard error.

The final model, f_c-PRF-PD-ED, contains all four variables. This is marginally better than the combination of f_c, PD and ED in terms of r² but somewhat worse in its standard error. There appears little reason to prefer one model to the other. To help resolve this dilemma, two additional statistics were investigated, linear and logarithmic versions of the rms error, see eqns (4) and (5) above. Table 3 gives the results for the four best models determined using the statistics in Table 2; the value for the MI is shown for comparison. Using these statistics, the complete model, f_c-PRF-PD-ED, is slightly better than f_c-PD-ED. However, the smallest linear rms errors are given by a different three-variable model and by a two-variable model, PRF-PD-ED and PD-ED, respectively. Because the models were actually fit using eqn (2), i.e., the logarithmic version of eqn (1), greater weight should be placed on the logarithmic rms error. Thus the complete four-variable model is selected as providing the best fit to the lung hemorrhage threshold data.

Table 3.

Additional Goodness-of-fit Statistics for the 4 Best Models and the MI.

Variable(s) Evaluated	(Name)	rms Error Linear	rms Error Logarithmic
PD, ED		0.5632	0.1231
fc, PD, ED		0.6033	0.1142
PRF, PD, ED		0.5557	0.1221
fc, PRF, PD, ED		0.5967	0.1139
√fc	(MI)	1.1632	0.2518

The estimated values and standard deviations for the five individual parameters in the “complete” model are given in Table 4. Also shown are the t-statistics and associated probabilities testing whether the estimates differ from 0. As may be seen, four of the 5 parameters are statistically significantly different from 0. Exponents D and E are both negative, indicating that the threshold decreases as either pulse duration or exposure duration increases, and their associated probabilities are small, indicating they are strongly correlated with threshold pressure. Exponent B is positive, thus the threshold increases with increasing frequency, although the effect is not as strong as for PD and ED. The exponent on PRF is not significantly different from 0, indicating that the term PRF^C in eqn (1) may be replaced by PRF⁰ = 1 without significant loss in the predictive power of the equation, an outcome that may have been anticipated from the results in Table 3. As shown in Table 5, the values of the parameters for this reduced model are essentially identical to those for the complete model.

Table 4.

The parameter estimates and standard deviations for log(p_r) in the complete model, f_c-PRF-PD-ED.

Variable	Parameter	Parameter Estimate	Standard Deviation	t-value	P-value
Constant	log(A)	0.617	0.114	5.405	8.24×10−6
log(fc)	B	0.276	0.132	2.087	0.04581
log(PRF)	C	0.040	0.101	0.398	0.69329
log(PD)	D	−0.271	0.077	−3.535	0.00139
log(ED)	E	−0.227	0.073	−3.135	0.00392

Table 5.

The parameter estimates and standard deviations for log(p_r) in the reduced model, f_c-PD-ED.

Variable	Parameter	Parameter Estimate	Standard Deviation	t-value	P-value
Constant	log(A)	0.638	0.099	6.451	3.98×10−7
log(fc)	B	0.284	0.129	2.207	0.03511
log(PD)	D	−0.284	0.069	−4.119	0.00028
log(ED)	E	−0.252	0.040	−6.253	6.89×10−7

New Mechanical Index

Based on the results of the preceding analysis, it seems both prudent and reasonably simple to suggest an improved definition of the MI for use when exposing organs containing relatively large volumes of gas, i.e., the lung. Either the complete model (f_c-PRF-PD-ED, Table 4) or reduced model (f_c-PD-ED, Table 5) would appear to offer a good starting point for the needed revision. One practical point may complicate their implementation however: the presence of the exposure duration. Because the threshold decreases with increasing ED, direct incorporation of either of these models (f_c-PRF-PD-ED or f_c-PD-ED), or of any model containing ED, into a new expression for the MI would necessarily cause the MI to become time-dependent. Further, the experiments upon which the models are based used fixed exposure geometries, i.e., they exposed a single volume of tissue for the entire extent of the ED. This is a condition rarely met in diagnostic medicine. Inclusion of ED in a new MI would thus require continuous tracking of beam direction and focal position, as well as force the development of a time-dependent safety parameter. These are difficult, if not currently intractable, problems.

Fortunately, reconsideration of Table 2 with this in mind leads to a potential solution. The three-variable model f_c-PRF-PD exhibits values for r² and standard error that are approximately as good as those of the PRF-PD-ED model, 0.8307 vs 0.8546 and 0.1402 vs 0.1300, respectively, and that are better than those of any two-variable model that does not include ED. The linear and logarithmic rms errors for the f_c-PRF-PD model are 0.6519 and 0.1317, respectively, both of which are considerably better than the corresponding values for the current MI (1.1623 and 0.2518, respectively).

The estimated values and standard deviations for the parameters in the reduced f_c-PRF-PD model are given in Table 6. Incorporating these values into eqn (1) leads to the following expression for the threshold for lung hemorrhage:

Table 6.

The parameter estimates and standard deviations for log(p_r) in the reduced model, f_c-PRF-PD.

Variable	Parameter	Parameter Estimate	Standard Deviation	t-value	P-value
Constant	log(A)	0.381	0.098	3.901	0.00050
log(fc)	B	0.242	0.150	1.614	0.11700
log(PRF)	C	0.303	0.065	4.679	0.00006
log(PD)	D	−0.235	0.086	−2.723	0.01067

$${\widehat{p}}_r=\frac{2.4f_c^{0.24}{\text{PRF}}^{0.30}}{{\text{PD}}^{0.24}}\hspace{0.17em}\text{MPa}\text{.}$$ (6)

The quality of the fit provided by this expression may be illustrated by plotting the predictions of eqn (6) vs the experimental threshold data as shown in Fig. 1. For comparison, the best fit obtainable using the expression for the MI,

Figure 1.

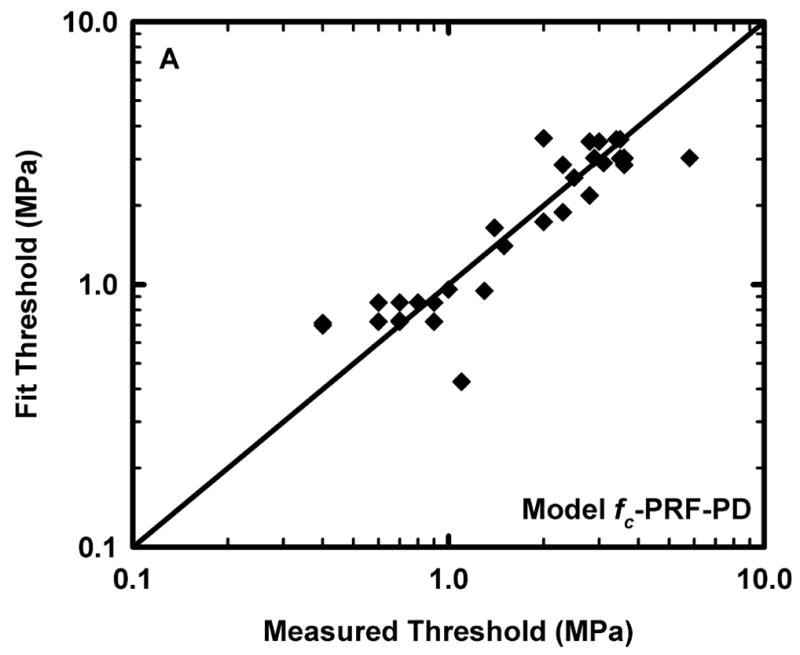
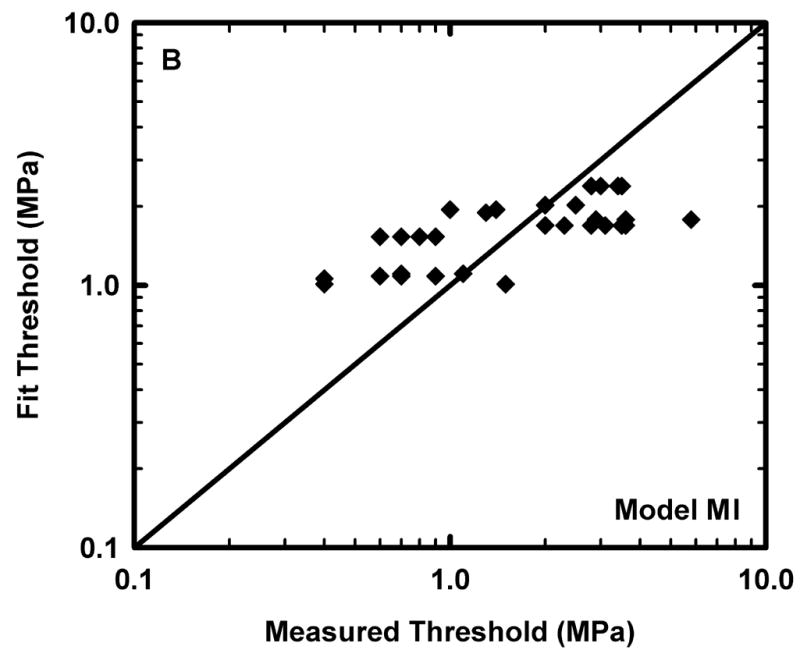
Comparison of the predicted and measured values of the threshold for lung hemorrhage for A) the reduced model, f_c-PRF-PD and B) the equivalent form of the MI. The diagonal line indicates equality between the measured and calculated values.

$${\widehat{p}}_{r,\text{MI}}=1.0f_c^{0.5}\hspace{0.17em}\text{MPa},$$ (7)

is also shown. The diagonal line in Fig. 1 indicates equality between measured values and those obtained from the respective fits. Points above the line indicate predictions greater than the measurements, while those below indicate predictions less than experimental values.

Comparison of eqns (6) and (7) shows that the form of eqn (6) is similar to the original expression developed in support of the MI (Apfel and Holland 1991) but with two additional parameters, PRF and PD. Rearranging to place all of the acoustic variables on the left-hand side produces:

$$\frac{{\widehat{p}}_r{\text{PD}}^{0.24}}{f_c^{0.24}{\text{PRF}}^{0.30}}=2.4\hspace{0.17em}\text{MPa}.$$ (8)

Because we are interested in the general functional relationship between the threshold for damage and the acoustic variables rather than the threshold itself, eqn (8) is made nondimensional by dividing by the value of the constant, 2.4 MPa. This yields the desired form for the mechanical index for lung:

$${\text{MI}}_{\text{Lung}}=\frac{p_r{\text{PD}}^{0.24}}{f_c^{0.24}{\text{PRF}}^{0.30}}.$$ (9)

Discussion

One of the goals of this study was to evaluate the validity of the current formulation of the MI as a predictor of the likelihood of the induction of an adverse bioeffect in patients whose lungs may be exposed to diagnostic ultrasound. As was shown above, the MI as presently calculated may be the worst possible approach to estimating the probability of an effect in exposed patients. Further, the acoustic frequency by itself has little predictive power for the induction of lung hemorrhage. Several significantly better models are available, and several of these have been considered as possible replacements for the MI, at least for lung exposures.

The best of the potential models for improving the MI all include the duration of exposure (ED) as one of the variables. Although it is a simple matter to formulate a new equation for the MI that includes ED, the implementation of such an expression presents several technical challenges. As noted above, incorporation of ED would necessarily cause the MI to become time-dependent. Because the threshold decreases with increasing ED (Tables 4 and 5), the displayed MI would continuously increase as an examination proceeded. The physician or sonographer would be required to direct some attention to this evolving display rather than focusing on the patient, and would also need to continuously compare the displayed value to some remembered and possibly arbitrary scale of safety. Another difficulty with including ED in the MI is that the experiments upon which the models are based used fixed exposure geometries, i.e., they exposed a single volume of tissue for the entire extent of the ED. In diagnostic medicine, the probe is frequently tilted and rotated, or simply moved from one site to another. Therefore, inclusion of ED in a new MI would require continuous tracking of probe location, beam direction and focal position, and because such an MI would be time-dependent, the display would have to be reset each time the motion stopped. A third difficulty concerns selection of which MI to display, the original or the new version. Would the scanner sense whether lung was being exposed and the display be changed automatically, or would the display be fixed based on the user’s selection of imaging mode, or would the user select the MI directly? Obviously, there is much more to this problem than simply establishing the best mathematical expression.

To simplify the process of implementation, eqn (9) was selected as the best overall expression for an MI for lung. This expression is based on eqn (6), which provides a fit to the threshold data nearly as good as the best of the remaining models. One point of concern may arise with this expression, however. As shown in Table 6, the exponent on the acoustic frequency f_c is not statistically different from 0. This result is consistent with previous results that show little correlation between threshold and frequency (O’Brien et al. 2006b). Therefore it is reasonable to ask why it should be included in the expression for the new MI, and to consider removing it.

Removing f_c from the three-variable model f_c-PRF-PD leaves the two-variable model PRF-PD. The goodness-of-fit parameters for this model, given in Table 2, show that removing f_c results in a slight decrease in the ability of the model to describe the results; the linear and logarithmic rms errors of this fit to the data are 0.6224 and 0.1373, respectively. As shown in Table 7, the values of the parameters for this reduced model are all highly statistically significantly different from 0. The quality of the fit provided by this model is illustrated in Fig. 2. Use of this model would result in the following expression for the new MI:

Table 7.

The parameter estimates and standard deviations for log(p_r) in the reduced model, PRF-PD.

Variable	Parameter	Parameter Estimate	Standard Deviation	t-value	P-value
Constant	log(A)	0.527	0.038	13.775	9.33×10−15
log(PRF)	C	0.319	0.066	4.872	0.00003
log(PD)	D	−0.207	0.076	−4.056	0.00031

Figure 2.

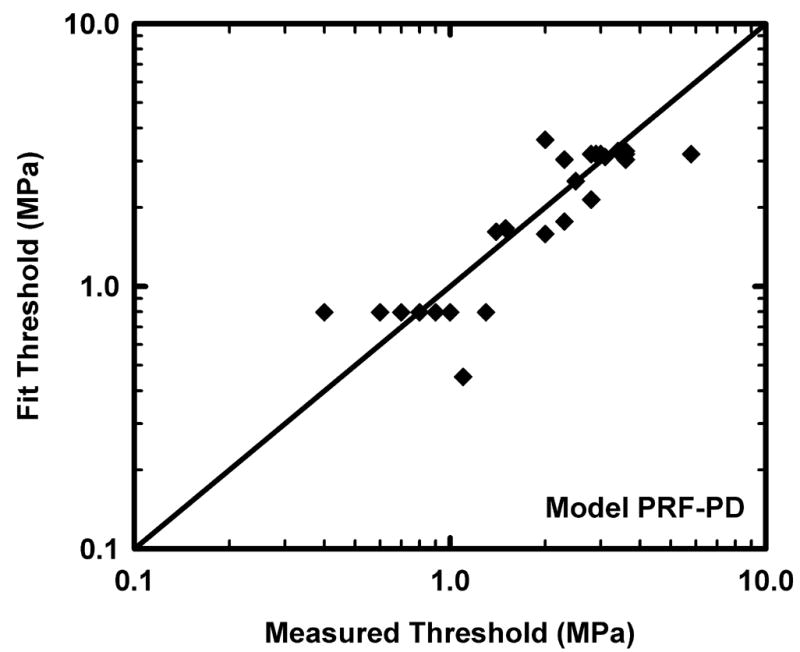
Comparison of the predicted and measured values of the threshold for lung hemorrhage for the alternative model, PRF-PD; the diagonal line indicates equality between the measured and calculated values.

$${\text{MI}}_{\text{Lung}}=\frac{p_r{\text{PD}}^{0.21}}{{\text{PRF}}^{0.32}}.$$ (10)

From a purely academic point of view, there seems little reason to prefer eqn (9) to eqn (10). However, the intention is for the expression to be used to quantify the risk of nonthermal effects resulting from exposures in humans, and such exposures result from the attempt to obtain diagnostically useful information. Removing the frequency parameter, as in eqn (10), tends to produce higher values for MI_Lung. Because this could unnecessarily limit the physician’s ability to acquire a diagnostic scan, eqn (9) is preferred.

One potentially significant parameter not considered in the analysis is the acoustic beam width. While the threshold for lung hemorrhage appears not to be a function of beam width (Child et al. 1990; O’Brien et al. 2001b), there is evidence that for superthreshold pressure amplitudes, the probability of inducing lung hemorrhage increases in a statistically significant manner as the width of the beam at the lung surface increases (O’Brien et al. 2001b). Unfortunately, too few data are available to quantify this effect in the present work. In any case, basing the suggested form for MI_Lung on the threshold for hemorrhage is consistent with the original work supporting the MI.

Although none of the studies analyzed in this report utilized diagnostic scanners, future studies on laboratory animals using well-calibrated diagnostic machines might offer a good means of testing the proposed lung-specific MI. Particularly useful would be machines which allow control of the beam width without affecting other acoustic parameters (or at least modifying them in known ways). Tightly focused beams or single scan line modes could test the proposed version of MI_Lung, while beams of increasing width could provide sufficient information to allow future modification of MI_Lung into a truly risk-based safety parameter.

Another parameter not explicitly assessed in this analysis is the imaging frame rate (FR), i.e., the rate at which visual frames are captured and/or displayed by a diagnostic scanner. Although this is really a property of the visual display, the PRF is related to the FR and the imaging modality chosen by the user. Thus FR is subsumed under PRF. However, there are some subtleties to this observation. First, the PRF examined here is not the same as the PRF sometimes displayed on the screens of diagnostic machines. Rather, the PRF in this work is the rate at which imaging pulses travel down each individual scan line. Thus for some imaging modalities, e.g., fundamental B-mode imaging, PRF = FR. Because some older imaging modes, e.g., color Doppler, and many recently developed modes, e.g., harmonic, pulse inversion, power modulation, etc., are multi-pulse techniques, this relation does not hold. A second point, one not examined in any study analyzed here, is that the rate at which pulses travel down a scan line is rarely regular. For example, a particular implementation of a pulse inversion mode may send two pulses down a line in quick succession to form one line of an image, and then not send another down the same line until the rest of the image has been formed. What effect this may have on the risk of such exposures, if any, is unknown.

Finally, it must be noted that the database lacks diversity in certain respects. As Table 1 shows, 27 of the 34 data points were taken with exposures having duty factors of 0.1 – 0.14 %, with only 3 points falling below this very narrow range and 4 points rising above it. In contrast, the thresholds reported for these 27 points are in the range 0.4 – 5.8 MPa, and the remaining 7 thresholds all lay within the same range. This may have influenced the results of the analysis in unanticipated ways. For example, it is surprising that the best combination of PD and PRF is not the product of the two, i.e., the duty factor, but rather the quotient. Based on previous results (O’Brien et al. 2006b), it was expected that duty factor would provide a very good fit to the data, but as shown in Table 2, this was not the case. In addition, neither of the fitting parameters, i.e., log (A) or the exponent on duty factor, was significantly different from 0, meaning that a simple horizontal line, p_r = 1 MPa, would fit the data as well. In retrospect, it is probably not surprising that this model cannot well account for the dependent variable when its entire range is contained within such a narrow part of relatively broad range of the independent variable. Therefore it is suggested that an additional study be undertaken to obtain thresholds for combinations of PD and PRF that are underrepresented in Table 1.

Summary

This study presents an analysis of fourteen experimental studies to determine the threshold for induction of lung hemorrhage in four common laboratory animals, mouse, rat, rabbit and pig. It was assumed that the threshold in situ peak rarefactional pressure (p_r) was a function of four acoustic variables: center frequency (f_c), pulse repetition frequency (PRF), pulse duration (PD) and exposure duration (ED). The threshold data were fit by linear regression to a multiplicative model of the four variables, p_r = Af_c^BPRF^CPD^DED^E, where A is a constant, to all other such models for which one or more of the four variables were not included, and to the general form of the current expression for the MI. The MI was shown to provide a poor fit to the threshold data, while the best fits were found for the complete model and for three others. All of the best-fitting models contain the exposure duration. Because the implementation of a time-dependent safety parameter would present significant practical difficulties, a different model, p_r = Af_c^BPRF^CPD^D, was chosen as the basis for the new, lung-specific mechanical index, MI_Lung. This is the first potential safety index developed as a direct result of experimental measurements rather than theoretical analysis.