Abstract
In both humans and experimental animals, the ability to perceive contours that are vertically or horizontally oriented is superior to the perception of oblique angles. There is, however, no consensus about the developmental origins or functional basis of this phenomenon. Here, we report the analysis of a large library of digitized scenes using image processing with orientation-sensitive filters. Our results show a prevalence of vertical and horizontal orientations in indoor, outdoor, and even entirely natural settings. Because visual experience is known to influence the development of visual cortical circuitry, we suggest that this real world anisotropy is related to the enhanced ability of humans and other animals to process contours in the cardinal axes, perhaps by stimulating the development of a greater amount of visual circuitry devoted to processing vertical and horizontal contours.
Humans and other animals process information at or near the vertical and horizontal meridians more efficiently than information projected onto the retina at oblique angles. This phenomenon—called the “oblique effect”—has been documented by differences in acuity, contrast sensitivity, orientation discrimination, and recognition rate (1, 2). In addition to humans, species as diverse as octopuses, goldfish, rats, cats, and chimpanzees show the oblique effect to some degree (2). Despite the prevalence of this perceptual bias, there is little or no consensus about how or why it occurs or what significance it has for human vision (see, for example, ref. 3).
Although contours in the visual environment obviously are distributed across the full range of orientations, it is possible that the visual system has been biased functionally and structurally by a predominance of visible contours near the cardinal axes. In fact, natural vistas have predictable frequency and chromatic characteristics (4, 5), and an earlier study using optical Fourier analysis has shown that a variety of scenes have anisotropic frequency spectra, with more power near the cardinal axes (6; see also ref. 7). Despite these intriguing reports, the distribution of oriented feature contours projected onto the retina by representative objects has never been determined in a way that would allow ready comparison of the distribution of orientations within and between different visual environments. Accordingly, we have examined a large number of real world scenes, taking advantage of recent advances in image analysis to measure the distribution of oriented projections that the visual system must process.
METHODS
To ensure an unbiased selection of scenes, we employed two naive subjects to collect representative images. The images were obtained with an automatic digital camera while the subjects walked about in three different settings: (i) indoor environments at Duke University; (ii) outdoor environments on the Duke University campus; and (iii) natural environments at Duke University (different regions of the Duke Forest, which comprises a variety of completely undeveloped terrains). In each of these settings, the subjects carried a device that produced a tone every 2 min. Each time the tone sounded, the observers took a picture of the scene confronting them at that moment. The only adjustment required was to level the tripod-mounted camera in the horizontal axis with a carpenter’s level to provide a consistent frame of reference. Thus, our subsequent analysis of the database reflects the distribution of orientations with respect to the horizon. At least 40 photographs were collected for the various settings by each observer. The digital images were reviewed, and any with technical imperfections (poor focus or low contrast) were eliminated. After this culling, 50 pictures for each of the three visual environments were randomly selected (the data obtained by each observer were represented equally).
Digital files (768 × 576 pixels) of the scenes were opened in photoshop 3.0 (Adobe Systems, San Jose, CA), and a circle 573 pixels in diameter was drawn in the center of the field; a circular mask was used to preclude any edge-effect bias. The circular scene within a featureless white background was then rescaled at 2562 pixels for subsequent analysis. Each image was processed by the Sobel direction and magnitude filters (8) in the Image Processing Tool Kit (CRC Press, Boca Raton, FL); these filters operate as plug-ins in nih image, a public domain program developed at the U.S. National Institutes of Health (9). A comparison of the Sobel and the “steerable filters” techniques for quantifying orientations (10, 11) (using computer code kindly provided by M. Gorkani, Machine Vision Group, IBM) showed that the results obtained with these two methods are similar. The Sobel filter was chosen because of its simplicity and ease of implementation.
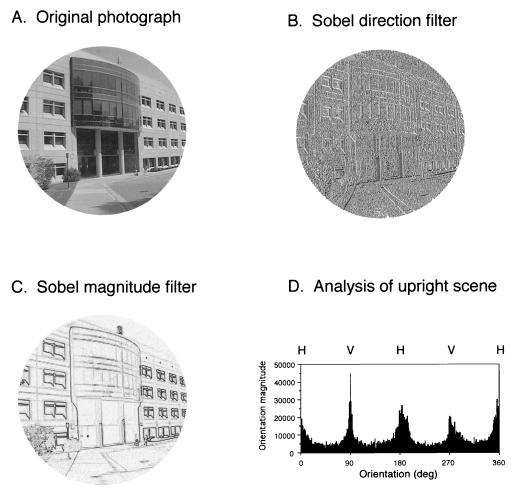
The Sobel direction filter determined the orientation of each pixel based on the direction of the local gray-scale gradient in a standard 9-pixel array; Sobel direction was calculated from the arc tangent of the partial derivative of brightness in a 3 × 3 kernel in the vertical direction, divided by this value in the horizontal direction. The Sobel magnitude filter determined the magnitude of the local gradient at each pixel, independent of orientation; Sobel magnitude was calculated from the square root of the sums of the squares of the partial derivatives of brightness in the vertical and horizontal directions. The results subsequently were exported as text files into statistical and graphics programs for analysis and display. The metric we chose for a comparison of various visual environments was the summed magnitude, i.e., the number of pixels at each particular orientation weighted by the magnitude of the gradient at that pixel. For statistical analysis, the results from 0 to 360° (the filter differentiated black to white and white to black transitions for each orientation) were collapsed to a 180° scale because 0°, 180°, and 360° represent identical orientations, as do 90° and 270°, etc. Fig. 1 illustrates these steps in the orientation analysis of a particular scene. Fig. 2 shows control observations that rule out methodological artifacts. The shifted, but otherwise similar histograms when the camera was upright (Fig. 1D) or tilted 45° (Fig. 2B), indicate that the magnitude differences are derived from the contours projected by the objects in the scene and not from any artifact associated with the analytic algorithms. A small artifact at 45° intervals is encountered in the presence of noise (e.g., extended surfaces without features) because of the kernel size (9 pixels). In the subsequent analyses (see Results), this deficiency was corrected by averaging the bins on either side of the 45° intervals to obtain values for these particular 9 bins. Fig. 2C shows an image of random noise, and Fig. 2D shows the combined analysis of 10 such images. The absence of any anisotropy in this latter control confirms that neither the algorithms nor other factors in the analysis produced spurious biases.
Figure 1.
Analysis of oriented contours in real-world scenes. (A) Digital photograph of the Neurobiology Building and its immediate surroundings at Duke University. (B) Image in A after the application of a Sobel direction filter. (C) Image in A after the application of a Sobel magnitude filter. (D) Plot of the summed pixel magnitudes, grouped by orientation. The peaks and troughs evident in the plot provide a quantitative measure of the predominance of projected contours near the vertical (V; 0/270°) and horizontal (H; 0/180°) axes in such scenes. A full 360° are shown because white to black transitions occupy half of the gray-scale, and black to white transitions occupy the other half.
Figure 2.
Control observations validating the techniques used here. (A) Same digital photograph as in Fig. 1 but tilted at a 45° angle. (B) Analysis showing that the magnitude of the orientation biases observed in Fig. 1D are similar but that their distribution is shifted by the expected amount. (C) Digital “scene” comprised of random noise. (D) Combined analysis of 10 such scenes. Note the absence of anisotropy in this control.
Technical limitations in the analysis include differences between a camera and the eye as optical systems, the inclusion of all spatial frequencies in the analysis, and the arbitrary selection of a kernel size (3 × 3 pixels). The latter two problems are mitigated by the random inclusion of pictures with focal distances ranging from <1 m to infinity. Because the results also could have been influenced by the scale of analysis, we repeated the image processing for a selected subset of the library at 5122, 1282, and 642 pixels. Although the orientation histograms were less smooth at the larger scales and comprised smaller numbers of pixels, the anisotropies we report were equally evident.
RESULTS
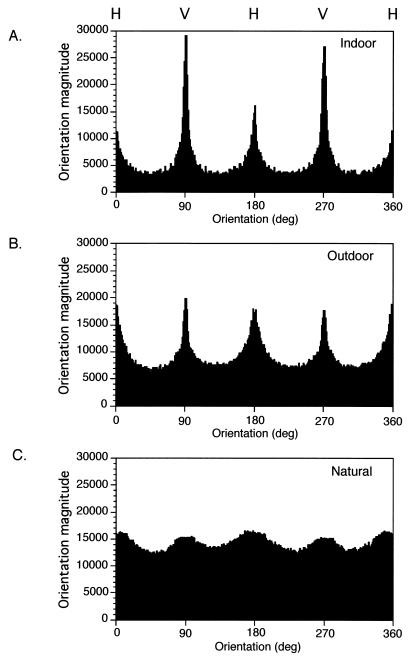
Fig. 3 shows examples of typical scenes from each setting. The distribution of orientations projected from objects in indoor scenes was strongly biased toward the cardinal axes (Fig. 3A). Indeed, simply looking at the original projections makes plain that the contours of corners, the edges of walls, windows, and doors dominate many of these images, thus biasing the distribution toward vertical and horizontal orientations. The near vertical and horizontal (±22.5°) orientation magnitudes were more than twice as strongly represented as the near oblique orientations (Fig. 4A; Table 1).
Figure 3.
Representative examples from a digitized library of 150 scenes obtained from indoor (A), outdoor (B), and entirely natural (C) environments at Duke University. The complete library of 150 digitized scenes is available on request.
Figure 4.
Distribution of oriented contours in indoor (A), outdoor (B), and entirely natural (piedmont forest) (C) environments. Each graph represents the average of the analyses of 50 representative scenes in the indicated setting. As in Fig. 1, vertical contours (V) are 90/270°, and horizontal contours (H) are 0/180°. The cardinal axes predominate, particularly in the indoor and outdoor scenes.
Table 1.
Summed magnitude values of horizontal and vertical contour projections compared with oblique angles in the four different settings analyzed
| Type of scene | Orientation | Mean ± SEM, ×1000 | P value |
|---|---|---|---|
| Indoor | Cardinal | 33.6 ± 1.70 | <0.0001 |
| Oblique | 15.5 ± 7.59 | ||
| Total | 49.16 ± 1.23 | ||
| Outdoor | Cardinal | 46.2 ± 1.95 | <0.0001 |
| Oblique | 31.2 ± 1.55 | ||
| Total | 77.49 ± 1.75 | ||
| Natural | Cardinal | 60.7 ± 1.21 | <0.0001 |
| Oblique | 53.6 ± 1.03 | ||
| Total | 114.41 ± 1.1 |
The statistical significance of the differences between the representations of contours in the cardinal axes vs. oblique angles is based on paired t tests.
A similar result was obtained for outdoor environments on the Duke campus (Fig. 3B). The projections from such scenes also were biased toward the cardinal axes, the magnitude of vertical and horizontal orientations being nearly 50% greater than the values determined for near oblique contours (Fig. 4B; Table 1). As expected, entirely natural scenes acquired in the various terrains encountered in the Duke Forest (Fig. 3C) showed a more uniform distribution of orientations. Even in this circumstance, however, near vertical and horizontal contours predominated (Fig. 4C; Table 1). Thus, the summed magnitudes of contour projections near the cardinal axes in natural scenes were ≈10% greater than the magnitudes of the projections near the right and left obliques. Because of the relatively greater complexity of natural scenes, the overall values of oriented contours weighted by their magnitude were substantially greater than in the indoor or outdoor settings. The greater summed magnitudes in outdoor and natural scenes compared with indoor scenes presumably derive from the prevalence of uniform surfaces (walls, ceilings, floors) in the latter setting. Because indoor scenes have more expanses such as walls or floors that have relatively few oriented contours (i.e., regions of the scene in which each pixel is surrounded by neighbors of similar or identical gray-scale value), there is a relative paucity of contours in this setting compared with outdoor and natural scenes.
A potential limitation of this sample of natural scenes is its provenance from a particular geographic region (the North Carolina piedmont; we assume that the indoor and outdoor scenes would be generally similar in other locations). Accordingly, an additional set of scenes was analyzed from a coastal region of North Carolina that featured marshes, dunes, beachscapes, and the maritime flora typical of the Outer Banks. The results were consistent with our original sample of natural scenes, showing a significant prevalence of vertical and horizontal contours relative to oblique angles.
The reason for a bias toward the cardinal axes in such different natural settings is presumably an omnipresent horizon dictated by the earth’s surface (which guarantees horizontal components in most scenes) and an abundance of plants that use vertical supports to counter the force of gravity and horizontal extension to capture sunlight with maximum efficiency.
DISCUSSION
Taken together, these results indicate that the oblique effect, i.e., the greater sensitivity of the visual system in humans and other animals to information oriented near the cardinal axes, accords with the biased distribution of contours projected onto the retinas from objects in the real world. What then is the link, if indeed there is one, between this aspect of visual behavior and the structure of the world with respect to oriented contours?
Several studies have addressed the anatomical and physiological basis of the oblique effect. Psychophysical tests of orientation processing using interference fringes, a technique for presenting an oriented stimulus to human subjects that essentially nullifies the optics of the eye, have shown that the cause of the oblique effect does not lie in the eye itself (12, 13). It has therefore been proposed that this asymmetrical visual behavior has its origin more centrally in the distribution and tuning properties of orientation-selective cells in primary visual cortex (14). Indeed, surveys of single-unit responses in the primary visual cortex of cat (14–17) and monkey (18, 19) have established that more neurons respond to orientations near the cardinal axes than to obliquely oriented stimuli. Moreover, vertical and horizontal stimuli evoke larger cortical potentials measured with surface electrodes than do obliquely oriented stimuli (20–23). In accord with these electrophysiological results, we recently have found that more primary visual cortex in ferrets responds to stimuli in the cardinal axes than to obliquely oriented stimuli (24). In the light of these several lines of evidence, it seems likely that the oblique effect is based on a greater amount of neural machinery devoted to the analysis of orientations near the cardinal axes.
A disproportionate allocation of cortical circuitry devoted to analyzing contours near the cardinal axes could be instantiated during phylogeny, ontogeny, or both. Although the prevalence of vertical and horizontal contours in real world scenes is consistent with either of these possibilities, the results we report here provide some encouragement to consider anew the role of normal experience in the establishment of the mature visual system. That orientation selectivity can be influenced by early experience is indicated by the phenomenon of meridional amblyopia in individuals who suffered from uncorrected astigmatism in early life (25). In such patients, some orientations are much better seen during development than others. As a result, these subjects develop a permanent inability to adequately resolve specific orientations, even when the astigmatism is fully corrected. If the quality of experience with oriented contours can affect the neural circuitry dedicated to analyzing specific orientations under these pathological circumstances, it is reasonable to imagine that a real world bias in the prevalence of oriented contours also influences the structure of the maturing brain. Further support for this view comes from recent work showing that, in the somatic sensory system at least, regions of cortex that are most active during development grow to a greater extent than less active cortical regions (26–29).
Despite this and other evidence that the environment can influence the circuitry concerned with orientation selectivity (30, 31), the influence of visual experience on the organization of cortical orientation domains is still debated. Because the development of ocular dominance columns is modified readily by early experience in cats, monkeys, and a variety of other species (32–34), it seemed likely that orientation columns would be similarly affected. However, the arrangement of orientation domains examined by optical imaging remains unchanged when mapped after vision through one eye and then the other for a prolonged period (ref. 35; see also ref. 36). Moreover, recent experiments indicate that vertical and horizontal orientation columns are detectable very soon after eye opening, implying a largely intrinsic mechanism for their formation (37, 38). The resolution of this apparently conflicting evidence may simply be that, whereas visual experience has little or no influence on the overall arrangement of cortical modules like orientation columns (or ocular dominance columns, for that matter; see ref. 39), it nonetheless has an important effect on the size of columns devoted to processing different orientations.
In summary, the results of digital scene analysis show a prevalence of contours near the cardinal axes in a wide variety of visual environments. Based on recent evidence about the effects of neural activity on cortical development, this biased experience may explain the greater ability of the adult visual system to process information about vertical and horizontal contours.
Acknowledgments
We are grateful to Len White, Darin Nelson, Larry Katz, David Fitzpatrick, Oren Yishai, and Mark Williams for helpful criticisms. This work was supported by National Institutes of Health Grant NS29187.
Footnotes
A commentary on this article begins on page 3344.
References
- 1.Appelle S. Psychol Bull. 1972;78:266–278. doi: 10.1037/h0033117. [DOI] [PubMed] [Google Scholar]
- 2.Howard I P. Human Visual Orientation. New York: Wiley; 1982. [Google Scholar]
- 3.Sekular R, Blake R. Perception. New York: McGraw Hill; 1994. [Google Scholar]
- 4.Field D J. J Opt Soc Am A Opt Image Sci. 1987;4:2379–2393. doi: 10.1364/josaa.4.002379. [DOI] [PubMed] [Google Scholar]
- 5.Burton G J, Moorhead I R. Appl Optics. 1987;26:157–170. doi: 10.1364/AO.26.000157. [DOI] [PubMed] [Google Scholar]
- 6.Switkes E, Mayer M J, Sloan J A. Vision Res. 1978;18:1393–1399. doi: 10.1016/0042-6989(78)90232-8. [DOI] [PubMed] [Google Scholar]
- 7.van der Schaaf A, van Hateren J H. Vision Res. 1996;36:2759–2770. doi: 10.1016/0042-6989(96)00002-8. [DOI] [PubMed] [Google Scholar]
- 8.Sobel I. Camera Models and Machine Perception. Aim 21. Palo Alto, CA: Stanford Artificial Intelligence Lab; 1970. [Google Scholar]
- 9.Russ J C. The Image Processing Handbook. 2nd Ed. Boca Raton: CRC Press; 1994. [Google Scholar]
- 10.Freeman W T, Adelson E H. IEEE TransPattern Anal Machine Intell. 1991;13:891–906. [Google Scholar]
- 11.Picard R W, Gorkani M. Spatial Vis. 1994;8:221–253. doi: 10.1163/156856894x00341. [DOI] [PubMed] [Google Scholar]
- 12.Campbell F W, Kulikowski J J, Leumson J. J Physiol. 1966;187:427–436. doi: 10.1113/jphysiol.1966.sp008100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mitchell D E, Freeman R D, Westheimer G. J Optical Soc Am. 1967;57:246–249. doi: 10.1364/josa.57.000246. [DOI] [PubMed] [Google Scholar]
- 14.Orban G A, Kennedy H. Brain Res. 1981;208:203–208. doi: 10.1016/0006-8993(81)90633-8. [DOI] [PubMed] [Google Scholar]
- 15.Pettigrew J D, Nikara T, Bishop P O. Exp Brain Res. 1968;6:373–390. doi: 10.1007/BF00233185. [DOI] [PubMed] [Google Scholar]
- 16.Leventhal A G, Hirsch H V B. J Neurophysiol. 1980;43:1111–1132. doi: 10.1152/jn.1980.43.4.1111. [DOI] [PubMed] [Google Scholar]
- 17.Berman N, Payne B R, Garcia-Kennedy R, Murphy E H. Invest Ophthalmol Vis Sci. 1981;20:147. [Google Scholar]
- 18.Mansfield R J W. Science. 1974;136:1133–1134. doi: 10.1126/science.186.4169.1133. [DOI] [PubMed] [Google Scholar]
- 19.Blakemore C B, Garey L J, Vital-Durand F. J Physiol (London) 1981;319:78P. (abstr.). [Google Scholar]
- 20.Mansfield R J W, Ronner S F. Brain Res. 1978;149:229–234. doi: 10.1016/0006-8993(78)90603-0. [DOI] [PubMed] [Google Scholar]
- 21.Campbell F W, Maffei L. J Physiol. 1970;207:635–652. doi: 10.1113/jphysiol.1970.sp009085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bonds A B. Exp Brain Res. 1982;46:151–154. doi: 10.1007/BF00238110. [DOI] [PubMed] [Google Scholar]
- 23.Bonds A, Casagrande V A, Norton T T, DeBruyn E J. Vis Res. 1987;27:845–857. doi: 10.1016/0042-6989(87)90001-0. [DOI] [PubMed] [Google Scholar]
- 24.Coppola D M, White L E, Fitzpatrick D, Purves D. Proc Natl Acad Sci USA. 1998;95:2621–2623. doi: 10.1073/pnas.95.5.2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mitchell D E, Freeman R D, Millodot M, Haegerstrom G. Vision Res. 1973;13:535–558. doi: 10.1016/0042-6989(73)90023-0. [DOI] [PubMed] [Google Scholar]
- 26.Riddle D, Richards A, Zsuppan F, Purves D. J Neurosci. 1992;12:3509–3524. doi: 10.1523/JNEUROSCI.12-09-03509.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Riddle D R, Gutierrez G, Zheng D, White L, Richards A, Purves D. J Neurosci. 1993;13:4193–4213. doi: 10.1523/JNEUROSCI.13-10-04193.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Purves D. Neural Activity and the Growth of the Brain. Cambridge, U.K.: Cambridge Univ. Press; 1994. [Google Scholar]
- 29.Zheng D, Purves D. Proc Natl Acad Sci USA. 1995;92:1802–1806. doi: 10.1073/pnas.92.6.1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Blakemore C, Cooper G F. Nature (London) 1970;228:477–478. doi: 10.1038/228477a0. [DOI] [PubMed] [Google Scholar]
- 31.Hirsch H V B. Cell Mol Neurobiol. 1985;5:103–121. doi: 10.1007/BF00711088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.LeVay S, Wiesel T N, Hubel D H. J Comp Neurol. 1980;191:1–51. doi: 10.1002/cne.901910102. [DOI] [PubMed] [Google Scholar]
- 33.Wiesel T N. Nature (London) 1982;299:583–591. doi: 10.1038/299583a0. [DOI] [PubMed] [Google Scholar]
- 34.Hubel D H. Eye, Brain, and Vision: Scientific American Library Series. New York: Freeman; 1988. [Google Scholar]
- 35.Gödecke I, Bonhoeffer T. Nature (London) 1996;379:251–254. doi: 10.1038/379251a0. [DOI] [PubMed] [Google Scholar]
- 36.Kim D-S, Bonhoeffer T. Nature (London) 1994;370:370–372. doi: 10.1038/370370a0. [DOI] [PubMed] [Google Scholar]
- 37.Chapman B, Bonhoeffer T. Soc Neurosci Abstr. 1994;20:214. (abstr.). [Google Scholar]
- 38.Chapman B, Stryker M P, Bonhoeffer T. J Neurosci. 1996;16:6443–6453. doi: 10.1523/JNEUROSCI.16-20-06443.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Horton J C, Hocking D R. J Neurosci. 1996;16:1791–1801. doi: 10.1523/JNEUROSCI.16-05-01791.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]