Hidden Markov Model Analysis of Multichromophore Photobleaching

Abstract

The interpretation of single-molecule measurements is greatly complicated by the presence of multiple fluorescent labels. However, many molecular systems of interest consist of multiple interacting components. We investigate this issue using multiply labeled dextran polymers that we intentionally photobleach to the background on a single-molecule basis. Hidden Markov models allow for unsupervised analysis of the data to determine the number of fluorescent subunits involved in the fluorescence intermittency of the 6-carboxy-tetramethylrhodamine labels by counting the discrete steps in fluorescence intensity. The Bayes information criterion allows us to distinguish between hidden Markov models that differ by the number of states, that is, the number of fluorescent molecules. We determine information-theoretical limits and show via Monte Carlo simulations that the hidden Markov model analysis approaches these theoretical limits. This technique has resolving power of one fluorescing unit up to as many as 30 fluorescent dyes with the appropriate choice of dye and adequate detection capability. We discuss the general utility of this method for determining aggregation-state distributions as could appear in many biologically important systems and its adaptability to general photometric experiments.

I. Introduction

In the past decade, single-molecule measurements have become an important technique for studying complex biochemical systems.^1,2 The field of single-molecule research is not strictly limited to measurements of one molecule but also includes multimolecular single active units as they function in some local environment (e.g., a dilute solution, polymer matrix, or the interior of a living cell). Some recent examples include enzyme^3,4 and ligand-binding⁵ dynamics, peptide-^6,7 and protein-folding⁸ dynamics, and molecular-⁹ and self-assembly.¹⁰

The sensitivity of single-molecule measurements has revealed aggregation that would be undetected in traditional measurements.^11,12 When the goal is to measure a single molecule, it is important to be able to distinguish aggregates of various orders so as to properly partition them in the analysis. Since photobleaching of the dyes serves as a verification of the presence of discrete fluorescing units, repeated photobleaching of multiple dyes will provide evidence of the number of dyes present in an aggregate. In some cases, aggregation of molecular systems is the focus of the experiment and the ability to quantify aggregation is of the utmost importance.^11–13

Fluorescence intermittency results from photophysical or photochemical transitions between emitting or “bright” states and nonemitting or “dark” states. Fluorescence intermittency is problematic because the photons deliver all the information about the system to the observer.¹⁴ When a molecule transits to a nonfluorescent state, no information is delivered about that state. From this point of view, photoblinking and photobleaching are indistinguishable as no dark state can provide information in photon detection experiments. However, since in photoblinking the molecule later returns to a fluorescent state, the distribution of dwell times in the nonfluorescent state can provide information regarding the nature of dark state(s) and can potentially distinguish multipath recovery.^3,15 In principle, it is possible to use this methodology to distinguish multiple dark states that are attributed to various damaged states of fluorescent probes.¹⁶

The dark state dwell times coupled with the identification of the preceding (prior) and succeeding (posterior) bright states are the only information that can provide knowledge about the dark states. Sorting the dwell-time distributions by prior and posterior states can limit the kinetic schemes, however this approach requires a large number of observations of dark states for each possible pair of prior and posterior states. Nevertheless, it is the information (from photons) that is obtained from the bright states that permits any inference about the dark states. Therefore, under certain circumstances, intermittency can be viewed as an advantage rather than an inherent problem for single-molecule fluorescence measurements. For example, the discretized loss of fluorescence is considered one of the standard pieces of evidence that the system under observation is a single fluorescent unit. In another example, the fluorescence of an oxazine dye was transiently interrupted by contact with a quencher attached to the other end of a peptide such that the intermittency itself provided the source of the dynamical information.¹⁷ Analysis of intermittency has also been used to learn about the electronic states of semiconductor quantum dots.¹⁸

The full potential of single-molecule experiments is realized when a state-to-state trajectory can be reconstructed from the data. This trajectory consists of transitions between states and dwell times within the states. The state-to-state trajectory allows greater kinetic detail to be inferred from the measurement of the time evolution of the system. Single-molecule spectroscopy simplifies the interpretation of the time evolution of a system because of the tractable state space, Z, that is present. If one is interested in extending the reach of “single” molecule (single-state) measurements to multiple molecules, then it is important that the number of states be reasonable. Models must be simple enough that the state space remains tractable but still adequately describes the underlying dynamics being studied.

If a single molecule has s states, then a distinguishable pair of molecules has Z = s² states. An indistinguishable pair has $Z=s^2-{\mathrm{\Sigma }}_{i=1}^{s-1}$ i states. In general, a system of N molecules with s states per molecule has states totaling

$$Z=\{\begin{array}{l}{s}^N,\text{distinguishable}\\ \left(\begin{array}{c}N+s-1\\ s-1\end{array}\right),\hspace{0.17em}\text{indistinguishable}\end{array}$$ (1)

This leads to an astronomical number of states for a system of many particles and many states. Even for systems with small numbers of available states, there will be a finite number of particles for which it will no longer be practical to attempt to approach analysis using the state-to-state trajectory paradigm because the information from the photon stream will not be adequate to distinguish between the states.¹⁴ By comparison, in a bulk measurement, one observes the ensemble average of this state space and typically will observe the properties of the state(s) of maximum multiplicity. One strategy, therefore, for multiple-molecule state-space reduction is to focus on the states of maximum multiplicity to simplify the interpretation of the dynamics.

Hidden Markov models (HMMs) have been extensively used in diverse fields such as speech recognition, bioinformatics, neuroscience, climatology, and finance, resulting in the rapid development of flexible methodology for their treatment.^19–25 We have previously reported the application of hidden Markov models to the “two-color problem” where a molecule fluctuates between two states that can be distinguished based on the color of the fluorescence.²⁶ In that work, it was observed that estimation of two-state kinetic parameters was robust even in the presence of considerable background and spectral crosstalk in the data and for kinetic rates comparable to the photon count rates. We introduced simple model selection methods that showed that the presence of “non-Markovian” two-state dynamics could be detected and justified statistically. Application of hidden Markov models to single-molecule photon counting experiments extracts maximal information from the photon data stream. When properly implemented, HMM analysis uses all the information from the photons prior and posterior to a given photon to make its state assignment.^14,26

In the present work, we exploit the intermittency of fluorescent probes in the analysis of multichromophoric experimental data. Our interest in discrete chromophore counting is motivated by the many important systems that self-assemble from simpler subunits. Our current applications are counting the number of dyes and trajectory reconstruction in the presence of intermittency for a multiply labeled polymer, however, the technology is readily applicable to other systems. Dendritic chromophores have generated interest for photonics applications.²⁷ Light harvesting complexes have multiple chromophores that behave as a strongly coupled system.²⁸ Many biological assemblies involve multiple copies of the same protein. Tubulin assembles to form microtubules;²⁹ crystallin forms transparent materials in the eye;³⁰ the bovine liver enzyme monoamine oxidase B self-regulates based on its oligomerization state;³¹ chromosomes have many copies of histone proteins;³² viruses self-assemble multiple copies of their capsid proteins;³³ and the aggregation of misfolded proteins and peptides into cross-β amyloid fibrils is implicated in many common diseases.¹³

We begin with a discussion of our input model, its assumptions, and methods for initializing the model parameters for HMM analysis. Next, we report the results of experimental photobleaching trajectories for dextran conjugated with multiple 6-carboxy-tetramethylrhodamine dyes analyzed using HMM and discuss the resolution of this technique. Then, we show via information theory and Monte Carlo simulations the extendibility and limits of this methodology. The limits are derived in terms of the dye quality factor, η, equal to the required number of photons detected prior to photobleaching, required to distinguish one dye blinking in the presence of varying numbers of identical fluorophores. We use results from bulk control experiments to support our model assumptions and discuss when these assumptions become invalid, that is, when a more complicated model is required to reconstruct the photon trajectory. We indicate some possible applications of this technique. Finally, we compare our technique to other methods in the current literature.

II. Materials and Methods

A. Samples and Preparation

Dextran conjugates were obtained from Invitrogen Molecular Probes (Eugene, OR) with molecular weights of 70 kD and 2000 kD. The former weight consisted of two separate conjugates with 3.8 (catalog # D-1818) and 5.8 (catalog # D-1819) mole and the latter 58 (catalog # D-7139) mole of tetramethylrhodamine (TMR) per mole of dextran. Steady-state excitation and emission spectra and fluorescence lifetimes of bulk TMR-labeled dextran solutions were taken for concentrations varying from micro- to millimolar to observe possible concentration-dependent effects. All bulk measurements were made on ~1 mL of sample solution. For single-molecule measurements, the conjugates were dissolved in 0.2 μm filtered HPLC water or HPLC methanol (Fisher Scientific, Pittsburgh, PA) and diluted to approximately 10 pM. Glass coverslips used for sample substrates were prepared in a standard solvent cleaning (SC-1) bath.³⁴ The SC-1 protocol is 10:1:1, H₂O/NH₄OH/30% H₂O₂ at 125 °C. The coverslips were rinsed with HPLC water and dried for immediate use. The cleaned substrates were imaged with the single-molecule microscope to verify the absence of any preexisting fluorescent particulates. A 5–20 μL aliquot of dextran solution was then applied to the coverslip.

B. Time-Correlated Single Photon Counting

An 80.00000 MHz Spectra-Physics Ti:Sapphire laser was operated at 1028 nm with a Gires-Tournois interferometer to control the spectral bandwidth and provide nearly Gaussian 12 ps fwhm pulses as measured from deconvoluting second harmonic-detected autocorrelation. The vertically polarized pulse train was sent through an acousto-optic modulator (Con Optics model 360–80) to pulse select for a pulse spacing of i × 12.50 ns with i = 2,3,4 and then frequency doubled to 514 nm by a type I second harmonic generating β-barium borate crystal (CSK Optronics, Culver City, CA).

For bulk solutions, the horizontally polarized, frequency-doubled beam was directed through a half-wave plate and a Glan-Thompson polarizer. The resulting vertically polarized light was incident upon a sample cuvette with a 1 cm optical path. Fluorescence was collected at 90° to the excitation path with a 50 mm biconvex lens and passed through a matched, second Glan-Thompson polarizer (set at 0°, 90°, or 54.7° to determine anisotropy). The polarized signal was scrambled with a quartz depolarizer (Optics for Research) to avoid the polarization dependence of the grating transmission and passed into an Acton Research Corporation SP-150 monochromator with entrance and exit slits set to 1.0 mm to limit the detected bandwidth to 5.0 nm. Photon arrival times were determined with a Hamamatsu microchannel plate (MCP) and a Becker-Hickl SPC-630 correlator using Becker-Hickl SPCM software. The instrument response function typically had a full-width at half-maximum (fwhm) of ~50 ps. TCSPC data collection was performed to up to numerical overflow of the photon counting board (65 535 photon peak count).

For single-molecule measurements, the frequency-doubled laser light was transformed to circular polarization with a quarter-wave plate (CVI Laser, model, QWPM-515-05-4-R10) and focused to a diffraction-limited spot via a 60X, NA 1.4 Olympus oil-immersion objective model (UIS2-PLAPON-60XO). A closed-loop nanopositioning stage (Mad City Labs–nano-bio) provided imaging capability with 3 nm digitally addressable resolution. The fluorescence emission was collected using the same objective, redirected using a dichroic mirror (Omega Optical, model, 540 DCLP), and filtered using bandpass (OptoSigma, models, 079-3360 and 079-4490)) and notch (Kaiser Optical, model: JSPF-514.5-1.0) filters to collect only the wavelength range of TMR emission (550–650 nm) and reject the excitation wavelength of 514 nm, respectively. Finally, a polarizing cube separated the emission into vertical and horizontal polarization components incident upon separate avalanche photodiodes (PerkinElmer, model SPCM-AQR-15) with a dark count of <50 Hz. A Becker-Hickl SPC-830 time-correlated single photon counting (TCSPC) board and a Pentium 4 computer with custom-made Lab VIEW virtual instruments controlled the experimental data collection.³⁵

The process for single-molecule data collection started with image scanning at low laser powers (0.25–1.0 μW) to locate single molecules (see Figure 2). Images were saved for later analysis of intensity vs number of TMR dyes. Fluorescent lifetimes collected during imaging were used to verify that a single molecule had the expected lifetime (2.5–2.8 ns) of TMR. A cursor system was used to mark the desired molecules for first-in-first-out (FIFO) data collection. In FIFO mode, each detected photon was stamped with detector, microtime (time of arrival with respect to the excitation pulse), and macrotime (time of arrival on total data collection time scale). During FIFO data collection, higher powers of 2–10 μW were used to intentionally photobleach the TMR dyes on a reasonable time scale of approximately 5 s to 5 min. The background photon rate was measured using the first recorded cursor, and all molecules were photobleached to the background level.

Figure 2.

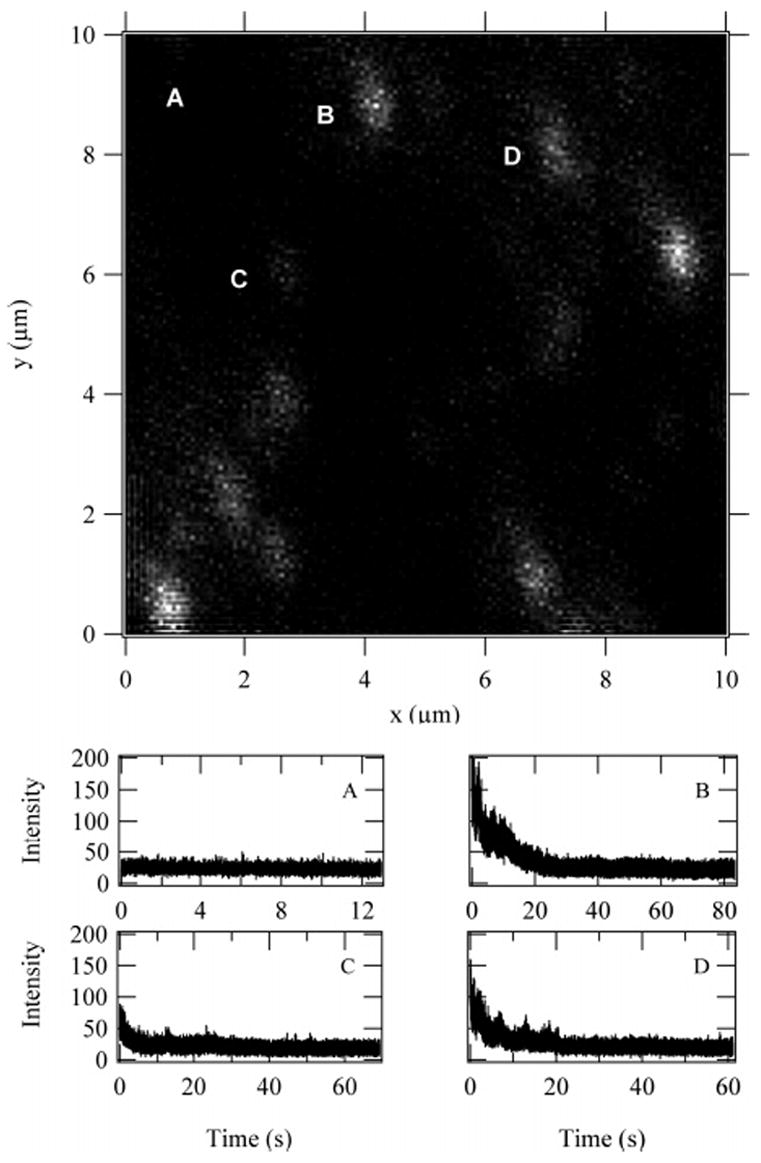
Scanned image of 5.8 TMR-conjugated 70 KD dextran: (A) the laser was centered away from any fluorescent molecules to obtain background intensity; (B) a bright spot that has nine states; (C) a dim spot that resulted in four states; (D) a spot that resulted in six states.

C. Fluorescence Decay Analysis

Fluorescence lifetimes were analyzed using a convolute-and-compare, nonlinear, least-squares technique.³⁶ In this technique, the instrument response function is convolved with a theoretical decay function. The theoretical decay was a single exponential corresponding to the fluorescent lifetime of TMR. In some cases described below, a weighted sum of two or more exponential decays was required. Single-molecule fluorescent lifetimes were fit both for the entire photon trajectory and dye-by-dye using the state reconstructions provided by the HMM analysis. The single-molecule microscope instrument response typically had a fwhm of approximately 400 ps.

D. Data Simulations

Simulated photon arrival trajectories were created using a C compiled external operation (XOP) in Igor Pro v.5 multi-platform analysis software (WaveMetrics, Oswego, OR). The XOP creates photon emission rates exponentially distributed according to input model parameters (detailed below). State-dependent sequential first-passage times were simulated from the sum of all rates. Transitions were determined by the branching ratios between fluorescence, bleaching, and recovery.

E. HMM Implementation

We have previously discussed²⁶ our implementation of a random-observation-time HMM data analysis for single photon streams using an approach inspired by Rabiner.¹⁹ In the present work, we have changed our implementation in several ways. The analysis is now performed by an Igor Pro XOP we have written for both Windows and Macintosh computers.³⁵ We perform all of our calculations using the first-passage-time solution to the kinetic equations rather than the random telegraph process master equation. This is justified in the limit where the photobleaching/blinking rate is much slower than the emission rate.

The model in the present work is based on two-state, on–off dynamics, discussed in detail in the following section and depicted in Figure 1. Analysis using this hidden Markov model requires initialization of five parameters: background and fluorophore emission rates, photobleaching and photorecovery rates, and total the number of states including the background as a state. Initialization was done using a statistical comparison test on binned photons. Starting from the end of the trajectory to detect the background level and final photobleaching event, the algorithm used a number of photons (100–5000) to calculate the first two statistical moments of the distribution for the emission rates. Proceeding backward through the photon stream, another collection of 100–5000 photons was used to calculate the second distribution’s statistical moments. The two distributions were compared using a Students T-test. If they were judged to be statistically indistinguishable, then the two distributions were combined to form one distribution. The algorithm repeated until the distributions were different and, thus, found a photo-bleaching step. The number of photons used to compute the distributions were varied to exclude the possibility of missing or averaging across a state transition.

Figure 1.

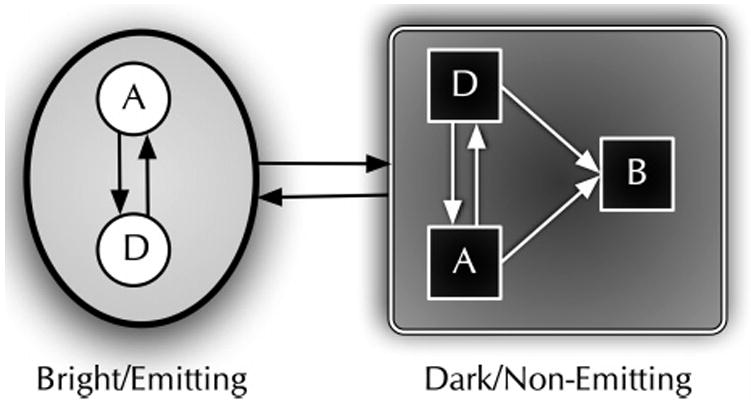
Reduced two-state model used for HMM analysis of single-molecule photobleaching trajectories. The shaded oval region represents spectroscopically indistinguishable emissive (bright) states with inset circles representing distinct bright states. The shaded rectangle region represents spectroscopically indistinguishable nonemissive (dark) states with inset squares representing distinct dark states. Active states, whether dark or bright (A), are considered to be related by reversible physical processes such as isomerization or intersystem crossing. Damaged states (D) are considered to be chemically modified dark or bright states. Bleached states (B) are dark and entered irreversibly. If there is only one connection between the emitting and nonemitting states, then the system can be reduced to a two-state system. The use of hidden Markov models can make it possible to extract both the emitting and nonemitting hidden states given enough state transitions to characterize them.

The amount of information provided by transition rates per single molecule was low enough compared to that of the emission rates that accurate reconstruction of a trajectory was possible with transition rate parameters that were within an order of magnitude of the true values. The transition rates (k_pb and k_rec) were initialized assuming that two photobleaching events occur for each dye during the experiment. This takes into consideration the possibility for one recovery event for each dye state during the observation time. Therefore, k_pb = 2/T and k_rec = 1/T, where T was the total observation time of the single molecule.

The total number of dyes in the model was incremented from 1 to 12 giving 2–13 total states including the background state. The four rates were optimized for each number of dye states using four different methods to calculate the maximum total likelihood for each case to determine which number of states was most likely. The three methods were as follows: Simplex minimization,³⁷ More–Hebdon using finite differences, and simulated annealing. The first method was implemented as an XOP in Igor Pro. The latter two methods were performed using Igor Pro’s Optimize operation. To evaluate the quality of the optimized solutions, we performed a discrete point integration of the probability space by storing the iterative probability results from the simulated annealing minimization. We also used an adaptive, recursive Monte Carlo integrator (also described in Numerical Recipes) to integrate the probability space of the model for the range of dye states to clear disagreement; however, this algorithm was not used consistently because it does not return the optimized rate parameters. Results from all of the methods were compared to determine the number of dye states in each molecule measured. In most cases, all techniques agreed with one another. For cases where there was disagreement, the solution that was most supported or the solution with the lowest number of states was chosen.

III. Results

A. HMM for Multi-dye Photobleaching

To be able to reconstruct trajectories of a multi-dye system, we must have a strategy to reduce the dimensionality of the state space such that a single-molecule measurement will be able to provide enough information to make state assignments. Equation 1 suggests that the state space can be greatly reduced by treating the dyes as indistinguishable. This assumption also simplifies the HMM since it requires that all the fluorophores be spectroscopically indistinguishable, that is, have the same mean emission (k_em) and transition rates at a given laser intensity.

Even after invoking dye indistinguishability, the total number of states will become intractable for even a modest individual-dye state space. Therefore, we will use the smallest number of states that can still reasonably reproduce the features observed in photobleaching trajectories (i.e., photobleaching with occasional photorecovery). We use two states in the model (Figure 1), corresponding to bright (emitting) and dark (nonemitting) states of the dye. The shaded oval of Figure 1 contains unique “on” (bright) states in circles, while squares in the shaded rectangle are unique “off’ (dark) states, and A, D, and B represent active, damaged, and bleached dyes, respectively. If various luminescent states exist and are not clearly distinguished directly from measurement, it is possible to extract them through hidden Markov model analysis. One way to do this is to construct distributions of dwell times and fit the nonexponential distribution to two or more exponentials. Each exponential would, then, represent a new state for the HMM. Examining the posterior and prior states for the new state can establish the connectivity to the rest of the HMM state diagram.

Dark states within the shaded rectangle of Figure 1 can include any nonradiative condition, for example, intersystem crossing into excited triplet states, intermolecular charge transfer of electrons or holes, proton transfer (intra- or intermolecular), cis–trans isomerization of double bonds, twisted intramolecular charge transfer, photooxidation, at high irradiation, two photon excitation leading to radical ion pairs, and so forth. The existence of these states in TMR and other organic dyes has been well established in the literature.^38–45

Transitions between the two domains of states are characterized by two rates: photobleaching from bright to dark (k_pb) and recovery from dark to bright k_rec). Reducing the state space using this two-state model brings the problem to a tractable level. The HMM analysis can then evaluate if an increase in model complexity is necessary.

When multiple indistinguishable fluorophores are present, the number of independent parameters does not increase under our two-state model as the on-state emission rates and the transition rates each are additive. The off-state of the nth fluorophore corresponds to the on-state emission of the (n − l)-th fluorophore. Under these assumptions, when N TMR fluorphores are present, the emission rate for n ≤ N dyes is nk_em and the rate for transitioning from this state is the sum of the bleaching (k_pb) and recovery (k_rec) rates, which scale with N and n as

$$k_{n,N}=n{k}_{\text{pb}}+(N-n)k_{\text{rec}}$$ (2)

By using this model, we increase the information available for the determination of the four fundamental rates.

To further simplify the model, we have assumed that between the individual observed photons only single dye state jumps are allowed. At the laser powers used in this study, the time for photobleaching and recovery are two or more orders of magnitude larger than the interphoton time. Therefore, we do not expect to observe an instantaneous change of more than one dye state. Observation of simultaneous multiple-dye events would suggest the possibility of cooperativity in the process-(es) leading to blinking and/or coupling between the dyes. In the dwell time analysis with our two-state model, multiple-state jumps would show up as additional exponential components with much higher rates than the single-state jumps because the state pathway is forced into instantaneous residence in the interstitial state. Equation 2 would contain an additional rate term for each multiple-state jump included in the model. The generalized rate matrix has the form

$$\begin{array}{c}\left(\begin{array}{llllll}{k}_{1,1}\hfill & k_{1,2}\hfill & 0\hfill & 0\hfill & \cdots \hfill & 0\hfill \\ k_{2,1}\hfill & k_{2,2}\hfill & k_{2,3}\hfill & 0\hfill & \cdots \hfill & 0\hfill \\ 0\hfill & k_{3,2}\hfill & k_{3,3}\hfill & k_{3,4}\hfill & \cdots \hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & \hspace{0.17em}\hfill & \ddots \hfill & ⋮\hfill \\ 0\hfill & 0\hfill & 0\hfill & \cdots \hfill & k_{N,N-1}\hfill & K_{N,N}\hfill \end{array}\right),\\ k_{i,i}=k_{\text{bg}}+(i-1)k_{\text{em}}\\ k_{i,j}=\{\begin{array}{ll}(i-1)k_{\text{pb}};\hspace{0.17em}i=j-1\hfill & i\hspace{0.17em}\epsilon \hspace{0.17em}\{1,N\},\hfill \\ (N-i)k_{\text{rec}};\hspace{0.17em}i=j+1,\hfill & j\hspace{0.17em}\epsilon \hspace{0.17em}\{1,N\}\hfill \end{array}\end{array}$$ (3)

The rates corresponding to transitions between nonadjacent states were set to zero under the assumption of no double-state jumps between photons. No change in model likelihood has been observed by allowing or disallowing these transitions, and no multiple bleaching or recovery events were observed within one interphoton time when the full N × N rate matrix was used. With this “ground-up” model approach, the model state space to be optimized consists of only four parameters for a given number of states.

B. Single-Molecule Data

Here, we report the analysis of 120 total 70 kD dextran molecules, of nearly equal numbers of the 3.8 and 5.8 TMR conjugates. The sample was dissolved in water then physisorbed and imaged on a glass coverslip. The fluorescent dextran polymers were typically in an adequate volume of water to maintain hydration; however, the physisorbed molecules remained at fixed positions throughout the experiment. A scanned single-molecule image of the 5.8 TMR-labeled dextran is shown in Figure 2. Four trajectories from this image were selected to illustrate typical observations in the photobleaching experiments. The plots below the image display the photon trajectories that correspond to the molecules labeled in the image: (A) the laser was focused on a region away from any fluorescent molecules to obtain the background photon detection rate; (B) a fluorescent spot that resulted in nine states when analyzed by HMM; (C) a four-state molecule as indicated by HMM analysis; (D) a six-state molecule. Each spot was analyzed using the HMM algorithm to determine the most likely number of dyes to include in the degree of labeling distribution.

The fluorescence photobleaching trajectories typically exhibit distinct photobleaching steps. After one or more photobleaching steps, fluorescence recovery was sometimes observed where the intensity made a steplike return to a higher intensity level. Eventually, all of the fluorophores are permanently photobleached to the background level. When the trajectory shows well-defined discrete states, HMM analysis of the trajectories for the total number of fluorophores gives the log-probability of the model and shows a sharp increase as one approaches the correct number of fluorophores. The log-probability has a less steep decrease for dye numbers higher than the correct value. Figure 8 shows a simulated trajectory with the log-probability as a function of the number of states in the inset. Figure 3 displays examples of experimental trajectories (discussed in more detail below) where the determination of the number of states using the techniques described above are (A) distinct, (B) near the limit of our detection technique, (C) identifiable to within a range of states, and (D) beyond the capability of detection using the intensity-based technique reported here.

Figure 8.

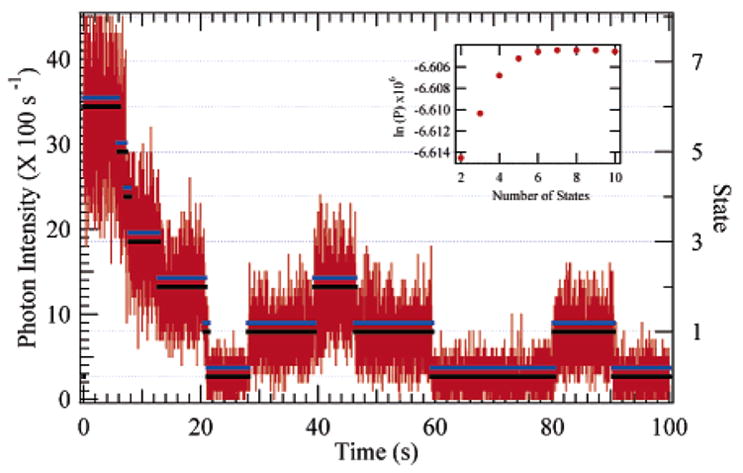
Simulated six-dye (seven-state) photon emission trajectory created using the two-state photobleaching model described in the text. The true and reconstructed trajectories are plotted over the 10 ms binned trajectory, and the dye state is shown on the right axis. The reconstructed trajectory has been shifted upward by 0.2 to facilitate viewing. Inset: the simplex optimized state-dependent log-probability, which shows maximum model likelihood (least negative ln(P) at seven states).

Figure 3.

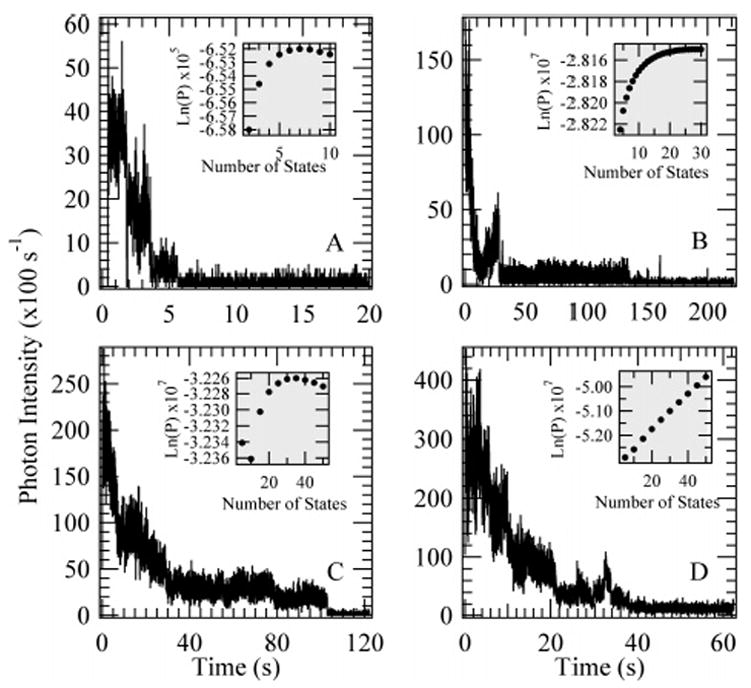
Experimentally obtained fluorescence trajectories of TMR-labeled dextran where the photobleaching steps are (A) sharp and readily detected for a total of 7 states, (B) less distinct but still resolved at a maximum likelihood of 28 states, (C) within the limits of our technique at 35 ± 4 states showing that the total number of states is not the only variable dictating the ability to determine the number of states, and (D) beyond the capability of this detection technique. The graph insets show the posterior log-probability optimized for each number of fluorophores analyzed in the context of our model.

The polarization trajectory of wet samples shows no preferential orientation of the fluorescence dipole as illustrated in Figure 4. The bottom panel of Figure 4 is the 10 ms binned photon trajectory with the HMM photon-by-photon state reconstruction overlaid. The top graph in Figure 4 shows the dipole angle implied by the polarization ratio. Li this experiment, we cannot distinguish between fluorescence from dipoles oriented at or near 45° and that from dipoles that are rapidly reorienting. Therefore, 45° corresponds to isotropic emission from the sample. The polarization trajectory of dry samples shows some fluctuating preferential orientation of the fluorescence dipole as illustrated in Figure 5. The bottom panel of Figure 5 is the 10 ms binned photon trajectory with the HMM photon-by-photon state reconstruction overlaid. The top graph in Figure 5 shows the dipole angle implied by the polarization ratio. Jumps in the polarization occur in sync with some, but not all, of the blinking events. Most of the polarization jumps were relatively small. These effects are overcome by combining the detected horizontal and vertical polarization components to get the total fluorescence intensity before applying the two-state multi-dye HMM described above to determine the best value for the single-dye intensity fit to all of the dyes on a given molecule.

Figure 4.

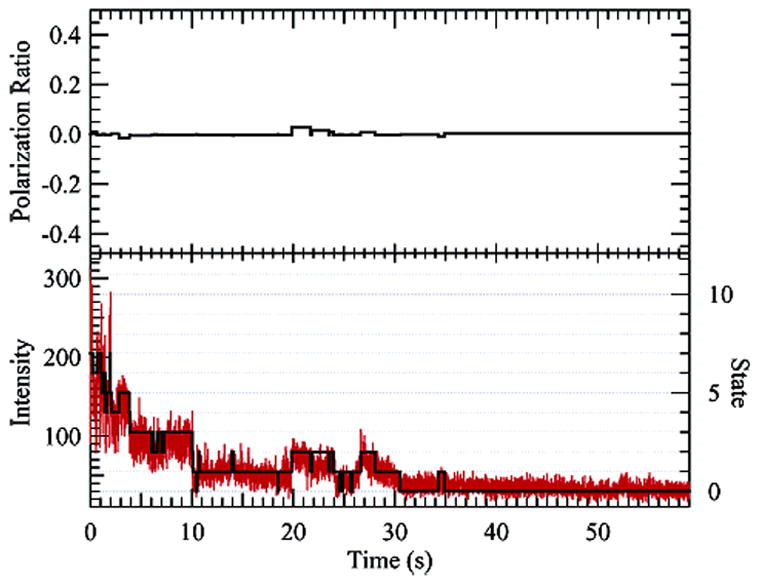
5.8 TMR-labeled (70 kD) dextran on a glass coverslip while still wet. Very little state-dependent polarization is observed (upper graph, polarization ratio of zero indicates isotropic emission). The bottom graph shows a histogram of the photon trajectory binned at 10 ms for the combined two-channel polarization data. The eight-state (seven-dye) reconstruction is overlaid.

Figure 5.

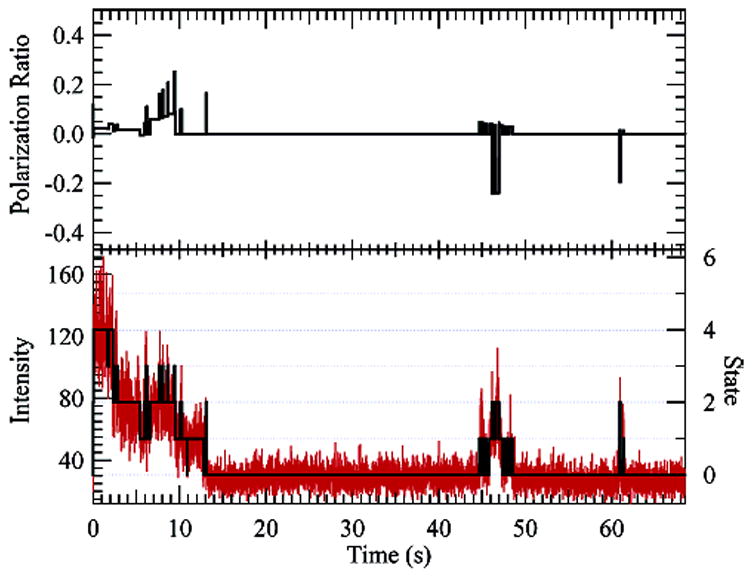
5.8 TMR-labeled (70 kD) dextran allowed to dry on a glass surface. Polarization effects can be seen in the upper graph, where the state-dependent polarization ratio is plotted (zero indicates isotropic emission). The bottom graph shows a histogram of the photon trajectory binned at 10 ms for the combined two-channel data. The five-state (four-dye) reconstruction is overlaid.

Wet single-molecule samples showed fluorescence decays that were best fit to a single exponential with the expected lifetime of ~2.5 ns. Figure 6 shows typical results from the nonlinear least-squares convolute-and-compare analysis for fluorescent lifetime. The fluorescent lifetime for each dye state is calculated by collecting the photons for each state from the HMM reconstruction. The shaded region indicates the statistical uncertainty bounds of the lifetime from the fluorescent lifetime fit to the entire photon trajectory. The state-dependent lifetime resides within the shaded region, indicating no individual TMR fluorophores experience quenching due to dye–surface or dye–dye interactions. The background measured after complete photobleaching typically showed a decay that was longer than what was typically measured in locations that had never shown fluorescent molecules. In addition, there were no quenching effects as a function of laser intensity in single-molecule measurements.

Figure 6.

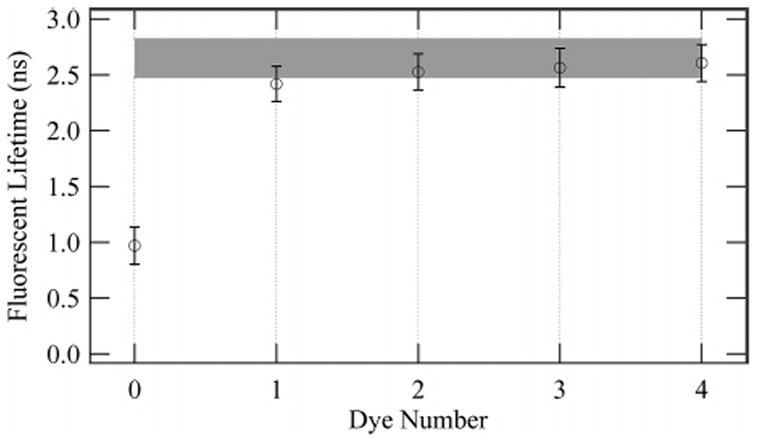
Fluorescent lifetimes evaluated from a convolute-and-compare algorithm (described in the text) for a typical dextran molecule. The lifetime is shown as a function of dye number (state) in the overall trajectory. The shaded region represents one standard deviation of the fluorescent lifetime from a fit to the entire photon trajectory. The state-dependent lifetime is within the statistical range of the entire trajectory (shaded region), and the completely photobleached state exhibits a much shorter lifetime.

From the reconstructed trajectories, we determined the most likely number of dyes and compiled these values into histograms for both the 3.8 and 5.8 TMR/70k dextran polymers. Figure 7 shows the resulting distributions of the degree of labeling. The solid lines show least-squares fits to the distributions using a zero-excluded Poisson distribution. Zero is excluded because this experiment cannot detect dextran without TMR conjugation. The Poisson fits to the 3.8 and 5.8 dye degree-of-labeling distributions had mean values of 3.96 ± 0.31 and 5.58 ± 0.27 dyes, respectively. Occasional outliers to the distributions were observed that contained more than 10 dyes. These spots have an anomalously high degree of labeling and are likely due to multiple polymers.

Figure 7.

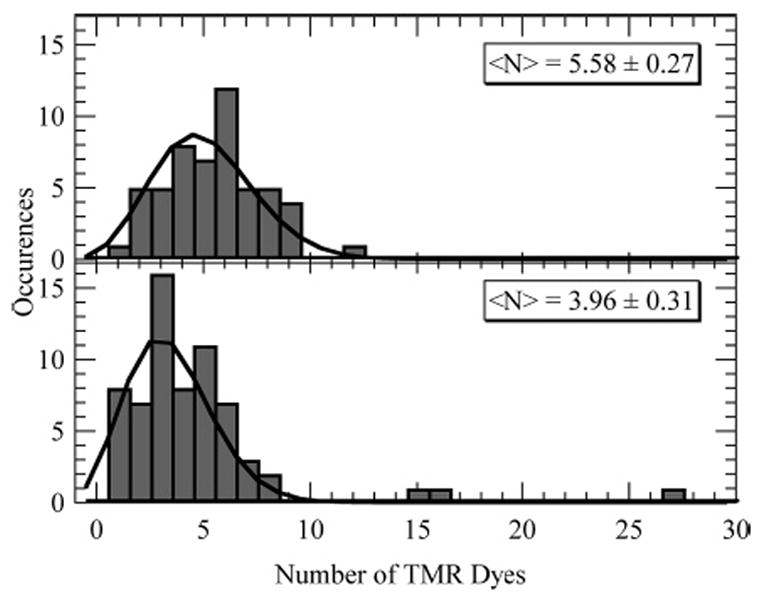
Comparison of the number distribution of TMR dyes on two conjugates, 3.8 and 5.8 TMR dyes/mole of dextran. The solid curves are the result of a fit to the data with a zero-excluded Poisson distribution. The fitting resulted in distributions with centers at 3.96 ± 0.31 and 5.58 ± 0.27 dyes.

C. Bulk Fluorescence Control Experiments

TCSPC polarized fluorescence decay measurements on bulk solutions of 3.8–70k and 58–2M dextran polymers show initial anisotropies of r₀ = 0.16 ± 0.01 and r₀ = 0.17 ± 0.02, respectively, which decay to zero with lifetimes of τ_r = 1.68 ± 0.04 ns and τ_r = 1.25 ± 0.02 ns, respectively. These values are independent of dextran concentration. The bulk measurements of absorption and emission spectra showed no evidence of spectral splitting or fluorescence quenching that are commonly observed when strong dye–dye interactions occur, typically at high TMR concentrations.⁴⁶

D. Theory and Simulations

To evaluate the HMM analysis, we performed Monte Carlo simulations of the photobleaching of varying numbers of dyes. Figure 8 shows an example of a simulated six-dye (seven-state) trajectory (binned to 10 ms for display in the figure) with the true and HMM reconstructed state trajectories overlaid. The state-dependent probability resulting from simplex optimization of the simulated trajectory of Figure 8 is shown in the figure inset. The reconstructed trajectory has been shifted up to make viewing easier. The true and reconstructed trajectories were not binned during the analysis; they represent the photon-by-photon trajectory. Because there were few bleaching and recovery events compared to the number of photons for each dye state, the ability to determine these transition rates accurately was difficult on a molecule-by-molecule basis. The amount of information provided by transition rates per single molecule was low enough compared to that of the emission rates that accurate reconstruction of a trajectory was possible with transition rate parameters that were within an order of magnitude of the true values. We found that the algorithm accurately identified photobleaching and recovery steps to within a few photons. The algorithm was most likely to miss steps at the beginning of the trajectory where the number of active dyes is at its maximum. The relative change in emission intensity is strongly dependent on the number of dyes.

$$\frac{I_N}{I_{N-1}}=\frac{N{k}_{\text{em}}+k_{\text{bg}}}{(N-1)k_{\text{em}}+k_{\text{bg}}}$$

The product of the excitation likelihood (Ik_excite), the quantum yield (φ_QY), and the collection (φ_coll) and detection (φ _det) efficiency gives the expected count rate at the detector. Under nonsaturating conditions, the excitation probability is proportional to the illumination fluence. Therefore, under conditions of linear response, the expected number of photons emitted before a dye photobleaches, η = (Ik_exciteφ_QYφ_collφ_detn)/(Ik_pbN_p) = k_em/k_pb, independent of intensity and the number of dyes present.

We can use the information theory to predict the limits of resolution of a photobleaching dye-counting experiment by examining the number of photons required prior to photobleaching/blinking to provide enough information to distinguish the N and N − 1 levels. The number of photons and the time to the first bleaching/blinking event are the two relevant observables for this problem. Neglecting any cooperativity or self-quenching of the dyes, the distribution of the number of photons emitted by the dyes prior to a photobleaching step is independent of the number of dyes present

$$\mathcal{P}(N_{\text{p}}\mid \eta )=\frac{{\eta }^{N_{\text{p}}}}{{(1+\eta )}^{1+N_{\text{p}}}}$$ (4)

The likelihood of observing photobleaching after time t and N_p photons in that time is

$$\mathcal{P}(N_{\text{p}},t\mid N)=\frac{k_{\text{em}}N}{N_{\text{p}}!}{\left(k_{\text{em}}t\left(\frac{1}{\gamma }+N\eta \right)\right)}^{N_{\text{p}}}{e}^{-k_{\text{em}}t((1/\gamma )+\text{N}(\eta +1))}$$ (5)

The data analysis method must distinguish between the N and N − 1 states using the number of photons N_p emitted prior to the bleaching event occurring at time t.

The information contained in the photon stream regarding the number of dyes present is

$$\mathcal{I}(N,N_{\text{p}},t\mid \eta )=\mathcal{H}(N\mid \eta )-\mathcal{H}(N\mid N_{\text{p}},t,\eta )$$ (6)

$$\mathcal{H}(N\mid N_{\text{p}},t,\eta )={\int }_0^{\infty }\underset{j=0}{\overset{1}{\Sigma }}\underset{N_{\text{p}}=0}{\overset{\infty }{\Sigma }}\mathcal{P}(N_{\text{p}},t\mid N-j)\mathcal{P}(N-j)\times {log}_2\left(\frac{\mathcal{P}(N_{\text{p}},t\mid N-j)\mathcal{P}(N-j)}{{\displaystyle \underset{k=0}{\overset{1}{\Sigma }}}\mathcal{P}(N_{\text{p}},t\mid N-k)\mathcal{P}(N-k)}\right)$$ (7)

Using eq 5 and the uniform prior = (N − 1) in eq 7, we can calculate the number of photons required to distinguish between N and N − 1 dyes by evaluating the integral and the first summation and solving for the minimum number of photons, N_p, which reduces the entropy to the point where it is 99% likely that the state will be correctly identified. The solid lines in Figure 9 show how the number of photons required increases with the number of dyes to be distinguished. To obtain this number of photons consistently, the quality of the dye must be substantially higher as suggested by eq 4. The results we calculate for N_p in Figure 9 are analogous to the empirical resolving power of the standardized Poissonian log-likelihood change-point formulation derived by Watkins and Yang. The broken lines in Figure 9 show how the dye quality parameter, η, needed to distinguish the first photobleaching/blinking step, increases with the number of dyes present.

Figure 9.

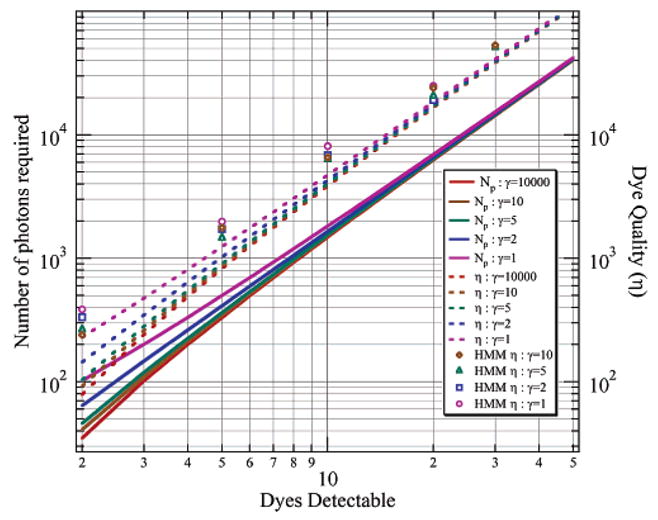
Number of photons that need to be emitted prior to the first photobleaching/blinking event to distinguish that initial level from the lower intensity level following the first photobleaching/blinking event. The solid lines are calculated from information theory. The dashed lines are also from information theory calculation and include a correction factor from eq 4 to represent the dye quality factor necessary for detection. The dots are Monte Carlo simulation results of the HMM capability of detecting a photobleaching step for a given dye quality factor. Results are shown for various signal to background (γ) values.

To evaluate the effectiveness of the HMM approach to detecting the first step, we evaluated Monte Carlo simulations of photobleaching for N = {2, 5, 10, 20, 30} at various levels of signal-to-background γ = {10, 5, 2, 1} and determined the quality of dye required for the HMM algorithm to successfully detect the step 99% of the time. The results of these simulations appear as the open symbols in Figure 9. The Monte Carlo simulations indicate that the HMM algorithm is operating near the information-theoretical limit for determining the number of dyes present as dictated by the detection of the first bleaching step. In general, the HMM algorithm should be expected to do slightly better than in these simulations since occasional recovery to the original level would provide additional photons for the detection of the highest intensity level.

IV. Discussion

A. Validation of Model Assumptions

The simplified two-state photobleaching model requires several assumptions that may not be valid for all systems or in all circumstances. The most important assumptions are that the dyes can be considered to be indistinguishable and independent. In the hidden Markov model, we additionally assume that only one dye will blink between photon observations.

Dye indistinguishability requires that the local environment be essentially identical for each active dye and remain so throughout the experiment. This dictates that there be no large dielectric discontinuities near the dye (e.g., an air-glass interface), otherwise the fluorescence properties will depend on a lab-fixed axis. At any instant in time, each dye will be in a slightly different environment and have a different orientation with respect to the laboratory. In the presence of local heterogeneity, the dyes must average over the different environments on a time scale that is short compared to the fastest relevant blinking time.

Samples on glass that were allowed to dry for at least 2 h showed fluorescence anisotropy and quenching, as well as nonexponential lifetimes. We attribute this to the orientation of the dipoles with respect to the air–glass dielectric interface. The dipole orientations become spatially frozen by TMR–glass interactions. This polarization effect results in trajectories that exhibit different fluorescent levels in horizontal and vertical polarization detection channels. It is likely that the fact that the polarization angle is different for different recoveries to the state containing a single active dye is reflective of multiple dyes being damaged but not permanently bleached. In the dry samples, as different dyes happen to recover, the polarization takes on the value reflective of that dye’s orientation with respect to the laboratory polarization axis.

By contrast, measurements made on wet samples resulted in little or no polarization effects and exponential lifetimes for most of the states observed. This would suggest that the wet samples are averaging over the conformational space rapidly compared to the relevant blinking times. The rare, nonexponential states observed in wet samples we attribute to dyes that are, by happenstance of the labeling reaction, very close together geometrically. Strong coupling of a pair of dyes that are close together will make them different and therefore distinguishable in our experiment.

The assumption of dye independence is suspect since one expects to observe dye–dye interactions on systems with multiple fluorophores in close proximity. In systems that have regular, or highly symmetric, geometries with the distance between chromophores that are small enough (~Å), strong coupling can occur resulting in spectral shifts and potentially cooperative behavior as has been observed in the light harvesting complex, LH2.^16,47 Structural fluctuations were observed to change the polarization properties of LH2 because of the sensitivity of chromophore electronic coupling on geometry.^16,47 In the case of TMR–dextran conjugates each polymer is of finite size and is labeled with several dyes. The dyes can, in principle, couple. Some possible mechanisms are excitonic dynamics and excimer formation (strong coupling) and fluorescent resonant energy homotransfer (weak coupling). However, the labeling of the dextran polymers is expected to be random and the dextran itself has little long-range structure to hold chromophores in a regular geometry. Therefore, strong coupling between all the dyes is unlikely. However, if the density of dyes is high enough, then the coupling will be strong some fraction of the time and the spectral properties of those dyes will be changed due to exciton formation.⁴⁸ The fraction in the case of the TMR–dextran conjugates that we studied must be small since the bulk measurements of absorption and emission spectra showed no evidence of spectral splitting or fluorescence quenching that are commonly observed at the high TMR concentrations that result in strong dye–dye interactions.

On the single-molecule level, strong coupling would manifest itself in the photobleaching trajectories. The sequential bleaching of dyes would have a very strong effect on the overall signal due to the changes in the coupling between the dyes that would occur upon blinking. The fact that the dipoles were randomly oriented and that there was no evidence of nonexponential decays for wet samples suggests that the dipoles were reorienting rapidly enough to average over the modest dielectric inhomogeneity at the water–glass interface.

Fluorescence self-quenching has often been observed when a system has multiple fluorescent probes in close spatial proximity (see, for example, refs ^{9, 16}, and ⁴⁷). Our data indicate that it was uncommon for the coupling to be strong enough to cause substantial spectral and lifetime changes in the dyes. In addition, there were no quenching effects as a function of laser intensity in single-molecule measurements. However, in the case of a few trajectories, as illustrated by Figure 3D, we found that the log-likelihood with respect to the number of states was not convex in the region of a reasonable number of dyes. We attribute this to TMR–dextran conjugates with dyes that are, by happenstance, very close together. When this occurs, small changes in distance and structure can cause intensity fluctuations that are not accounted for in the two-state model.

In the case of weak coupling, where Förster homotransfer is expected to be the dominant mechanism, the expectation is that the luminescence would experience a decay of anisotropy on the time scale of the energy transfer. Bulk fluorescence anisotropy measurements showed clear evidence of weak coupling between the dyes in the form of fluorescent resonant energy transfer. The fastest decay component will come from the dyes that are closest together. Assuming a dextran polymer is approximately spherical, then the distribution of nearest-neighbor distances between dyes depends on whether the TMR labels uniformly on the surface of the sphere or uniformly along the chain length of dextran. The calculated Förster radius (R₀) for FRET homotransfer between isotropically oriented TMR is 4.49–5.66 nm depending on the actual quantum yield. Molecular probes suggest a quantum yield of ~0.45, which corresponds to R₀ = 5.14 nm. Assuming the nanosecond time-scale depolarization occurs by FRET homotransfer between two dyes, the mean distance between nearest neighbors would need to be approximately 1.08R₀ = 5.6 nm and 1.20R₀ = 6.2 nm for the 70 and 2000 kD dextran, respectively. Literature values⁴⁹ for the hydrodynamic radius (r_H) of various molecular weights of dextran in phosphate-buffered saline were determined to be r_H-(70 kD) = 3.5 ± 0.2 nm and r_H(2 MD) = 14.4 ± 0.6 nm. If the labeling occurs randomly on the surface of a sphere, then the mean distances between nearest neighbors for the 3.8–70k, 5.8–70k, and 58–2M conjugates are ~2.9, ~2.5, and ~3.4 nm, respectively. If the labeling is uniformly distributed along the dextran chain, and therefore uniformly distributed inside the volume of the globular polymer, then the mean distances between nearest neighbors for the 3.8–70k, 5.8–70k, and 58–2M conjugates are ~2.6, ~2.9, and ~3.4 nm, respectively. This suggests that either the hydrodynamic radii are underestimated by approximately a factor of 2 or that the depolarization due to the nearest neighbors will occur in < 100 ps. Indeed, we observe that the samples are depolarized to an anisotropy value of 0.16 and 0.17 within our instrument response of ~40 ps. These initial anisotropy values correspond to depolarization cone angles of 57–58°. This suggests that the observed nanosecond anisotropy decay is due to a phenomenon other than the FRET homotransfer. A likely explanation would be rotation of the TMR dyes that has been slowed by interactions with the dextran local environment.

The observed depolarization is expected to be a benefit for this methodology because it will facilitate polarization scrambling, reducing the effect of incomplete dipole orientation averaging on the fluorescence signal from a single multichromophoric molecule. We observed that even in the case of dried samples there was substantial depolarization of the fluorescence, most likely due to homotransfer between dyes.

Even when the dyes are independent when fluorescent, they may not be independent once one or more dyes has been damaged or bleached. Nearby dyes could photochemically react. This would appear as occasional pairwise correlated irreversible jumps in fluorescence intensity. If a state that causes fluorescence intermittency is absorptive, then it might act as an energy transfer acceptor and result in the appearance of cooperativity in the intermittency. This would appear as correlated multiple-dye jumps in intensity. If either of these phenomena occurs for the TMR-dextran conjugates, then the likelihood must be small compared to coincidental photobleaching. The tridiagonal rate matrix prevents such transitions from occurring by setting the nonstepwise rate constants to zero, yet when we performed our analysis with the rate matrix allowing multiple synchronous blinking events, there was essentially no improvement in the log-likelihood. Since we get a convex log-likelihood for the majority of TMR–dextran conjugates, we take this as further evidence that our assumptions are usually valid.

B. Trajectory Reconstruction

The Monte Carlo simulations showed that with reasonable signal levels, trajectories could be reconstructed with level-change identification accuracy to within a few photons. Most of the photobleaching trajectories we measured fit well to our HMM and showed a most-likely number of dyes. However, in the case of a few trajectories, as illustrated by Figure 3D, we found that the log-likelihood with respect to the number of states was not convex. Bulk experiments suggested that our assumptions of dye indistinguishability and dye independence were valid, however trajectories such as this one illustrate how minority components of a sample can give substantially different behaviors. In this case, we attribute this behavior to polymers that happen to have dyes in very close proximity. In this case, even small geometry changes can cause dramatic intensity and lifetime fluctuations. This will prevent single-molecule trajectory reconstruction under the assumptions of dye indistinguishability and independence.

There is a slight decrease in lifetime as the number of dyes decreases. This is likely due to the increasing fraction of background. The background photon lifetime measured after complete photobleaching is indicated by dye number zero. This lifetime was much shorter than that of TMR, as expected. However, it was also longer than that typically measured in locations that never showed fluorescent molecules. The low intensity of the final state reduces the reliability of lifetime measurements. The fitting has difficulty distinguishing between a combination of uncorrelated plus instantaneous scattering background and a 1 ns decay. Less than 100 fluorescent photons (≤2% of the total detected in this case) can add enough decay to the tail of the exponential distribution to significantly alter the evaluation of the fluorescence lifetime relative to the instrument response. Also there may also be some contribution due to residual fluorescence from photodamaged molecules. The simplified HMM will gather very dim, damaged states together with fully photobleached states in the reconstruction (see Figure 1).

If one is interested in quantifying the kinetics from the trajectory reconstructions, then only the appropriate model will result in Markovian dynamics and thus give meaningful numbers for kinetic parameters that describe bleaching, blinking, multiple damaged states, and environmental sensitivity. Though it was successful in counting dyes and reconstructing trajectories, the two-state model we used is apparently invalid in the presence of photoblinking that is different from photobleaching, damaged dyes that emit nearly as intensely as undamaged ones, environmental sensitivity of the dye, and so forth. We have found that the kinetics from this model are indeed non-Markovian. Since only a small number of kinetic events are observed for these processes in any particular trajectory, the reconstruction is relatively insensitive to non-Markovian state dwell time distributions. Constructing appropriate hidden Markov models from non-Markovian state dwell-time distributions will be the subject of future papers.

C. Dye Counting

The ability to identify all of the individual dye levels relies on the collection of a sufficient number of photons from each level. Intensity fluctuations within individual levels can have a significant impact on the identification ability as well. For these reasons, careful selection of the dye is critical, as we have shown through information theory and simulations. Information theory shows that dye photostability is ultimately the limiting factor for the number of dyes that can be counted using this method. However, the choice of model is also important. It must be flexible enough to accommodate non-Markovian behavior, but still be simple enough to be tractable for several dyes. In the interest of counting dyes, we have used an additive two-state model that allows detection of states that may be fluctuating about an average intensity and easily identifies short-lived dyes that might be missed by assuming unique intensity and transition rates for each dye. The two-state model also expedites optimization of the rate parameters so that the number of dyes can be quickly identified.

The degree of labeling distribution is expected to depend on the nature of the polymer being labeled and the labeling methodology. When preparing a fluorescently labeled protein, there are typically a small number of labeling sites. Every protein should have the same number of active sites. If all sites have approximately the same reactivity, then the degree of labeling distribution is expected to follow a binomial distribution.

$$\mathcal{P}(l\mid \mu ,m)=\left(\begin{array}{c}m\\ N\end{array}\right){\left(\frac{\mu }{m}\right)}^N{\left(1-\frac{\mu }{m}\right)}^{m-N}$$

If the different labeling sites have different reactivities, then the labeling will follow a multinomial distribution. When the number of available label sites is much greater than the degree of labeling, the labeling will be randomly located among the sites and have a Poisson distribution.

$$\mathcal{P}(l\mid \mu ,m)=\frac{{\mu }^N}{e^{\mu }N!}$$

This is the behavior expected for polymers with sparse labeling such as the TMR-labeled dextran from Invitrogen.⁵⁰ If the labeling of the polymer is not sparse with respect to the number of labeling sites, then the distribution of polymer lengths can become relevant. In this case, the labeling distribution will be a convolution of the binomial behavior with the distribution of the number of labeling sites.

The distinction between the 3.8 and 5.8 TMR conjugates is easily made, demonstrating the capability of observing multi-molecular systems of this order (Figure 7). The outlying molecules for the 3.8 dye distribution (i.e., the three molecules with number of TMR dyes greater than 10) are likely aggregate dextrans included in the analysis, however, fitting to a bimodal distribution does not provide better or significantly different results. The ability to obtain distributions with uncertainties smaller than a single dye indicates the strength of this HMM technique for distinguishing any distribution with this order of multiplicity.

There are limits to the ability of this method to determine the degree of labeling distribution. The hidden Markov model probability calculation is not limited to analysis of any maximum number of states. In fact, this type of analysis has been applied to continuous/diffusive systems with much success.⁵¹ However, as the number of fluorophores increases, the emission rate approaches a continuous variable (see, for example, Füreder-Kitzmüller et al.⁵²). The first bleaching step will most often be the limiting factor in accurately determining the number of dyes present. As the number of dyes increases, the bleaching occurs on an ever-faster time scale as described by eq 2. Though the intensity of the signal also increases proportionally, the signal-to-noise ratio that is limited by shot noise does not increase as rapidly. At some number of dyes, the bleaching rate will be too fast, on average, to allow for detection of the first bleaching step. Therefore, the limit of accuracy of a dye-counting experiment is dependent primarily on the number of photons that a dye emits, on average, prior to photobleaching.

Under conditions of moderate excitation power, the photo-bleaching rate is proportional to excitation intensity.^38,40,42 The intensity range for the experiments reported here was (5–20) × 10³ W/cm². According to Dittrich and Schwille, TMR in water (air atmosphere) reaches saturation of one photon (514 nm) excitation near power densities of 2 × 10⁵ W/cm², well above the laser intensities used in this study. Therefore, no power-dependent fluorescence quenching is expected or was observed.

Combining the results of information theory, simulations, and single-molecule measurements of aggregated 70 kD dextran and the 58 TMR-labeled 2000 kD dextran, we are confident that this technique can be extended to systems with multiplicity orders of 30 and higher. At these levels, we might expect to under-count the number of dyes because of the rapid photobleaching of the first dye or two. Having a good estimate of the bleaching rate constants would allow a correction to be applied to the final distribution based on the fraction of the time the dyes would be expected to photobleach before delivering enough information to identify that first level.

Photobleaching dye counting can be used to calibrate photometric experiments. With careful calibration of dye intensity, complete photobleaching of the fluorescence of the system under study would not be required to have high confidence in the number of molecular constituents. For data collected on a particular day, the background and individual dye intensities are the same for every molecule within some experimental uncertainty. By analyzing approximately 10 molecules, these values can be ascertained and analysis can proceed by simply observing the maximum intensity of each molecule. The implications of this result are that one may use fluorescence imaging strategies either by scanning APDs or CCD to simultaneously collect data for > 100 molecules.

In the case where molecules are free to diffuse, the analysis would require the addition of diffusive terms to the HMM. Distinction between individual dye levels would require resolution of individual photons within a fluorescence burst. Discrete intensity steps associated with blinking would need to be distinguished from continuous changes resulting from diffusion. Observation of a few discrete steps would allow the initial instantaneous brightness and step size to be determined. The ratio of these quantities is the dye number. This approach would make this technique applicable to various diffusive experiments or to flowing experiments in micro and nanofluidic devices.

D. Comparison of HMM to Other Methods

HMM analysis provides a photon-by-photon reconstruction of the data. These reconstructions allow one to determine many of the parameters of interest in single-molecule trajectories (e.g., state-dependent dwell times, fluorescent lifetimes, absence of correlation within a particular state) with more accuracy than any other proposed technique. HMM analysis of a photon stream benefits from the statistical simplifications that occur because of the Markov property.^19–21,53 The Markov chain of molecular states is not directly observed. However, since each state has associated with it emission probabilities and transition probabilities, this hidden sequence can be reconstructed from the photon stream if enough information is present in the entire trajectory to distinguish the states.

Recently, a method to analyze the changepoints of photon trajectories based on likelihood calculations of photon emission rates was proposed.⁵⁴ This technique when compared to hidden Markov models indeed overcomes the issue of model initialization. However, computation time using this technique scales as N²_cpN_p ln(N_p). N_cp is the number of state-to-state changepoints and N_p is the number of photons, which can be greater than 10⁶ for multiple fluorophores. On the other hand, hidden Markov models calculate the probability of a model as N_pN, where N is the number of states in the model. Including an optimization step requiring 1000 iterations for the HMM analysis results in far shorter computation times even when linearizing the changepoints technique by analyzing overlapping sections of 1000 photons as suggested by Watkins and Yang. In addition to being computationally slower, the changepoints analysis does not directly return a trajectory reconstruction, transition rates, or state connectivity, that is, kinetic pathways, and is not sensitive to short dwell times within a particular state. In fact, for their test simulations, they specifically eliminated short dwell times. The dwell time distributions for directly connnected states are functions that monotonically decrease from time zero implying that a large number of dwell times will be short. HMM analysis is capable of detecting state occupations of a single interphoton time should there be adequate statistical information to justify it. Moreover, molecular parameters are optimized to include statistically weighted contributions from transitions that may have occurred but that may not have provided enough information to justify assignment at a 95% or greater confidence level.

V. Conclusions and Further Work

Bulk experiments such as dynamic light scattering are often used to identify sizes of molecular components in solution and extract number distributions. Heterogeneity, particle shape, and sample contamination often convolute the results of these experiments making an accurate assessment difficult. On the single-molecule level, there are many experiments that involve multiple molecular copies or a variety of interacting components. The ability to identify and distinguish these components is of utmost importance to understanding the results of these experiments.

We have developed hidden Markov model analysis algorithms that directly determine input model probability and reconstruct the most likely state-to-state trajectory on a photon-by-photon basis. In this report, we have shown that HMM analysis operates near the information–theoretical limit to provide the highest possible resolution. Applying HMM analysis to photobleaching of multiply labeled dextran, a system with a known average degree of labeling, we showed that one is able to accurately determine the number of molecular constituents, making this method applicable to many experiments related to aggregation, multimolecular, or assembly processes. From simulations and information theory, we have shown it is possible to extend our experimental results to systems with much higher multiplicity (as high as 30) and provided a framework for determining when the information content is sufficient for making certain inferences.

We analyzed our data using the simplest two-state model possible. The HMM reconstructed trajectories provide state-to-state dwell times. Dwell time analysis (not shown here) using this two-state model resulted in non-Makovian dynamics. Analysis of the multiexponential (non-Markovian) dwell time results is currently underway to identify the nature of the hidden states. We aim to determine whether oxygen or triplet states play a role in these TMR-dextran photobleaching dwell times by studying these polymers in the presence of reducing agents (dithiolthriotol and β-mercaptoethanol) and triplet quenchers (cystamine). These results will be the subject of a forthcoming paper.