The Kinematic Filling Efficiency Index of the Left Ventricle: Contrasting Normal vs. Diabetic Physiology

Abstract

An index of filling efficiency incorporating stiffness and relaxation (S&R) parameters has not been derived or validated although numerous studies have focused on the effects of altered relaxation or stiffness on early rapid filling and diastolic function. Previous studies show that S&R parameters can be obtained from early rapid filling (Doppler E-wave) via kinematic modeling. E-wave contours are governed by harmonic oscillatory motion, modeled via the parameterized diastolic filling (PDF) formalism. The previously validated model determines three (unique) oscillator parameters from each E-wave having established physiologic analogues: x_o (load), c (relaxation/viscoelasticity), and k (chamber stiffness). We define the dimensionless, filling-volume based kinematic filling efficiency index (KFEI) as the ratio of the velocity-time integral (VTI) of the actual clinical E-wave contour fit via PDF to the VTI of the PDF model-predicted ideal E-wave contour having the same x_o and k, but with no resistance to filling (c=0). To validate the new index, Doppler E-waves from 36 subjects with normal ventricular function, 17 diabetic and 19 well-matched non-diabetic controls, were analyzed. E-wave parameters x_o, c, and k and KFEI were computed for each subject and compared. In concordance with prior human and animal studies in which c differentiated between normal and diabetic hearts, KFEI differentiated (p<0.001) between non-diabetics (55.8±3.3%) and diabetics (49.1±3.3%). Thus, the new index introduces and validates the concept of filling efficiency, and using diabetes as a working example, provides quantitative and mechanistic insight into how S&R affects ventricular filling efficiency.

Introduction

It is well-known that in certain dysfunctional hearts, the Doppler E-wave exhibits a ‘delayed relaxation’ pattern (Kameyama et al. 1992, Riordan et al. 2005). The concomitant alterations of chamber physiology, which generate this ‘delayed relaxation’ pattern, result in a reduction of the volume of blood aspirated by the left ventricle (LV) during early rapid filling. This results in an alteration of E-wave shape and reduction of the E/A ratio.

Diabetic cardiomyopathy is characterized clinically by ventricular hypertrophy and impaired diastolic function, which may precede the onset of systolic dysfunction (Borbély et al. 2005, Dent et al. 2001, Dhalla et al. 1998, Dhalla et al. 1985, Gustafsson et al. 2001, Mahgoub et al. 1998, McNeill et al. 1986, Riordan et al. 2005). However, while diabetes is associated with altered cellular structure and extracellular matrix disorganization (Thompson 1994), the effects of such physiologic alterations on diastolic function have not been fully characterized prior to the overt manifestation of diabetic cardiomyopathy, particularly in the setting of normal left ventricular ejection fraction (LVEF).

Though much work has been devoted to understanding how the velocity contour of the E-wave changes in both disease and aging, the concept of diastolic filling efficiency has not been previously considered. One of the reasons for this conceptual gap is that no idealized framework for ventricular filling, representing 100% efficiency, has been theoretically proposed or empirically observed. In previous work, we have derived and validated the Parametrized Diastolic Filling (PDF) formalism, a kinematic model that extracts physiologic parameters from the E-wave contour (Kovács et al. 1987). Each contour is uniquely determined by three (lumped) parameters: a relaxation/viscosity parameter c, a stiffness parameter k, and a load parameter x_o. The framework of the PDF model characterizes filling in terms of a driving force (the atrioventricular pressure gradient), a damping/viscous force that resists transmitral flow, and an inertial force. Since, from a kinematic modeling perspective, an increased relaxation/viscosity constant c generates increased damping (opposing filling), a natural choice for ideal ventricular filling is a kinematic scenario without damping (c=0). New insight is provided by the union of the physiology of diastole and a kinematic model that relates cause (stiffness, relaxation, load) to effect (transmitral flow). Specifically, the physiologic concept of idealized or optimal filling (frictionless in the modeling sense) has never been proposed. In this study, we define an index of filling efficiency by considering the dimensionless ratio of actual volume entering the LV (velocity-time integral (VTI) of real E-wave) to the ideal volume (VTI of ideal E-wave (c=0)). We show that a new, kinematic filling efficiency index (KFEI) can be derived through a simple mathematical relationship between c and k. Additionally, to determine utility, we assess the ability of KFEI to differentiate E-waves in diabetic subjects from those in normal subjects. This work is motivated in part by previous results showing that the relaxation/viscosity parameter c differentiates between the filling patterns of diabetic and non-diabetic hearts, all with normal LVEF (Dent et al. 2001, Riordan et al. 2005).

Analysis of transmitral flow contours (Doppler E-waves) via the PDF formalism (Hall et al. 1994a, Hall et al. 1993, Hall et al. 1994b, Hall et al. 1998, Kovács et al. 1987, Kovács et al. 2000, Lakshminarayan et al. 1993) has shown that diabetes alters the relaxation parameter c of early rapid filling in both rats (Dent et al. 2001) and humans (Riordan et al. 2005). Importantly, these two studies showed that for hearts with normal LVEF, conventional E-wave indexes such as peak E-wave velocity (E_peak) or deceleration time (DT) were unable to differentiate between normal and diabetic filling patterns, whereas the relaxation/viscosity parameter c differentiated between normal (lower c) and diabetic subjects (higher c). Recently, a simultaneous catheterization-echocardiography human study showed that this same kinematic relaxation parameter c is linearly related to active relaxation characterized by τ, the time-constant of isovolumic relaxation (Chung et al. 2006).

The PDF formalism models early LV filling in analogy to the motion of a damped simple harmonic oscillator (SHO) (Kovács et al. 1987). The governing equation of motion is:

$$m\frac{d^{2}x}{d{t}^2}+c\frac{dx}{dt}+kx=0$$ [1]

The formalism solves the ‘inverse problem’ of filling by providing (mathematically) unique parameters c, k, and x_o that determine each Doppler E-wave contour (Kovács et al. 2001). The initial displacement of the oscillator x_o (cm) is linearly related to the E-wave VTI (i.e. related to volumetric preload) (Kovács et al. 2000). Chamber stiffness (dP/dV) is linearly related to the SHO spring constant k (g/s²) (Kovács et al. 1997), while the oscillator’s damping constant or chamber viscoelasticity/relaxation index c (g/s) characterizes the resistance (relaxation/viscosity) of the filling process (Kovács et al. 2000). Because the formalism is kinematic and is species independent, it provides a novel, volume-based physiologic paradigm by which the efficiency of filling can be modeled and assessed.

Methods

Patient Selection

The methodology has been previously described (Chung et al. 2006, Dent et al. 2001, Kovács et al. 1997, Lakshminarayan et al. 1993, Lisauskas et al. 2001, Riordan et al. 2005). Briefly, after informed consent, in accordance with Human Studies Committee criteria via a protocol approved by the Washington University Human Studies Committee (IRB), simultaneous echocardiographic transmitral flow data and high-fidelity LV pressure were acquired. Thirty-six patients (17 with a previously established historical diagnosis of diabetes, 19 with no history of diabetes) were selected from an existing database (Lisauskas et al. 2001). All subjects (both non-diabetic and diabetic) had normal LVEF (LVEF ≥ 55%), normal sinus rhythm, clearly discernible E-waves, and normal valvular function. None of the 36 subjects had previously diagnosed diabetic cardiomyopathy, myocardial infarction, peripheral vascular disease, bundle branch block, ongoing ischemia, congestive heart failure or any other discernible cardiovascular co-mobidities (other than diabetes or treated hypertension) determined clinically or by LVEF. All subjects were normotensive at the time of data acquisition; some were normotensive by history, while others were on anti-hypertensive medicines. There was no difference between the number of subjects on anti-hypertensive agents between groups. Specifically, 9 of the subjects in each group were on anti-hypertensive agents at the time of data acquisition. The selection criterion for inclusion in the diabetic group was based on the previously established diagnosis (and associated treatment) for elevated blood sugar as documented by medical record review. The duration of diabetes was not specifically recorded.

Transmitral Doppler images were obtained using a standard clinical imaging system (Acuson, Mountain View, CA). With the patient supine, apical four-chamber views were obtained with the sample volume gated at 1.5 to 2.5 mm and placed at the tips of the mitral valve leaflets with the insonification direction orthogonal to the valve plane using color Doppler as a guide. The data were acquired in accordance with American Society of Echocardiography standard 2D/Doppler echocardiographic guidelines (Gottdiener et al. 2004). The wall filter was set at 125 Hz or 250 Hz, the baseline adjusted to take advantage of the full height of the CRT display, and the velocity scale adjusted to exploit the dynamic range of the output without aliasing. Simultaneous limb lead II ECG was displayed on all images. Images were captured simultaneously with LV pressure data and recorded continuously via VHS or magneto-optical disk. Images were digitized offline via a dedicated custom video capture station. Five beats of transmitral flow were analyzed for each subject. LVEDP, LVEF and LVEDV were determined from clinical catheterization data. Acquired data reflected steady-state physiology, and load was not varied in accordance with the IRB approved protocol.

Kinematic Modeling of Filling

The PDF formalism uses a linear, bi-directional spring to approximate early filling according to the kinematics of a damped SHO. In accordance with Newton’s second law, the equation of motion for a SHO is given by Eq. 1 (Kovács et al. 1987). Because the E-wave has zero initial velocity, the SHO initial velocity is zero (v(0)=0). However, the SHO has a non-zero initial spring displacement, x_o. Systole stores elastic strain energy, which at mitral valve opening, is available as potential energy to power the mechanical recoil, ventricular suction process. Setting m=1 in Eq. 1 allows calculation of parameters c and k per unit mass. The contour of the clinical E-wave is predicted by the underdamped solution for the velocity of a damped oscillator, given by:

$$v(t)=-\frac{x_{o}k}{\omega m}{e}^{-\alpha t}sin(\omega t)$$ [2]

where α = c/2m, $\omega =\sqrt{4mk-c^2}/2m$. Determination of PDF parameters from each E-wave by solving the ‘inverse problem’ results in a unique solution for x_o, c, and k (Hall et al. 1993, Kovács et al. 2001) for each E-wave contour. Additional PDF-derived indexes denote the stored elastic strain energy driving ventricular suction (1/2kx_o²) and the peak atrio-ventricular pressure gradient (kx_o) (Kovács et al. 1987). PDF parameter values for x_o, c, and k were determined using the Levenberg-Marquardt algorithm fit (Press et al. 1992) to the maximum velocity envelope via a custom LabVIEW (National Instruments, Austin, TX) interface (Chung et al. 2006, Dent et al. 2001, Hall et al. 1994a, Kovács et al. 2000, Riordan et al. 2005).

Kinematic Filling Efficiency Index

Optimal diastolic function maximizes filling volume relative to available stored elastic strain energy at mitral valve opening. The actual kinematic process of ventricular filling is necessarily accompanied by energy-loss phenomena (viscoelasticity and relaxation), whose components can be characterized in biological or physical terms. The model-based image processing (MBIP) determined fit to actual E-waves always generates a non-zero value for c. This reflects the fact that part of the stored elastic strain energy that initiates ventricular filling via mechanical suction is dissipated during early filling. The consequence of a non-zero value for the parameter c (c≠0) manifests in the E-wave contour in three easily understood ways. First, relative to an ideal, model-predicted lossless (c=0) filling contour, which has the shape of an undamped sine wave, a non-zero value for the viscosity term reduces the peak amplitude of the E-wave. Second, it shortens the acceleration time of the E-wave contour by shifting the peak closer to the onset of filling (Riordan et al. 2005). Third, it introduces an inflection (d²v/dt² = 0) in the deceleration portion of the E-wave, which is usually disregarded in conventional E-wave analysis where E-wave shape is approximated as a triangle. Because the triangle approximation disregards the inflection, the slight lengthening of the deceleration is not appreciated (Dent et al. 2001, Riordan et al. 2005). Reduction of the peak of the E-wave decreases the VTI of the E-wave contour. Assumption of a constant effective mitral valve area relates the VTI directly to the volume of blood entering the ventricle during early filling.

The effect of c≠0 on filling can be assessed by comparing the VTI of a model-predicted ideal or optimal (lossless) E-wave contour generated by the same numerical values for x_o and k, but with c=0 in Eq. 2 and the actual VTI of the same E-wave with c≠0. According to Eq. 2, the contour of an ideal E-wave is a simple sine wave with a slightly shorter period and higher peak velocity than the actual clinically fit E-wave, i.e.:

$$v(t)=-\frac{x_{o}k}{{\omega }^{\prime }m}sin({\omega }^{\prime }t)$$ [3]

where ${\omega }^{\prime }=\sqrt{k/m}$. Fig. 1 illustrates typical E-waves for a non-diabetic and diabetic subject and the corresponding fit to each E-wave contour generated by the solution of Eq. 2 using best-fit PDF parameters. For each subject, the ideal E-wave contour generated using the same values for x_o and k, but with c=0 (Eq. 3), is superimposed. Although the E-wave deceleration times for these two patients in Figure 1 are comparable (Riordan et al. 2005), the shapes of the deceleration portions, which carry information on (c-dependent) energy loss during filling, are different.

Figure 1.

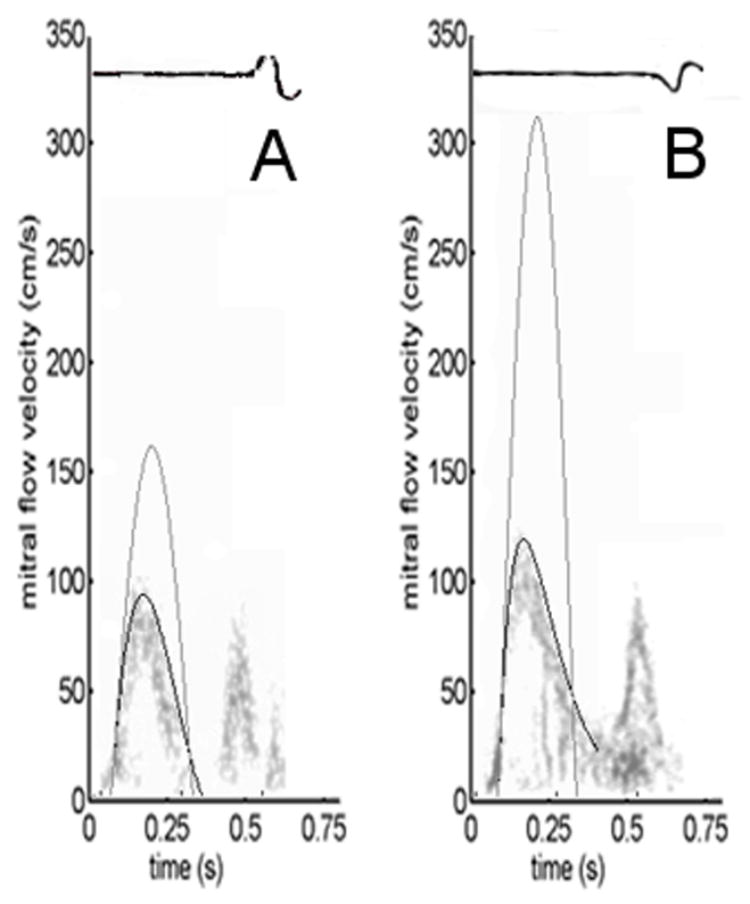
Comparison of actual (c≠0) vs. idealized (c=0) E-waves for both a) non-diabetic and b) diabetic subjects (having similar chamber stiffness parameter k). The ratio of the VTIs (areas) of the respective actual (black) and idealized (gray) contours defines the kinematic filling efficiency index KFEI. a) Non-diabetic E-wave parameters: x_o=−6.0 cm, k=244/s², c=9.9/s. b) Diabetic E-wave parameters: x_o=−20.3 cm, k=228/s2, c=27.7/s. The diabetic E-wave, with higher c, generates a visible inflection point in the deceleration portion (around 0.25 s in panel b). Note that stiffness parameter k remains indistinguishable between clinical and ideal contours. See text for details.

We define the filling volume based (dimensionless) kinematic filling efficiency index (KFEI) as the ratio of the VTI of the clinical E-wave contour fit via PDF (c≠0) and the VTI of the PDF predicted ideal E-wave contour with the same x_o and k, but with viscoelastic parameter c=0. Mathematically, KFEI is defined as:

$$\mathit{KFEI}=\frac{\underset{0}{\overset{\mathit{Edur}}{\int }}{v}_{c\ne 0}dt}{\underset{0}{\overset{\mathit{Edur}}{\int }}{v}_{c=0}dt}=\frac{\underset{0}{\overset{\mathit{Edur}}{\int }}\frac{x_{o}k}{\omega }{e}^{-\alpha t}sin(\omega t)dt}{\underset{0}{\overset{\mathit{Edur}}{\int }}\frac{x_{o}k}{{\omega }^{\prime }}sin({\omega }^{\prime }t)dt},$$ [4a]

for underdamped (4k>c²) E-waves which end prior to the onset of the A-wave where E_dur is the duration of the E-wave (E_dur = π/ω). After analytically calculating the integrals in the numerator and denominator, KFEI can be expressed as:

$$\mathit{KFEI}=\frac{1+e^{-\frac{c}{2}\times \mathit{Edur}}}{2}=\frac{1+e^{-\frac{c\pi }{\sqrt{4k-c^2}}}}{2}$$ [4b]

For overdamped E-waves (4k<c²), that exhibit delayed relaxation and merged E- and A-waves, KFEI can be lower than the limiting value of Eq. 4b, which is 0.5, because E_dur is taken as the time between the onset of E-wave and A-wave. In such cases, KFEI is calculated directly from Eq. 4a.

Statistical Analysis

As in previous work (Riordan et al. 2005), we compared diabetic and non-diabetic subjects on the basis of traditional echocardiographic and hemodynamic indexes (LVEDP, LVEF, and E_peak and DT) and expected no difference. We also compared PDF derived parameters (c, k, x_o) and related indexes (kx_o, 1/2kx_o²) and expected no significant difference in stiffness (k), but significant differences in relaxation/viscosity (c), peak atrioventricular pressure gradient (kx_o) and stored energy (1/2kx_o²). Five beats were analyzed for each subject and average values were calculated for comparison.

KFEI was calculated from derived parameters as described above [Eq. 4b]. While most subjects (n=32 of 36) had clearly separated E- and A-waves, 4 subjects exhibited merged waves due to delayed relaxation, resulting in KFEI values of <50%. The model-predicted KFEI vs. c relation [Eq. 4b] was also tested using data from all subjects whose E-waves were fit by Eq. 2. Linear least-squares fitting was employed to determine the relationships between KFEI and other parameters such as age, x_o and k for both the non-diabetic and diabetic groups. P-value of the linear least-squares fitting intercept is calculated.

Results

The clinical descriptors and PDF parameters for the non-diabetic and diabetic groups are listed in Table 1. Statistics are concordant with those previously reported (Riordan et al. 2005). No conventional index was able to differentiate between groups, viscosity/relaxation parameter c differentiated among the groups in concordance with previous results (Dent et al. 2001, Riordan et al. 2005). VTI and KFEI for both groups are listed in Table 2. KFEI differentiated between the diabetic and non-diabetic groups (p<0.001), but does not appear to have any meaningful correlation with LVEDP, LVEF, LVEDV, etc (data not shown).

Table 1.

Clinical descriptors and PDF parameters for non-diabetic and diabetic groups.

	Non-Diabetic (n=19, 15 male)	Diabetic (n=17, 11 male)	p value
Age (y)	50 ± 10	55 ±11	NS
Heart Rate (bpm)	66 ± 12	71 ± 10	NS
Ejection Fraction(LVEF) (%)*	67 ± 8	70 ± 10	NS
LVEDV (ml)	162 ± 47	170 ± 50	NS
LVEDP (mm Hg)	14 ± 3	16 ± 6	NS
Peak E-wave Velocity Epeak(m/s)	0.68 ± 0.10	0.75 ± 0.19	NS
E-wave Deceleration Time DT (ms)	163 ± 61	223 ± 75	NS
− xo(cm)	9.3 ± 1.9	12.3 ± 3.6	0.01
k (s−2)	206 ± 54	219 ± 56	NS
c (s−1)	16.6 ± 3.9	26.3 ± 4.6	<0.001
kxo (dynes)	−1840 ± 390	−2650 ± 860	<0.01
(1/2)kxo2(ergs)	8570± 2480	17280 ±9880	<0.01

^*LVEF determined by ventriculography

Data are presented as mean ± (SD)

LVEDV = Left ventricular end-diastolic volume from ventriculography

Table 2.

Velocity time integrals (VTI) and KFEI for diabetic and non-diabetic subjects

	Non-diabetic (n=19)	Diabetic (n=17)	p-value
VTI (c ≠ 0) (cm)	10.3± 1.8	12.0 ± 3.3	NS
VTI (c = 0) (cm)	18.6± 3.7	24.7 ± 7.1	<0.01
KFEI (%)	55.8 ± 3.3	49.1 ± 3.3	<0.001

Data are presented as mean ± (SD)

As shown in Eq. 4b, KFEI is a function of both c and k while the increase of relaxation/viscosity c directly increases the energy loss and lowers KFEI. To provide a graphical demonstration of the dependence of KFEI on the parameter c, we used the mean value of x_o for all the subjects and three different k values (mean and mean ± standard deviation of 32 subjects having separated (underdamped) E- and A-waves) to obtain the mathematically predicted curves (Eq. 4b) relating KFEI and c, as shown in Fig. 2 (The four diabetic subjects that don’t fall into ‘underdamped’ regime (c²<4k) and with merged E- and A-waves are not included in Fig. 2 and Fig. 3, but are included in Fig. 4). This range of k values, consisting of the mean (k=217 1/s²), bracketed above and below by one standard deviation (k=163 to 272 1/s²), represents the physiologic range in the 32 (19 non-diabetic, 13 diabetic) of 36 subjects whose E-waves fell into the underdamped (4k > c²) regime. Clinically measured KFEI versus c is plotted on the same graph; note the displacement among the three contours, accounted for the dependence of KFEI on k. We plotted the model-predicted KFEI versus c curves using three different k values to show the extent to which the clinical data agrees with our model-predicted relation between KFEI and c. This figure shows the dependence of KFEI on c within the k value in this study.

Figure 2.

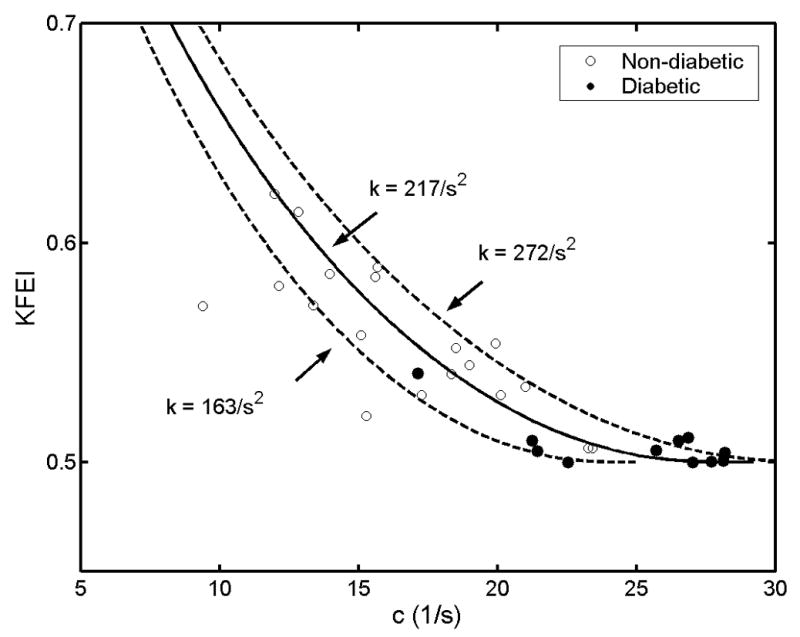
Predicted dependence of KFEI on c. The predicted curve was based on average values of x_o for the group (x_o=−10.3 cm) of diabetic and non-diabetic subjects with unmerged E-waves fit by Eq. 2a (‘underdamped’ c²<4k, kinematics, n=13 for diabetic subjects, n=19 for non-diabetic subjects). Three curves correspond to three different k values (average - solid line [k=217/s²], average ± standard deviation - dashed lines [k=163 and 272/s²]). Hollow circles denote non-diabetic subjects; Solid circles denote diabetic subjects. See text for details.

Figure 3.

The relation between KFEI and chamber stiffness (k) in the same subjects as in Figure 2, whose E-waves are fit by ‘underdamped’ kinematics (c²<4k) (19 non-diabetics = open circles, 13 diabetics = solid circles). Black circles denote non-diabetic subjects, solid circles denote diabetic subjects. Note tendency of solid circles to reside near the bottom of the figure. KFEI as a function of k, for three different, but constant, values of viscoelasticity/relaxation c are also shown (mean = 20.3/s solid; mean + 1SD = 26.2/s dashed, mean−1SD= 14.4/s dashed). Consider the 6 data points (3 solid circles, 3 open circles) closest to the solid line, e.g. 6 data points with c values very near c=20.3/s (within the black rectangle), Note k values for these 6 subjects are quite different, ranging from 150 (1/s²) to 300 (1/s²). This illustrates the effect of k on KFEI when c is essentially unchanged. For these 6 subjects c would not differentiate between the groups as well as KFEI. See text for details.

Figure 4.

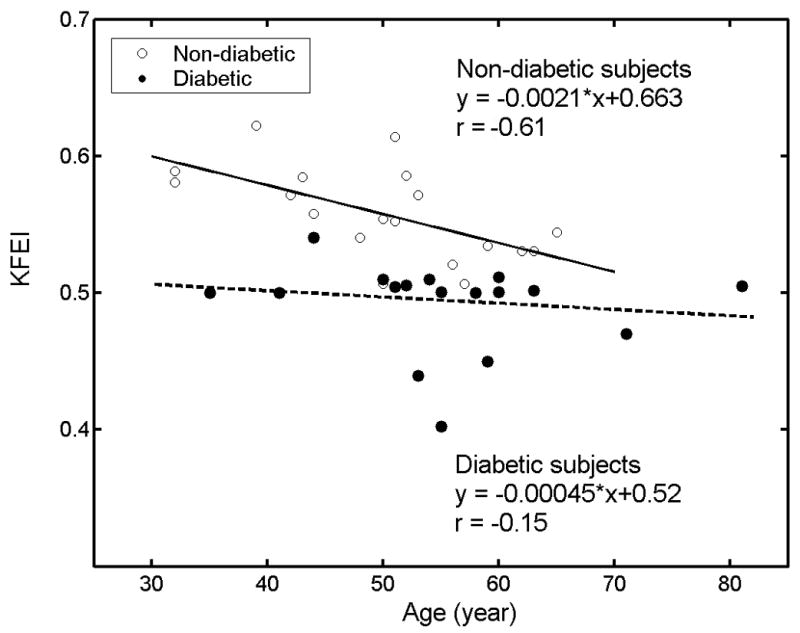
The relation between KFEI and age for all subjects. 19 open circles = non-diabetic group, solid line, linear regression between KFEI and age in non-diabetic group, 17 solid circles = diabetic group, dashed line, linear regression between KFEI and age in diabetic group. The diabetic group appears to ‘age’ (KFEI decreases) more rapidly than subjects without diabetes. See text for details.

Because KFEI is mainly dependent on c, it was not significantly dependent on k (r = 0.06, p=0.80 in controls, r = 0.32, p=0.22 in diabetics) statistically in this study. However as shown by Eq. 4b, KFEI depends on the stiffness k, in the mathematical sense. In Fig. 3, we show KFEI as a function of k for three different, but constant, values of viscoelasticity/relaxation c (mean = 20.3/s, solid; mean + 1SD = 26.2/s, dashed; mean − 1SD = 14.4/s, dashed). The subjects plotted on this figure are the same as those in Fig. 2. The superposition of the lines of constant viscoelasticity (c) in the figure more clearly shows why stiffness (k) is an important factor in KFEI. Considering the 6 points (3 solid circles, 3 open circles) closest to the solid line, e.g. 6 data points with c values very near c=20.3/s (within the black rectangle), we see that the values of k for these 6 subjects are quite different, ranging from 150 (1/s²) to 300 (1/s²), and that KFEI is also different, varying from 50% to 55%. Subjects with the same c can have different KFEI purely due to having different values of k since KFEI is mathematically determined by both stiffness k and viscoelasticity/relaxation c.

KFEI is the dimensionless ratio of two stroke volume analogues. As shown in Eq. 4b, there is no algebraically simple mathematical relationship between x_o and KFEI. Nevertheless, we observe a positive correlation between KFEI and x_o in both the non-diabetic (r = 0.49, p<0.05) and diabetic groups (r = 0.44, p = 0.08). The weak relations obtained are due to the physiology-imposed relationship between x_o, c and k.

Figure 4 illustrates the relationship between KFEI and age for all the subjects in both the non-diabetic and diabetic groups. KFEI shows a significant negative correlation with age in the non-diabetic group (r = −0.61, p<0.01). Disease breaks the age correlation, resulting a non significant regression relationship in the diabetic group (r = −0.15, p=0.57). In concert with the relation between KFEI and age, c correlates well with age in the non-diabetic group (r= 0.54, p=0.02) and non-significantly in the diabetic group (r = −0.098, p=0.71) (not shown in Fig. 4).

Discussion

None of the myriad of phenomenologic Doppler echo-based parameters proposed to date for diastolic function characterization involves the concept of efficiency (Gilbert et al. 1989, Little et al. 1990). Accordingly, by deriving an efficiency-based index from a predictive, kinematic (species-independent) model of filling that can be determined using routine echocardiography, we sought to characterize the filling process in a causal, rather than correlative terms. The conceptual advance of devising an optimal velocity contour permits comparison of ‘actual physiology’ to ‘ideal physiology’ in numerical and functional terms and computation of a dimensionless efficiency index. One of the reasons why filling efficiency has not been well characterized previously is because there was no established framework for ideal filling. According to the first law of thermodynamics,

$$\mathrm{\Delta }U=Q-W$$ [5a]

where ΔU is the increase in the internal energy of the system, Q is the heat added to the system, and W is the work done by the system on the environment (Young et al. 2004). Diastolic filling is powered by the stored potential strain energy at end-systole (Helmes et al. 1996, Katz 1930, Robinson et al. 1986), and its release is modulated by Ca²⁺ cycling (Kass et al. 2004). For the LV during diastole,

$$\mathrm{\Delta }PE=W+Q$$ [5b]

where ΔPE represents the change in potential energy during diastolic filling, W represents the work done by the LV in aspirating blood from the left atrium and including mitral annulus displacement and tissue deformation, etc., and Q represents all mechanisms by which energy is converted to heat during the filling process. Optimal filling corresponds to maximizing work W and minimizing Q or E_loss (wasted energy). More explicitly,

$$E_{\mathit{total}}=E_{\mathit{potential}}+E_{\mathit{kinetic}}+E_{\mathit{loss}}$$ [6a]

At the initiation of transmitral flow, stored elastic (potential) energy manifests as mechanical suction (dP/dV < 0) that generates the atrioventricular pressure gradient, thereby converting potential energy into kinetic energy by moving the tissue and accelerating the blood into the ventricle. The total energy is conserved according to Eq. 6a, as energy in the system is converted from potential to kinetic and viscous losses. During the actual filling process, a certain amount of energy must always be dissipated due to damping/viscosity in accordance with the Second Law (i.e. the process is thermodynamically irreversible). We now invoke the PDF paradigm, where motion is driven by a bi-directional, linear spring, and re-express Eq. 6a as:

$$\frac{1}{2}k{x}_o^2=\frac{1}{2}k{(x_o+x)}^2+\frac{1}{2}m{v}^2+\underset{0}{\overset{x}{\int }}\mathit{cvdx}$$ [6b]

In the second term on the right hand side of Eq. 6b, m is normalized to 1 as in PDF model. Notice that the last term of Eq. 6b corresponds to heat Q in Eqs. 5a and 5b. Optimal filling is achieved only when the viscoelastic/relaxation parameter c=0, which we define as ideal filling. The corresponding filling volume, i.e. VTI, is the maximum possible volume that could be aspirated into the ventricle using the available end-systolic potential elastic strain-energy.

In this work, we define the kinematic filling efficiency index as the ratio of actual blood volume (VTI) entering the ventricle during early filling to the ideal, maximum possible volume (VTI) that an E-wave could deliver using the same end-systolic potential energy (1/2kx_o²). This index conveys the modulating effect that the viscoelasticity/relaxation parameter c has on the filling volume (VTI). We apply it in the in-vivo physiologic setting to the clinically and physiologically challenging problem of: “Can the proposed KFEI differentiate between normal and abnormal hearts that are otherwise indistinguishable?” As shown in Table 1, all of the diabetic and control subjects had clinically similar physiologic function (e.g. ejection fraction) and no evidence that diabetes was affecting their heart function. Hence conventional echocardiographic parameters (EF, E_dur, E_peak, DT, EDV) were unable to differentiate between the groups. The new KFEI, however, can differentiate between the groups. Although in percentage terms, the difference between groups was a modest 7% in absolute terms, discriminating between groups is assured because the p-value for KFEI between the diabetic and non-diabetic groups was p<0.001. The previously reported ability of c (Riordan et al. 2005) and our current finding of the ability of KFEI to discriminate between non-diabetic and diabetic groups yield essentially the same results, i.e. p<0.001. However, the advantage of KFEI relative to the viscoelasticity/relaxation parameter c is that c is an absolute measure obtained from E-wave fitting and thus cannot convey direct information about filling efficiency. In contrast, KFEI is dimensionless and in this particular pathophysiologic group having diabetes, whose filling is primarily c, rather than k dependent, represents the effect of viscoelasticity/relaxation on filling efficiency, KFEI conveys the concept of efficiency as a numerical percentile index, which is widely understood and accepted.

The dependence of KFEI on stiffness k is not statistically significant in our results due to the extent to which the diabetic data set is only modestly k dependent. However, as shown in Figs. 2 and 3, the relationship between KFEI and c or k is not assured. For instance, in Fig. 3, we see up to six data points with constant c values, but varying KFEI and k values, suggesting the importance of KFEI as a more inclusive index of ventricular function. Importantly, datasets for different pathologic groups (hypertensives, for example) may be highly stiffness (k) dependent but only modestly viscoelasticity (c) dependent. KFEI could accommodate these parameter-dependent variations.

As expected, model-based analysis shows that KFEI (Eq. 4b) in diabetics is primarily a function of viscoelasticity/relaxation. It has the limiting value of 1 (100% efficiency) as c approaches 0. It decreases exponentially to the 0.5 range (50% efficiency) for larger c (especially in the diabetic group). For E-waves exhibiting a delayed relaxation pattern, the A-wave usually starts before the E-wave velocity reaches zero; hence, the calculated KFEI could be less than 50%. Using an energy-based paradigm, 100% efficiency means that all of the potential energy (1/2kx_o²) available at mitral valve opening is converted to kinetic energy of motion (i.e. into transmitral flow), thereby maximizing filling volume relative to the energy available. A volume-based efficiency of around 50% is not physiologically unreasonable. As mentioned in Kameyama et al. (Kameyama et al. 1992), the mechanical efficiency during the cardiac cycle among normal subjects is about 22%. Therefore, the kinematic filling efficiency (KFEI) of early filling is higher than that of the whole cardiac cycle. Also, the total work efficiency of the whole cardiac cycle has been reported to be 69%, which is comparable in magnitude with the kinematic filling efficiency (Kameyama et al. 1992).

We noticed that KFEI has a strong negative correlation with age in non-diabetic patients as shown in Fig. 4. Previous work shows that conventional Doppler indexes of diastolic function in non-diabetic subjects change dramatically with age (Benjamin et al. 1992). The current result is consistent with previous research which shows impaired relaxation to be a feature of aging (Benjamin et al. 1992). The negative correlation between KFEI and age is indicative of the established, age-associated decline of diastolic function in terms of the efficiency of early filling. If we take the negative linear correlation in non-diabetic subjects as a reference, the average KFEI for the diabetic group gives a nominal age of 81, while their actual average age is 55±11. Thus, a pathophysiological state such as diabetes appears to expedite the age-related alteration in relaxation, affecting filling. That the expected age-related decrease in diastolic function can be delayed or even reversed by caloric restriction has only recently been reported.

The effect of diabetes on the heart is multifactorial (Mahgoub et al. 1998, McNeill et al. 1986, Poornima et al. 2006). In general, the diagnosis of diabetic cardiomyopathy is based on impairment of LVEF. Previous work has established that diabetes has a discernible effect on diastolic function. Specifically, analysis of filling in diabetic rat and human hearts compared to non-diabetic controls using the PDF formalism has shown that diastolic function is affected by diabetes through an increase in the value of the PDF parameter c with k unchanged (Dent et al. 2001, Riordan et al. 2005). This suggests that, even in the pre-clinical (LVEF>55%) stages, diabetes alters filling efficiency primarily through viscoelasticity or relaxation (c-dependent) rather than chamber stiffness (k-dependent) mechanisms. The net result is an alteration in the ability to deliver a specific filling volume via mechanical suction-initiated filling. Our choice of diabetes as a working example was arbitrary; any other pathophysiologic group can be selected. Parenthetically, KFEI could be used to determine efficiency in other clinical groups such as hypertensives, cardiomyopathies, congenital anomalies, and mitral stenosis, etc. In this study, LVEDP did not differ between the two groups. As a result, KFEI cannot function as a ‘pseudo-normal pattern’ detector in these subjects. It will be interesting to apply KFEI to pseudo-normalized subjects to elucidate the underlying mechanisms in terms of efficiency.

Because the derivation of the index is species-independent, it can also be used in animal studies, including genetically altered species, as well as tests of pharmacologic agents that affect heart function.

Study Limitations

Data acquisition was conducted while subjects were in physiologic steady-state during catheterization. In light of the data acquisition methodology as part of diagnostic catheterization, alteration of load was not part of the IRB approved protocol. Accordingly, the load dependence of the kinematic filling efficiency index cannot be assessed. Future studies will need to be performed to evaluate load dependence.

Blood viscosity has been observed to be higher in diabetic subjects (Savage 1996). This effect might contribute to higher c values in diabetics. While in this study blood viscosity was not explicitly measured, Hb/Hct values were not significantly different between the diabetic and non-diabetic groups (data not shown),

Because the focus of this work was a global diastolic function, i.e E-wave derived diastolic filling efficiency index, we did not examine Doppler Tissue Imaging (DTI) measurements of annular motion –which reflect regional i.e. longitudinal function.

Additionally, whether efficiency is decreased in other pathologic groups (hypertension, amyloidosis, congenital heart disease, etc), as we expect, and if so, is it due to changes in k, c or x_o or a combination of these is not yet known, nor can we predict this from first principles. Accordingly, determination of KFEI in other well-defined pathophysiologic groups has merit.

Conclusion

The filling-volume based dimensionless, kinematic filling efficiency index (KFEI) is defined as the ratio of the VTI of the actual clinical E-wave contour and the VTI of an ideal (lossless) E-wave having the same PDF parameters (x_o, k) but with the viscosity parameter c=0. Because the dependence of KFEI on c is that of a decaying exponential, E-waves having greater values of c have lower filling efficiencies. As previously observed in normal LVEF human and animal studies for the parameter c, KFEI differentiated between diabetics and non-diabetic controls, whereas conventional indexes such as E_peak and DT did not. KFEI characterizes the modulating effect of both stiffness and viscosity/relaxation on E-wave VTI and elucidates the manner in which it affects filling efficiency. Diabetes decreases filling efficiency in subjects with normal LVEF relative to non-diabetic controls by increasing chamber viscous losses while maintaining chamber stiffness relatively unaltered. The load dependence of KFEI is under investigation.