Different levels of I_h determine distinct temporal integration in bursting and regular-spiking neurons in rat subiculum

Abstract

Pyramidal neurons in the subiculum typically display either bursting or regular-spiking behaviour. Although this classification into two neuronal classes is well described, it is unknown how these two classes of neurons contribute to the integration of input to the subiculum. Here, we report that bursting neurons posses a hyperpolarization-activated cation current (I_h) that is two-fold larger (conductance, 5.3 ± 0.5 nS) than in regular-spiking neurons (2.2 ± 0.6 nS), whereas I_h exhibits similar voltage-dependent and kinetic properties in both classes of neurons. Bursting and regular-spiking neurons display similar morphology. The difference in I_h between the two classes of neurons is not responsible for the distinct firing patterns, as neither pharmacological blockade of I_h nor enhancement of I_h using a dynamic clamp affects the qualitative firing patterns. Instead, the difference in I_h between bursting and regular-spiking neurons determines the temporal integration of evoked synaptic input from the CA1 area. In response to stimulation at 50 Hz, bursting neurons, with a large I_h, show ∼50% less temporal summation than regular-spiking neurons. The amount of temporal summation in both neuronal classes is equal after pharmacological blockade of I_h. A computer simulation model of a subicular neuron with the properties of either a bursting or a regular-spiking neuron confirmed the pivotal role of I_h in temporal integration of synaptic input. These data suggest that in the subicular network, bursting neurons are better suited to discriminate the content of high-frequency input, such as that occurring during gamma oscillations, than regular-spiking neurons.

The subiculum functions as the main output structure of the hippocampus proper and gets its main inputs from the CA1 area and the entorhinal cortex as well as from other subcortical and cortical areas. Functionally, the subiculum plays a role in certain forms of spatial memory and in mnemonic processing (O'Mara et al. 2001). The identification of the electrophysiological properties of subicular neurons has led to a categorization into bursting and regular-spiking neurons (Taube, 1993; Stewart & Wong, 1993; Mason, 1993) but there are controversies concerning the ion currents responsible for the intrinsically generated bursting behaviour. Some studies suggest that a Ca²⁺-dependent conductance is responsible for bursting, because TTX-resistant spikes and humps are present in bursting neurons (Stewart & Wong, 1993; Taube, 1993). In contrast, others (Mattia et al. 1993, 1997) have suggested that a Na⁺ conductance is responsible for burst generation, whereas Ca²⁺-dependent K⁺ conductances might be important for burst termination. More recently, it has been suggested that a Ca²⁺ tail current, mediated by multiple Ca²⁺ channel subtypes, drives bursting (Jung et al. 2001).

Independent from the discussion on which conductance underlies the ability to fire bursts in subicular neurons, few studies have compared the electrophysiological properties of the two classes of neurons in detail and, to date, no study compared the functional roles of specific voltage-gated conductances in the two classes of subicular neurons. However, the studies that have examined the electrophysiological properties of subicular neurons suggest that there are no obvious differences between the two classes (Taube, 1993; Stewart, 1997; Staff et al. 2000). The only distinct difference between bursting and regular-spiking neurons that has been reported is the lack of a prominent sag and of rebound potentials in regular-spiking neurons (Stewart & Wong, 1993; Greene & Totterdel, 1997; Menendez de la Prida et al. 2003), although others have not shown this difference (Taube, 1993; Behr et al. 1996; Staff et al. 2000). Depolarizing sags are caused by the activation of the hyperpolarization-activated cation current (I_h) (Pape, 1996; Robinson & Siegelbaum, 2002). We therefore investigated whether bursting and regular-spiking neurons express different levels of I_h and whether I_h displays similar properties in both classes of subicular neurons. As I_h has an important role in synaptic integration in both hippocampal and neocortical pyramidal neurons (Magee, 1998, 1999; Williams & Stuart, 2000; Berger et al. 2001), we also studied the temporal summation of synaptic input from the CA1 area in subicular bursting and regular-spiking neurons. We show that I_h in bursting neurons has a two-fold larger conductance than I_h in regular-spiking neurons, whereas the voltage-dependent and kinetic properties of I_h do not differ between the two classes of neurons. Furthermore, using a computer model of a reconstructed subicular neuron, we show that the difference in I_h is necessary and sufficient to account for the ∼50% difference in temporal summation between bursting and regular-spiking neurons as observed experimentally. Together, these results suggest that bursting neurons are better suited to discriminate the frequency content of high-frequency input than regular-spiking neurons because of their large I_h conductance.

Methods

Preparation of slices

Parasaggital slices including the hippocampus and entorhinal cortex (250 μm) were prepared from male 14- to 28-day-old Wistar rats (Harlan, Zeist, the Netherlands). Experiments were conducted according to the guidelines on animal experimentation of the Ethics Committee of the University of Amsterdam. After decapitation using a small animal guillotine without prior use of anaesthesia, the brain was rapidly removed and placed in ice-cold artificial cerebrospinal fluid (ACSF) containing (mm): NaCl 120, KCl 3.5, CaCl₂ 2.5, MgSO₄ 1.3, NaH₂PO₄ 1.25, glucose 25 and NaHCO₃ 25, equilibrated with 95% O₂–5% CO₂; pH 7.4. Subsequently, slices were cut using a vibroslicer (VT1000S, Leica Microsystems, Nussloch, Germany) and were left to recover for 1 h at 31°C. Slices were kept at room temperature (20–23°C) until use.

Electrophysiological recordings

Subicular pyramidal neurons were visualized using an upright microscope (Zeiss Axioskop FS2, Oberkochen, Germany) with Hoffman modulation contrast optics and with a VX44 CCD camera (PCO, Kelheim, Germany). Patch-clamp recordings for characterization of I_h were made at room temperature and at physiological temperatures (30–33°C) during experiments in which synaptic stimulation was performed. For whole-cell somatic recordings, patch pipettes were pulled from borosilicate glass and had a resistance of 2–4 MΩ when filled with pipette solution containing (mm): potassium gluconate 140, Hepes 10, EGTA 5, CaCl₂ 0.5, Mg-ATP 2 and sucrose 10; pH adjusted to 7.4 with KOH. For experiments in which I_h was characterized, biocytin (5 mg ml⁻¹) was added to this pipette solution. After firing characteristics were determined in current-clamp mode, 1 μm tetrodotoxin (TTX, Latoxan, Valence, France) was added and I_h was recorded in voltage-clamp mode. Cells were voltage-clamped at −50 mV and currents were evoked by hyperpolarizing voltage steps (1 s). Series resistance was 6–20 MΩ during whole-cell recordings and was compensated for by at least 80%. For cell-attached I_h recordings pipettes were filled with solution containing (mm): KCl 120, Hepes 10, MgCl₂ 1, CaCl₂ 2, tetraethylammonium chloride 20 and 4-aminopyridine 5 (pH adjusted to 7.4 with KOH) and had a resistance of 2–3 MΩ. Current signals in voltage clamp were acquired at 1 kHz and filtered at 500 Hz, whereas voltage signals in current clamp were acquired at 10 kHz and filtered at 3.3 kHz using an EPC9 amplifier and Pulse 8.31 software (HEKA Electronik, Lambrecht, Germany) run on an Apple Mac G3 computer. No correction was made for liquid-junction potentials.

Synaptic stimulation

A pair of tungsten stimulation electrodes (diameter, 70 μm), separated by ∼40 μm, was used for bipolar stimulation of the alveus on the border of CA1 and subiculum. The intensity of the 200-μs stimuli ranged from 300 to 900 μA and the distance from the site of stimulation to the recording electrode ranged from 200 to 1000 μm. Glutamatergic NMDA receptors were blocked with 50 μmd(-)-2-Amino-5-phosphonopentanoic acid and GABA_A receptors were blocked with 20 μm bicuculline methochloride. GABA_B receptors were blocked with 200 μm saclofen. For blockade of I_h, 20 μm ZD7288 was used. All chemicals were purchased from Tocris (Bristol, UK).

Dynamic clamp

A dynamic clamp, in which a model of I_h provided the I_h current depending on the actual recorded cell voltage, was used to artificially manipulate the amplitude of I_h, as previously described (van Welie et al. 2004). A PC with data acquisition card (National Instruments, Austin, TX, USA) sampled membrane voltage at 5 kHz and injected I_h with the same sampling rate. The voltage dependence and kinetics of I_h were as previously described (van Welie et al. 2004), and the amplitude of I_h was controlled by the external input gain of the recording amplifier. The static and dynamic properties of I_h in the dynamic clamp were verified with standard voltage-clamp protocols.

Morphological analysis

Cells were filled with biocytin (5 mg ml⁻¹, dissolved in the pipette solution) during recordings. Slices were fixed overnight in 4% paraformaldehyde and 1% glutaraldehyde at 4°C. After washing in PBS, slices were treated with 3% hydrogen peroxide in order to quench endogenous peroxidases and permeabilized with 2% Triton. Biocytin was visualized using an avidin–horseradish peroxidase–DAB (3,3'-Diaminobenzidine Tetrahydrochloride) reaction (ABC Elite peroxidase kit, Vector Laboratories, Burlingame, CA, USA) according to the manufacturer's instructions. Slices were coverslipped with Mowiol. Cells were reconstructed using a drawing tube, and the drawings were digitized using a graphical tablet.

Data analysis

For whole-cell experiments, hyperpolarization-activated currents were leak-corrected off-line using a custom-made procedure in Igor Pro (Wavemetrics Inc., Lake Oswego, OR, USA). The time constant of activation of I_h was determined by fitting a single exponential function to the start of current traces. The I_h conductance (g_h) was calculated using:

where V_rev is the experimentally recorded reversal potential of I_h (mean, −25 mV, see Fig. 3) The relationship of g_h as a function of voltage (V) was fitted by a Boltzmann equation:

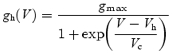where g_max is the maximal conductance, V_h is the voltage of half maximal activation and V_c is the slope factor. The input resistance was determined at the end of the voltage responses to hyperpolarizing current injections. In current-clamp recordings, the sag ratio was calculated by dividing the steady-state voltage by the peak voltage response to a hyperpolarizing current injection of 200 pA. In experiments in which synaptic stimulation was used, temporal summation was calculated as the relative increase in the amplitude of the synaptic depolarization during a train of five EPSPs:

Traces were averaged over 10–30 sweeps. All values are given as means ± s.e. Differences were tested with Student's t test unless stated otherwise. P < 0.05 indicates a significant difference.

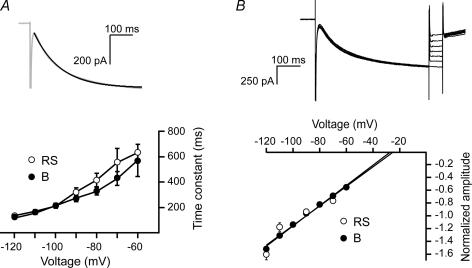
Figure 3. I_h characteristics in bursting and regular-spiking neurons.

A, I_h current traces were fitted to single exponential functions to obtain time constants of activation for both bursting (B) and regular-spiking (RS) neurons. Time constants of activation did not differ significantly between the two classes of neurons. Example trace is recorded from a regular-spiking neuron. Black line indicates the mono-exponential fit. B, reversal potentials of I_h in bursting and regular-spiking neurons were determined by a voltage protocol in which depolarizing steps (−120 to −60 mV) were given from a hyperpolarized holding potential (−120 mV). Black lines represent linear fit of the data points and the reversal potential was obtained by extrapolation. Data represent means ± s.e. of 17 bursting cells and nine regular-spiking cells recorded at room temperature.

Computer modelling

The interpretation of our data was verified by a modelling study, using the NEURON simulation environment (v5.6, Hines & Carnevale, 1997). First we used the NeuroLucida program to quantify the morphological organization of the soma and the dendritic tree of a typical subicular neuron. The morphology defines a compartment model consisting of a realistically dimensioned soma with apical and basilar dendrites (see Fig. 6A). A Scholl analysis (Scholl, 1953) of dendrite crossings as a function of distance from the soma (see Fig. 6B) concurred with previously reported data on the morphology of subicular neurons (Staff et al. 2000). Because the aim of our model study was to investigate subthreshold synaptic summation, we did not implement the firing patterns of subicular neurons. I_h was modelled to reproduce the voltage dependence and kinetics as observed experimentally at 30–33°C in the soma of bursting and regular-spiking neurons. The current was described by:

and

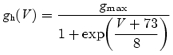and the voltage-dependent time constant was (τ_h) defined as:

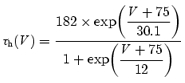using previously published data (Magee, 1998) that were corrected for extracellular Na⁺ concentration. For all I_h channels located in the dendritic compartments more than 100 μm away from the soma, the activation function was shifted by 8 mV in the depolarizing direction, based on dendritic recordings made in hippocampal CA1 pyramidal neurons (Magee, 1998). All other sodium and potassium currents were grouped into two leak conductances, their values determined by specific boundary conditions (see Results). All ion concentrations were implemented as stationary values, resulting in fixed reversal potentials for the ionic currents. This model is available in the Senselab database: (http://senselab.med.yale.edu/senselab/).

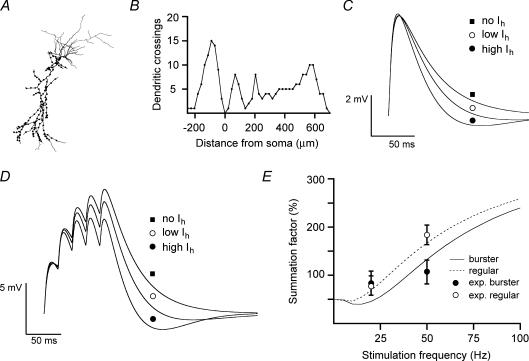
Figure 6. Computer simulation of the role of I_h in temporal summation.

A, morphology of the cell used in the modelling study. Dots represent the sites of excitatory synapses. B, Scholl analysis relates dendrite crossings of the reconstructed neuron to distance from the soma. C, single EPSPs as recorded from the soma of the model neuron with high levels of I_h (lower trace) and low levels of I_h (middle trace). In the absence of I_h, simulating the pharmacological block of I_h by ZD7288, the EPSPs from the bursting and regular-spiking model neuron overlap completely (upper trace). D, temporal summation of simulated EPSPs at 50 Hz under the same conditions as described in C. E, simulation of the frequency-dependence of temporal summation in the bursting (continuous curve) and regular-spiking (dashed curve) model neuron. Data points are the experimentally obtained values for the summation recorded in bursting (•) and regular-spiking (○) neurons (see Fig. 5).

Results

Morphology and distribution of bursting and regular-spiking neurons

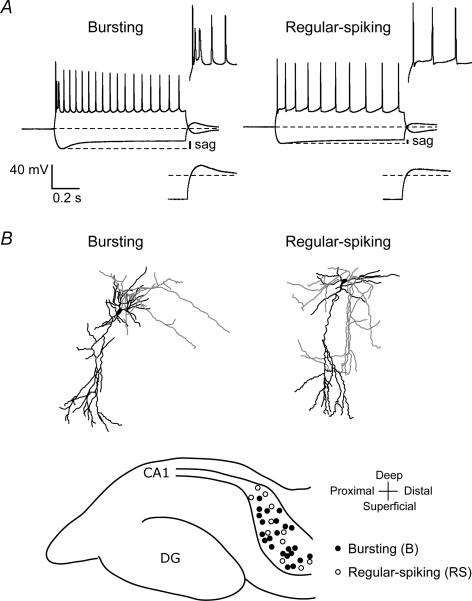
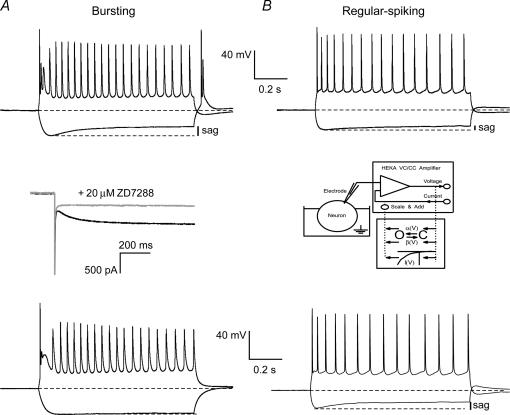
Combined current- and voltage-clamp experiments were performed in neurons from the subiculum. Filling neurons with biocytin present in the pipette solution allowed staining of recorded neurons to investigate morphology and location. From a total of 55 neurons recorded from locations randomly chosen in the subiculum (see lower schematic diagram in Fig. 1B), 35 (64%) were classified as bursting neurons, 17 (31%) as regular-spiking neurons and three (5%) as fast-spiking neurons. A burst was defined by a high frequency of the first two action potentials (>200 Hz) that rode on a depolarizing potential followed by a long (tens of milliseconds) afterhyperpolarizing potential (Fig. 1A). A distinction between weak-bursting (one burst per current injection) and strong-bursting (multiple bursts per current injection) neurons was not made. Regular-spiking neurons responded to current injections with trains of action potentials and never with a burst, regardless of the amplitude of the depolarization. Fast-spiking neurons presumably were interneurons and they were not further considered in this study.

Figure 1. Bursting and regular-spiking neurons in rat subiculum.

A, typical voltage responses of a bursting and a regular-spiking neuron in rat subiculum in response to hyperpolarizing (200 pA) and depolarizing (250 pA) current injections. Insets are enlargements to show burst and regular-spiking patterns in response to depolarizing current injections (upper insets) and anodal break potentials following hyperpolarizing current injections (lower insets). Note that the depolarizing sag and anodal break potentials are larger in bursting neurons. B, staining of biocytin-filled neurons showed that both bursting and regular-spiking neurons appeared to be projection neurons with pyramidal-like somas. The location of all successfully stained neurons is shown in the lower schematic diagram of the hippocampal formation, showing that both bursting and regular-spiking neurons are located throughout the deep–superficial and proximal–distal axes.

Both bursting and regular-spiking neurons were typical projection neurons with pyramidal-shaped somata (Fig. 1B). The axonal arbors could be followed in some neurons, but quantitative analysis of projection areas was not feasible due to the frequent cutting of axons by the slicing procedure. Figure 1B schematically shows the location of all successfully stained neurons, indicating that there is no relation between the location of subicular neurons and their firing pattern. Both classes of neurons are present throughout the deep–superficial and proximal–distal axes of the subiculum. The membrane properties determined in current-clamp mode (Table 1) showed no differences in resting membrane potential or capacitance between bursting and regular-spiking neurons at both room temperature (20–23°C) and physiological temperature (30–33°C). However, at room temperature, bursting neurons displayed a larger sag in response to a 1-s, 200-pA, hyperpolarizing current injection (sag ratio: bursting, 0.69 ± 0.02, n = 22; regular-spiking, 0.88 ± 0.02, n = 13, P < 0.05). Furthermore, the input resistance, determined at the end of hyperpolarizing current injections, of bursting neurons (79 ± 3 MΩ, n = 22) was considerably smaller than the input resistance of regular-spiking neurons (115 ± 12 MΩ, n = 13, P < 0.05). These differences in membrane properties were maintained at physiological temperature (see Table 1). The difference in input resistance suggests that bursting neurons have a larger conductance at resting membrane potential. Both bursting and regular-spiking neurons displayed anodal break potentials that in some cases initiated rebound potentials, but as for the sags, these were larger in bursting neurons than in regular-spiking neurons (Fig. 1A).

Table 1.

Membrane properties of bursting and regular-spiking subicular neurons at 23°C and 33°C

	Sag ratio	R-input (MΩ)	Capacitance (pF)	RMP (mV)
23°C
Bursting (n = 22)	0.69 ± 0.02	79 ± 3	32 ± 4	−59 ± 2
Regular spiking (n = 13)	0.88 ± 0.02*	115 ± 12*	29 ± 7	−58 ± 2
33°C
Bursting (n = 18)	0.74 ± 0.02	59 ± 5	17 ± 3	−59 ± 1
Regular spiking (n = 7)	0.83 ± 0.04*	97 ± 13*	14 ± 4	−58 ± 1

Sag ratio was calculated by dividing the steady-state voltage by the peak voltage response to a hyperpolarizing current injection of 200 pA. R-input, input resistance; RMP, resting membrane potential.

^*Significant difference between bursting and regular-spiking neurons (P < 0.05).

Two-fold difference in I_h conductance between bursting and regular-spiking neurons

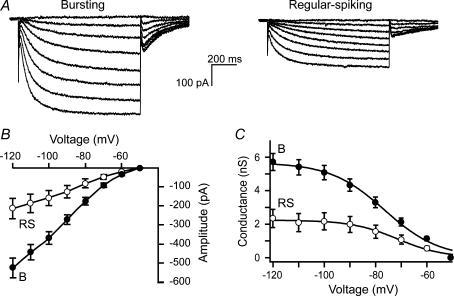
After determining the firing mode of subicular neurons in current-clamp mode, the recording configuration was switched to voltage clamp and I_h was characterized. A protocol in which a range of hyperpolarizing voltage steps were given from a holding potential of −50 mV was used to elicit I_h. In bursting neurons, this resulted in slowly activating inward currents that were considerably larger in amplitude in bursting neurons than those in regular-spiking neurons (Fig. 2A). The current–voltage (I–V) relationship of I_h displayed inward rectification and showed that the threshold for I_h activation is around −60 mV in both classes of neurons (Fig. 2B). At room temperature, the maximal conductance of I_h in bursting neurons was 5.3 ± 0.5 nS (n = 22) and in regular-spiking neurons was 2.2 ± 0.6 nS (n = 11; Fig. 2C, P < 0.05). The potential of half maximal activation (V_h) was −76 ± 2 mV for bursting neurons and for regular-spiking neurons was −73 ± 2 mV. Slope parameters (V_c) were 8.8 ± 0.2 and 8.7 ± 0.6 mV, respectively. V_h and V_c were not significantly different in the two classes of neurons. At physiological temperature, the maximal conductance of I_h in bursting neurons was 6.1 ± 0.5 nS (n = 18) and in regular-spiking neurons was 3.2 ± 0.9 nS (n = 7), with no differences in either V_h or V_c (Table 2). These results show that bursting neurons in the subiculum posses an I_h that is two-fold larger than I_h in regular-spiking neurons, whereas the voltage-dependence of I_h is similar in both classes of neurons.

Figure 2. I_h in bursting and regular-spiking subicular neurons.

A, subicular neurons were voltage clamped at the soma and I_h was evoked by a range of hyperpolarizing voltage steps (−50 to −120 mV) from a holding potential of −50 mV. The amplitude of I_h in bursting neurons is two-fold larger than that in regular-spiking neurons. B, current–voltage relationship of I_h in bursting (B) and regular-spiking (RS) subicular neurons displaying inward rectification and a threshold of activation around −60 mV. C, mean I_h conductance as a function of voltage in bursting (B, •) and regular-spiking (RS, ○) neurons. Mean conductance plots were fitted to a Boltzmann equation. Data represent means ± s.e. of 22 bursting cells and 13 regular-spiking cells recorded at room temperature.

Table 2.

Properties of I_h at 23°C and 33°C in bursting and regular-spiking subicular neurons

	gmax (nS)	Vh (mV)	Vc (mV)	τ (ms)
23°C
Bursting (n = 22)	5.3 ± 0.5	−76 ± 2	8.8 ± 0.2	117 ± 6
Regular spiking (n = 13)	2.2 ± 0.6*	−73 ± 2	8.7 ± 0.6	133 ± 9
33°C
Bursting (n = 18)	6.1 ± 0.5	−72 ± 1	10.7 ± 0.8	35 ± 3
Regular spiking (n = 7)	3.2 ± 0.9*	−75 ± 2	10.8 ± 1.1	42 ± 8

The parameters maximal conductance (g_max), voltage of half maximal activation (V_h) and slope factor (V_c) were determined from the fit of the Boltzmann equation to the voltage-dependent activation. τ is the time constant of activation at −120 mV.

^*Significant difference between bursting and regular-spiking neurons (P < 0.05).

I_h currents typically activate slowly, and the time constant of activation decreases upon hyperpolarization. The different subunits that underlie functional I_h channels (HCN1–4) display different activation kinetics. To investigate whether the I_h in bursting and regular-spiking neurons display differences in kinetics, we fitted current traces with single exponential functions to determine the time constants of activation as a function of voltage (Fig. 3A). In bursting as well as regular-spiking neurons, the time constant of activation decreased with increasing hyperpolarization, indicating a faster activation. However, at no given voltage did the mean time constant differ significantly between the two classes of neurons at either room temperature or at physiological temperature (Table 2). The reversal potential of I_h was determined by a voltage protocol in which a hyperpolarization to −120 mV was followed by a range of step depolarizations (Fig. 3B). Extrapolation of a linear fit between −120 and −60 mV resulted in the reversal potential of I_h. The mean reversal potential of I_h in bursting neurons was −26 ± 2 mV (n = 17), which was not significantly different from the mean reversal potential in regular-spiking neurons (−24 ± 2 mV, n = 9). These results show that the voltage-dependent characteristics of I_h do not differ between bursting and regular-spiking neurons, suggesting that a substantial difference in subunit composition of I_h in the two classes of neurons is unlikely.

Whole-cell recordings are potentially distorted as a result of space-clamp issues; therefore, in addition we determined cell-attached I_h amplitude and kinetics. Double-patch recordings were performed at 30–33°C with one electrode used in the whole-cell current-clamp configuration to determine cell type and one electrode used to establish a cell-attached voltage clamp to record I_h at a patch membrane potential of −120 mV. This showed a mean cell-attached I_h amplitude of 10.4 ± 1.9 pA (n = 10) in bursting neurons and 4.3 ± 1.2 pA (n = 7) in regular-spiking neurons (P < 0.05). The mean time constant of I_h at a patch membrane potential of −120 mV was 44 ± 6 ms (n = 9) in bursting neurons and 55 ± 5 ms (n = 5) in regular-spiking neurons, which is not significantly different. These results confirm the two-fold difference in whole-cell I_h conductance and the similarity in I_h kinetics in bursting and regular-spiking neurons and indicate that these are not the result of potential space-clamp problems arising from differential gradients of I_h along the somato-dendritic axis.

I_h does not determine firing mode of subicular neurons

Given the two-fold difference in I_h between bursting and regular-spiking neurons, we examined the role of I_h in determining the firing pattern of the two classes of neurons. In bursting neurons, we blocked the large I_h with the I_h antagonist ZD7288 (20 μm). Application of ZD7288 abolished I_h (Fig. 4A, middle panel) and consequently abolished the depolarizing sag (Fig. 4A, compare upper and lower panels). Furthermore, blockade of I_h abolished anodal break potentials and rebound action potentials. Although blocking I_h in three of four neurons affected the number of action potentials within the burst, the qualitative nature of the burst did not change (Fig. 4A, lower panel). In regular-spiking neurons, we enhanced the relatively small I_h by making use of a dynamic clamp (Fig. 4B, middle panel). Increasing I_h two- to eight-fold enhanced the sag and tended to reduce the frequency of action potentials. Increasing I_h also augmented the anodal break potentials. However, increasing I_h in the regular-spiking neurons never resulted in burst firing. These results indicate that the sole manipulation of the amplitude of I_h does not change the firing mode of subicular neurons from bursting into regular-spiking or vice versa.

Figure 4. I_h does not determine firing mode of subicular neurons.

A, upper panel shows the voltage responses of a bursting neuron in response to a hyperpolarizing current injection (200 pA) and a depolarizing current injection (250 pA). After blocking I_h with 20 μm ZD7288 (middle panel), the sag in response to the hyperpolarizing current injection was abolished and the number of action potentials within the burst was affected (lower panel). Also, the anodal break potential and the rebound potential were abolished by blockade of I_h. However, the qualitative nature of the burst did not change following blockade of I_h. B, upper panel shows the voltage responses of a regular-spiking neuron to injection of a hyperpolarizing current (200 pA) and a depolarizing current (250 pA). Note the small depolarizing sag as a result of the small I_h in regular-spiking neurons. Increasing the current amplitude of I_h by eight-fold using a dynamic clamp (middle panel, see Methods) increased the sag and the anodal break potential, but did not convert regular-spiking neurons into bursting neurons (lower panel).

Bursting neurons display less temporal summation of EPSPs

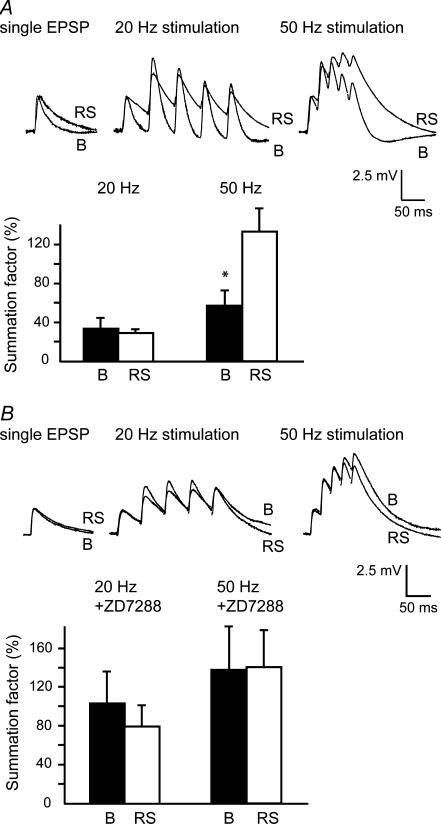
I_h strongly affects the temporal integration of synaptic inputs in both hippocampal CA1 and neocortical pyramidal neurons (Magee, 1998, 1999; Williams & Stuart, 2000; Berger et al. 2001). Therefore we investigated the temporal integration of synaptic input in subicular bursting and regular-spiking neurons. As the CA1 area is one of the main input pathways to the subiculum and the final synaptic relay in the hippocampus proper, the alveus, at the border of the CA1 area and the subiculum, was stimulated to evoke single subthreshold EPSPs (1.5–4 mV) in subicular neurons. Single EPSPs in regular-spiking neurons had similar rise times (2.8 ± 0.4 ms), but slower decay kinetics (44 ± 11 ms, n = 7) than the single EPSPs observed in burst-firing neurons (3.0 ± 0.2 ms and 18.2 ± 0.2 ms, respectively, n = 13, P < 0.05 for the decay, Fig. 5A). The EPSCs that underlie these EPSPs, recorded from the somata of the neurons under voltage clamp, were not different between bursting and regular-spiking neurons (rise time: bursting, 1.7 ± 0.2 ms, n = 15; regular-spiking, 1.5 ± 0.3 ms, n = 6; time constant of decay: bursting, 7.4 ± 0.7 ms, n = 16; regular-spiking, 7.4 ± 2.4 ms, n = 6). Temporal summation of synaptic input was investigated in current clamp at two different stimulation frequencies: 20 and 50 Hz. At 20 Hz, bursting and regular-spiking neurons showed the same moderate level of temporal summation (bursting, 34 ± 11%, n = 10; regular-spiking, 29 ± 4%, n = 6, Fig. 5A). However, in response to input of higher frequency (50 Hz), bursting neurons showed only half the temporal summation (57 ± 16%, n = 9) of that observed in regular-spiking neurons (133 ± 24%, n = 6, P < 0.05, Fig. 5A). To confirm the pivotal role of I_h in temporal summation of synaptic input, we blocked I_h with ZD7288 (20 μm) in both classes of neurons. In bursting neurons, ZD7288 increased the time constant of decay of the EPSPs (43 ± 11 ms, n = 5, Fig. 5B), whereas in regular-spiking neurons, ZD7288 had little effect on the time constant of decay (43 ± 3 ms, n = 4, Fig. 5B). In addition, the difference in temporal summation between the two classes of neurons was abolished in the presence of ZD7288. The mean level of summation at a stimulation frequency of 50 Hz while I_h was blocked was 138 ± 45% (n = 4) in bursting neurons and 141 ± 38 (n = 4) in regular-spiking neurons (Fig. 5B). The mean level of summation at a stimulation frequency of 20 Hz while I_h was blocked was 104 ± 32% (n = 5) in bursting neurons and 79 ± 22% (n = 4) in regular-spiking neurons. These results indicate that bursting neurons display less temporal summation than regular-spiking neurons, particularly in response to high-frequency input. Furthermore, the different levels of I_h between bursting and regular-spiking neurons appear to be crucial for the distinct levels of temporal summation between the two classes of neurons.

Figure 5. Bursting neurons display less temporal summation of EPSPs.

A, EPSPs in response to a single subthreshold stimulation and to stimulation at 20 Hz and 50 Hz in both bursting and regular-spiking neurons. Stimulation was performed at 30–33°C. Summation factors were expressed as the percentage increase in synaptic depolarization during a train of five EPSPs (see Methods). In response to stimulation at 50 Hz, bursting neurons display significantly less temporal summation of EPSPs. Stimulation artifacts in current traces were deleted for displaying purposes. Data represent mean ± S.E. of 13 bursting and seven regular-spiking neurons. Asterisks indicate P < 0.05. B, blockade of I_h by 20 μm ZD7288 abolished the difference in temporal summation between bursting and regular-spiking neurons. Data represent means ± s.e. of five bursting and four regular-spiking neurons.

Computer simulations confirm the role of distinct levels of I_h in temporal summation of synaptic input

In order to verify the role of I_h in determining the different temporal summation of synaptic input in bursting and regular-spiking neurons, we implemented a quantified subicular neuron with different levels of I_h and examined how this affected synaptic integration. In accordance with our measurements and previously reported data (Staff et al. 2000), the same neuronal morphology was used for bursting and regular-spiking neurons (Fig. 6A and B). Assuming an intracellular resistivity of 150 kΩ cm⁻¹, the model was then tuned to the following boundary conditions. (1) I_h was implemented assuming a density gradient in the dendrite that reached its maximum 500 μm from the soma. We implemented a gradient of 1: 7 (i.e. somatic density to density at 350 μm from the soma) based on previous physiological studies of I_h in hippocampal CA1 pyramidal neurons (Magee, 1998). Simulated voltage-clamp experiments on the model cell with a somatic electrode were performed in the final configuration of the model to confirm that I_h as measured in the soma matched the experimental data, giving a somatic g_max of 0.0120 mS cm⁻² for bursting neurons and 0.0045 mS cm⁻² for regular-spiking neurons. (2) The ratio for K⁺ and Na⁺ leak currents in each compartment was adjusted to attain a uniform resting membrane potential of −65 mV. The absolute value of the leak was scaled to match the recorded impedance of bursting and regular-spiking neurons and to correspond to the experimentally determined response to synaptic stimulation under I_h blockade, resulting in a leak conductance of 0.025 mS cm⁻² for both classes of neurons. (3) Uniformly over the membrane surface of the dendrite (starting at 100 μm below the soma, dots in Fig. 6A), glutamatergic synapses were implemented as changes in membrane conductance with a reversal potential of 0 mV, a peak conductance of 300 pS, and rise and decay time constants of 0.5 and 3 ms, respectively, which, when recorded from the soma, reproduced the experimentally observed EPSC rise and decay time constants. A fraction of the synapses (36 in total) were activated synchronously and this resulted in an EPSP at the soma with an amplitude of ∼5 mV and time constants for rise (bursting, 3.2 ms; regular-spiking, 3.4 ms) and decay (bursting, 24 ms; regular-spiking, 44 ms) similar to those obtained experimentally (Fig. 6C).

Temporal summation of synaptic input as a function of frequency was analysed in both model neurons (high and low levels of I_h), revealing differences that matched the experimental observations (Fig. 6E). The values calculated from simulations with stimulation at 50 Hz corresponded well with the experimentally obtained data (bursting, 83%; regular-spiking, 117%). Deleting I_h from the model to simulate the pharmacological block of I_h by ZD7288 increased these values to 142% and 141%, respectively (Fig. 6D). Simulations with a stimulation frequency of 20 Hz also corresponded well to the experimental data for the regular-spiking neuron (experimental, 29 ± 4%; simulated, 19%), whereas for the bursting neuron, the model predicted less summation than was actually observed (experimental, 34 ± 11%; simulated, −4%, Fig. 6E). The lower degree of summation could be due to the fact that the model does not take potential presynaptic mechanisms of facilitation that might be relevant at these stimulation frequencies into account.

Discussion

The main finding we report here is that bursting and regular-spiking neurons of the rat subiculum exhibit a considerable difference in I_h. Bursting neurons posses a two-fold larger I_h conductance than regular-spiking neurons. The voltage-dependent properties of I_h in both classes of neurons were similar. The large I_h conductance, which is not causally related to the ability to fire in bursts, ensures less temporal summation of evoked synaptic input onto bursting neurons, which implies that they are better suited to discriminate the frequency content of a high-frequency input. This important intrinsic difference between bursting and regular-spiking neurons may provide information about the physiological relevance of bursting and regular-spiking neurons in the subicular network.

From randomly chosen neurons in the rat subiculum, we found fractions of bursting (64%), regular-spiking (31%) and fast-spiking neurons (6%) that agreed well with previous studies in rat (Taube, 1993; Greene & Totterdel, 1997; Gigg et al. 2000) and guinea-pig (Stewart & Wong, 1993). Bursting and regular-spiking neurons did not appear to differ in obvious morphological characteristics and were both dispersed throughout the subiculum, which also corresponds well with previously reported data (Greene & Totterdel, 1997). Bursting neurons displayed larger sags and lower input resistance than regular-spiking neurons, which correlated with a two-fold difference in maximal I_h conductance at both room temperature (bursting, 5.3 ± 0.5; regular-spiking, 2.2 ± 0.6 nS) and at physiological temperatures (bursting, 6.1 ± 0.5; regular-spiking, 3.2 ± 0.9 nS). The difference in sag ratio was not reported in a previous detailed study of the cellular properties of subicular neurons (Staff et al. 2000). This discrepancy most probably results from the fact that only small hyperpolarizing current steps (5–10 mV) were given from resting membrane potential to test sag ratios in the study by Staff et al. (2000); such steps are not likely to activate much I_h. The voltage-dependence, reversal potential and kinetics of I_h did not differ between the two classes of neurons. No detectable difference in membrane potential between the two classes of neurons was noted, although one would expect a relatively depolarized resting membrane potential in bursting neurons because of the larger I_h, which has a reversal potential around −25 mV. This suggests that, in addition to I_h, there may be other voltage-gated or leak conductances that are different between bursting and regular-spiking neurons.

In hippocampal CA1 and neocortical layer 5 neurons, I_h is present in relatively low densities at the soma whereas I_h density steadily increases along the apical dendrite towards the distal dendrites (Magee, 1998; Berger et al. 2001). For subicular pyramidal neurons, a gradient for HCN1, one of the subunits underlying functional I_h channels, was shown to exist using high-resolution immunolocalization (Lörincz et al. 2002). In this study, no link was made to the physiology of subicular neurons and direct evidence for a dendritic gradient of I_h in both classes of subicular neurons is therefore still lacking. However, the fact that the authors did not report distinct quantitative differences for sampled neurons could indicate that both bursting and regular-spiking neurons might exhibit somato-dendritic gradients of I_h channels. In our model, using a ratio of 1: 7 (at 350 μm), similar to the distribution of I_h in hippocampal CA1 pyramidal neurons (Magee, 1998), we show that the temporal summation of synaptic input in both bursting and regular-spiking neurons can be qualitatively reproduced (Fig. 6D and E). However, because the parameters of the model solely relied on the somatic whole-cell measurements and were restricted by the use of a uniform synaptic input to the dendritic tree, the model could not confirm that a somato-dendritic gradient for I_h as implemented was necessary to explain the experimental data (data not shown).

It has been suggested that bursting and regular-spiking neurons project to different areas. Thus, Stewart (1997) reported that subicular neurons do not differ in their input pathways, but that they differ in their projection areas. This study showed that whereas the responses of bursting and regular-spiking neurons to orthodromic stimulation from either CA1, presubiculum or entorhinal cortex did not differ qualitatively, they differed significantly in their responses to antidromic stimulation from these areas. Thus, bursting neurons were antidromically driven from presubiculum, but not from the entorhinal cortex or CA1, whereas regular-spiking neurons were antidromically driven from entorhinal cortex and CA1, but not presubiculum. As we show here that bursting neurons are better suited to discriminate high-frequency input, this could mean that such information is preferentially relayed to the presubiculum whereas lower-frequency input is distributed to all projecting areas by both classes of subicular neurons.

The ability to fire in bursts has been proposed to ensure reliable synaptic transmission at synapses that have a low probability of transmitter release in response to single action potentials (Miles & Wong, 1986; Lisman, 1997; Snider et al. 1998). This means that potentially, bursting neurons more reliably transmit input at any frequency compared to regular-spiking neurons. Here we report that bursting neurons will also more reliably discriminate the frequency content of high-frequency (>20 Hz) synaptic inputs compared to regular-spiking neurons. In vivo, during waking and rapid eye movement (REM) sleep, high-frequency input to the subiculum occurs in the form of gamma oscillations (∼40–60 Hz), which result from the temporally organized discharge of hippocampal and entorhinal neurons (Bragin et al. 1995; Chrobak & Buzsaki, 1998). Our results suggest that during gamma oscillations, bursting neurons will better discriminate the frequency content of its inputs than regular-spiking neurons. This might be useful for the transfer and storage of information during learning processes, but may also have a role in the transmission of seizures in the subiculum during epilepsy (Harris & Stewart, 2001; Cohen et al. 2002).