Intrinsic Dynamic Behavior of Fascin in Filopodia

Abstract

Recent studies showed that the actin cross-linking protein, fascin, undergoes rapid cycling between filopodial filaments. Here, we used an experimental and computational approach to dissect features of fascin exchange and incorporation in filopodia. Using expression of phosphomimetic fascin mutants, we determined that fascin in the phosphorylated state is primarily freely diffusing, whereas actin bundling in filopodia is accomplished by fascin dephosphorylated at serine 39. Fluorescence recovery after photobleaching analysis revealed that fascin rapidly dissociates from filopodial filaments with a kinetic off-rate of 0.12 s⁻¹ and that it undergoes diffusion at moderate rates with a coefficient of 6 μm²s⁻¹. This kinetic off-rate was recapitulated in vitro, indicating that dynamic behavior is intrinsic to the fascin cross-linker. A computational reaction–diffusion model showed that reversible cross-linking is required for the delivery of fascin to growing filopodial tips at sufficient rates. Analysis of fascin bundling indicated that filopodia are semiordered bundles with one bound fascin per 25–60 actin monomers.

INTRODUCTION

Filopodia are thin rod-like cellular protrusions that serve an exploratory role in motile cells. In the growth cones of migrating axons, filopodia effectively “scan” the local environment “in search” of guidance cues that direct the axon toward its target (Albrecht-Buehler, 1976; Davenport et al., 1993; Dent and Gertler, 2003; Koleske, 2003). Filopodial turning, elongation, and retraction are key events involved in this process and require filopodia to be flexible enough to wave about yet rigid enough to protrude many microns past the cell surface. To identify the physical and molecular properties which underlie the reorganization of filopodia we must understand how actin filaments are cross-linked and how those cross-links are subsequently taken apart. Because fascin is the primary actin cross-linker in filopodia and is essential for filopodia formation (Vignjevic et al., 2006), we investigated features important to its function and dynamics. Specifically, we focused on questions regarding the initiation and elongation stages of filopodia formation as well as their maintenance and retraction: What is the origin of fascin in filopodia? How does fascin get delivered to tips of growing filopodia? How is it organized within actin bundles? How does that organization change over time, and what implications does this reorganization of filaments have on filopodia dynamics and stiffness?

Filopodia are thought to form by at least two mechanisms, one mechanism that is based on the reorganization of the dendritic network in a process that involves actin filament elongation and convergence at the barbed ends (Svitkina et al., 2003) and a formin-mediated process, which involves the formation of actin bundles in an unbranched network (Kovar and Pollard, 2004; Zigmond, 2004; Pellegrin and Mellor, 2005). Under the former mechanism, merged filaments elongate by polymerization of actin to form precursors to filopodia, so called lambda precursors. Actin filaments that come in proximity to one another are cross-linked into unipolar parallel bundles to form mature filopodia (Vignjevic et al., 2006). However, there is no established molecular mechanism that explains how fascin molecules are recruited to filopodia. One possibility is a higher affinity for actin filaments in filopodia than elsewhere in the cell. Activation by dephosphorylation is one way that has been reported to achieve this higher affinity (Ono et al., 1997; Yamakita et al., 1996; Adams et al., 1999; Vignjevic et al., 2006).

Cross-linking of actin filaments carries implications both for the elongation of filopodia and for their response to mechanical stress. Cross-linking is presumed essential for filopodial protrusion, because single actin filaments are insufficiently stiff to resist compressive forces (Mogilner and Rubinstein, 2005). Experimental support for this conclusion comes from observation of fascin-depleted filopodia that are typically bent and buckled under the cell membrane (Brieher et al., 2004; Vignjevic et al., 2006). It has been established that elongation of filopodia is mediated by actin assembly at their tips (Mallavarapu and Mitchison, 1999). Presumably, a supply of fascin is also required to cross-link the newly polymerized actin. Otherwise, the nascent actin filaments would not be sufficiently rigid to support protrusion of the filopodium. To reach the growing (barbed) end of nascent actin filaments, fascin must be translocated from the cell body into the filopodium and out to the tip. However, when filopodia reach long lengths or elongate rapidly, diffusion, alone, may not be a sufficient mechanism for protein transport. What other mechanisms does the cell invoke to overcome the limitations of simple diffusion?

If filaments are physically attached to each other by cross-linking, how can they reorganize to relieve intra- and extracellular stresses without compromising structural integrity? Others have shown that dynamic interactions exist between α-actinin and actin filaments in stress fibers and that the dissociation rate of the cross-linker governs the mechanical properties of these bundles (Sato et al., 1987; Xu et al., 1998, 2000). We and others recently reported that fascin rapidly exchanges between filopodial actin filaments (Nakagawa et al., 2006; Vignjevic et al., 2006). The time-scale for fascin dissociation may provide clues as to how filopodia respond to mechanical stress that may have implications for the relationship of such response to cell morphology.

The purpose of this work is to advance our understanding of filopodia formation, which currently lacks detailed information regarding the fascin–actin interaction and how that interaction influences the molecular organization, remodeling, and mechanical properties of filopodia during its dynamic life cycle. Therefore, we undertook a quantitative, biophysical, and kinetic analysis of fascin dynamics. We quantified kinetic rates for fascin turnover in filopodia and we determined whether these rates are regulated or whether they are intrinsic to the cross-linker. We probed the role of phosphorylation cycles in regulating the active pool of fascin available for actin cross-linking by using phosphomimetic fascin mutants. Finally, we examined the limitations of fascin transport by diffusion and we developed a quantitative, computational model to analyze mechanisms for the delivery of cross-links to filopodial tips.

MATERIALS AND METHODS

Proteins

Actin was purified from rabbit muscle as described previously (Spudich and Watt, 1971). Tetramethylrhodamine (TMR)-actin was prepared by labeling F-actin with 5- (and 6)-carboxytetramethylrhodamine succinimidyl ester (NHSR) (Invitrogen, Carlsbad, CA) as described in Isambert et al. (1995) and stored at −80°C. Biotinylated actin was prepared with biocytin maleimide (Invitrogen) by the method of Rock et al. (2000). Before use, labeled G-actin was recycled by polymerization for 2 h on ice in the presence of 50 mM KCl, 2 mM MgCl, and 1 mM ATP, sedimentation at 100,000 × g for 1.5 h at 4°C, resuspension in cold G-buffer (2 mM Tris-HCl, 0.2 mM CaCl, 0.2 mM ATP, and 0.5 mM dithiothreitol [DTT]) to a final concentration of 2 mg/ml, and dialysis was conducted overnight against G-buffer using microdialysis buttons (Pierce Chemical, Rockford, IL).

Recombinant human fascin was prepared by a modification of the method of Ono et al. (1997). Escherichia coli carrying the plasmid was grown at 37°C until the A₆₀₀ reached 0.6. Protein expression was induced by adding 0.1 mM isopropyl β-d-thiogalactoside at 20°C for 4 h. Cells were harvested by centrifugation and extracted with B-PER in phosphate buffer (Pierce Chemical) plus 1 mM phenylmethylsulfonyl fluoride (PMSF) and 1 mM DTT. The lysate was centrifuged at 20,000 × g for 20 min, and the supernatant was mixed for 1 h at room temperature (RT) with 2 ml of glutathione-Sepharose 4B (GE Healthcare, Little Chalfont, Buckinghamshire, United Kingdom) equilibrated with phosphate-buffered saline (PBS) plus 1 mM DTT. The glutathione-Sepharose was poured into a column and washed with 20 ml of PBS plus 1 mM DTT. Then, 80 μl of thrombin (GE Healthcare) was added, and digestion was allowed to proceed overnight at 4°C. Flowthrough fractions were collected in 2 mM PMSF and concentrated by Centricon 10 (Millipore, Billerica, MA). Fascin was labeled with AlexaFluor 488 carboxylic acid, and succinimidyl ester (Alexa 488-NHS; Invitrogen). The pH of the fascin solution was raised to 8.3 by the addition of 1/20 volume of 0.1 M NaHCO₃, pH 9.3. A 10-fold molar excess of Alexa 488-NHS was added from a stock solution of 25 mg/ml in dimethyl sulfoxide and reacted for 1 h at RT. Free dye was separated from labeled fascin on an Excellulose desalting column (Pierce Chemical).

In Vitro Bundling Assay

Coverslips (22 × 22 mm) were cleaned with 70% ethanol and blown dry with air (same applies to microscope slides). Coverslips were coated with nitrocellulose (1% collodion in amyl acetate (Electron Microscopy Sciences, Hatfield, PA) and allowed to air dry for 1 h. Chambers were created by placing two strips of double-sided tape onto microscope slides, 0.5 inch apart, and placing coverslip (nitrocellulose coating face down) on top of taped slide. Neutravidin mix (1 μl of 5 mg/ml Neutravidin in 50 mM PBS, pH 8.0, to 20 μl of actin polymerization buffer [10 mM imidazole, pH 7.0, 50 mM KCl, 1 mM MgCl₂, and 1 mM EGTA]) was infused into perfusion chamber and allowed to incubate at RT for 1 min. Chamber was washed two times with 1 mg/ml bovine serum albumin in actin polymerization buffer to block any nonspecific binding. The bundle mixture (1 μM TMR-actin, 3 μM unlabeled actin, and 1 μM biotinylated-actin) was infused into chamber. Chamber inlet and outlet was sealed with petroleum jelly:lanolin:paraffin (1:1:1).

The bundle mixture was added to an Eppendorf tube and allowed to polymerize in actin polymerization buffer. To bundle actin filaments, 3 μM unlabeled fascin and 1.5 μM Alexa488-fascin were added to the test tube and allowed to incubate at RT for 1 h. The following were used to inhibit photobleaching: 4.5 mg/ml glucose, 0.86 mg/ml glucose oxidase (G-2133; Sigma-Aldrich, St. Louis, MO), and 0.14 mg/ml catalase (C-3155; Sigma-Aldrich) added to bundle mixture before imaging.

Cell Culture

B16F1 mouse melanoma and Neuro2a mouse neuroblastoma lines were provided by Drs. C. Ballestrem (Weizmann Institute of Science, Rehovot, Israel) and A. Ferreira (Northwestern University, Chicago, IL), respectively, and they were maintained in DMEM supplemented with 10% fetal bovine serum (FBS) at 37°C. Cells were plated onto coverslips, which were coated with 20 μg/ml mouse laminin (Invitrogen) for 1 h and thereafter incubated with 1% heat-inactivated bovine serum albumin in phosphate buffered saline for 20 min. pEGFP–fascin construct was provided by Dr. J. Adams (Cleveland Clinic Foundation, Cleveland, OH). QuikChangeII site-directed mutagenesis kit (Stratagene, La Jolla, CA) was used to create point mutations. Transfection of plasmids in B16 cells was carried out by FuGENE6 (Roche Diagnostics, Indianapolis, IN) and TransIT-Neural (Mirus, Madison, WI) for Neuro2a cells per the manufacturers' instructions. For live cell imaging, cells were transferred into L-15 medium (Invitrogen) supplemented with 10% FBS.

Quantitative Immunoblotting

B16 cells were lysed in buffer containing 10 mM Tris, pH 7.5, 150 mM NaCl, 1% Triton X-100, 10% glycerol, and protease inhibitor tablet (Roche Diagnostics). Lysate and purified fascin protein were loaded onto an SDS-polyacrylamide gel electrophoresis (PAGE) (4–20% polyacrylamide) and immunoblotted with anti-fascin primary antibody (DakoCytomation, Carpinteria, CA) and secondary mouse antibody (Sigma-Aldrich) using standard protocols. The amount of fascin in cell lysates was evaluated by comparing the intensity of the bands of each sample with the pure fascin standard by densitometry using NIH ImageJ software (http://rsb.info.nih.gov/ij/).

Microscopy

FRAP and Fluorescence Loss in Photobleaching (FLIP).

FRAP and FLIP experiments were performed on a Zeiss LSM 510 Meta confocal microscope (Carl Zeiss, Thornwood, NY) with a 100×/1.3 numerical aperture planapochromat oil objective. TMR-actin was excited with the 543-nm line of a HeNe laser (1 mW), whereas green fluorescent protein (GFP)- and Alexa488-tagged proteins were excited with the 488-nm line of an argon laser (25 mW). We photobleached fluorescence using a rectangular region of 1 μm² area for 0.7–1.7 s by using 100% laser power for photobleaching, and we recorded images at attenuated laser settings.

FRAP data were analyzed as follows. The average intensity in the bleached zone was measured over the time course of the experiment. Before quantifying the fluorescence recovery, the measurements were corrected for photobleaching during image acquisition by a bleaching correction factor. This factor was determined by curve-fitting the fluorescence decay of a filopodium located far from the site of bleaching during a FRAP experiment (nonbleached bundle in the in vitro experiments) with a single exponential function, exp(−k_decayt), to extract a decay constant, k_decay. We then multiplied the intensity in the bleached zone by the correction factor, exp(−k_decayt), for each time point, t, in the experiment to obtain a normalized recovery profile. We curve fit the in vivo FRAP profile with a double exponential function, I(t) = I_f − 0.75 × exp(−k_fastt) − 0.25 × exp(−k_slowt), and single exponential function, I(t) = I_f + (I_o − I_f)exp(−k_fastt), for the in vitro experiment, because fluorescence recovered rapidly to prebleach values, where I_f is the intensity of the bleached zone at the final time of the experiment relative to the prebleach state, I_o is the intensity immediately postbleach relative to the prebleach state, k_fast is the constant reflecting the recovery to quasi-steady state when fascin cross-links have redistributed evenly within the filopodium, and k_slow is the constant reflecting the recovery to prebleach intensity. The half time for dissociation was calculated as t_1/2 = ln2/k_fast, with average values along with their 95% confidence interval reported.

FLIP data were analyzed by measuring the loss in fluorescence near the filopodial tip. The intensity loss was multiplied by a photobleaching correction factor, which was determined in the same manner as above. Once normalized, the decay in fluorescence was fit with a single exponential function, I(t) = I_o exp(−k_offt), where I_o is the initial intensity relative to the prebleach state and k_off is the dissociation rate constant.

Epifluorescence Live Cell Imaging: Determination of Percentage of Fascin Localizing in Filopodia.

B16 mouse melanoma cells expressing GFP-fascin were visualized by fluorescence microscopy using Nikon Diaphot CH-300 (Nikon, Tokyo, Japan), equipped with a 63× objective, at 300-ms exposure. Cells were kept on the microscope stage at 37°C during observation. Images were analyzed using MetaMorph imaging software (Molecular Devices, Sunnyvale, CA). MetaMorph line function was used to trace and measure the whole-cell perimeter.

Confocal Microscopy: Determination of Percentage of Fascin Bound in Filopodia.

B16 mouse melanoma cells expressing GFP-fascin were imaged using the LSM510 Meta confocal microscope and kept at 37°C with consistent settings throughout imaging and analyzed using the LSM510 Meta image analyzer software (Carl Zeiss).

Determination of the Operating Fascin:actin Ratio in Filopodia

Quantitative immunoblotting was used to determine the concentration of cellular fascin protein to be 100–300 nM in B16 cells (350–500 nM in N2a cells). That value was converted to number of fascin molecules per cell by dividing the amount of fascin protein by molecular weight of fascin (55 kDa) and Avogrado's number, yielding 1.0–2.5 × 10⁵ molecules per B16 cell (3.0–4.6 × 10⁵ per N2a cell). Using fluorescence microscopy, we determined the percent of total fascin molecules in a cell which localize to filopodia, 11% in B16 (29% in N2a). To calculate the number of fascin molecules in one filopodium, we divided by the average number of filopodia per cell (number of filopodia in B16 cells = 30, n = 88; number of filopodia in N2a cells = 60, n = 30), or

Similar calculations yielded 1450–2200 fascin per N2a filopodium. We found that, on average, B16 filopodia were 3 μm long (Vignjevic et al., 2006) and N2a filopodia were 8 μm (current study). By assuming that filopodia contain 20 actin filaments (Lewis and Bridgman, 1992; Mogilner and Rubinstein, 2005) and using the accepted incremental extension of an actin monomer of 2.7 nm, which gives 370 actin monomers per μm of filament, we found that the filopodia contain:

Similar calculations yielded 27–41 actin per fascin in neuronal N2a filopodia.

RESULTS

Fascin Undergoes Rapid Local Exchange in Filopodia and Simultaneous Slow Exchange with the Cytoplasmic Pool

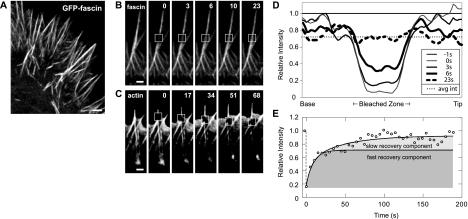
Our previous work on fascin dynamics (Vignjevic et al., 2006) was performed in melanoma cells. To extend those studies to a neuronal cell type and to evaluate the conserved features of fascin exchange, we determined the dynamics of fascin in Neuroblastoma 2a cells, a cell line that generates numerous filopodia. We compared the distribution and turnover of fascin in filopodia by using fluorescence microscopy and FRAP analysis. We found that fascin localizes throughout the entire length of filopodia in these cells (Figure 1A), just as in B16F1 mouse melanoma cells (Vignjevic et al., 2006). In addition, FRAP experiments revealed rapid recovery of GFP-fascin in filopodia, on the order of 10 s (Figure 1B), and this behavior did not require the turnover of actin, which moved with retrograde flow (Figure 1C). The time scale for fascin exchange was consistent between phases of filopodial protrusion, retraction, and stationary periods. This result is consistent with findings in other cell types (Nakagawa et al., 2006; Vignjevic et al., 2006), which indicates that the dynamic behavior is a general phenomenon. The conserved behavior implies that the localization and dynamics of fascin may be critical to filopodia remodeling and intimately connected to their biological function.

Figure 1.

Fascin exchanges rapidly in filopodia. (A) Confocal image of N2a cell expressing GFP-fascin. GFP-fascin localizes along the entire length of filopodia. Time-lapse sequence of photobleaching experiments on GFP-fascin (B) and GFP-actin (C). Fluorescence of GFP-fascin recovered quickly, whereas GFP-actin did not recover. Instead, the bleached zone moved with retrograde flow. Bars, 1 μm. Time given in seconds. (D) Recovery profile of bleached zone over time course of FRAP experiment. By 6 s, half of bleached cross-links have fully exchanged with neighboring molecules. The postbleach average intensity along the filopodium matches the average intensity at the time when fluorescence has evenly distributed, or fascin has fully exchanged, suggesting that fascin turnover is primarily intrafilopodial on this time scale. (E) At longer time scales, the bleach zone recovers fully (to prebleach values), suggesting that filopodial-cytoplasmic exchange restores fluorescence to the prebleach intensity. The recovery profile is curve-fit with a double exponential function with a recovery constant for fast intrafilopodial exchange and a second recovery constant for slower filopodial–cytoplasmic exchange (see Materials and Methods). Fast and slow recovery components are shown in shaded regions, with the recovery profile for rapid intrafilopodial exchange separating the two.

Although our FRAP data demonstrate the existence of fascin exchange, by itself, it does not reveal the source of fascin turnover, specifically, whether the exchange is accomplished predominantly within the filopodium, with the cytoplasmic pool, or a combination of both. Assessing the source of fascin exchange requires the evaluation of recovery profiles, because they provide information about the time scale for protein exchange and the origin of that exchange. FRAP data were quantified by tracing the fluorescence intensity along bleached filopodia, normalizing for global loss of fluorescence during image acquisition along with prebleach intensity values, and data were plotted for varying times in the experiment (Figure 1D). The trough in intensity at 0 s (thin gray line) corresponds to the region bleached in the experiment, whereas the nearly flat profile at 23 s (dashed black line) corresponds to the time when fluorescence had evenly redistributed within the filopodium. The average half time of this recovery was t_1/2 = 6.0 ± 1.6 s (n = 24). Although fluorescence within the filopodium became uniform by 23 s, it had not recovered to the prebleach level. Instead, it recovered to the average fluorescence at the postbleach time (0 s), indicating that little fascin exchange had occurred with the pool in the cell body (Figure 1D, dotted line). Therefore, the initial recovery process predominantly represented a redistribution of fascin cross-links originally within the filopodium.

What is the significance of recovery that is uniform but to less than prebleach values? One possibility is that a fraction of the bleached molecules have been rendered immobile. Another possibility is the existence of a second, slower mode of recovery. Extending image acquisition to >100 s showed essentially full restoration of prebleach fluorescence (Figure 1E). Because we could infer that the initial rapid recovery was predominantly due to intrafilopodial exchange, the secondary slow recovery process suggests two additional conclusions: first, that essentially all the fascin has remained mobile, and, second, that fascin in filopodial cross-links can exchange with the cytoplasmic pool of fascin. FRAP experiments along the entire length of filopodia containing GFP-fascin revealed recovery times that matched those of the secondary recovery phase, confirming these conclusions (Supplemental Figure 1).

FRAP Data Reveal Kinetic Off-Rate of Fascin in Filopodia

What is the kinetic significance of the fast fascin recovery seen in the FRAP data? Is this recovery a measure of fascin association, dissociation, or a mixture of both events? Theoretical considerations indicate that in a simple binding reaction (A + B ⇌ AB), recovery is exponential (1 − exp(−k_offt)) and that the exponent k_off indicates the rate constant of dissociation from the complex (Sprague et al., 2004). On this basis, we calculate an off rate of k_off = 0.12 s⁻¹.

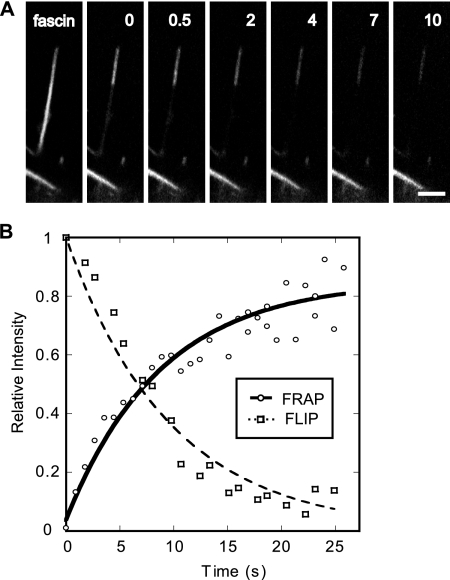
We sought to confirm this value by independent FLIP experiments, which provided a more direct measure of the fascin dissociation rate constant in filopodia. Here, we repeatedly bleached a proximal domain of a filopodium containing GFP-fascin, while monitoring the loss of fluorescence over time in a distal domain (Figure 2A). Because the bleaching light was confined to the proximal domain, any loss of fluorescence in the distal domain was due to fascin molecules that dissociated from actin filaments in that domain and diffused into the proximal domain. If we assume that a fascin molecule typically diffused out of the distal zone before rebinding, the diminishing brightness of the distal domain was a direct indicator of the rate of fascin dissociation. The decay of fluorescence in the FLIP experiment was plotted versus time (Figure 2B) and curve-fit using a single exponential function, exp(−k_offt), revealing an off rate, k_off = 0.1 s⁻¹ (n = 19), corresponding to a half-time for fascin dissociation of ≈6 s. As expected, the half-time for dissociation matches the half time of recovery from FRAP studies, shown by the complementary profiles of the curves plotted in Figure 2B, reinforcing the conclusion that fascin dissociates from actin filaments with a k_off = 0.12 s⁻¹.

Figure 2.

Kinetic analysis of fluorescence recovery of fascin in filopodia reveals k_off. (A) FLIP of GFP-fascin in filopodia. Fluorescence decay near the tip represents exchange of GFP-fascin with bleached and endogenous cross-links. Bars, 1 μm. Time given in seconds. (B) Plot of relative intensity versus time in both FRAP and FLIP experiments on GFP-fascin in filopodia. Relative decay of fluorescence in FLIP experiment was curve fit with a single exponential function, exp(−k_offt), and directly reveals a half-time of dissociation of 6 s. The corresponding FRAP curve shows a half-time of fluorescence recovery of 6 s as well. This half time also yields the dissociation rate of fascin from actin because, assuming that the total concentration of fascin remains unchanged in the filopodium over time, the recovered fluorescence is equal to the difference between the total amount of fascin and the amount that dissociated. Therefore, the FRAP data were curve fit with the function, 1 − exp(−k_offt), where k_off = 0.12 s⁻¹.

The Characteristic Cycles of Fascin Association and Dissociation Are an Intrinsic Property of the Fascin–Actin Interaction

Is each cycle of fascin association and dissociation in filopodia directly regulated, such as by enzymatic phosphorylation/dephosphorylation or by binding/dissociation of a G protein, or is it an intrinsic property of the fascin–actin interaction? To test for intrinsic fascin exchange in filopodia, we carried out FRAP experiments in reconstituted filopodia-like bundles composed strictly of purified fascin and actin proteins (Vignjevic et al., 2003), thereby excluding any proteins that potentially regulate fascin exchange. If the recovery behavior of fascin in purified bundles matched that in filopodia, then it would be evidence that fascin turnover is an intrinsic property of the cross-linker.

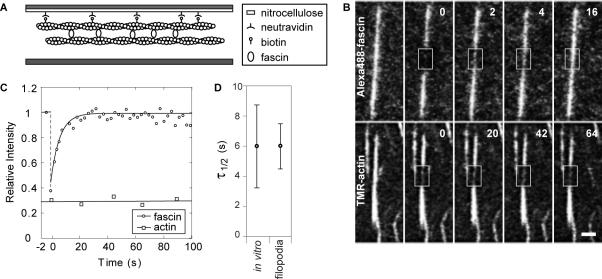
We tethered in vitro bundles to coverslips via a biotin–avidin interaction in a sealed perfusion chamber so that fluorescence recovery could be monitored over time (Figure 3A). FRAP experiments revealed rapid fluorescence recovery of Alexa488-fascin (Figure 3B, top). In contrast, fluorescence recovery of TMR-actin was negligible (Figures 3B, bottom, and C), confirming our in vivo result that fascin undergoes cycles of dissociation and association within actin bundles. The recovery data were normalized for global bleaching and fit with a single exponential function as shown in Figure 3C. The half time of recovery for fascin in vitro is t_1/2 = 6 ± 3 s (n = 28), nearly identical to that found in filopodia (Figure 3D). Because the time scale for fascin exchange was recapitulated in vitro, we conclude that fascin exchange is an intrinsic property of the fascin–actin interaction and that it does not require assistance by an auxiliary molecule(s) for either binding or release from filopodial actin.

Figure 3.

Fascin is dynamic in reconstituted filopodia-like bundles. (A) Profile view of perfusion chamber design. Actin–fascin bundles are tethered to nitrocellulose-coated coverslip via a biotin-neutravidin interaction. (B) Top, photobleaching of Alexa488-fascin in reconstituted filopodia-like bundles reveals rapid recovery of fluorescence. Bottom, photobleaching experiment on TMR-actin yields no fluorescence recovery. Bleached zone marked by boxes. Bar, 1 μm. Time given in seconds. (C) Recovery curves show intensity relative to prebleach value per time of the experiment for fascin and actin, with average half time of recovery for fascin of 6 s and recovery to prebleach level by 20 s. (D) Plots show the mean (circle) recovery half-times for FRAP experiments performed in vitro and in vivo, along with their respective 95% confidence intervals. The matching fast recovery kinetics for fascin in filopodia and reconstituted bundles reveal that dynamic exchange in filopodia is an intrinsic property of the fascin cross-linker.

Whereas the half-times for fast recovery were similar in vitro and in filopodia, in vitro fluorescence recovered fully to prebleach intensity levels within ∼20 s, whereas full filopodial recovery required a slower component of exchange between the filopodium and cell body. The rapid full recovery in vitro was expected, as the bundles were surrounded by a large unbound pool of fascin that could undergo three-dimensional diffusion over shorter distances to unoccupied binding sites. In contrast, full filopodial recovery required long-distance exchange with the cell body and diffusion through a more crowded space.

Because such an intrinsic property precludes a multistep association reaction (e.g., with a catalyst), we can use the value of a previously measured affinity constant (K_A = 6.7 μM⁻¹, Yamakita et al., 1996) and our measured k_off to calculate the kinetic on-rate, k_on, of the fascin–actin association reaction as follows: k_on = K_A· k_off = 0.8 μM⁻¹ s⁻¹.

Fascin-Mediated Actin Bundling in Filopodia Requires That Fascin Be in the Nonphosphorylated State

Several studies have shown that the formation and lifetime of filopodia seem dependent upon the state of fascin phosphorylation; when activated by dephosphorylation, fascin yielded numerous, long-lived filopodia, whereas phospho-fascin yielded sparse, short-lived filopodia (Yamakita et al., 1996; Adams et al., 1999; Anilkumar et al., 2003; Vignjevic et al., 2006). These observations suggest that phosphorylation limits the availability of fascin for actin bundling in filopodia. However, phosphorylated fascin is not excluded from filopodia (Vignjevic et al., 2006); therefore, its contribution to actin bundling needs to be tested. Here, we quantified and compared the preference for localization in filopodia and the turnover rates of fascin phospho-mimetic mutants to determine the extent of binding of phosphorylated fascin in filopodia.

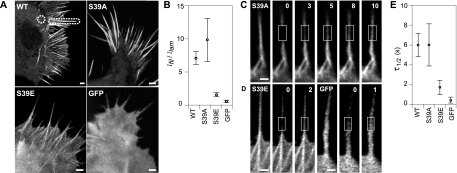
To directly test whether the incorporation of fascin in filopodia was dependent on the phosphorylation state, we analyzed the fluorescence distribution of soluble GFP, GFP-tagged wild-type fascin, and GFP-tagged mutant fascin proteins that mimic the inactive phosphorylated (S39E) and active nonphosphorylated (S39A) states (Figure 4A). Proteins were expressed in N2a cells (on a background of endogenous levels), because these cells generate many filopodia that are easy to study. We used confocal microscopy to obtain images of consistent optical depth so that measured intensities would indicate relative GFP concentrations, and we plotted the ratio of filopodial-to-lamellipodial fluorescence for each protein in Figure 4B. As a control for uniform optical depth, we first measured this ratio for GFP-expressing cells, and we found that I_fil/I_lam = 0.9 ± 0.1 ≈ 1 (n = 26), as expected for a uniformly soluble marker. Also as expected, wild-type GFP-fascin showed significantly greater preference for filopodia (I_fil/I_lam = 7.4 ± 1.0; n = 27) than did diffuse GFP. Although both mutants localized along filopodial shafts, the active S39A mutant showed strong preference for filopodia (I_fil/I_lam = 10.0 ± 2.9; n = 27), whereas filopodia containing inactive S39E exhibited only marginal localization (I_fil/I_lam = 1.3 ± 0.1; n = 27) and a uniform diffuse fluorescence in the cell body. The comparison of intensity distribution among fascin mutants implies that fascin incorporation in filopodia is strongly increased by fascin dephosphorylation.

Figure 4.

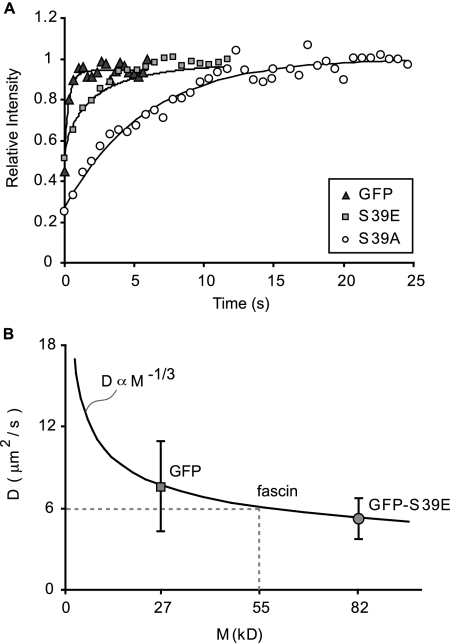
Localization and dynamics of fascin mutants in filopodia. (A) Fascin wild type (WT) and phosphomutant expression patterns in N2a cells. WT and S39A are enriched in filopodia, whereas S39E shows weaker localization in filopodia. Soluble GFP localizes uniformly throughout cell. (B) The relative intensities of filopodia and cytoplasm for WT, S39A, and S39E fascin and those of soluble GFP, as measured in protruding filopodia and lamellipodia indicated in dashed outlines in A. Average relative intensity ratios, I_fil/I_lam, (circles) and 95% confidence intervals are similar and overlap for WT and S39A, whereas those for S39E and GFP are much lower and similar to each other, suggesting that S39E weakly localizes to filopodia. FRAP experiments reveal recovery of GFP-S39A fascin (C), GFP-S39E fascin (D, left), and GFP (D, right) in filopodia. Bars, 1 μm. Time given in seconds. Although FRAP leaves a distinctly visible bleached zone in the S39A experiment, it leaves nearly the whole filopodium bleached in the S39E and GFP experiments, even though the same size bleached zone was used to perform the bleaching experiments, suggesting that S39E undergoes a diffusion process similar to that of GFP in filopodia. (E) Plots show the distribution of half-times of recovery for fascin WT and mutants alongside GFP. Although recovery of S39E and GFP occur in t_1/2 = 1.7 ± 0.9 s (n = 13) and t_1/2 = 0.5 ± 0.3 s (n = 10), respectively, the recovery is slower and identical for WT and S39A, with average t_1/2 = 6 s, suggesting that filopodial filaments are primarily bundled by dephosphorylated fascin.

The weak localization of phospho-fascin in filopodia suggests either limited access to, or low retention within, filopodia. We compared the mobility of fascin mutants by using FRAP to test the dependence of fascin lifetime in filopodia on phosphorylation state. Filopodia containing GFP-tagged S39A mutant revealed recovery after photobleaching (Figure 4C) with t_1/2 = 6 ± 2 s (n = 17), which is nearly identical to that exhibited by the wild-type fascin protein (Figure 4E) and on the same order as that found in B16 cells (Vignjevic et al., 2006). These results suggest that the bound fascin cross-links in filopodia exist predominantly in the dephosphorylated state and that this feature is conserved among neuronal and nonneuronal cells. In contrast, the recovery profile for the GFP-tagged S39E mutant (Figure 4D, left) closely resembled that of soluble GFP (Figure 4D, right), with t_1/2 = 1.7 ± 0.6 s (n = 13) and t_1/2 = 0.5 ± 0.2 s (n = 10), respectively (Figure 4E). Instead of revealing a distinct bleached zone, as in the wild-type and S39A FRAP experiments, the bleached zone and the region distal to it seemed to be generally nonfluorescent after photobleaching despite bleaching a zone of identical size (1-μm² area). We infer from the similar mobilities of GFP and the S39E mutant that neither protein appreciably bind actin. Instead, both GFP and S39E likely diffused into the bleached zone during the bleaching interval before redistributing into the distal domain of the filopodium, leaving the bleached zone and the region distal to it nonfluorescent.

Fascin Undergoes Free Diffusion in Filopodia with a Moderate Diffusion Coefficient, D = 6 μm²/s

The tight packing of actin filaments and closely apposed plasma membrane of filopodia suggest an environment of limited diffusive mobility. We sought a measure of the diffusion coefficient of fascin in filopodia to understand the relative difficulty of movement compared with that in the cell body. Using experimentally derived images of FRAP as inputs of filopodia cross-sections and initial and final protein concentrations, we simulated the recovery process of both GFP and GFP-S39E by using a mathematical model of one-dimensional diffusion (Appendix A). Typical experimental recovery profiles and their simulation results are plotted versus time in Figure 5A. By matching the recovery half-times between experiment and simulation, we determined values of mean diffusion (D) coefficient for GFP and GFP-S39E of 7.5 μm²/s and 5.1 μm²/s, respectively. Given the purely diffusive motion of soluble GFP, the Stokes–Einstein relationship predicts a diminished diffusion coefficient with increasing molecular weight: D ∝ M^−1/3. We fit this relationship through the experimentally determined diffusion coefficient of GFP, and we plotted the experimental value for GFP-S39E on the same plot (Figure 5B). The match between the experimentally measured diffusion coefficient for GFP-S39E and the predicted value based on molecular weight confirms that the phosphomimetic protein is not measurably slowed by actin binding or small network pore size in filopodia. Had the recovery process for GFP-S39E been significantly slowed by kinetics, the measured D value would have fallen below the curve.

Figure 5.

Phospho-fascin undergoes pure diffusion in filopodia. (A) FRAP recovery curves for soluble GFP and fascin mutants S39E and S39A (symbols). Simulations of recovery data (curves) yield diffusion coefficients for GFP and S39E. Recovery data with curve-fitting for S39A follows reaction-dominant process, plotted for comparison. (B) Median values of measured diffusion coefficients for GFP (7.5 μm²/s; n = 12) and S39E (5.1 μm²/s; n = 14) plotted versus molecular weight. Given a purely diffusive motion of GFP, the Stokes–Einstein relationship predicts a diminished diffusion coefficient with increasing molecular weight that matches S39E recovery data, suggesting the phosphomimetic mutant is negligibly slowed by adhesion or small network pore size. This relationship allows for interpolation of diffusion coefficient for unlabeled fascin, yielding D = 6 μm²/s.

The agreement between the experimentally determined and predicted diffusion coefficients allows for the use of the Stokes–Einstein relationship to interpolate a free diffusion coefficient for native fascin in filopodia. Fascin's untagged molecular weight of 55 kDa corresponds to a diffusion coefficient of D = 6 μm²/s (Figure 5B; discussion of effective diffusion in Appendix B). This value resembles the D value for GFP; therefore, it supports the conclusion that the FRAP recovery profiles used to calculate k_off were indeed kinetically limited. It is also less than one-tenth the diffusion coefficient previously measured for GFP in the cell body (Swaminanthan et al., 1997), reflecting the increased rate of collisions with immobile proteins, the more tortuous paths within the tight filopodial network, or both.

Incorporation of Fascin Cross-links in Filopodia

Individual actin filaments cannot impart sufficient stiffness to filopodia extended beyond the leading edge, but bundling by fascin allows for protrusion and maintenance of filopodia (Brieher et al., 2004; Mogilner and Rubinstein, 2005; Vignjevic et al., 2006). It is not known, however, what the fascin-to-actin ratio is in filopodia. Additionally, although our FRAP data reveal the existence of bound and free populations of fascin in filopodia, we do not know the fraction bound. We designed two approaches to calculate the relative fascin to actin concentration and solved for the ratio of bound to free fascin. Together, these relationships provide an estimate for the number of bound fascin molecules per actin in filopodia.

Filopodia Contain One Fascin Cross-link per 25–60 Actin Monomers

To solve for the stoichiometry of fascin to actin in filopodia, we developed a two-part technique that involves quantitative immunoblotting and fluorescence ratiometry based on previously established methods (Zhai and Borisy, 1994; Wu and Pollard, 2005). Immunoblotting was used to calculate the total number of fascin molecules in cells, and fluorescence microscopy was performed to determine the proportion of cellular fascin molecules that localize to filopodia. The measurements were combined to calculate the number of fascin cross-links per actin residing in filopodia.

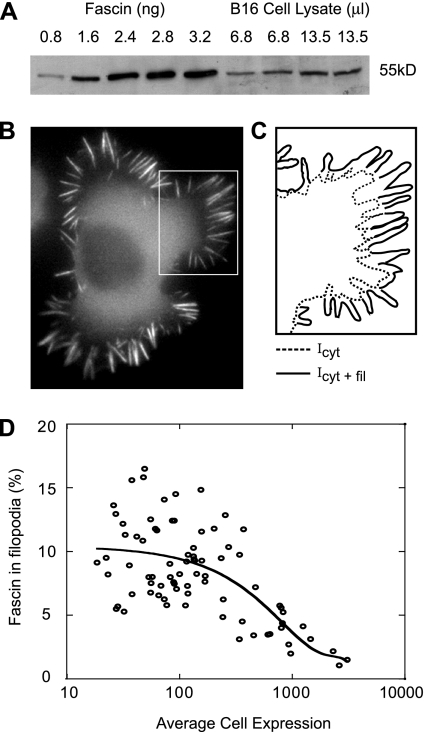
To determine the concentration of fascin in a cell, nontransfected cells were plated in a dish and counted by phase microscopy. Lysates of the counted cell population along with known amounts of pure fascin protein were loaded onto an SDS-PAGE and incubated with fascin antibody. The blot was visualized by chemiluminescence and shown in Figure 6A and Supplemental Figure 2. The intensity of the bands corresponding to amount of fascin in cell lysate and pure protein were quantified using NIH image software. We determined that B16 and N2a cells contain roughly 100–500 nM (n = 20).

Figure 6.

Filopodial bundles contain 1 fascin cross-link per 25–60 actin monomers in B16 cells. (A) Western blot of B16 cell lysate (in duplicate) and varying amounts of pure fascin protein. Comparison of band intensity reveals that B16 cells typically contain 100–300 nM [Fascin]. (B) Epifluorescent image of a B16 cell expressing GFP-fascin along with schematic representation of inset (C). Peripheries of cell (solid) and cytoplasm (dashed) are outlined to indicate borders of integrated intensity measurements, where I_cyt+fil is the total cell intensity and I_cyt is the intensity in nonfilopodial parts. (D) Percentage of fascin localized to filopodia was calculated using the expression, (I_cyt+fil − I_cyt)/I_cyt+fil × 100 and plotted versus average intensity in cells for varying expression levels. The data were fit with a third order polynomial with y-intercept equal to the percentage of endogenous fascin that localizes to filopodia in wild-type, nonexpressing cells. Using this technique, we determined that ∼11% of total fascin molecules in the cell localize to filopodia, or 11–33 nM [Fascin] reside in filopodia. Comparing the fascin to actin concentration in filopodia yields a ratio of 1 fascin per 25–60 actin (Appendix B).

Fluorescence ratiometry was used to determine the local concentration of fascin molecules in filopodia. Cells expressing GFP-fascin were imaged at varying expression levels in order to evaluate intensity variation in filopodial versus nonfilopodial parts over a wide expression range. Figure 6B shows a typical epifluorescent image of a B16 cell expressing GFP-fascin with inset illustrated in Figure 6C. The solid line demarcates the perimeter of the cell, whereas the dotted line outlines the outer boundary of the cytoplasm. By assuming that intensity is proportional to protein concentration, the ratio of total fascin localized to filopodia was calculated by dividing the integrated intensity in filopodia by that of the entire cell; filopodia plus cytoplasm. The percentage of fascin in filopodia was plotted versus average cell intensity for cells expressing GFP-fascin and fit with third order polynomial (Figure 6D and Supplemental Figure 2). The y-intercept of the fitted curve yields the percentage of total cellular endogenous fascin cross-links that localize to wild-type filopodia to be ∼10–30% (n = 118). Together, quantitative immunoblotting and fluorescence fractionation revealed that average filopodia contain one fascin cross-link per 25–60 actin monomers (calculation shown in Materials and Methods).

Most Fascin Molecules in Filopodia Are Bound at Any Instant

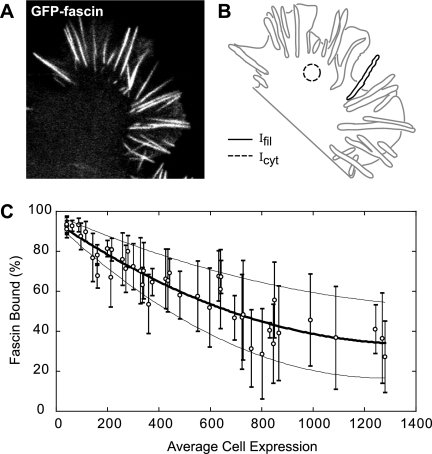
The stoichiometry of fascin to actin in filopodia determined above includes the total population of fascin molecules in filopodia; both bound and unbound fractions. Here, we used a fluorescence ratiometric technique to determine the proportion of fascin molecules that are bound. We examined the difference between intensity in filopodia and cytoplasm in confocal images of cells expressing GFP-fascin at varying expression levels. Confocal microscopy serves as an advantage to wide-field microscopy in that an image of the same optical depth is acquired. Therefore, intensity levels between different cellular structures, namely, filopodia and cytoplasm, can be directly compared. Figure 7A shows a representative confocal image of a B16 cell expressing GFP-fascin. Based on the assumption that the cytoplasmic pool in the cell body is unbound and that this concentration is uniform throughout the cell and filopodia, the per-pixel fluorescence intensity in the cell body (dashed circular region in Figure 7B) was taken as proportional to free fascin concentrations, whereas the fluorescence intensity in the filopodium (solid black outline in Figure 7B) was taken as proportional to the sum of bound and free fascin. The assumption that fascin is predominantly soluble in the cell body is supported by FRAP experiments in which rapid diffusion precluded any discernible bleached zone within lamellipodia or the cell body (data not shown). Therefore, dividing the fluorescence intensity in the cell body by the filopodial intensity yields the proportion of unbound fascin population in the filopodium. Subtracting this value from 1 gives the proportion of bound fascin molecules in filopodia. We plotted the percentage of bound fascin molecules in filopodia against average intensity values in the cytoplasm of cells at varying expression levels (Figure 7C and Supplemental Figure 2C). To determine the percentage of bound fascin molecules in wild-type filopodia, we curve fit our data with a second order polynomial and extrapolated to zero cell intensity. The y-intercept of the curve revealed that, on average, 97% (B16 cells: n_cells = 51, n_fil = 615; N2a cells: n_cells = 26, n_fil = 353) of endogenous fascin molecules are bound in filopodia, with a range of 94–98%.

Figure 7.

Nearly all fascin molecules (95–98%) in filopodia are bound. (A) Confocal slice of a B16 cell expressing GFP-fascin along with (B) schematic representation of the same cell. Average intensities in filopodia (sold line) and cytoplasm (dashed circle) were measured. The intensity in filopodia, I_fil, is proportional to total concentration of fascin, bound and unbound, whereas intensity in the lamellipodium, I_cyt, is proportional to amount of unbound fascin in filopodia. (C) Thus, percentage of fascin bound in filopodia was calculated as (1 − I_cyt)/I_fil and plotted versus average cytoplasmic intensity over a range of expression levels. Both the range and mean values for percentage of fascin bound in filopodia were fit with a second-order polynomial function, where the y-intercept yields the percentage of endogenous protein bound in filopodia of wild-type, nonexpressing cells. Using this method, we found that 95–98% of filopodial fascin is bound, with a mean value of 97%.

Dynamic Fascin Cross-Linking Allows for Increased Filament Bundling at Growing Filopodial Tips

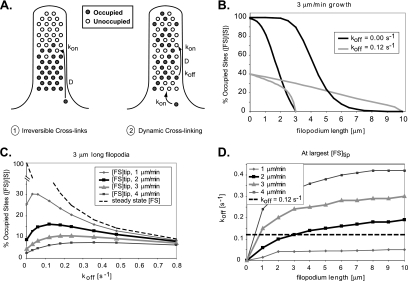
Growing filopodia require fascin cross-linking near their tips, necessitating fascin diffusion at a sufficient rate from the cell body over the entire length of the filopodium. Do binding reactions along the length preclude fascin delivery to the tips of long or rapidly growing filopodia? With the k_on and diffusion coefficient values reported in this study (Table 1), the average distance a fascin molecule diffuses before a binding reaction is ≈1.2 μm. In filopodia significantly longer than this distance and with irreversible cross-links (i.e., k_off = 0), diffusing fascin would permanently fill binding spots nearest the base first, and an elongation rate that exceeds fascin supply would leave the tips very low in fascin (Figure 8A). This rapid local transport but slow long-distance diffusion is the same phenomenon observed in the fast and slow recovery components in Figure 1. Diffusion with dynamic cross-linking (k_off > 0) might permit a sufficient supply rate to the tip region at longer lengths, by allowing dissociation of bound fascin and continued diffusion and redistribution along the length of the filopodium.

Table 1.

Parameters determined in this study

Parameter	Value
koff	0.12 s−1
kon	0.8 μM−1 s−1
D	6 μm2 s−1
fascin:actin	1:25–60
fascin (bound:free)	19–49:1

Figure 8.

Effective fascin transport to the tips of growing filopodia require dynamic cross-links. (A) A numerical model was developed to compare the suitability of fascin delivery to tips of growing filopodia via diffusion with irreversible cross-linking (1) and dynamic cross-linking via dissociation (2). (B) Under mechanism 1, cross-linkers diffuse toward barbed-ends and attach permanently near the first available binding site (k_off = 0) precluding delivery to the growing tips of moderate or long filopodia (black curves). In mechanism 2, fascin dissociation allows for cross-links to contribute farther along the filopodial length and near the tips (gray curves). (C) The percentage of occupied binding sites near the tips of 3-μm filopodia was plotted against fascin dissociation rate constants for growth rates of 1–4 μm/min. The curves reveal an increase in fascin–actin complex concentration, [FS], near tips for low rate constants, as well as a decrease at high rates due to a diminishing steady-state bound concentration (dashed curve). The peaks in the curves reflect optimal off rates for given conditions. (D) A plot of the optimal off-rate for various lengths and growth speeds show that a value of k_off = 0.12 s⁻¹ is optimal for 3-μm-long filopodia growing at 2 μm/min.

To quantify this predicted effect, we designed a numerical, one-dimensional (1D), reaction-diffusion model of filopodial elongation (Appendix A), and we compared the ability of these two mechanisms to accommodate growth over a range of filopodial lengths. The value of k_on was kept constant at 0.8 μM⁻¹ s⁻¹ throughout all simulations, such that changing k_off was equivalent to changing K_A. Unoccupied binding sites at [S] = 10 μM (Appendix A) were added to the tip of the model filopodium to simulate elongation rates of 1–4 μm/min, with typical rates of 2–3 μm/min determined by subtracting the rate of actin retrograde flow from the rate of filopodial protrusion in FRAP data. A constant pool of free, active fascin [F] = 0.1 μM was maintained at the base (cell body). Because growth extends unoccupied binding sites and k_on is finite, the extreme tip itself was always theoretically devoid of bound fascin. Accordingly, we compared concentrations of occupied binding sites, [FS], at a position 0.5 μm from the filopodial tip. Plots could have alternatively been made of the bound fascin-to-actin ratio ([FS]/([S] + [FS])), but these curves would be of identical shape, because the total binding site concentration ([S] + [FS]) is proportional to the actin concentration and remains constant along the length.

As expected, the advantage of fascin dissociation increased with filopodial length at typical rates of elongation. With irreversible cross-links, the profile of bound fascin concentration fell sharply toward the tip of 3-μm-long filopodia (Figure 8B, black curve). With dynamic cross-linking, the concentration of occupied sites near the base decreased due to a lower equilibrium (i.e., maximum) value, but increased by a factor of 1.5 near the tip (Figure 8B, gray curve). When filopodia continued to grow to 10 μm, a markedly sigmoidal concentration profile indicated low fascin transport to the tip when k_off = 0 s⁻¹, but a 100-fold increase in bound fascin concentration was observed with k_off = 0.12 s⁻¹. Thus, a process which involves diffusion and rapid, irreversible association can supply fascin only to short filopodia, but dynamic cross-linking is required to sustain longer filopodia.

Is there an optimal off-rate for delivery of fascin to filopodial tips? Figure 8C plots the concentrations of bound fascin [FS] near the tips of growing, 3-μm-long filopodia as a function of k_off. Consistent with Figure 8B, tip concentrations initially increased with k_off. At higher k_off; however, concentrations decreased due to a diminishing equilibrium bound fascin concentration. The peaks in the curves represent an optimal value of k_off for maximum bound fascin concentration near the tips of growing filopodia. Our measured off-rate compares well with the range of dissociation rates, 0.05–0.25 s⁻¹, that are optimal for filopodia growing at rates of 1–4 μm/min.

Figure 8D plots the optimal k_off as a function of length for several growth velocities. At growth rates of 2 μm/min and lengths of 3 μm, our measured value of k_off = 0.12 s⁻¹ provides the highest bound fascin concentration near the tip. At 3 μm/min filopodial growth rate, k_off is optimized for short, 0.8 μm filopodia. At slow growth rates of 1 μm/min, bound fascin concentrations near the tip would be higher with a decreased k_off at any length. Thus, the k_off measured in this study seems to be a good compromise among lengths to generate the highest tip concentrations of bound fascin at typical growth rates.

DISCUSSION

Filopodia are highly dynamic cellular protrusions that require precise mechanisms for recruitment, maintenance, and turnover of their molecular components. In this study, we showed that filament bundling in filopodia requires fascin dephosphorylation, that instantaneous fascin cycling between filaments optimizes filopodial growth conditions, and that, on average, filopodia contain fascin:actin ratios of 1:25–60. Here, we explore the implications of these results on mechanisms for filopodia elongation and physical properties.

Fascin Phosphorylation Acts as a Molecular Switch for Filopodia Formation

Cells have the capacity to form filopodia in response to a variety of signals that arise from environmental cues, particular substrates, or other cells. Such a capacity implies the existence of a regulatory mechanism. In this work, we tested phosphorylation/dephosphorylation cycles in regulating key events in filopodia. Because fascin phosphorylation has been reported to inhibit actin bundling (Yamakita et al., 1996; Ono et al., 1997; Adams et al., 1999), we suspected that the role of these cycles may be to regulate fascin exchange in filopodia and to limit concentrations of fascin available for actin cross-linking. Unexpectedly, we found that the time scale for fascin dissociation in reconstituted filopodial bundles mimicked those in filopodia, indicating that the dynamic exchange does not require an enzymatic reaction but that it is an intrinsic property of the fascin cross-linker. In contrast, photobleaching data on fascin phosphomutants revealed that phosphorylation alters the mobility of fascin in filopodia. Although the nonphosphorylated fascin mutant imitated wild-type kinetic reactions in filopodia, the phospho-fascin mutant underwent a predominantly diffusive process. The phosphomimetic mutant S39E contains one active binding site and one site that is inactivated by a single-site mutation. Although the nonmutated binding site is presumably free to associate with actin, it is likely that, without the cooperation of the other binding site, fascin does not undergo appreciable binding to filaments. Therefore, only the nonphosphorylated form seems to participate in filament cross-linking, whereas the purpose of fascin phosphorylation is likely to limit the size of that pool. On basis of our results, we propose that phosphorylation/dephosphorylation cycles serve as a molecular switch to turn fascin activity on or off, which in so doing determines whether filopodia form.

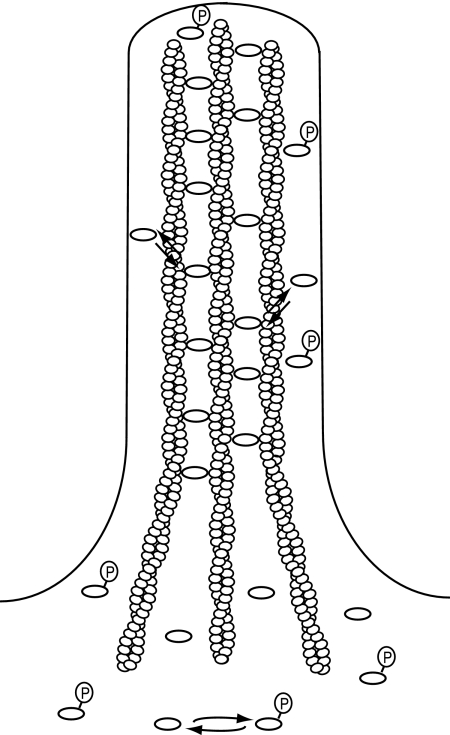
In summary, we propose a model for the formation and maintenance of filopodia (Figure 9). In our model, activation of fascin by dephosphorylation allows for high-affinity actin binding in filopodia. Actin cross-linking provides filopodia with the rigidity necessary for protrusion, whereas intrinsic fascin exchange between filaments allows for elongation and filopodial remodeling. Fascin inactivation by phosphorylation decreases the availability of fascin to bundle actin, which in turn inhibits filopodia formation.

Figure 9.

Illustrative model of fascin dynamics and organization in filopodia. Fascin is activated by dephosphorylation, which allows for high-affinity interaction with actin filaments in filopodia. Active fascin undergoes intrinsic dynamic exchange, which facilitates and ensures efficient remodeling of the filopodium during shape changes.

Filopodia Represent Semiordered Bundles of Actin

Our study reveals that filopodia contain one bound fascin molecule per 25–60 actin monomers. Due to the dynamic nature of the cross-links, this ratio represents unsaturated binding sites. The saturation stoichiometry can be calculated from equilibrium kinetics:

where [actin] is the filopodial actin concentration, [F] is the soluble, active fascin concentration, and [S] and [FS] are the available and occupied binding sites on the filaments, respectively. Even more fascin could theoretically be bound in a perfect filament lattice. Considering each helix of an actin filament separately, if the pitch allowed for a 360° rotation precisely every 12 monomers, each monomer would contribute a 30° rotation. If these filaments were hexagonally packed, for example, every second actin monomer in the helix would be aligned with an adjacent filament and perhaps accommodate a cross-link. Because each fascin is connected to two filaments, this repeating arrangement would result in a molecular ratio of one fascin per four actin monomers. (Note that each helix of each filament repeats this geometry, such that, neglecting bundle edge effects, the ratio remains 1:4 for the entire bundle.) Indeed, lattices seeming hexagonal are apparent in some reconstituted or chemically fixed bundles (Tilney and DeRosier, 1986; Tilney et al., 2000; Volkman et al., 2001), and bound ratios of up to 1:4.6 have been measured in vitro (Bryan and Kane, 1978; Yamashiro-Matsumura and Matsumura, 1985). However, it seems unlikely that the geometry of filopodia would allow for this precise packing. The pitch of each actin helix of a free filament is imperfect for hexagonal packing, rotating 360° per ∼13.7 monomers, or only 26.3° (instead of 30°) per monomer. Because one bound fascin per 25–60 actin monomers equates to one cross-link every 6th to 15th monomer along a double helix, a torque aligning the filament for hexagonal packing would result in an cumulative angle strain of (30–26.3° per monomer) × (6–15 monomers) = 22–56° between successive cross-links on a filament. Electron micrographs of filopodia formed by convergent elongation in fact seem imperfectly packed (Svitkina et al., 2003), and Stokes and DeRosier (1991) have described bundles formed in vitro with one bound fascin per 33–66 actin monomers as plentiful but “poorly ordered,” both suggesting a somewhat reduced binding site concentration. The lower range of our bound fascin-to-actin ratio (1:25) would translate to a binding site to actin ratio of 1:4.6 if either K_A was as low as 2.3 μM⁻¹ or the free fascin concentration, [F], was as low as 0.03 μM (an order of magnitude lower than our measured 0.1–0.5 μM).

In summary, filopodia seem to represent semiordered bundles, reducing the possible fascin:actin (saturation) stoichiometry from a 1:4 theoretical value to 1:10–24. However, given their dynamic nature and limited soluble concentration, they only operate at ratios of 1:25–60 in vivo.

Fascin Dynamics Impart Rate-dependent Resistance to Filopodial Deformation

A key function of fascin as an actin cross-linker is its ability to stiffen filopodia. Individual actin filaments are insufficiently rigid to resist compressive forces (Janmey et al., 1991; Mogilner and Rubinstein, 2005), and filopodia in fascin-depleted cells are typically bent and buckle under the cell membrane (Vignjevic et al., 2006). Although the function of stiffening would apparently be best served by high-affinity fascin binding, this counteracts the need for filopodia to undergo necessary remodeling (e.g., fusion of neighboring filopodia, accommodation to obstacles, or cycling between growth and breakdown). The dynamic nature of the fascin cross-links allows for both requirements.

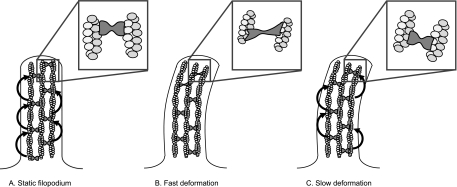
The filopodium as a whole undergoes two main loading regimes, with a different mechanical response to each. Slow-scale displacement of the filopodium occurs on the time scales of cell motility itself, on the order of 1 μm/min, and it may occur over small or large distances. A growing filopodium may be displaced as it encounters other cells, for example, or be displaced by lamellipodial retraction or the motion of adjacent cells. Displacement may also occur on rapid time scales due to Brownian (thermal) motion, under which a single, 10-μm-long actin filament bends considerably (persistence length, Isambert et al., 1995). We have shown that the half-time of fascin exchange in filopodia is 6 s, indicating a time scale of motion that divides two types of mechanical responses: displacement rates that build little strain in the cross-links over this time-scale result in little resistance to displacement from those cross-links, whereas rates that build up significant strain on this time scale encounter resistance due to the additional stiffness that fascin imparts to the bundle. This resistance rises with the filopodial fascin:actin ratio, which we estimated to be high, at 1:25–60. Although it is difficult to predict the rate at which strain builds in the cross-links of a displaced filopodium without detailed knowledge of the system geometry, it is likely that the slow displacements do not build appreciable resistance from fascin over the course of a single binding period, whereas the displacement due to thermal motion almost certainly does. The dynamics of fascin exchange therefore mediate a differential, visco-elastic-like response to the two common loads, allowing slow remodeling but resisting rapid fluctuations with additional stiffness (Figure 10).

Figure 10.

Rapid fascin exchange may endow filopodia with a rate-dependent response mode to mechanical stress. Schematic models depicting the behavior of fascin in filopodial bundles under different rates of deformation. (A) Fascin undergoes continuous exchange within unstressed bundles. (B) Moderate rates of fascin exchange allow for filopodia to resist rapid deformations (C) but to reorganize when stress is applied slowly. In the latter case, fascin provides little resistance against the load since cross-links rearrange faster than filaments are displaced.

Similar stress-strain relationships have been observed in stress fibers incorporating alpha-actinin (Sato et al., 1987; Pollard et al., 1990). Like fascin-mediated actin bundles, the mechanical properties of such actin networks depend on the rate of displacement, where the stiffness can increase by an order of magnitude at fast displacements. One significant difference is that the rate of dissociation of α-actinin is an order of magnitude faster than that of fascin (Xu et al., 2000). The variance in the time scales of protein exchange between the two bundlers yield different limits for the rate of deformation. Such limits may be critical for the ability of actin bundles to withstand the different types of stresses they encounter in their respective subcellular locations. It would be interesting to compare such properties between filopodia and other protrusive actin networks such as pseudopodia, microvilli, and stereocillia.

Fascin Turnover Is a Key Process in Rapid Filopodial Assembly

Filopodia are naturally subject to selective evolutionary pressures as dictated by their required sensory functions. Such pressures include the formation and maintenance of ordered parallel bundles; remodeling of filopodial structure at adequate rates under appropriate loads, with resistance to other loads; providing the necessary, perhaps nonuniform, stiffness along the filopodial length; and transport of cytoskeletal proteins to growing filopodial tips at rates compatible with elongation velocities. Such requirements must operate over filopodial lengths of 1–50 μm, diameters of only 0.1–0.5 μm (Mitchison and Cramer, 1996), and growth rates from a typical 2 μm/min (Mallavarapu and Mitchison, 1999; current study) to as fast as 25 μm/min (Sheetz et al., 1992). As our numerical analysis shows, filopodia growing at 2 μm/min seem to operate near a k_off that delivers maximum fascin cross-links to the extending tip. Lower k_off values allow less dissociation of bound fascin and continued diffusion toward the tip, whereas higher values further limit the equilibrium bound concentration throughout the length. Among the pressures affecting filopodial rigidity and morphology, the optimal value of k_off to supply fascin to the tip at the typical growth rate seems to be of particular importance. Altogether, filopodia may have selected dynamic cross-links to form adequately stiff bundles at appropriate rates and allow for remodeling.

Abbreviations used:

FLIP

fluorescence loss in photobleaching

FRAP

fluorescence recovery after photobleaching

GFP

green fluorescent protein

RT

room temperature

TMR

tetramethylrhodamine

WT

wild type.