Heritability of ultimatum game responder behavior

Abstract

Experimental evidence suggests that many people are willing to deviate from materially maximizing strategies to punish unfair behavior. Even though little is known about the origins of such fairness preferences, it has been suggested that they have deep evolutionary roots and that they are crucial for maintaining and understanding cooperation among non-kin. Here we report the results of an ultimatum game, played for real monetary stakes, using twins recruited from the population-based Swedish Twin Registry as our subject pool. Employing standard structural equation modeling techniques, we estimate that >40% of the variation in subjects' rejection behavior is explained by additive genetic effects. Our estimates also suggest a very modest role for common environment as a source of phenotypic variation. Based on these findings, we argue that any attempt to explain observed ultimatum bargaining game behavior that ignores this genetic influence is incomplete.

It is frequently pointed out that humans exhibit unusually high rates of cooperation among non-kin (1), and it has further been suggested that one important factor for enhancing cooperation is that humans appear willing to forego material payoffs to punish unfair behavior (2–4). Such fairness preferences have been widely studied by using experimental games, in particular the ultimatum game (5–7).

In the ultimatum game, two subjects are assigned the role of either proposer or receiver, and then they bargain over a sum of money (the “cake”). The proposer makes an offer on how to divide the cake. If the receiver accepts the proposer's offer, the players are paid accordingly, whereas if the offer is rejected, both players receive a zero payoff. In a one-shot game, rational and money-maximizing responders should accept any positive offer because the alternative is a zero payoff. Two stylized facts about responder behavior emerge from the ultimatum game literature: first, that unfair offers are often rejected and second, that the acceptance threshold varies substantially between individuals (5, 6). The average responder behavior has been shown to be relatively stable across Western cultures (8), whereas more variation has been observed among non-Western small-scale societies (9).

Although there is a voluminous literature discussing the cultural and evolutionary origins of observed fairness preferences, the relative social and genetic contributions have hitherto been left unexplored. In this work, we use the classical twin design to estimate the heritability of the propensity to reject unfair offers in the ultimatum bargaining game. In doing so, we not only provide the first decomposition of the social and genetic contributions to ultimatum game rejection behavior but also to behavior in experimental games in general. The virtue of the twin design is that by comparing monozygotic (MZ) twins, who share the same set of genes, and dizygotic (DZ) twins, whose genes are imperfectly correlated, we can estimate the proportion of variance in phenotype due to genetic, shared, and nonshared environmental effects (10).

Results

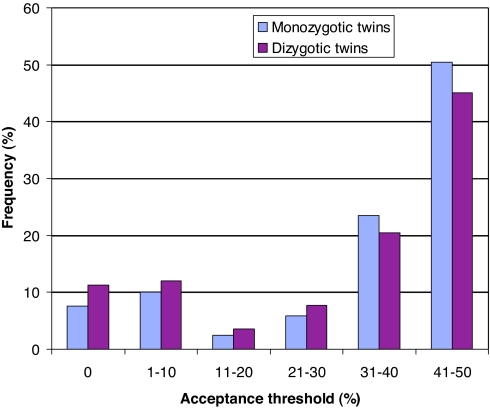
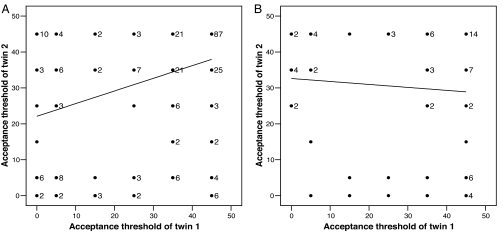
In Fig. 1 we report the distribution of acceptance thresholds for MZ and DZ twins. As can be seen, the distributions are very similar, and we cannot reject the null hypothesis of identical distributions (χ² test; χ² value = 4.292, df = 5, n = 653, P = 0.491).^¶ The average acceptance threshold is 32.68 SEK, implying that on average a responder demands ≈33% of the cake to accept the proposer's offer in the ultimatum game.^‖ Fig. 2 illustrates the correlation in acceptance thresholds within MZ and DZ twin pairs. The Spearman rank correlation is 0.39 (95% confidence interval, 0.26–0.49) for MZ twin pairs and −0.04 (95% confidence interval, −0.25 to 0.18) for DZ twin pairs. The difference in the correlation coefficients is highly significant (t test; t = 3.212, P < 0.01, two-sided) and thus provides strong evidence in favor of a genetic effect on ultimatum game responder behavior.

Fig. 1.

Distribution of acceptance thresholds in the ultimatum game for MZ and DZ twins. The distributions do not differ significantly.

Fig. 2.

Scatterplot of ultimatum game acceptance thresholds for twin pairs. (A) Scatterplot for MZ twin pairs. The acceptance thresholds are highly correlated. (B) Scatterplot for DZ twin pairs. There was no significant correlation in acceptance thresholds.

We also use a standard threshold model to decompose phenotypic variation into additive genetic effects, common environmental effects, and nonshared environmental effects. The model assumes that there is an underlying, continuous and normal distribution of fairness preferences, with arbitrary cutoffs (thresholds) observed by the researcher. In Table 1 we present maximum likelihood estimates of the model parameters as well as its nested submodels.** Additive genetic effects are estimated to account for 42% of the variation in the best-fitting model, and this estimate is significantly different from zero (P < 0.01). The point estimate of the effect of common environment is zero, and its confidence interval has an upper boundary at 21%, suggesting that common environmental influences are at most a moderately important source of variation. The remaining variation is accounted for by nonshared environment. The estimate of nonshared environment also includes any measurement error.

Table 1.

Maximum likelihood estimates of the structural equation ACE model and its submodels (95% confidence intervals in parentheses)

Model	χ2 value	P	df	Mean squared error	A (genetic contribution)	C (common environmental contribution)	E (unique environmental contribution)
ACE	79.44	0.08	63	0.02	0.42 (0.17–0.54)	0.00(0.00–0.21)	0.58(0.46–0.72)
AE	79.44	0.09	64	0.02	0.42 (0.28–0.54)		0.58(0.46–0.72)
CE	86.96	0.01	64	0.04		0.32(0.19–0.4)	0.68(0.56–0.81)
E	109.30	0.00	65	0.04			1

The genetic contribution (A) is highly significant in the full ACE model with a point estimate of 42% of the variation. The common environmental contribution (C) has a point estimate of zero and is not significant. The AE submodel is the best-fitting model; comparing this model with the ACE model, we cannot reject the null hypothesis of a zero effect of common environment (χ ² test; χ ² value = 0, df = 1, P = 1). The ACE model significantly outperforms the CE submodel (χ ² test; χ ² value = 7.52, df = 1, P < 0.01) and the E submodel (χ ² test; χ ² value = 29.88, df = 2, P < 0.001).

Finally, we consider the results stratified by sex because pooling may not always be appropriate. Our data set is fairly unbalanced with respect to sex, approximately three-quarters of subjects being women. There was no evidence that pooling by sex is inappropriate because we could not reject the null hypothesis that the distribution of the acceptance threshold is the same for men and women (χ² test; χ² value = 2.653, df = 5, n = 653, P = 0.778) (11). When we estimate separate models for men and women, the estimates of additive genetic effects were practically identical: 0.412 for women and 0.435 for men.

Discussion

This work has demonstrated that genetic influences are important determinants of rejection behavior in the ultimatum game. In our best-fitting model, additive genetic effects account for 42% of the observed variation in responder behavior, and our point estimate for common environment is zero. However, note that the estimate for the genetic effect should be considered a lower boundary because it presumes perfect reliability in the measurement of responder behavior. If there is noise in eliciting acceptance thresholds, the estimate of additive genetic effects will be downward-biased.

Our finding of substantial genetic effects on ultimatum game rejection behavior is consistent with previous research in behavioral genetics and neuroscience. For instance, survey based studies repeatedly find sizeable genetic effects on a wide range of economically relevant social attitude variables such as personality and political preferences (15–18). Furthermore, recent studies have shown that the responder stage in the ultimatum game is associated with increased activation in the dorsolateral prefrontal cortex as well as responders' circulating testosterone levels (19–21). The dorsolateral prefrontal cortex is a brain region whose structure is under pronounced genetic influence (22, 23), as are individual testosterone levels (24).

The etiology of fairness preferences has been intensely debated. Some authors have argued that the willingness to engage in costly punishment reflects fundamental and universal fairness preferences that evolved through a process of gene–culture coevolution in early modern Homo sapiens, preferences that are considered crucial for maintaining cooperation among non-kin (3, 25). Others have argued that indirect reciprocity models based on an evolved psychology for reputation management provide a more parsimonious explanation (1, 26–31). Although our results are consistent with an evolutionary origin for fairness preferences, it is important to remember that heritability measures the genetically determined variation around some average behavior. Hence, it does not provide us with any direct evidence with regard to the evolutionary dynamics that brought it about.

However, the fact that there seems to be a substantial genetically determined heterogeneity in ultimatum game rejection behavior is an interesting finding in and of itself. First of all, it suggests that economic theory and policy need to address the potential importance of genetic influences on economic preferences, behavior, and outcomes (32). It also suggests that the current debate on the evolutionary origins of ultimatum game rejection behavior, and the preferences it proxies, should perhaps be brought into the broader context of the evolution of variation in personality. If we observe a mean phenotypic expression in behavior with substantial genetic variation, then any evolutionary model of its origin must not only account for average phenotype but also phenotypic variation.

In humans as well as in other species there is substantial genetically determined variation for a great number of personality traits (33–35). Unfortunately, this variation is not well understood because the observed patterns seldom correspond to the simplest evolutionary genetic models of fixation. Many authors have therefore resorted to the default explanation that observed variation is nonadaptive (33). This is, however, not necessarily the case, and a number of recent papers have examined these questions in more detail. For instance, Dall et al. (33) emphasize the combination of frequency-dependent selection and state-dependent behavioral specialization as a possible source of adaptive variation, whereas Penke et al. (35) argue that balancing selection by environmental heterogeneity explains individual variation in personality.^††

Finally, on a more general note, our findings suggest that it is time to take seriously the proposition that experimental behavior may be substantially heritable, which may explain why, despite ample experimental evidence, the origins of individual variation remain elusive, and most attempts to find theoretically appealing and empirically stable correlates to experimentally derived preferences have had only mixed success.

Materials and Methods

This work was undertaken in collaboration with the Swedish Twin Registry at Karolinska Institutet. The registry is the largest twin registry in the world and has been described in detail elsewhere (36). Same-sex twins born 1960–1985 were solicited by e-mail and recruited in all major Swedish cities through the summer and fall of 2006. A condition for participation was that both twins in a pair be able to attend the same experimental session. In total, 658 individuals (71 DZ and 258 MZ pairs of twins) participated. Zygosity was assigned by questionnaire items that have been shown to have a reliability of up to 98% (36).

In the first stage of the experiment, all subjects played the role of proposer and were asked to divide 100 SEK (approximately $15) between themselves and a randomly selected anonymous counterpart not partaking in the same experimental session. In the second and final stage, all subjects played the role of responder and were once again matched with a randomly selected anonymous counterpart, different from that in stage 1, not partaking in the same session. We used the strategy method to extract acceptance thresholds (6). Each subject determined whether he or she would accept or reject every possible proposal in multiples of 10% before learning the actual proposal. This method allows for the recovery of the entire strategy of each participant. We then recorded the lowest offer that the responder indicated a willingness to accept in the range of offers between 0% and 50%. In this region, all subjects, except for the very few idiosyncratic responses referred to below, exhibit simple, monotonic behavior. The mean acceptance threshold is therefore uniquely defined.^‡‡

Of the 658 participants, two failed to respond to the ultimatum game question and had to be dropped from the analysis. In addition, eight subjects provided inconsistent responses.^§§ Of these inconsistent responses, five were clarified by an e-mail follow-up question (two subjects did not respond to the e-mail, and one subject wanted to keep the inconsistent answer). Thus, our dataset in the analysis consists of 653 individual observations (511 MZ twins and 142 DZ twins), and 324 complete twin pairs (253 MZ pairs and 71 DZ pairs).^¶¶

Abbreviations

DZ

dizygotic

MZ

monozygotic.