Hydrophobic cooperativity as a mechanism for amyloid nucleation

Abstract

The kinetics of amyloid fibril formation are in most cases explained by classical nucleation theory, yet the mechanisms behind nucleation are not well understood. We show using molecular dynamics simulations that the hydrophobic cooperativity in the self-association of the model amyloidogenic peptide STVIYE is sufficient to allow for nucleation-dependent polymerization with a pentamer critical nucleus. The role of electrostatics was also investigated. Novel considerations of the electrostatic solvation energy using the Born-Onsager equation are put forth to rationalize the aggregation of charged peptides and provide new insight into the energetic differences between parallel and antiparallel β-sheets. Together these results help explain the influence of molecular charge in the class of fibril-forming hexapeptides recently designed by Serrano and collaborators.

Introduction

Amyloid diseases are characterized by the extracellular deposition of insoluble plaques comprised of polypeptides aggregated into ordered fibril structures rich in β-sheet content.¹ Classical nucleation theory is often used to explain amyloid phenomena as the kinetics of fibril formation are in most cases consistent with a nucleation-dependent polymerization mechanism.^2–6 Nucleation theory posits that the initial association of monomers to form small oligomers is energetically unfavorable; once an oligomer of sufficient size, the critical nucleus, is formed, monomer addition becomes energetically favored and polymerization is a downhill process (Fig. 1A). The physical rationale for such a free energy profile is as follows. While the loss in entropy associated with aggregating a monomer out of solution can be presumed to be approximately independent of the size of the oligomer with which it aggregates, there is likely to be cooperativity in the enthalpy of adding successive monomers to oligomers of increasing size. If this cooperativity is sufficient, the enthalpic term will eventually overcome the entropic cost and monomer addition will become energetically favorable. One argument that has been proposed to account for the necessary cooperativity in the association enthalpy is that monomers are able to participate in more new interactions when binding to larger rather than smaller oligomers (Fig. 1B).

Fig. 1.

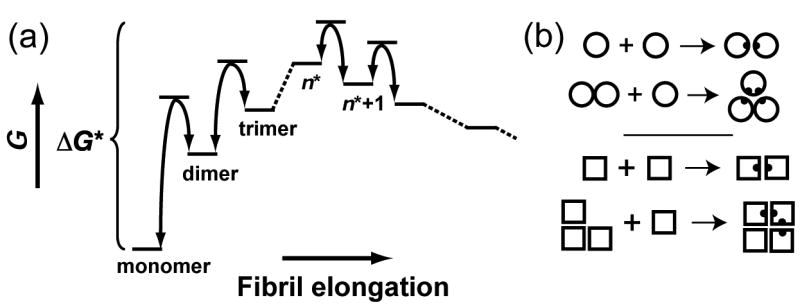
(a) Classical nucleation theory. Monomer addition is unfavorable until the critical nucleus is formed, which consists of n* peptides and is defined as the state with the highest free energy; addition of a monomer to an oligomer of n* or more peptides results in a lowering of the free energy. The rate of nuclei formation is proportional to e^−ΔG*/k_BT. (b) A cartoon illustrating the nature of cooperative association; two new interactions are formed when a monomer binds a dimer or trimer, whereas only one interaction is formed when two monomers associate.

A growing body of evidence points to small oligomeric intermediates on the fibril elongation pathway, rather than fully formed fibrils, as the disease-causing agents in many amyloid pathologies.^7–10 To understand amyloid disease it is thus necessary to characterize the entire amyloid assembly pathway and its various intermediates. Molecular simulations have been used in recent years to investigate early aggregation events in amyloidogenic peptides. In detailed atomistic molecular dynamics (MD) simulations peptide fragments were observed to associate into disordered trimers and tetramers that subsequently organized into β-sheets.^11–13 At the other extreme, the spontaneous formation of 100-peptide fibrillar structures has been observed in coarse-grained simulations.^14,15 Such studies demonstrate the usefulness of simulation as a tool for studying transient intermediates in the fibril formation pathway that have proved difficult to characterize experimentally.

Understanding amyloid nucleation in particular remains an important problem. The critical nucleus cannot be detected directly as it exists only transiently and at low concentrations; its size, however, can be inferred from the concentration dependence of the lag time (i.e., the time required for nuclei formation). Kinetic characterization has been used to study nucleation in the Ure2p yeast prion and polyglutamine. The Ure2p critical nucleus was reported to consist of six monomers,¹⁶ while the polyglutamine nucleus was shown to be equal to one, suggesting that its nucleation can be regarded as a highly unfavorable folding reaction.¹⁷ Simulation studies of nucleation have been hindered by the fact that attaining convergence in all-atom simulations of association equilibria remains intractable due to the large number of degrees of freedom involved. Attempting to circumvent this, Wu et al. simulated the tetramerization of the NFGAIL peptide at extremely high concentration (233 mM).¹³ Extrapolating their results for the cooperativity they observed between the trimer and tetramer, they speculated that at the “physiological” peptide concentration of 1 nM the nucleus is an octamer. Nucleus size has also been explored in coarse-grained simulations, which show that the nucleus increases in size upon destabilization of the amyloid-competent state.¹⁵

Our present studies focus on the direct detection and characterization of the critical nucleus for a small model amyloidogenic peptide. Rather than trying to sample all of association/dissociation configurational space, we performed atomistic simulations on intact oligomers of different size and measured the cooperativity in their enthalpy. These enthalpy measurements were then coupled with entropic considerations, allowing us to compute the free energy profile for aggregation. Our studies concentrated on the peptide STVIYE, which was designed by Serrano and collaborators to form homopolymeric antiparallel β-sheets and was demonstrated to form amyloid fibrils in vitro at pH 7.4 but not at pH 2.6. (The N- and C-termini are acetylated and amidated, respectively, so that the glutamate bears the only potential charge group in the peptide.) By examining seven other similar sequences Serrano et al. were able to show that peptides with a net charge of ±1 had a marked preference for fibril formation over their electrically neutral counterparts.¹⁸ We performed simulations on the STVIYE system with both protonated and deprotonated glutamate to explore the molecular basis for this trend. Simulations were performed using replica exchange molecular dynamics (REMD) with the all-atom CHARMM force field¹⁹ and a generalized Born (GB) implicit solvent model.²⁰

Results and Discussion

REMD trajectories

Four sets of simulations were performed, which we denote I–IV; in each set homo-oligomers comprised of two to eight peptides were simulated. Sets I and II consisted of antiparallel β-sheet oligomers of STVIYE^(-) and STVIYE, respectively (Fig. 2; see also Fig. S1 in Supplementary Data). In sets III and IV multiple copies of either STVIYE^(-) or STVIYE, respectively, were randomly oriented in space and allowed to diffuse together to form amorphous aggregates. Monomeric STVIYE^(-) and STVIYE were also simulated. The mean thermal energy for each oligomer was computed by averaging its potential energy throughout the 303 K simulation; using these mean energies we calculated the enthalpy changes for adding successive monomers to oligomers of increasing size. To wit, we computed ΔH_n^th, the enthalpy change for the reaction, ${\text{P}}_{\text{1}}+{\text{P}}_{n-1}\rightleftharpoons {\text{P}}_n$, which is the association of the n^th monomer with an oligomer of n − 1 peptides to form an oligomer of n peptides.

Fig. 2.

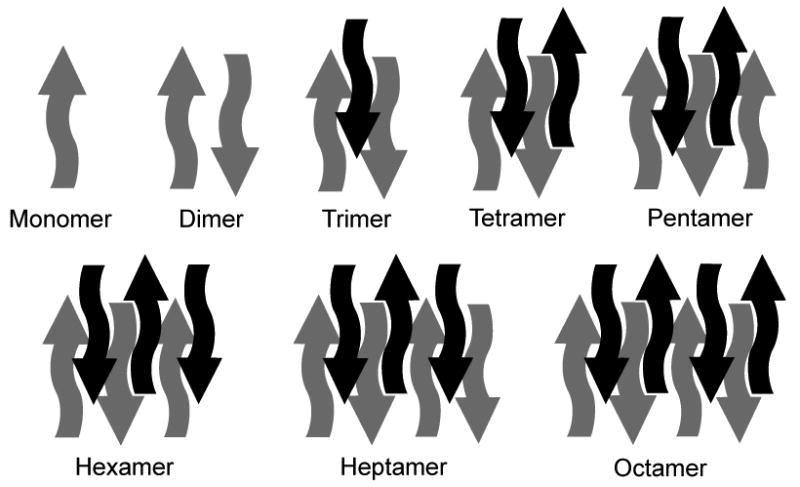
β-sheet oligomers were constructed with up to eight peptides and consisted of two stacked antiparallel β-sheets.

Monomeric STVIYE^(-) and STVIYE simulations started from the extended conformation. However, within 1 ns of REMD each peptide backbone collapsed on itself. During the next 3 ns of simulation the peptides formed more or less compact structures, often forming transient helical structures with i, i + 3 and i, i + 4 backbone hydrogen bonds. Heptameric and octameric β-sheet oligomers were stable throughout the entire REMD simulation, with most of their inter-strand hydrogen bonds remaining intact. The smaller β-sheet oligomers were less stable, and, though the peptides remained associated, some of the backbone hydrogen bond network was lost by the end of the simulation. These results are consistent with the observation by Nussinov et al. that as many as eight peptides are needed to form a β-sheet oligomer that is stable in the nanosecond regime in explicit solvent MD simulations.^21,22 Despite the gradual decrease in hydrogen bonds over the course of the simulation, the overall energy was quite stable in the smaller β-sheet simulations, and hence we were able to compute meaningful thermal energies for the metastable β-sheet oligomers. We note that significantly longer simulations would have led to dissociation of the oligomers.

Amorphous aggregate simulations started with a random configuration of compact monomer structures. Monomers were not constructed in the extended conformation in this case because such structures were rare in the MD ensemble in monomeric simulations. In each of the aggregates simulated, all of the monomers associated within 1 ns, forming roughly globular aggregates of more or less compacted monomers randomly oriented with respect to each other. Once formed, aggregates remained associated throughout the entire simulation.

Association enthalpies

The ΔH_n^th values obtained for n = 2 to 8 for sets I–IV reveal a high degree of cooperativity in the association enthalpy (Fig. 3). Dimer formation is favored by 17 to 20 kcal/mol, and in each set monomer addition to the larger oligomers ends up being nearly twice as favorable. To determine the origin of this cooperativity, ΔH_n^th values were decomposed into parts for different energy components (i.e., the bond, angle, dihedral, van der Waals, and electrostatic energy terms as well as the GB terms for polar and nonpolar solvation). The solvation free energy for solutes in water is typically expressed as the sum of polar (electrostatic) and nonpolar contributions: ΔG_solv = ΔG_els + ΔG_np. The sum of the contributions of the van der Waals and nonpolar surface burial terms to the association enthalpy²³ (ΔH_vdw+np,n^th) represents the change in ΔG_np upon association, and can be regarded as the hydrophobic interaction strength. The sum of the polar GB and electrostatic contributions, ΔH_gb+elec,n^th, represents the change in ΔG_els as well as solvent-screened electrostatics upon association. Energy decomposition reveals that the observed cooperativity in ΔH_n^th is dominated by hydrophobic interactions. While both ΔH_vdw,n^th and ΔH_np,n^th became more negative with increasing n, all other contributions to ΔH_n^th fluctuate about zero and play only minor roles in determining the magnitude of the association enthalpy (Fig. 4A).

Fig. 3.

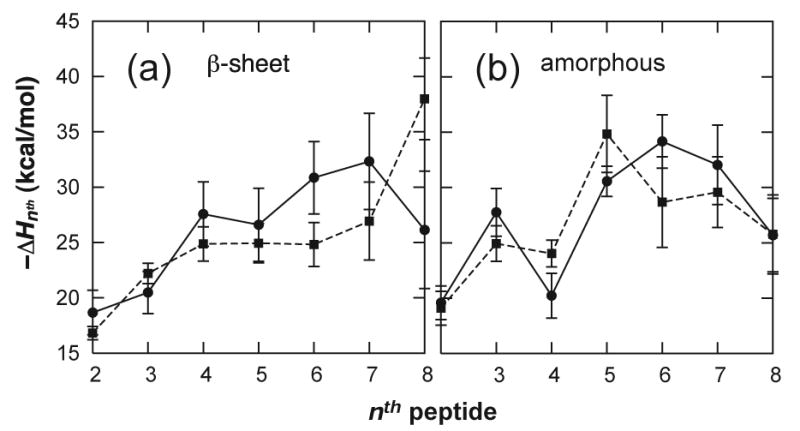
Association enthalpies, ΔH_n^th, for β-sheet oligomers (a) and amorphous aggregates (b), from MD simulations of STVIYE^(-) (circles) and STVIYE (squares).

Fig. 4.

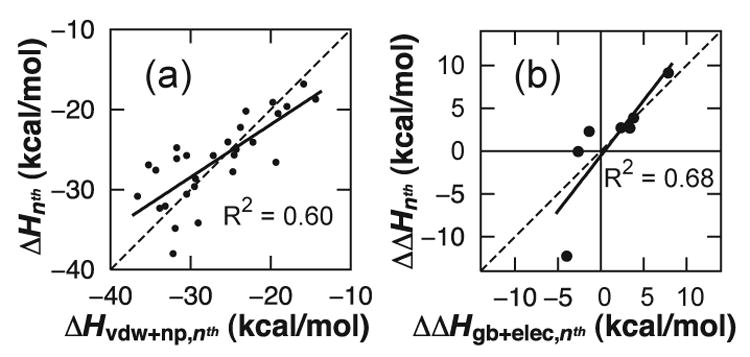
(a) The magnitude of the association enthalpy is determined primarily by hydrophobic interactions, as indicated by the strong correlation between ΔH_n^th and ΔH_vdw+np,n^th for data sets I–IV, with a regression line (solid) that lies nearly on the diagonal (dashed). By comparison, the correlation between ΔH_n^th and ΔH_gb+elec,n^th has an R² = 0.06 (Fig. S3A). (b) Analogously, the differences between the β-sheet and amorphous enthalpies for STVIYE (ΔΔH_n^th) are explained largely by shifts in the electrostatic/polar solvation contribution to the enthalpy (ΔΔH_gb+elec,n^th). The correlation between ΔΔH_n^th and ΔΔH_vdw+np,n^th has an R² = 0.19 (Fig. S3B.).

For the β-sheet oligomers, STVIYE has a weaker association enthalpy than STVIYE^(-) for n = 4 to 7 and exhibits less cooperativity in this region (Fig. 3A), consistent with the fact that STVIYE^(-) forms amyloid fibrils high in β-sheet content whereas STVIYE does not but may aggregate amorphously.¹⁸ No significant difference was observed in the energetics of amorphous aggregation between STVIYE^(-) and STVIYE (Fig. 3B), and these two curves are comparable to the β-sheet profile for STVIYE^(-) (see, e.g., Fig. S2). It is interesting that while STVIYE^(-) does form amyloid its amorphous oligomers were just as stable as its β-sheet oligomers. The reason STVIYE^(-) does not aggregate amorphously is likely that for higher order oligomers (n > 8) it becomes energetically unfavorable to self-associate charged peptides in random orientations due to the accumulation of electrostatic charge repulsion. Serrano et al. have suggested that terminally charged peptides aggregate into fibrillar antiparallel β-sheets rather than amorphous aggregates in order to maximize charge separation and keep charge groups exposed to solvent.¹⁸ Charge repulsion is de-emphasized in the amorphous aggregates studied here because of the small aggregate size.

Role of electrostatic solvation

Energy decomposition reveals that β-sheet destabilization in STVIYE oligomers arises from the electrostatic/polar solvation contribution. The differences between the amorphous and β-sheet association enthalpies for STVIYE, which we denote ΔΔH_n^th,²⁴ were computed and decomposed into their energy contributions. The shifts in the association enthalpy correlate fairly well with the shifts in ΔH_gb+elec,n^th (Fig. 4B).

Consideration of the Born-Onsager relation²⁵ provides an explanation for β-sheet destabilization in STVIYE. The Born-Onsager equation expresses that there is a favorable contribution to the electrostatic solvation energy for a solute with an electric dipole moment. During the aggregation of peptides into antiparallel β-sheets, the dipole moments of adjacent strands become aligned in opposite directions in a manner that they approximately cancel each other out. Calculations presented in Supplementary Data demonstrate that this cancellation of dipoles can result in a destabilization of 1.4 kcal/mol per pair of adjacent STVIYE strands. This would explain why the β-sheet ΔH_n^th values for STVIYE are on average 1.2 kcal/mol weaker than its amorphous values (Fig. S2B). During the formation of parallel β-sheets, on the other hand, strand dipoles add up constructively rather than destructively and no destabilization is predicted to be present. Lack of dipole destabilization could help explain why parallel β-sheets are observed frequently in proteins despite backbone hydrogen bond networks being regarded as more energetically favorable in antiparallel β-sheets.

For the aggregation of charged peptides such as STVIYE^(-) the monopole term in the Born-Onsager expression, which scales as the inverse radius, dominates. Since ΔG_els scales as the square of the charge, a favorable decrease in solvation energy is predicted to accompany the aggregation of charged peptides. We show in Supplementary Data that this favorable monopole contribution is quite large and, interestingly, appears to be sufficient to overcome the electrostatic repulsion experienced between terminal charge groups in STVIYE^(-) β-sheets.

Aggregation free energy profile

We can estimate the free energy profile for the oligomerization process by combining an estimate of the entropy change accompanying the aggregation of the n^th monomer from solution, ΔS_n^th, with the calculated enthalpy of association. A peptide monomer binding to a pre-existing oligomer loses translational, rotational, and conformational entropy; to a good approximation these contributions can be assumed constant (i.e., independent of n). Moreover, as STVIYE^(-) and STVIYE differ by only a proton, their entropic contributions should be nearly identical. It is known from kinetic studies that the lag phase for hexapeptide fibrillogenesis is of the order of hours;^18,26 based on simple analysis using transition state theory²⁷ this means the activation energy for nucleus formation (ΔG*) must be between 20 and 25 kcal/mol. Given the association enthalpies measured for STVIYE^(-) β-sheets, such a value of ΔG* is obtained only when TΔS_n^th ≈ −28.5 kcal/mol (see Fig. S6). In Supplementary Data we use statistical mechanical models for the translational and rotational entropy along with conformational entropies for the helix-coil transition to show that this value of ΔS_n^th is quite reasonable. In Fig. 5 we present the resulting free energy profiles for data sets I–IV.²⁸

Fig. 5.

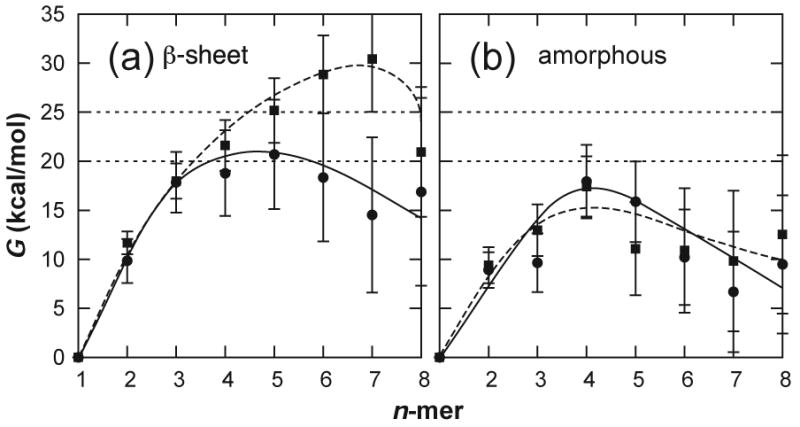
Oligomer free energies expressed relative to the monomeric state for β-sheet oligomers (a) and amorphous aggregates (b), for STVIYE^(-) (circles) and STVIYE (squares). The free energy curves were calculated from the enthalpies shown in Fig. 3 using a constant entropic cost, TΔS_n^th = −28.5 ± 1.0 kcal/mol. These free energies correspond to a 1 mM concentration of monomeric peptide—the concentration at which STVIYE^(-) and other hexapeptides form fibrils in vitro.¹⁸,²⁶

Each of the four free energy profiles appears to turn over, implying that the enthalpic cooperativity is sufficient to overcome the entropic cost of association. In Fig. 5A the free energy for STVIYE^(-) turns over at n* = 5. This provides a direct estimate for the size of the critical nucleus in STVIYE^(-) fibril formation. The free energy for STVIYE β-sheet oligomerization doesn't turn over until after it has reached a height of 30 kcal/mol, a barrier that would take 35 years to cross at 300 K. Evidently, β-sheet destabilization in STVIYE is large enough to prevent fibril formation. The 17 kcal/mol barrier for amorphous STVIYE aggregation (Fig. 5B) implies that this peptide can aggregate non-specifically, though. The profiles for STVIYE^(-) β-sheet and amorphous oligomerization are qualitatively similar, though at large n we would expect the amorphous profile to start rising due to accumulated charge repulsion. The initial similarity in the two free energy profiles for STVIYE^(-) suggests that its fibrillogenesis could proceed through small amorphous oligomeric intermediates—a mechanism that has been suggested by others.^11,14 Tracing the curve in Fig. 5B backwards, amorphous STVIYE^(-) octamers would have to overcome a barrier of 10 kcal/mol in order to dissociate into monomers, indicative of a lifetime on the order of microseconds. Such an intermediate could persist long enough for an amorphous to β-sheet structural rearrangement to occur. The resulting β-sheet octamer could then serve as a stable seed for initiating fibril formation as it persists on the order of nanoseconds (5 kcal/mol dissociation barrier), consistent with suggestions by Nussinov and coworkers that small peptide octamers are the minimal β-sheet oligomer stable on the nanosecond timescale.^21,29

Conclusions

We characterized the critical nucleus for a model amyloidogenic peptide and established a mechanistic role for hydrophobic cooperativity in nucleation. The lack of electrostatic cooperativity in the β-sheet enthalpies is in accordance with electronic structure calculations suggesting that the enthalpic cooperativity in β-sheet hydrogen bond networks is insignificant.³⁰ While the calculated association enthalpies arise predominately from hydrophobic interactions, electrostatic solvation appears to play an important role in determining aggregation. This duality between hydrophobicity and electrostatics reinforces the general view that the hydrophobic effect is the primary thermodynamic driving force in protein folding while electrostatics provide mostly for specificity. In addition to driving aggregation, hydrophobic interactions are responsible for structural collapse of the protein core during proper folding of the native state. We suggest that a mechanism of hydrophobic cooperativity such as reported here, perhaps akin to the hydrophobic zipper model proposed by Dill et al.,³¹ is involved in core collapse during folding. Such a mechanism could account for the marvelous degree of cooperativity observed in the folding of evolved proteins. We thus offer that hydrophobic cooperativity is a general property of polypeptides and is crucial in shaping both folding and misfolding behavior.

Note added in proof

Three reports were published at the time of revision that further speak to the applicability of this study. Firstly, a simple relationship was observed between the lag time and growth rate of several amyloidogenic peptides, suggesting that nucleation mechanisms may be quite similar across different peptide systems.⁴⁰ The fact that we observed a similar degree of cooperativity for both amorphous and β-sheet oligomerization (Figs. 3A and 3B) suggests to us that hydrophobic cooperativity may be a general nucleation mechanism (i.e., one that is independent of the structures presupposed in Fig. 2) that can also be applied at least qualitatively to other amyloid systems. A second recent report also attests to the mechanism's universality: coarse-grained simulations of Aβ_1–40 revealed that increase in the hydrophobic residue density with oligomerization allows for a turn over in free energy at the 10-mer.⁴¹ Thirdly, a diverse set of amyloidogenic proteins were shown to aggregate as non-fibrillar ‘particulates’ under pH conditions resulting in low net charge,⁴² suggesting that the electrostatic principles we have put forth for STVIYE aggregation may also be of relevance to larger, physiologically significant polypeptides.

Materials and Methods

Simulation details

Molecular dynamics (MD) simulations were performed using CHARMM¹⁹ version c31a2 with the param22 all-atom force field³² and the CMAP backbone torsional corrections.^33,34 A generalized Born (GB) implicit solvation model²⁰ incorporating Nina radii³⁵ was employed using a surface tension coefficient (γ) of 0.03 kcal/(mol-Ų). Nonpolar (i.e., non-electrostatic) contributions to the solvation free energy were incorporated in this model by including the term ΔG_np = γS in the CHARMM energy function, where S denotes the solvent-accessible surface area. Simulations employed the SHAKE algorithm³⁶ and the time step was set at 2.0 fs. Langevin dynamics with a 5.0 ps⁻¹ friction coefficient was used to maintain thermal equilibrium. Periodic boundary conditions employing a cubic box of side 60 Å ensured a fixed concentration of peptide in each simulation. Nonbonded interactions were cut off at 20 Å with a switching function beginning at 16 Å. The simulations were performed using the replica-exchange method (replica exchange molecular dynamics, REMD)³⁷ within the MMTSB Tool Set³⁸ in order to achieve more robust sampling of the conformational space. Conformational snapshots were recorded every 500 dynamics steps.

Oligomer construction

For the construction of β-sheet homo-oligomers an octamer of STVIYE^(-) was first built using two four-stranded, planar, antiparallel β-sheets. The peptides were in an extended conformation, with backbone torsions (Φ, Ψ) = (−139°,+135°) and were placed 4.7 Å apart; the two sheets were positioned 10.0 Å apart (this geometry was proposed by Serrano et al. based on X-ray fiber diffraction data).¹⁸ Side chains were then relaxed by performing 100 ps of conventional MD at 300 K with backbone atoms harmonically restrained in Cartesian space. Next, 100 ps of MD was performed with distance restraints placed on backbone amide oxygen and nitrogen atoms to further relax the structure while maintaining inter-strand hydrogen bonds. During this segment of dynamics the β-sheets adopted a 15°–20° right-handed twist (Fig. S1A) - a twist angle that is common for antiparallel β-sheets in the Protein Data Bank.³⁹

A set of β-sheet homo-oligomers of two to seven peptides (Fig. 2) was then created for STVIYE^(-) by successively deleting individual peptides from the structurally refined octamer and performing energy minimization. These oligomers, along with monomeric STVIYE^(-) in an extended conformation, were then each subjected to 4 ns of REMD. For the simulation of the amorphous aggregates, eight monomers of STVIYE^(-) were randomly placed in a 60 Å cubic box (Fig. S1B); individual peptides were successively deleted from this arrangement to obtain a set of configurations containing two to eight peptides, for each of which 4 ns of REMD was performed. The starting structure used for the peptides in the amorphous simulations was obtained from the final snapshot of the 4 ns STVIYE^(-) monomer simulation. The entire process described in the two preceding paragraphs was then repeated using protonated glutamate (STVIYE), resulting in a composite simulation length of 120 ns.

REMD details

For each oligomer simulation twelve identical replicas of the system were constructed and simulated using the following temperature windows (in Kelvin): 285, 303, 321, 341, 362, 384, 408, 433, 460, 488, 518, and 550. Conformational exchanges between temperature windows were attempted every 500 dynamics steps. The exchange frequency remained between 10% and 40% for all simulations performed. All data presented in this communication were extracted from the 303 K replicas.

Mean thermal energies

The energy in all simulations typically stabilized after 1 to 2 ns of REMD (see Fig. S7 for a representative time series), and the time period during the initial equilibration was not included when averaging the potential energy to obtain the mean thermal energies for use in computing enthalpy changes. To estimate the uncertainty in the mean energy the averaged region was divided up into three equally sized segments, for each of which the average energy was computed; the standard deviation of these three averages was then taken as an estimate of the uncertainty in the mean energy. The association enthalpy, ΔH_n^th, was calculated using ΔH_n^th = <E(P_n)> − <E(P_n−1)> − <E(P₁)>, where we have used the time-averaged potential energy of the n-mer, (n − 1)-mer, and monomer, respectively. Error propagation was used to estimate the uncertainty in each association enthalpy (error bars are represented as ±1 standard deviation).