Detection of changes in pairwise interactions during allosteric transitions: Coupling between local and global conformational changes in GroEL

Abstract

A protein engineering approach for detecting and measuring local conformational changes that accompany allosteric transitions in proteins is described. Using this approach, we can identify interactions that are made or broken during allosteric transitions. The method is applied to probe for changes in pairwise interactions in the chaperonin GroEL during its ATP-induced allosteric transitions. Two pairwise interactions are investigated: one between subunits (Asp-41 with Thr-522) and the other within subunits (Glu-409 with Arg-501). We find that the intraring intersubunit interaction between Asp-41 and Thr-522 changes little during the allosteric transitions of GroEL, indicating that the hydrogen bond between these residues is maintained. In contrast, the intrasubunit salt bridge between Glu-409 and Arg-501 becomes significantly weaker during the ATP-induced allosteric transitions of GroEL. Our results are consistent with the electron microscopy observations of an ATP-induced hinge movement of the apical domains relative to the equatorial domains.

Structure–function studies of allosteric proteins are often hampered by the fact that structural information on the different allosteric states of the protein is not available. An interesting example of an allosteric protein is the chaperonin GroEL from Escherichia coli, which facilitates protein folding both in vivo and in vitro (for reviews see refs. 1–4). GroEL consists of 14 identical subunits that form two stacked heptameric rings with a central cavity (5, 6). Each subunit consists of three domains: (i) a large equatorial domain that forms all of the interring contacts and most of the intraring contacts between subunits; (ii) a large apical domain that forms the opening of the central cavity; and (iii) an intermediate domain that connects the apical and equatorial domains. Key to GroEL’s mechanism of action is its allosteric regulation by adenine nucleotides. GroEL has 14 ATP binding sites and a weak K⁺-dependent ATPase activity that is cooperative with respect to ATP (7–10) and K⁺ ions (11). Upon the cooperative binding of ATP, GroEL rings switch from a high-affinity (T) state for nonfolded proteins to a protein release (R) state, which has low affinity for nonfolded proteins (12, 13). The molecular events that accompany the allosteric transitions of GroEL are still mostly not known. In an effort to obtain such information, we have applied the technique of double-mutant cycles to study allosteric transitions. Using this approach, we can identify interactions that are made or broken during allosteric transitions as we describe in what follows.

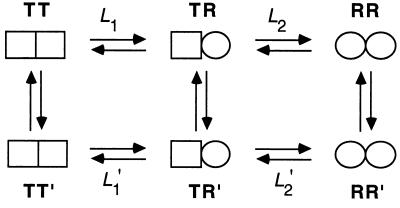
A nested model for cooperativity in ATP hydrolysis by GroEL was recently put forward (10, 14) in which GroEL is in equilibrium between three allosteric states: TT, TR, and RR (Fig. 1). In this model, there are two levels of allostery: one within each ring and the second between rings. In the first level, each heptameric ring is in equilibrium between a low- (T) and high- (R) affinity state for ATP, in accordance with the Monod–Wyman–Changeux representation (15). A second level of allostery is between the rings of GroEL, which undergoes, in the presence of increasing concentrations of ATP, sequential Koshland–Némethy–Filmer-type transitions (16) from the TT state via the TR state to the RR state (Fig. 1). Positive cooperativity in ATP hydrolysis at low concentrations of ATP (≤100 μM in the case of wild type) reflects the transition of the GroEL particle from the TT state to the TR state. Owing to negative cooperativity between rings, the transition of the GroEL particle from the TR state to the RR state is observed only at higher concentrations of ATP or at low concentrations of ATP in the presence of the cochaperonin GroES (17).

Figure 1.

Measurement of changes in free energy during the allosteric transition of GroEL. In the absence of ATP, GroEL is mainly in the TT state. In the presence of low concentrations of ATP, the equilibrium is shifted toward the TR state (L₁ = [TT]/[TR]). Higher concentrations of ATP further shift the equilibrium toward the RR state (L₂ = [TR]/[RR]). For simplicity, we designate by R the ATP-bound rings in both the TR and RR states although their conformation may differ. The difference in free energy between the TR and TT states of wild-type GroEL is given by ΔG_TR-TT = −RTlnL₁. Likewise, the difference in free energy between the RR and TR states of wild-type GroEL is ΔG_RR-TR = −RTlnL₂. The difference in free energy between the TR and TT states of wild-type GroEL and a mutant [designated by prime (′)] is given by ΔΔG_TR-TT = −RTln(L₁/L₁′). Likewise, the difference in free energy between the RR and TR states of wild-type GroEL and a mutant is given by ΔΔG_RR-TR = −RTln(L₂/L₂′).

Electron microscopy studies have shown that adenine nucleotide binding induces large conformational changes in GroEL (18–20). In contrast, surprisingly little difference was found between the high-resolution crystal structures of a double mutant of GroEL in the absence of and in complex with ATPγS (21). In this paper, we describe a protein engineering approach for detecting local conformational changes that accompany allosteric transitions, which is conceptually related to earlier work of Ackers and coworkers (22). We then apply it to probe for changes during the allosteric transitions of GroEL in two pairwise interactions: one between subunits (Asp-41 with Thr-522) and the other within subunits (Glu-409 with Arg-501). Our results are consistent with the observation by electron microscopy (20) of ATP-induced hinge movements of the apical domains relative to the equatorial domains, which lead to a more elongated structure of GroEL.

Detection of Changes in Interactions During Allosteric Transitions

The method of double-mutant cycles enables the detection of pairwise interactions in one thermodynamic state of a protein relative to another (23–25). Two residues, X and Y, are mutated separately and together to give rise to a cycle that comprises wild-type protein (P-XY), two single mutants (P-X and P-Y), and the double-mutant protein (P). The change in free energy upon mutation of X, associated with a functional or structural property of the protein, may be expressed relative to wild-type as ΔG_P-XY→P-Y. Similarly, the change in free energy associated with this property upon mutation of X, when Y has already been mutated, is ΔG_P-X→P. If the effect of mutation of X is independent of Y, then ΔG_P-XY→P-Y = ΔG_P-X→P. If the effects of the mutations are not independent of each other, then ΔG_P-XY→P-Y ≠ ΔG_P-X→P. The free energy of coupling, ΔΔG_int, between residues X and Y is given by:

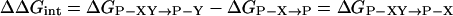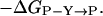1

Previously, free energies of coupling between two residues were measured in the folded relative to unfolded states of a protein (for example, see ref. 26) and in a protein–ligand complex relative to the unbound state (for example, see ref. 27). Here, we have measured the coupling free energies between two residues in one allosteric state relative to another.

The crystal structure of GroEL (5, 6) was inspected and two pairwise interactions were identified. A double-mutant cycle was constructed for each interaction. The allosteric constants, L₁ and L₂, were measured for wild-type GroEL and the mutants (Fig. 1). The difference between wild-type GroEL and a mutant [designated by prime (′)] in the free energy of the TR state relative to the TT state is ΔΔG_TR-TT = −RTln(L₁/L₁′). Likewise, the difference between wild-type GroEL and a mutant in the free energy of the RR state relative to the TR state is given by ΔΔG_RR-TR = −RTln(L₂/L₂′). The free energy of coupling, ΔΔG_int, between two residues in the TR state relative to the TT state is calculated from the cycle, as follows (Fig. 2):

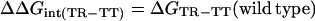2

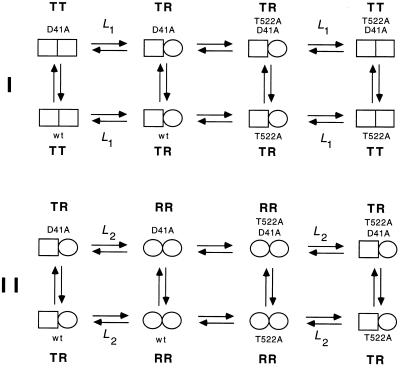
The free energy of coupling, ΔΔG_int(RR-TR), between two residues in the RR state relative to the TR state is calculated in a similar manner. Double-mutant cycles for the interaction of Asp-41 with Thr-522 in the TR state relative to the TT state and in the RR state relative to the TR state are shown in Fig. 2 I and II, respectively.

Figure 2.

Measurement of changes in coupling free energies between Asp-41 and Thr-522 during the allosteric transition of GroEL. The coupling energy, ΔΔG_int, between two residues (Asp-41 and Thr-522) in the TR state relative to the TT state is given by (I) ΔΔG_int(TR-TT) = ΔG_TR-TT(wild-type) − ΣΔG_TR-TT(single mutants) + ΔG_TR-TT(double mutant). The coupling energy between the two residues in the RR state relative to the TR state is (II) ΔΔG_int(RR-TR) = ΔG_RR-TR(wild-type) − ΣΔG_RR-TR(single mutants) + ΔG_RR-TR(double mutant). The change in coupling energy during the allosteric transition of one ring may depend on the conformation of the adjacent ring. A measure of this dependence is given by ΔΔΔG_int = ΔΔG_int(RR-TR) − ΔΔG_int(TR-TT). Similar cycles may be constructed for the interaction between Glu-409 and Arg-501. Single-letter notation for amino acids is used.

Experimental Procedures

Site-directed mutagenesis was carried out as before (28) using the following mutagenic oligonucleotides: Asp-41 → Ala, 5′-TGCACCGAAAGATTTAG*CCAGAACTACGTTACG-3′; Glu-409 → Ala, 5′-ACCAGCAACCACGCCTG*CTTCTACCGCAGCACG-3′; Arg-501 → Ala, 5′-GTACTGCAGAGCAGAAG*C*AGTTACTTTGGTTGG-3′; and Thr-522 → Ala, 5′-GTTTTTCGGCAGGTCGGC*AACCATGCATTCGGT-3′. An asterisk follows the mismatched bases. Protein expression was carried out as before (28), and purification was achieved as described earlier (11) with some modifications (10). ATPase assays were carried out at 25°C as previously described (28). Initial velocities of ATP hydrolysis as a function of ATP concentration were fitted, using kaleidagraph, version 2.1, to the previously derived equation for a three-state nested allosteric model (14):

3

where [S] is the substrate (ATP) concentration, L₁ and L₂ are the respective apparent allosteric constants for the transitions TT → TR and TR → RR, V₀ is the initial rate of ATP hydrolysis, V_max(1) and V_max(2) are the respective maximal initial rates of ATP hydrolysis of the TR and RR states, and K_R is the dissociation constant of ATP. Estimates of parameters ± SE are given.

Results and Discussion

Two pairwise interactions were targeted for mutagenesis: one within subunits and the other an intraring interaction between subunits. The intraring interaction is between the O^δ2 atom of Asp-41 in one subunit and the O^γ1 atom of Thr-522 in a neighboring subunit, which are separated by 2.78 Å and are involved in a hydrogen bond (Table 1). The intrasubunit interaction is between Glu-409 and Arg-501, which together form a salt bridge (Table 1). The mutations in this study were to alanine to remove the interactions under study and minimize the possibility of new interactions being formed. Mutations of key residues involved in the stabilization of the double-ring structure of GroEL (5, 29) were also avoided.

Table 1.

List of important contacts made by Asp-41, Thr-522, Glu-409, and Arg-501 in the crystal structure of GroEL

Atom 1	Atom 2	Average distance,* Å
Asp-41 Oδ1 (subunit 1)	Lys-42 N (subunit 1)	2.79
Asp-41 Oδ2 (subunit 1)	Thr-522 Oγ1 (subunit 2)	2.78
Thr-522 Oγ1 (subunit 1)	Asp-523 N (subunit 1)	2.86
Glu-409 Oɛ1 (subunit 1)	Arg-501 Nɛ (subunit 1)	2.90
Glu-409 Oɛ1 (subunit 1)	Arg-501 NH2 (subunit 1)	3.17
Glu-409 Oɛ2 (subunit 1)	Arg-501 NH2 (subunit 1)	2.94
Arg-501 NH1 (subunit 1)	Gln-505 Oɛ1 (subunit 1)	2.91

^*Owing to differences in interatomic distances between different subunits, average distances in the refined crystal structure of GroEL (6) were calculated. 

The Interaction Between Asp-41 and Thr-522.

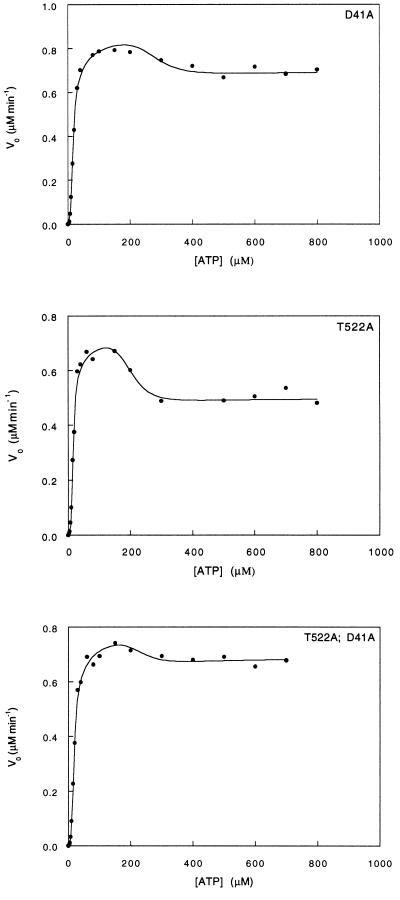
The single mutation Asp-41 → Ala has little effect on the stability of the TR state relative to the TT state, and it stabilizes the TR state relative to the RR state by ≈2 kcal·mol⁻¹ (Fig. 3; Table 2). The single mutation Thr-522 → Ala stabilizes both the TT state relative to the TR state and the TR state relative to the RR state by about 1 and 1.5 kcal·mol⁻¹, respectively (Fig. 3; Table 2). The double mutation Asp-41 → Ala, Thr-522 → Ala has no effect on the stability of the TR state relative to the TT state and is found to stabilize the TR state relative to the RR state by ≈1 kcal·mol⁻¹ (Fig. 3; Table 2). The mutations had no effect on the dissociation constant for ATP and only small effects on the k_cat for ATP hydrolysis in the TR and RR states. Using Eq. 2, we calculate the overall coupling energies, ΔΔG_int(TR-TT) and ΔΔG_int(RR-TR), between Asp-41 and Thr-522 in the TR state relative to the TT state and in the RR state relative to the TR state to be 0.88 ± 0.75 and 2.38 ± 1.20 kcal·mol⁻¹, respectively. Assuming that binding of ATP affects only the seven intersubunit contacts in the ATP bound ring, then the coupling free energies, ΔΔG_int(TR-TT) and ΔΔG_int(RR-TR), between Asp-41 and Thr-522 are only 0.13 ± 0.11 and 0.34 ± 0.17 kcal·mol⁻¹ per interaction, respectively.

Figure 3.

Initial velocity of ATP hydrolysis by the Asp-41 → Ala and Thr-522 → Ala GroEL mutants and the corresponding double mutant at different concentrations of ATP. The data were fitted to the previously derived equation for a three-state nested allosteric model (see Experimental Procedures and ref. 14). The oligomer concentration of GroEL is 25 nM. The reactions were carried out at 25°C as previously described (28).

Table 2.

Free energies of the allosteric transitions TT → TR and TR → RR of wild-type GroEL and mutants

GroEL	ΔGTT → TR,* kcal·mol−1	ΔGTR → RR,* kcal·mol−1
Wild-type	−3.48 (± 0.37)	−11.09 (± 0.48)
Asp-41 → Ala	−3.55 (± 0.32)	−12.97 (± 0.60)
Thr-522 → Ala	−4.47 (± 0.47)	−12.69 (± 0.62)
Asp-41 → Ala, Thr522 → Ala	−3.66 (± 0.32)	−12.19 (± 0.69)
Glu-409 → Ala	−2.54 (± 0.50)	−14.58 (± 0.86)
Arg-501 → Ala	−2.49 (± 0.43)	−4.49 (± 0.33)
Glu-409 → Ala, Arg501 → Ala	−4.90 (± 0.98)	−12.83 (± 1.15)

^*Average free energies determined from two independent experiments are given. The free energies correspond to the intrinsic allosteric constants which are related to the apparent allosteric constants as follows: L₁(app) = 2L₁ and L₂(app) = L₂/2 (14). 

The Interaction Between Glu-409 and Arg-501.

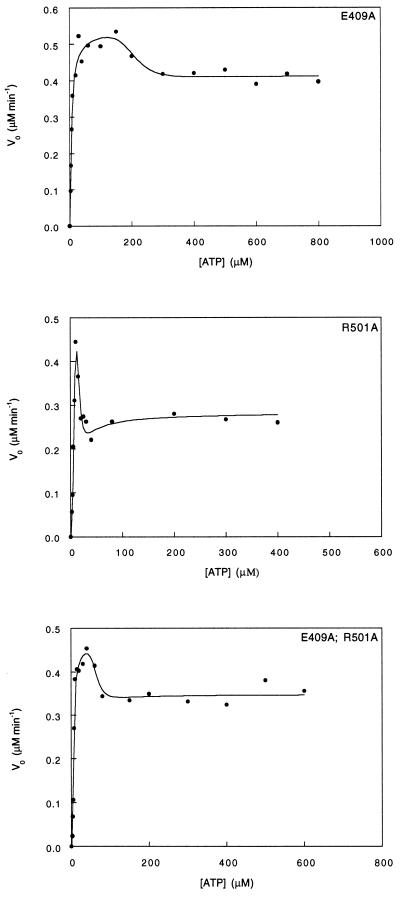
The single mutation Glu-409 → Ala destabilizes the TT state relative to the TR state by ≈1 kcal·mol⁻¹ and stabilizes the TR state relative to the RR state by >3 kcal·mol⁻¹ (Fig. 4; Table 2). The single mutation Arg-501 → Ala destabilizes both the TT state relative to the TR state and the TR state relative to the RR state by about 1 and 6 kcal·mol⁻¹, respectively (Fig. 4; Table 2). The double mutation Glu-409 → Ala, Arg-501 → Ala stabilizes both the TT state relative to the TR state and the TR state relative to the RR state by ≈1–2 kcal·mol⁻¹ (Fig. 4; Table 2). Using Eq. 2, we calculate the overall coupling energies, ΔΔG_int(TR-TT) and ΔΔG_int(RR-TR), between Glu-409 and Arg-501 in the TR state relative to the TT state and in the RR state relative to the TR state to be −3.35 ± 1.23 and −4.84 ± 1.56 kcal·mol⁻¹, respectively. Assuming that ATP binding affects only the seven intrasubunit contacts in the ATP bound ring, then the respective coupling energies, ΔΔG_int(TR-TT) and ΔΔG_int(RR-TR), between Glu-409 and Arg-501 are −0.48 ± 0.18) and −0.69 ± 0.22 kcal·mol⁻¹ per interaction. The mutations in this cycle also affect the k_cat of ATP hydrolysis by the TR and RR states and the dissociation constant for ATP. The dissociation constant for ATP of all the mutants is 5 μM compared with 10 μM in the case of wild-type GroEL (14). The k_cat of ATP hydrolysis by the Glu-409 → Ala single mutant and the double mutant is reduced by a factor of ≈2 in both the TR and RR states. The k_cat of ATP hydrolysis by the Arg-501 → Ala mutant in the TR and RR states is reduced by factors of about 2 and 4, respectively.

Figure 4.

Initial velocity of ATP hydrolysis by the Glu-409 → Ala and Arg-501 → Ala GroEL mutants and the corresponding double mutant at different ATP concentrations. The data were fitted to the previously derived equation for a three-state nested allosteric model (see Experimental Procedures and ref. 14). The oligomer concentrations of GroEL is 25 nM except for the Arg-501 → Ala mutant, which is 37.5 nM. The reactions were carried out at 25°C as previously described (28).

Changes in Pairwise Interactions in GroEL During Allosteric Transitions.

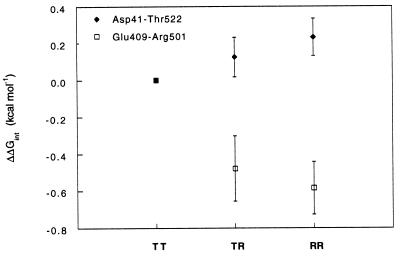
Pairwise coupling energies in the RR state were also calculated relative to the TT state [ΔΔG_int(RR-TT) = ΔΔG_int(TR-TT) + ΔΔG_int(RR-TR)]. A plot of ΔΔG_int as a function of the reaction coordinate of the allosteric transition is shown in Fig. 5. The change in coupling energy for the interaction between Asp-41 and Thr-522 is small and positive. Since the strength of a hydrogen bond is typically between 1 and 3 kcal·mol⁻¹ (30, 31), we conclude from these results that the hydrogen bond between Asp-41 and Thr-522 is maintained during the allosteric transitions of GroEL. In contrast, the changes in coupling energy for the interaction between Glu-409 and Arg-501 are larger and negative (Fig. 5). The change in coupling energy between Glu-409 and Arg-501 in the RR state relative to the TT state is ≈0.6 kcal·mol⁻¹, which corresponds to the energy of partially masked or otherwise weakened salt bridges (32). These results indicate that the salt bridge between Glu-409 and Arg-501 is weakened in both the TR and RR states. They support the observation that ATP binding induces a hinge movement of the apical domains relative to the equatorial domains, which involves weakening of the Glu-409–Arg-501 salt bridge. Interestingly, coupling energies for these pairwise interactions in the transition state of hydrolysis relative to the ATP-bound states that are calculated from the k_cat values also show similar large changes in the case of the Glu-409–Arg-501 interaction but not the Asp-41–Thr-522 interaction.

Figure 5.

Changes in pairwise coupling energies as a function of the reaction coordinate of the allosteric transition of GroEL relative to the TT state. Coupling energies between Asp-41 with Thr-522 and between Glu-409 with Arg-501 in the TR state relative to the TT state, and in the RR state relative to the TR state, were calculated from the data in Figs. 3 and 4 using Eq. 2. The coupling energy in the RR state relative to the TT state, ΔΔG_int(RR-TT), was calculated from ΔΔG_int(TR-TT) + ΔΔG_int(RR-TR). Coupling energies were divided by seven to be for a single interaction.

For simplicity, we have assumed that the R conformation in the TR and RR states is similar. A test for this assumption is the higher-order coupling energy, ΔΔΔG_int [= ΔΔG_int(TR-TT) − ΔΔG_int(RR-TR)], which measures to what extent the coupling energy between two residues in the R state depends on the conformation of the adjacent ring. In other words, ΔΔΔG_int measures the effect of the coupling between two residues on the coupling between rings. We find that the values of ΔΔΔG_int for the Asp-41–Thr-522 and Glu-409–Arg-501 interactions are 0.22 ± 0.20 and −0.21 ± 0.28 kcal·mol⁻¹, respectively. These close-to-zero values suggest that, for the pairwise interactions examined in this study, the coupling energies in one ring are close to being independent of the conformation of the adjacent ring.

In conclusion, we have described a strategy for measuring changes in pairwise (and higher-order) coupling energies during allosteric transitions. We have applied this strategy to show that the Asp-41–Thr-522 interaction is maintained, whereas the Glu-409–Arg-501 interaction is weakened during the ATP-induced allosteric transitions of GroEL. This strategy complements standard structural methods by providing information on energetic changes during allosteric transitions at the amino acid residue level. Such information may, with caution, be interpreted in structural terms and thus shed light on the structural basis of allosteric transitions.