Cooperative effects of photodynamic treatment of cells in microcolonies

Abstract

Microcolonies of 2-8 Madison–Darby canine kidney cells (MDCK II) and Chinese hamster lung fibroblasts (V79) cells were incubated with the photosensitizer Photofrin and exposed to light, and the resulting number of dead cells per colony was determined. The distribution of this number was found to be incompatible with the assumption that cells are inactivated independently. The experimental distributions were significantly different from the binomial distribution expected from this assumption, but in accordance with a model in which an inactivated cell can inactivate adjacent cells with a certain probability. These findings are contrary to the common view that damage caused by radiation is limited to the cell in which the primary damage takes place. Our findings clearly indicate some kind of cooperativity between cells treated with Photofrin and light.

It is generally believed that radiation-induced biological damage is limited to the cell in which the primary energy deposition takes place. However, experiments reported by Little and coworkers (1–5) indicate that damage caused by ionizing radiation may be transmitted to cells not directly affected by the radiation. Their results also shed doubt on the hypothesis that DNA is the all-important primary target for ionizing radiation. Hence, they put into question a paradigm of current radiobiology.

In an earlier paper on cell inactivation by photodynamic treatment (PDT) (6) it was noted that when colonies of 2–4 cells were treated with doses of porphyrin and light so as to inactivate about half of the cells, there was an overabundance of colonies where either all or none of the cells were inactivated. This “colony effect” may indicate that some kind of interaction between cells within the same colony is involved in the inactivation. However, that work did not contain sufficient data to rule out the possibility that the observations could be merely the result of statistical fluctuations. Furthermore, we could not rule out several trivial explanations—e.g., that the colony effect was simply due to a high degree of synchrony within such small colonies in combination with cell cycle-dependent susceptibility to PDT, or reflecting a clonal difference in susceptibility.

Thus, the present study was undertaken to determine more decisively if the colony effect is indeed real, in the sense that it is statistically verifiable, and if it means that cooperative effects do have a significant role in cell inactivation by PDT. For this purpose we have carried out experiments with colonies of 2–8 cells as well as confluent layers of cells from two different cell lines. By comparing the results with mathematical models we have verified a significant degree of cooperativity in PDT-induced cell inactivation.

MATERIALS AND METHODS

Cell Lines and Culture Conditions.

Madison–Darby canine kidney cells (MDCK II) and Chinese hamster lung fibroblasts (V79) were used in this study. The cells were subcultured twice a week in RPMI 1640 medium and minimal essential medium (MEM), respectively, both with Hank’s balanced salt solution (GIBCO) supplemented with 10% fetal calf serum, 100 units/ml penicillin, and 100 μg/ml streptomycin. The cells were incubated at 37°C in a humidified atmosphere of 5% CO₂ for 22 to 48 h after seeding from a single cell suspension.

Irradiation Procedures.

Irradiation was carried out at room temperature using a bank of four fluorescent light tubes (model 3026, Applied Photophysics, Surrey, U.K.) with fluence rate of 2.3 mW/cm² and emission mainly in the wavelength region 370–450 nm.

Distribution of Dead Cells in Microcolonies.

The cells were seeded at a density of 3-4000 cells/cm² in 28.3 cm² plastic tissue culture dishes (Falcon). When grown to a suitable colony size, they were incubated with fresh medium containing 5 μg/ml Photofrin for 1 h before light exposure and further incubation. To stain the dead cells, 14 μl of 0.5 mg/ml propidiumiodide (PI) (Sigma) were pipetted into the cell medium 2–18 h after exposure, which gave a final concentration of 2 μg/ml. Thus, by fluorescence microscopy, using a filter block composed of a 546 nm excitation band filter, a 580 nm beam splitter, and a 590 nm long pass emission filter, it was possible to determine the number of fluorescing (dead) cells per colony. The fraction of fluorescing cells was found to reach a constant level from about 2 h after light exposure. Hence, cell death was scored after 2–4 h in most of the experiments. The total number of cells and the number of fluorescing cells per microcolony (2–8 cells) were counted by phase contrast and fluorescence microscopy, respectively, using a ×40 water immersion objective (Axioplan; Zeiss), and low levels of analyzing light. Each area on the dishes was observed only once to ensure that the analysis did not cause extra inactivation. Seven separate clones of MDCK II cells were used to check whether the distributions obtained were due to the presence of clones with different sensitivity to PDT. There was a clear distinction between dead and live cells. Thus, the average total fluorescence intensity of fluorescent (i.e., dead) cells was 2.4 times times higher than that of nonfluorescent (i.e., vital) cells, while the relative variation within each group was less than a factor 0.5.

BrdUrd Immunoassay.

The response of a cell to PDT may vary with its position in the cell cycle (7). This could lead to colonies with different sensitivity to PDT provided that a significant degree of synchrony existed within the colonies.

To assess the degree of synchrony, 35 μl 5 mg/ml BrdUrd (Sigma) was added to MDCK II cells (seeded out on plastic dishes 2 days before) for 30 min to give a final concentration of 50 μg/ml. Subsequently, the cells were fixed in 25% acetic acid and 75% methanol for 30 min before washing with PBS at 4°C, and denaturation of DNA in 2 ml 0.2% pepsin (porcine stomach mucosa pepsin, type P7125; Sigma) for 30 min in the dark at room temperature. The cells were then labeled with fluorescein isothiocyanate (FITC)-conjugated BrdUrd antibody according to Gerlyng et al. (8). Subsequently, all the nuclei were stained with 0.4 μM 4′-diamidino-2-phenylindole (DAPI) (Sigma). Thus, by fluorescence microscopy, using a filter block composed of a 365 nm excitation band filter, a 395 nm beam splitter, and a 420 nm long pass emission filter, and two exchangeable excitation band filters: a UV-filter for DAPI excitation and a 480 nm filter for FITC excitation, it was possible to determine the total number of cells per colony and the number of cells in S-phase by counting DAPI-stained nuclei and FITC-positive cells, respectively.

Terminal Deoxynucleotid Transferase (TdT) Assay.

To investigate whether the MDCK II cells were inactivated by a apoptotic mechanism, we used the TdT assay that is based on detection of the extensive DNA breakage that characterizes apoptosis (9). The 3′-hydroxyl termini of DNA breaks are labeled with FITC-dUTP.

Two hours after illumination the MDCK II cells were washed with 4°C PBS and fixed in −20°C methanol. After removal of the methanol 30 μl fresh TdT solution (terminal transferase kit, Boehringer Mannheim) was put on a previously marked area of cells under a coverslip to spread out the solution. The cells were incubated in this solution for 30 min at 37°C in a humidified atmosphere of 5% CO₂. After removing the coverslip carefully the cells were washed once with 4°C PBS and twice with 4°C PBS containing 0.1% Triton X-100. Subsequently, 12 μl anti-fade (Vectashield mounting medium for fluorescence, H-100; Vector Laboratories) with 0.4 μM DAPI was pipetted carefully on the same area of cells and a coverslip was laid on. Thus, by fluorescence microscopy it was possible to determine the number of apoptotic cells by counting the FITC positive cells and the total number of cells by counting the DAPI stained nuclei.

Mathematical Models for the Inactivation of Cells.

The experimental distributions were compared with three different mathematical models for the inactivation of cells. The first two models are special cases of the last.

Primary hit model (H0).

In this model cells within microcolonies are inactivated independently of each other after PDT. The expectation values for dead cells are binomially distributed:

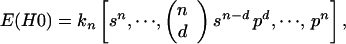1

where n is the number of cells per colony (the multiplicity); k_n is the number of colonies with n cells; p is the probability of inactivation by primary damage and s = 1 − p; d is the number of cells inactivated by primary hits in a colony. For example, for n = 2: E(H0) = k₂^·[s², 2sp, p²], and with k₂ = 100 and s = 0.3: E(H0) = [9, 42, 49], s = 0.5: E(H0) = [25, 50, 25], s = 0.8: E(H0) = [64, 32, 4].

Neighbor inactivation model (H1).

In this model each cell in a colony can be inactivated, with probability b, via an adjacent cell that has been inactivated by primary damage. This is called a bystander hit. A cell inactivated via its neighbor cannot inactivate the remaining, surviving neighbor cells. The vector for the expected number of colonies with t = d + i inactivated cells is obtained by matrix multiplication between a matrix, G, containing the probabilities for bystander hits (see Appendix), the vector for the distribution of primary hits (Eq. 1), and the total number of colonies, k_n:

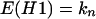2

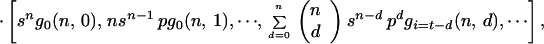where g_i(n, d) is the probability for i bystander hits in colonies with multiplicity n, and d is the number of cells inactivated by primary damage. This gives for example for n = 2: E(H1) = k₂[s², 2spa, 2spb + p²], and with k₂ = 100, s = 0.3, and b = 0.2: E(H1) = [9, 34, 57], s = 0.5 and b = 0.2: E(H1) = [25, 40, 35], s = 0.8 and b = 0.2: E(H1) = [64, 26, 10].

Propagated inactivation model (H2).

In this model a cell inactivated via a neighbor may inactivate its other adjacent cells with the same probability b. The expected values for the number of colonies with t dead cells are obtained by matrix multiplication (see Appendix):

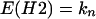3

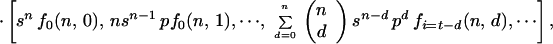where f_i(n, d) is the probability for i bystander hits in colonies with multiplicity n and d cells inactivated by primary damage. k_n is the total number of colonies.

The vectors in Eqs. 2 and 3 were fitted to the experimental distributions by using the values of p and b that gives the smallest value for the χ² random variable defined in Eq. 4:

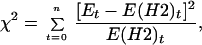4

where E_t is entry number t in the vector containing the experimental values. The value of the χ² random variable was calculated using a modified version of the square root transformation for counts (10). The minimization was carried out using routines in mathematica 2.2.3 (Wolfram Research, Champaign, IL). The experimental distributions were tested for statistically significant deviation from the model distributions by using the minimized chi square values.

RESULTS

The majority of the experiments were done with MDCK II cells. In eight experiments we used V79 cells to check whether the results were cell line-specific.

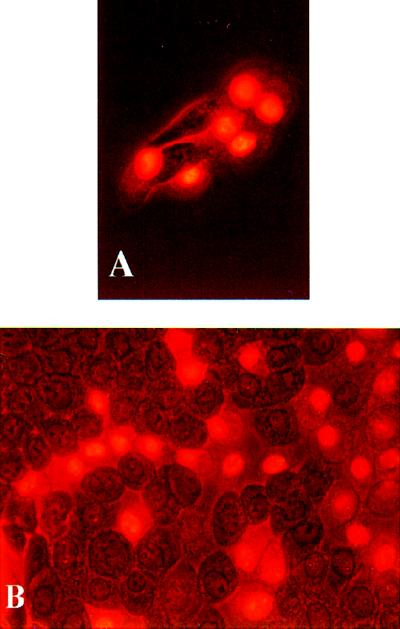
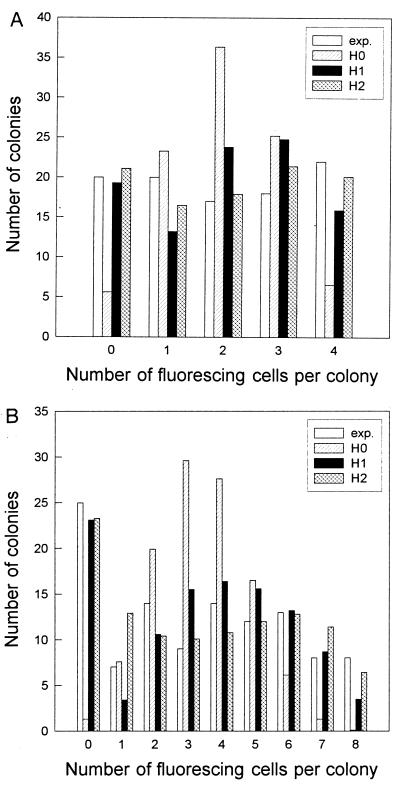
The photomicrographs in Fig. 1 show typical examples of the cells observed. As noted above, fluorescing, inactivated cells, and nonfluorescing surviving cells were clearly distinguishable. Fig. 2 A and B show examples of the distribution of inactivated cells in microcolonies with four and eight cells, respectively. In both cases the experimental distribution is clearly different from the binomial distribution. It appears that the H2 model (propagated inactivation) yields the best fit to the experimental data. This impression is confirmed by Table 1, which gives the sum of χ² random variables for all experiments. Model H2 is not significantly different from the experimental distribution neither for V79 cells nor for MDCK II cells. The deviation of the neighbor model (H1) from the experimental distribution was larger for the MDCK II cells than for the V79 cells. The binomial distribution (H0) of inactivated cells was significantly different from the experimental distributions for both cell lines in 35 of 39 experiments.

Figure 1.

Combined fluorescence and phase-contrast charged-coupled device (CCD)-pictures of MDCK II cells stained with 2 μg/ml PI 2 hr after PDT. (A) An octet with 6 fluorescing cells irradiated for 5 min. (B) A confluent layer, irradiated for 8 min, with fluorescing cells in distinct patches.

Figure 2.

Examples of the distribution of inactivated cells. (A) The V79 quartets were illuminated for 2 min to give a surviving fraction of 51%, k₄ = 97 [χ²(H0) = 52; χ²(H1) = 9.1; χ²(H2) = 1.5]. (B) The MDCK II octets were illuminated for 5 min to give a surviving fraction of 57%, k₈ = 110 [χ²(H0) = 36.1; χ²(H1) = 7.1; χ²(H2) = 7.8]. Exp. is the experimental distribution. H0, H1 and H2 are the corresponding model distributions explained in Materials and Methods.

Table 1.

Sum of χ² random variables from all experiments

	V79			MDCK II
	H0	H1	H2	H0	H1	H2
∑χ2	230.4	19.8	2.9	2536.5	375.8	172.4
φ	<0.0001	0.71	1.00	<0.0001	<0.0001	0.18

The χ² random variables for the compairson between the model distributions and eight experimental distributions from V79 cells (4 doublet and 4 quartet experiments, 24 df) and 31 experimental distributions from MDCK II cells (10 doublet, 8 quartet, and 13 octet experiments, 156 df) were added together. φ is the probability that a χ² random variable was greater than this sum. 

Tables 2 and 3 show the median of the χ² random variable and the fraction of experiments that support the three different models. From the χ² median values we arrive at the same conclusion as from Table 1, namely that the H2 propagation model gives the best fit to the data.

Table 2.

Median of the χ² random variable and fraction of experiments with MDCK II cells that support the current hypothesis

n	Median			Fraction
	2	4	8	2	4	8
H0	20	84	126	2/10	1/8	0/13
H1	pf	13	19	pf	4/8	3/13
H2	pf	3	9	pf	7/8	12/13

n, multiplicity; pf, the models give a perfect fit to any doublet distribution. The value of the χ² random variable has to be above 5.99 for doublets, 9.49 for quartets and 15.51 for octets to give significant deviation between two distributions within the 5% level of significance. 

Table 3.

Median of the χ² random variable and fraction of experiments with V79 cells that support the current hypothesis at a level of significans of 5%

n	Median		Fraction
	2	4	2	4
H0	31	35	0/4	1/4
H1	pf	3	pf	4/4
H2	pf	0.7	pf	4/4

n, multiplicity; pf, the models give a perfect fit to any doublet distribution. The value of the χ² random variable has to be above 5.99 for doublets and 9.49 for quartets to give significant deviation between two distributions within the 5% level of significance. 

Conceivably, distributions deviating significantly from a binomial distribution like the one shown in Fig. 2 could be the result of clones with different sensitivity to PDT. This possibility was tested by performing the same experiment as described on seven separate MDCK II cell cultures cloned 20–30 cell divisions earlier. The resulting distributions were similar to the experiments described above.

For doublets we have a perfect fit between the experimental distribution and the two cooperativity models (which are identical for doublets) because the number of experimental values (0, 1 and 2 dead cells) equals that of model parameters (t = d + i, p, and b).

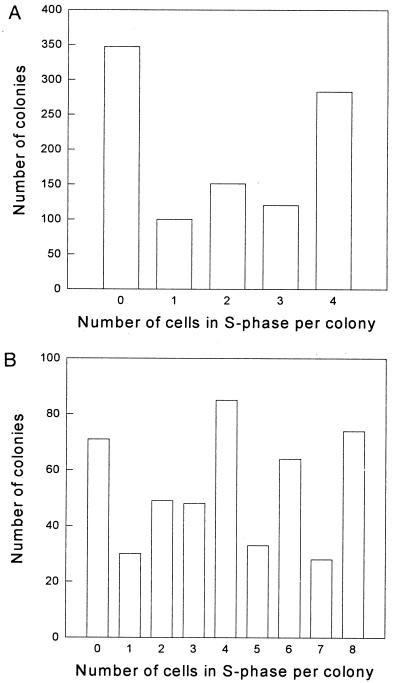
The results of the BrdUrd experiments carried out to assess the degree of synchrony are shown in Fig. 3, where the distribution of cells in S-phase in MDCK II quartets (Fig. 3A) and octets (Fig. 3B) are depicted. A total of 49% of the cells were in S-phase, while 35% of the quartets and 15% of the octets had no cells in S-phase, and 28% of the quartets and 15% of the octets had all cells in S-phase. There were significantly more colonies with an even number of cells in S-phase than with an odd number. Such a synchrony could influence our results. Thus, if cells in S-phase were more sensitive to PDT, colonies with a large fraction of cells in S-phase would be more sensitive than the other colonies. As discussed below, a quantitative evaluation of the data show that this effect cannot explain the present results.

Figure 3.

The distribution of cells in S-phase in MDCK II quartets (A) and octets (B) as determined by the BrdUrd immunoassay. A total of 49% of the cells were in the S-phase of the cell cycle. Numbers are the sum of five experiments (k₄ = 1001 colonies observed, k₈ = 482 colonies observed).

In three experiments confluent layers of cells were exposed to PDT so that ≈50% of the cells were inactivated. As seen in Fig. 1B, the PI-stained cells were not homogeneously distributed but localized in patches, as expected if collective effects are important.

Cooperativity could be mediated via secretion of signal molecules from dying cells into the cell culture medium. This hypothesis was investigated by keeping the culture dishes on a rocking platform subsequent to PDT exposure, so that excreted substances became uniformly distributed. However, this resulted in the same experimental distributions of inactivated cells as before.

In three experiments on MDCK II cells using the TdT assay, less than 1% of the cells were found to be apoptotic.

DISCUSSION

The present experiments do seem to confirm the phenomenon indicated by the experiments reported by Moan et al. (6). We have shown that the deviation of the distribution of the number of dead cells per colony from that expected if cells are killed independently of adjacent cells is statistically highly significant. We have extended the experiments to include two cell lines that were different from that studied in ref. 6, colonies of various multiplicities as well as confluent cultures. We have also investigated several alternative explanations of the data, including (i) that the cultures contained clones of different susceptibility to PDT, (ii) synchronous growth within colonies, (iii) that the cooperativity is mediated by some factor which diffuses through the culture medium, and (iv) that apoptosis was triggered by signals transmitted from damaged to undamaged cells. The agreement between the observations and the mathematical models which assume transfer of damage between adjacent cells strongly suggests that this phenomenon is due to cooperativity between adjacent cells, in the sense that one inactivated cell significantly increases the risk for its adjacent neighbors. The finding that several monoclonal cultures yielded similar distributions seems to rule out the possibility that the results were due to clones with different sensitivity to PDT.

Light exposure in the presence of Photofrin leads to damage of cell membranes (11). Thus, it is possible that leakage of PI from a damaged to an undamaged cell could influence our results. However, gap junctions between damaged and undamaged cells are generally closed (12). This is in agreement with experiments on MDCK II cells (data not shown) showing a 40% reduction of intercellular gap junction communication 2 h after a PDT-dose inactivating 10% of the cells (clonogenic assay).

Comparisons between the experimental distributions of inactivated cells and the independent inactivation model H0 and the two cooperativity models H1 and H2 do not only rule out the former alternative, but enable us to discriminate between the two interaction models, H1 and H2. The data of Tables 1–3 strongly favor the H2 model, which assumes that damage is propagated from cell to cell. Thus, we are led to believe that the mechanisms for cell inactivation by PDT involve intercellular communication of some kind.

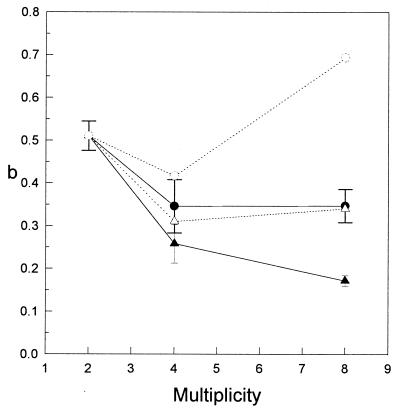
As the multiplicity of a microcolony increases, a given cell cannot be in contact with all of the other cells. Thus, the number of cells with which a cell can interact becomes less than the multiplicity. The value of the neighbor inactivation probability, b, should therefore decrease with increasing colony size, as shown in Fig. 4. If we make corrections for this decrease, by calculating the number of nearest neighbors, the mean value of b(H2) for higher multiplicities is still below the value of b for doublets. This can be explained if there is a tighter connection between two cells from the same mitosis during the first interphase after division than between other cells of the same colony. The adjusted mean value of b(H1), on the other hand, was higher for octets than for doublets. This cannot be explained within the framework of the present models, and is interpreted as an artificial attempt to compensate for the absence of long range effects in model H1.

Figure 4.

The mean value of b, the probability of inactivation via an adjacent cell, for all experiments as a function of multiplicity. •, Mean value of b as given by model H1; ○, value of b(H1) adjusted for the size of the colony; ▴, mean value of b as given by model H2; ▵, adjusted value of b(H2). (Error bars = standard error.)

Christensen et al. (7) reported that, for four cell lines, including V79, cells in S-phase were more sensitive to PDT than cells in the other phases of the cell cycle by a factor of two, whereas other investigators have found nearly flat cell cycle response curves (13–15). If the cells in a microcolony were highly synchronous and if the sensitivity to PDT varied sufficiently through the cell cycle, the distribution of inactivated cells could conceivably become similar to those observed. We have tried to investigate this possibility using the distribution of cells in S-phase shown in Fig. 3 and assuming that cells in a microcolony are inactivated independently of each other (model H0). By assigning hypothetical values to the probability of inactivating cells in S-phase (pS) and the probability of inactivating cells in the remaining part of the cell cycle (pG), we adjusted the distributions in Fig. 3 to fit the different experimental distributions of inactivated cells. Thus, we calculated that to reproduce the experimental distributions of inactivated cells the sensitivity of cells in S-phase had to be from 9 to 54 times larger than the sensitivity of cells in the other phases of the cell cycle. Hence, it seems highly unlikely that the combination of synchrony and different sensitivity through the cell cycle can explain the experimental distributions.

Table 4 shows that there was a higher number of colonies with an even than with an odd number of inactivated cells. Similarly, Fig. 3 shows that there was a higher number of colonies with an even rather than an odd number of cells in S-phase. Thus, the results of Table 4 can be explained if we assume that cells are in closer contact during the first interphase than later. Conceivably, two cells arising from the same mother cell share cytoplasm at the start of G₁, and are tighter together in the ensuing cell cycle.

Table 4.

Ratio between the total number of colonies with an odd and an even number of inactivated cells

n	MDCK II			V79
	2	4	8	2	4
odd
even	0.4	0.5	0.7	0.7	1.0

The colonies with no inactivated cells have been omitted. 

One difference between the MDCK II cell line and V79 cell line was that the MDCK II cells formed tighter colonies. As can be seen from Tables 1–3, both cell lines display cooperativity effects, since their distribution of inactivated cells are significantly different from the H0 model distribution. However, the MDCK II cell distributions have a larger χ² value when compared with the H0 model, and also gives a significant preference for the H2 model vs. H1, thus suggesting a closer cooperativity in agreement with the histology of the cultures.

The present experiments indicate that cells in microcolonies interact with each other so as to mediate the effect of PDT, and that lethal cell damage can be propagated trough a chain of adjacent cells. There are many possible mechanisms for this phenomenon. The passage of water from one cell to another because of membrane damage could mediate the effect. Preliminary experiments with hypo- and hyperosmolar media do not favor this explanation. Experiments with hydrophilic photosensitizers localized mostly in the cytoplasm of the cells and not in their membranes have also shown cooperativity (unpublished results), indicating that cooperative effects are not unique for photoinactivation caused by membrane damage. Finally, the possibility that apoptosis is triggered by signals transmitted from damaged to undamaged cells, is not a likely explanation of the data because our cells did not die by apoptosis. Cooperativity could be mediated through gap junctional intercellular communication during or shortly after irradiation. Further investigations are needed to identify the mechanisms by which the cooperativity phenomenon works.

ABBREVIATIONS

DAPI

4′-diamidino-2-phenylindole

FITC

fluorescein isothiocyanate

PDT

photodynamic treatment

PI

propidiumiodide

TdT

terminal deoxynucleotid transferase

Appendix

The matrices containing the entries for the probabilities of inactivation by interactions between cells have terms that can be calculated by the following recursion formulas:

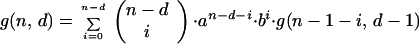A1

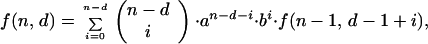A2

where n is the colony multiplicity, d is the number of cells in the colony inactivated by primary hits, i is the number of cells in the colony inactivated by neighboring interactions, a is the probability that a cell will survive the actions from an inactivated neighbor cell, and b = 1 − a. g(n, d) and f(n, d) represent the sum (over i) of the columns in the matrices. g(n, 0) = g(n, n) = 1, because no further inactivation of cells can take place. We also see that f(2, 1) = g(2, 1) = a + b, and that the use of binomial coefficients in the recursions ensures that the sums ∑_df(n, d) and ∑_dg(n, d) will be polynomial expansions of powers of (a + b), and thus equal to 1. The difference between the recursion formulas (A1 and A2) arises when one detaches the dth primary hit cell. In the H1 case one also removes the i cells inactivated by it, since they have no influence on the effect on the remaining cells. The i cells inactivated by the dth cell in the H2 case can on the other hand inactivate their neighbors equivalently to primary hit cells. The resulting matrix for H1 (and similar for H2) is:

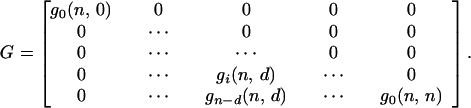A3