Direct in vivo measurement of targeted binding in a human tumor xenograft

Abstract

Binding is crucial to the function of most biologically active molecules, but difficult to quantify directly in living tissue. To this end, fluorescence recovery after photobleaching was used to detect the immobilization of fluorescently labeled ligand caused by binding to receptors in vivo. Measurements of mAb affinity to target antigen within human tumor xenografts revealed a saturable binding isotherm, from which an in vivo carcinoembryonic antigen density of 0.56 nmol/g (5.0 × 10⁵/cell) and an association constant of K_a ⩽ 4 × 10⁷ M⁻¹ were estimated. The present method can be adapted for in vivo studies of cell signaling, targeted drugs, gene therapy, and other processes involving receptor-ligand binding.

Specific receptor–ligand binding is crucial to the function of many biologically active molecules and is the basis for a wide range of novel therapeutic and diagnostic strategies. Controversy regarding the performance of receptor-targeting agents (1–3) has arisen, in part, from uncertainties in evaluating binding in situ. In vitro measurements may be misleading due to in vivo differences in receptor density, presentation, and accessibility, and due to microenvironment-related changes in binding kinetics (4–6). We devised a method to measure binding directly at a microscopic level in living tissue by applying fluorescence recovery after photobleaching (FRAP) to detect receptor-mediated immobilization of fluorescently labeled ligand.

With the FRAP technique, the movement of fluorescently labeled molecules is made evident by exposing the region of interest to a pulse of focused laser light to create a microscopic photobleached pattern that then dissipates due to local transport phenomena. This approach has been used extensively to detect binding in cell membranes (7, 8), cytoplasm (9, 10), and various in vitro preparations (11–16). We previously applied FRAP in vivo to measure the interstitial diffusion and convection of albumin within a tumor tissue preparation (17), and we report here the application of FRAP to measure binding in vivo. Fluorescent ligand is introduced into tissue, and the fluorescence redistribution after laser exposure is recorded as a series of digital images from which the molecular mobility is calculated. Apparent binding affinity K_app, the ratio of bound to free ligand, is inferred from the mobility reduction compared with an equivalent nonspecific molecule. An in vivo binding isotherm is then constructed by measuring apparent affinity at various ligand concentrations.

MATERIALS AND METHODS

Fluorescent Ligand.

In this study, the tumor-associated antigen carcinoembryonic antigen (CEA) and the CEA-specific mAb ZCE025 constitute the receptor–ligand system. We examined both bivalent (intact IgG) and monovalent (Fab′ fragment) forms of the ligand. Control measurements were performed using S1, a nonspecific mAb of the same IgG₁ isotype. The antibodies (provided by Hybritech) were labeled with fluorescein (Molecular Probes) at approximate molar ratios of 6 per IgG and 2.3 per Fab′. A competitive binding assay confirmed that the conjugated anti-CEA molecules retained their high binding affinity: suspensions of LS174T cells were incubated at various ratios of labeled/unlabeled mAb, and the mean cell fluorescence was measured by flow cytometry. For both IgG and Fab′, the data (not shown) indicated an association constant K_a (M⁻¹) 80–90% of the value for its unlabeled counterpart. The association constant of ZCE025 was previously measured in vitro to be 6 × 10⁹ M⁻¹ (IgG) and 9 × 10⁸ M⁻¹ (Fab′).

Stock solutions of labeled antibody in PBS (≈3 mg/ml) were diluted to the desired concentration (100–3000 μg/ml) in sterile saline containing 1 mg/ml BSA. Higher concentrations of intact mAb (3000–30,000 μg/ml) were obtained by mixing the labeled material with unlabeled molecules (≈30 mg/ml). The free diffusion coefficient (D₀) of each molecule was determined by performing FRAP measurements on 0.1-mm-thick glass capillary tubes containing 0.1 mg/ml fluorescein-conjugated protein.

Animal Model.

A transparent window chamber allowed noninvasive microscopic observation of human tumor xenograft tissue in athymic nude mice. The xenografts were derived from the LS174T colon carcinoma cell line shown to express CEA in vitro (18) and in vivo (19–21). Immunohistochemical analysis of xenograft tissue sections confirmed that CEA expression was dense and uniform (data not shown). As described previously (19), a portion of folded skin was replaced with a glass coverslip to expose the striated muscle and subcutaneous tissue of the opposing skin layer, upon which a suspension of cultured cells (2 × 10⁵ in 2 μl) was deposited.

When the solid tumor xenograft reached an approximate diameter of 4 mm (15–17 days after cell implantation), fluorescently labeled protein (20–6000 μg in 0.2 ml of sterile saline solution) was administered by tail vein injection, and the filling of the vasculature within the dorsal chamber was observed by fluorescence microscopy (see Fig. 1A). For the highest dose level, an additional 0.1 ml of ligand solution was injected after a 30-min interval. At each dose level, measurements were performed on three mice. All procedures were performed in accordance with Massachusetts General Hospital guidelines for research animal care.

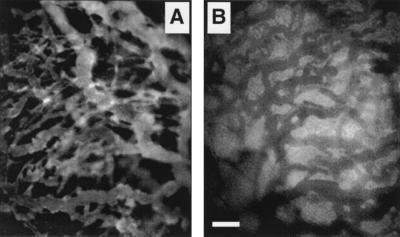
Figure 1.

Extravasation of fluorescein-labeled protein (nonspecific IgG) in a tumor xenograft is observed through a window in the mouse dorsal skin. (A) Ten minutes after injection, IgG is largely confined to the vascular space. (B) After 24 h, the fluorescence emission of the interstitial space exceeds that of the vasculature due to free and bound protein in the interstitial compartment. Although the image in B suggests a substantial level of nonspecific binding, the image does not accurately quantify the vascular-interstitial concentration difference because of differences in optical properties: the interstitium exhibits increased intensity due to scattered out-of-focus fluorescence above and below the plane of focus, whereas the red blood cells strongly absorb fluorescence in the vascular space. (Bar = 100 μm, approximately twice the diameter of the photobleached spot.)

Fluorescence Photobleaching Data Acquisition.

FRAP measurements of interstitial mobility were performed 24 h after i.v. administration of various doses of fluorescently labeled mAb. The 24-h timepoint was selected on the basis of previous studies (22, 23) to allow sufficient accumulation and establishment of a quasi-equilibrium between bound and free antibody within the interstitial compartment. An argon ion laser (model 2020; Spectra-Physics), tuned to a wavelength of 488 nm, was focused onto the tissue through the microscope objective (×20, NA 0.4) to form a circular spot with nominal diameter of 40 μm and incident power of 30 mW. After a brief (100-ms) exposure to laser illumination, wide-field epifluorescence images were projected onto an intensified charge-coupled device camera (model 2400; Hamamatsu Photonics, Hamamatsu City, Japan), digitized, and stored at a rate of 5 image/s for a period of 100 s.

Photobleaching recoveries were quantified by spatial Fourier analysis (24, 25) in which each sequential image is subtracted from a prebleach image and multiplied by a windowing function, as described (26), to obtain an array f(x,y,t), where t is the time after laser exposure (s), and x and y are the spatial coordinates (μm). Each array describing the time-dependent photobleached pattern is then converted by two-dimensional discrete Fourier transform (27) into the spatial frequency domain F(u,v,t), where u and v are coordinates of a two-dimensional spatial frequency vector (cm⁻¹). For the purposes of this study, in which diffusion is assumed to be isotropic, the spatial frequency magnitude (q, in radian/cm) was defined as q² = 4π²(u² + v²). The transformation of individual images is illustrated in Fig. 2.

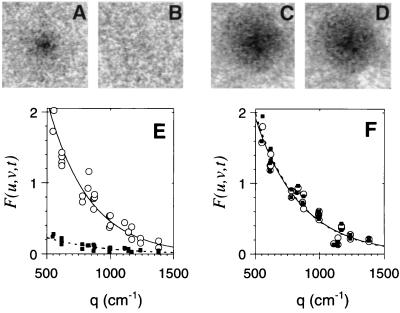
Figure 2.

Quantification of photobleached patterns in tumor tissue. Photobleached patterns are shown for xenograft tissue containing control S1 mAb (A and B) and CEA-specific ZCE025 (C and D) at times of 1 s (A and C) and 100 s (B and D) after laser exposure. Spatial detail of the pattern is quantified by two-dimensional Fourier transform of the images (E and F). An image is converted into a two-dimensional array of Fourier coefficients, each element with its own spatial frequency vector (u,v). The pattern is characterized by the plot of Fourier coefficient amplitude versus the spatial frequency magnitude q, where q² = 4π²(u² + v²), at t = 1 s (○) and 100 s (▪). Specific mAb (F) shows a greater persistence compared with the equivalent nonspecific molecule (E).

Direct Mobility and Affinity Calculation from FRAP Data.

The dissipation of an arbitrary photobleached pattern is driven by interstitial diffusion, characterized by the effective interstitial diffusion coefficient D_eff (cm²·s⁻¹) and by a characteristic diffusion distance. In the Fourier transform domain, the diffusion length is defined by the spatial frequency of each Fourier component. Each periodic spatial frequency component relaxes at a rate q²D_eff (s⁻¹) that is independent of other components and unaffected by distortion due to the optical transfer function of the microscope/imaging system (25). Binding, which acts to preserve the photobleached pattern, is characterized by the effective forward and reverse binding rates k_f (s⁻¹) and k_r (s⁻¹). The forward rate k_f is actually a pseudo-first-order rate that is the product of intrinsic association rate k_f′ (M⁻¹·s⁻¹) and concentration of free receptors B (M); therefore this effective rate will vary with ligand concentration. The measured fluorescence pattern, F(u,v,t) (consisting of a free and bound fraction, F_free and F_bound) is assumed to obey a simple first-order reaction-diffusion relation in which only the free fraction diffuses. The relation is given by the following set of ordinary differential equations:

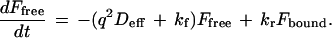1

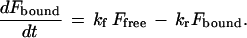2

The assumptions that a chemical quasi-equilibrium exists and that free and bound molecules are photo bleached at the same rate provide the following initial condition:

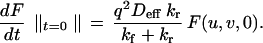3

The exact solution to the coupled differential equations is a biexponential decay, for which the eigenvalues are:

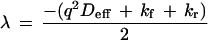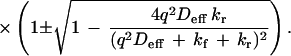4

To reduce the number of curve-fitting parameters, we derived simplified forms appropriate to the observed recovery data. A dimensionless time variable, τ = q²D₀t, was defined based on the diffusion rate in water. Whenever possible, the two binding rates were combined into a single equilibrium affinity, K_app = k_f/k_r, or were expressed as an immobile fraction φ, defined by the simple algebraic identity φ = K_app/(1 + K_app).

A “low-affinity,” “reaction-limited” simplification is valid when the association and dissociation rates are of similar magnitude and both much slower than the diffusion rate (q²D_eff ≫ k_f ≈ k_r), meaning that a significant portion of molecules is unbound and that dissociated molecules are likely to diffuse long distances before rebinding.

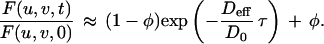5

Eq. 5 was used to analyze the photobleaching recoveries of all nonspecific control molecules to calculate D_eff and φ for each molecule.

Under “high affinity” conditions (k_f ≫ k_r) most molecules are bound, and the mobile fraction in Eq. 5 is undetectable. The recovery is described by:

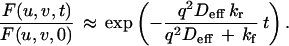6

Interpretation of the FRAP recovery rate under high affinity conditions depends on the relative magnitudes of the diffusion rate and the binding rate (i.e., how far unbound molecules travel before rebinding). Because typical dissociation rates for receptor–ligand binding vary over many orders of magnitude (28), both reaction-limited and diffusion-limited models were considered. In the reaction-limited case, rebinding is rare (q²D_eff ≫ k_f), and the recovery rate is simply the dissociation rate k_r. But in the diffusion-limited case, rebinding is common (k_f ≫ q²D_eff), and the recovery rate depends on the apparent equilibrium affinity K_app:

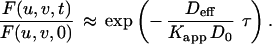7

For FRAP experiments involving specific ligand, the recovery rate k_obs (s⁻¹) was compared with that of the control ligand (from which a mean value of D_eff was obtained with Eq. 5). Eq. 7 was then used to calculate the apparent affinity by K_app = q²D_eff/k_obs. In the reaction limit, (k_obs = k_r), by virtue of the reaction-limit condition (k_f ≪ q²D_eff) this calculated apparent affinity value is only the upper limit (K_app < q²D_eff/k_obs). Therefore Eq. 7 provides at least an upper limit estimate of the in vivo affinity.

Use of Pharmacokinetic Model to Interpret FRAP Measurements of Apparent Affinity.

FRAP measurements yield a direct measure of apparent affinity (K_app), the product of intrinsic affinity and local ligand concentration. Noninvasive measurement of local ligand concentration in tumor interstitial fluid is problematic; therefore, to extract the intrinsic affinity we applied a simple two-compartment pharmacokinetic model (3) to estimate the interstitial fluid concentration based on the total dose injected into the tail vein. The extravasation rate of fluorescent ligand is assumed proportional to the plasma-interstitial fluid concentration difference.

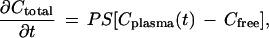8

where C_total, the interstitial ligand concentration, is the sum of free and bound (specific and nonspecific) components with respect to interstitial fluid volume (taken to be 20% of the total tumor volume). The vascular permeability surface area product per unit tissue volume, PS, has been measured in this xenograft model [2.5 × 10⁻³·min⁻¹ for IgG, 5.1 × 10⁻³·min⁻¹ for Fab′ (29)]. The initial plasma concentration was calculated from the injected dose divided by a 1.0 ml plasma volume, and the plasma clearance kinetics, C_plasma(t), of the injected agents in nude mice have been measured previously (22). The accumulation of labeled ligand was calculated by numerical integration of the extravasation rate over 24 h. A chemical quasi-equilibrium was assumed to exist among free and bound states in the tumor compartment, including nonspecific nonsaturable binding affinity, K_ns (measured in control experiments), and specific saturable binding. K_app, the ratio of all bound species to free ligand, was calculated as a function of the parameters K_a (intrinsic receptor-ligand association constant, M⁻¹) and B_max (receptor density, M):

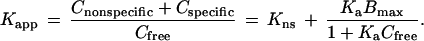9

For comparison with other measurements of CEA content in the literature, the tissue receptor content (nmol/g) was calculated as the product of interstitial receptor density B_max and interstitial volume fraction (assumed to be 0.2 ml/g). To obtain the mean binding sites per cell, a 70% cellular volume fraction and a mean single-cell volume of 1000 (±500) μm³ were assumed. Volume fraction and cell size estimates were made based on histological examination of fixed tissue sections.

RESULTS

Extravasation and accumulation within the xenograft was evident for each putative ligand studied. Fig. 1 illustrates the initial appearance of fluorescently labeled material in the vascular component of the tumor, followed by fluorescent staining of the extravascular compartment over the next 24 h. At the lowest doses administered (0.13 nmol for IgG), accumulation of nonspecific antibody could not be detected, whereas a measurable increase of tissue fluorescence was observed after administering the same dose of specific mAb. At larger doses, there was no obvious difference in the images of the fluorescently stained xenograft tissue, and hence no way to judge the extent of binding based simply on appearance.

Comparison of photobleached spot images provides qualitative evidence for tumor-specific binding (Fig. 2 A and B, and C and D). In the presence of control mAb, the nearly complete rapid dissipation of the photobleached spot indicates a high level of molecular mobility. In contrast, the photobleached pattern remained almost static in the presence of specific mAb, revealing the immobilization of mAb due to binding. Fig. 2 E and F illustrates the quantification of the photobleached pattern in terms of spatial frequency. Representative plots of the pattern decay under various conditions (Fig. 3) further illustrate the difference between nonspecific and specific molecules. FRAP measurements made upon the control S1 molecule or its fragment were all fit to Eq. 5 to determine the effective interstitial diffusion coefficients and nonspecific binding affinity of IgG and Fab′, as summarized in Table 1. For the control molecules, both the immobile fraction (shown in Fig. 4A) and the initial recovery rate (hence D_eff) were dose-independent, in support of the hypothesis that the recovery is a reaction-limited process with first-order nonsaturable binding.

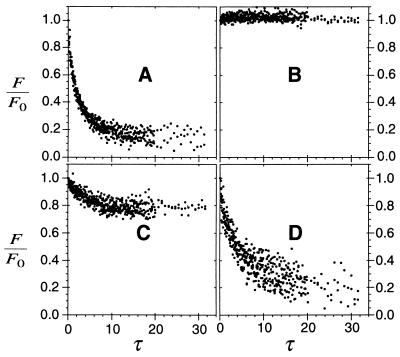
Figure 3.

Quantification of photobleaching recovery rate in tumor tissue. The decay of Fourier components (with spatial frequencies, q, from 500 to 900 cm⁻¹) is shown for nonspecific S1 mAb, 6 nmol total injected dose (A); specific ZCE025 mAb, 0.3 nmol (B); ZCE025, 5 nmol (C); and ZCE025, 70 nmol (D). The dimensionless time parameter τ is scaled by the diffusion rate in free solution. Measurements were performed 24 h after i.v. injection of the specified dose. Notably biphasic decays that suggested discrete bound and unbound components (A, C, and D) were fit to Eq. 5, whereas slow, incomplete recoveries were fit with Eq. 7.

Table 1.

Summary of FRAP mobility measurements for nonspecific molecules

Molecule	D0 × 107 (cm2·s−1)	Deff × 107 (cm2·s−1)	Deff/D0	φ
Fab′	6.6 (±0.3)	2.7 (1.4-5.4)	0.41	0.37 (±0.14)
IgG	3.9 (±0.2)	1.3 (0.7-2.2)	0.32	0.26 (±0.14)

The effective interstitial diffusion coefficient (D_eff) and immobile fraction (φ) in tumor xenograft tissue were measured in 18 (IgG) and 9 (Fab′) xenografts at doses shown in Fig. 4. All diffusion coefficients are scaled to 20°C according to the Stokes–Einstein equation. The standard deviation (in parentheses) is asymmetric about the mean for D_eff due to a log-normal distribution of measurements. 

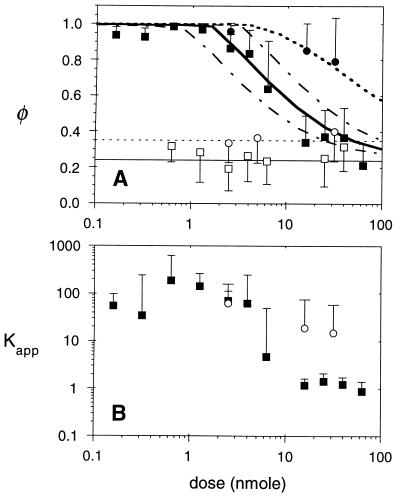
Figure 4.

In vivo binding isotherms. (A) Bound fractions of nonspecific S1 IgG (□) and S1 Fab′ (○) were independent of the total injected dose (mean values indicated by thin solid and dotted lines, respectively). Intact ZCE025 mAb (▪) exhibited near complete immobilization at low doses and binding site saturation above 2.5 nmol. ZCE025 Fab′ (•) exhibited a large bound fraction at all doses. Each data point represents the mean and standard deviation of at least 18 FRAP measurements in three xenografts. Theoretical binding curves are shown (thick solid line, intact IgG; dotted line, Fab′) for an in vivo CEA content of 0.56 nmol/g, calculated as described in the text. To show the sensitivity to the model parameters, IgG binding curves are also shown for 2-fold reduction (lower dashed line) and enhancement (upper dashed line) of binding site density (0.25 and 1.0 nmol/g). (B) The apparent binding affinity of anti-CEA molecules is calculated using Eq. 7, based on the observed initial rate of fluorescence recovery k_obs and the diffusion coefficient of the nonspecific control molecule, D_eff, taken from Table 1. The K_app value is the factor by which specific binding slows the photobleaching recovery; values around 1 imply negligible specific binding. Median values for intact IgG (▪) and fragment (○) are plotted with error bars showing the 90th percentile values for K_app. At low doses, K_app should approach the product of the intrinsic association constant K_a and the binding site concentration B_max.

FRAP measurements performed on CEA-specific molecules produced clear evidence of saturable high affinity binding. As Fig. 3 B–D illustrates, the relative persistence of the pattern depended on the dose. At high doses, the initial decay rates were comparable to those exhibited by control molecules, and hence these decays were fitted also to the low affinity model, Eq. 5. However, in the absence of a detectable initial rapid recovery phase (as in Fig. 3B), binding affinity was estimated by comparing the diminished decay rate with the mean decay rate of the equivalent nonspecific molecule using Eq. 7. Fig. 4 shows the construction of binding isotherms based on these data. The relation between bound fraction and total dose (Fig. 4A) shows the saturation phenomenon clearly. Below a critical dose nearly all of the specific ZCE025 mAb was bound; above that dose, the bound fraction declined toward the nonspecific level. In contrast to its intact form, the monovalent ZCE025 Fab′ fragment exhibited a reduced mobility relative to the control Fab′ (Fig. 4A), even at the highest doses we were able to administer (1500 μg).

To estimate the intrinsic binding parameters responsible for the observed binding isotherms, the data were compared with predictions of a simple pharmacokinetic model that estimates the local ligand concentration based on the injected dose and the independently measured extravasation (29) and plasma clearance rates (22). The fit of the model to the data (Fig. 4A) indicates a high level of CEA expression in this tumor xenograft, ≈0.56 nmol/g of tissue or 5.0 (±2.5) × 10⁵ binding sites/cell, based on the assumptions listed above. This estimated antigen (receptor) density is approximately directly proportional to the assumed vascular permeability surface area parameter. Therefore, if the permeability were assumed to be a smaller by a factor of two (which is within the error of that measurement), the estimated receptor density would be half the value given above (e.g., 0.28 nmol/g).

The reduced recovery rates observed for the specific molecules compared with the related control molecule were interpreted using Eq. 7 as described above. The upper limit of apparent affinity K_app is the ratio of recovery rates of the nonspecific control molecule (q²D_eff) and the specific molecule (k_obs). Affinity values of up to 1000 were estimated; as shown in Fig. 4B, the median affinity at doses below 4 nmol was ≈100, without a strong dose dependence. If K_app is taken to be the product of intrinsic association constant and the binding site concentration (adjusted for the interstitial fluid volume fraction as described in the methods), an upper limit of K_a ≤ 4 × 10⁷ M⁻¹ is calculated based on the median measurements for both the intact mAb and its fragment. If intrinsic affinity is calculated based on a more conservative estimate of tissue receptor content (B_max = 0.28 nmol/g) and based on the highest measurements of apparent affinity (the 90th percentile for K_app at low doses of intact IgG is 510) then the K_a value is ≈4 × 10⁸ M⁻¹, still well below the in vitro value (6 × 10⁹ M⁻¹).

A comparison of Fab′ and intact IgG revealed no substantial difference in the maximum detected affinity, but a continued high Fab′ affinity at high doses. The pharmacokinetic model reveals that the higher apparent affinity of Fab′ compared with the intact ZCE025 at high doses results not from a greater number of available binding sites but from the use of total injected dose in plotting the binding isotherm rather than the free ligand concentration in interstitial fluid (C_free). As has been noted in other studies (30, 31), the shorter plasma residence time of Fab′ compared with intact IgG means that a smaller fraction of the injected dose is delivered to the interstitial fluid over a 24-h period.

DISCUSSION

The FRAP experiments described here measured transport over distances on the scale of 10–100 μm within a tissue volume on the order of 0.1 nl. Experiments conducted upon more controlled in vitro preparations such as single cells or receptor-coated artificial surfaces may be more appropriate for elucidating the biophysics of receptor–ligand binding, but the attraction of the present method is its ability to reveal the effective binding behavior of tissue, capturing complexities that are not reproduced in model systems. Not only is receptor density likely to vary depending on the microenvironment, but the presentation and accessibility of receptors may also be modulated by effects on cell metabolism or by indirect effects of the extracellular matrix. The in vivo method reveals binding parameters relevant to tissue function such as the accessible receptor concentration, effective binding affinity, and the interstitial diffusion rate, and may be particularly useful for studies of physiology or drug delivery. In conventional pharmacokinetic studies, tissue binding parameters are among the many parameters that can be obtained by fitting the time-dependent ligand biodistribution to a model. This FRAP method provides an independent assessment of the compartmentalization between bound and free ligand within a tissue. The high spatial resolution of the method suggests that it will be feasible to assess microscopic variations in binding affinity and relate those differences to the local structure and composition of the tissue.

Binding isotherms were generated by performing FRAP measurements of effective binding affinity for a range of doses at a particular timepoint after injection. A Scatchard or similar solid-phase binding analysis can be applied to the measured binding curve to determine the true association constant (K_a, in units of M⁻¹) and antigen concentration. In practice such analysis is problematic because the tumor tissue is not a well mixed medium. Antibody extravasation and antigen density in a solid tumor are spatially heterogeneous, and there is likely a gradient in the local binding site occupancy such that regions of tissue near sites of extravasation become saturated at a lower dose than the more distant regions (32, 33). An additional source of variation is the possible presence of shed antigen in the tumor interstitial fluid. (A complex of antibody and soluble antigen would appear unbound to the FRAP method.) Nevertheless, estimates of these basic binding parameters were made by comparing the measurements with predictions of a simple pharmacokinetic model. This approach allowed calculation of the CEA expression in this tumor xenograft; the estimate of 0.56 nmol/g of tissue (101 μg/g) corresponds very closely to the mean CEA content of 105 μg/g measured by Esteban et al. (20), using the same experimental system (LS174T xenograft grown subcutaneously in nude mice to a size of ≈5 mm diameter). It is notable that the in vivo CEA expression per cell (based on our estimate of mean cell size) is 5.0 × 10⁵ sites/cell, markedly less than levels of over 10⁶/cell measured in vitro (18).

Fluorescence recoveries observed at low doses of each specific molecule generally occurred at detectable rates indicating that the in vivo intrinsic association constant, K_a, is no greater than 4 × 10⁷ M⁻¹, an order of magnitude lower than measured in vitro for Fab′ and two orders of magnitude lower than for IgG (30). This reduced in vivo affinity may be attributable to factors discussed above (presence of shed antigen, differences in antigen presentation, and spatial heterogeneity of delivery). It is unlikely to be an artifact of the fluorescein conjugation required for the FRAP technique, because the in vitro competitive binding measurements mentioned previously detected at most a minor reduction (<20%) in the binding affinity of both the antibody and its Fab′ fragment. Previous in vitro FRAP measurements (12) suggest fluorescein conjugation either abolishes specific binding entirely or has minimal effect on affinity.

The failure to detect a higher intrinsic binding avidity for intact IgG (due to bivalent binding) compared with its monovalent fragment suggests that IgG binding is primarily monovalent in this system. Moreover, the pharmacokinetic simulation of the IgG and Fab′ binding isotherms gave a better fit to the data when monovalent binding was assumed (same receptor density for each molecule).

The greatest potential source of error lies in the determination of the local free ligand concentration. Unfortunately, in most tissue preparations, this value cannot be calculated directly from fluorescence intensity, but it could be determined either by direct collection of interstitial fluid (34) or by an analysis of fluorescence partitioning in an excised tumor (35). Both methods are problematic, particularly in terms of invasiveness, but could provide useful additional information such as the concentration of soluble receptor–ligand complex.

The results of the specific binding measurements demonstrate the feasibility of in vivo detection and quantification of binding at the microscopic level. This experimental method provides a valuable tool to examine, within living tissue, a wide range of physiological phenomena involving receptor–ligand binding.

ABBREVIATIONS

FRAP

fluorescence recovery after photobleaching

CEA

carcinoembryonic antigen