Direct phase determination in protein electron crystallography: The pseudo-atom approximation

Abstract

The crystal structure of halorhodopsin is determined directly in its centrosymmetric projection using 6.0-Å-resolution electron diffraction intensities, without including any previous phase information from the Fourier transform of electron micrographs. The potential distribution in the projection is assumed a priori to be an assembly of globular densities. By an appropriate dimensional re-scaling, these “globs” are then assumed to be pseudo-atoms for normalization of the observed structure factors. After this treatment, the structure is determined directly by conventional direct methods, followed by Fourier refinement, leading to a mean phase deviation of only 20° (from the values originally found from the image transform) for the 45 most intense reflections.

Recently, there has been increasing interest in using direct phasing methods to aid the electron diffraction determination of macromolecular structures at low resolution. Much of this attention has been focused on the problem of phase extension, i.e., starting with a partial phase set and extending it into the whole range of the recorded data set to obtain a clearer view of the molecular envelope. In original x-ray crystallographic studies, such efforts have started with partial information obtained from multiple isomorphous replacement (1, 2). In electron crystallography, the partial phase set would typically be determined from the Fourier transform of experimental electron micrographs after image averaging (3). In either case, successful application of traditional direct methods, such as the Sayre equation (4–6), or newer methods, including maximum entropy and likelihood (7), have shown that the low-resolution data from many macromolecules are accessible to such analyses. Only when the node of averaged intensity occurring near (5 Å)⁻¹ is reached, are significant problems encountered in the phase extension (4).

The prospect of actual ab initio phase determinations, assuming that no preliminary information is available, also has been explored. The Sayre equation, followed by phase annealing steps, was quite successful in one case (8), as was the use of maximum entropy and likelihood (9). However, if such multisolution methods are to be effective, there must also be a robust figure of merit that allows identification of the correct structure solution. This requirement may not be easily satisfied, despite the approximate validity of smoothness and flatness criteria (10) for the density distribution when structures are determined at low resolution (6). [The log-likelihood gain criterion in maximum entropy procedures may be a suitable way to solve this problem (9).]

Another approach to such phasing problems, especially in cases where the structures have appropriate distributions of mass, would be to adopt a pseudo-atom approach. The concept of using globular sub-units as quasi-atoms was discussed by David Harker in 1953, when he showed that an appropriate globular scattering factor could be used to normalize the low-resolution diffraction intensities with higher accuracy than the actual atomic scattering factors employed for small molecule structures (11). In a sense, this idea has already been employed (in real space) for phase determination in protein x-ray crystallography, when clusters of globular subunits, randomly arrayed in numerous patterns, have been generated to seek an adequate approximation to the density distribution in the unit cell (12).

There is, possibly, a more straightforward use of this idea in reciprocal space, and that is to test the suitability of intensity data normalized by a “glob” transform for analysis of crystallographic phases by conventional direct methods, as if the structure were that of a small molecule. The successful analysis of a projected membrane protein structure is described in this paper.

ANALYSIS

Data Set.

Electron diffraction intensity data, which had been collected at 120 kV to 6-Å resolution from frozen-hydrated two-dimensional (Halobacterium halobium) halorhodopsin crystals by Havelka et al. (13), were used in this analysis. There were 101 unique reflections in the published list. The centrosymmetric plane group for the square projection (a = 102.0 Å) is p4 gm (# 12). The crystallographic phases, derived from the Fourier transform of averaged electron micrographs, had been published in the original report of this structure (13).

Normalization of Structure Factors.

Harker (11) had treated the globular subunits of a protein as hard spheres in his original treatment and, if these were to have a diameter x, then their Fourier transforms would have cross-sectional terms containing the function sinc(πx) = sin(πx)/πx. Since it is only the first envelope of the two-dimensional “Airy disc” transform that would be used to approximate a globular scattering factor, it might be preferable to replace this function by a Gaussian term (or something close to a Gaussian function), since the Fourier transform of this function (i.e., another Gaussian function) does not produce the “edge diffraction” effect found in the sinc function. It is also well known that several functions (e.g., Gauss and sinc) can be used as good approximations of one another in the most intense part of their envelopes (14).

Indeed, the scattering factors of atoms are approximately Gaussian, since they can be expressed as a weighted sum of Gaussian functions (15). [The actual Lorentzian shape of this sum (15) is assumed not to be a significant deviation.] In this study, therefore, it was assumed that all details of the structure could be rescaled dimensionally by a factor of 10. The rationale for this 10-fold rescaling (and the choice of an approximate scattering factor) is easily found by comparing the center-to-center distance for two touching α-helices (16), i.e., ≈15 Å, to the distance, 1.54 Å, of a carbon–carbon single bond (17). Thus, a square unit cell with a = 102.0 Å would become one with a′ = 10.20 Å edges, and the data resolution would then be assumed to be recorded to 0.6-Å resolution instead of just 6 Å. Therefore, for normalization after this rescaling of dimensions, the glob transform was approximated by the electron scattering factor of carbon (15). [This approach is to be distinguished from a “globular” approximation on another scale, i.e., where an atomic scattering factor (7) or a more accurate phenomenological distribution (18) simulates the Fourier transform of an amino acid residue, for example.]

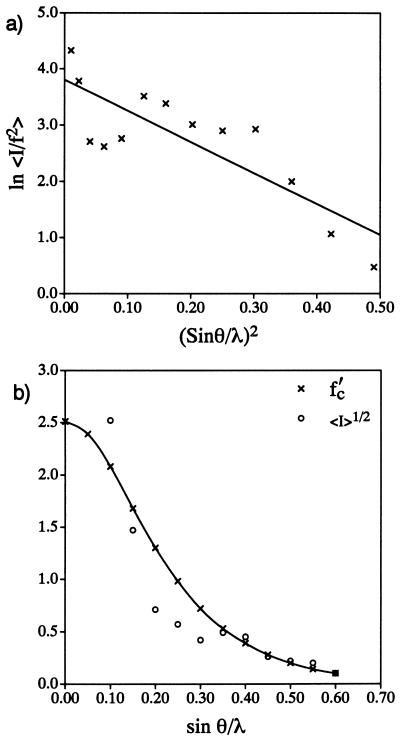
As usual, the intensities were evaluated with a Wilson plot (19), based on ln 〈I_h^obs/∑f²〉 = ln C − 2B_iso(sin²θ/λ²), to determine the overall temperature factor B_iso = 2.8 Å (2), as shown in Fig. 1a. After adjusting the carbon scattering factor, f′ = f exp(−B sin²θ/λ²), i.e., the approximation for the glob transform after rescaling, for “thermal motion,” normalized structure-factor magnitudes |E_h| were calculated from the observed intensities in the usual way (20): |E_h| = I_h^obs/ɛ∑(f′)². Here the statistical weight ɛ compensates for certain reflection index classes due to the symmetry properties of the plane group. After these normalized quantities were calculated, 95 were found to have suitably high values to be used for direct phase determination.

Figure 1.

(a) Wilson plot made after rescaling of halorhodopsin electron diffraction intensities. (b) Fit of rescaled plot of average-observed structure-factor magnitudes vs. resolution to the carbon scattering factor curve (with temperature factor included).

Direct Phase Determination.

Three-phase structure invariants (20), defined φ_h = φ_k + φ_h−k, were employed for the analysis. (Here φ_h is the phase of a reflection with Miller indices h = h₁k₁ℓ₁ and k = h₂k₂ℓ₂. When all indices are different, the equality defines a so-called Σ₂ invariant, but when h = 2k, it defines a Σ₁ invariant. The former is the most useful.) These generate simultaneous equations in the crystallographic phases that can be ranked according to their decreasing reliability of being correctly predicted according to, e.g., A = (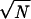/2)|E_hE_kE_h−k| for the Σ₂ invariants. Here N is the number of atoms in the unit cell (assumed to be equally weighted). (Note that the correct number of globs, i.e., seven in the asymmetric unit, was used in this determination. This exact number is not absolutely required since, to a first approximation, it will only affect the relative scaling of the A terms but not their ordering.) Using a convergence procedure (21), all possible phase contributors (from a total set of 507 triples generated to a minimum value of A = 0.5) to a given reflection h were considered in the sequence most optimal for finding the phases of the most number of reflections after definition of a small basis set.

Crystallographic phases were determined by a procedure termed “symbolic addition” by some researchers (22). Only one reflection could be used for origin definition in this projection, since both gg0 and uu0 combinations are phase seminvariants for this plane group (23). (Here, g = “gerade” = even and u = “ungerade” = odd index values.) From the sequential rank of |E_h| terms, a ug0 reflection, the phase φ₅₆₀ = π, was assigned. [The other possible value, 0, also could have been used legitimately, but this term was chosen to preserve the origin used in earlier determinations (5, 9, 13), just to facilitate phase comparison.] From the most probable Σ₁ relationships, the phases: φ_12,12,0 = φ₈₈₀ = φ_0,16,0 = φ_0,10,0 = φ_2,10,0 = 0, were also accepted. Finally, two other reflections were initially given algebraic phase values, φ₀₈₀ = a, φ₅₉₀ = b. Their actual values (respectively, 0 and π) were determined unequivocally in the course of the phase solution.

Fourier Refinement.

As will be shown below, the initial phase set yielded a potential map [via ρ(r) = 1/V∫|F_h^obs| exp(iφ_h) exp(−2πih·r)dr] with a partial structure solution. Glob positions were picked from the map as atoms would have been for a small molecule structure and structure factors were then calculated with these identified positions to find new phase terms, again using the scaling approximation above and the carbon scattering factor. In successive cycles, new atom positions are identified and their positions used for new structure-factor calculations, etc.

In this refinement procedure, it was assumed that the normal indicators for small molecule structure determinations were valid. That is to say, density profiles of maps could suggest new atom sites and these were accepted if the new map, based on the revised phase set, retained the peak as reinforced density. However, the crystallographic R-factor was not used as a figure of merit (see below), nor were difference maps calculated during this refinement.

RESULTS

After definition of the basis set, 32 phase values were determined, the derived set containing 7 errors (mostly associated with weaker reflections). Combining these values with |F_h^obs| to calculate the first potential map, four globular sites were observed strongly (Fig. 2a), with the weak indication of a fifth. After a structure-factor calculation based on the five sites to find phases for all unique reflections, a second map (Fig. 2b) was calculated, reinforcing the position of the fifth site and indicating a sixth position. The next structure-factor calculation produced a revised phase list. The resultant potential map reinforced the sixth position. It should also be noted that one glob was elongated (Fig. 2c), and so an estimated position was given near the end of the elongation. After the next structure-factor calculation, the revised phase list resulted in a potential map (Fig. 2d), which is very close in appearance to the one found originally (13) from the Fourier transform of electron micrographs (Fig. 2e).

Figure 2.

Progress of structure determination. (a) Initial potential map after symbolic addition. (b) Map after first structure-factor calculation. (c) Map after second structure-factor calculation. (d) Map after third structure-factor calculation. (e) Structure determined by electron microscopy (13). Helix positions are numbered (to match to those given in Table 2).

The positions of identified α-helix centers (the globs) found in this determination were very close to the ones located in the original determination (Table 1). If all reflections were considered, the mean phase difference to those found from the image transform was 〈|Δφ|〉 = 56.8°. For the 45 most intense reflections this difference was only 20.0°.

Table 1.

Mean phase errors for halorhodopsin compared with previous determinations

	This determination	Previous direct phasing	Phase extension
To 6 Å, all data	56.8°	74.8°	55.2°
To 6 Å, IFhI ≥ 1.0	20.0°	44.0°	24.0°

DISCUSSION

The results of this straightforward phasing procedure, based on the symbolic addition procedure often employed in small molecule crystallography, are found to be much more accurate for this example than the results obtained earlier by another direct phasing technique, involving an annealing step after expansion in shells of reciprocal space (9). No figure of merit was needed for identification of the structure, and the usual rules for accepting new peaks during refinement were also accepted, again without the reinforcement of the crystallographic R-factor.

From this determination, it is apparent that the globular scattering factor suggested by Harker (11) is quite appropriate for determination of optimal normalized structure factors. With this normalization, and assuming that pseudo-atom positions will be sought later in the potential maps, it is clear also that standard direct phasing procedures will be effective for determining what is essentially a small molecule structure problem. Obviously, if the globular pseudo-atoms account well for the unit cell density, then their transforms should faithfully simulate the unit cell Fourier transform (diffraction pattern).

However, it is obvious too that the rescaling device used for this determination is somewhat of an artifice, even if the tabulated atomic scattering factor (15) was a convenient approximation for the globular transform. Just how well did the carbon atom model serve in this case? If a cluster of seven carbon atoms were used to simulate the globs (but with somewhat higher thermal values than found in the Wilson plot above), after rescaling the dimensions of the problem, the crystallographic R-factor was calculated to be 0.41, not a highly accurate portrayal of the intensity transform. However, for the complete phase list, there were only 28 errors (for 101 reflections) and these were mostly associated with weaker reflections. The determined phases were, of course, combined with observed structure factors to calculate the potential maps in Fig. 2, so the density distribution would be expected to be quite good. This is shown by the comparison of helix sites in Table 2.

Table 2.

Helix positions for halorhodopsin found by direct methods.

Position	This determination		Image analysis
	x/a	y/b	x/a	y/b
1	0.199	0.018	0.201	0.016
2	0.199	−0.069	0.211	−0.078
3	0.237	−0.164	0.239	−0.144
4	0.330	−0.180	0.339	−0.188
5	0.404	−0.114	0.378	−0.115
6	0.306	−0.045	0.319	−0.045
7	0.294	0.042	0.294	0.045

It is clear, therefore, that further work could be devoted to the formulation of more accurate scattering factors for protein subunit globs (including anisotropic distributions of density to simulate tilted helices, for example). The fit of the carbon atom scattering factor curve, adjusted for thermal motion, to the fall-off of 〈I_h^obs〉^1/2 with sin θ/λ is found to be only a fair approximation (Fig. 1b), e.g., the curves fall to a near zero value at about the same resolution, a criterion that should be used as an a priori test of any model for the glob transform. (It is probably not worthwhile to overcomplicate the simulation by allowing globs of various sizes, since thermal motion can be used as another variable when the map indicates that it might be needed for improving the fit to density.) Thus, the fit to the scattering envelope could be much better, although the present approximation does not have too serious an effect on the results observed in this study.

One serious limitation of this rescaling model is that it restricts the determination to the spatial frequency limit of the phenomenological scattering factor, or else there would be problems with hyper-resolved data sets. In other words, the technique is only suited to a modest diffraction resolution (e.g., the 6 Å limit of this study), because the success of the structure determination probably also relies on the favorable analytical properties of the intensity transform for direct phase determinations (4–8) up to the nodal zero of average scattered intensity observed near 5 Å.

As will be shown in a future communication, there are other protein structures with pseudo-atomic subunits, such as the lipid-containing (3) or delipidized (24) forms of bacteriorhodopsin, that can also be determined in projection by this technique, even when the projected density distribution is noncentrosymmetric. On the other hand, other nonglobular secondary structure, e.g., β-sheets, may not be so conveniently visualized by this approach.