Direct observation of ligand transfer and bond formation in cytochrome c oxidase by using mid-infrared chirped-pulse upconversion

Abstract

We have implemented the recently demonstrated technique of chirped-pulse upconversion of midinfrared femtosecond pulses into the visible in a visible pump–midinfrared probe experiment for high-resolution, high-sensitivity measurements over a broad spectral range. We have succeeded in time-resolving the CO ligand transfer process from the heme Fe to the neighboring Cu_B atom in the bimetallic active site of mammalian cytochrome c oxidase, which was known to proceed in <1 ps, using the full CO vibrational signature of Fe–CO bond breaking and Cu_B–CO bond formation. Our differential transmission results show a delayed onset of the appearance of the Cu_B-bound species (200 fs), followed by a 450-fs exponential rise. Trajectories calculated by using molecular-dynamics simulations with a Morse potential for the Cu_B–C interaction display a similar behavior. Both experimental and calculated data strongly suggest a ballistic contribution to the transfer process.

Internal dynamics in proteins are crucial for the accomplishment of protein function. In proteins interacting with small ligands, ligand dynamics has been shown to be adapted and optimized for the protein function: e.g., fast rebinding in ligand sensor/receptor proteins versus efficient diffusion away from the active site in ligand synthesizing proteins (1).

Ultrafast ligand shuttling has been studied in heme proteins by photodissociating diatomic ligands from the heme with a visible pump pulse in pump-probe experiments. A probe in the visible domain (2) is sensitive to the ligand arrival and departure from the heme through its effect on the heme electronic transitions, a mid-infrared (mid-IR) probe (3–5) allows the observation of the ligand trajectory via the ligand's vibrational frequency changes, whereas an x-ray probe (6) is directly sensitive to the atomic positions.

The observation of the first steps of the ligand evolution after dissociation requires femtosecond (fs) time resolution. Because pump-probe x-ray diffraction measurements in proteins with fs resolution still remain a challenge (7), mid-IR absorption experiments are currently the most direct way to follow the ligand trajectory. Mid-IR experiments, however, optimally require high concentrations of protein compared with experiments in the visible because of the smaller extinction coefficients and limitations due to solvent absorption. Most fs IR studies, like the pioneering work of Hochstrasser and Anfinrud, have therefore focused on proteins that are readily available at high concentration, like myoglobin and hemoglobin (3, 8–11).

Another limitation is that spectrally resolved measurements, although straightforward in the visible because of detection with CCD cameras, are more difficult to implement in the mid-IR. IR pump-probe spectroscopy approaches have relied either on time-consuming frequency (3, 9) or delay scanning (12) or, more recently, on expensive mercury cadmium teluride (HgCdTe) detector arrays (10, 11, 13, 14) for detection of the IR probe. Here, we measure the transmitted mid-IR pulse using the recently demonstrated technique of upconversion into the visible range by sum-frequency generation with a chirped 800-nm pulse (15). This technique benefits from highly mature silicon CCD technology for detection in the visible and has already been successfully applied to two-dimensional IR spectroscopy (16). It allows for high-resolution, high-sensitivity measurements over a broad spectral range currently unattainable with IR-detector technology.

We applied this detection scheme to the observation of ligand transfer in the key enzyme cytochrome c oxidase (CcO). CcO aa₃ is the terminal respiratory-chain enzyme present in the mitochondrial inner membrane of eukaryotes and the cell membrane of many prokaryotes. It reduces oxygen to water by using four electrons delivered by cytochrome c and couples the energy of this reaction to the pumping of four protons across the membrane to set up a transmembrane proton gradient (17). The mammalian enzyme has 13 subunits, three of which (subunit I, which contains the active site, and subunits II and III) show a high degree of homology with the three subunits of bacterial enzymes. It contains two a-type hemes: heme a participates in electron transfer from cytochrome c to the active site and heme a₃ binds dioxygen via its central Fe atom. The enzyme's bimetallic active site where dioxygen reduction takes place, contains the heme a₃ Fe atom and the nearby (5.3 Å away) Cu_B (18, 19). Whereas both metal centers can bind small ligands, the heme has a higher overall affinity. This arrangement constitutes a unique opportunity to study ligand traffic between two intraprotein binding sites located at close distance.

Physiologically present NO and CO act as competitive ligands for the O₂-binding site. This competitive binding has been shown to have a regulatory role in the case of NO (20). As in other heme proteins, the protein environment at the active site is responsible for fine tuning the heme affinity for the various competitive ligands. In contrast to O₂, CO forms a stable complex with the enzyme and has thus been used in numerous experiments aimed at elucidating ligand binding and transfer in CcO (21, 22). CO binds to Cu_B before binding to the heme Fe (23) as well as after photodissociation from the heme Fe (24). A doorstep role for ligands on their way into and out of the active site has thus been attributed to Cu_B (see Fig. 1 for a representation of the active site of CcO with CO bound to the heme-a₃ Fe and to Cu_B). Nevertheless, before this work, the CO transfer from the heme Fe to Cu_B has not been directly time resolved. Previous studies used either a visible probe leading to conclusions based on the heme dynamics (25) or a 2-ps mid-IR probe (4, 26). A stepwise population of the nonliganded heme-a₃ ground state was deduced in the first case and attributed to concerted motions of the active site participating in ligand transfer (25). The mid-IR work, on the other hand, measured an upper limit of 1 ps for the CO transfer time and pointed out the rapidity of the process incompatible with diffusive transfer of CO toward Cu_B (4, 26).

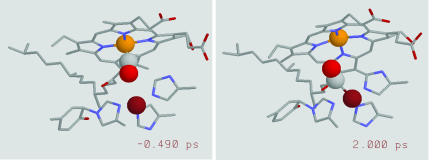
Fig. 1.

Active site of CcO with the CO bound to the heme Fe (Left) and to Cu_B (Right) before and after photodissociation, respectively. The orange, magenta, and gray and red spheres represent the van der Waals radii for the heme-a₃ Fe atom, Cu_B, and CO, respectively. The two images correspond to two snapshots of a trajectory calculated by using molecular-dynamics simulations.

In this work, we report on fs visible pump–mid-IR probe experiments that allow direct time resolution of the arrival of CO on Cu_B after its release from the heme. The mid-IR probe was detected in the visible after sum-frequency generation with a chirped 800-nm pulse. The results demonstrate a ballistic contribution, on the fs time scale, to the transfer process and are in good qualitative agreement with molecular-dynamics simulations using a Morse potential to explicitly model formation of the Cu_B–CO bond.

Differential Transmission Results

Our experimental setup (Fig. 2) is based on the one used for mid-IR electric field characterization with a visible CCD camera using chirped-pulse upconversion into the visible (15). In the present work, we measured the spectral amplitude of the mid-IR field and did not make use of the spectral phase measurement capability (15). The use of a highly chirped, 150-ps pulse ensures that the mid-IR pulse overlaps only with a well defined frequency inside the chirped pulse. One hundred twenty-five pixels are available over the full 200-cm⁻¹ width of the probe spectrum, the detection range being limited solely by the probe spectral width.

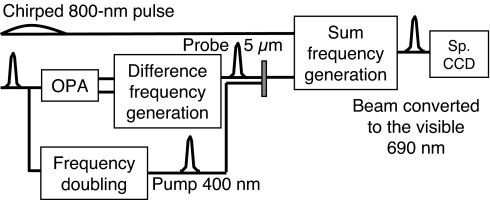
Fig. 2.

Scheme of the experimental setup.

The main difference with respect to the previous setup (15) is that, instead of using the zero-order diffraction off the compressor grating, the chirped 800-nm pulse is split from the stretched pulse inside the amplifier just before the compressor stage by using a λ/2 waveplate and a polarizing beam splitter. This allows for a chirped pulse of higher and variable power. This is particularly important for beef heart CcO: this ≈150-kDa membrane protein is not easily obtained at very high concentrations. To increase the absorption and hence the differential signal, we resort to relatively large sample thicknesses (200 μm) that translate into very weak transmission levels (≈2% at 1,960 cm⁻¹ and 0.8% at 2,064 cm⁻¹) even after H₂O substitution by D₂O. Consequently, the power of the chirped pulse used for the upconversion was increased to 500 μJ to maximize the signal arriving at the CCD and minimize the photon shot noise. With a count number of ≈20,000 at the maximum of the probe spectrum for a single laser shot, we are close to the optimal operation conditions for our 16-bit CCD camera (65,536 counts).

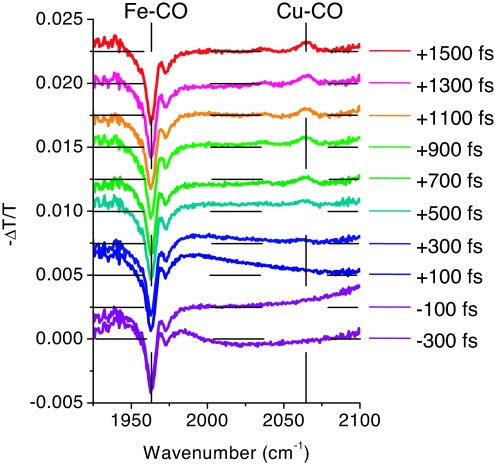
Differential transmission spectra were recorded for delay times between −300 fs and +1,500 fs with a delay step of 200 fs and are shown in Fig. 3. The probe spectrum was chosen to encompass both the Fe–CO and the Cu_B–CO vibrational frequency (probe centered at 2,030 cm⁻¹ with a full width at half-maximum of 80 cm⁻¹). The most prominent feature of the spectra is the gradual appearance, after the pump-probe delay of +300 fs, of an induced absorption peak at 2,064 cm⁻¹ representing the arrival of CO at Cu_B. The departure of CO from its initial Fe-binding site is observed as an induced transmission peak at 1,963 cm⁻¹. Both the Fe–CO and Cu_B–CO vibrational frequencies determined here are in agreement with previous observations (4, 27). We also performed spectrally integrated absorption anisotropy experiments (data not shown) confirming the angles of 160° and 55° for Fe- and Cu_B-bound CO with respect to the heme normal, respectively, measured in ref. 4. A weaker induced absorption peak is also observed at 2,036 cm⁻¹. Finally, a small side peak of the Fe–CO signal at 1,972 cm⁻¹ is probably due to protein degradation (28). The area of this peak gradually increases with exposure time (data not shown) and is 20% of the total Fe–CO signal for the data shown here.

Fig. 3.

Differential transmission spectra for different pump-probe delays displaced vertically for clarity (horizontal dashed lines indicate the origin). Vertical dashed lines show the position of the Fe–CO and the Cu_B–CO vibrational peaks at +1.5 ps.

The noise in the differential transmission spectra is 5 × 10⁻⁵ (2.2 × 10⁻⁵ OD) for a total acquisition time of 1 h, i.e., 3.3 min per pump-probe delay value, excluding the time needed for the delay variation, and is limited by the photon shot noise. This is the reason why the noise is higher at ≈1,925 and 2,100 cm⁻¹ at the edge of the probe spectrum where the photon number is smaller. The noise due to the laser fluctuations is efficiently eliminated by the use of the maximum, 500-Hz, chopping frequency. Residual noise due to laser fluctuations is probably the origin of the deviations from the zero baseline of the differential spectra at +500 and +700 fs. The large-period oscillations observed at negative and close-to-zero delays (−300, −100, and +100 fs) as well as the bleaching of the CO band at negative delays are due to the pump-induced perturbed polarization decay effect (29, 30).

Pump-probe fs experiments in the visible have determined the CO photodissociation time from the heme Fe to be <50–100 fs (2, 31) for heme excitation in the α-band as well as in the Soret band at 400 nm (32). Confirming CO departure dynamics based on the mid-IR differential transmission spectra is difficult because of the presence of the perturbed polarization effect. In principle, spectrally integrating the peak at 1,963 cm⁻¹ and the coherent spectral oscillations both on the high- and low-frequency side should reveal the departure dynamics. In our present data, however, the signal after spectral integration is too weak compared with the noise resulting from laser fluctuations.

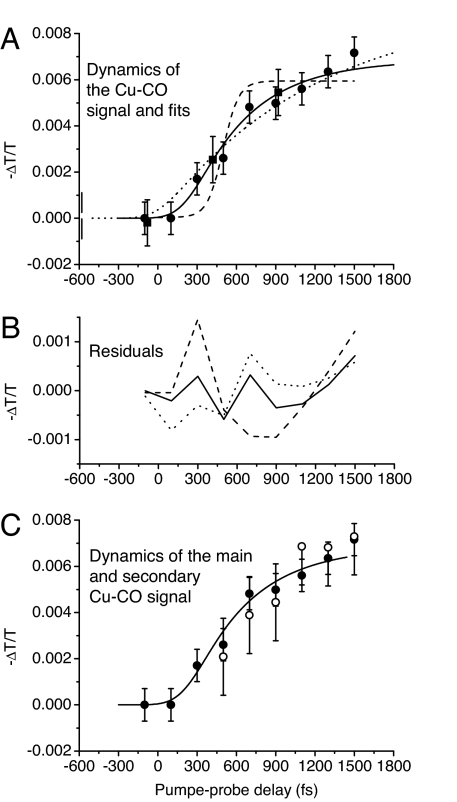
Let us now turn to the dynamics of the signal at 2,064 cm⁻¹ due to the arrival of CO at the Cu_B-binding site. We fitted the signal with Gaussians and then plotted the area under the Gaussian as a function of delay time (see Fig. 4A). If the transfer process were purely ballistic, we would expect a Heaviside-like form convoluted with the instrument response function such as the fit shown for a step function at 500-fs delay (dashed line, Fig. 4A). The measured dynamics is clearly slower. If, on the other hand, the dynamics were purely diffusive, an exponential signal rise would be expected, as in the case of CO arrival at the docking site of myoglobin (3). The dotted line in Fig. 4A corresponds to such an exponential fit with a characteristic time of 1,200 fs convoluted with the instrument response function. The difference between the experimental data and this fit is first negative and then positive (Fig. 4B). Indeed, a pure delay is observed before the signal starts rising after 300 fs. This feature cannot be reproduced by an exponential fit and is indicative of a ballistic contribution to the transfer process. Furthermore, spectrally integrated experiments demonstrate that the arrival dynamics is over at 1.5 ps (J.T., J. P. Ogilvie, T. Polack, M.H.V., M.J., and A.A., unpublished data), whereas the exponential fit continues to increase. We therefore resorted to a transfer model including both a ballistic and a diffusive component described by a delayed exponential convoluted with the instrument response function. Fitting the experimental data with this function gave the best agreement for a delay of 200 fs and a characteristic time of 450 fs (see residuals in Fig. 4B).

Fig. 4.

Dynamics of the Cu–CO signal. (A) Area under the Cu_B–CO vibrational peak at 2,064 cm⁻¹ as a function of pump-probe delay time. The circles (squares) are data obtained at a 1 kHz (25 Hz) rate. The lines are fits with (i) the instrument response function displaced by 500 fs (dashed), (ii) a 1200-fs exponential convoluted with the instrument response function (dotted), and (iii) a 450-fs exponential displaced by 200 fs and convoluted with the instrument response function (solid). (B) Residuals corresponding to the different fits. (C) Comparison between the signal rise of the main peak at 2,064 cm^M1 (filled circles; same data as in A) and that of the secondary peak at 2,036 cm⁻¹ (open circles; data multiplied by a factor of 2.38) together with the solid-line fit of A.

The weaker induced absorption peak at 2,036 cm⁻¹ shows the same dynamics as the main Cu_B–CO peak (see Fig. 4C) and should therefore also be related to the arrival of CO at the Cu_B-binding site. This signal may be due either to a different CcO conformation or to the absorption of the excited vibrational state v = 1. Two conformations have been observed in rat heart CcO–CO at low temperature (120 K) with CO vibrational frequencies of 1,964 and 1,951 cm⁻¹ for the Fe–CO forms and frequencies of 2,063 and 2,044 cm⁻¹ for the Cu_B–CO forms, respectively (33). In our room-temperature data, the shoulder seen at ≈1,951 cm⁻¹ may be due to the presence of a second conformation with the peak at 2,036 cm⁻¹ being related to its Cu_B–CO form. In the second case (excited vibrational transition), the frequency difference between the ground state and the v = 1 excited state absorption would be 28 cm⁻¹, comparable with the values of 26 cm⁻¹ for ¹³CO at the hemoglobin docking site (34) and 25 cm⁻¹ for Fe-bound CO in hemoglobin (12). The area under the 2,036-cm⁻¹ peak is 29% of the total area under the 2,036- and 2,064-cm⁻¹ peaks. A fraction of the Cu_B–C bond formation energy may be transformed into CO vibrational energy, thus giving rise to an excited-state vibrational population. A decay time of the peak at 2,036 cm⁻¹ similar to the vibrational relaxation rate of CO complexes of a few 10s of ps (12) would indicate that this peak is a vibrational hot band. However, conformational interconversion of one species into the other taking place on the same time scale cannot be excluded. Therefore, the most unambiguous way to distinguish between the two hypotheses would be 2D-IR spectroscopy (35).

The width of both the main Fe–CO peak and the main Cu_B–CO peak is 8–9 cm⁻¹. Their surface ratio is equal to 7, in agreement with ref. 4. The Gaussian fits of the main Cu_B–CO peak show a small shift from 2,062.4 to 2,064.3 cm⁻¹ between the pump-probe delays of 500 and 1,500 fs. The precision of this determination, however, varies from ±1.6 to ±0.7 cm⁻¹ and does not allow a definitive conclusion on the existence of this frequency shift. Confirming this behavior will have important implications for the transfer process by answering the question: is free CO formed in the transfer process or is there a gradual change from Fe–CO to Cu–CO without free CO formation? Density-functional theory calculations have shown that the CO vibrational frequency increases as the Fe–C distance increases (5) as expected from the higher free CO frequency (2,130 cm⁻¹). Similarly, we expect a frequency decrease for “free” CO progressively binding to Cu_B. Observing the opposite would imply that CO progressively transforms from Fe-bound to Cu_B-bound without intermediate “free” CO formation.

Molecular-Dynamics Simulations

We have further investigated the ligand transfer dynamics in the active site of CcO by molecular-dynamics simulations. The main difference with previous work (36) lies in the inclusion of a Morse potential for the binding of CO to Cu_B. Contrary to the case of CO binding to the heme Fe (spin change from S = 2 to S = 0), there is no spin change inherent to the Cu_B–CO bond formation. We therefore chose for the Cu_B–CO bond a Morse potential, E = D(e^{−2α(r−r₀)} − 2^{e−α(r−r₀)}), the simplest and most commonly used potential allowing binding and dissociation, where r is the Cu_B–C distance, r₀ its equilibrium value, −D the potential energy at r = r₀, and α the anharmonicity parameter given by the equation $\omega =\alpha \sqrt{2D/\mu }$ with ω the Cu_B–C vibrational frequency and μ the reduced mass of the Cu_B–C vibrator. The parameters of the Morse potential were chosen as follows: density-functional theory calculations including CO bound to Cu_B⁺ coordinated with three imidazole rings representing the three histidine residues bound to Cu_B⁺ gave an r₀ of 1.87 Å and a vibrational frequency of 379 cm⁻¹ (C. Meier and M.-C. Heitz, personal communication). This r₀ value is in good agreement with experimental data on Cu⁺–CO-containing molecules (37, 38). The potential energy D is equal to the sum of the activation energy, determined from the temperature dependence of the rate of thermal dissociation of the Cu_B–CO bond to be ≈315 meV (39), and the ground-state vibrational energy of 23.5 meV, i.e., equal to 340 meV. Given the reduced mass of Cu–C, the anharmonicity parameter we used was 2.87 Å⁻¹.

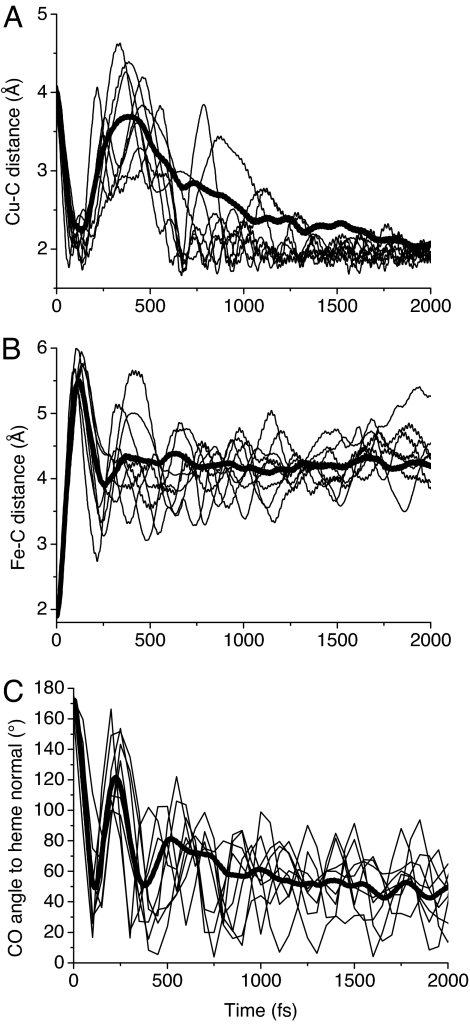
This Cu_B–C Morse potential allowed the simulation of CO binding to Cu_B [see supporting information (SI) Movie 1]. Fig. 5 shows the Cu_B–C (A) and the Fe–C (B) distance and the angle between CO and the normal to the heme plane (C) as a function of time after CO photodissociation at t = 0 for 8 trajectories as well as the mean of 30 trajectories. These trajectories show that the CO molecule moves away from the Fe toward the Cu_B within ≈100 fs and then bounces off the atoms surrounding Cu_B, losing part of its kinetic energy, and reapproaches to form a bond at times varying from 500 to 2,000 fs (Fig. 5 A and B). Interestingly, there is no clear correlation between the initial kinetic energy of CO and the bond formation time with Cu_B.

Fig. 5.

Time evolution, after CO dissociation at t = 0, of the distance between the Cu_B and the CO carbon atom (A), the distance between the Fe and the CO carbon atom (B), and the angle formed by the CO and the normal to the heme a₃ plane (C). Eight individual trajectories (thin lines) as well as the average (thick lines) of 30 trajectories calculated for different initial conditions are shown.

The main features of the simulated trajectories are in agreement with the experimental dynamics. During the first hundreds of fs, the various trajectories show a similar behavior indicating a ballistic process with almost no CO molecules binding to Cu_B before 500 fs. Similarly, in the experiment no Cu_B–CO signal appears before 300 fs. The various CO molecules then reach the final Cu_B–C distance of 1.9 Å after a time ranging from 500 to 2,000 fs, suggestive of the exponential rise observed in the experiment.

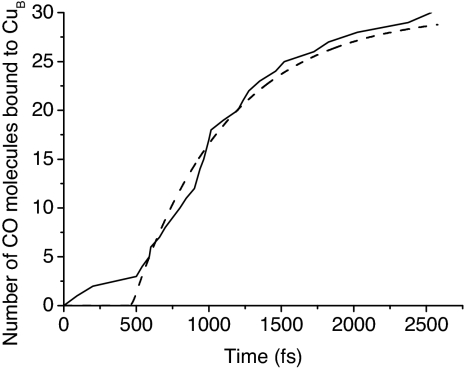
To quantify the arrival time distribution in the simulated trajectories, we considered that a CO molecule is bound to Cu_B at the time after which the sum of the kinetic energy of the CO center of mass and the potential energy in the Morse potential remains negative. We then generated a figure simulating the signal produced at 2,064 cm⁻¹ by these 30 trajectories by plotting the number of Cu_B-bound CO molecules as a function of time (Fig. 6). Similar results were obtained with a distance criterion considering that a CO molecule is bound to Cu_B at the time after which the Cu_B–C distance remains <2.8 Å (150% of its bound equilibrium value). Fig. 6 shows the same characteristics as the experiment: delayed onset, followed by an exponential rise, and can be fitted by an exponential delayed by 470 fs with a characteristic time of 660 fs. This analysis confirms the presence of both ballistic and diffusive contributions.

Fig. 6.

Number of Cu_B-bound CO molecules as a function of time after CO dissociation from the heme Fe. The dashed line is a fit with an exponential delayed by 470 fs with a characteristic time of 660 fs.

The angle between CO and the heme normal shows similar features: a fast initial rotation from the initial angle of ≈160° to a value close to the final one within ≈100 fs, a rebound at ≈250 fs, followed by a weaker one. No potential was used in the simulations for the angle of Cu_B-bound CO. Nevertheless, the final angle reached by the trajectories is in agreement with the angle of 55° measured in ref. 4, indicating that the equilibrium angle is mainly determined by steric effects.

Further improvement of molecular-dynamics simulations will require density-functional theory calculations of the Cu_B–C potential energy surface and its angular dependence.

Discussion

The active site of heme–copper oxidases provides a unique opportunity to study an ultrafast and experimentally accessible ligand transfer reaction between two well defined binding sites within a protein. Previous suggestions of a ballistic contribution to the transfer process were based on indirect assessments (4, 25). By directly resolving the CO transfer dynamics, our results provide evidence for the presence of such a ballistic contribution to the transfer. This indicates an active site optimized for the ligand transfer from the heme Fe to Cu_B. The heme doming after ligand dissociation may play an important role in giving the CO molecule the necessary impulse and torque to move in the direction of Cu_B. In addition, the nonzero initial angle of CO with respect to the heme normal (4) may favor its rotation for ultrafast binding to Cu_B. Although the precise role of CO in CcO is currently unknown, it is tempting to conjecture that this optimized transfer has a protective role for the enzyme, given the fact that, after reaching Cu_B, the probability of CO rebinding to the heme Fe is extremely low compared with that of releasing it to the solvent (21).

Although the exponential distribution of CO arrival times at the Cu_B-binding site seems to indicate a diffusive component in the transfer process, this distribution may be due, at least partly, to the distribution of initial conditions (CO kinetic energy, CO angle with respect to the heme normal, and angle of the CO projection on the heme plane) as well as the distribution of the positions of the atoms surrounding Cu_B due to thermal fluctuations at room temperature. Indeed, a simple, purely ballistic, classical model considering free CO evolving in the attractive Morse potential of Cu_B taking into account a distribution of initial conditions also shows a delayed exponential behavior for the CO arrival time in the absence of any collisions. The main role of the protein in the transfer process thus appears to be to hold the two metal-binding sites of CO in position in close proximity to each other. Molecular-dynamics simulations, however, have shown that the active-site configuration and, in particular, the unusual Tyr–His bond delimiting the active site play an important role in maintaining the CO in the proximity of Cu_B (36).

Several open questions remain: is free CO formed in the transfer process? Experiments at the “free” CO frequency of 2,130 cm⁻¹ would help to answer this question, but even if free CO exists, it will persist for only a very short time, and its spectrum will therefore be broadened and very difficult to detect. Experiments with further improved signal-to-noise ratio should allow a more precise determination of the Cu_B–CO vibrational frequency and thus possibly a confirmation of a vibrational frequency increase during the transfer process indicating an absence of free CO, as discussed above. Is there a stepwise population of the Cu_B–CO state as was deduced from the fs pump-probe data in the visible (25)? The signal-to-noise ratio is currently not sufficient to answer this question in a more direct way, although the experimental data do indicate a small plateau between 700 and 900 fs.

Conclusions

We have directly observed, with fs resolution, the transfer of the ligand CO in the bimetallic active site of CcO from the heme Fe to Cu_B using the ligand's vibrational signature. The transfer process shows an onset delayed by 200 fs, indicating a ballistic contribution followed by an exponential behavior with a characteristic time of 450 fs. Beyond suggesting a possible protective role for the enzyme, these results may have far reaching implications for understanding the mechanisms of short-distance ligand shuttling reactions in proteins in general. Indeed, the CO transfer from the heme Fe to Cu_B can be seen as a model system for such processes. The rapidity of the process suggests that the protein environment surrounding the CO molecule and the two binding sites plays an important role in the efficiency of the transfer process.

Our pump-probe results were obtained by using chirped-pulse upconversion detection of the mid-IR probe that offers a promising alternative to existing techniques. Indeed, spectral resolution and noise levels compare favorably with those obtained with HgCdTe detector arrays. In particular, high spectral resolution over a range limited solely by the probe width (200 cm⁻¹ in our case) is possible. Our upconversion method with an intense 800-nm beam benefits from the high quantum yield and low-noise characteristics of CCD detectors that are especially important for weakly transmitting samples where the IR photon number is limited. These results thus open the way for the application of the chirped-pulse upconversion technique to a large variety of proteins and ligands and mid-IR experiments in general.

Materials and Methods

Experimental Setup.

A 1-kHz, 100-fs, 550-μJ, regenerative amplifier (Hurricane; Spectra Physics, Mountain View, CA) is used to pump a white-light continuum-seeded double-pass optical parametric amplifier (OPA). The signal and idler output at 1.4 and 1.9 μm, respectively, are then focused onto a 1-mm GaSe crystal to yield a 1-μJ mid-IR probe at ≈5 μm by difference-frequency mixing. A 300-nJ, 400-nm pump beam is obtained by frequency doubling in a 0.5-mm, type-I β barium borate (BBO) crystal of a portion of the 800-nm amplifier output. Pump and probe beams are focused slightly noncollinearly to 90 μm at the sample. The transmitted mid-IR pulses are then focused onto a 425-μm MgO:LiNbO₃ (5% MgO, θ = 46°, type I) crystal together with a chirped, 150-ps, 800-nm pulse for upconversion toward the visible (≈700 nm) by noncollinear sum-frequency mixing. The visible upconverted pulse is dispersed by a 600-groove/mm grating in a 0.46-m spectrometer (SPEX HR 460) and detected with a 1,340 × 100 pixel, back-illuminated silicon CCD camera with 16-bit, 2-MHz analog-to-digital conversion (Princeton Instruments, Trenton, NJ).

An important improvement with respect to ref. 15 concerns detection at a 1-kHz rate and pump chopping at 500 Hz achieved by limiting the active CCD chip to 20 lines instead of 100 by vertical binning of all lines and by transferring the read-out spectra to the LabVIEW acquisition program by groups of 100 individual spectra packaged in “virtual” images of 1.340 × 100 pixels by using a custom LabVIEW driver (SITK for Lab, VIEW, R-Cubed).

We used a Kr spectral lamp for the spectrometer frequency calibration in the visible. The offset between the visible and mid-IR frequency was determined from the well known vibrational absorption of carbonmonoxy myoglobin (MbCO) at 1,945 cm⁻¹ by using a 10-mM, 200-μm-thick sample mounted between 2-mm CaF₂ windows of identical thickness to those used for the CcO sample. This allows the determination of the exact frequency value (precision 1 cm⁻¹) involved in the upconversion process that remains valid as long as no change of the mid-IR/chirped-pulse path length difference takes place. Based on the MbCO frequency shift in the visible as a function of the delay introduced in the chirped-pulse path length, we measured the second derivative of the spectral phase to be equal to 5.47 × 10⁶ fs² and deduced a spectral resolution of 1.6 cm⁻¹. This spectral resolution is currently limited by the upconversion pulse chirp and not by the spectrometer resolution (1.4 cm⁻¹ in this spectral range) but can be further improved by using correction techniques.

The pump-induced, instantaneous free-carrier absorption in GaAs placed behind a 2-mm CaF₂ window was used for determining the pump-probe zero delay (precision: ±50 fs) and the instrument response function (300-fs width). The zero delay is given for 2,064 cm⁻¹ and changes only slightly throughout the probe spectrum (−20 fs shift at 1,963 cm⁻¹). The probe (pump) duration was 170 (250) fs. We avoided excitation of the same spot by subsequent pump pulses and heating effects by rotating the sample. The pump polarization was set to 54.7° with respect to the probe polarization to avoid photoselection effects. The percentage of photodissociated molecules was estimated to be 14%. The differential transmission spectra were obtained on a pulse-to-pulse basis by taking the difference between spectra of consecutive transmitted probe pulses in the presence and the absence of the pump.

Sample Preparation.

CcO was isolated from the mitochondria of beef heart (INRA; Theix/Clermont–Ferrand, France) by using the protocol of ref. 40, with minor modifications as described in ref. 41, and suspended in a 50 mM Tris·HCl, 0.1% β-DM (pH 7.6) D₂O buffer. The protein solution was then concentrated up to 500 μM by using centrifugation in cellulose-membrane, 100-kDa concentrators (Amicon Ultra-4; Millipore, Billerica, MA). The sample was subsequently degassed, reduced with an excess of dithionite, and exposed to 1 atm CO for 10 min. One hundred microliters was then placed between two 2-mm CaF₂ windows with a 200-μm spacer. The final H₂O concentration was estimated from steady-state IR transmission spectra to be 30% because of D₂O–H₂O exchange with ambient water molecules and H₂O inside the protein molecules that are not efficiently substituted.

Molecular-Dynamics Simulations.

Simulations of the CO dissociation from heme a₃ were performed by using the molecular-modeling program CHARMM (42) and the CHARMM22 force field (43). Because of its smaller size, we constructed, as described (36), a model of the Paracoccus denitrificans CcO, whose subunits I, II, and III show a high degree of homology with those of beef heart CcO. Briefly, we use the PDB (44) file code 1AR1 (19) to generate a model with 531 residues of subunit I, 256 residues of subunit II, 2 hemes (a and a₃), 3 copper, 1 magnesium, and 1 calcium atom, 1 CO ligand, 44 structural water molecules, 14 phosphatidylcholine molecules, and 1,189 additional water molecules. A covalent bond was added between His-276 Nε₂ and Tyr-280 Cε₂.

A time integration step of 1 fs was used, and the nonbonded interactions were gradually switched to zero between 8 and 14 Å. The structure was heated to 300 K and equilibrated for 250 ps, and several free-dynamics runs were performed to obtain different CO dissociation initial conditions.

We used the sudden approximation (45) to simulate the CO dissociation and a Morse potential to simulate the CO binding to Cu_B. A CO dissociation simulation is started by deleting the Fe–C bond, switching to deoxy-heme parameters and to a three-site charge CO model, introducing the Cu_B–C Morse potential, and canceling nonbonded interactions between the C ligand atom and the Cu_B site (the Cu_B atom and the three imidazole rings of the histidine Cu_B ligands). Fe, Cu_B, C, and O coordinates were saved each femtosecond, and entire model coordinates were saved each 50 fs.

Abbreviation

CcO

cytochrome c oxidase.