Computer-Assisted Measurement of Vessel Shape from 3T Magnetic Resonance Angiography of Mouse Brain

Abstract

Blood vessel morphology (vessel radius, branching pattern, and tortuosity) is altered by a multitude of diseases. Although murine models of human pathology are important to the investigation of many diseases, there are few publications that address quantitative measurements of murine vascular morphology. This report outlines methods of imaging mice in vivo using magnetic resonance angiograms obtained on a clinical 3T unit, of defining mouse vasculature from these images, and of quantifying measures of vessel shape. We provide examples of both healthy and diseased vasculature and illustrate how the approach can be used to assess pathology both visually and quantitatively. The method is amenable to the assessment of many diseases in both human beings and mice.

1. Introduction

Blood vessels surround and permeate mammalian organs. Almost every disease from cancer to the common cold thus affects vessel attributes. These attributes include not only vessel number but also vessel morphological measures such as radius, tortuosity, and branching pattern. Primary vascular diseases such as stroke, aneurysm, arteriovenous malformation, and Moya-Moya disease provide immediately obvious examples. Many other diseases also affect the vasculature, however. Cancer induces new vessel growth and is associated with abnormal vessel tortuosity [1, 2], diseases such as hypertension, diabetes, and autoimmune disorders produce vessel narrowing and an increase in vessel tortuosity [3, 4], vasopasm and many vasculopathies alter vessel radius [5], infection induces angiogenesis [6], and even the common cold produces vasodilation [7]. Automated, quantitative measurement of three-dimensional (3D) vessel attributes as defined from high resolution, magnetic resonance (MR) images thus provides a new method of evaluating many diseases.

Despite the emerging importance of murine models to the study of disease, relatively little has been published on the quantitative analysis of murine vascular morphology. This report describes methods of acquiring magnetic resonance angiograms (MRA) of mouse brain in vivo using a clinical 3T MR unit. This report also describes methods of computer-assisted quantification of vessel number and shape from these images. Although our own work has concentrated primarily upon the assessment of cancer-associated vessel tortuosity [8, 9], the general approach is immediately applicable to the noninvasive evaluation of stroke, vasospasm, diabetes, and the plethora of other diseases that affect blood vessels. Since the imaging method is non-invasive, it can also be used to image an individual subject over time.

2. Description of method

2.1 Image acquisition All protocols were approved by our Institutional Animal Care and Use Committee. In order to ensure that animals remain motionless during image acquisition, isoflurane (2% induction and 1% maintenance) is used throughout the imaging procedure. Two advantages of isoflurane are that anesthetic depth is readily maintained and that animals recover rapidly once the agent is discontinued. Isoflurane is delivered through a nose cone which fits snugly with the small animal MR coil (described below) to further minimize animal motion.

Images are acquired in the coronal plane on a Siemens 3T Allegra head only scanner (Siemens Medical Inc., Erlangen, Germany) with a maximum gradient strength of 40 mT/m and a slew rate of 400 mT/m/msec. Since the scanner is a clinical scanner rather than a dedicated small animal MR scanner, a custom-made, birdcage, volume transmit/receive coil measuring 2.1 cm in diameter is utilized. This coil surrounds the mouse’s head and does not require fixation to the mouse’s skull or skin. Mice are anesthetized prior to placement of the coil.

Images are acquired using high-resolution, time-of-flight MRA without injection of gadolinium. Velocity compensation along both the slice select and frequency encoding directs is used to minimize intravoxel dephasing. In addition, in order to minimize spin saturation and to improve vascular visualization, a long TR (53 msec) is used. A FOV of 30 mm² with a matrix size of 256×256 and a slice thickness of 0.1 mm provide an isotropic voxel size of 0.1×0.1×0.1mm³. Two averages are used to improve signal-to-noise ratio which lead to a total data acquisition time of 23 min and 11 sec while also permitting coverage of the entire brain.

Figure 1 illustrates both a coronal section of a murine MRA and a volume rendering of that mouse’s brain. This mouse represents an example of a healthy control animal.

Figure 1.

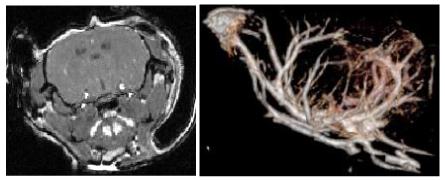
Murine MRA. Left: typical coronal section through the brain of a healthy mouse. Right: volume rendering of the brain shown from a lateral point of view (the mouse’s nose is to the left). The image was produced using VolView (Kitware, Inc, Clifton Park, NY). The images are noisy, making it difficult to separate small vessels from brain using intensity windowing alone; no vessel segmentation was employed in these images.

2.1 Vessel extraction and vessel tree formation

One of the difficulties in defining detailed vessel trees from MRA images is that MRA images are noisy (see Figures 1 and 2). We handle this problem both by the vessel extraction method itself and by a post-processing step.

Figure 2.

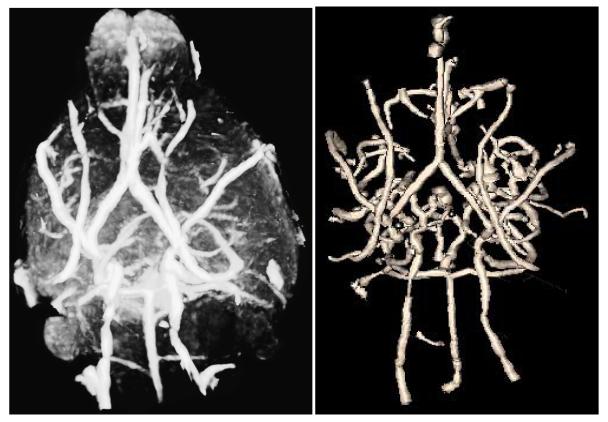
Maximum intensity projection (MIP) (left) and segmented vessels (right) from the same mouse shown in Figure 1 and as seen from a base view. The MIP image was produced using VolView (Kitware, Inc, Clifton Park, NY)

Vessel extraction is performed by the method of Aylward [10]. Segmentation of each vessel begins from a seed point. The method then automatically tracks the image intensity ridge representing the vessel skeleton in 3D, using dynamic scaling and automated calculation of vessel width at each skeleton point. Since the method extracts only objects approximately circular in cross-section, it resists inclusion of non-vessel objects. The output of the program is a set of directed, 4-dimensional points indicating the (x,y,z) spatial position of each sequential vessel skeleton point with an associated radius at each point. Each vessel skeleton is defined as a spline, subsequently sampled at regularly spaced intervals. We have experimented with sampling rates using synthetic data, and find that for tortuosity evaluation a sampling distance of one voxel allows adequate estimation of arc length while avoiding noise that can appear with sub-voxel sampling [11]. It takes 15-20 minutes to define vessels within the murine brain. Figure 2 illustrates a maximum intensity projection (MIP) of the same mouse shown in Figure 1 and the set of vessels segmented from that mouse.

The output of the vessel segmentation program provides a detailed but disconnected set of vessels, each of whose directions (from the first point to the last) may or may not correctly indicate the direction of blood flow within that vessel. The segmentation may also contain veins and portions of the extracranial vasculature. We therefore post-process the initial segmentation to produce a set of connected vessel trees. The method requires the user to define one or more roots; for the brain, roots are manually defined as the two carotid arteries and the basilar artery. The program then automatically calculates parent-child relationships on the basis of distance and the existence of supporting image intensity information using a modified minimum spanning tree algorithm [12]. If the connection distance is too large or if the image intensity data does not support the connection, the potential child vessel is discarded. Only bifurcations are allowed; “X” connections are not permitted. This process automatically discards most venous structures as well as most spurious “vessels” representing short lengths of image noise while also correctly including small connected vessels of one voxel diameter [12]. It takes about a minute to perform this post-processing step.

In this report, we use the term “vessel” to describe a single, unbranched structure that can be modeled as a curving tube of variable radius in three-dimensional space. An individual vessel can be long and can proceed past multiple branch points. At each such branch point, the path not taken is defined as a new vessel.

Figure 3 illustrates a set of vessel trees defined from the same healthy mouse shown in Figures 1-2. Connected circulatory groups are color-coded, with the anterior cerebral circulation shown in red, the left carotid and left middle cerebral circulation in green, the right carotid and right middle cerebral circulation in blue, and the basilar circulation in gold.

Figure 3.

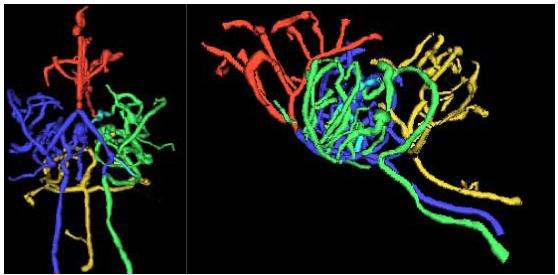
Segmented vessel trees shown from a base (left) and lateral (right) point of view.

2.2 Calculation of vessel attributes

Once a set of connected vessels has been mathematically defined, it is possible to calculate many shape measurements over an arbitrarily selected subset of these vessels. Vessel attributes can be calculated for an individual vessel, for a subtree of vessels, for vessels clipped to a region of interest, or for the entire set of extracted vessels. This paper describes four attributes that seem useful when assessing pathology regardless of the vessel subset employed. These attributes include vessel number, vessel radius, vessel tortuosity as measured by the “Sum of Angles Metric” (SOAM), and vessel tortuosity as measured by the “Inflection Count Metric” (ICM). Each measurement is discussed individually below. Table 1 provides the means and standard deviations of radius, SOAM, and ICM values for 6 major named arteries (the two carotid arteries, the basilar artery, the two middle cerebral arteries, and the paired anterior cerebral arteries extracted as a single entity) defined from 10 healthy mice. These individual vessel examples were selected as major named arteries that can be defined readily across animals. An example of pathology against which to compare healthy values is given later.

Table 1.

Means and standard deviations for the average radius (AVRAD) in mm, tortuosity as measured by the Sum of Angles Metric (SOAM) in radians/mm, and tortuosity as measured by the Inflection Count Metric (ICM) as a dimensionless number for the left carotid (LCar), right carotid (RCar), basilar, left middle cerebral artery (LMCer), right middle cerebral artery (RMCer), and anterior cerebral arteries (Ant Cer) for 10 healthy mice.

	AVRAD	SOAM	ICM
LCar	0.14 ± 0.02	10.28 ± 2.51	3.34 ± 1.25
RCar	0.13 ± 0.02	8.56 ± 3.26	2.56 ± 3.26
Basilar	0.13 ± 0.01	10.50 ± 2.47	4.08 ± 1.78
LMCer	0.10 ± 0.01	12.18 ± 4.87	2.76 ± 1.24
RMCer	0.10 ± 0.01	11.04 ± 3.40	3.43 ± 1.90
AntCer	0.10 ± 0.01	13.42 ± 1.99	6.11 ± 3.33

2.2.1 Vessel number

Vessel number is the number of extracted vessels comprising a designated subtree, lying within and clipped to a region of interest, or as counted within the entire brain. The number is always an integer. For 10 healthy mice examined at the MRA resolution described here, the number of segmented vessels comprising all intracerebral vessel trees was 90.2 ± 19.07.

2.2.2 Average vessel radius

Average vessel radius is calculated for each vessel by summing the radius defined at each vessel skeleton point and by dividing by the number of points. Results are provided in mm. Table 1 provides the average radius for six major named vessels as defined from ten healthy animals. As appropriate, the radii of the extracted carotid and basilar arteries are larger than the radii of child branches. At the MR resolution employed, we are rarely able to separate the paired and closely juxtaposed anterior cerebral arteries from each other. These paired arteries are therefore usually defined together as a group.

As shown by Table 1, the largest vessels in our MRA images of the brain tend to be the carotid arteries, which have an average radius slightly less than 0.15 mm. The smallest vessels defined in these murine MRA studies have a radius of 0.05 mm (a diameter of 100 microns). These are the smallest vessels we can define using MRA images of voxel size 100 × 100 × 100 μm² because of the resolution limits of the image data.

2.2.3 Tortuosity as measured by SOAM

The term “abnormal tortuosity” as used by clinicians can apply to more than one type of vessel shape abnormality [11]. We therefore employ two different tortuosity metrics that can be used in isolation or in weighted combination to assess different disease states [8, 9, 10].

Tortuosity as measured by the “Sum of Angles Metric” (SOAM) calculates for each vessel the angle between the vector pair defined by each successive trio of ordered, equally spaced, vessel skeleton points. Such angles are then summed along each vessel and normalized by dividing by the total path length [11]. Results in this paper are represented in radians/mm. Table 1 illustrates SOAM values for six major named vessels extracted from ten healthy mice.

More specifically, the method of determining the angle ϕ between a trio of consecutive, equally spaced, three-dimensional points indicating the position of the vessel skeleton is as follows:

1. Name the three ordered skeleton points X, Y, and Z

2. Define the two vectors Y - X and Z - Y

3. Normalize each vector

4. The cosine of ϕ is the dot product of the two vectors.

The metric as currently employed does not incorporate torsion (the out-of-plane angle made by a space curve when considering successive quartets rather than trios of points). Although torsion can be readily incorporated into the equation [11], we have not found this addition to be useful when comparing healthy to diseased subjects since the inclusion of the additional derivative appears to add noise.

In general, SOAM is high when a curve exhibits high curvature over a short distance. Figure 4 illustrates a vessel extraction from a genetically engineered mouse with cancer (choroid plexus carcinoma; genetic engineering details are provided under [13]). One of the features of cancer-associated vasculature is development of “many smaller bends upon each larger bend” [2, 8]. SOAM tortuosity assessment captures the smaller bends. In Figure 4, arrows point to two of m any examples of vessels with grossly elevated SOAM values. The SOAM value for the first vessel is 35.5 and for the second 28.2, each many standard deviations above the healthy vessel norms outlined in Table 1. This type of high-frequency, low-amplitude tortuosity abnormality appears in cancer-associated vessels in both mice and human beings [2, 8, 9].

Figure 4.

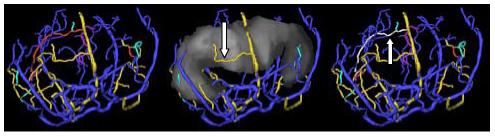
Vasculature associated with a murine carcinoma shown from an AP view. Left: Vessels segmented from brain with the same color-coding by anatomical grouping as in Figure 2. Center: The ventricular region of interest (grey) is shown together with the vessels. The vessel color coding in this and the next panel has changed to indicate relationship to the surface of the region of interest, with red vessels lying inside, gold vessels traversing, cyan vessels exiting, purple vessels entering, and blue vessels outside the region of interest. The distinction between entering and exiting vessels is enabled by the vessel tree structure. An arrow points to an obvious example of an abnormal traversing vessel (gold) with high curvature per unit distance (high tortuosity by SOAM). Right: The ventricular region is hidden; vessel color coding is the same as in the central panel except that a particular vessel of interest is colored white to make it easier to see.. An arrow points to a second example of an overtly abnormal vessel (colored white) with high-frequency, low-amplitude “wiggles” producing a high tortuosity value by SOAM.

2.2.4 Tortuosity as measured by ICM

Tortuosity as measured by the “Inflection Count Metric” (ICM) multiples the number of a space curve’s “inflection points” by the total curve length and divides by the distance between curve endpoints [11]. This approach enhances the sensitivity of the traditional Distance Metric (which divides the total curve length by the distance between endpoints) to determine not only how far a curve deviates from straight but also to provide a higher value if the curve frequently changes direction. In general, elevated ICM values are associated with long vessels that exhibit high-amplitude, undulating paths.

The number of “inflection points” is determined by using a Frenet frame and by counting the number of times (plus one) the Frenet normal axis rotates close to 180 degrees [11]. More specifically, for the consecutive, three-dimensional skeleton points X, Y, Z

1. Define vector T1 as Y - X and vector T2 as Z - Y

2. Define the velocity vector V at point Y as Z - X

3. Define the acceleration vector A at point Y as T2 - T1

4. The three axes of the Frenet frame (T, N, and B) can then be calculated at point Y as

   $$\mathbf{T}=\mathbf{V}∕\mid \mathbf{V}\mid$$

   $$\mathbf{N}=\mathbf{V}\times \mathbf{A}\times \mathbf{V}∕\mid \mathbf{V}\times \mathbf{A}\times \mathbf{V}\mid$$

   $$\mathbf{B}=\mathbf{T}\times \mathbf{N}$$

5. Passage through an inflection point is recognized by searching for local maxima of ΔN•ΔN when ΔN•ΔN is greater than 1.0.

One problem with the Frenet frame is that it is undefined whenever the acceleration vector has no length, as occurs at inflection points or during passage over a straight line. We handle this problem by checking the length of the acceleration vector, and if this length is less than 10^-6 mm we simply skip the point and redefine the frame at the next vessel point [11].

The anterior cerebral arteries in the mouse tend to have relatively high ICM values as compared to the carotid, basilar, and middle cerebral arteries since the anterior cerebral vessels possess relatively high-amplitude, undulating curves (Table 1). An example of a vessel with a pathologically elevated ICM value in a mouse with cancer is illustrated in the right panel of Figure 4 (the vessel is white and is pointed to with an arrow; ICM is 12.5 for this vessel).

Concluding remarks

This paper describes methods of imaging mouse brain vasculature in vivo on a clinical 3T MR unit and of quantifying several measures of vascular morphology. We provide examples of differing radius and tortuosity values for six major named vessels as assessed across 10 healthy animals and outline tortuosity differences between healthy and cancer-associated vasculature.

The MR images employed in this report were acquired on a 3T head-only scanner. Similar murine images could be similarly acquired on a 3T whole body scanner as long as the small animal receiving coil continued to be employed. With the exception of the small animal coil (birdcage volume transmit/receive coil), no special hardware is needed. It would also be feasible to obtain the same studies on a 1.5T unit. However, the signal to noise ratio of images acquired at 3T is approximately twice that of images obtained at 1.5T. Acquisition time on a 1.5T unit would thus be about four times longer if one wished to obtain the same signal to noise ratio for the images shown here.

A limitation of the described method is that vessel segmentation is limited by the voxel acquisition size. Nevertheless, given 100×100×100 μm³ voxels, the method can discriminate between healthy and pathological vessels of radius 50u or more throughout the mouse brain. In a study of emerging malignancy in mice, this resolution level was sufficient to define emerging cancers as malignant on the basis of vessel shape once the cancer had reached a volume of 1 mm³ or greater [9]. Image acquisition time is less than 25 minutes on a 3T unit. Vessel segmentation requires approximately 20 minutes, and, if no registration is required, the entire image processing time is less than 30 minutes.

The particular segmentation method described in this report is effective in extracting small vessels from noisy images. It is thus well-suited to defining detailed vessel trees and to analyzing large vessel populations that include small branches visualized during image acquisition. Since the method assumes that vessels are approximately circular in cross-section, however, it is much less useful when attempting to detail irregularities of the vessel lumen, as may be important to the analysis of atherosclerotic plaque or of asymmetrical aneurysms. Alternative vessel segmentation approaches are likely to be preferable for these types of applications. Our vessel segmentation and tree formation programs are freely available on request, however, to those interested in using them for research purposes.

One area for future extension is the mathematical description of vessel morphological measures. The four vessel attributes described here (vessel number, radius, and two tortuosity measures) represent only a few of the many possible vessel attribute descriptions. This report does not consider branching pattern (as might be useful in the analysis of stroke), nor does it consider irregularities of radius (as might be useful in assessing the “beading” associated with vasculopathies). The image processing approach described in this report is arbitrarily extensible to many other types of vessel morphological analyses.