Simulating replica exchange simulations of protein folding with a kinetic network model

Abstract

Replica exchange (RE) is a generalized ensemble simulation method for accelerating the exploration of free-energy landscapes, which define many challenging problems in computational biophysics, including protein folding and binding. Although temperature RE (T-RE) is a parallel simulation technique whose implementation is relatively straightforward, kinetics and the approach to equilibrium in the T-RE ensemble are very complicated; there is much to learn about how to best employ T-RE to protein folding and binding problems. We have constructed a kinetic network model for RE studies of protein folding and used this reduced model to carry out “simulations of simulations” to analyze how the underlying temperature dependence of the conformational kinetics and the basic parameters of RE (e.g., the number of replicas, the RE rate, and the temperature spacing) all interact to affect the number of folding transitions observed. When protein folding follows anti-Arrhenius kinetics, we observe a speed limit for the number of folding transitions observed at the low temperature of interest, which depends on the maximum of the harmonic mean of the folding and unfolding transition rates at high temperature. The results shown here for the network RE model suggest ways to improve atomic-level RE simulations such as the use of “training” simulations to explore some aspects of the temperature dependence for folding of the atomic-level models before performing RE studies.

One of the key challenges in the computer simulation of proteins at the atomic level is the sampling of conformational space. The efficiency of many common sampling protocols, such as Monte Carlo (MC) and molecular dynamics (MD), is limited by the need to cross high free-energy barriers between conformational states and rugged energy landscapes. One class of methods for studying equilibrium properties of quasi-ergodic systems that has received a great deal of recent attention is based on the replica exchange (RE) algorithm (1, 2) (also known as parallel tempering). To accomplish barrier crossings, RE methods simulate a series of replicas over a range of temperatures. Periodically, coordinates are exchanged by using a Metropolis criterion (3) that ensures that at any given temperature a canonical distribution is realized. RE methods, particularly REMD (4), have become very popular for the study of protein biophysics, including peptide and protein folding (5, 6), aggregation (7–9), and protein–ligand interactions (10, 11). Previous studies of protein folding appear to show a significant increase in the number of reversible folding events in REMD simulations versus conventional MD (12, 13). Given the wide use of REMD, a better understanding of the RE algorithm and how it can be used most effectively for the study of protein folding and binding is of considerable interest.

The effectiveness of RE methods is determined by the number of temperatures (replicas) that are simulated, their range and spacing, the rate at which exchanges are attempted, and the kinetics of the system at each temperature. Although the determination of “optimal” Metropolis acceptance rates and temperature spacings has been the subject of various studies (2, 14–19), the role played by the intrinsic temperature-dependent conformational kinetics that is central to understanding RE has not received much attention. Recent work (19–22) recognizes the importance of exploration of conformational space and the crossing of barriers between conformational states as the key limiting factor for the RE algorithm. Molecular kinetics can have a strong effect on RE beyond the entropic effects that have been discussed (20, 22), particularly if the kinetics does not have simple temperature dependence. It is known from experimental and computational studies that the folding rates of proteins and peptides can exhibit anti-Arrhenius behavior, where the folding rate decreases with increasing temperature (23–28). Different models have been proposed to explain the physical origin of this effect (29, 30).

In this paper, we investigate the impact of simulation parameters and anti-Arrhenius kinetics on the RE method. Because RE simulations of protein systems that display anti-Arrhenius behavior are difficult to converge, we developed a network RE (NRE) model that allows us to simulate the RE algorithm of two-state protein folding. This network model reduces the atomic complexity of the system to a set of discrete conformational states that evolve in continuous time according to Markovian kinetics for both conformational transitions and exchange between replicas.

The NRE model studied here does not capture all of the complexities of the “real” molecular simulation because various kinds of non-Markovian behavior are not captured in the network model. However, it does capture some of the essential features of RE and allows us to study these fundamental aspects of the algorithm in a controlled setting and at low computational cost, which allows us to separate some of the interacting parameters and study their effects on the simulation individually. Many of the limitations in the convergence rates and efficiency observed with NRE also will be present in full atomic-level RE simulations, allowing us to identify promising avenues of inquiry for future atomic-level simulations.

Theory

The RE Method and the NRE Model.

In a standard RE simulation with M replicas corresponding to M inverse temperatures β_i = (k_BT_i)⁻¹ (β₁ > β₂ > … > β_M), the state of the extended ensemble is specified by a joint configuration of M replicas X = {x₁, x₂, …, x_M}, where x_i stands for the configuration of replica i. To simulate the extended ensemble, a propagation algorithm such as MC or constant-temperature MD is used to locally sample the conformational space within each replica, and exchanges of configurations between pairs of replicas, e.g., X = {…, x_i, …, x_j, …} → X′ = {…, x_j, …, x_i, …} are attempted periodically with an acceptance probability w(X → X′). For the equilibrium distribution to remain invariant with respect to these exchanges, it is sufficient to impose a detailed balance condition on the transition probability. For the potential energy function U(x), the appropriate transition probability is given by (4)

To isolate some of the essential features of the RE algorithm, we construct a kinetic NRE model, which we can use to study the effects of the parameters of the model on efficiency and convergence. We consider a system in which the configurational space can be partitioned into two macrostates of interest separated by a free-energy barrier that makes transitions between the conformations an activated process. Motivated by protein folding, we call these macrostates F and U (for “folded” and “unfolded”). Transitions between F and U in a (non-RE) MD or kinetic MC simulation can be approximated by a Poisson process in which the waiting times between folding and unfolding transition events are exponentially distributed random variables with means equal to the reciprocal of the folding or unfolding rates, respectively.

If the transition events are Markovian, then we can represent the simultaneous behavior of two noninteracting replicas in terms of the four composite states {F₁F₂, F₁U₂, U₁F₂, U₁U₂}. In each symbol, the first letter is the configuration of replica 1, the second letter is the configuration of replica 2, and the subscripts are the temperatures of each replica. Therefore, F₁U₂ represents the composite state that replica 1 at temperature T₁ is folded, while replica 2 at temperature T₂ is unfolded. The kinetics in the composite state space can be represented as a continuous-time Markov process with discrete states (31).

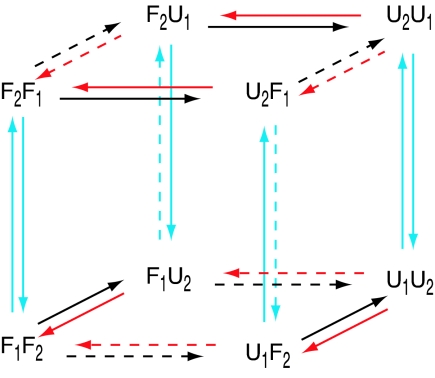
The four-state composite system corresponding to noninteracting replicas can be extended to create a discrete-state model of RE by introducing temperature exchanges between replicas. For example, suppose the current state is F₁U₂. After a successful temperature exchange, replica 1 is at T₂ and replica 2 is at T₁, thus the new state can be represented as F₂U₁. The introduction of temperature exchange therefore creates four additional states, leading to the eight-state system {F₁F₂, F₁U₂, U₁F₂, U₁U₂, F₂F₁, F₂U₁, U₂F₁, U₂U₁}. These states are arranged into two subnetworks defined by the “horizontal” folding and unfolding transitions, which are connected to each other by “vertical” temperature-exchange transitions, forming a cubic network (Fig. 1). In general, the network for an N-replica system consists of N! subnetworks, each of which has 2^N states connected by folding/unfolding transitions. The model description in this section will focus primarily on the two-replica case; all of the details can be generalized easily to the case of N replicas.

Fig. 1.

The kinetic network of the composite states corresponding to the simplified RE model with two replicas. The state labels represent the conformation (letter) and temperature (subscript) for each replica. For example, F₂U₁ represents the state in which replica 1 is folded and at temperature T₂ while replica 2 is unfolded and at temperature T₁. Red and black arrows correspond to folding and unfolding transitions, respectively, and the temperature at which the transition occurs is indicated by the solid and dashed lines (for T₂ and T₁, respectively). The cyan arrows correspond to temperature-exchange transitions, with the solid and dashed cyan lines denoting transitions with rate parameters α and wα, respectively.

We require that the equilibrium populations of the states be such that the canonical ensemble is recovered at each temperature. This is the case if the equilibrium populations are proportional to the product of the equilibrium populations for the two-state systems, e.g.,

where the factor of 1/2 accounts for the presence of the two equivalent manifolds. For these probabilities to be preserved under temperature exchanges, it is sufficient that detailed balance is satisfied, e.g., the transition probabilities w(F₁U₂ → F₂U₁) and w(F₂U₁ → F₁U₂) satisfy P_eq(F₁U₂)w(F₁U₂ → F₂U₁) = P_eq(F₂U₁)w(F₂U₁ → F₁U₂) or

If the equilibrium favors the folded state at T₁ and the unfolded state at T₂, then w < 1. The ratios of forward and reverse transition probabilities for F₁F₂ ⇌ F₂F₁ and U₁U₂ ⇌ U₂U₁ are equal to one because interchange of temperatures does not change the equilibrium populations.

In atomic-level RE simulations, temperature-exchange attempts usually are made periodically in time, i.e., the MC or MD evolution is interrupted, temperature swap proposal(s) are made, and the proposals are either accepted or rejected (4, 6). In keeping with the continuous-time nature of our network model, we simulate the effect of temperature exchanges by introducing an additional rate parameter α, which controls the overall scaling of the temperature-exchange rate relative to the folding and unfolding rates. We set the forward and reverse rates of the F₁F₂ ⇌ F₂F₁ and U₁U₂ ⇌ U₂U₁ “reactions” equal to α, while the other rates are set to α or wα (Fig. 1) as required by detailed balance (Eq. 2), and where we choose w < 1. For example, the states U₁F₂ and U₂F₁ differ in population, with U₂F₁ being more populated if the equilibrium favors the folded state at T₁ and the unfolded state at T₂. We therefore set the U₁F₂ → U₂F₁ “reaction rate” equal to α and the reverse rate equal to wα, where w is defined in Eq. 2.

The NRE model can be simulated by using a standard method for continuous-time Markov processes with discrete states (31), also known as the “Gillespie algorithm.” The algorithm remains efficient even when the number of replicas is large (e.g., 20 replicas, corresponding to 10²⁴ states) because of the fact that each state is connected to a small number of neighboring states (those connected by single temperature exchanges involving neighboring temperatures and folding/unfolding transitions of each replica).

The convergence or efficiency of a simulation is monitored by measuring N_TE(τ∣T₁), the number of “round-trip” transitions between the U and F states, conditional on the temperature of interest T₁ that occurs in a given observation time τ. In the context of the network model, suppose that we follow replica 1, and at a given time the system is in a state where that replica is folded at temperature T₁ (e.g., F₁F₂). We then wait for the first occurrence of a state in which replica 1 is unfolded at T₁ (e.g., U₁F₂) and then for the first occurrence of a state in which that replica is folded again at T₁ (e.g., F₁F₂). At this point, we say that a transition event has occurred. Conceptually, a transition event is a transit of a given replica from one conformation at low temperature to the other conformation at low temperature and back again regardless of route, i.e., whether it was the result of a direct barrier crossing at T₁ or indirectly via a barrier crossing at T₂ combined with temperature exchanges. The number of transitions as defined corresponds to the number of “reversible folding” events studied in all-atom simulations of peptide systems (12, 13).

Thermodynamic Model for Anti-Arrhenius Behavior.

The Arrhenius equation relates a reaction rate k to the temperature:

where ΔG^†(T) is the free energy of activation. The temperature dependence of the reaction rate customarily is described by means of the Arrhenius plot, the plot of ln k(T) with respect to 1/T. The slope of ln k(T) in the Arrhenius plot is proportional to the activation energy, ΔE^†(T), at temperature T. When the activation energy is temperature-independent, the Arrhenius plot appears as a line of constant slope. Moreover, if the activation energy is positive, the reaction rate increases with increasing temperature. This behavior is referred to as normal Arrhenius behavior. When the activation energy is negative, however, increasing the temperature causes the rate to decrease. This nonintuitive phenomenon sometimes observed in protein folding kinetics (23–28) is referred to as anti-Arrhenius behavior. In these circumstances, the transition state is energetically favored but entropically disfavored with respect to the reactants.

Often protein folding rates follow normal Arrhenius behavior at low temperatures, switching to anti-Arrhenius behavior at higher temperatures. This mixed behavior can be understood in terms of a constant activation heat-capacity model in which the activation energy and entropy vary linearly with respect to the temperature and its logarithm, respectively (24, 32):

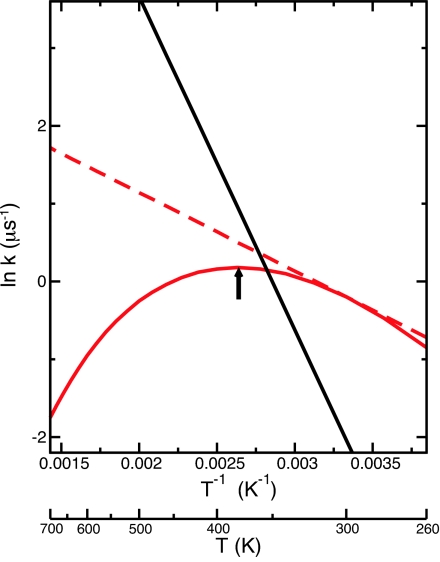
where ΔC_p^† < 0 is the activation heat capacity, which is assumed here to be independent of temperature. Summing Eqs. 4 and 5, we obtain the expression for ΔG^†(T) corresponding to this model. Shown in Fig. 2 are the Arrhenius plots for the unfolding and folding rates, k_u(T) and k_f (T), used in this work that result from inserting this expression in Eq. 3, setting ln A/s⁻¹ = 22, T₀ = 300 K, and ΔE^†(T₀), ΔS^†(T₀), and ΔC_p^† to be 2 kcal/mol, −0.01 kcal/mol·K, and −0.025 kcal/mol·K for folding, and 8.5 kcal/mol, 0.008 kcal/mol·K, and 0 kcal/mol·K for unfolding, respectively. For the case of Arrhenius folding (Fig. 2, dashed line), the parameters are identical with the exception that ΔC_p^† for folding is zero. The unfolding rate follows normal linear Arrhenius behavior, whereas the anti-Arrhenius folding rate decreases with increasing temperature above T* = 380 K (the temperature at which the activation energy for folding is zero and the folding rate is maximal). The general behavior of k_u(T) and k_f (T) shown in Fig. 2 is typical for experimentally determined peptide folding kinetic rates (23, 25, 28).

Fig. 2.

Arrhenius plot of the folding and unfolding rates from a thermodynamic model for the temperature dependence of protein folding rate constants. The black line corresponds to the unfolding rate, and the red lines correspond to the folding rates. The solid line is for the ΔC_p^† ≠ 0 case displaying anti-Arrhenius behavior, whereas the dashed line corresponds to the same parameters with ΔC_p^† = 0. The arrow indicates the temperature T* at which the folding rate is maximal (≈380 K).

Results

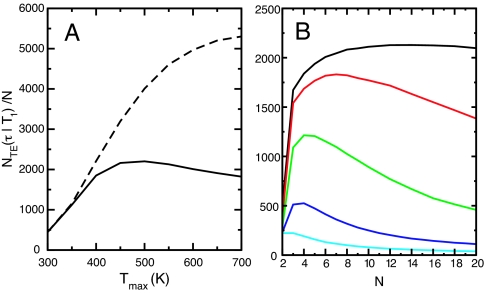
We have measured the number of conformational transitions for the NRE model by using both Arrhenius and anti-Arrhenius models for the folding and unfolding rates with various choices of the number of replicas, their temperatures, and the temperature-exchange rate parameter α. The goal of these calculations is to study factors that affect the increased efficiency that RE can provide. We define the efficiency in the context of NRE to be the total number of transitions divided by the number of replicas N_TE(τ∣T₁)/N. We make several general observations. First, increasing the total temperature range for a given number of replicas can degrade the efficiency of reversible folding if the kinetics is anti-Arrhenius (Fig. 3A). To understand this behavior, we first examine the behavior of NRE for the simple case of two replicas (N = 2), where the rate of temperature exchanges is large compared with the folding/unfolding kinetics. The condition that α be very large relative to the conformational kinetic rates simplifies the problem because in that limit the behavior is independent of the precise choice of α and depends on the (temperature-dependent) folding and unfolding rates. We fix T₁ at 300 K and sweep T₂ over the range 300 K to 700 K. In Fig. 4A, we show the dependence of N_TE(τ∣T₁) normalized by the number of replicas as a function of T₂ for the anti-Arrhenius kinetic model. We see that N_TE(τ∣T₁)/N is small at low and high T₂ and reaches a maximum near 440 K (Fig. 4A, solid black line).

Fig. 3.

Number of transition events in NRE simulations (normalized by the number of replicas) for various temperature ranges, exchange rates α, and number of replicas N. In all cases, the system was simulated for τ = 4 ms. For the simulations in A, α was set to 1,000 μs⁻¹, the dashed and solid lines correspond to Arrhenius and anti-Arrhenius kinetics, respectively, and six replicas were exponentially distributed between 300 K and T_max. The simulations in B were performed with anti-Arrhenius rates, N replicas exponentially distributed from 300 K to 700 K, and α values of 10,000 μs⁻¹ (black), 1,000 μs⁻¹ (red), 100 μs⁻¹ (green), 10 μs⁻¹ (blue), and 1 μs⁻¹ (cyan).

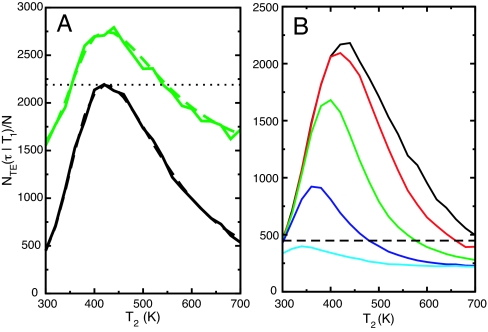
Fig. 4.

Number of transition events per replica in NRE simulations using the anti-Arrhenius folding rates for a simulation time τ = 4 ms conditional on temperature T₁ = 300 K, while T₂ is scanned from 300 K to 700 K. (A) Solid black and green lines show simulation results for two-replica and three-replica systems (with T₃ = 440 K), respectively. Dashed black and green lines show the number of transition events predicted by using the average of harmonic means for two and three replicas, respectively. All simulations were performed with α = 10 ns⁻¹. (B) Results for two-replica NRE simulations using the anti-Arrhenius folding rates and α values of 10 ns⁻¹ (solid black), 1 ns⁻¹ (red), 100 μs⁻¹ (green), 10 μs⁻¹ (blue), and 1 μs⁻¹ (cyan). The dashed black line corresponds to the predicted number of transitions for a single uncoupled simulation at T₁.

The number of transition events at the low temperature T₁ obtained by simulation in the large α limit is very well approximated by the average of the harmonic means of the folding and unfolding rates at both temperatures:

(Fig. 4A, dashed black line). For the uncoupled, non-RE case, the rate of transition events at each temperature is simply the harmonic mean of the rate constants. Therefore, our observation (Eq. 6) suggests that the number of transition events observed at the lowest temperature in the coupled RE case can be no larger than the number of transitions at an “optimum” temperature defined as that temperature for which the number of folding/unfolding transitions for the uncoupled system is maximized. Because the number of transitions for the uncoupled system is a harmonic mean of the rate constants, the overall convergence of NRE at low temperature is limited by the smallest rate at this optimum (higher) temperature.

Next, we examine how the number of replicas affects the convergence as monitored by the number of transition events. In Fig. 4A, we examine whether a third replica results in an improvement over the optimum behavior with two replicas by fixing T₁ at 300 K and T₃ at 440 K (the two-replica optimum) and scanning T₂ from 300 K to 700 K (i.e., we do not require T₁ < T₂ < T₃). We see in Fig. 4A (solid green line) that the number of transitions per replica again reaches a maximum near T₂ ≈ 440 K, corresponding to the case in which one replica is at the temperature of interest (300 K) and the other two are both placed at the “optimal” temperature of 440 K. As in the two-replica case, N_TE(τ∣T₁)/N is very well approximated by the average of the harmonic means of the rates at all three temperatures (Fig. 4A, dashed green line).

The relevant question is whether the addition of the third replica is an improvement over having two. It is important in this regard to distinguish the convergence rate from the computational efficiency of the simulation. In the cases seen in Fig. 4A, the total number of transition events (not normalized by the number of walkers) is larger for three replicas than the maximum total number of transition events for two replicas, and therefore we expect the convergence to be better. In general, adding an additional replica always will improve overall convergence, because the additional transition pathways opened up always will have a positive contribution to the total number of transition events. However, the computational efficiency of NRE as measured by N_TE(τ∣T₁)/N of the three-replica simulation is improved relative to the two-replica simulation only if the additional temperature T₂ has values between 350 K and 550 K (Fig. 4A, dotted black line). Although the addition of a replica always improves convergence, it improves efficiency only if the harmonic mean of the rates at the additional temperature is large relative to the harmonic means of the other replicas. If not, then the presence of the additional slow paths will reduce the efficiency. For the general case of NRE with N replicas, we expect that, in the large α limit, optimal efficiency (and convergence) will be obtained when one replica is at the temperature of interest and all of the other replicas are placed at the temperature that maximizes the harmonic mean of the folding and unfolding rates. Thus, the replica with the largest harmonic mean sets a “speed limit” for the amount of efficiency improvement that an RE simulation can have over an uncoupled simulation run for the same amount of CPU time. The addition of replica N + 1 will increase the efficiency only if the harmonic mean at the new temperature is greater than the average of the harmonic means of the original N replicas.

In the results described above, the rate of temperature exchanges is so large that convergence is limited only by the rates of conformational transitions at each temperature. When α is comparable to or smaller than the rates of conformational transitions, the waiting time for a temperature exchange to occur becomes comparable to or even larger than the timescale of configuration changes within each replica. Therefore, there can be multiple folding or unfolding events at higher temperatures before any of these events are transmitted to the temperature of interest. These events are “lost” and make no contribution to the number of transition events at low temperature. Therefore, in the NRE model (where conformational transitions are instantaneous and strictly Markovian), the optimal convergence (and efficiency) is achieved in the limit where α overwhelms the kinetic rates, and smaller values of α only degrade the performance of the algorithm. It should be noted that, because of non-Markovian effects present in real molecular systems, it may not be possible to achieve the large α limit in molecular RE simulations.

In Fig. 4B, we show the effect of α on the number of transition events per replica for two replicas as a function of the high temperature T₂. As expected, the number of transition events becomes smaller as α decreases. The drop in the number of events is most dramatic when α approaches the magnitude of the conformational transition rate constants (10–100 μs⁻¹). If we compare N_TE(τ∣T₁)/N with the expected number of transitions for a single-temperature simulation at T₁ (Fig. 4B, dashed line), we see that for some combinations of α and T₂ the efficiency of two-replica NRE is less than an uncoupled non-RE simulation, whereas for others the efficiency is improved.

The value of T₂ that maximizes the number of transition events also decreases as α decreases. This result arises because of a competition between the increase in the number of transition events at high temperature as T₂ approaches 440 K (the temperature at which the harmonic mean rate is maximized) and the decrease in the efficiency in transfer of those transitions to the low temperature by temperature exchanges caused by the decrease of w with increasing temperature gap. Thus, there is a temperature for which there is an optimal balance between the increasing number of conformational transition events at high temperature and the decreasing efficiency of transfer to low temperature. This optimum occurs when the two competing effects are of comparable magnitude, leading to a decrease in the optimum temperature as α decreases.

The finite-α behavior of NRE for many replicas is more complex because issues related to the size of the state space become important. Although in the limit of infinite α, any conformational transition in a replica at any temperature is “communicated” via rapid temperature exchanges to T₁ before the replica has had a chance to move back, this is not the case for finite α. The most apparent symptom of this is that a simulation with more replicas can be less efficient than one with fewer, which can be seen in Fig. 3B, where the insertion of additional replicas into a fixed temperature range can lead to a decrease in N_TE(τ∣T₁)/N. This result is related to the rapid increase in the combinatoric size of the NRE state space as N increases.

Conclusions

In this paper, we have used a kinetic NRE model to explore the effects of anti-Arrhenius behavior of the conformational kinetics on the convergence of RE protein folding simulations. We have constructed a NRE model inspired by protein folding and have studied its convergence behavior as a function of the number of replicas, their temperatures, the kinetics at each temperature, and the rate of temperature exchange. The number of folding transitions is used as an indicator for convergence. The results demonstrate that the convergence of NRE for a two-replica system in the limit of very rapid temperature exchanges is fastest when the high temperature is chosen to maximize the harmonic mean of the folding and unfolding rates. Additional replicas improve the efficiency in the NRE model only if the harmonic mean of the kinetic rates at the temperature of the additional replica is larger than the average of the harmonic means of the original set of replicas. Both the convergence rate and efficiency are reduced if the temperature-exchange rate is finite, and the optimal temperature of the high temperature is reduced.

The conclusions obtained here are based on the behavior of a simplified NRE model, which is completely Markovian. More of the characteristics of molecular RE could be incorporated into the NRE model to enhance its realism. For example, continuous energy distributions could be used to simulate the effects of energy-distribution overlaps. Non-Markovian effects, such as nonexponential waiting time distributions also could be modeled, either directly or by dividing the F and U macrostates into “hidden” microstates. Even though many proteins are observed to follow simple two-state kinetics for folding under some conditions, the underlying free-energy landscape is undoubtedly more complex. The NRE model also can be extended to simulate more complex landscapes represented by three or many more macrostates. It could turn out that the best strategies for optimizing RE simulations are different for such cases as compared with those in which the kinetics is described by two-state anti-Arrhenius behavior as has been observed for some peptides (25, 28).

The results shown here for the NRE model nevertheless are likely to be relevant for atomic-level RE simulations, and they suggest that more extensive “training” simulations to explore the temperature dependence of the kinetics will be useful for optimizing the efficiency of RE. Training simulations have been used to construct asynchronous variants of RE (33) and to find the optimum temperature ladder by maximizing the diffusion in temperature space (6, 19). However, maximizing the diffusion of replicas in temperature space regardless of the actual kinetics at each temperature does not necessarily optimize the RE simulation. If the rate constants have anti-Arrhenius behavior, then there exists an optimal temperature with the fastest kinetics. Additional replicas beyond that temperature decrease the efficiency of the simulation relative to the case in which the same number of replicas are used but the additional replicas are placed close to the optimum temperature. The reason for this is because in the anti-Arrhenius case the optimum temperature has more favorable kinetic properties than any higher temperature and can contribute more to the convergence of the low temperature of interest. In this context, finding the optimum high temperature should take priority, and the remaining replicas then can be distributed to optimize temperature diffusion and efficiency. On the other hand, in the context of Arrhenius-like rates, there is no optimum high temperature, and the focus on the optimization of diffusion to the highest temperature is justified.

The possibility that an arbitrary choice of highest temperature may be too high is increased further by the observation that finite temperature-exchange rates lower the optimal highest temperature significantly below that predicted by the harmonic mean of the forward and reverse rates at high temperature. Superficially, it could be argued that this result is not relevant to atomic-level simulations, which already are conducted in the “large-α” limit, given that the folding and unfolding timescales of peptides and small proteins are on the order of tens to hundreds of nanoseconds, whereas temperature exchanges typically are done on a picosecond timescale. However, unlike the NRE model, for which temperature exchanges of any magnitude can occur freely, in a molecular simulation the rate of temperature exchanges is limited by the rate of diffusion in energy space. For example, a replica must first find low-energy configurations to be able to exchange temperature with a replica at a lower temperature. Therefore, the rate of conformational transitions places an upper limit on the effective value of α that can be achieved in a molecular simulation.

NRE also provides some insights into the choice of the number of replicas and their temperature distribution. In molecular RE simulations, the temperature spacing is dictated primarily by the overlap of energy distributions at different temperatures. However, if we wish to add additional replicas beyond those required to obtain sufficient energy overlap (for example, in a large-scale cluster or grid computing environment), the NRE results indicate that additional replicas will be most beneficial to efficiency if they are placed at temperatures such that the average of the harmonic means is increased. Additionally, it may be possible to use reweighting methods such as T-WHAM (34), which generate estimates of thermodynamic quantities based on data from more than one temperature, to further accelerate convergence properties because folding transitions are not required to occur between identical temperatures to be “productive.” RE methods that are based on the exchange of energy function parameters (35) also may have more favorable convergence properties for some systems.

The RE technique is a powerful conformational sampling method for the study of quasi-ergodic systems while preserving canonical thermodynamic properties. For these reasons, it has become a very popular tool in computational biophysics research. This study identifies some characteristics of the method that are key for the effective use of RE to study processes with anti-Arrhenius kinetic behavior, such as protein folding and binding.

Abbreviations

RE

replica exchange

T-RE

temperature RE

MC

Monte Carlo

MD

molecular dynamics

NRE

network RE.