Electrostatic interactions in phospholipid membranes revealed by coherent 2D IR spectroscopy

Abstract

The inter- and intramolecular interactions of the carbonyl moieties at the polar interface of a phospholipid membrane are probed by using nonlinear femtosecond infrared spectroscopy. Two-dimensional IR correlation spectra separate homogeneous and inhomogeneous broadenings and show a distinct cross-peak pattern controlled by electrostatic interactions. The inter- and intramolecular electrostatic interactions determine the inhomogeneous character of the optical response. Using molecular dynamics simulation and the nonlinear exciton equations approach, we extract from the spectra short-range structural correlations between carbonyls at the interface.

As a constituent organelle in a cell, the membrane sets the information and energy gradients necessary for life. Carbonyl, phosphate, and choline are the common structural moieties in the polar surface of cellular membranes (1), mediating molecular recognition and signal transduction (1–4). Unfortunately, our knowledge on their arrangement and dynamics is rather limited due to experimental difficulties. In a lipid bilayer, lateral irregularity smears the diffraction pattern in neutron scattering measurements, and NMR resonances are broad because of the restricted motions that result in incomplete motional narrowing. IR spectroscopy, on the other hand, is known to be helpful in application to such systems. Since 1972, the IR resonance of carbonyl moieties in phospholipid membranes has attracted considerable attention (5–9). The absorption band shows a clear inhomogeneous character and can be described as a superposition of several substates (5–7). The carbonyl stretching line-shapes in membranes could yield direct information about molecular architecture and fluctuations in the membrane interface (10, 11), provided that the origin of the spectral inhomogeneity of the carbonyl IR response in phospholipid membranes is understood. The inhomogeneity was attributed to differences in the local environment of the sn-1 and sn-2 carbonyl moieties stemming from the packing arrangements (6, 8), the local chain conformations (8, 9, 12–14), the relative positions of the two CO groups with respect to the interface (9, 15), and the degree of hydration (16, 17). In an elegant work, Blume et al. (16) ruled out all of the scenarios involving local structural differences except hydrogen bonding. In a recent study, we eliminated the variance in hydration as a possible source of inhomogeneity (18).

Here we employ 2D IR spectroscopy (19, 20) to explore whether and to what extent the inhomogeneities of the carbonyl absorption can be attributed to electric field fluctuations. 2D IR techniques are femtosecond optical analogues of 2D NMR that generate 2D correlation plots that can separate homogeneous and inhomogeneous broadenings along the diagonal and antidiagonal axis and provide a rich cross-peak pattern (21). Electrostatic interactions strongly contribute to the optical response of molecular crystals (22), polypeptides (23, 24), and neat liquids (25). In a previous study the Coulomb coupling between sn-1 and sn-2 carbonyls in a phospholipid molecule was considered negligible (8). In this study, we use the 2D IR response, which measures the electrostatic interactions, whether of inter- or of intramolecular origin, to determine the role played by such interactions at the polar interface of a phospholipid bilayer.

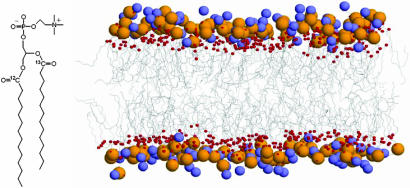
Our investigation focuses on membrane fragments of dimyristoyl-phosphatidylcholine (DMPC), where the sn-2 chain contains a ¹³C-labeled carbonyl (see molecular structure and schematic representation of the DMPC bilayer in Fig. 1). The details on the phospholipid synthesis are provided in ref. 18. To prepare membrane fragments, first we dissolved DMPC in chloroform and dried it on a glass plate. Second, after addition of deuterium oxide, the phospholipid suspension underwent mechanical mixing until the sample (10-μm film between two CaF₂ windows) demonstrated proper optical quality. Lipid:²H₂O molar ratio of 1:6 for the prepared sample suggests a moderate level of hydration. We performed experiments at 38°C; at this temperature the membrane fragments are in the lamellar liquid phase (26, 27).

Fig. 1.

Chemical structure of the DMPC phospholipid and a snapshot of the DMPC bilayer taken from the MD simulation (for reasons of clarity the water molecules are not shown). The orange, blue, and red spheres represent phosphorus, nitrogen, and oxygen atoms, respectively. The hydrophobic tails are shown with sticks.

The spectral degeneracy of the sn-1 and sn-2 carbonyls was lifted, giving two broad vibrational bands at 1,740 and 1,697 cm⁻¹, respectively (see linear IR spectrum in Fig. 2A) for nonlinear spectral probing. The 2D IR experiment uses 1.2-ps pump pulses and 0.1-ps probe pulses with 16 and 200 cm⁻¹ full bandwidth, respectively. This hole-burning technique uses the narrow band pump to select a subensemble of vibrational modes within an inhomogeneous distribution. The detected 2D correlation spectra were obtained by scanning the pump frequency and spectrally resolving the probe transmission. The 2D IR response was analyzed by using the theoretical approach described in refs. 28–30 combined with molecular dynamics (MD) simulations.

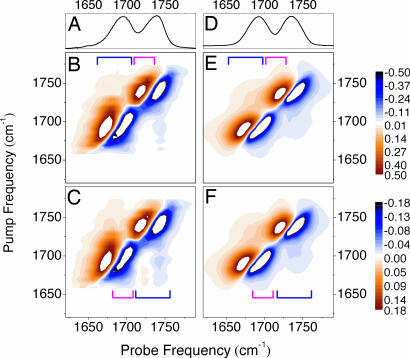
Fig. 2.

Experimental and calculated spectra. (A) FTIR optical absorption of the carbonyls in phospholipid membrane fragments. (B and C) Experimental 2D IR spectra recorded under parallel (B) and perpendicular (C) polarization conditions for pump and probe pulses. (D) Calculated linear optical absorption. (E and F) Calculated 2D IR spectra for parallel (E) and perpendicular (F) polarization conditions. Blue and magenta brackets show the spectral regions of the inter- and the intraband cross-peaks, respectively. Color scale bars show the experimental signal amplitudes in mOD (milli-optical density).

Fig. 2 B and C shows the 2D IR spectra at early delay time under parallel and perpendicular polarization geometry for the pump and probe pulses. We noticed that the diagonal resonances in the 2D IR spectra do not show time evolution on the time scale of vibrational relaxation, which means that frequency–fluctuation correlation function decays much slower than the vibrational lifetime. The spectra reveal two strong diagonal resonances corresponding to absorption of the two carbonyls (see also the linear IR spectrum in Fig. 2A). The elongation of these resonances along the diagonal direction of the 2D IR spectrum confirms the inhomogeneous character of the absorption bands of the carbonyl moieties (10, 11, 16). Each resonance has a negative (blue) contribution due to ground-state bleaching and to stimulated emission from the first excited state and a positive (red) contribution due to first excited-state absorption. The red shift of the excited-state absorption band reflects the anharmonicity of the carbonyl stretching mode. The 2D IR spectra also show off-diagonal features, known as cross-peaks, that are due to the coupling of the resonantly excited states with the states of different frequency within the same band (intraband cross-peaks) and with the states which belong to the other resonance (interband cross-peaks). In the perpendicular polarization configuration (Fig. 2C), the cross-peaks are more pronounced. In Fig. 3B we present selected horizontal slices of Fig. 2 B and C recorded with the pump frequency at 1,675 and 1,752 cm⁻¹ (see arrows). The cross-peaks provide a direct measure of vibrational coupling between carbonyl moieties. As in the case of neat liquids (25) and peptides (19), the interaction between transition dipole moments (23, 24) of carbonyl groups is responsible for such coupling, giving rise to delocalized vibrational states, i.e., to vibrational excitons.

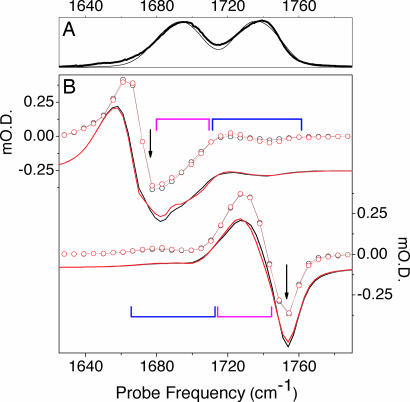
Fig. 3.

Experimental and calculated spectra. (A) FTIR optical absorption (thick line) and calculated linear optical absorption (thin line). (B) Experimental (open circle lines) and calculated (solid lines) hole-burning spectra under pump excitation at 1,675 and 1,752 cm⁻¹ (see arrows). Black and red colors indicate spectra under parallel and perpendicular polarization conditions, respectively. The spectra under perpendicular polarization are scaled by a factor of three. Blue and magenta brackets specify the spectral regions of the inter- and intraband cross-peaks, respectively (see also Fig. 2).

The interface of a phospholipid membrane is a highly disordered system (31). To model its linear and nonlinear optical response, we employ an MD simulation of a bilayer system consisting of 112 DMPC molecules (18, 32) to obtain the atomic trajectories. Definition of vibrational states is accomplished by using an N × N vibrational Hamiltonian matrix, where N = 112 is the number of coupled CO groups in one leaflet of the membrane. The diagonal elements are the zero-order local frequencies corrected by the effect of the electric field acting on each oscillator (33, 34). The Stark frequency shift is Δω = k E_proj, where E_proj is the projection of the electric field along the CO bond. The electric field on each CO oscillator is calculated in the middle point of the bond following Coulomb's law, i.e., by using the positions and the charges of the atoms known from the MD simulation. The off-diagonal elements of the Hamiltonian matrix are obtained by using the transition dipole coupling mechanism (23, 24, 34), which is based on the dipole–dipole approximation for the electrostatic interaction among the transition dipole moments:

where e_kl is the unit vector connecting the transition dipole moments μ_k and μ_l of the carbonyl oscillators k and l at distance R_kl and ε is the dielectric constant (in our case, set to 1). Diagonalization of the Hamiltonian matrix yields the eigenvectors (excitons) in the carbonyl basis and the corresponding eigenvalues, i.e., the excitonic frequencies. Once the excitons and their frequencies are known, the linear absorption can be calculated as follows:

In this equation, as in the following ones, the angular brackets represent an average over the configurations obtained from the simulation, and Φ_im is the contribution (eigenvector coefficient) of the carbonyl i to the exciton of frequency ω_m. The traditionally adopted procedure for calculating the nonlinear spectra requires the explicit evaluation of the two-exciton states, which are obtained by diagonalizing the two-exciton Hamiltonian matrix of rank N(N + 1)/2 (6,328 in our case). According to the sum-over-states approach, the nonlinear optical response is then obtained as the sum of the transitions between the two-exciton eigenstates. For large systems, the calculation becomes prohibitively expensive due to the N⁴ scaling. In the present paper, we use the alternative nonlinear exciton equations approach (28–30), which avoids the calculation of the two-exciton states. In the nonlinear exciton equations method, the nonlinear signal originates from the scattering event in which two one-exciton states are eliminated upon collision to create a pair of new excitons. This process is described by a scattering matrix, which contains the effect of the molecular anharmonicity. Therefore, the 2D IR signal is proportional to the product of the scattering matrix with a Green's function term, which describes the propagation of the free excitons before and after the scattering event. Multiplication by the four-point correlation function of the transition dipole moments of the four excitons gives the final nonlinear spectrum (28–30).

Optimization of the calculated linear and nonlinear spectra gives the following parameters: excitonic Lorentzian half-with at half maximum γ is equal to 2 cm⁻¹; zero-order resonant frequencies are equal to 1,755 and 1,708 cm⁻¹ for the native and the ¹³C-labeled carbonyls, respectively; Stark coefficient k = 2.1 × 10⁻⁴ e a_o⁻¹ m_e⁻¹; transition dipole moment 3.4 D Å⁻¹ amu^−1/2 (34, 35). The anharmonicity of the CO oscillators used to calculate 2D IR spectra is 20 cm⁻¹. Fig. 2 D–F shows the calculated linear IR spectrum, and the 2D IR response under different polarization conditions. The calculated spectra reproduce the experimental band widths and their inhomogeneous (diagonally distributed) character. They account for the presence of both intraband and interband cross-peaks. In Fig. 3B we compare two horizontal slices of the calculated nonlinear signals with experiment. The intensities and the spectral shape of intraband and interband cross-peaks are fairly well reproduced.

In vivo the native membrane determines structural and functional constraints important for cellular activity. On the 10⁻⁹ to 10⁻⁶ second time scale, according to the temporal hierarchy of rotation and translational (lateral) diffusion, the interface of the phospholipid membrane is a quasistatic electrically decorated scaffold. Structural and dynamic properties of guest molecules, such as water (18, 36) or polypeptides (37, 38), are in specific correlation with the local membrane architecture and fluctuations. Nonlinear IR spectroscopy provides a unique experimental measure of the electrostatic interactions in such systems and therefore offers the opportunity to verify the nature of the vibrational states as predicted from the theoretical modeling.

The possibility of extracting local structural information from the spectroscopic data depends on the degree of delocalization of the vibrational states. We may estimate the degree of delocalization of the excitonic states by calculating the vibrational amplitude correlation function g(R,ω) and the frequency-dependent participation ratio η(ω) (39, 40)

where R_ij is the distance between the transition dipole moments i and j. For excitons of frequency ω, the g(R,ω) function describes the average correlation of the vibrational amplitudes between two oscillators at distance R. The participation ratio provides the average number of oscillators participating in the vibrational exciton of frequency ω.

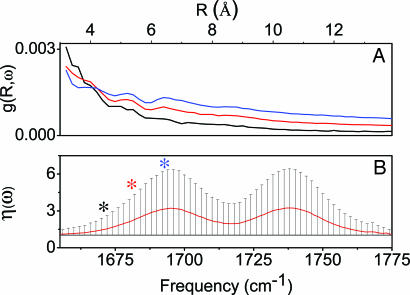
Fig. 4A shows g(R,ω) for three specific values of ω (1,670, 1,682, and 1,694 cm⁻¹). The correlation between the transition dipole moments of carbonyls extends up to 10 Å (and beyond) for frequencies in the central part of the band, which is in agreement with the frequency distribution of the participation ratio (Fig. 4B). In fact, even though η(ω) shows that, on average, less than three oscillators contribute in one-exciton states, its standard deviation indicates the presence of excitons of larger size. Furthermore, we note that, in the tails of the IR bands, the excitons are expected to be localized on single oscillators. Such localization may provide an opportunity to assess the local structural properties. In fact, under excitation on the very red side of the ¹³CO band, the measured anisotropy r = (I_‖ − I_⊥)/(I_‖ + 2I_⊥) of the interband cross-peak is ≈0.26. Here, I_‖ and I_⊥ are the cross-peak excursions for parallel and perpendicular polarization conditions, respectively. On the basis of the ansatz r = (3cos²θ − 1)/5 (see ref. 20), the possible anisotropy values range from 0.4 (parallel arrangement of the transition dipole moments) to −0.2 (perpendicular arrangement). The relatively large anisotropy measured in our case is indicative of a rather narrow angular distribution. In particular, it suggests an average angle θ of 29° (or equivalently 151°) between the transition dipole moments of the paired carbonyls. The anisotropy of the cross-peaks becomes vanishingly small when the pump frequency is tuned to the central part of the ¹³CO band. This is expected in view of the increasing delocalized nature of those vibrational states.

Fig. 4.

Characteristics of the excitonic states from MD simulation. (A) Correlation functions of vibrational amplitudes, g(R,ω) for three specific frequencies: 1.670 cm⁻¹ (black line), 1,682 cm⁻¹ (red line), and 1,694 cm⁻¹ (blue line). The three curves show that the intermolecular correlation extends to longer distance for exciton states closer to the maximum of the band. (B) Participation ratio, η(ω) (red line), and its standard deviation (bars). The asterisks show the frequencies we used for the calculation of g(R,ω).

The anisotropy recovered from the 2D IR spectra suggests the existence of preferential mutual arrangements of the transition dipole moments and, hence, of the carbonyl moieties. In this respect, the atomistic detail of the MD simulation provides the opportunity of determining the pairing geometry of two transition dipole moments, expressed in terms of mutual distance R and angle θ, that mostly contributes to the cross-peak intensity. The contribution of a given pair arrangement (R, θ) is proportional to the number of transition dipole moment pairs in that arrangement, each pair being weighted by a coupling factor calculated in the context of the transition dipole coupling mechanism. In particular we define a weighted radial–angular pair distribution function as follows

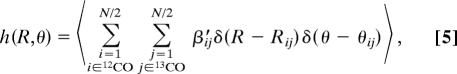where the sums over i and j run over the¹²CO and ¹³CO carbonyls, respectively. The weight factor β′_ij is a pair coupling factor correlated to the parameter β_ij (see Eq. 1) and to the difference of the diagonal frequencies, ω_i⁰ − ω_j⁰. It is defined as follows:

where ω_i and ω_j are the vibrational frequencies of the two carbonyls obtained considering their coupling in the excitonic fashion, i.e., by diagonalizing the reduced Hamiltonian matrix,

In Fig. 5, we report the h(R,θ) function calculated considering all¹²CO–¹³CO pairs, only the ¹²CO–¹³CO intermolecular pairs and only the intramolecular pairs, respectively. In Fig. 5A we note that for distances of >6.5 Å, the h(R,θ) function vanishes, implying that only neighboring carbonyls give a significant contribution to the cross-peaks, which is in general agreement with the results obtained for the participation ratio reported above. A further interesting feature of the distribution function is its structure. In the total h(R,θ) (Fig. 5A), we observe the presence of several structural families whose origin (intermolecular or intramolecular) can be easily understood by comparison with Fig. 5 B and C. It is relevant to remark that the intermolecular h(R,θ) function is far from showing random orientation even if it is broader than the intramolecular counterpart. The sharp peak at θ of ≈40° and R = 5 Å in Fig. 5C corresponds well with the angle between the transition dipole moments obtained from the experimental anisotropy, suggesting that it is mainly originated by the intramolecular pairs. However, we notice that, for this angular value, the intermolecular carbonyl pairs also contribute significantly (up to 26 ± 5%) to the total h(R,θ) function (see Fig. 5B).

Fig. 5.

β′-weighted radial–angular distribution functions (Eq. 5) calculated considering all ¹²CO–¹³CO pairs (A), ¹²CO–¹³CO intermolecular pairs (B), and ¹²CO–¹³CO intramolecular pairs (C). The red dotted lines indicate the angular values obtained from experimental spectral anisotropy. The chromatic bar shows the range of the statistical distribution according to Eq. 5.

The present experimental and MD simulation study of linear and nonlinear IR response of carbonyl moieties in a phospholipid bilayer reveals the importance of electrostatic interactions at the polar interface. Both the transition dipole moment coupling and the variance of the electric field contribute to the shape and to the bandwidth of the linear IR spectrum. The two contributions, which cannot be distinguished in the linear response, can be clearly separated in the diagonal and in the off-diagonal parts of the 2D correlation plots. The cross-peak intensity is a direct measure of the contribution of coupling to the overall line shape. The diagonal spectral distribution is due to both the frequency dispersion of the excitonic states and the broadening originating from the local electric field. The 2D line shapes allow the unambiguous interpretation of the IR response and specific modeling of the vibrational excitations. The increased localization of the excitonic states in the wings of the IR response allows us to assess local structural properties for the nearest chromophores. 2D IR spectroscopy, in conjunction with the nonlinear exciton equations approach, provides an opportunity to model effectively the structural relations in the phospholipid membranes. This strategy is promising for structural studies through intermolecular coupling in composite phospholipid bilayers, host–guest lipid–protein complexes, lipid systems of reduced dimensionalities, and polymers.

Abbreviations

MD

molecular dynamics

DMPC

dimyristoyl-phosphatidylcholine.