Metabolic rate does not calibrate the molecular clock

Abstract

Rates of molecular evolution vary widely among lineages, but the causes of this variation remain poorly understood. It has been suggested that mass-specific metabolic rate may be one of the key factors determining the rate of molecular evolution, and that it can be used to derive “corrected” molecular clocks. However, previous studies have been hampered by a paucity of mass-specific metabolic rate data and have been largely limited to vertebrate taxa. Using mass-specific metabolic rate measurements and DNA sequence data for >300 metazoan species for 12 different genes, we find no evidence that mass-specific metabolic rate drives substitution rates. The mechanistic basis of the metabolic rate hypothesis is discussed in light of these findings.

Molecular dating (the use of DNA sequences to estimate evolutionary divergence times) can provide extremely useful historical information on the timing of evolutionary events. Molecular dating analyses were initially premised on the assumption that the rate of molecular evolution is constant; however, there is increasing evidence that the rate of molecular evolution varies widely among lineages (1–4). For example, previous studies have indicated that smaller-bodied vertebrates tend to have higher rates of molecular evolution than larger-bodied vertebrates (2, 5, 6). One explanation for this effect is the metabolic rate hypothesis. This hypothesis suggests that smaller-bodied vertebrates generate higher levels of mutagenic oxygen radicals than larger vertebrates (5) as a consequence of their higher mass-specific metabolic rates (7). Oxygen radicals, which are byproducts of normal metabolism (8), can cause damage to DNA in a variety of ways, and this damage has been shown to induce mutations (9).

Although some studies have reported a correlation between mass-specific metabolic rate and molecular evolutionary rate (5, 10), other studies using larger data sets found no evidence for the metabolic rate hypothesis, even when the covariation of metabolic rate with other life history variables (such as generation time) was taken into account (2, 6). Despite this, a number of studies have invoked the metabolic rate hypothesis to explain patterns of variation in the rate of molecular evolution (5, 11, 12).

In a recent study, Gillooly et al. (13) used measurements of body size and temperature to derive predictions of metabolic rate in a range of animal species and compared these predicted mass-specific basal metabolic rate (BMR) values to substitution rates gathered from the literature. They concluded that “there is indeed a single molecular clock… but that it ‘ticks’ at a constant substitution rate per unit of mass-specific metabolic energy rather than per unit of time” (13). However, there are a number of reasons why this claim requires further empirical validation.

First, as the authors acknowledge, their model did not distinguish between the metabolic rate and generation time hypotheses (the hypothesis that organisms with faster generation times tend to accumulate more copy errors and hence substitutions, per unit time; e.g., ref. 14). Second, only 10 of 60 data points in the study were invertebrates, which makes it difficult to assess the generality of the conclusions beyond vertebrate animals. Third, estimates of substitution rate were collected from the literature from studies by using widely differing methods and are thus not directly comparable (a point acknowledged by the authors). Fourth, independent contrasts were not used, which led to some data being counted multiple times in a single analysis, violating the assumption of statistical independence inherent in the analyses.

To overcome limitations in previous studies, we undertook a taxonomically broad test of the metabolic rate hypothesis among the Metazoa using measured values of mass-specific metabolic rate. We collected mass-specific BMR data from the literature and genetic data from GenBank (www.ncbi.nlm.nih.gov) for a range of >300 metazoan species from 11 different phyla, including representatives from all three major bilaterian clades (Ecdysozoa, Lophotrochozoa, and Deuterostomia). We then used phylogenetic comparative methods (e.g., ref. 15) to test for an association between mass-specific BMR and rates of molecular evolution. We found significant evidence of variation in the rate of molecular evolution. However, we found no evidence that the variation in the rate of molecular evolution is correlated with differences in mass-specific metabolic rate.

Results

Evidence for Rate Variation.

Significant rate variation was observed in 9 of 12 genes and more than one-third of the comparisons used in this study [see Table 1 and supporting information (SI) Appendix 1], despite the low power of Likelihood Ratio Tests to detect differences in the rate of molecular evolution (16).

Table 1.

Summary of sequence data used in this analysis

Abbreviation	Full name	Genome	Coding	Comparisons
12S	12S RNA	Mitochondrial	RNA	36
16S	16S RNA	Mitochondrial	RNA	32
COX1	Cytochrome oxidase 1	Mitochondrial	Protein	49
COX2	Cytochrome oxidase 2	Mitochondrial	Protein	2
CYTB	Cytochrome B	Mitochondrial	Protein	54
ND2	NADH dehydrogenase 2	Mitochondrial	Protein	11
ND5	NADH dehydrogenase 5	Mitochondrial	Protein	5
18S	18S ribosomal RNA	Nuclear	RNA	33
28S	28S ribosomal RNA	Nuclear	RNA	18
H3A	Histone 3 alpha	Nuclear	Protein	4
VWF	von Willebrand factor	Nuclear	Protein	14
ATP7A	ATPase 7 alpha	Nuclear	Protein	3

Abbreviations and full names are given for each gene included in this study. ″Genome″ indicates whether the gene is of mitochondrial or nuclear origin, ″Coding″ indicates whether the gene is RNA or protein coding, and ″Comparisons″ indicates the number of independent comparisons available for each gene.

No Evidence for a Metabolic Rate Effect.

We found no evidence for a relationship between mass-specific BMR and rate of molecular evolution. No significant association between substitution rate and mass-specific BMR was seen in any of the nonparametric sign tests, including those in which all comparison pairs were included and those in which different taxonomic or genomic (i.e., mitochondrial or nuclear) subsets of the data were analyzed independently (Table 2). Results were qualitatively identical if sign tests used only those comparisons with both significant variation in substitution rate and at least 2-fold differences in mass-specific BMR (see SI Appendix 1). Tortoise/Hare sign tests, which included only those comparisons with the largest differences in mass-specific BMR, showed no significant association between mass-specific BMR and substitution rate, despite comparisons having an average 17-fold difference in mass-specific BMR (see SI Appendix 2).

Table 2.

Results of sign tests

Taxa	Genes	Protein coding				RNA coding
		BLdN (+/−)	P	BLdS (+/−)	P	BLT (+/−)	P
All	All	(53/54)	0.500	(56/58)	0.537	(52/39)	0.104
	Mitochondrial	(49/51)	0.540	(49/56)	0.721	(22/21)	0.500
Mammalia	Mitochondrial	(18/11)	0.133	(11/18)	0.868	(19/11)	0.100
	Nuclear	(9/5)	0.212	(9/5)	0.212	n/a	n/a
Aves	Mitochondrial	(8/15)	0.895	(12/12)	0.500	n/a	n/a
Mollusca	Mitochondrial	(11/5)	0.105	(8/9)	0.500	(6/4)	0.377
	Nuclear	n/a	n/a	n/a	n/a	(5/5)	0.500
Arthropoda	Mitochondrial	(8/12)	0.748	(10/12)	0.584	(11/10)	0.500
	Nuclear	n/a	n/a	n/a	n/a	(12/8)	0.252

All tests are one-tailed. Shown are the origin of the genes used in the analysis: mitochondrial, nuclear, or both (″all″); BL_dN, nonsynonymous branch lengths; BL_dS, synonymous branch lengths; BL_T, total branch for RNA-coding genes; the number of comparisons in which the sign of the difference in substitution rate and mass-specific BMR is the same, ″+,″ or different, ″–″; and P value. ″n/a″ indicates that comparisons were not available in that particular subset of the data.

Parametric regression revealed no significant association between mass-specific BMR and substitution rate in any of the genes analyzed in any of the taxa. These included tests of both nuclear and mitochondrial genes in the Arthropoda (18S, COX1, and 16S), Mollusca (18S, COX1, and 16S) and Mammalia (VWF, CYTB, and 12S), and mitochondrial genes in the Aves (CYTB and ND2). Removal of outliers (see Methods) had no qualitative effect on this result (Table 3). Z tests indicate there is no evidence for an association between BMR and substitution rate when the results of different regressions are combined across all taxa or combined separately within the Arthropoda, Mollusca, Mammalia, or Aves (Table 4).

Table 3.

Regressions of phylogenetically independent comparisons of molecular branch lengths on mass-specific BMR

Taxon	Gene	y axis	All data points				Outliers removed
			n	r2	β	P	n	r2	β	P
Arthropoda	18S	BLT	13	0.027	0.123	0.573	10	0.120	0.262	0.297
Arthropoda	COX1	BLdN	18	0.041	−0.192	0.408	14	0.028	0.124	0.551
Arthropoda	16S	BLT	16	0.063	−0.148	0.327	14	0.026	−0.105	0.565
Mollusca	18S	BLT	7	0.059	0.209	0.564	6	0.064	−0.134	0.583
Mollusca	COX1	BLdN	16	0.032	0.128	0.489	13	0.180	0.226	0.130
Mollusca	16S	BLT	10	0.002	0.031	0.886	8	0.002	−0.022	0.901
Mammalia	VWF	BLdN	14	0.136	0.153	0.176	11	0.006	0.018	0.813
Mammalia	VWF	BLdS	13	0.001	0.012	0.929	11	0.114	0.176	0.282
Mammalia	CytB	BLdN	28	0.002	−0.005	0.964	24	0.033	0.001	0.857
Mammalia	CytB	BLdS	12	0.052	0.840	0.455	11	0.145	−0.462	0.222
Mammalia	12S	BLT	29	0.008	−0.060	0.641	26	0.017	0.067	0.520
Aves	CytB	BLdN	21	0.011	0.168	0.645	17	0.004	0.109	0.807
Aves	CytB	BLdS	8	0.032	−0.395	0.644	7	0.003	0.155	0.893
Aves	ND2	BLdN	10	0.051	−0.587	0.503	9	0.247	−0.617	0.143
Aves	ND2	BLdS	7	0.011	−0.259	0.804	6	0.099	−0.422	0.492

Regressions were Type I and forced through the origin. Shown are the number of comparisons: n, the r², the estimated slope: β, and the P value. BL_dN, nonsynonymous branch lengths; BL_dS, synonymous branch lengths; BL_T, total branch for RNA-coding genes.

Table 4.

Results of Z tests on P values from regressions of substitution rates on life history traits

Trait	Taxon	n	P (all data points)	P (outliers removed)
BMR	All	15	0.405	0.394
BMR	Arthropoda	3	0.764	0.270
BMR	Mollusca	3	0.207	0.314
BMR	Mammalia	5	0.227	0.341
BMR	Aves	4	0.677	0.812
M	All	15	0.479	0.042*
M	Arthropoda	3	0.823	0.733
M	Mollusca	3	0.095	0.053
M	Mammalia	5	0.423	0.005**
M	Aves	4	0.673	0.644
G	All	15	0.302	0.050
G	Arthropoda	3	0.726	0.635
G	Mollusca	3	0.071	0.062
G	Mammalia	5	0.462	0.065
G	Aves	n/a	n/a	n/a

M, body mass; G, metabolic rate estimated from mass and temperature (13).

*, P < 0.05;

**, P, < 0.01.

Some Evidence for an Effect Using Proxies of Metabolic Rate.

To facilitate comparison of our results with those of previous studies, we consider whether a previously reported predictor of mass-specific BMR [a function of body size and environmental temperature (17) that we term G] or body size (M) might explain some of the variation in substitution rates observed here. Both of these quantities have been reported to correlate with substitution rates, although these studies have been limited almost exclusively to vertebrate taxa (2, 5, 6, 11, 18).

After removing outliers (see Methods), regression revealed significant positive correlations between G and substitution rate in one gene for mammals (VWF synonymous substitutions, P = 0.048) and one gene for molluscs (COX1 nonsynonymous substitutions, P = 0.012). A significant negative correlation between body size (M) and substitution rate was observed in one gene for mammals (12S, P = 0.002).

Z tests indicate there is a highly significant negative association between body size and substitution rate across all taxa, (P = 0.042; Table 4), but analyzing taxa separately suggests that this entirely stems from a strong effect in the mammals (P = 0.005, with P > 0.05 in all other taxa; Table 4). Z tests indicate that there are no significant associations between G and substitution rate in any taxa when treated individually (P > 0.05 in all cases; Table 4) or when results from all taxa are combined (P = 0.05; Table 4). These results are in accordance with previous studies, which show a significant body-size effect in mammalian species (2) but find no evidence of a body size effect in invertebrate species (3). Despite the lack of significant associations between G and substitution rate in the Z tests, it is of note that P values obtained for G closely mirror those obtained for body size (Table 4). It therefore seems possible that Gillooly et al.'s (13) result primarily reflects a body size effect on the rate of molecular evolution in mammals rather than a universal metabolic rate effect.

Discussion

The results of this study show no evidence that measured mass-specific BMR drives substitution rate in any of the genes or taxa studied. This result is in accordance with previous studies, which find no evidence for the metabolic rate hypothesis in either mammals (2) or birds (6). The parameter G (predicted metabolic rate based on temperature and body mass) explains a significant proportion of the variance in substitution rates in only 2 of 11 data sets examined, and these correlations are not significant after correction for multiple tests (Table 4). These results cast doubt on the claim that there exists a single molecular clock that can be calibrated with measurements of body size and temperature. Because we analyze data sets from each of the three major groupings of the modern tree of bilaterians (Deuterostoma, Ecdysozoa, and Lophotrochozoa) and find no evidence for the metabolic rate effect, we conclude that the metabolic rate effect is not a universal feature of metazoan molecular evolution.

We are confident there is sufficient power in our analysis to detect an effect of mass-specific metabolic rate on substitution rate. First, we use the largest data set so far compiled to test the metabolic rate hypothesis. Second, we analyze a broad range of taxa and genes, both together and separately, to reduce the possibility that a significant metabolic rate effect in some taxa or genes was obscured by the lack of an effect in other taxa or genes. Third, in the parametric regression we exclude very small or saturated branches and reanalyze the data after removal of outliers. We are therefore confident that the failure to detect an effect was not because of the influence of a small number of highly influential data points. Finally, the Tortoise/Hare sign tests, which use only those comparisons with the largest differences in mass-specific BMR, are unlikely to suffer a lack of power because of measurement error in mass-specific BMR, yet none of these tests show any evidence of a relationship between metabolic rate and rate of molecular evolution.

The Metabolic Rate Hypothesis: A Reevaluation.

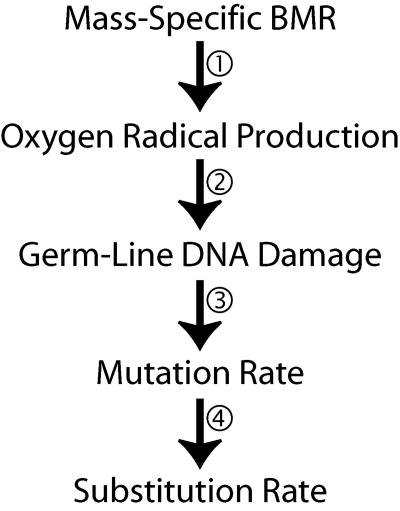
Although the mechanistic basis of the metabolic rate hypothesis is reasonable (5), a number of assumptions are made to link mass-specific BMR and substitution rate (Fig. 1). The first assumption is that species with higher mass-specific BMR values have higher levels of oxygen radical production (Fig. 1, link 1). However, there are at least two mechanisms by which this link between BMR and oxygen radical production may have been decoupled during metazoan evolution. First, the efficiency with which mitochondria generate ATP varies between species. This can lead to very different rates of mitochondrial oxygen radical generation in taxa with similar mass-specific BMRs (8, 19–21). Second, mitochondrial oxygen radical production can be decoupled from oxygen intake (which is often used as a proxy of BMR) by various mitochondrial proteins, which allow protons to leak across the mitochondrial membrane without the generation of ATP (22). In this way, it is possible for higher rates of oxygen intake (and by inference, higher mass-specific BMR) to be associated with lower rates of oxygen radical production.

Fig. 1.

For mass-specific BMR to influence substitution rates as predicted by the metabolic rate hypothesis, a number of assumptions must be made. In particular, each numbered link (discussed individually above) shown above indicates an assumption of a monotonic positive relationship between the two linked quantities.

The second assumption of the metabolic rate hypothesis is that the species with higher organism-wide rates of oxygen radical production will suffer higher rates of germ-line DNA damage (Fig. 1, link 2). There are a number of reasons why this may not be the case. Both the high reactivity of oxygen radicals and the presence of an array of antioxidant defenses (23) in eukaryotic cells mean that oxygen radicals do not travel far. Indeed, although oxidative damage to both mitochondrial and nuclear DNA is extensive in mammalian cells (24), oxygen radicals generated in the mitochondria are not responsible for the damage to nuclear DNA (25). It is therefore unlikely that the organism-wide rate of oxygen radical production provides a reliable estimate of the concentration of oxygen radicals (and thus the oxygen radical induced DNA damage) in the germ-line tissue, especially if the germ-line mitochondria are under selection to remain largely inactive (see, e.g., refs. 26 and 27).

The third assumption of the metabolic rate hypothesis is that species with higher levels of DNA damage should have higher mutation rates (Fig. 1, link 3). Although data on DNA repair in nonmodel organisms are scarce, there is evidence that DNA repair efficiency varies in natural populations (28, 29) and may thus be influenced by natural selection. It is therefore possible that differences in DNA repair efficiency may arise in response to changes in rates of DNA damage, which could confound any simple relationship between the rate of DNA damage and the rate of mutation. Finally, it is not certain that an increase in mutation rate will lead to a proportionate increase in the rate of substitution (Fig. 1, link 4). Indeed, there are plausible models of adaptive substitution in which the two rates are largely independent (30).

In conclusion, there are a number of ways in which the relationship between mass-specific BMR and substitution rate proposed by the metabolic rate hypothesis may be obscured. Many of the assumptions required for such a relationship do not always hold, even among closely related species, and others are predicted to be directly counteracted by the effects of natural selection. Although there may be a role for metabolically induced mutation in molecular evolution, particularly for the mitochondrial genome, the results presented in this study reject the hypothesis that mass-specific BMR is a universal driver of rates of substitution.

Conclusions

This study provides an empirical test of the hypothesis that metabolic rate is a primary determinant in variation in rate of molecular evolution between species. We find no evidence of any kind of association between metabolic rate and substitution rate for a wide range of animal taxa and many different genes. However, we do detect some evidence of a body size effect on rates of molecular evolution in mammals. Our detection of the mammalian body size effect, which has been reported in several previous studies, suggests that our data set has sufficient power to detect life history correlates of rates of molecular evolution. It seems possible that the body size effect explains why the proxy for metabolic rate used in a previous study has some explanatory power for rate variation in several genes in mammals and molluscs; however, this requires further investigation. Even if the proxy, G, is shown to explain a significant proportion of variation in rate of molecular evolution for some taxa, our results suggest two important qualifications. First, the correlation between G and substitution rate is not universal, but specific to particular genes and taxonomic groups. Second, we do not know the mechanism underlying the relationship between G and substitution rate, but we are confident it is not explained by BMR. If it were, then we would expect to see a relationship between substitution rate and metabolic rate. We find no hint of such a relationship in our database of 300 metazoan species, even when we consider only those comparisons with dramatic differences in metabolic rate.

Methods

Data Collection.

Data on the BMR, body mass, and the temperature at which measurements were taken were collected from the literature. We excluded data that did not represent the BMR of the species under study (e.g., animals that were under stress, were not of representative adult mass, or were not measured within the normal temperature range of that species). When more than one measurement existed for a species, the arithmetic mean of all measurements was taken. If sample sizes were also reported, weighted arithmetic means were calculated based on sample size. Much of the data for marine invertebrate species were taken from a database collated by T.B. (available from the authors on request), and the rest was taken from the literature (see SI Appendices 1 and 2). Data for the Mammalia and the Aves were taken from recent compendia (31, 32). For the Mammalia, measurements of mass-specific BMR from the Artiodactyla, Macropodidae, Lagomorpha, and Soricidae were excluded because of methodological difficulties in obtaining accurate measurements (32). In the Aves, BMR values were taken exclusively from wild-caught birds, because significant differences in BMR values have been observed between wild-caught and captive specimens (31). We converted all body mass data into grams of wet mass and all BMR data to mass-specific BMR in Watts per gram by using conversion factors gathered from the literature (see SI Appendices 1 and 2).

Available genetic data for each species were taken from GenBank (www.ncbi.nlm.nih.gov). Where possible, we included at least one example of a protein- and RNA-coding gene from both the mitochondrial and nuclear genomes for all species pairs. The final data set comprised seven mitochondrial (cytochrome oxidase 1, COX1; cytochrome oxidase 2, COX2; mitochondrial 12S RNA, 12S; mitochondrial 16S RNA, 16S; cytochrome B, CYTB; NADH dehydrogenase 2, ND2; and NADH dehydrogenase 5, ND5) and five nuclear (18S ribosomal RNA, 18S; 28S ribosomal RNA, 28S; histone 3 alpha, H3A; von Willebrand factor, VWF; and ATPase alpha, ATP7a) genes, with each gene represented in an average of just over 40 species (see Table 1 and SI Appendix 1).

Comparative Method.

Most commonly used statistical tests assume that all data points are independent of one another. To avoid counting single instances of trait change multiple times, we use independent pairs of species from the terminal branches of the phylogeny (e.g., ref. 15). In this method, each data point is calculated as the difference in the value of a trait between a pair of lineages, where all pairs of lineages are monophyletic with respect to all other pairs. Because reliable phylogenies are not available for many taxa included in this analysis, independent pairs were selected by using the taxonomy published on the National Center for Biotechnology Information's Taxonomy database (www.ncbi.nlm.nih.gov). To do this, we assumed that all families and genera were monophyletic, and we chose a maximum of one independent pair per genus. Where we had data for more than two species in a particular genus, we chose the two that maximized the difference in mass-specific BMR. This approach yielded 156 independent comparisons from 11 phyla: 74 comparisons from the Chordata (comprising 48 pairs from Mammalia, 25 from Aves, and 1 from Ascidiacea); 36 from Arthropoda; 25 from Mollusca; 10 from Echinodermata; 3 from Cnidaria; 3 from Annelida; 2 from Nematoda; and 1 each from Chaetognatha, Nemertea, Platyhelminthes, and Porifera (see SI Appendix 1). We avoid very deep comparison pairs (e.g., between phyla), because we are less confident that life history trait values of single species are representative of widely divergent groups.

Substitution Rate Estimation.

Sequences were first aligned by eye into global alignments for each gene by using Se-Al (33). Regions of genes that could not be confidently aligned (e.g., hypervariable regions of rRNAs) were excluded. Triplet alignments of the two species in each comparison and one outgroup species (see SI Appendix 1 for accession numbers) were then extracted from the global alignment and edited by hand. Alignments are available from the authors at www.tempoandmode.com. Triplet alignments were used to estimate maximum likelihood branch lengths on unrooted trees with substitution rates free to vary across the tree (see SI Appendices 1 and 2). For each comparison, the National Center for Biotechnology Information's Taxonomy database was used to select the most closely related outgroup with appropriate sequence data. The branch length of each of the two ingroup species represents an estimate of the number of changes that have occurred in the DNA sequence of each lineage since the two species diverged. Thus, the species with the longest branch length is inferred to have the higher rate of molecular evolution. For RNA-coding sequences, branch lengths were estimated by using baseml (34), with the TN93 (35) model of nucleotide substitution and gamma distributed rates across sites. This model was selected as the best from the suite of 29 possible substitution models implemented in PAML using the Akaike Information Criterion (36); calculations were performed in MODELTEST version 3.6 (37). For coding sequences synonymous (dS) and nonsynonymous (dN), branch lengths were estimated in codeml (34), with codon frequencies estimated from the data and dN/dS ratios free to vary across the tree. Model parameters were estimated independently for each triplet of species.

Statistical Analysis.

Each point in our analysis represents the difference in a trait between two sister species. The independent variable was calculated as ln(B₁/B₂), where B₁ is the mass-specific BMR of species 1, B₂ is the mass-specific BMR of species 2, and species 1 and species 2 are randomly assigned to the two species of a comparison pair. The dependent variable was calculated as ln(λ₁/λ₂), where λ₁ is the branch length of species 1, and λ₂ is the branch length of species 2. Comparisons in which one of the branch lengths was zero were excluded from the analysis.

We analyzed the data in two ways. First, we tested for an association between substitution rate and mass-specific BMR using a nonparametric sign test. For this test, we score each comparison pair as a “+” if the sign of the difference in metabolic rate and substitution rate are identical and as a “−” if the sign of the difference in metabolic rate and substitution rate are different. We then assess whether there is a significant excess of either “+” or “−” signs by comparing our observed numbers of each to a binomial distribution. Because the metabolic rate hypothesis is predicted to operate in a similar manner on all genes, and the sign test considers only the direction, not the magnitude, of the difference in substitution rate, this test allowed us to include branch length data from different genes (e.g., COX1 and ND2) into one analysis (see Table 1). However, we never included the same taxon multiple times in a single analysis. In cases where one comparison had more than one gene available within a particular subdivision of the data, we used branch lengths from the gene with the most significant difference in substitution rate between the two species (assessed using a likelihood ratio test; see below), such that each comparison was represented only once in each sign test. We tested subdivisions of the data to ascertain whether there was evidence for a metabolic rate effect on a universal scale (all genes in all taxa), a genome-specific scale (either mitochondrial or nuclear genes in all taxa), or a taxon- and genome-specific scale (either mitochondrial or nuclear genes in some taxa). Protein and RNA coding sequences were treated separately in all cases, because previous studies have suggested that some patterns are evident only for analyses of protein coding sequences (see, e.g., ref. 2).

In the sign test, it is important that the sign of the difference of a trait between a species pair (e.g., the difference in substitution rate or in metabolic rate) be known with confidence, because a small number of incorrect signs may drastically decrease the power of the test to detect an effect. We therefore performed an additional sign test on each subdivision of the data set, where we included only those comparisons in which the difference in substitution rate was significant, and in which the measured mass-specific BMR of the two species differed by ≥2-fold. We used a likelihood ratio test to ascertain the significance of the difference in substitution rate between the two ingroup species in each comparison pair. This test compares the likelihood of a tree in which the two ingroup species were forced to have the same rate of molecular evolution, to one in which their rates of molecular evolution were allowed to differ. Significance is assessed by comparing twice the difference in the likelihood scores of the two trees to a χ² distribution with degrees of freedom equal to the difference in the number of parameters of the two models (one in this case). Because tests of this kind are known to have relatively low power to detect rate variation (16), significance levels of both 5% and 25% were used to assess the significance of rate variation. Although a 5% significance level is likely to be conservative (i.e., exclude a number of comparisons which show substantial rate variation), a 25% significance level should be thought of as removing those comparison pairs most likely to yield false negatives in the sign tests. The results of analyses using both significance levels are presented.

We performed three additional sign tests to ensure that potential measurement error in mass-specific BMR was not influencing our ability to detect an effect. These tests, which we term Tortoise/Hare tests, included only the 20 comparisons with the largest ratios in mass-specific BMR. The first of these tests placed no restrictions on the significance of the difference in branch lengths, the second considered only those comparisons with substitution rate variation significant at the 5% level, and the third considered only those comparisons with substitution rate variation significant at the 25% level.

In the second set of analyses, we used type I (least squares) regression to test for an association between substitution rate and three possible independent variables: mass-specific BMR, body size, and the proxy of metabolic rate derived by Gillooly et al. (13). All regressions were forced through the origin. Contrasts in mass-specific BMR were calculated as above. Contrasts in body size were calculated as ln(M₁/M₂), where M₁ is the average mass (in grams) of species 1, and M₂ is the average mass of species 2. Contrasts in Gillooly et al.'s (13) proxy of mass-specific metabolic rate (here termed G) were calculated as ln(G₁/G₂), where G₁ is the average G for species 1, and G₂ is the average G for species 2. G values were calculated for each measurement for which both body size and temperature data were available, using the following formula (17):

where b is a constant that cancels out when ratios of G values are taken between comparison pairs (and whose value is thus unimportant), M is the mass (in grams) of the individual, T is the temperature (in Kelvins) at which the measurement was made, k is Boltzmann's constant, and E is the average activation energy, which is taken to be 0.65 eV (13). Contrasts for G were not calculated for avian taxa, because measurements of temperature were not available, and assumption of a constant temperature for all avian taxa would simply reduce contrasts in G to be equivalent to contrasts in M. Contrasts using M and G were calculated for four additional pairs of mammalian taxa, for which measured mass-specific BMR measurements were excluded because of methodological issues (see above). In total, 154 contrasts were calculated for M, and 116 contrasts were calculated for G.

In type I regression analyses, multiple genes cannot be combined in the same analysis, and so separate tests were carried out for each gene for which sufficient data were available (Table 2). These comprised two nuclear (18S and VWF) and five mitochondrial genes (COX1, 16S, 12S, CYTB, and ND2) from four different taxonomic groups (Arthopoda, Mollusca, Mammalia, and Aves). Comparisons in which either one of the branch lengths was very small (<0.0001 substitutions per site) were excluded, because the error variance in such short branches is likely to be high. Comparisons in which either one of the branches was saturated (branch length >1) were also excluded. Visual inspection of the data indicated that outliers may be having undue influence on some results; we therefore repeated each analysis after excluding outliers. Outliers were identified by first calculating the leverage, h_i, of each point as follows (38):

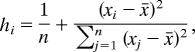where n is the number of points in the analysis, x_i is the data point of interest, and x̄ is the arithmetic mean of x variable. We then excluded all points for which h_i>(4 p/n), where p is the number of parameters of the model. This cutoff for h_i is twice that which indicates a highly influential point (38). This procedure was carried out on both the x and y variables for each regression. Tests for homogeneity of variance were carried out as described by Garland et al. (39), and contrasts were normalized with the square root of the sum of the branch lengths when appropriate.

To combine tests performed on different taxa and different genes, the P values from the various regressions were analyzed by using the Z test (40). The Z test requires P values to be one-tailed. In this case, we converted P values from regressions (which are two-tailed) to one-tailed values by assuming that substitution rate would be positively associated with BMR and G (as predicted by the metabolic rate hypothesis) and negatively associated with M (as observed by other investigators; see, e.g., ref. 2).

Abbreviation

BMR

basal metabolic rate.