Myosin V stepping mechanism

Abstract

We observe the myosin V stepping mechanism by traveling wave tracking. This technique, associated with optical tweezers, allows one to follow a scattering particle in a two-dimensional plane, with nanometer accuracy and a temporal resolution in the microsecond range. We have observed that, at the millisecond time scale, the myosin V combines longitudinal and vertical motions during the step. Because at this time scale the steps appear heterogeneous, we deduce their general features by aligning and averaging a large number of them. Our data show that the 36-nm step occurs in three main stages. First, the myosin center of mass moves forward 5 nm; the duration of this short prestep depends on the ATP concentration. Second, the motor performs a fast motion over 23 nm; this motion is associated to a vertical movement of the myosin center of mass, whose distance from the actin filament increases by 6 nm. Third, the myosin head freely diffuses toward the next binding site and the vertical position is recovered. We propose a simple model to describe the step mechanism of the dimeric myosin V.

Molecular motors convert the chemical energy, obtained from ATP hydrolysis, into mechanical work in a very efficient way. Understanding this active system, which is constantly driven away from the thermodynamics equilibrium, has been a challenge for physicists, biologists, and chemists. Nowadays, the genetic approach, together with an increasing amount of structural information (1, 2) and single-molecule studies (3–10), has supplied a detailed description of molecular motor dynamics. To describe how those machines move and develop force, several hypothesis have been proposed. They range from purely mechanical models, in which a conformational change takes place during the chemical cycle and drives the motor to the final state (11–13), to stochastic descriptions based on thermal ratchets. In the latter models, the molecular motor thermally explores the energy landscape and the arrival to the final state triggers the chemical cycle and prevents the motor from stepping back (14–21).

A detailed description of the mechanical cycle (existence of internal subcycles and their dynamics) is essential to discriminate among the various theoretical models. The myosin V–actin complex is naturally a good candidate for this study: at each chemical cycle the myosin V center of mass moves toward the plus-end of the actin filaments, by steps of 36 nm (5). This movement is among the widest steps observed in molecular motors, and it facilitates the observation and characterization of the mechanical substeps. In addition, myosin V, like many dimeric machines, moves along the filament in a hand-over-hand manner (9), which seems to be a very general feature of processive motors (22, 23).

The single-molecule approach has been indispensable to understand the myosin V dynamics: this motor steps back only occasionally at zero load, whereas the backward/forward step ratio increase drastically near the stall force (2–3 pN). The wild-type myosin V makes steps of 36 nm, corresponding to the actin pitch, with two internal phases (13, 24–26): the working stroke and the diffusive search of the next binding site. Steps smaller than 36 nm have also been reported when the lever arm is shortened (27).

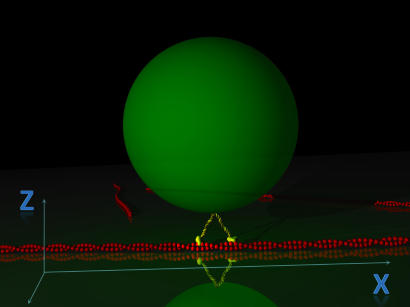
Previous work has shown that the step occurs relatively fast (≈10⁻³ s), compared with its whole ATPase cycle (≈10⁻¹ s). To investigate such a fast conformational change requires techniques with a high spatial and temporal resolution. With this intention, we have developed an optical method for single-molecule tracking, combining subnanometer precision with a temporal resolution of 2 μs: traveling wave tracking (TWT) (28). Compared with other detection methods (25), TWT allows one to follow a small scattering center in a two-dimensional plane, as schematically described in Fig. 1. In addition, with an increased bandwidth, the temporal resolution is limited only by the size of the probe and can be improved by the use of smaller particles.

Fig. 1.

Schematic view of a single-molecule bead assay in TWT. The bead trajectory is recorded along the two directions x and z, respectively parallel and perpendicular to the actin filament.

Here, the motion of a single myosin V has been recorded by TWT in a classical optical tweezers assay, in which a 200-nm polystyrene bead is coated with the molecule and is held in contact with the actin filament. This approach allowed us to supply a detailed description of the motor dynamics during its mechanical cycle.

Results

Heterogeneous Steps.

We use the optical tweezers to bring the myosin-coated bead in contact with the actin filaments and we record its motion by TWT. The myosin V concentration is progressively decreased, until only 10% of the molecules move processively along the actin filaments. In agreement with previous work (29), we observe that this concentration (and lower) optimizes the probability of finding single steps and stall forces not exceeding 2.5 pN.

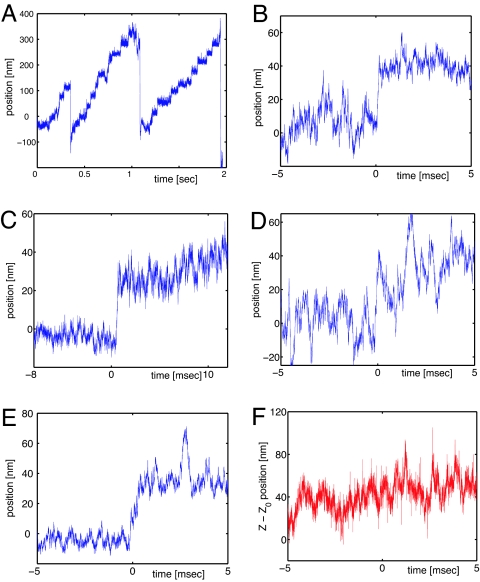
Fig. 2A shows the position of a myosin-coated bead as a function of time, during a run at saturating ATP concentration (2 mM). The optical tweezers stiffness is (3.6 ± 0.3)·10⁻⁶ N/m and stalls the myosin at 1.6 pN. Higher stall forces (up to 2.5 pN) have been observed in other runs (data not shown).

Fig. 2.

Myosin V stepping. (A) A single myosin V moving against the optical tweezers. In this run the measured stall force is 1.6 pN. (B–D) Examples of single 36-nm steps, extracted from the curve in A. (E and F) Bead motion during a single step. The trajectory is projected along the x axis (parallel to the actin filament) and the z axis (perpendicular to the actin filament).

In Fig. 2 B–E we present four examples of myosin steps extracted from this run. Despite a well preserved step size, statistically distributed around 36 nm (±9 nm), these steps are considerably different. In particular, the step shown in Fig. 2B is faster than 100 μs and the bead moves straight to the final position. Thus, the step time t₀ can be determined with a precision of a few tens of microseconds. The bead trajectory is much more complex in the examples C and D, where it reaches the final position through an intermediate position (C) and an (apparently) noisy pathway (D), which lasts a few milliseconds (≈3 ms). This behavior is quite common in our observations and seems to be representative of myosin stepping (26). In this case the initial time of the step t₀ is ambiguously determined. Finally, Fig. 2E shows an event in which the bead covers the 36 nm in >500 μs. Even though t₀ is almost unequivocal for some steps, for others it is less clear. Strong heterogeneities also appear from these examples.

The two steps presented in Fig. 2 C and D show that a sudden increase of the bead fluctuations may appear in the vicinity of the myosin steps. This effect has already been described in the literature [Veigel et al. (24)] and explained as a transitory weakening of the actomyosin bridge, due to the detachment of the trailing head. Surprisingly, we have observed such wide fluctuations also between two steps, as shown in the Fig. 2C (beginning of the track) and 2E (t ≈ 3 ms). Such isolated and wide fluctuations cannot be interpreted as a simple thermal motion of the bead, and they might be put down either to a deeper conformational change of the myosin V or to an aborted attempt of stepping.

After these isolated events have been removed, the rms amplitude of the bead fluctuations is 3.9 ± 1.0 nm. This corresponds to a stiffness κ = (2.4 ± 0.7)·10⁻⁴ N/m of the myosin-bead link (the value is obtained by using 428 portions of trajectories, which corresponds to a total acquisition time of 5 s).

Perpendicular Motion During the Step.

Using the two-dimensional TWT, we recorded the bead motion in a plane passing by the actin filament and perpendicular to the glass surface (see Fig. 1). Thus, the myosin V motion can be measured simultaneously along and perpendicular to the actin filament. Fig. 2 E and F shows the bead trajectory during a step, projected on the two directions x and z, respectively. Note that the absolute vertical position z(t) is not accessible and only variations Δz(t) are measurable (see Eq. 3). In addition, we observe that the absence of the lock-in detection makes the z signal very noisy when the bandwidth exceeds 1 kHz. Nevertheless, despite a poor signal-to-noise ratio (z signal showed in Fig. 2F), we will see in the following that it may provide useful information about the myosin V step (see Analysis).

Analysis

Averaging Method.

The aim of this work is to describe the myosin stepping features and determine how the motor moves. The examples shown in Fig. 2 reveal an extreme heterogeneity in the myosin steps. The extraction of the general stepping features is thus difficult.

A general way to extract information about the myosin step has been described in previous papers (28, 30, 31): a sequence of N steps is averaged, in such a way that the random fluctuations are erased, whereas the signal, which adds coherently, survives. This averaging process would increase the signal-to-noise ratio proportionally to the square root of the number of steps (N^1/2), but is meaningful only if the steps are properly synchronized and do not contain a stochastic sequence themselves. The step synchronization is implemented as described in the following.

We first choose an exponential function, corresponding to the trajectory of the bead subsequent to an instantaneous motor step:

where τ is fixed by time response of the bead, A is the step size, and t₀ is an arbitrary chosen time origin. A_n and t₀ⁿ are determined by fitting Eq. 1 to each experimental step n. To characterize the most straightforward artifacts, resulting from the averaging process, the synchronization method has been run on a wide set of numerically simulated steps [see supporting information (SI) Appendix].

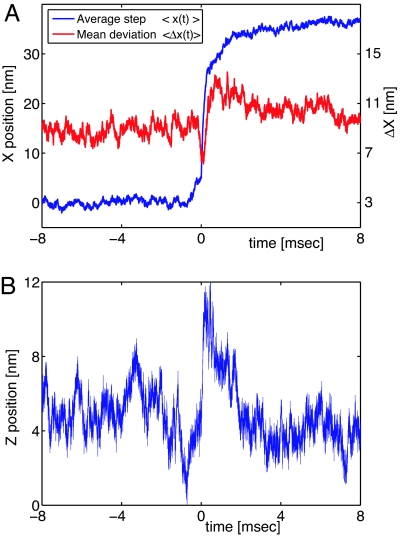
We average the data over 188 chosen among the best 268 experimental steps; data biased by multiple motor attachment, multiple steps (72 nm), or incomplete steps (steps followed by a back step) are discarded. The average step x̄(t) = 〈x_n(t − t₀ⁿ)〉_n=1,N is shown in Fig. 3A together with its mean deviation $\overline{\Delta x}(t)=\sqrt{{\langle \Delta x_n^2(t-t_0^n)\rangle }_{n=1,N}}$. In agreement with the previous work, the mean step amplitude is 36.3 ± 0.7 nm.

Fig. 3.

Average step. (A) Parallel motion (blue curve). The step requires a few milliseconds to be completed and presents a small kink (0 → 5 nm) before the steeper slope. We note the transitory increase of the mean deviation (red curve) in the last part of the step. This indicates that the steps differ in this part. This effect seems to be due to the diffusive search for the next binding site. (B) The mean distance between the bead and the surface increases when the trailing head unbinds.

We observe that the step does not occur suddenly, as observed for other molecular motors, such as the conventional kinesin (31) and the Neurospora kinesin (28). On the contrary, the myosin V step requires a few milliseconds to be completed; this value is long compared with the bead response time, which is ≈100 μs. In addition, the average step presents a small kink immediately before the main movement.

Complementary information is provided by the deviation from the mean step: Δx(t) (Fig. 3A, red line). The deviation is sensitive to the differences between steps, and noticeably changes around t₀: a deep minimum immediately precedes the step synchronization time and is followed by a broad maximum lasting a few milliseconds. The variance interpretation being subtle, we tested the synchronization algorithm on different sets of simulated steps (see SI Appendix). From these simulations, we deduce that the narrow variance minimum is mainly produced by the step alignment: the similarities between steps are maximized around t₀, where the larger slope makes the step detection algorithm more sensitive. Conversely, the variance increase after the step is mainly due to the heterogeneities in the step profiles. This feature is also observable by a direct comparison of single steps (Fig. 2), as discussed previously, and it is in good agreement with the experiments carried by Veigel et al. (24); the authors observe that, during the myosin V step, the bead fluctuates more, and they attribute this fluctuation increase to the detachment of the trailing head, with the consequent weakening of the myosin–actin bond.

As explained in the previous section, x(t) and z(t) are recorded simultaneously. The z measurements, being deduced from signal amplitude, are sensitive to the laser intensity fluctuations, and thus more noisy than the phase measurements that yield x. However, this uncorrelated noise can also be reduced by step averaging. The synchronization time t₀ⁿ provided by the x(t) tracks is used to align and average all of the z(t) trajectories.

The average z̄(t) is shown in Fig. 3B; it shows that the bead moves away from the surface, where the actin filament is attached, during the main substep. After this motion, whose mean amplitude is 6 ± 1 nm, the bead recovers its initial position.

Step and Substeps.

The myosin-coated bead follows a complex trajectory during the myosin V stepping. This trajectory includes a sequence of coupled motions along the two directions, perpendicular and parallel to the actin filament. Here we propose a mechanical interpretation of the myosin stepping, based on our findings and compatible with previous observations (24, 32).

The bead trajectory showed in Fig. 3 exhibits three main phases:

1. Before the main step (≈0.7 ms) the bead moves forward over ≈5 nm. On average, the motion happens in 160 ± 40 μs, then the myosin stops for the next ≈300 μs. (Quantitative values associated to each phase of the step are summarized in Table 1.)

2. The widest myosin substep consists of a coupled motion forward and away from the surface. While the myosin center of mass moves forward ≈23 nm, its distance from the surface increases by 6 nm. Both these movement happen in a very short time: 160 and 80 μs for x and z, respectively.

3. The bead returns to the initial vertical position, with an additional longitudinal translation of 8–9 nm. The mean characteristic time of this phase is in the millisecond range.

Table 1.

Summary of the three phases in myosin V stepping

Phase	Δx, nm	τx, μs	Δz, nm	τz, μs
1 (2 mM)	4.8 ± 0.3	300 ± 50	(0)	(0)
(10 μM)	5.5 ± 0.5	5,000 ± 500	(0)	(0)
2	23 ± 1.5	160 ± 20	6 ± 1	80 ± 20
3	8.7 ± 1.4	1,300 ± 300	−7 ± 1	2,600 ± 500

Because the duration of phase 1 depends on the ATP concentration, the table includes the values for [ATP] = 2 mM (saturating) and [ATP] = 10 μM.

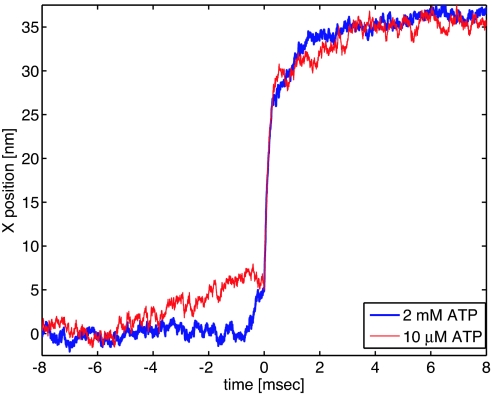
Phase 1 is observable only in the average step, whereas in the single steps it is hidden by the fluctuations of the bead. To associate a chemical state to the this part of the step, the experiments have been repeated at low ATP concentration (10 μM). At low ATP, most of the dwell time between steps would reflect a nucleotide-free state. In Fig. 4 we compare the two average steps, at saturating ATP (2 mM, blue line) and at low ATP (red line) respectively. We observe that the lack of ATP mainly affects the first part of the step (phase 1), whereas the second part remains identical, within the experimental uncertainty. In particular, the time scale of the prestroke (5-nm substep) increases from a few hundred microseconds to five milliseconds.

Fig. 4.

Average step of myosin V for two ATP concentrations. The last part of the steps behaves similarly at different concentration of ATP. In contrast, the prestep lasts several milliseconds with 10 μM ATP (red curve) and only a few hundred microseconds at saturating ATP (blue curve).

Discussion

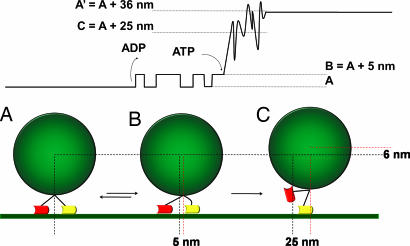
Our results show that the myosin V steps in three stages. With the backing of electron micrographs (32), we propose to associate the three stages to the three conformations schematized in Fig. 5(A, B, and C, respectively). The most natural interpretation for phase 2 (transition from state B to state C) is that the trailing head unbinds from the actin filament. This involves both a transversal and a longitudinal motion. In a purely symmetric configuration of the head, the bead would move to 36/2 = 18 nm. As already shown elsewhere (13, 24, 26), the position of the bead in configuration C exceeds this value and strongly indicates that a strain is accumulated during phase 1 at the level of the leading head. The main step fits well with an exponential relaxation, whose characteristic time is ≈150 μs. This exponential profile can be also observed on each single step (before averaging) and can be interpreted as the motion of the bead relaxing from position B to C (Fig. 5). In practice the viscous drag of the bead intrinsically limits our temporal resolution in this phase of the step; this limit implies that 150 μs is a pessimistic evaluation and the myosin V might complete this substep even faster.

Fig. 5.

Myosin V stepping model. (Upper) Example of a step, in which only the first transition (A ⇄ B) is reversible, whereas B → C and C → A′ are irreversible. (Lower) This schematic view of the myosin dimer stages during the step was suggested by electron micrographs (32) and is consistent with our experimental data.

Even though phase 3 takes on average 2.6 ms, it cannot be directly observed in the single steps. The noise dominates in this phase, probably because the unbinding of the trailing head produces a weakening in the myosin–actin bridge. During this phase the detached head looks for the next binding site in a diffusive manner. This hypothesis, already proposed in the literature (13, 24), is strongly supported by the increased mean deviation Δx(t) (plotted in Fig. 3 together with x̄(t)). We note that Δx is mostly sensitive to the discrepancies between different steps, and its increase indicates that the bead follows a different trajectory for each step.

Our experiments have also shown a certain number of aborted steps: the motor never finds the next binding site and goes back to configuration A (Fig. 5). The unfinished/finished step ratio is quite low (≈5%, data not shown), but it is certainly underestimated. In fact, only the steps for which phase 3 is clearly identified are considered.

Concerning the short substep appearing in phase 1, there are other reports for 5-nm steps observed in a monomeric myosin (24). The authors interpret this forward motion as the power stroke of the myosin V. They also propose that this substep is associated with either ADP release or isomerization of the myosin V head in the ADP state. In our experiments, we observe the 5-nm substep with a myosin V dimer. The interpretation of this motion as the transition between the states A and B, induced by ADP release, would be compatible with the enzymatic data (33).

In ref. 24 the authors propose that the ATP binding triggers the myosin head unbinding. Qualitatively, our observations agree with this hypothesis, because the 5-nm prestep duration is strongly affected by the ATP concentration. However, with an ATP concentration of 10 μM and a binding rate of 1 μM⁻¹·s⁻¹, the motor is expected to stay in state B for ≈100 ms before stepping to 28 nm. This seems to contradict our experiments, which showed a prestep lasting, at most, 5 ms at this ATP concentration. Nevertheless, these remarks would be true only if the chemical and the mechanical transitions were tightly coupled and with a single stochastic process (or a sequence of irreversible processes). On the contrary, this is not the case if the transition from A to C includes two, or more, stochastic processes, one of which is reversible, with different characteristic time scales. In such a framework, their time scales would mix and the duration time of the prestep may not scale linearly with the ATP concentration (see simulations in the SI Appendix). As a counterexample, we supply a simple model accounting for this effect (Fig. 5). We make the hypothesis that, after ADP release, the dimeric myosin V fluctuates between states A and B. In such a model the first transition A ⇄ B is reversible, whereas B rarrow C is irreversible and triggered by the ATP binding. If the residence time t_B in the state B is long compared with the ATP binding time scale (t_ATP) the transition rate B → C is limited by the ATP arrival, and the alignment procedure provides essentially the time t_ATP. In contrast, when t_ATP is much larger than t_B (low ATP concentration), the waiting time before the jump to state C is still controlled by the ATP arrival time t_ATP, but the alignment procedure provides a measure of the time t_B. Thus, it is not surprising to find, in the average step, a time scale of t_B = 5 ms, which is shorter than the ATP binding rate. We note that this 5-nm substep bears many similarities with the one observed by Veigel et al. (24) using a monomeric myosin V; it is triggered by the ADP release and its duration depends on the ATP concentration. Nevertheless, the authors did not report any clear evidence for the reversibility of the transition A ⇄ B. To understand this discrepancy, we should mention that, even though state B would be energetically favorable after the ADP release, a dimeric myosin V can store a large amount of elastic energy when the leading lever arm is bent (34). This energy might counterbalance the power stroke and drastically reduce the energy difference ΔE_A⇄B, until the trailing head unbinds. In this framework, the two models would be compatible; experiments with different loads should be done to verify this hypothesis and to estimate the energy difference ΔE_A⇄B.

A more detailed analysis of this model is supplied in the SI Appendix. We simulated 200 steps, according to this model, and we aligned them by using the algorithm proposed above. There, we show how, at low ATP concentration, the time scale t_B dominates in the average step, whereas the t_ATP dominates at higher ATP concentration. We also verified that, at this time scale, the alignment procedure does not introduce artifacts. In particular, it does not introduce long presteps for simple models containing only irreversible transitions. In contrast, the 5-nm reversible fluctuation shown in Fig. 5 might result in an alteration in the apparent position distribution between steps. In particular, at very low ATP concentration, the average position of the bead immediately before the step would be slightly increased. At this stage, neither in our experimental data nor in the numerical simulations can a baseline rise be clearly seen. The simulations indicate that a higher statistics and a different analysis are required (P.P. and G.C., unpublished work) to confirm this effect and refine the model.

We should mention that our observations are partially inconsistent with those of Uemura et al. (25). Those authors also reported myosin V substeps, but they observed a sequence of two substeps, 12 and 24 nm, respectively. In addition, they have shown that the intermediate step is not affected by the ATP concentration, which is in contradiction with our findings. At present, we do not have a theoretical argument to justify this discrepancy.

Conclusion

The high temporal and spatial resolution achieved by using two-dimensional TWT allowed us to investigate the dynamics of the myosin V stepping mechanism. In such a way, we have followed the fast conformational changes associated to the chemical cycle of ATP hydrolysis in a two-dimensional plane and with unprecedented time resolution.

In particular, the motion can be described as a sequence of three main steps: (i) After the ADP release, the myosin center of mass moves forward 5 nm (A ⇄ B); our data also indicate that this conformational change is reversible for a dimeric myosin V. (ii) This conformational transition is followed by a wide coupled motion forward (≈23 nm) and away from the actin filament (≈6 nm); this motion, whose time scale is shorter than 200 μs, probably corresponds to the unbinding of the trailing head. Our experiments at different ATP concentrations indicate that this motion is triggered by the ATP binding (B → C). (iii) In the last phase, the myosin V moves toward the next binding site and recovers the initial conformation (after a translation of 36 nm). This search for the next binding site occurs in a diffusive manner with a statistically distributed time lapse and is associated with a recovery of the initial distance between the bead and the actin filament. The time elapsed between the stroke and the rebinding follows an exponential distribution with a characteristic time of 1–2 ms (C → A). Our observations confirm that the myosin step happens in a hybrid manner, including a power stroke and a diffusive search.

In conclusion, our results highlight the existence of a prestroke conformation, with the trailing head in a free-nucleotide state, and indicate that the head unbinding is associated with ATP arrival. Additional measurements of force–velocity relations at very low ATP concentration (in the nanomolar range) would help to clarify the nature of the different phases here observed.

Methods

TWT.

The optical detection method TWT (28, 35) is based on an interference pattern, which continuously shifts through the sample, at constant speed. A sinusoidally modulated illumination is obtained by interference of two laser beams with opposite wave vectors k_x. These beams have a slightly different frequency (Δω ≈4 MHz) and undergo total internal reflection at the glass/water interface. As a consequence, the sample is illuminated by a progressive wave, whose amplitude decays exponentially with the distance from the surface:

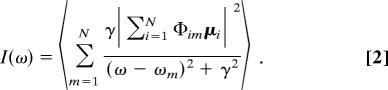where the fringe period is π/k_x = 197 nm and the characteristic penetration depth ζ ≈215 nm.

A small particle (i.e., a 100-nm polystyrene bead immobile in the pattern) scatters the light proportionally to the local intensity I(x, z; t) and hence blinks at the frequency Δω. An avalanche photo diode (APD) records the scattered light, whose phase ϕ(t) and amplitude A(t) depend, respectively, on the bead position x(t) and its distance from the surface z(t):

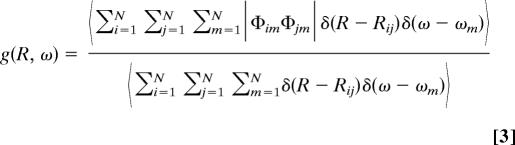Both ϕ(t) and A(t) are extracted by using a lock-in amplifier with a bandwidth of 300 kHz and are recorded with a sampling rate of 625,000 samples per second. Note that, as shown in Eq. 3, the absolute z position is not accessible, but relative positions z(t) − z₀ are measurable.

The resolution and the performances of the TWT setup have been characterized by using a piezoelectric stage, which moves a bead stuck to the coverglass by steps of 10 nm. The steps are easily observed and their internal structure can be determined with subnanometer precision [see Busoni et al. (28)].

In our experiments, the TWT detection is coupled to a simple optical tweezers setup, which allows us to manipulate the myosin-coated beads and measure the motor stall force.

Bead Assays.

Chick brain myosin V and rabbit skeletal F-actin are purified and processed as described in refs. 36–39. Myosin V (30 pM) is adsorbed on polystyrene beads (diameter: 194 nm, 1% solid; Polysciences, Eppelheim, Germany) preblocked with 10 μg/ml BSA and diluted 1/100 in assay buffer (25 mM imidazole·HCl, pH 7.4/25 mM KCl/1 mM EGTA/10 mM DTT/4 mM MgCl₂). Motility buffer additionally contained 2 mM ATP and an oxygen-scavenging system (20 mM d-glucose, 20 μg/ml glucose oxidase, and 8 μg/ml catalase). The rhodamine-phalloidin-stabilized actin filaments are introduced in a flow chamber and attached to the coverslip by myosin II treated with N-ethylmaleimide (37). The chamber is rinsed with motility buffer, supplemented with 1 mg/ml of BSA to prevent nonspecific interaction, then the myosin-coated beads are introduced. The coverslip is sealed with VALAP (Vaseline, lanolin, and paraffin at 1:1:1, wt/wt). Observations are performed at room temperature (≈25°C).

The trap stiffness is calibrated for the trapped bead from the amplitude of the thermal fluctuations (40). Typical values of stiffness are between 2·10⁻⁶ and 8·10⁻⁶ N/m.

Abbreviation

TWT

traveling wave tracking.