Time-dependent clearance of mycophenolic acid in renal transplant recipients

Abstract

Aims

Pharmacokinetic studies of the immunosuppressive compound mycophenolic acid (MPA) have shown a structural decrease in clearance (CL) over time after renal transplantation. The aim of this study was to characterize the time-dependent CL of MPA by means of a population pharmacokinetic meta-analysis, and to test whether it can be described by covariate effects.

Methods

One thousand eight hundred and ninety-four MPA concentration-time profiles from 468 renal transplant patients (range 1–9 profiles per patient) were analyzed retrospectively by nonlinear mixed effect modelling. Sampling occasions ranged from day 1–10 years after transplantation.

Results

The pharmacokinetics of MPA were described by a two-compartment model with time-lagged first order absorption, and a first-order term for time-dependent CL. The model predicted the mean CL to decrease from 35 l h⁻¹ (CV = 44%) in the first week after transplantation to 17 l h⁻¹ (CV = 38%) after 6 months. In a covariate model without a term for time-dependent CL, changes during the first 6 months after transplantation in creatinine clearance from 19 to 71 ml min⁻¹, in albumin concentration from 35 to 40 g l⁻¹, in haemoglobin from 9.7 to 12 g dl⁻¹ and in cyclosporin predose concentration from 225 to 100 ng ml⁻¹ corresponded with a decrease of CL from 32 to 19 l h⁻¹. Creatinine clearance, albumin concentration, haemoglobin and cyclosporin predose concentration explained, respectively, 19%, 12%, 4% and 3% of the within-patient variability in MPA CL.

Conclusions

By monitoring creatinine clearance, albumin concentration, haemoglobin and cyclosporin predose concentration, changes in MPA exposure over time can be predicted. Such information can be used to optimize therapy with mycophenolate mofetil.

Introduction

The pharmacokinetics of mycophenolic acid (MPA), the active immunosuppressive compound of the prodrug mycophenolate mofetil (MMF), have been extensively investigated in renal transplant recipients [1, 2]. One of the most important results from these studies was the elucidation of a relationship between area under the curve (AUC(0,12 h) of MPA and the risk of acuterejection [3–6]. Most studies also found a large between-patient variability in the pharmacokinetics of MPA [2, 3, 7]. This had led some clinicians to employ therapeutic drug monitoring for MMF therapy using a MPA AUC(0,12 h) value of 30 mg l⁻¹ h, as the minimum concentration to prevent acute rejection episodes [8]. The pharmacokinetics of MPA are further complicated by a gradual rise of 30–50% in MPA exposure over the period between the first weeks of dosing and 1–6 months after renal transplantation despite the use of fixed [2, 7, 9–12] or sometimes smaller doses of MMF [3]. The change in exposure is the result of decreasing MPA clearance (CL) over time [10], the reason for which is not completely understood. A decreasing effect of improving renal function on MPA CL has been shown [10], but also other time-varying factors may play a role. Examples of these are increasing albumin concentrations in the first months after transplantation and the gradual tapering of cyclosporin (CsA) dose and CsA target concentrations during the same period [7]. In order to maintain or achieve MPA target exposure, knowledge about the characteristics of the time-dependent CL is necessary. The aim of this study was to characterize the time-dependent CL of MPA and to test whether improving renal function, changes in concomitant immunosuppressive therapy and time-varying patient factors contribute to the time dependency. To this end a population pharmacokinetic meta-analysis was conducted combining concentration-time data from the first day to the first year after transplantation.

Methods

Patients and sampling procedures

MPA concentration-time data from six clinical studies were combined. Details of these studies have been published previously [3, 4, 13–16]. Approval was obtained from the respective ethics committees at the time each study was conducted. Patients in study 1 used 1, 1.5 or 1.75 g MMF twice daily in combination with CsA, which was begun after transplantation when creatinine concentrations dropped below 3 mg dl⁻¹. Plasma samples were drawn from 18 renal transplant patients on days 1 and 20 after transplantation for the measurement of MPA. Samples were taken predose and at 0.5, 1, 2, 4, 8 and 12 h after MMF administration. In study 2, samples were taken predose and at 0.5, 1, 2, 4, 8 and 12 h after 1 or 1.5 g MMF given twice daily to 62 renal transplant recipients on days 1 and 5 after transplantation and at hospital discharge (range day 6–day 21) [13, 14]. In these patients, CsA was begun after the first week. Study 3 was a concentration-controlled trial in which 141 CsA treated renal transplant recipients were randomized to three AUC(0,12 h) target groups, low, intermediate or high [3, 4]. Starting MMF doses were 0.45, 0.95 and 1.7 g MMF twice daily, which were adjusted to achieve AUC(0,12 h) targets of 16.1, 30.3 or 60.6 mg l⁻¹ h, respectively. Full concentration-time profiles were obtained on days 3, 7 and 11 after transplantation. Samples were taken predose and at 0.33, 0.67, 1.25, 2, 6, 8 and 12 h after oral MMF intake. On day 21 and at months 1, 2, 3, 4, and 5 after transplantation, abbreviated 2 h profiles were obtained over the first five sampling time points. In study 4, pharmacokinetic data were collected from 44 renal transplant patients given 1 g of MMF. On day 4, only a predose sample was drawn, and full concentration-time profiles were obtained on day 7 and at months 1, 3 and 6. Samples were drawn predose and at 0.33, 0.67, 1.25, 2, 3, 4, 6, 8 and 12 h after oral MMF intake. In 14 patients, MMF was combined with CsA, and in the remaining 30 patients sirolimus was used instead of CsA. In study 5, samples were drawn predose and at 0.33, 0.67, 1.25, 2, 3, 4, 6, 8 and 12 h after 0.75 or 1 g MMF twice daily from 118 renal transplant recipients on day 7 and at months 3, 7 and 12 [15]. CsA also given according to three different regimens: a standard dose, a low dose or a low dose which was withdrawn after 3 months. Study 6 included 85 stable renal transplant recipients, at least 6 months after surgery, treated with 1, 1.25 or 1.5 g MMF twice daily [16]. One full concentration-time curve was obtained from every patient. Samples were taken predose and at 0.33, 0.67, 1.25, 2, 3, 4, 6, 8 and 12 h after MMF intake. All patients also received CsA. In each study prednisone was used according to routine practice. In study 4 and in a subset of patients in study 5, induction therapy with standard doses of daclizumab was administered.

Different high performance liquid chromatography (HPLC) methods were used to measure total MPA concentrations in the six different studies. All six methods complied with the FDA guidance for bioanalytical method validation [17], and had a limit of quantification for total MPA of 0.1 mg l⁻¹. The method used in study 3 [3, 4] is described elsewhere [18]. The intra-assay precision of this method, expressed as coefficients of variation, at the limit of quantification, 1 mg l⁻¹ and 20 mg l⁻¹ was 10.2%, 2.06% and 0.89%, respectively [18]. The corresponding interassay precision at the limit of quantification, 1 mg l⁻¹ and 20 mg l⁻¹ was 2.85%, 1.40% and 1.85%, respectively [18].

Pharmacokinetic analysis

After appropriate pooling, all data were analyzed simultaneously using the nonlinear mixed effects modelling software program NONMEM (double precision, Version V, level 1.1, GloboMax LLC, Hanover, USA). Because NONMEM estimated pharmacokinetic parameters for MPA, MMF doses were converted to the equivalent MPA content. Data were transformed to their natural logarithm and the first order estimation method was used throughout the entire model building process, because of the high computational intensity of the first order conditional estimate method (FOCE).

Basic model

The first step was the development of a compartmental model, in which pharmacokinetic variability and time dependent CL of MPA were characterized. Values for CL, central and peripheral volumes of distribution (V1 and V2, V3) and intercompartmental clearances (Q2, Q3) were estimated. Since bioavailability (F) could not be measured, apparent values of oral CL, Q and V were estimated, these being the ratios CL/F, Q/F and V/F, respectively. Between-patient variability in these parameters was estimated using exponential models. Covariance was estimated between the parameters for between-patient variability. Within-patient variability was also modelled [19]. The difference between observed and model predicted MPA concentrations (residual variability) was modelled as additive to the log of the observed MPA concentration [20].

The time-dependency of MPA CL was modelled as a first order process shown in equation 1:

(1)

where θ_ss is the population value of MPA CL at steady-state, θ_Δ is the change in MPA CL from its steady-state value and θ_rate is a first order rate constant determining the rate at which CL changes over time.

Covariate model

The second step was an analysis of the influence of covariates on the pharmacokinetic parameters. Relationships were investigated in the basic model without time-dependent CL, according to a two-stage approach. In the first stage covariates were introduced separately and tested for their significance in an univariate analysis. Continuous covariates, that could have a value of 0, for example CsA dose, were modelled in a proportional manner with the value centred around its population median as shown in equation 2:

(2)

where θ_pop is the MPA CL in individuals taking the median CsA daily dose of the population (325 mg) and θ_{CsA dose} is the fractional change in CL per mg CsA.

Continuous covariates that cannot have a value 0, for instance weight, were modelled in an exponential manner, which allows for estimation of nonlinear relationships (equation 3):

(3)

in which θ_pop is the MPA CL in individuals with the median weight of the population (71 kg) and θ_Weight is an exponent determining the shape of the relationship. Categorical variables, for example gender, were modelled as shown in equation 4:

(4)

where θ_pop is the population value of MPA CL in females (gender = 0) and θ^gender is the fractional change in CL in males (gender = 1). Covariates with less than 4% of missing data were imputed with population median values during the following time frames after transplantation: days 0–4, days 5–8, week 2, week 3, week 4, month 2, month 3, month 4, month 5, month 6, the second half of the first year and beyond the first year. The population median used for imputation corresponded with the time after transplantation at which covariate data were missing. The value of 4% for the missing data was arbitrarily chosen. When this value was exceeded, an adjustment was made in the model according to equation 5, which is derived from equation 3:

(5)

where the indicator variable FLAGij has the value of 1 when covariate data are present for the i^th individual on the j^th occasion and 0 when data are missing. The consequence of this is that observed MPA concentration-time data from patients with missing covariate data are ignored for estimation of the effect of that covariate (θ_Weight), and are used in the estimation of θ^1–FLAGij. θ^1–FLAGij has no further pharmacokinetic meaning.

Whether a covariate had a significant effect was determined by the difference between the minimum value of objective function (OFV) generated by NONMEM for two hierarchical models [21]. When inclusion of a covariate caused a decrease in the OFV of >10.8 units (P < 0.001, 1 degree of freedom), it was considered to be statistically significant. In addition, a decrease in the estimate for between- and within-patient variability was a criterion for covariate selection.

All covariates selected during the first stage were then included in an intermediate model, and were excluded separately from the intermediate model in a backward elimination procedure. If the elimination of a covariate significantly worsened the fit of the model (i.e. an increase of OFV >10.8), the covariate remained in the model. The result of the backward elimination procedure was the final model.

The final model was refined by testing models for covariates structurally changing over time as described by Wählby et al. [22], when visual inspection of a correlation between time and the covariates indicated such a trend. Models for time-varying covariates may provide more valuable information than time-constant covariate models (equations 2 and 3), because the effect of a covariate on between-patient variability in a pharmacokinetic parameter can be estimated separately from the effect of that covariate on within-patient variability [22]. These models also allow the magnitude of an effect of a covariate on a pharmacokinetic parameter to vary between individuals, thus allowing the estimation of between-patient variability as shown in equation 6, which is derived from equation 3[22]:

(6)

where η_Weight is a random variable with mean 0 and variance ω² allowing the effect of weight on CL (θ_Weight) to vary between individuals.

The time-dependent CL term (equation 1) was included in the final model again to test the hypothesis that the selected covariates could describe all the time-dependency in this parameter.

The adequacy of these NONMEM models was evaluated using the precision of the parameter estimates and goodness-of-fit plots [23]. Goodness-of-fit plots were generated in Xpose (version 3.010), an S-PLUS based (Version 6.2, professional edition, Seattle, USA) modelling aid [24].

Model validation

The stability and the performance of the final model were assessed by an internal validation, using the bootstrap resample technique [25]. During this procedure approximately 65% of the original data were resampled with replacement, which produces different combinations of data sets. The final model was fitted to each artificial sample and estimates for all parameters were produced. For this purpose the bootstrap option in the software package Wings for NONMEM (Nick Holford, version 405, November 2003, Auckland, New Zealand) was used.

Results

In total, 1894 concentration-time profiles were available from 468 renal transplant recipients, ranging from one to nine profiles per patient. Demographic data are summarized in Table 1. Sampling occasions varied from day 1 to day 3795 (>10 years) after transplantation and MMF doses ranged from 250 mg to 2200 mg twice daily. Data were simultaneously fitted to several compartmental models. A two-compartment model with a time lagged first order absorption resulted in the best goodness-of-fit. Typical population estimates of the pharmacokinetic parameters for this basic model are summarized in Table 2. Coefficients of variation for between- and within-patient variability were estimated for the first order absorption rate constant (k_a), V1, CL and Q (Table 2). Estimates for within-patient variability (κ) in this model showed a skewed distribution with mean (± SEM) values significantly greater than zero soon after transplantation (e.g. 0.074 ± 0.010 at the first sampling time, P < 0.001) and mean values significantly less than zero on later occasions (e.g. −0.037 ± 0.010 for the last sampling time, P < 0.001).

Table 1.

Patient demographics and biochemical parameters on four sampling occasions after renal transplantation (median (range))

Characteristics	Missing data	Days 0–4	Month 1	Month 6	Year 1
Gender (n)
Male	0%	157	119	87	104
Female	0%	89	69	47	67
Race (n)
Caucasian	0%	217	168	121	131
Black	0%	17	7	4	37
Other	0%	12	13	9	3
Diabetes mellitus (n)	0%	49	17	15	16
DGF (n)	3.8%	34	–	–	–
Use of antacids (n)	0%	56	24	0	1
Use of proton pump inhibitors (n)	0%	7	13	0	0
Use of H2-receptor antagonists (n)	0%	66	82	3	5
Use of antiviral agents (n)	0%	68	8	1	0
Use of sirolimus (n)	20%	21	27	17	2
Age (years)	0%	50 (18–72)	50 (19–70)	49 (28–70)	52 (22–73)
Body weight (kg)	0.1%	71 (37–151)	68 (38–151)	80 (42–151)	75 (49–122)
Serum creatinine (µmol l−1)	2.9%	424 (66–1379)	128 (53–913)	124 (62–195)	125 (52–221)
Creatinine clearance (ml min−1)	2.9%	19 (4–132)	55 (7–203)	71 (44–132)	64 (34–113)
Plasma albumin (g l−1)	14%	35 (23–51)	35 (26–50)	36 (29–45)	42 (31–48)
Serum ALT (U l−1)	12%	17 (2–653)	17 (4–144)	25 (10–128)	20 (11–1759)
Serum total bilirubin (mg dl−1)	12%	0.5 (0.2–3.0)	0.6 (0.1–1.9)	0.5 (0.1–1.6)	0.7 (0.2–3.3)
Serum alkaline phosphatase (U l−1)	12%	64 (17–870)	86 (25–221)	99 (46–218)	171 (41–347)
Red blood cell count (×1012 l−1)	20%	3.2 (1.5–4.8)	3.4 (2.1–4.9)	4.3 (3.5–5.9)	4.4 (3.7–9.5)
Haemoglobin (g dl−1)	3.5%	9.7 (4.9–17)	11 (6.7–15)	12 (9.6–18)	13 (7.8–18)
Prednisone daily dose (mg)	11%	30 (20–1365)	19 (7.5–35)	10 (0–10)	9.4 (0–10)
Cyclosporin daily dose (mg)	4.8%	530 (0–1000)	350 (0–1400)	100 (0–200)	138 (0–300)
Cyclosporin predose concentration (ng ml−1)	5.3%	171 (0–806)	237 (0–571)	93 (0–316)	155 (0–1337)
Patients not using cyclosporin (n)	4.8%	102	27	17	34
Mycophenolate mofetil dose (mg twice daily)	0%	1150 (400–2200)	1000 (250–2200)	1000 (1000–1000)	1000 (250–1250)

Data were collected from 468 renal transplant recipients participating in six clinical studies. Because of different sampling times after transplantation in the studies, the number of individuals from whom data were available differs for the four presented occasions. n = number of renal transplant recipients, DGF = delayed graft function. Normal values as used at Erasmus MC, Rotterdam, the Netherlands for creatinine: 65–115 mol l⁻¹ for males and 55–90 mol l⁻¹ for females, for plasma albumin: 35–50 g l⁻¹, for serum ALT: < 41 U l⁻¹ for males and < 31 U l⁻¹ for females, for serum total bilirubin: < 1 mg dl⁻¹, for serum alkaline phosphatase: < 120 U l⁻¹, for red blood cell count: 4.4–5.6×¹⁰¹²l⁻¹ for males and 3.9–4.9 × ¹⁰¹²l⁻¹ for females, for haemoglobin: 13.8–16.9 g dl⁻¹ for males and 12.1–15.3 mg dl⁻¹ for females.

Table 2.

Parameter estimates for the basic model with and without time-dependent (td) CL, the final model and the bootstrap procedure and their coefficients of variation (CV)

Parameter	Basic model without tdCL	Basic model with tdCL Estimate (CV%)	Final model	500 Bootstrap replicates of the final model Mean estimate (CV%)
Minimum OFV	454.9	163.5	−505.5
PK parameters
ka (h–1)	4.4 (6%)	3.6 (5%)	4.0 (7%)	4.0 (8%)
V1 (l)	131 (8%)	111 (10%)	69 (6%)	70 (4%)
CL (l h–1)	27 (4%)	–	23 (2%)	23 (3%)
V2 (l)	449 (10%)	388 (9%)	298 (8%)	299 (8%)
Q (l h–1)	64 (11%)	49 (10%)	34 (7%)	35 (9%)
tlag (h)	0.21 (2%)	0.24 (1%)	0.24 (1%)	0.23 (5%)
Time-dependent parameters
CLss (l h–1)	–	20 (3%)	–	–
CLΔ (l h–1)	–	14 (6%)	–	–
θrate (h–1)	–	8.8 × 10−4 (12%)	–	–
Between-patient variability
ka (%)	156 (13%)	112 (15%)	101 (14%)	109 (12%)
V1 (%)	148 (13%)	113 (17%)	90 (16%)	94 (9%)
CL (%)	44 (9%)	38 (9%)	36 (9%)	36 (5%)
Q (%)	104 (25%)	78 (22%)	60 (21%)	61 (12%)
Covariance (r) in estimates for between-patient variability
rka–V1	0.74 (15%)	–	0.45 (28%)	0.49 (18%)
rka–CL	0.14 (67%)	–	−0.13 (67%)	−0.13 (66%)
rka–Q	0.54 (29%)	–	0.21 (72%)	0.23 (66%)
rV1–CL	0.40 (21%)	0.44 (19%)	0.45 (17%)	0.43 (16%)
rV1–Q	0.46 (27%)	0.55 (24%)	0.33 (30%)	0.31 (34%)
rCL–Q	0.50 (19%)	0.56 (17%)	0.54 (18%)	0.51 (19%)
Within-patient variability
ka (%)	137 (12%)	124 (14%)	116 (10%)	117 (6%)
V1 (%)	89 (11%)	80 (13%)	71 (12%)	71 (6%)
CL (%)	34 (7%)	24 (10%)	21 (10%)	21 (5%)
Q (%)	77 (23%)	74 (22%)	41 (39%)	41 (21%)
Residual variability
Additive error (mg l–1)*	0.42 (2%)	0.44 (2%)	0.44 (2%)	0.43 (2%)
Covariate effects
CsA dose on ka	–	–	9.8 × 10−4 (20%)	9.4 × 10−4 (20%)
Factor for missing data			0.99 (12%)	0.98 (14%)
Albm on V1	–	–	−1.2 (17%)	−1.2 (17%)
Factor for missing data	–	–	1.0 (6%)	1.1 (6%)
CLCR on V1	–	–	−0.49 (10%)	−0.48 (10%)
Antacids on V1	–	–	1.4 (8%)	1.4 (8%)
CsA predose concentration on CL	–	–	4.8 × 10−4 (16%)	4.8 × 10−4 (16%)
Factor for missing data	–	–	0.96 (5%)	0.96 (5%)
Albm on CL	–	–	−0.72 (13%)	−0.71 (13%)
Factor for missing data	–	–	1.1 (3%)	1.1 (3%)
CLCR on CL	–	–	−0.22 (7%)	−0.22 (8%)
Hb on CL	–	–	−0.48 (16%)	−0.48 (16%)
Between-patient variability in covariate effects
CLCR on CL (%)	–	–	66 (29%)	67 (15%)
Albm on CL (%)	–	–	112 (44%)	115 (23%)

^*Residual variability is on a natural logarithmic-scale as data were logarithmically transformed.tdCL = time-dependent CL, OFV = objective function, k_a = first order absorption rate constant, V1 = central distribution volume, CL = clearance, V2 = peripheral distribution volume, Q = intercompartment clearance, t_lag = lag time, CL_ss = steady-state value of CL, CL_Δ = change of MPA CL from its steady-state value, θ_rate = first order rate constant determining the rate with which CL changes over time, r = correlation coefficient, CL_CR = creatinine clearance, Albm = plasma albumin concentration, Hb = haemoglobin, CsA = cyclosporin. Typical k_a, V1 and CL values can be calculated as follows:

k_a = 4.0 × (1 + 9.8 × 10⁻⁴ × (CsA dose-325) × FLAG3ij) × 0.99^1–FLAG3ij

V1 = 69 × (CL_CR/50)^−0.49 × (Albm/38)^{–1.18 ×FLAG1ij} × 1. 0^1–FLAG1ij × 1.4^antacids

CL = 23 × (CL_CR/50)_CR^{−0.22 ×exp(ηCL}) × (Albm/38)_Albm^{−0.72 ×exp(η}) ^×FLAG1ij × 1.1^1–FLAG1ij × (1 + 4.8 × 10⁻⁴ × (CsA predose−200) × FLAG2ij) × 0.96^1–FLAG2ij × (Hb/11)^−0.48

where FLAG1ij, FLAG2ij and FLAG3ij are 1 when Albm, CsA predose concentration and, respectively, CsA dose data are present and 0 when covariate data are missing.

When time-dependent CL (equation 1) was incorporated into this basic model, the goodness-of-fit improved and estimates for between- and within-patient variability decreased (Table 2). The decrease in OFV was 291 units, but this cannot be used formally as a criterion for goodness-of-fit in this situation. Within-patient variability in CL decreased from 34 to 24% and κ estimates had mean (± SEM) values much closer to 0 on all occasions relative to the basic model without the time-dependent CL, e.g. −0.01 ± 0.01 at the first sampling time. Time-dependent CL was characterized as follows (equation 7):

(7)

The value of 8.8 × 10⁻⁴ h⁻¹ for θ_rate was used in the expression ln2/8.8 × 10⁻⁴ to derive an estimate for the half-life of MPA CL of 33 days. According to equation 7, the model predicts a MPA CL of 34 l h⁻¹ (θ_{ss +} θ_Δ) immediately after renal transplantation, which decreases over a period of 165 days (five times the MPA CL half-life) to 20 l h⁻¹ (Table 2, Figure 1a).

Figure 1.

a) Time after renal transplantation vs. mycophenolic acid (MPA) clearance (CL) based on the basic model with time-dependent CL. Open circles are individual Bayesian estimated CL values, and the solid line represents the model estimated relationship between time and CL according to equation 7. b) Time after renal transplantation vs. MPA CL based on the final model. Open circles are Bayesian estimated CL values and the solid line represents the median MPA CL–time course

Although equation 7 is able to describe the changes in MPA CL over time, a model in which covariates describe this time-dependency is more useful for therapeutic drug monitoring. In order to identify such covariates the following variables were tested in the basic model without time-dependency: ethnic group (Caucasian, African-American, other), age, gender, weight, plasma albumin concentration (Albm), ALT, bilirubin, alkaline phosphatase, haemoglobin (Hb), red blood cell count, delayed graft function (DGF, defined as the need for dialysis during the first 2 weeks after transplantation), diabetes mellitus, MMF dose, CsA dose, CsA predose concentration, corticosteroid dose, the use of antiviral agents, antacids, H₂-receptor antagonists and sirolimus. Renal function was assessed from the creatinine clearance (CL_CR) according to Cockcroft & Gault [26] and the glomerular filtration rate using the abbreviated Modification of Diet and Renal Disease method (aMDRD) [27]. Because univariate correlations between pharmacokinetic parameters and CL_CR explained more variability than correlations with aMDRD, CL_CR was used as the measure for renal function.

After the backward elimination procedure, CsA dose was significantly correlated with k_a; CL_CR, Albm and the use of antacids was significantly correlated with V1; CL_CR, Albm, CsA dose and Hb had a significant effect on CL (Table 2). Exclusion of each of these covariates during the backward elimination procedure resulted in an increase in OFV of at least 20 units (P < 0.001). Despite a weaker correlation between CsA predose concentration and CL compared with CsA dose in the backward elimination procedure, the former parameter was included in the covariate model as exposure to CsA, and thereby the effectiveness of CsA therapy is better reflected by the predose concentration than by CsA dose. Equation 8 shows the results of the covariate analysis for MPA CL:

(8)

where FLAG1ij is 1 when Albm covariate data are present and 0 when they are missing. The same applies for FLAG2ij with regard to CsA predose concentration data. In equation 8, a change in CL_CR from 19 to 71 ml min⁻¹ in a typical patient (Albm 38 g l⁻¹, Hb 11 mg dl⁻¹, CsA predose 200 ng ml⁻¹) was asociated with a decrease in MPA CL from 28 to 21 l h⁻¹ (Figure 2a). This relationship explained no between-patient variability, but 19% within-patient variability, as determined by the comparison between the variability estimates in the final model containing and not containing the relationship. An increase in Albm from 35 to 40 g l⁻¹ was associated with a decrease of CL from 24 to 22 l h⁻¹ (Figure 2b). This correlation explained 5% between and 12% within-patient variability. An increase in Hb from 9.7 to 12 mg dl⁻¹ was asociated with a decrease in CL from 24 to 22 l h⁻¹. A further 5% between and 4% within-patient variability was explained by this correlation. Finally, a decrease in CsA predose concentration from 225 to 100 ng ml⁻¹ was associated with a decrease in MPA CL from 23 to 22 l h⁻¹. This relationship explained 3% between and 3% within-patient variability. These changes in covariate values are representative for the changes within a patient during the first 6 months after transplantation (Table 1). When they occur simultaneously, equation 8 predicted a decrease of MPA CL from 32 to 19 l h⁻¹, indicating that the covariates can describe the time-dependent decrease in CL (Figure 1b).

Figure 2.

a) Correlation between creatinine clearance (CL_CR) and mycophenolic acid (MPA) clearance (CL) as identified in the final model. The solid line represents the model predicted relationship for a typical patient with an albumin concentration of 38 g l⁻¹, a haemoglobin of 11 g dl⁻¹ and a cyclosporin predose concentration of 200 ng ml⁻¹ according to equation 8. b) Correlation between albumin concentration and MPA CL as identified in the final model. The solid line represents the model predicted relationship for a typical patient with a CL_CR of 50 ml min⁻¹, a haemoglobin of 11 g dl⁻¹ and a cyclosporin predose concentration of 200 ng ml⁻¹ according to equation 8. The broken lines in both (a) and (b) represent the 5 and 95%iles of the between-patient variability in both relationships, illustrating that the magnitude of the effect of CL_CR and albumin concentration on MPA CL varies between individuals. Thus a given change in CL_CR or albumin concentration can have a large effect on MPA CL in one patient (95%ile, dotted line), but a small effect in another patient (5%ile, dashed line). The between-patient variability in the effects of CL_CR and albumin concentration on MPA CL was modelled according equation 6. Because CL_CR values above 120 ml min⁻¹ are not physiologically plausible in renal transplant patients, the solid and broken lines in (a) are truncated at 120 ml min⁻¹. Data for CL_CR above 150 ml min⁻¹ are not shown (n = 4)

During model refinement, introduction of between-patient variability in the effect of CL_CR and Albm on MPA CL according to equation 6, resulted in a significant improvement in fit, with the OFV decreasing by 28 and 36 units, respectively (P < 0.001) and within-patient variability in CL decreasing from 23% to 20% [21]. Between-patient variability in the effect of CL_CR and Albm on CL was 66% and 112%, respectively (equation 8, Table 2, Figures 2a, b).

Introduction of a time-dependent CL term (equation 1) into the final model produced an OFV which was 160 units lower than the model without this. Although an improvement in fit is suggested, this model did not converge successfully, in contrast to the covariate model without the time-dependent CL. The latter allowed the estimation of time-dependent CL through the effect of covariates as shown in Figure 1b and had κ estimates with mean (±SEM) values close to 0 on all occasions (e.g. −0.003 ± 0.005 on the first and −0.006 ± 0.003 on the last occasion). For these reasons, this model was accepted as the definitive final model.

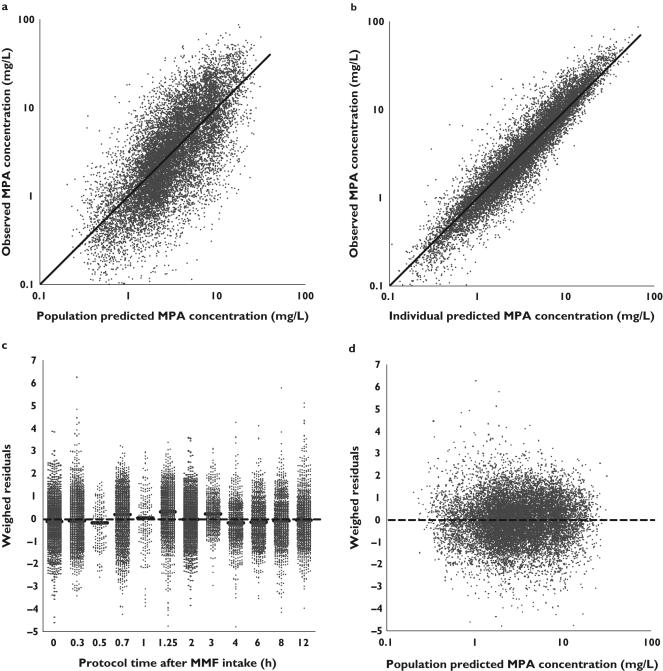
The goodness-of-fit plots of the final model are presented in Figure 3(a–d) and show a random distribution of data points around the line of identity (Figures 3a, b) and the line WRES = 0 (Figures 3c, d), indicating that the model is free from bias. However, Figure 3c shows that maximum MPA concentrations, occurring between 0.7 and 1.25 h after MMF administration, are slightly underestimated by the model. Because these underpredictions are within acceptable limits (95.2% of all WRES fall between −2 and 2), we conclude that the model describes the data adequately.

Figure 3.

Goodness-of-fit plots for the final model. a) Population predicted mycophenolic acid (MPA) concentration vs. observed MPA concentration, b) Individual Bayesian predicted MPA concentration vs. observed MPA concentration, c) Protocol sample time vs. weighed residuals and d) population predicted MPA concentration vs. weighed residuals. The solid lines in (a) and (b) represent the lines of identity. The dotted lines in (c) and (d) represents the line y = 0. The small solid horizontal lines in (c) represent the median weighed residual for the protocol sampling times

Five hundred bootstrap replicates were carried out and all converged successfully. No bootstrapped parameter estimate differed by more than 9% from its corresponding estimate in the final model (Table 2).

Discussion

The pharmacokinetics of MPA are complex as a result of large between-patient variability in MPA exposure and a gradual increase in MPA concentration over time after renal transplantation [2, 3, 8, 10]. The time-dependent changes in MPA pharmacokinetics result in at least a 30% to 50% increase in AUC(0,12 h) during the first weeks after transplantation [2]. The present study has shown that the time-dependent change of exposure to MPA is caused by decreasing MPA CL, due to a combination of improving CL_CR, increasing Albm, increasing Hb and decreasing CsA predose concentrations during the first 6 months after transplantation. A number of observations from the present analysis provide evidence for this statement. First, whereas the final model successfully minimized without error messages, a model in which both the time-dependent CL term and the covariate effects were included, did not converge successfully. Convergence could not be effected by changing the significant digits or the initial estimates of the model. Unsuccessful convergence could be indicative of over-parameterization, suggesting that the data did not contain sufficient information to support reliable estimation of all the parameters in the model. Second, the estimated change in MPA CL as predicted by the basic model with the time-dependent CL-term (equation 7) from 34 to 20 l h⁻¹ over a period of the first 165 days after transplantation, is very similar to the change in CL from 32 l h⁻¹ to 19 l h⁻¹ in the final model described by typical changes in covariate values over that same period of time (Table 1, Figures 1a, b). Third, whereas within-patient variability (κ) should have a normal distribution around 0, estimates of κ in the basic model without time-dependent CL showed a skewed distribution with mean values >0 early after transplantation and mean values < 0 on later occasions. This suggests that the structural time-dependent effect is taken into account by the estimates for within-patient variability. In contrast, κ estimates in the basic model with time-dependent CL as well as in the final model had mean values much closer to 0 on all occasions.

The influence of CL_CR on MPA CL may be explained through an effect on MPA protein binding. Acidosis and uraemia are associated with impaired renal function and will decrease MPA binding to albumin [10]. Moreover, accumulation of the glucuronide metabolite of MPA (MPAG) during renal impairment will displace MPA from its albumin binding sites [28]. As MPA is thought to be a restrictively cleared drug, the resulting increase in MPA free fraction will lead to an increase of the amount of MPA available for glucuronidation and hence to a higher MPA CL [10, 29, 30]. In addition, the increase in MPA CL associated with low albumin concentrations is likely to be due to an increased free fraction of the drug. The same mechanism might also explain the effect of Hb on CL, but in an in vitro study, the fraction MPA found in red blood cells was very small (0.001%), making this possibility uncertain [28].

The effect of CsA predose concentration on MPA CL can be explained by an inhibitory effect of CsA on the enterohepatic recirculation of MPA [31–33].

The use of antacids was associated with a 40% higher V1. Antacids containing aluminium or magnesium ions are known to be capable of interacting with co-administered drugs through formation of nonabsorbable complexes. As V1 represents apparent oral V1 (V1/F), patients who used antacids may have a 40% lower F as a consequence of the binding of MPA to these drugs in the gut [1]. However, an effect of antacids on apparent oral CL, which would also be expected, was not detected, and thus the mechanism of the effect of antacids on V1 remains uncertain.

The covariates affecting MPA CL, namely CL_CR, Albm, Hb and CsA predose concentration, are frequently measured in renal transplant recipients to monitor their clinical status. The easy availability of these parameters offers opportunities for clinicians to optimize MMF therapy. The first week after renal transplantation the population CL was 32 l h⁻¹, resulting in an AUC(0,12 h) of 31 mg l⁻¹ h after a standard MMF dose of 1000 mg. Consequently, a large proportion of the population will be below the AUC(0, 12 h) target limit of 30 mg l⁻¹ h [8]. These are most likely patients with poor renal function, low Albm, low Hb and those concurrently treated with CsA. Therefore, it is advisable to measure MPA exposure in these patients to select those who need a dose increase to reach target exposure. By monitoring CL_CR, Albm, Hb and CsA predose concentrations, changes in MPA CL over time can be compensated for. Measurement of MPA exposure after the abovementioned variables have stabilized, or after CsA dose tapering, can identify those with high AUC(0,12 h) values (above 60 mg l⁻¹ h [8]) and who may benefit from a MMF dose reduction. As the recommended target AUC(0,12 h) values for MPA have only been validated for the first half year after transplantation, studies relating MPA exposure to long-term outcomes would be of benefit [8].

Despite having identified significant correlations between MPA CL and CL_CR, Albm, Hb and CsA predose concentration, therapeutic monitoring of MPA remains advisable for MMF dose adjustment for the following reasons: 1) large between-patient variability was observed for the effect of CL_CR and Albm had on MPA CL (66 and 112%, respectively). Thus a given change in CL_CR or Albm does not necessarily lead to the same change in CL in all patients [22]. Consequently, a change in these covariates is not an indication for dose adjustment, but provides a rationale for measuring MPA concentration to assess whether exposure has changed and whether MMF dose adjustments are needed [8] and 2) the identified covariates explained insufficient between- and within-patient variability in MPA CL to serve as a basis for MMF dose selection.

The validity of the final model was confirmed by the results of the bootstrap procedure, and the parameter estimates and covariate effects are, in general, in agreement with previous population pharmacokinetic studies of MPA [33–39]. However, an underestimation of the observed maximum MPA concentrations was seen. The likely reason for this is that with orally administered drugs, conventional compartmental models with a lag time and a first or zero order absorption rate constant are often not able to predict accurately a rapid initial increase in plasma concentration [40]. Models with time-dependent absorption or with a dual sequential first order absorption process were tested on a subset of the data, but the fit was not significantly improved.

Only two of the previous population studies of MPA included enterohepatic circulation in their final model [33, 37], which is a well-known feature of MPA pharmacokinetics [1]. The present final model did not incorporate it. Nevertheless, ignoring this phenomenon did not result in gross model misspecification. Four hundred and thirty-eight out of the 468 patients were treated with CsA during at least a part of the study, and CsA is known to inhibit the enterohepatic circulation of MPA [31, 32]. However, the observed small overestimation of low MPA concentrations, occurring at the end of a dosing interval, may be the result of the inability to fit secondary peak concentrations.

In conclusion, on the basis of a population pharmacokinetic meta-analysis, the time-dependent CL of MPA could be described by changes in CL_CR, Albm, Hb and CsA predose concentration. This can be used to decide when to measure MPA exposure to reach and maintain predefined MPA target concentrations with a limited number of sampling occasions [41, 42].