Population pharmacokinetic and pharmacodynamic models of remifentanil in healthy volunteers using artificial neural network analysis

Abstract

Aims

An ordinary sigmoid E_max model could not predict overshoot of electroencephalographic approximate entropy (ApEn) during recovery from remifentanil effect in our previous study. The aim of this study was to evaluate the ability of an artificial neural network (ANN) to predict ApEn overshoot and to evaluate the predictive performance of the pharmacokinetic model, and pharmacodynamic models of ANN with respect to data used.

Methods

Using a reduced number of ApEn instances (n = 1581) to make NONMEM modelling feasible and complete ApEn data (n = 24 509), the presence of overshoot was assessed. A total of 1077 measured remifentanil concentrations and ApEn data, and a total of 24 509 predicted concentrations and ApEn data were used in the pharmacodynamic model A and B of ANN, respectively. The testing subset of model B (n = 7352) was used to evaluate the ability of ANN to predict overshoot of ApEn. Mean squared error (MSE) was calculated to evaluate the predictive performance of the ANN models.

Results

With complete ApEn data, ApEn overshoot was observed in 66.7% of subjects, but only in 37% with a reduced number of ApEn instances. The ANN model B predicted 77.8% of ApEn overshoot. MSE (95% confidence interval) was 57.1 (3.22, 71.03) for the pharmacokinetic model, 0.148 (0.004, 0.007) for model A and 0.0018 (0.0017, 0.0019) for model B.

Conclusions

The reduced ApEn instances interfered with the approximation of true electroencephalographic response. ANN predicted 77.8% of ApEn overshoot. The predictive performance of model B was significantly better than that of model A.

Introduction

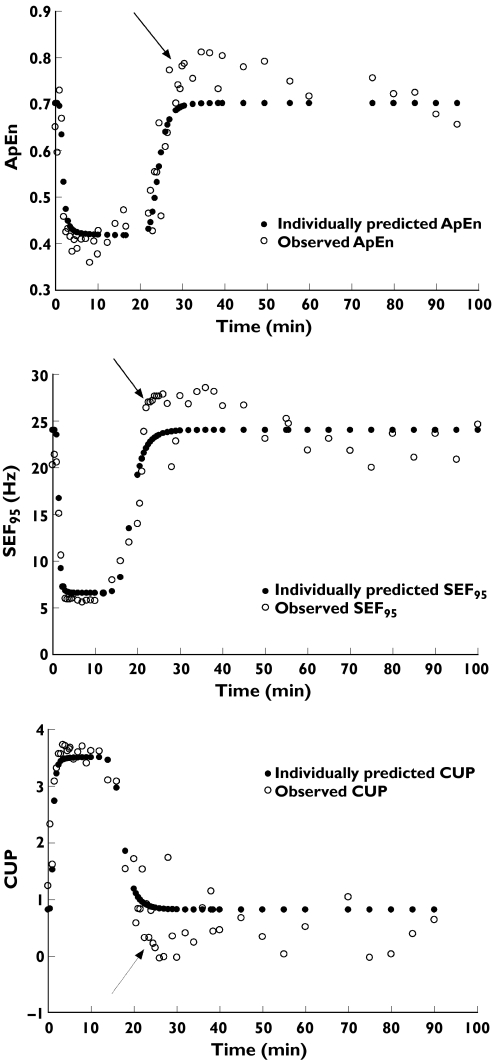
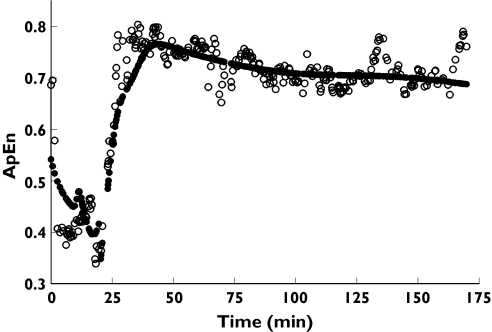
In a clinical investigation evaluating electroencephalographic (EEG) approximate entropy (ApEn) changes in healthy volunteers during remifentanil infusion [1], we observed overshoot of ApEn [2], 95% spectral edge frequency (SEF₉₅) and canonical univariate parameter (CUP) [3], which were used as surrogate measures of the central nervous system effect of remifentanil, during recovery from profound remifentanil effect (Figure 1).

Figure 1.

Typical examples of overshoot of electroencephalographic approximate entropy (ApEn), 95% spectral edge frequency (SEF₉₅) and canonical univariate parameter (CUP) during recovery from profound remifentanil effect (arrow). ApEn (upper panel, volunteer ID 1), SEF₉₅ (middle panel, volunteer ID 14), and CUP (lower panel, volunteer ID 18)

There have been a few studies of the population pharmacodynamic model of remifentanil using an ordinary sigmoid E_max model fitted by NONMEM (GloboMax LLC, Hanover, MD, USA), in which SEF₉₅ was used as a surrogate measure of the central nervous system effect of remifentanil [4, 5]. No study has indicated that the initial EEG response to opioid administration differs from that during recovery from the effect of opioids on the human central nervous system. Additionally, in these and our own studies, the number of processed EEG parameters such as ApEn, SEF₉₅ and CUP should have exceeded that of measured concentrations of remifentanil because these EEG metrics can be calculated every 10–20 s from continuously recorded raw EEG data. For example, we selected 1581 points (59 ± 6 points per individual, mean ± SD) out of 24 509 measurements of ApEn for population pharmacodynamic modelling using an ordinary sigmoid E_max model fitted by NONMEM [1]. Because the default maximum number of observations per subject is set to 50, and with increasing this number the computing time should be prolonged, NONMEM requires reduction of these abundant EEG data for the sake of efficient computing, which might interfere with the approximation of the true EEG response to remifentanil.

The overshoot of processed EEG parameters during recovery and the probable loss of information in the selected EEG data may advocate an alternative pharmacodynamic modelling method, other than an ordinary sigmoid E_max, to model the EEG response to opioids.

Several new methods for mathematical modelling have emerged in pharmacokinetics and have shown good performance in solving pharmacokinetic problems [6–8]. One of them, artificial neural network (ANN), is a powerful empirical pattern-recognition and mapping tool for approximation of complex nonlinear relationships. Instead of imposing an a priori model on the data, ANN learns input and output relationships directly from the data. The flexibility of the ANN models has led to successful application in population pharmacokinetic and pharmacodynamic data analysis [9–12].

Using the blood concentrations of remifentanil and EEG data obtained from our previous clinical investigation [1], the primary objective of this study was to evaluate if the pharmacodynamic model of ANN, in which complete ApEn data (n = 24 509) were used, can predict the overshoot of ApEn during recovery from profound remifentanil effect. The secondary objective was to evaluate the predictive performance of the pharmacokinetic model, and the pharmacodynamic models of ANN with respect to datasets used in the pharmacodynamic analysis, i.e. measured concentrations of remifentanil and corresponding ApEn data (n = 1077) vs. predicted concentrations of remifentanil calculated from the pharmacokinetic model of ANN and complete ApEn data (n = 24 509).

Methods

Electroencephalographic analysis

In addition to electroencephalographic ApEn derived from the raw EEG data in the previous study [1], we calculated total power, relative δ, θ, α and β band power from 5-min segments that showed overshoot during recovery after termination of remifentanil infusion, and from the baseline EEG activity recorded before remifentanil infusion.

ANN model

SAS ENTERPRISE MINER Release 4.1 was used for ANN analysis (SAS Institute Inc., Cary, NC, USA). Of many different architectures of ANN, the multilayer perceptron (MLP) network has been most commonly used to analyse pharmacokinetic data [10, 13]. An ANN of MLP architecture is capable of approximating any existent nonlinear solution and has demonstrated advantages in at least one population pharmacodynamic analysis [14]. A three-layered MLP, with input, hidden and output layers, was used for pharmacokinetic and pharmacodynamic modelling. A hyperbolic tangent function was used as the activation function. By standard deviation method, the continuous input variables (time, amount, rate, age, height and weight in pharmacokinetic modelling; time, age, height, weight, concentrations of remifentanil in pharmacodynamic modelling) were normalized to a mean of 0 and a SD of 1 [15].

Due to its robustness and fast convergence, the Levenberg–Marquardt method was used for training of pharmacokinetic and pharmacodynamic models [11]. This method adjusts the network weights using the following formula.

(1)

where w is the network weight, J is the Jacobian matrix that contains first derivatives of the network output with respect to the weights, e is the vector of network errors and I is the identity matrix. The coefficient μ controls the step size of the weight update and is varied based on the error convergence. When μ is large, the method becomes gradient descent with a small step size, whereas for μ close to zero, it acts as Newton's method with an approximate Hessian [11].

It is often difficult to generalize the ANN models because of their tendency to over-fit the data. Over-fitting is the circumstance in which ANN fits the specific training data instances so closely that it uses random variance or other idiosyncracies of the training dataset to predict outcome. To prevent this over-fitting, a method to incorporate validation and testing subsets has been adopted [16]. The datasets for pharmacokinetic and pharmacodynamic models were randomly divided into three subsets: training (40%), validation (30%) and testing subset (30%).

The number of iterations was determined by the mean squared error (MSE) of both training and validation subsets. Final pharmacokinetic and pharmacodynamic models were selected according to MSE of the testing subset.

Pharmacokinetic analysis

The input variables, number of instances and number of hidden layer neurons (processing elements) are described in Table 1. The output was transformed using a logistic activation function.

Table 1.

Number of instances, input variables and number of hidden layer neurons of pharmacokinetic (PK) and pharamcodynamic (PD) models of the artificial neural network (ANN)

	PK	PD
		Model A	Model B
Number of instances	1340*	1077†	24 509‡
Input variables	Time	Time	Time
	Amount	Infusion	Infusion
	Infusion	Age	Age
	Rate	Sex	Sex
	Age	Weight	Weight
	Sex	Height	Height
	Weight	Measured concentrations	Predicted concentrations
	Height	of remifentanil	of remifentanil
Number of hidden layer neurons	12	10	9

^*Measured concentrations of remifentanil.

^†Measured concentrations of remifentanil vs. corresponding approximate entropy (ApEn) values.

^‡Predicted concentrations of remifentanil calculated from the pharmacokinetic model of ANN vs. complete ApEn data. Time, time elapsed from the beginning of remifentanil infusion (minutes); Amount, total dose infused (mg); Infusion: 1 during remifentanil infusion, 0 after termination of remifentanil infusion; Rate (mg min⁻¹), Age (years), Sex: 1 male, 0 female, Weight (kg), Height (cm).

Pharmacodynamic analysis

The input variables, number of instances and number of hidden layer neurons characterizing the pharmacodynamic model A and B of ANN are found in Table 1. Model A is the pharmacodynamic model of ANN created with reduced ApEn data (measured concentrations of remifentanil vs. corresponding ApEn values, n = 1077) and model B is the pharmacodynamic model of ANN built with the complete ApEn data (predicted concentrations of remifentanil calculated from pharmacokinetic model of ANN vs. complete ApEn dataset, n = 24 509).

The time delay between measured concentrations of remifentanil and ApEn values in model A was within 10 s, whereas time of predicted concentrations in model B was identical to that of ApEn.

Model performance

MSE, mean absolute error (MAE) and R² were calculated to evaluate the predictive performance of pharmacokinetic and pharmacodynamic models.

Median absolute weighted residual (MDAWR) and mean of the individual mean absolute weighted residuals (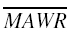) were calculated to assess the predictive performance of pharmacokinetic models. We used the weighted residual to describe the quality of the prediction in each individual, calculated as (measured-predicted)/predicted [17]. Median absolute residual (MAR) was calculated to assess the performance of pharmacodynamic models.

These indices for the pharmacokinetic model of ANN were estimated using fivefold cross-validation with random subsampling. All indices of model performance were calculated from testing subsets of the pharmacodynamic models of ANN and the results of population pharmacokinetic and pharmacodynamic models of NONMEM in our previous study [1].

The corresponding 95% confidence intervals of MSE, MAE and 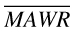were calculated and the statistical differences of MSE, MAE and 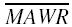between NONMEM and ANN models were tested by a paired t-test or t-test, as appropriate.

Overshoot of ApEn

The overshoot of ApEn during recovery was defined as follows: (i) the ApEn values within 30 min after termination of remifentanil infusion should be > 110% of individual baseline ApEn values; (ii) these overshot values of ApEn should last at least 30 s.

The selection criteria of ApEn data in the previous study [1], which were similar to the work of Minto and associates [5], were as follows: (i) every 30 s during the first 5 min, every 1 min during the second 5 min, every 2 min during the third 10 min after the beginning of remifentanil infusion; (ii) every 30 s during the first 5 min, every 1 min during the second 5 min, every 2 min during the third 10 min after the termination of remifentanil infusion; (iii) and thereafter, every 5–10 min until 170 min after the beginning of remifentanil infusion.

These 1581 measurements of ApEn vs. time, which were selected for the population pharmacodynamic modelling by NONMEM in the previous study [1], were used to assess the presence of overshoot. The number of subjects who showed overshoot of ApEn during recovery was counted on the basis of the relationships between the individually predicted and observed ApEn over time.

According to the previously described criteria for overshoot of ApEn during recovery, the number of subjects in whom overshoot of ApEn was well predicted by the model B of ANN (number of ApEn data = 24509) was counted. The presence of overshoot was assessed using complete ApEn data vs. time. The testing subset of model B (n = 7352) was used to evaluate the ability of model B to predict overshoot of ApEn. Criteria for the prediction of overshoot in testing data of model B were defined as follows: maximal predicted ApEn value should be larger than both baseline observed ApEn value and baseline predicted ApEn value.

Results

Previously, processed EEG parameters and blood concentrations of remifentanil were modelled by the sequential approach of pharmacokinetic and pharmacodynamic modelling [1]. Table 2 shows the final population pharmacokinetic model fitted by NONMEM which was not described in our first study [1]. A total number of 1340 remifentanil blood concentrations was available for pharmacokinetic analysis. All models were fitted using the first-order estimation procedure. A full variance–covariance matrix was estimated for the different distributions of ηs. The minimal value of the objective function (OFV, equal to minus twice the log likelihood) provided by NONMEM was used as the goodness-of-fit characteristic to discriminate between hierarchical models using the log likelihood ratio test. A P-value of 0.05, representing a decrease in OFV of 3.84 points, was considered statistically significant [χ² distribution, degrees of freedom (d.f.) = 1]. A nonparametric bootstrap analysis was performed as an internal model validation, using the software package Wings for NONMEM (N. Holford, Version 404, June 2003, Auckland, New Zealand) [18]. This process was repeated 3000 times.

Table 2.

The estimates of population pharmacokinetic parameters and median parameter values (2.5–97.5%) of the nonparametric bootstrap replicates of the final pharmacokinetic model of NONMEM

Parameter		Estimate	Median	2.5–97.5%	Bias
V1 (θ1)		9.95	10.00	7.95–17.00	0.05
	θ2	0.3	0.3	0.1–0.5	0
	θ9	0.0939	0.0978	0.01–0.23	0.0039
	θ10	0.0491	0.0512	0.01–0.22	0.0021
k12 (θ3)		0.159	0.160	0.115–0.256	0.001
k21 (θ4)		0.136	0.135	0.116–0.154	−0.001
k13 (θ5)		0.0185	0.02	0.01–0.07	0.0015
k31 (θ6)		0.00204	0.002	0.001–0.005	−0.00004
ω2 for V1		0.112	0.346	0.110–0.769	0.234
ω2 for k10		0.159	0.462	0.150–1.269	0.303
ω2 for k12		0.188	0.508	0.112–1.061	0.32
ω2 for k21		0.0157	0.161	0.012–0.422	0.1453
ω2 for k13		12.1	3.6	0.8–13.0	−8.5
ω2 for k31		18.5	4.5	0.7–19.0	−14
σ21 (additive)		0.0496	0.0464	0.003–0.068	−0.0032
σ22 (proportional)		0.247	0.25	0.21–0.44	0.003

BSA, body surface area. Bias = Median – Estimate. ω² and σ², Variance of random effects parameters in log domain (interindividual random variability) and variance of residual random variability, respectively. Interindividual random variability and residual random variability was modelled using log-normal model and additive plus proportional error model, respectively.

ANN model

To avoid multicollinearity, height/body weight/sex, body surface area (BSA)/sex, or lean body mass (LBM) exclusively entered the pharmacokinetic and pharmacodynamic models of ANN. Of these, the combination of height/body weight/sex was selected for both pharmacokinetic and pharmacodynamic models, as it improved the model performance better than BSA/sex or LBM did. These findings are different from the covariates of pharmacokinetic and pharmacodynamic models of NONMEM. In ANN, demographic factors enter a model as independent variables.

Pharmacokinetic analysis

A pharmacokinetic model was selected according to MSE of the testing subset previously described. The number of iterations was 41.

The n-fold cross-validation approach to training and testing has often been used for relatively small numbers of instances [19]. In a preliminary analysis, 10-fold cross validation resulted in a large variability in the performance estimates from fold to fold. Stratification into fivefold cross-validation produced more homogeneous testing subsets and showed less variability in the performance estimates. Because fivefold cross-validation maximizes the number of instances available for both training and testing, the fivefold cross-validation performance estimate was considered a fairly good estimate of true performance. Therefore, performance of the pharmacokinetic model of ANN, selected according to MSE of the testing subset, was estimated using fivefold cross-validation with random subsampling, in which 80% (n₁ = 1072) and 20% (n₂ = 268) of data were used as training and testing subset, respectively [20]. The dataset was randomly split into five mutually exclusive subsets (the folds) D₁, D₂, D₃, D₄, D₅ of equal size. For five experiments, a model structurally identical to the selected pharmacokinetic model of ANN (same architecture, training parameters, inputs and number of hidden layer neurons) was trained (weight adjustment) with n₁ = 1072 training instances, then tested using n₂ = 268 testing instances. Performance estimates were then calculated from all five testing subsets, including every instance (n = 1340). This method enabled optimal performance estimation on the limited dataset, by maximizing the data used for training and simultaneously maximizing the data used for testing. The five test subsets were homogeneous (P = 0.3, one-way anova).

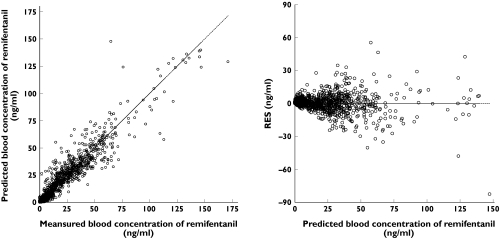
Figure 2 illustrates the relationship between the predicted and measured concentrations of remifentanil in the ANN analysis. The residuals of pharmacokinetic models of NONMEM and ANN showed similar range of values (−42.2 to 76.75 ng ml⁻¹vs.− 82.65 to 55.45 ng ml⁻¹, respectively). At the clinical range of concentrations (<25 ng ml⁻¹), the residuals were much lower than those at higher concentrations of remifentanil.

Figure 2.

The goodness-of-fit plots of the final pharmacokinetic model of artificial neural network (ANN). Left: predicted vs. measured blood concentration of remifentanil, right: residuals (RES) vs. predicted blood concentration of remifentanil

The statistical measures of the performance of the final pharmacokinetic models of NONMEM and ANN are found in Table 3. MSE and MAE of the pharmacokinetic model of ANN were smaller than those of the pharmacokinetic model of NONMEM. 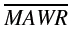of the pharmacokinetic model of ANN was considerably higher than that of the pharmacokinetic model of NONMEM, which resulted from the excessive underprediction of the lower range of remifentanil concentrations in ANN analysis. The median value of the 198 points of measured concentrations, which showed 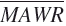≥ 2.0, was 0.4 ng ml⁻¹.

Table 3.

Predictive performance of the pharmacokinetic models of NONMEM and artificial neural network (ANN)

	NONMEM (95% CI)	ANN*(95% CI)
MSE	95.8 (79.2, 112.3)	57.1 (3.22, 71.03)
MAE	5.4 (4.99, 5.87)	4.1 (3.76, 4.44)
MDAWR	0.27	0.31
	0.37 (0.31, 0.42)	2.22 (1.66, 2.78)
R2	0.83	0.90

^*Five testing sets of fivefold cross-validation were combined to obtain predictive performance estimates for ANN. P< 0.001 vs. NONMEM. MSE, mean squared error; MAE, mean absolute error; MDAWR, median absolute weighted residual; 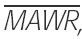mean of the individual mean absolute weighted residuals.

Pharmacodynamic analysis

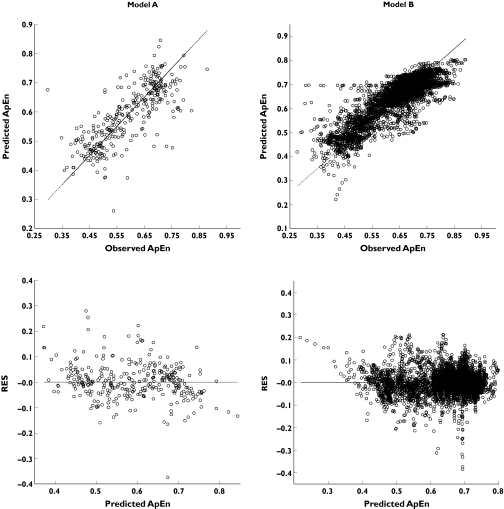
The number of iterations was 9 for model A and 49 for model B. The results of model performance were obtained using testing subsets (n = 323 for model A, 7352 for model B). The predictive performance of the pharmacodynamic models of NONMEM and ANN is summarized in Table 4. The performance of model B was better than that of the ordinary sigmoid E_max model fitted by NONMEM and model A, but there was no difference in model performance between ordinary sigmoid E_max model and model A. The plots of predicted ApEn against observed ApEn, residuals against predicted ApEn in model A and B are illustrated in Figure 3. The residuals of model A and B ranged from − 0.38 to 0.28 and − 0.37 to 0.23, respectively, which were similar to those of the ordinary sigmoid E_max model (−0.40 to 0.29).

Table 4.

Predictive performance of the pharmacodynamic models of NONMEM and artificial neural network (ANN)

	NONMEM	ANN
	Ordinary sigmoid Emax model (95% CI)	Model A (95% CI)	Model B (95% CI)
MSE	0.00725 (0.00594, 0.00731)	0.148 (0.004, 0.007)	0.0018* (0.0017, 0.0019)
MAE	0.058 (0.056, 0.061)	0.052 (0.047, 0.058)	0.0300* (0.0293, 0.0307)
MAR	0.04	0.04	0.02
R2	0.52	0.58	0.74

^*P < 0.01 vs. ordinary sigmoid E_max model. N = 1581 for the pharmacodyanmic model of NONMEM [1]. ANN – model A, the dataset was measured concentrations of remifentanil vs. corresponding approximate entropy (ApEn) values (n = 1077). ANN – model B, the dataset was predicted concentrations of remifentanil calculated from the pharmacokinetic model using ANN vs. complete ApEn data (n = 24 509). MSE, mean squared error; MAE, mean absolute error; MAR, median absolute residual.

Figure 3.

The goodness-of-fit plots of the final pharmacodynamic models of artificial neural network (ANN). Model A: number of approximate entropy (ApEn) instances = 1077 (measured concentrations of remifentanil vs. corresponding ApEn values), model B: number of ApEn instances = 24 509 (predicted concentrations of remifentanil calculated from the pharmacokinetic model of ANN vs. complete ApEn data)

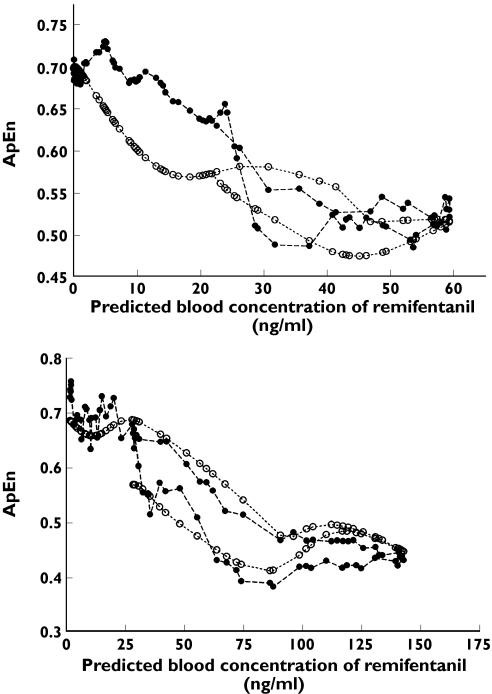
Figure 4 shows the plots of predicted ApEn and observed ApEn against predicted concentrations of remifentanil in two volunteers. ANN accurately predicted the change in observed ApEn at predicted concentrations of remifentanil. The hysteresis loop was seen in Figure 4, suggesting ANN differentially predicted the ApEn values at the same predicted concentrations of remifentanil in the ascending and descending limbs.

Figure 4.

The predicted (○) and observed (•) approximate entropy (ApEn) against predicted blood concentrations of remifentanil, calculated from the final pharmacokinetic model of artificial neural network (ANN), in two volunteers (upper panel: n = 67 for volunteer ID 6, lower panel: n = 66 for volunteer ID 21)

Overshoot of ApEn

In the previous study [1], 1581 measurements of ApEn vs. time were selected for the population pharmacodynamic modelling by NONMEM. When the same dataset was used to assess the presence of overshoot, the number of subjects who showed overshoot of ApEn during recovery was 10 (37.0% of all volunteers). This overshoot was not predicted by the individually predicted ApEn of the final pharmacodynamic model by NONMEM [1].

The number of subjects who showed overshoot of ApEn during recovery was 18 (66.7% of all volunteers), as determined by evaluating complete ApEn data vs. time. Total power, relative δ, θ, α and β band powers in these volunteers are found in Table 5. The increase of β band power, and hence increase of total power during recovery from profound remifentanil effect, is believed to cause the overshoot of ApEn. Using the testing subset of model B, ANN predicted this overshoot in 14 subjects (77.8%) of 18 volunteers who showed overshoot of ApEn. Figure 5 shows observed and predicted ApEn against time in one volunteer (ID 1), in which the overshoot of ApEn was well predicted by model B. The reason we did not examine the prediction of overshoot in model A was that the number (323) of instances in the testing subset of model A was too small.

Table 5.

Total power, relative δ, θ, α and β band powers in volunteers who showed overshoot of the electroencephalographic (EEG) approximate entropy during recovery from profound remifentanil effect

	Baseline	Overshoot
Total power (μV2)	142.4 ± 25.0	340.0 ± 63.8*
Relative δ (%)	53.3 ± 3.5	43.7 ± 3.1*
Relative θ (%)	13.5 ± 0.9	14.5 ± 1.3
Relative α (%)	21.6 ± 3.4	22.5 ± 2.5
Relative β (%)	12.6 ± 1.0	20.6 ± 2.6*

Data are stated as mean ± SE. Five-minute segments of raw EEG data were used to calculate total power, relative δ, θ, α and β band powers for both baseline and overshoot during recovery.

^*P < 0.05 vs. baseline.

Figure 5.

The observed (○) and predicted (•) approximate entropy (ApEn) against time in one volunteer (ID 1). Overshoot of ApEn was well predicted by model B of the artificial neural network

Discussion

The increase of β band power, and hence increase of total power during recovery from profound remifentanil effect, is believed to cause the overshoot of ApEn. This β activation may indicate an increase in vigilance and awareness [21]. The filtering level r of ApEn is calculated as a percentage of the SD of the amplitude values [22]. Thus the increase of the total power is reflected in the calculation of ApEn. Remifentanil is often administered by target controlled infusion (TCI), which is implemented in commercialized TCI devices in the field of anaesthesia [5]. Both the effect-site or plasma concentration of remifentanil can be a target to be controlled during anaesthesia. Pharmacokinetic parameters and k_e0 are needed to calculate the effect-site concentration of remifentanil. Typically, k_e0 was obtained by sequential pharmacokinetic and pharmacodynamic modelling in which three compartmental pharmacokinetic models with added effect compartment and an ordinary sigmoid E_max model were used [1, 5]. However, an ordinary sigmoid E_max model can not predict overshoot of the processed EEG parameters during recovery from profound remifentanil effect on the central nervous system [1]. With complete ApEn data (n = 24 509, model B), the percentage of volunteers who showed overshoot of ApEn during recovery from profound remifentanil effect was 66.7%. However, when the number of ApEn instances was reduced to make NONMEM feasible, this percentage was decreased to 37%, suggesting that the reduction of pharmacodynamic data resulted in inaccurate representation of the real features of response to a drug. Moreover, the ANN model B predicted 77.8% of the overshoot of ApEn, whereas the ordinary sigmoid E_max model fitted by NONMEM could not predict the overshoot at all because it restricted the highest predicted ApEn to E₀. The predictive performance of the pharmacokinetic model of ANN was better than that of NONMEM. However, ANN excessively underpredicted the lower range of measured concentrations of remifentanil (especially below 0.4 ng ml⁻¹). The predictive performance of the ordinary sigmoid E_max model fitted by NONMEM and the pharmacodynamic model A of ANN was similar, suggesting that the model performance of ANN could not be improved with the limited number of pharmacodynamic data. However, the ANN model B using complete ApEn data showed significantly better performance than did the ordinary sigmoid E_max model. This differences of performance between the ordinary sigmoid E_max model and the ANN model B were attributed to the predictive ability of the ApEn overshoot during recovery from profound remifentanil effect. Originally, population pharmacokinetic data analysis technique was developed to analyse sparse within-patient concentration–time data. With the dosing history and clinically relevant measures of response to a drug, we can obtain further insight into the effects of different demographic factors on the behaviour of a drug and pharmacodynamic characteristics. The purpose of pharmacokinetic modelling is to obtain the absorption, distribution, metabolism, excretion and toxicity (ADMET) properties of drugs. In this point of view, ANN might provide us with only limited information on a drug, because a fitting itself for given data can not tell us the mechanistic parameters regarding ADMET properties of drugs. However, if we want to know the natural or real features of response to a drug and a large quantity of pharmacodynamic data can be obtained, ANN may be an excellent alternative to NONMEM, especially in pharmacodynamic modelling. The purpose of calculating the predicted concentrations from the pharmacokinetic model of ANN in the ANN model B was to match the concentration data to all of the ApEn data. Therefore, this approach differed from the NONMEM method to collapse hysteresis loop by k_e0. For the final pharmacokinetic model of NONMEM, interindividual variability of k₁₃ and k₃₁ was very high. This is possibly because there was a considerable number of volunteers who did not have the third compartment, as reported previously [5], or perhaps because of the relatively small sample size. Both the pharmacokinetic and pharmacodynamic models using first-order conditional estimation (FOCE) of NONMEM failed to converge. Joint estimation of θ and η by FOCE may cause computational difficulty, especially when sample size is small [23, 24], which may partly account for convergence failure of FOCE models. For the validation of both the pharmacokinetic and pharmacodynamic models of first-order estimation by NONMEM, nonparametric bootstrap analyses were performed. Estimates of all the structural parameters were similar to the median values of bootstrap replicates and estimates of all the structural and statistical parameters were within 2.5–97.5 percentile (Table 2 in this report and Table 4 in our previous report [1]). Additionally, prediction probability of the calculated remifentanil effect-site concentration for ApEn, which was assessed as described by Smith et al.[25], was good enough to accept that the models were optimal [1, 25]. Minto et al. reported that age/LBM and age were significant covariates for their pharmacokinetic and pharmacodynamic models, respectively [5]. In the pharmacokinetic model of NONMEM in this study, age and BSA were significant covariates of central clearance, which decreased by approximately 24.6% with increasing age. Age was the only significant covariate for both t_1/2k_e0 and Ce₅₀, and t_1/2k_e0 increased by approximately 31.7% and Ce₅₀ decreased by 77.1% with increasing age [1]. These characteristic pharmacokinetic and pharmacodynamic findings in elderly patients are consistent with a previous report [5] and suggest considerable dose reduction in clinical practice. In conclusion, the reduction of pharmacodynamic data to make NONMEM modelling feasible for efficient computation resulted in inaccurate representation of the real features of response to remifentanil. ANN could predict overshoot of ApEn during recovery from profound remifentanil effect using complete ApEn data. The predictive performance of the pharmacokinetic model of ANN was better than that of NONMEM, but tended to underpredict the lower range of measured concentrations of remifentanil. The predictive performance of the pharmacodynamic model of ANN using complete ApEn data was superior to that of the pharmacodynamic model of ANN using measured concentrations of remifentanil vs. corresponding ApEn data.