Abstract
What is already known about this subject
When characterizing an exposure–response relationship it has been suggested that the randomized concentration-controlled trial (RCCT) is potentially a more informative design than a randomized dose-controlled trial design (RDCT).
Traditionally, these trials have been analysed by group-wise comparison or similar statistics.
The aim of this study was to compare different randomization schemes when a model-based analysis has been performed.
What this study adds
Alternative randomization schemes may not have the proposed advantages if a model-based analysis is employed.
Aims
In the literature, five potential benefits of randomizing clinical trials on concentration levels, rather than dose, have been proposed: (i) statistical study power will increase; (ii) study power will be less sensitive to high variability in the pharmacokinetics (PK); (iii) the power of establishing an exposure–response relationship will be robust to correlations between PK and pharmacodynamics (PD); (iv) estimates of the exposure–response relationship are likely to be less biased; and (v) studies will provide a better control of exposure in situations with toxicity issues. The main aim of this study was to investigate if these five statements are valid when the trial results are evaluated using a model-based analysis.
Methods
Quantitative relationships between drug dose, concentration, biomarker and clinical end-point were defined using pharmacometric models. Three randomization schemes for exposure-controlled trials, dose-controlled (RDCT), concentration-controlled (RCCT) and biomarker-controlled (RBCT), were simulated and analysed according to the models.
Results
(i) The RCCT and RBCT had lower statistical power than RDCT in a model-based analysis; (ii) with a model-based analysis the power for an RDCT increased with increasing PK variability; (iii) the statistical power in a model-based analysis was robust to correlations between CL and EC50 or Emax; (iv) under all conditions the bias was negligible (<3%); and (v) for studies with equal power RCCT could produce either more or fewer adverse events compared with an RDCT.
Conclusion
Alternative randomization schemes may not have the proposed advantages if a model-based analysis is employed.
Keywords: clinical trial simulation, model-based analysis, pharmacometrics, randomized concentration-controlled trial, randomized dose-controlled trial, study design
Introduction
The randomized dose-controlled trial (RDCT) is presently the most used clinical trial design. The simplicity in assigning the patients to different dose groups makes the RDCT easy to perform and cost effective compared with alternative designs. However, when characterizing an exposure–response relationship it has been suggested that the randomized concentration-controlled trial (RCCT) is potentially a more informative design [1, 2], and as an extension to the RCCT the randomized biomarker-controlled trial (RBCT) design has been described [3]. The idea is that since the randomization point is moved closer to the clinical end-point in the chain of causal events, randomizing patients to defined target concentrations or biomarker levels, as opposed to dose, makes it possible to reduce the within-group variability in the response variable in relation to the randomization variable. The drawback with an RCCT/RBCT, on the other hand, is that it is necessary to titrate each patient by some adaptive feedback strategy to ensure that the defined target concentration or biomarker level is reached. This is complicated and costly. A further issue is that it may not be possible to reach the specified target level in some patients, so-called formal data loss, meaning that the desired reduction in variability due to the randomization scheme will not be achieved. These practical complications, in particular the first, in carrying out an RCCT or RBCT have limited their use.
For the sake of this discussion, the evaluation of randomized clinical trials can be divided into two approaches. The first is a ‘traditional’ analysis, e.g. a group-wise comparison, where the aim is to investigate differences between treatment arms [4]. The second is a model-based analysis, where the goal is to establish a hypothesized mathematical model for the relationship under investigation. One benefit of the traditional analysis strategy is that it is relatively objective since the explanatory variable, i.e. the randomization group assignment, is defined prior to the analysis. A model-based analysis is more complicated and requires assumptions about the general underlying form of the exposure–response relationship as well as other assumptions of a more technical nature [5]. On the other hand, it has been shown that a model-based analysis can increase the statistical power of a study by using all the observed data according to their relative information content and by obviating the need for missing data imputation (by, for example, the last observation carried forward algorithm) [6].
From the literature, the expected general benefits of an RCCT over an RDCT can be summarized in five points. As the general ideas are the same for the RCCT and RBCT, these points are expected to apply to the RBCT design also.
Study power will be less sensitive to high variability in the pharmacokinetics (PK) [1, 2, 7].
The power of establishing an exposure–response relationship will be less sensitive to correlations between PK and pharmacodynamics (PD) [1, 2, 7].
The estimates of the exposure–response relationship are likely to be less biased [1, 2, 7].
The studies will provide a better control of exposure in situations with toxicity issues [1, 2].
Statements 1–4 originate from a traditional data analysis point of view [2, 7], where the underlying assumption is that interindividual variability is a confounding factor. Statement 5 refers to the fact that side-effects are related to the level of exposure, similarly to the desired drug effect. Therefore, controlling the exposure levels should also control the incidence of adverse events.
In the early 1990s Sanathanan and Peck [2] published a simulation study where they investigated the improvement in sample size efficiency that can be gained from the RCCT design (i.e. statement 1). Later, Endrenyi and Zha [8] showed that Sanathanan and Peck's results were dependent on the restricted model they used. None of the previous authors on the topic has addressed all five of the potential benefits (mentioned above) of using the RCCT design.
A MEDLINE search of clinical studies with an RCCT design [9–46] shows that most RCCTs were analysed with a traditional statistical approach. Since model-based drug development is becoming more popular and is even being advocated by some regulatory authorities [4, 47], it is of interest to investigate the consequences of different randomization schemes under the assumption of a model-based analysis.
The aim of this simulation study was to investigate the five potential benefits outlined above assuming a model-based analysis and contrast it with a traditional group-wise analysis.
Methods
Data simulation
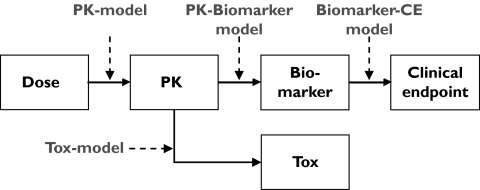
In this study the events caused by administrating the drug to the body is defined as a sequence of dose, plasma concentrations, biomarker and clinical end-point responses, i.e. a mechanistic pathway of drug response, shown in Figure 1. Each step in the sequence was defined by a mathematical model which will be described in further detail. Each simulation setup was replicated 1000 times. The simulations and analyses were made using the software package NONMEM, version VIβ[48] and automated by the use of the programming language perl.
Figure 1.
The model for the mechanistic pathway of drug response consists of: a pharmacokinetic (PK) model for the dose–exposure relationship, a pharmacokinetic biomarker model for the exposure–biomarker relationship and biomarker clinical end-point model for the biomarker–clinical end-point relationship and a pharmacokinetic toxicity (Tox) model for the exposure–toxicity relationship.
Pharmacokinetic model
The dose–concentration relationship was described by a PK model where steady-state conditions were assumed and the ith individual's mean concentration and clearance (CLi) was related to the administered dosing rate (Di) by Equation 1. Interindividual variability in CLi around the typical value of clearance in the population (θCL) was assumed to be log-normally distributed according to Equation 2, where ηCL is a zero mean, normally distributed random variable [ηCL∈N(0,ω2)], explaining the differences between individuals.
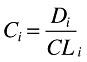 |
(1) |
| (2) |
Biomarker model
An Emax model was used to describe the relationship between the exposure and the change from the baseline biomarker response (ΔB) (Equation 3). The variability in the individual EC50 values (EC50,i) was assumed to be log-normally distributed according to Equation 4, where θEC50 is the typical value of the EC50 in the population and ηEC50 is a zero mean, normally distributed random variable. To constrain the individual Emax values (Emax,i) to fall between 0 and 1 the random variability [ηEmax∈N(0,ω2)] was added to the typical value of the Emax in the population through a logit function (Equations 5 and 6).
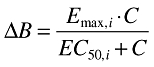 |
(3) |
| (4) |
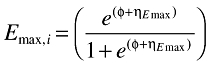 |
(5) |
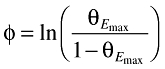 |
(6) |
Toxicity model
The concentration–toxicity relationship was described by a Tmax model (Equation 7), where Tmax = 1. The variability in the individual TC50 values (TC50,i) was assumed to be log-normally distributed according to Equation 8, where θTC50 is the typical value of the TC50 in the population and ηTC50 is a zero mean, normally distributed random variable. The therapeutic interval was varied by defining θTC50 as a function of θEC50, according to Equation 9, where x = 1, 2, 3 and 4. The therapeutic interval describes the differences between the concentrations which give rise to the desired effect and the concentrations that lead to side-effects. An adverse event was defined as T > 0.75·Tmax.
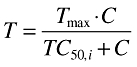 |
(7) |
| (8) |
| (9) |
Clinical end-point model
A dichotomous clinical end-point was simulated using a logistic model. The logit function (Equation 10) defines the shape of the probability function (Equation 11) for the clinical end-point given a biomarker value (change from baseline response). α and β are constants that describe the baseline and the slope, respectively, of the logit function.
| (10) |
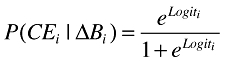 |
(11) |
In the simulations the value of the probability, P(CE = 1|ΔB), was compared with a uniformly distributed random number (R) [R∈U(0,1)]. If R was <P(CE = 1|ΔB), the value of the clinical end-point was set to 1, i.e. a response, otherwise 0. The probability of an effect at baseline was set to 20% and a maximum change in the biomarker would lead to a 65% probability of a response.
Study design
The trials were randomized according to three schemes: RDCT, RCCT and RBCT. Each simulated clinical trial consisted of four parallel groups, one placebo and three active, with 50 subjects per group. One observation per individual was made for all the variables, i.e. dose, concentration, biomarker and clinical end-point. It was assumed that there was no measurement error in the observations. When the biomarker was the randomization variable there was a possibility that an individual Emax value was lower than the targeted change in biomarker, i.e. the occurrence of formal data loss. In those cases the simulated change in biomarker was set to 95% of the individual Emax value. In the RDCT and RCCT it was assumed that it was possible to reach the target doses/concentrations exactly.
Simulation setup
A number of simulation setups were defined involving different permutations of randomization schemes (RDCT/RCCT/RBCT) and variability magnitudes in the parameters. The default simulation setup was defined as 30% variability in CLi, 40% variability in EC50,i, 30% variability in Emax,i and 25% variability in the baseline value (α) in the clinical end-point model. The other simulation setups are described in Table 1. The RBCT design was used as the reference design, meaning that the dose and concentration levels used in the RDCT and RCCT were calculated from the biomarker levels considering the variability between the biomarker and dose/concentration. To compute the corresponding doses and concentrations in the RDCTs and RCCTs, respectively, 2500 individual biomarker values were generated for each target level and the defined models were used to calculate the corresponding individual concentrations and doses necessary to reach the target biomarker levels. The doses and concentrations used for randomization were set to the median values of these 2500 individual concentrations and doses for each target level. To investigate the impact of the choice of randomization levels two ranges of biomarker levels were simulated: WIDE and LOW with 0%, 25%, 50%, 75% and 0%, 15%, 35%, 55% change from biomarker baseline, respectively.
Table 1.
Numerical values used in the simulations
| Fixed effects parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| θCL | θEC50 | θEmax | θTC50 | θα | θβ | ||||
| 10 | 25 | 0.8 | 1/2/3/4·θEC50 | −1.386 | 0.0224 | ||||
| Random effects parameters | |||||||||
| CV(CL) % | CV(EC50) % | CV(Emax) % | CV(TC50) % | CV(α) % | CV(β) % | ||||
| 0/20/30/50/100 | 40 | 0/30* | 0/30/50/75 | 0/25* | 0 | ||||
| Correlation levels | |||||||||
| ρ (CL < = > EC50) | ρ (CL < = > Emax) | ||||||||
| −0.8 | −0.2 | 0 | 0.2 | 0.8 | −0.8 | −0.2 | 0 | 0.2 | 0.8 |
The figures in bold indicate the values used in the default simulation setup.
The parameters are used within a logit transform and the numerical values for the standard deviation were ωEmax = 1.875 and ωα = 0.3465.
Data analysis
In the model-based analysis, different independent variables were used depending on the randomization scheme. The independent variables for the RDCT were dose, concentration and biomarker. For RCCT the independent variables were concentration and biomarker. For RBCT the only independent variable was the biomarker. Since only one observation was available for each individual it was not possible to separately estimate different variability components (between subjects and between observations within subjects) and the analysis models did not therefore include any terms for the interindividual variability in the parameters.
Two models were fitted to each simulated dataset. The first model constituted the null hypothesis (H0) in which the logit function for the clinical end-point did not include a term related to drug exposure. The second model, which constituted the alternative hypothesis (H1), altered depending on the independent variable. In the case where the biomarker was the independent variable the H1 model was the same as the simulation model (except for the interindividual variability term). When the independent variable was either dose or concentration they were related to the clinical end-point through an Emax-shaped logit function. This is because the Emax model that was used to simulate the relationship between concentration and biomarker.
The models were estimated in NONMEM and compared using the likelihood ratio (LR) test (see below).
In the traditional analysis, a group-wise comparison was made to investigate the differences between treatment groups. Since the clinical end-point is dichotomous, a χ2 test for independent observations was used to compare the responses from all treatment groups simultaneously, i.e. the test statistic (Q) to be used in the test is a function of the observed frequencies and the expected frequencies in all the groups.
The next sections describe the methods used for investigating the five potential benefits of an RCCT/RBCT.
Potential for higher statistical power
In the investigation of a potential gain in statistical power, the default simulation setup was used and the simulated trials were analysed with model-based analysis and by group-wise comparison.
In the model-based analysis the significance testing of the models was made by using the LR test. The LR test is based on the difference in objective function value (OFV), computed by NONMEM, between the model with (H1) and without (H0) a relationship between the clinical end-point and the independent variable. The statistical power was calculated according to Equation 12,
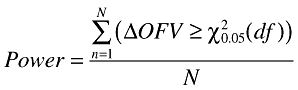 |
(12) |
where d.f. is degrees of freedom, i.e. the difference in number of parameters between models and N is the total number of simulated trials. The significance level required to reject the null hypothesis was set to 5%. This corresponds to differences in OFV of 3.84 and 5.99 for 1 and 2 degrees of freedom, respectively.
In the traditional analysis, the statistical power was calculated as the sum of trials where the χ2 test showed statistical significance divided by the total number of simulated trials (Equation 13),
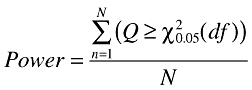 |
(13) |
where the degrees of freedom are the number of treatment groups minus one. The required significance level was 5%.
Sensitivity to high pharmacokinetic variability
When addressing the impact of high PK variability on statistical power, the default setup was compared with one where the variability in CLi was set to 100%. In all other respects the simulation setup was the same as in the default setup. The power was computed as described above.
Sensitivity to correlation between PK and PD parameters
By simulation a correlation (ρ) between PK and biomarker response was introduced between CLi and EC50,i or Emax,i. Five different levels of parameter correlations were investigated (Table 1). The correlated data were simulated using both the default and high variability in CLi, i.e. 30 and 100%.
Less biased estimates of exposure–response relationships
In the investigation of the contribution of the study design to a potential bias in the estimated parameters in the exposure–response relationships, the simulations were performed without any variability in the biomarker–clinical end0point model. This was done to avoid any bias caused by simplification of the model due to the necessary omission of the interindividual component in the logit function for the clinical end-point.
The bias in the estimated parameters was calculated according to
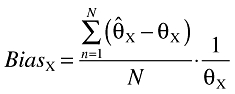 |
(14) |
where 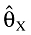 is the parameter estimate, θX is the true value, N is the number of simulated datasets and the index X is the parameter of interest.
is the parameter estimate, θX is the true value, N is the number of simulated datasets and the index X is the parameter of interest.
Control of exposure in situations of toxicity issues
To investigate the impact of the randomization scheme and data analysis strategy on the number of adverse events, the number of subjects in the simulated trials was calibrated so that each trial would result in an 80% statistical power. Five levels of interindividual variability in CL and TC50 and four sizes of the therapeutic interval, shown in Table 1, were simulated. The average number of adverse events (from 1000 simulated trials) between an RCCT with group-wise analysis and an RDCT and RCCT with model-based analysis with concentration and biomarker as the independent variable was compared.
Results
Potential for higher statistical power
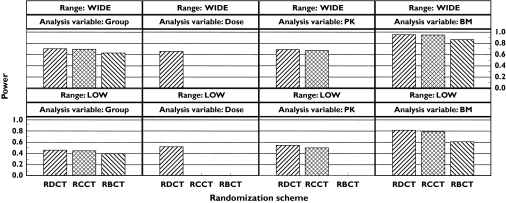
The effect of the dose range, randomization scheme and analysis strategy on the statistical power are shown in Figure 2. The trends between the randomization schemes were the same regardless of dose range and analysis strategy. With respect to randomization scheme, the statistical powers decrease in the following order: RDCT, RCCT and RBCT. However, the main differences in statistical power appear within a randomization scheme between different independent variables. With the LOW dose range, in the RDCT there is approximately a 30% gain (from 52% to 81%) in statistical power by using biomarker as the independent variable compared with dose.
Figure 2.
The effect of randomization and independent variable on statistical power under the default simulation setup with both wide and low dose ranges. The independent variable group indicates a traditional statistical analysis.
Sensitivity to high pharmacokinetic variability
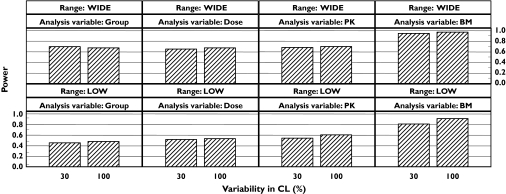
The effect on the statistical power in an RDCT of the different sizes of interindividual variability in the pharmacokinetics is shown in Figure 3. The trends, increased power with increased PK variability, are the same in all cases except when using the WIDE dose range with a traditional analysis. With the model-based analysis, the power increased with independent variable in the order dose, concentration and biomarker. The power with the model-based analysis was comparable to or higher than the group-wise analysis regardless of independent variable. The statistical power for all the other randomization scheme and independent variable options was not affected by the variability in CL (results not shown).
Figure 3.
Effect of high variability in CL with a randomized dose-controlled trial (RDCT) design. The randomized concentration-controlled trial (RCCT) and randomized biomarker-controlled trial (RBCT) designs are not affected by the variability in CL. The independent variable group indicates a traditional statistical analysis.
Sensitivity to correlation between PK and PD parameters
The effect of the correlations between PK and PD (with the default parameter variabilities), dose range, randomization scheme and analysis strategy on the statistical power is shown in Table 2. Regardless of all other factors, the statistical power in a model-based analysis is robust to correlations between CL and EC50 or Emax. The same is true in a group-wise analysis with respect to a correlation between CL and EC50. The formal data loss which is caused by, in particular, high correlations between CL and Emax leads to higher sensitivity in the statistical power with the group-wise analysis. The results of effect of the correlations between PK and PD when the variability in CL was 100% did not add any new conclusions and for the sake of clarity the results are not shown.
Table 2.
Statistical power when introducing different magnitudes of correlation between CL and EC50 or CL and Emax
| RDCT | RCCT | RBCT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model-based | Traditional | Model-based | Traditional | Model-based | Traditional | |||||||
| Magnitude of correlation | EC50 | Emax | EC50 | Emax | EC50 | Emax | EC50 | Emax | EC50 | Emax | EC50 | Emax |
| LOW dose range | ||||||||||||
| −0.8 | 0.81 | 1 | 0.46 | 0.52 | 0.87 | 0.82 | 0.44 | 0.39 | 0.61 | 0.63 | 0.39 | 0.32 |
| −0.2 | 0.81 | 0.86 | 0.46 | 0.47 | 0.82 | 0.79 | 0.47 | 0.44 | 0.61 | 0.60 | 0.39 | 0.39 |
| 0 | 0.85 | 0.85 | 0.50 | 0.50 | 0.80 | 0.80 | 0.46 | 0.46 | 0.61 | 0.61 | 0.39 | 0.39 |
| 0.2 | 0.86 | 0.83 | 0.51 | 0.45 | 0.81 | 0.78 | 0.46 | 0.44 | 0.61 | 0.60 | 0.39 | 0.40 |
| 0.8 | 0.94 | 0.80 | 0.46 | 0.22 | 0.86 | 0.81 | 0.46 | 0.38 | 0.61 | 0.61 | 0.39 | 0.33 |
| WIDE dose range | ||||||||||||
| −0.8 | 0.95 | 1 | 0.70 | 0.65 | 0.96 | 0.96 | 0.67 | 0.63 | 0.86 | 0.86 | 0.62 | 0.50 |
| −0.2 | 0.95 | 0.96 | 0.70 | 0.71 | 0.95 | 0.95 | 0.71 | 0.71 | 0.86 | 0.85 | 0.62 | 0.62 |
| 0 | 0.96 | 0.96 | 0.72 | 0.72 | 0.95 | 0.95 | 0.70 | 0.70 | 0.86 | 0.86 | 0.62 | 0.62 |
| 0.2 | 0.96 | 0.95 | 0.73 | 0.69 | 0.95 | 0.95 | 0.71 | 0.69 | 0.86 | 0.87 | 0.62 | 0.62 |
| 0.8 | 0.99 | 0.93 | 0.63 | 0.34 | 0.96 | 0.96 | 0.68 | 0.63 | 0.86 | 0.86 | 0.62 | 0.52 |
The default parameter variability levels are used and the independent variable is biomarker.
Less biased estimates of exposure–response relationships
Under all conditions the bias in parameter estimates was negligible (<3%) and unaffected by study design, variability in the PK or correlation between PK and PD.
Control of exposure in situations of toxicity issues
Since the statistical power is a function of randomization scheme and analysis strategy (see above), it was necessary to simulate trials of different sizes depending on randomization and analysis conditions, to ensure a statistical power of 80%. The required number of individuals ranged between 140 and 460, as shown in Table 3. In all but one case (RDCT with analysis on concentration and 100% variability in CL) the number of individuals was less in a model-based analysis than in a group-wise comparison.
Table 3.
The number of subjects needed to reach a statistical power of 80% under different analysis strategies and levels of interindividual variability in CL
| Number of subjects to reach a statistical power of 80% | |||||
|---|---|---|---|---|---|
| Interindividual variability in CL (%) | RCCTGroup | RDCT(B) | RDCT(C) | RCCT(B) | RCCT(C) |
| 0 | 410 | 200 | 380 | 200 | 380 |
| 20 | 420 | 200 | 380 | 210 | 380 |
| 30 | 430 | 200 | 400 | 220 | 400 |
| 50 | 420 | 180 | 400 | 210 | 380 |
| 100 | 410 | 140 | 460 | 210 | 380 |
The letters in parentheses denote the independent variable in a model-based analysis. RCCT, Randomized concentration-controlled trial; RDCT, randomized dose-controlled trial.
It is worth pointing out that the analysis strategy affects only the number of adverse events through the statistical power and its effect on study size. This means that since the model-based analysis under an RCCT always resulted in a lower than or equal study size compared with the group-wise analysis, the corresponding number of adverse events for the RCCT was also always lower than or equal to the adverse events found in the group-wise analysis.
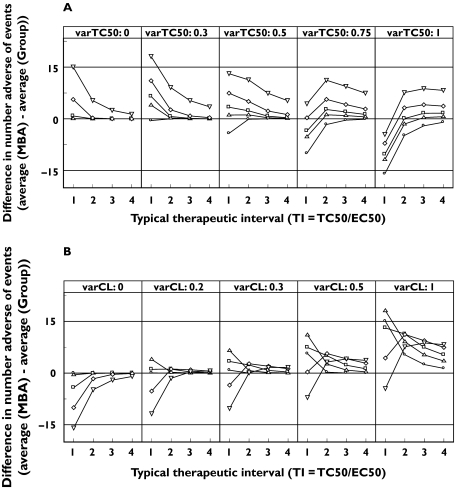
Figure 4 shows the difference in the average number of adverse events between an RDCT with analysis on biomarker with model-based analysis, and an RCCT with group-wise comparison vs. the size of therapeutic interval. Each line in Figure 4a represents one level of variability in TC50, while each panel displays one level of variability in CL. In Figure 4b the lines represent the different levels of variability in CL and the panels display the levels of variability in TC50. Generally, the difference in number of adverse events increases with increasing variability in CL, whereas it decreases with increasing variability in TC50. Since the number of adverse events is decreasing with increasing therapeutic interval, the difference in the number of adverse events tends towards zero as the therapeutic interval increases.
Figure 4.
The difference in number of adverse events vs. the size of therapeutic interval (TI = TC50/EC50) between a randomized dose-controlled trial (RDCT) with model-based analysis (MBA) with biomarker as independent variable and a randomized concentration-controlled trial (RCCT) with group-wise analysis. The graphs are conditioned on variability in (a) TC50 ( , 0 varCL;
, 0 varCL;  , 0.2 varCL;
, 0.2 varCL;  , 0.3 varCL;
, 0.3 varCL;  , 0.5 varCL;
, 0.5 varCL;  , 0 varTC50) and (b) CL (
, 0 varTC50) and (b) CL ( , 0 varTC50;
, 0 varTC50;  , 0.3 varTC50;
, 0.3 varTC50;  , 0.5 varTC50;
, 0.5 varTC50;  , 0.75 varTC50;
, 0.75 varTC50;  , 1 varTC50). The variability is noted as the CV.
, 1 varTC50). The variability is noted as the CV.
Discussion
The results consistently show that, when using a model-based analysis approach, the more variability in the independent variable the more information in the data, i.e. higher statistical power. For traditional analyses it is often assumed that to obtain an increase in statistical power a decrease in within-group variability in the data is needed. As seen in some of these results, the trend can be the opposite.
One explanation of why this happens is that the biomarker values are allowed to be higher than the targeted values in the RBCT and thus give rise to higher responses. This is due to the log-normal distribution of the biomarker values and that the RDCT/RCCT targets the median biomarker value. The decrease in power with the RBCT, with both methods of analysis, is also caused by formal data loss. Formal data loss occurs when patients randomized to a target, e.g. a certain biomarker level, fail to reach that target. Another cause of formal data loss is when the target, in a large fraction of the patients, gives rise to a response that is outside the informative exposure–response range, for example at Emax. This has been recognized as one of the disadvantages with the RCCT [8]. Without formal data loss, the statistical power will increase, as expected, with decreasing within-group variability in a group-wise analysis (results not shown). However, it is difficult to avoid formal data loss in a randomized clinical trial and will probably become a problem in any RBCT or RCCT regardless of analysis strategy. In this study the underlying concentration-biomarker model is an Emax model and the formal data loss problem increases with increasing variability in the Emax parameter.
According to the present results, there is generally no gain in statistical power by randomizing on either concentration or biomarker with increased variability in CL. From a modelling point of view, the increase in variability increases the information content in the data, i.e. the greatest statistical power is obtained with a high variability in CL, randomization on dose and using the biomarker as the independent variable. In the group-wise analysis the statistical power is also dependent on the randomization target range. When the target range is close to baseline response (LOW in our simulations), increased variability in CL leads to a slightly higher statistical power in an RDCT. This is because the increased variability in the response makes it easier to contrast between the placebo response and the highest exposure group. When the target range is closer to the maximal response (WIDE in our simulations), on the other hand, the increased variability in CL leads to formal data loss and therefore lower statistical power. The effect of randomization scheme and target range with a group-wise analysis is illustrated in Figure 2. From a practical point of view, this means that the effect on the statistical power after a model-based analysis is more predictable to the consequences of a high variability in PK compared with a group-wise analysis.
One of the arguments for using the RCCT has been in situations where there is a correlation between PK and PD. According to the present results, a model-based analysis is quite robust to such correlations, regardless of whether the correlation is between CL and EC50 or CL and Emax, and regardless of the randomization scheme and independent variable. The only case when the statistical power is sensitive to correlations is in a group-wise analysis when the correlation is between CL and Emax, which can be explained by the occurrence of formal data loss.
Another of the suggested benefits of an RCCT in a traditional statistical analysis is that the decreased variability in the randomization variable would decrease the parameter bias. Our results from the model-based analysis show no appreciable parameter bias in any parameter regardless of simulation setup.
In the MEDLINE search of RCCTs [9–46], half of the number of trials were aimed towards investigating safety/toxicity and most of the other studies stated that the reason for controlling the concentrations was a narrow therapeutic window or other safety reasons. This shows that safety issues are the most common reasons to choose an RCCT (RBCT) design. However, the simulations in this study have shown that, with a moderate variability in PK and a high variability in the toxicity response, an RDCT combined with a model-based analysis strategy may be a more effective means of minimizing the number of adverse events in a clinical trial. The reason is that a model-based analysis leads to a higher statistical power and therefore allows for smaller study populations. On the other hand, if the variability in the toxicity response or PK is unknown, the most conservative approach is to use an RCCT, assuming a well-defined model. This is especially true if the expected adverse events are serious, in which case it is particularly important to use a model-based data analysis approach to minimize the study size and therefore the number of side-effects.
A model-based analysis is robust to the choice of the target exposure levels [49]. For example, if the PD model is an Emax model, it is possible to choose dose levels such that only a fraction of the concentrations are above the EC50 value and still obtain a high statistical power. This explains the small differences in statistical power between the two target exposure ranges used in this study. It also means that the target ranges in an RDCT study subject to model-based analysis can be lower than the target range for a corresponding RCCT study with group-wise analysis. This may also influence the incidence of adverse events.
In this study only one set of models has been tested. However, the models used are relatively general and therefore quite robust to deviations from assumptions. It is thereby possible to generalize the conclusions.
When using model-based analysis, it is beneficial to use a biomarker as the independent variable in the analysis. Using a biomarker as an independent variable in a model-based analysis should be distinguished from a postrandomization on a biomarker in a single treatment arm trial. In a postrandomization there is a risk of experiencing bias in the estimated parameters, since, for example, patients with high clearance will end up in a low biomarker group. In the model-based analysis strategy we propose, no new groupings are made on the basis of the biomarker value, it is just an observation with high information content about the clinical end-point. However, when using an RDCT design and analysing an exposure–response relationship there is a possibility of experiencing parameter bias if the randomization variability is less than the interindividual variability. One example of this is when the variability between the dose levels (randomization variability) is less than the interindividual variability in the pharmacokinetics. In this study the randomization variability was always greater than the interindividual variability.
In conclusion, even though conditions are maximally favourable for RBCT and RCCT (ability to target the randomization levels exactly, having no residual error in the concentration and biomarker observations and biomarker on the mechanistic pathway), the results of this study indicate that alternative randomization schemes have no beneficial effect on the statistical power, regardless of whether a model-based or group-wise analysis is employed. A model-based analysis will result in higher statistical power and therefore smaller group sizes compared with a group-wise analysis, given the same randomization scheme. In addition, this study has demonstrated that under certain conditions, and maintaining equal power across trial designs and analysis options, an RDCT may well result in fewer adverse events than an RCCT. On the other hand, randomization on the closest predictor to the toxicity effect, RCCT or RBCT, and model-based analysis is the most conservative approach and can be expected to yield the lowest number of adverse events regardless of PK and toxicity response variability. With a model-based analysis the practical and economic gain in performing an RDCT further outweighs the possible benefits of performing an alternative randomization scheme.
K.E.K. was supported by a grant from AstraZeneca, Södertälje, Sweden.
References
- 1.Kraiczi H, Jang T, Ludden T, Peck CC. Randomized concentration-controlled trials: motivations, use, and limitations. Clin Pharmacol Ther. 2003;74:203–14. doi: 10.1016/S0009-9236(03)00169-3. [DOI] [PubMed] [Google Scholar]
- 2.Sanathanan LP, Peck CC. The randomized concentration-controlled trial: an evaluation of its sample size efficiency. Control Clin Trials. 1991;12:780–94. doi: 10.1016/0197-2456(91)90041-j. [DOI] [PubMed] [Google Scholar]
- 3.Grahnen A, Karlsson MO. Concentration-controlled or effect-controlled trials: useful alternatives to conventional dose-controlled trials? Clin Pharmacokinet. 2001;40:317–25. doi: 10.2165/00003088-200140050-00001. [DOI] [PubMed] [Google Scholar]
- 4.Department of Health and Human Services. CDER and CBER guidance for industryExposure–Response Relationships—Study Design, Data Analysis, and Regulatory Applications. 2003. [2005-May-16]. Available from http://www.fda.gov/cber/gdlns/exposure.pdf.
- 5.Karlsson MO, Jonsson EN, Wiltse CG, Wade JR. Assumption testing in population pharmacokinetic models: illustrated with an analysis of moxonidine data from congestive heart failure patients. J Pharmacokinet Biopharm. 1998;26:207–46. doi: 10.1023/a:1020561807903. [DOI] [PubMed] [Google Scholar]
- 6.Jonsson EN, Sheiner LB. More efficient clinical trials through use of scientific model-based statistical tests. Clin Pharmacol Ther. 2002;72:603–14. doi: 10.1067/mcp.2002.129307. [DOI] [PubMed] [Google Scholar]
- 7.Peck CC. Concentration-controlled versus concentration-defined trials [reply] Clin Pharmacol Therapeutics. 1993;53:385–7. doi: 10.1038/clpt.1993.37. [DOI] [PubMed] [Google Scholar]
- 8.Endrenyi L, Zha J. Comparative efficiencies of randomized concentration- and dose-controlled clinical trials. Clin Pharmacol Ther. 1994;56:331–8. doi: 10.1038/clpt.1994.144. [DOI] [PubMed] [Google Scholar]
- 9.A randomized trial of propranolol in patients with acute myocardial infarction. I. Mortality results. JAMA. 1982;247:1707–14. doi: 10.1001/jama.1982.03320370021023. [DOI] [PubMed] [Google Scholar]
- 10.Bever CT, Jr, Young D, Anderson PA, Krumholz A, Conway K, Leslie J, Eddington N, Plaisance KI, Panitch HS, Dhib-Jalbut S, Fossler MJ, Devane J, Johnson M. The effects of 4-aminopyridine in multiple sclerosis patients: results of a randomized, placebo-controlled, double-blind, concentration-controlled, crossover trial. Neurology. 1994;44:1054–9. doi: 10.1212/wnl.44.6.1054. [DOI] [PubMed] [Google Scholar]
- 11.Bowden CJ, Figg WD, Dawson NA, Sartor O, Bitton RJ, Weinberger MS, Headlee D, Reed E, Myers CE, Cooper MR. A phase I/II study of continuous infusion suramin in patients with hormone-refractory prostate cancer: toxicity and response. Cancer Chemother Pharmacol. 1996;39:1–8. doi: 10.1007/s002800050531. [DOI] [PubMed] [Google Scholar]
- 12.Brundage RC, Yong FH, Fenton T, Spector SA, Starr SE, Fletcher CV. Intrapatient variability of efavirenz concentrations as a predictor of virologic response to antiretroviral therapy. Antimicrob Agents Chemother. 2004;48:979–84. doi: 10.1128/AAC.48.3.979-984.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burch JE, Ahmed O, Hullin RP, Mindham RH. Antidepressive effect of amitriptyline treatment with plasma drug levels controlled within three different ranges. Psychopharmacology (Berl) 1988;94:197–205. doi: 10.1007/BF00176845. [DOI] [PubMed] [Google Scholar]
- 14.Christensen J, Andreasen F, Poulsen JH, Dam M. Randomized, concentration-controlled trial of topiramate in refractory focal epilepsy. Neurology. 2003;61:1210–8. doi: 10.1212/01.wnl.0000091867.09720.6b. [DOI] [PubMed] [Google Scholar]
- 15.Eisenberger MA, Sinibaldi VJ, Reyno LM, Sridhara R, Jodrell DI, Zuhowski EG, Tkaczuk KH, Lowitt MH, Hemady RK, Jacobs SC, VanEcho D, Egorin MJ. Phase I and clinical evaluation of a pharmacologically guided regimen of suramin in patients with hormone-refractory prostate cancer. J Clin Oncol. 1995;13:2174–86. doi: 10.1200/JCO.1995.13.9.2174. [DOI] [PubMed] [Google Scholar]
- 16.Flechner SM, Goldfarb D, Modlin C, Feng J, Krishnamurthi V, Mastroianni B, Savas K, Cook DJ, Novick AC. Kidney transplantation without calcineurin inhibitor drugs: a prospective, randomized trial of sirolimus versus cyclosporine. Transplantation. 2002;74:1070–6. doi: 10.1097/00007890-200210270-00002. [DOI] [PubMed] [Google Scholar]
- 17.Flechner SM, Kurian SM, Solez K, Cook DJ, Burke JT, Rollin H, Hammond JA, Whisenant T, Lanigan CM, Head SR, Salomon DR. De novo kidney transplantation without use of calcineurin inhibitors preserves renal structure and function at two years. Am J Transplant. 2004;4:1776–85. doi: 10.1111/j.1600-6143.2004.00627.x. [DOI] [PubMed] [Google Scholar]
- 18.Fletcher CV, Anderson PL, Kakuda TN, Schacker TW, Henry K, Gross CR, Brundage RC. Concentration-controlled compared with conventional antiretroviral therapy for HIV infection. AIDS. 2002;16:551–60. doi: 10.1097/00002030-200203080-00006. [DOI] [PubMed] [Google Scholar]
- 19.Flexner C, van der Horst C, Jacobson MA, Powderly W, Duncanson F, Ganes D, Barditch-Crovo PA, Petty BG, Baron PA, Armstrong D, Bricmont P, Kuye O, Yacobi A, DesJardins R, Polsky B. Relationship between plasma concentrations of 3′-deoxy-3′-fluorothymidine (alovudine) and antiretroviral activity in two concentration-controlled trials. J Infect Dis. 1994;170:1394–403. doi: 10.1093/infdis/170.6.1394. [DOI] [PubMed] [Google Scholar]
- 20.Frank E, Kupfer DJ, Perel JM, Cornes C, Jarrett DB, Mallinger AG, Thase ME, McEachran AB, Grochocinski VJ. Three-year outcomes for maintenance therapies in recurrent depression. Arch General Psychiatry. 1990;47:1093–9. doi: 10.1001/archpsyc.1990.01810240013002. [DOI] [PubMed] [Google Scholar]
- 21.Gelenberg AJ, Kane JM, Keller MB, Lavori P, Rosenbaum JF, Cole K, Lavelle J. Comparison of standard and low serum levels of lithium for maintenance treatment of bipolar disorder. N Engl J Med. 1989;321:1489–93. doi: 10.1056/NEJM198911303212201. [DOI] [PubMed] [Google Scholar]
- 22.Groth CG, Backman L, Morales JM, Calne R, Kreis H, Lang P, Touraine JL, Claesson K, Campistol JM, Durand D, Wramner L, Brattstrom C, Charpentier B. Sirolimus (rapamycin)-based therapy in human renal transplantation: similar efficacy and different toxicity compared with cyclosporine. Sirolimus European Renal Transplant Study Group. Transplantation. 1999;67:1036–42. doi: 10.1097/00007890-199904150-00017. [DOI] [PubMed] [Google Scholar]
- 23.Hale MD, Nicholls AJ, Bullingham RE, Hene R, Hoitsma A, Squifflet JP, Weimar W, Vanrenterghem Y, Van de Woude FJ, Verpooten GA. The pharmacokinetic–pharmacodynamic relationship for mycophenolate mofetil in renal transplantation. Clin Pharmacol Ther. 1998;64:672–83. doi: 10.1016/S0009-9236(98)90058-3. [DOI] [PubMed] [Google Scholar]
- 24.Holford N, Black P, Couch R, Kennedy J, Briant R. Theophylline target concentration in severe airways obstruction—10 or 20 mg/L? A randomised concentration-controlled trial. Clin Pharmacokinet. 1993;25:495–505. doi: 10.2165/00003088-199325060-00007. [DOI] [PubMed] [Google Scholar]
- 25.Holford N, Hashimoto Y, Sheiner LB. Time and theophylline concentration help explain the recovery of peak flow following acute airways obstruction. Population analysis of a randomised concentration controlled trial. Clin Pharmacokinet. 1993;25:506–15. doi: 10.2165/00003088-199325060-00008. [DOI] [PubMed] [Google Scholar]
- 26.Joel S, O'Byrne K, Penson R, Papamichael D, Higgins A, Robertshaw H, Rudd R, Talbot D, Slevin M. A randomised, concentration-controlled, comparison of standard (5-day) vs. prolonged (15-day) infusions of etoposide phosphate in small-cell lung cancer. Ann Oncol. 1998;9:1205–11. doi: 10.1023/a:1008437805286. [DOI] [PubMed] [Google Scholar]
- 27.Kramer BK, Neumayer HH, Stahl R, Pietrzyk M, Kruger B, Pfalzer B, Bourbigot B, Campbell S, Whelchel J, Eris J, Vitko S, Budde K. Graft function, cardiovascular risk factors, and sex hormones in renal transplant recipients on an immunosuppressive regimen of everolimus, reduced dose of cyclosporine, and basiliximab. Transplant Proc. 2005;37:1601–4. doi: 10.1016/j.transproceed.2004.09.026. [DOI] [PubMed] [Google Scholar]
- 28.Kreis H, Cisterne JM, Land W, Wramner L, Squifflet JP, Abramowicz D, Campistol JM, Morales JM, Grinyo JM, Mourad G, Berthoux FC, Brattstrom C, Lebranchu Y, Vialtel P. Sirolimus in association with mycophenolate mofetil induction for the prevention of acute graft rejection in renal allograft recipients. Transplantation. 2000;69:1252–60. doi: 10.1097/00007890-200004150-00009. [DOI] [PubMed] [Google Scholar]
- 29.Laskow DA, Vincenti F, Neylan JF, Mendez R, Matas AJ. An open-label, concentration-ranging trial of FK506 in primary kidney transplantation: a report of the United States Multicenter FK506 Kidney Transplant Group. Transplantation. 1996;62:900–5. doi: 10.1097/00007890-199610150-00005. [DOI] [PubMed] [Google Scholar]
- 30.Mathew T, Kreis H, Friend P. Two-year incidence of malignancy in sirolimus-treated renal transplant recipients: results from five multicenter studies. Clin Transplant. 2004;18:446–9. doi: 10.1111/j.1399-0012.2004.00188.x. [DOI] [PubMed] [Google Scholar]
- 31.Mattson RH, Cramer JA, Collins JF. A comparison of valproate with carbamazepine for the treatment of complex partial seizures and secondarily generalized tonic-clonic seizures in adults. The Department of Veterans Affairs Epilepsy Cooperative Study, 264 Group. N Engl J Med. 1992;327:765–71. doi: 10.1056/NEJM199209103271104. [DOI] [PubMed] [Google Scholar]
- 32.McMichael J, Lieberman R, McCauley J, Irish W, Marino I, Doyle H. Computer-guided randomized concentration-controlled trials of tacrolimus in autoimmunity: multiple sclerosis and primary biliary cirrhosis. Ther Drug Monit. 1996;18:435–7. doi: 10.1097/00007691-199608000-00021. [DOI] [PubMed] [Google Scholar]
- 33.Morales JM, Wramner L, Kreis H, Durand D, Campistol JM, Andres A, Arenas J, Negre E, Burke JT, Groth CG. Sirolimus does not exhibit nephrotoxicity compared to cyclosporine in renal transplant recipients. Am J Transplant. 2002;2:436–42. doi: 10.1034/j.1600-6143.2002.20507.x. [DOI] [PubMed] [Google Scholar]
- 34.Pascual J. Concentration-controlled everolimus (Certican): combination with reduced dose calcineurin inhibitors. Transplantation. 2005;79(9 Suppl.):S76–9. doi: 10.1097/01.tp.0000162434.62591.f3. [DOI] [PubMed] [Google Scholar]
- 35.Pledger GW, Sackellares JC, Treiman DM, Pellock JM, Wright FS, Mikati M, Sahlroot JT, Tsay JY, Drake ME, Olson L, Handforth CA, Garnett WR, Schachter S, Kupferberg HJ, Ashworth MR, McCormick C, Leiderman D, Kapetanovic IM, Driscoll S, O'Hara K, Torchin CD, Gentile J, Kay A, Cereghino JJ. Flunarizine for treatment of partial seizures: results of a concentration-controlled trial. Neurology. 1994;44:1830–6. doi: 10.1212/wnl.44.10.1830. [DOI] [PubMed] [Google Scholar]
- 36.Riese NE, Buswell L, Noll L, Pajak TF, Stetz J, Lee DJ, Coleman CN. Pharmacokinetic monitoring and dose modification of etanidazole in the RTOG 85–27 phase III head and neck trial. Int J Radiat Oncol Biol Phys. 1997;39:855–8. doi: 10.1016/s0360-3016(97)00454-9. [DOI] [PubMed] [Google Scholar]
- 37.Solomon DA, Ryan CE, Keitner GI, Miller IW, Shea MT, Kazim A, Keller MB. A pilot study of lithium carbonate plus divalproex sodium for the continuation and maintenance treatment of patients with bipolar I disorder. J Clin Psychiatry. 1997;58:95–9. doi: 10.4088/jcp.v58n0301. [DOI] [PubMed] [Google Scholar]
- 38.Temkin NR, Dikmen SS, Wilensky AJ, Keihm J, Chabal S, Winn HR. A randomized, double-blind study of phenytoin for the prevention of post-traumatic seizures. N Engl J Med. 1990;323:497–502. doi: 10.1056/NEJM199008233230801. [DOI] [PubMed] [Google Scholar]
- 39.Torti C, Quiros-Roldan E, Regazzi M, De Luca A, Mazzotta F, Antinori A, Ladisa N, Micheli V, Orani A, Patroni A, Villani P, Lo Caputo S, Moretti F, Di Giambenedetto S, Castelnuovo F, Maggi P, Tinelli C, Carosi G. A randomized controlled trial to evaluate antiretroviral salvage therapy guided by rules-based or phenotype-driven HIV-1 genotypic drug-resistance interpretation with or without concentration-controlled intervention: the Resistance and Dosage Adapted Regimens (RADAR) study. Clin Infect Dis. 2005;40:1828–36. doi: 10.1086/429917. [DOI] [PubMed] [Google Scholar]
- 40.van der Maaten JM, Epema AH, Huet RC, Hennis PJ. The effect of midazolam at two plasma concentrations of hemodynamics and sufentanil requirement in coronary artery surgery. J Cardiothorac Vasc Anesth. 1996;10:356–63. doi: 10.1016/s1053-0770(96)80097-8. [DOI] [PubMed] [Google Scholar]
- 41.van Gelder T, Hilbrands LB, Vanrenterghem Y, Weimar W, de Fijter JW, Squifflet JP, Hene RJ, Verpooten GA, Navarro MT, Hale MD, Nicholls AJ. A randomized double-blind, multicenter plasma concentration controlled study of the safety and efficacy of oral mycophenolate mofetil for the prevention of acute rejection after kidney transplantation. Transplantation. 1999;68:261–6. doi: 10.1097/00007890-199907270-00018. [DOI] [PubMed] [Google Scholar]
- 42.van Hest RM, van Gelder T, Vulto AG, Mathot RA. Population pharmacokinetics of mycophenolic acid in renal transplant recipients. Clin Pharmacokinet. 2005;44:1083–96. doi: 10.2165/00003088-200544100-00006. [DOI] [PubMed] [Google Scholar]
- 43.Wassef AA, Dott SG, Harris A, Brown A, O'Boyle M, Meyer WJ, 3rd, Rose RM. Randomized, placebo-controlled pilot study of divalproex sodium in the treatment of acute exacerbations of chronic schizophrenia. J Clin Psychopharmacol. 2000;20:357–61. doi: 10.1097/00004714-200006000-00011. [DOI] [PubMed] [Google Scholar]
- 44.Volavka J, Cooper T, Czobor P, Bitter I, Meisner M, Laska E, Gastanaga P, Krakowski M, Chou JC, Crowner M, Douyon R. Haloperidol blood levels and clinical effects. Arch General Psychiatry. 1992;49:354–61. doi: 10.1001/archpsyc.1992.01820050018002. [DOI] [PubMed] [Google Scholar]
- 45.Woo E, Chan YM, Yu YL, Chan YW, Huang CY. If a well-stabilized epileptic patient has a subtherapeutic antiepileptic drug level, should the dose be increased? A randomized prospective study. Epilepsia. 1988;29:129–39. doi: 10.1111/j.1528-1157.1988.tb04408.x. [DOI] [PubMed] [Google Scholar]
- 46.Vozeh S, Kewitz G, Perruchoud A, Tschan M, Kopp C, Heitz M, Follath F. Theophylline serum concentration and therapeutic effect in severe acute bronchial obstruction: the optimal use of intravenously administered aminophylline. Am Rev Respir Dis. 1982;125:181–4. doi: 10.1164/arrd.1982.125.2.181. [DOI] [PubMed] [Google Scholar]
- 47.Food and Drug Administration. Challenge and Opportunity on the Critical Path to New Medical Products. 2004. [2005-May-13]. Available at http://www.fda.gov/oc/initiatives/criticalpath/whitepaper.pdf.
- 48.Beal SL, Sheiner LB. NONMEM Users Guides. Hanover, MD: Globomax, Inc.; 1989–1998. [Google Scholar]
- 49.Jonsson EN, Wade JR, Karlsson MO. Nonlinearity detection: advantages of nonlinear mixed-effects modeling. AAPS Pharmsci. 2000;2:E32. doi: 10.1208/ps020332. [DOI] [PMC free article] [PubMed] [Google Scholar]