Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2006 Aug 31;577(Pt 1):81–95. doi: 10.1113/jphysiol.2006.115204

Craniocentric body-sway responses to 500 Hz bone-conducted tones in man

Miriam S Welgampola 1,2, Brian L Day 1
PMCID: PMC2000670  PMID: 16945974

Abstract

Whole-body responses evoked by bone-conducted sound, a stimulus known to activate vestibular afferents, were recorded in standing subjects deprived of vision. With the head facing forward, unilateral mastoid vibration (500 Hz, 2 s, 136 dB force level) produced an oblique body sway with a consistent lateral component away from the stimulated ear and an average forward component. The side of stimulation had a powerful influence on the direction but not the magnitude of sway. Individuals' mean response directions were significantly clustered between subjects, as well as within subjects for 12 of 16 subjects when tested on five occasions. Single trial analysis did not reveal any habituation of the response. To investigate whether muscle spindle activation might be responsible for the response, vibration was applied directly over posterior and anterior neck muscles and tendons. This generally produced responses that were smaller and with different direction characteristics than with mastoid vibration. In contrast, stimulation over the temporal fossa produced responses similar in magnitude and direction to mastoid stimulation. When the head was turned in yaw to face in different directions the sway response changed direction by the same amount but with no change in magnitude, suggesting response organization in a craniocentric reference frame. Whole-body sway evoked by 500 Hz vibration delivered over sites close to the ear is thus likely to represent a vestibular-evoked balance response. When compared with sway responses evoked by 500 Hz vibration of the left temporal fossa, responses to 1 mA left cathodal galvanic vestibular stimulation were of similar magnitude, yet significantly different in direction, suggesting differences in the end organ afferents activated by these two stimuli. This may enable investigation of previously inaccessible aspects of vestibular function in intact freely behaving human subjects.

Vestibular hair cells are primarily responsive to linear and angular accelerations of the head. Forces parallel with the apical cellular surface activate the hair cells by deflection of the hair bundle's tip, movement towards and away from the kinocilium producing depolarization and hyperpolarization of the cell membrane (Hudspeth & Corey, 1977). There are problems in using this type of stimulus to study vestibular contributions to the control of balance because externally applied forces that accelerate the head in space also inevitably stimulate non-vestibular sense organs, and any contact of the body with an earth-fixed actuator may interfere with the balance task. In some species of fish, amphibians and mammals, vestibular hair cells can also be activated by sound and vibration (Lowenstein & Roberts, 1951; Moffat & Capranica, 1976; Young et al. 1977). Such stimuli could offer an alternative to sustained accelerations as a means of probing vestibular contributions to balance processes.

Large oscillatory mechanical stimuli exert a net excitatory effect upon the hair cell bundles through an imbalance between the maximal amplitudes of depolarizing and hyperpolarizing phases of the response (Hudspeth, 1989). Similar mechanisms may underlie activation of vestibular hair cells by sound and vibration conveyed through the endolymph. In experimental animals (cats, guinea pigs, squirrel monkeys) intense air-conducted sound, in addition to being a cochlear stimulus, activates vestibular afferents arising predominantly from the sacculus (Young et al. 1977; McCue & Guinan, 1994; Murofushi et al. 1995). The value of this stimulus for human experimentation is limited by the intensities that are required. Although it is safe to apply short-duration stimuli (clicks and tone bursts), which usefully evoke neck and leg muscle responses (Colebatch et al. 1994; Watson & Colebatch, 1998; Murofushi et al. 1999), the long-duration stimuli required to produce functional whole-body balance responses could be unsafe. In recent studies performed in guinea pigs, audio-frequency bone-conducted sounds of relatively low intensity (median threshold of 44 dB above that for brainstem auditory-evoked potentials) delivered via a clinical bone conductor have been found to selectively activate the irregular afferents of otolith origin (Curthoys et al. 2006). In man, 250–1000 Hz bone-conducted tones (at 70–80 dB above hearing threshold) delivered via the mastoid produces short-latency vestibular-evoked myogenic potentials (VEMPs) recorded from sternocleidomastoid (SCM) muscles (Sheykholeslami et al. 2000; Welgampola et al. 2003). This method therefore is a good candidate for a safe means of activating human vestibular afferents with the long-duration stimuli required to evoke functional balance responses.

In the present study, we wished to determine whether a bone-conducted tone delivered via the mastoid is capable of producing whole-body sway responses in standing subjects, and if so whether the response is consistent with being of vestibular origin. As this study is the first of its kind, we have measured some fundamental characteristics of the sway response (time course, magnitude and direction) and its intra- and intersubject reproducibility. We used a stimulus frequency (500 Hz) known to activate vestibular afferents in guinea pig and man (Curthoys et al. 2006; Welgampola et al. 2003), and a stimulus duration (2–3 s) known to evoke a well-developed whole-body balance response to galvanic vestibular stimulation (Day et al. 1997).

Although we deliberately stimulated over bone, the vibration could be transmitted to muscle spindles by conduction along the bone and tendons. When applied directly to relaxed human muscles and tendons, vibration stimulates muscle spindle primary endings resulting in an abrupt increase in group Ia afferents' discharge rates at the stimulus frequency (up to 200 Hz) or sub-harmonic frequencies (Burke et al. 1976). In the cat, vibration-evoked spindle responses have been reported at frequencies as high as 500 Hz (Brown et al. 1967), the vibration frequency used in the present study. If neck muscle spindle afferents are excited by bone-transmitted vibration then they could produce a whole-body sway response. We therefore compared the direction and magnitude of body sway responses upon stimulation of bone (mastoid and temporal fossa) and of neck musculature at different sites. We specifically chose posterior neck muscles and sternocleidomastoid muscles, which insert over the mastoid process and are the most likely postural muscles to receive transmitted vibration.

To test further whether the sway response might be of vestibular origin we examined the dependence of the evoked sway direction on changes in head position with respect to the feet. Since the vestibular system signals accelerations in craniocentric coordinates, the sway direction of a pure vestibular-evoked response must change by the same amount and in the same direction as a change in head yaw angle.

Finally, we compared the time course and direction of sway produced by the unilateral bone-conducted tone stimulus with that produced by unilateral cathodal galvanic vestibular stimulation (GVS) of the same side. We expected that comparison of these sway profiles in the same subjects would yield information on the end organs activated by the stimulus. GVS activates otolith and semicircular canal afferents (Lowenstein, 1955; Goldberg et al. 1984), but by a process of vector addition and cancellation (Fitzpatrick & Day, 2004; Day & Fitzpatrick, 2005) the net vestibular input is thought to be dominated by the canal component. This is reflected in the directional properties of the whole-body sway response (Cathers et al. 2005) and in the oculomotor response (Schneider et al. 2000) to GVS. If the bone-conducted tone selectively activates otolith afferents with negligible activation of semicircular canal afferents (Curthoys et al. 2006), different sway directions would be expected from the two modes of stimulation. Part of these data has been presented in abstract form (Welgampola & Day, 2004).

Methods

Sixteen healthy subjects aged 23–51 years were recruited with written informed consent and local ethics committee approval, in accordance with the Declaration of Helsinki. Four separate studies, which used common methods of stimulus delivery, data collection and analysis, were performed.

Stimuli and equipment

Bone-conducted tones

Tones were generated using a custom-made gated oscillator controlled by a logic signal and delivered via B71 clinical bone vibrators (Radioear Corporation, New Eagle, PA, USA) which were placed over each mastoid. The B71 is a commonly used piece of audiometric equipment, with a total weight of 19.9 g. The vibrator is housed in (3.0 cm × 1.5 cm × 1.5 cm) plastic casing with a (circular) mastoid contact plate of 1.77 cm2. Each vibrator is secured with a steel spring head-band, which holds it against the mastoid with a force of 4.5–5 N.

The bone conductors were calibrated using a Bruel and Kjaer 4930 artificial coupler and a Bruel and Kjaer 2203 Sound Level Meter (calibrated to read 0 dB at 1 μV). The force sensitivity constant of the coupler was 132 mV N−1 (or 132 × 10−9 V μN−1). The reference equivalent threshold force levels for bone conductors are given in decibells referenced to 1 μN (1 μN = 0 dB). The intensity of our bone-conducted tones using this reference are noted as dB FL (force level). The difference in dB between the μV scale (on the sound level meter) and μN scale is 17.6 (20 log (1 × 10−6/132 × 10−9)).

Stimuli of 500 Hz, 20 V peak-to-peak (p-p) (136 dB FL) lasting 2 s (experiments 1–3) or 3 s (experiment 4) were used. Mastoid vibration was delivered using two B71 clinical bone vibrators placed approximately 3 cm posterior and 2 cm superior to the external acoustic meatus. Care was taken to ensure contact between bone and the entire contact surface of the conductor. The final position of the stimulator was marked such that the same location would be used during the entire study.

Visible startle responses were seen in the first few trials of most subjects. We therefore gave 10 trial stimuli to all subjects before commencing data collection

Galvanic stimulation

In experiment 4, 1 mA monaural cathodal galvanic stimulation was delivered using 2.5 cm diameter circular neurostimulation electrodes (PALs plus, Nidd Valley Medical Ltd, Knaresborough, UK). The active electrode was placed over the left mastoid process and the reference over the T2 spinous process using Micropore. adhesive surgical tape (3M). Electrode gel (Dracard, Maidstone, UK) was used over the electrode–skin interface to improve conductance.

Accelerometer recordings

Peak acceleration was measured in response to a 500 Hz, 136 dB FL, 2 s stimulus (over the standard location) in a single subject using an Entran egaXT-50 uniaxial accelerometer (Fairfield, NJ, USA) attached to the mastoid tip with double-sided adhesive tape. The sensitive axis was aligned mediolaterally, normal to the plane of the mastoid.

Data collection and analysis

Before commencement of each trial, subjects stood quietly on the force platform with their feet together and eyes shut. Data collection was initiated by the experimenter with a button press and commenced after a random delay of 50–500 ms. Each collection lasted for 8 s in total. For every condition tested, each subject's mean response was obtained by averaging 20 trials offline, using a program written in MATLAB (MathWorks Inc., Natick, MA, USA). To quantify whole-body mean responses, we measured three parameters: the changes in ground reaction forces, the velocity of body motion and the body's position change. These measures were expressed in terms of magnitude and direction.

Ground reaction force data were collected using a fixed (Kistler type 9281B, Kistler Instrumente AG, Switzerland) force plate. Forces acting upon the body in mediolateral (x), anteroposterior (y) planes were measured from 0 to 450 ms post stimulus onset. The magnitude and direction of their vector sum (horizontal force response) was calculated. The position of the point of application of the ground reaction force in the horizontal plane (centre of pressure; CoP) was calculated.

The 3-dimensional position and velocity of an infrared marker attached to the prominence overlying the C7 spinous process was measured at 200 Hz using a CODA mpx 30 motion detection system (Charnwood Dynamics, Rothley, UK). For the final study, additional markers were placed at other sites on the body (see experiment 4 below). The magnitude and direction of the peak velocity of the C7 marker between 0.75 s and 2 s from stimulus onset was measured. The magnitude and direction of position change of the C7 marker in the horizontal plane was measured at a fixed interval of 0–2 s from stimulus commencement.

For single-trial analysis, we estimated the magnitude of response displacement in each individual trial by measuring the component of body displacement that occurred in the direction of the subject's mean response, normalized to the magnitude of the mean response. Thus, if in a single trial the subject swayed in the same direction and by an equal amount as her mean response, the single-trial response would be assigned a value of one. If she swayed by the same amount at either 90 or 180 deg to the mean angle, the single-trial response would be assigned values of 0 and −1, respectively. This method was chosen to take into account both the magnitude and direction of movement.

Experimental protocols

Experiment 1. Baseline study

Ten subjects stood facing forwards and were randomly presented with a right mastoid, left mastoid or a null stimulus. Sixty responses (20 per condition) were recorded and averaged separately for each of the three (left, right, null) conditions.

Experiment 2. Comparison of muscle vibration with mastoid vibration

Sixteen subjects were studied facing forwards. One bone conductor was placed over the left mastoid (standard location/control stimulus). The second one was placed in 1 of 5 alternative locations on the left side: the upper 1/3 of the sternocleidomastoid muscle (SCM) overlying the tendon; the middle 1/3 of the SCM overlying the muscle belly; the lower 1/3 of the SCM over it's clavicular head; on the posterior neck muscles, lateral to the superior part of trapezius; over the temporal fossa 4 cm directly above the external acoustic meatus. This experiment was conducted in five blocks. During each block, 40 stimuli were randomly delivered at one every 60 s over the standard or alternative locations. Between blocks the stimulators were removed from the head and subjects were allowed to sit down and rest for a minimum duration of 10 min.

Experiment 3. Effect of head yaw position

Eight subjects participated in this study. Their naso-occipital axes were approximately aligned to each of the five following directions presented in random order: 90 deg to the left, 45 deg to the left, directly forwards, 45 deg to the right, 90 deg to the right. The feet were always aligned to the sagittal plane. The head position was recorded, using infrared markers attached to symmetrical sites over both tragii. Left or right mastoid stimuli were presented randomly with 40 trials recorded for each head yaw angle.

Experiment 4. Comparison of galvanic vestibular stimulation and vibration

Ten subjects were studied, using 3 s, 136 dB FL, 500 Hz tones delivered over the left temporal fossa or 3 s, 1 mA GVS delivered over the left mastoid. This study also enabled us to observe the effects of a longer duration stimulus. The order of stimulus presentation was randomised. Twenty stimuli were delivered for each condition. Displacement of markers placed over the occiput, C7, T7 and L3 spinous processes, ground reaction forces and centre of pressure (CoP) displacement were measured.

Statistical methods

Measures of magnitude

The parameters measured (magnitude of force, velocity, position) were analysed using repeated measures ANOVA (version 11, SPSS Inc., Chicago, IL, USA). Planned contrasts were used for comparison between levels. When required, further post hoc comparisons were performed using paired t tests. Significance was taken as P < 0.05. The descriptive data are given as mean ±s.e.m. unless otherwise specified.

Measures of direction

Although linear statistical methods can be applied to directional data when the values are closely clustered, angular measures that are widely separated cannot be treated statistically as linear data. This is true for descriptive statistics as well as inferential statistics.

Conventions used to describe angles

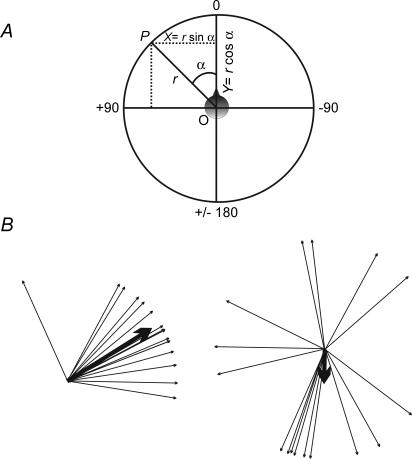
All directional data were expressed as angles ranging from 0 to ±180 deg using the convention of 0 deg pointing forward and horizontally in the mid-sagittal plane, with directions to the left of zero being positive and directions to the right being negative (Fig. 1A).

Figure 1. Representation of circular data.

Figure 1

Open in a new tab

A, convention used in representing angular data. B, example of a non-random distribution (left; r = 0.88, P < 0.001) and a random distribution of angles (right; r = 0.27, P = 0.3). The mean angles and their concentration (r) are shown by the direction and length of the thicker arrows.

Descriptive statistics for angular data

When measuring the mean of a group of angles, their arithmetic mean is a poor measure of central tendency (Batschelet, 1981; Rao & Sengupta, 2001). For analyses, angles were regarded as points (P) on the circumference of a unit circle with a radius (r) = 1, and perpendicular axes X and Y passing through its origin O. The rectangular coordinates of a point P on this circle (Fig. 1A) are:

graphic file with name tjp0577-0081-m1.jpg

A sample of angles α1, α2, …αn, would thus have a series of x and y coordinates x1, x2, …xn and y1, y2, …yn. The mean x- and y-values can be calculated as follows:

graphic file with name tjp0577-0081-m2.jpg (1)

Using the mean X and Y coordinates, the mean angle for this sample α can now be calculated as follows:

graphic file with name tjp0577-0081-m3.jpg

Therefore:

graphic file with name tjp0577-0081-m4.jpg (2)

This mean angle α represents the direction of the mean vector of the sample α1, α2, …αn.

The length of the mean vector (r) is equal to the resultant vector (of all the x and y coordinates) R divided by n (sample size). For a series of angles α1, α2, …αn the resultant vector is calculated as follows: the x coordinate of the resultant vector is the sum of all the x coordinates for α1, α2, …αn, or (Σsin α). Its y coordinate is the sum of all the y coordinates for α1, α2, …αn (Σcos α). The resultant of the summed x and y coordinates is then calculated.

graphic file with name tjp0577-0081-m5.jpg (3)
graphic file with name tjp0577-0081-m6.jpg (4)

In a situation where all the angles are identical, the value of r = 1. Where the sample points fall close together (e.g. in an arc < 20 deg) r will be almost 1 (Batschelet, 1981). Where there is no concentration around a single direction, r will be close to 0. In unimodal samples, r serves as a measure of concentration or clustering (see Fig. 1B).

Tests of significant clustering of angles

For each sample of angular data we used the Rayleigh test (using r as the test statistic) to check whether there was statistical evidence of ‘directedness’ (i.e. whether the population from which the angles are drawn differ significantly from randomness). When r is large (i.e. close to 1), the null hypothesis of randomness can be rejected in favour of directedness (Batschelet et al. 1981). The critical level of r for a sample varies with its size. We used a significance level of 0.05. Examples of a significantly clustered group of angles and a randomly distributed group are given in Fig. 1B.

Pair-wise comparisons

To examine differences between paired angular observations (α1, β1;α2, β2 … αn, βn) we used Moore's modification of Rayleighs test, a non-parametric method of pair-wise comparison (Moore, 1980; Zar, 1999; Sparto & Schor, 2004) using the following steps:

  1. X and Y coordinates of each sample were first calculated (Xα = sin α; Xβ = sin β; Yα = cos α; Yβ = cos β);

  2. Difference between the pairs for these coordinates were computed as follows:
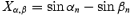
    graphic file with name tjp0577-0081-m7.jpg
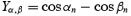
    graphic file with name tjp0577-0081-m8.jpg

  3. The resultant vector length r = [(Xα,β)2+ (Yα,β)2]1/2

  4. The angular difference corresponding with the subtracted coordinates θ = tan−1 = Xα,β/Yα,β

  5. r is rank ordered and the following values are calculated.
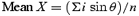
    graphic file with name tjp0577-0081-m9.jpg
    graphic file with name tjp0577-0081-m10.jpg
    where i is the rank order of (r)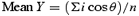

The test statistic R′ is then calculated as in eqn (5) and compared against critical values provided by Moore (1980).

graphic file with name tjp0577-0081-m11.jpg (5)

Correlations

When examining correlations between two sets of angular data (α1, β1;α2, β2 … αn, βn), we first used conventional linear scatterplots and linear regressions. Conventions of −360 to +360 deg were used to avoid discontinuity between data points that lay close to each other but across the ±180 deg line. However, this sometimes required subjective assessment of where a data point should lie. Therefore, we performed a more rigorous parametric circular–circular correlation using a modified correlation coefficient R2 (Batschelet, 1981; Mardia & Jupp, 2000) with angles within ±180 deg. This modified coefficient incorporates the following six correlation coefficients and is computed using eqn (6):

graphic file with name tjp0577-0081-m12.jpg
graphic file with name tjp0577-0081-m13.jpg
graphic file with name tjp0577-0081-m14.jpg
graphic file with name tjp0577-0081-m15.jpg
graphic file with name tjp0577-0081-m16.jpg
graphic file with name tjp0577-0081-m17.jpg
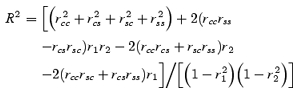graphic file with name tjp0577-0081-m18.jpg (6)

Independence of αn, βn is rejected for large values of R2. Under independence, nR2 = χ2 (Batschelet, 1981).

Results

Peak accelerations measured at the skin overlying the mastoid during ipsilateral and contralateral mastoid vibration were 1 g and 0.1 g, respectively. Since the accelerometer was not fixed directly to the bone surrounding the vestibular organs, it is unlikely that these values represent the true magnitude of acceleration transmitted to the inner ear. However, they provide an order of magnitude estimate of the attenuation of the stimulus across the head.

Whole-body response characteristics

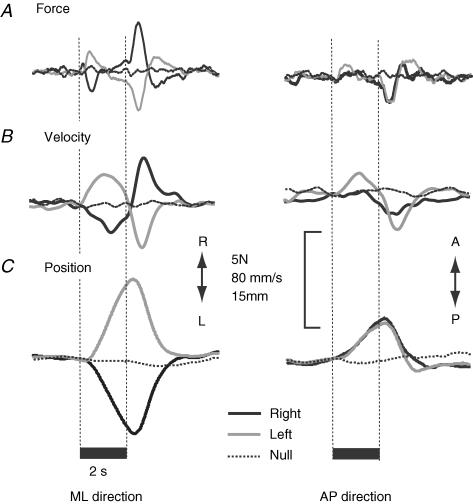
With the subject facing forward and eyes closed, 500 Hz vibration applied unilaterally to the mastoid process produced a consistent whole-body response. In single trials the response was superimposed on the random body sway of bipedal stance. Stimulus-locked averaging of 20 trials largely cancelled out the random spontaneous sway to reveal the mean stimulus-evoked response. In our recordings the earliest manifestation of the response was a force impulse between the feet and ground. It began ∼250 ms after stimulus onset and peaked at ∼450 ms (Fig. 2A). On average, it caused the body to sway in an anterolateral direction away from the stimulated mastoid (Fig. 3A). The magnitude of body velocity peaked around 0.75–1.5 s after stimulus onset (Fig. 2B). Displacement of the body began at ∼400 ms. By the end of the 2 s stimulus the body had moved to a new position relative to its start position, maximal displacement being achieved some 400–500 ms later (Fig. 2C). Following stimulus cessation, a similar but oppositely directed sequence of events returned the body approximately to its start position. We measured the magnitude and direction of three variables (initial force, peak velocity, position change) to define the average on-response at different stages of its development.

Figure 2. Group mean raw records.

Figure 2

Open in a new tab

Traces show the mediolateral (ML) and anteroposterior (AP) components of: A, horizontal ground reaction force; B, body horizontal velocity; C, body horizontal position before, during and after 2 s of mastoid vibration. Each trace represents mean responses to right, left and null stimuli in 10 subjects. The vertical dashed lines mark stimulus onset and cessation. Traces have been aligned at stimulus onset.

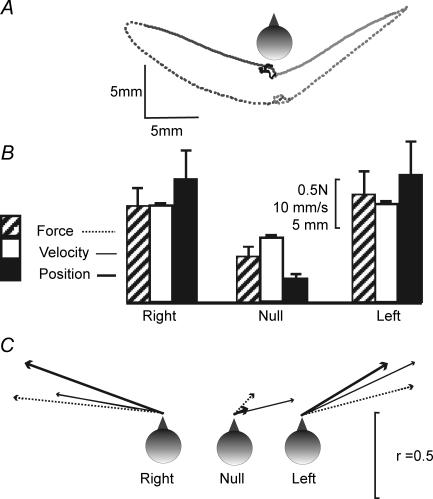
Figure 3. Effect of side of stimulation.

Figure 3

Open in a new tab

Data from mean responses in 10 subjects facing forward. A, group mean sway paths of the C7 marker during stimulation (continuous line) and 2 s post stimulus (dashed line) for 3 stimulus conditions [left (light grey), right (dark grey), null (black)]. B, mean (+s.e.m.) magnitude of the initial force response, peak velocity and position change during the 2 s stimulation period for right, left and null stimuli. C, mean directions of force (dotted line), velocity (thin continuous line) and position (thick continuous line). The direction of each arrow represents the mean angle and the arrow length represents r, a measure of concentration of the directions for each condition (r = 1 if all subjects respond in the same direction; see Statistical methods).

Response magnitude

The mean magnitudes of the initial force, peak velocity and position change for the on-response are shown in Fig. 3B and Table 1 for the three stimulation conditions (right stimulus, null stimulus, left stimulus). There was a significant effect of stimulation condition for all three measures of response magnitude (force: F2,18 = 8.89, P = 0.002; velocity: F2,18 = 8.29, P = 0.003; displacement: F2,18 = 10.16, P = 0.001). Planned contrasts showed that these effects stemmed from the null stimulus response being smaller than both the right stimulus response (force: P = 0.003; velocity: P = 0.019; position: P = 0.005) and the left stimulus response (force: P = 0.014; velocity: P = 0.008; position: P = 0.01). There were no significant differences between the right and left stimulation conditions (paired t test; force: P = 0.5; velocity: P = 0.72; position: P = 0.828).

Table 1.

Initial ground reaction force, body velocity and body position responses measured during right, left or null stimulus conditions

Right Left Null
Force change 0–450 ms (N) 1.02 ± 0.17 1.12 ± 0.24 −0.48 ± 0.08
Direction of force 0–450 ms (deg) 84.0 (0.86) −75.4 (0.66) −43.4 (0.16)
Peak force (N) 1.30 ± 0.13 1.55 ± 0.22 0.64 ± 0.09
Time of peak force (ms) 405 ± 36 473 ± 65 470 ± 98
Peak velocity (mm s−1) 20.0 ± 3.8 20.1 ± 3.8 13.3 ± 3.1
Direction of peak velocity (deg) 80.21 (0.61) −64.7 (0.71) −76.28(0.35)
Time of peak velocity (ms) 1290 ± 130 1103 ± 90 1346 ± 10
Position change 0–2 s (mm) peak 12.95 ± 2.97 11.47 ± 3.2 2.41 ± 0.47
Direction of position 0–2 s (deg) 69.9 (0.83) −58.9 (0.57) −66.2 (0.08)
Maximum displacement (mm) 13.58 ± 2.9 13.4 ± 3.5 2.94 ± 0.28
Open in a new tab

All linear values represent mean ±s.e.m. For left and right mastoid stimulation, linear values significantly different from those of the null condition are in italic. Directional data are given as mean angle and its concentration (r) in parentheses (see Statistical methods). Angles that were significantly clustered (non-random in distribution) are in bold type.

Response direction

The mean directions of the on-response initial force, peak velocity and position change are shown in Fig. 3C and Table 1 for the three stimulation conditions (right stimulus, null stimulus, left stimulus). The between-subject response directions were significantly clustered during right stimulation (force: 84.0 deg, r = 0.86, P < 0.001; velocity: 80.2 deg, r = 0.61, P = 0.023; position: 69.9 deg, r = 0.83, P < 0.001) and left stimulation (force: −75.4 deg, r = 0.67, P = 0.009; velocity: −64.7 deg, r = 0.71, P = 0.005; position: −58.9 deg, r = 0.57, P = 0.03), but were randomly distributed during null stimulation (force: r = 0.17, P = 0.78; velocity: r = 0.34, P = 0.32; position: r = 0.07, P = 0.5). For all three measures the mean response directions were significantly different for the left and right stimulation conditions (force: P < 0.001; velocity: P = 0.005; position: P < 0.001). The intersubject variability in response direction is illustrated for the position response in Fig. 4A.

Figure 4. Response variability.

Figure 4

Open in a new tab

A shows between-subject direction variability. The arrows represent the mean directions of displacement measured for 10 subjects under 2 stimulus conditions, right mastoid stimulation (black) and left mastoid stimulation (grey). Both groups of angles were significantly clustered (r = 0.83 and 0.57; P < 0.001 and P = 0.03). B shows within-subject direction variability. The bar graph represents the values obtained in 16 subjects for concentration (r) of response direction obtained in 5 successive experiments that used left mastoid vibration. Significant clustering (P < 0.05) is denoted by the horizontal dashed line. Four of the 16 subjects showed non-significant clustering while 12 show significant clustering. The mean directions of the position response recorded in the 5 separate experiments are shown on the right for 2 subjects. C shows trial-by-trial variability as the normalized component of sway size measured in the direction of each subject's mean position response direction. Shown are individual data from a single subject (upper plot) and group mean (±s.e.m.) data (lower plot) from all 10 subjects.

Within-subject variability and single trial responses

Sixteen subjects were stimulated over the left mastoid in five separate blocks (experiment 2), each containing 20 trials. Reproducibility of the mean response direction for each subject was examined by measuring the clustering of the mean angle of displacement for these five blocks using the Rayleigh test. Calculated r values for the five mean angles of displacement recorded for each subject are depicted in Fig. 4B. Of the 16 subjects, 12 had significant clustering of the mean angles (r values of 0.76 and above, P < 0.05).

To investigate the possibility of response habituation, we analysed data on an individual trial basis from the baseline study (experiment 1) in which each subject was stimulated 40 times. Figure 4C shows the trial-by-trial normalized displacement for a single subject and the mean normalized displacement for all 10 subjects. Linear regression of the normalized displacement against trial number gave an r value of 0.17 (P = 0.3) and no evidence of response habituation.

Comparison with direct neck muscle vibration

The mean sway paths to vibration delivered at five different sites over the skull or neck muscles together with the standard mastoid site are shown in Fig. 5A. In this experiment mastoid vibration trials were randomly interleaved with vibration at one other site in five blocks of trials. However, for the purpose of statistical analyses we have taken the mastoid response as the average of all mastoid trials.

Figure 5. Comparison of skull and muscle vibration.

Figure 5

Open in a new tab

A, group mean (n = 16) sway paths described by the C7 marker during the 2 s of stimulation (continuous line) and 2 s after stimulus cessation (dashed line), when the stimulus was applied over the left mastoid (M: black traces) or one of 5 alternative left-sided sites (grey traces): T, temporal fossa; P over the posterior neck muscles; S1, upper 1/3 of the SCM, 1 cm below the mastoid; S2, middle 1/3 of the SCM, over the muscle belly; S3, lower 1/3 of the SCM over the clavicular head. B, mean (+s.e.m.) magnitudes of the force (hatched bars) and position change (black bars) for the 6 stimulus locations. Magnitudes that were significantly reduced compared with the mastoid are marked with an asterisk. C, mean directions of force (dotted arrow) and position (continuous arrow) responses. The direction of each arrow represents the mean angle and the arrow length represents r, a measure of concentration of the directions (r = 1 if all subjects respond in the same direction; see Statistical methods). Note the similarity in the directions of force and displacement for mastoid and temporal fossa stimulation. Angles for S1–3 were randomly distributed between subjects and are marked with an asterisk.

Response magnitude

Stimulus location had a significant effect on the magnitudes of the initial force (F5,75 = 3.99, P = 0.003) and position response (F.5,75 = 5.69, P < 0.001) but not on the maximum velocity (F5,75 = 2.79, P = 0.085). Planned contrasts compared the mastoid response with the response at each of the other sites. As shown in Fig. 5B and Table 2, both force and position changes were significantly smaller only for the SCM belly or clavicular head sites (force: P = 0.006, 0.02; position: P < 0.001, 0.002, respectively). For the posterior neck site the magnitude of force was similar to mastoid stimulation (P = 0.95) but the magnitude of position change was significantly smaller (P = 0.025).

Table 2.

Initial ground reaction force, body velocity and body position responses following stimulation over two skull locations (mastoid and temporal fossa) and four locations over anterior and posterior neck muscles

Measurement Mastoid Temporal SCM tendon (S1) SCM belly (S2) SCM clavicular head (S3) Posterior neck
Force change 0–450 ms (N) 0.84 ± 0.11 0.97 ± 0.13 0.79 ± 0.11 0.43 ± 0.06 0.56 ± 0.06 0.84 ± 0.1
Direction of force 0–450 ms (deg) −49.76 (0.61) −85.2 (0.61) −107.9 (0.46) 152.7 (0.28) −173.5 (0.15) 27.3 (0.49)
Peak velocity (mm s−1) 14.6 ± 1.0 16.7 ± 2.0 14.3 ± 2.0 12.4 ± 1.0 12.4 ± 1.0 12.8 ± 1.0
Direction of peak velocity (deg) −61.4 (0.89) −61.6 (0.75) 178.7 (0.13) 173.9 (0.35) 42.7 (0.03) −33.2 (0.19)
Position change 0–2 s (mm) 10.83 ± 1.64 13.65 ± 2.9 8.19 ± 3.09 5.36 ± 1.11 4.8 ± 1.05 6.23 ± 1.34
Direction of position 0–2 s (deg) −57.99 (0.89) −67.57 (0.78) −135.7 (0.19) 178.8 (0.28) −72.8 (0.12) 6.05 (0.68)
Open in a new tab

Directional data are given as mean angle and its concentration (r) in parentheses (see Statistical methods). Angles that were significantly clustered (non-random in distribution) are in bold type. The italicised figures represent linear values that were significantly different from the control mastoid values on repeated measures ANOVA with contrasts, and angular values that were significantly different on pair-wise comparison with mastoid stimulation (angles with a random distribution were not used in such analyses).

Response direction

The response directions for left mastoid stimulation were significantly clustered and similar to those recorded in the baseline study (mean directions for force, velocity and displacement: −49.76 deg (r = 0.61, P < 0.002), −61.4 deg (r = 0.89, P < 0.001), −57.99 deg (r = 0.89, P < 0.001)).

For all three SCM sites there were no consistent directions of response within the group (see Table 2 and Fig. 5C) and so were not analysed further. For the posterior neck muscle site there was significant clustering of force and position directions (r = 0.49, 0.68; P = 0.022, P < 0.001, respectively), but the mean directions (force: 27.3 deg; position: 6.05 deg) were significantly different to the mastoid site (P < 0.001 for both). For the temporal fossa site there was significant clustering of force, velocity and position directions (r = 0.61, 0.75, 0.78; P < 0.002, P < 0.001, P < 0.001, respectively). In this case the mean directions (force: −85.2 deg; velocity: −61.6 deg, position: −67.57 deg) were not significantly different to the mastoid site (P > 0.1 for all 3).

Effect of head yaw position

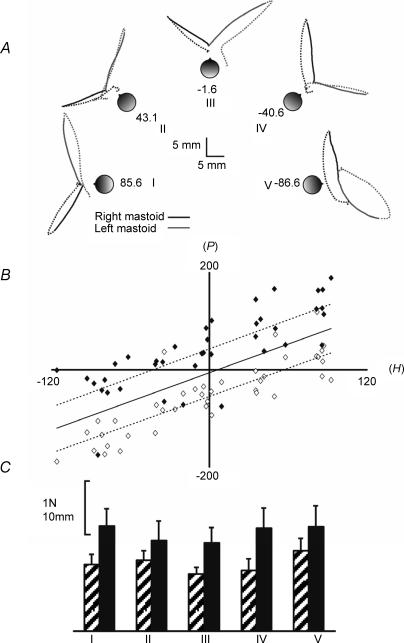
Figure 6A illustrates the effect of five head yaw angles (+ 90, +45, 0, −45, −90 deg) on the mean sway paths in eight subjects. It shows that response direction was not fixed in body or room coordinates but was a function of head angle. The scatter plot shown in Fig. 6B suggests there was a linear relationship between sway direction and head yaw angle. Statistically, the direction of the initial force (F), the direction of body motion at peak velocity (V) and the direction of displacement (P) were significantly correlated with head yaw angle (H). Thus, the circular–circular correlations between F, V, and P with H for left mastoid stimulation yielded modified correlation coefficients (Mardia & Jupp, 2000) of 0.79, 0.92 and 1.2, respectively (corresponding values for nr2 = 31.6, 36.9, 48.0; probability of independence < 0.001 for all 3). For right mastoid stimulation, the modified coefficients for F, V and P were 0.83, 0.49, 0.75 (nr2 = 33.2, 19.6, 30.0; P < 0.001 for all 3). The slopes of the relationships obtained from linear regression were close to unity (1.01, 1.07 and 0.98, respectively, for F, V and P) suggesting the response was organized in a craniocentric reference frame. The response magnitudes were unaffected by head yaw angle (F4,56 = 2.1, 0.362, 0.89, P = 0.08, 0.83, 0.48 for F, V and P, respectively) (Fig. 6C).

Figure 6.

Figure 6

Open in a new tab

Effect of head direction A, group mean (n = 8) paths taken by the C7 marker during 2 s of stimulation (bold lines) and 2 s following stimulus cessation (dashed lines) for left (grey) and right (black) mastoid stimulation. Subjects' feet were always aligned to the sagittal plane. The naso-occipital axes were aligned to angles of +90, +45, 0, −45 and −90 deg from the saggital plane (conditions I–V). The values noted for conditions I–V represent the average angle of the naso-occipital axes in the 8 subjects. B, scatterplot of the direction of position change (P) against head yaw angle (H) during stimulation. Angles relating to right- and left-sided stimulation are marked black and white, respectively. The regression lines for left- or right-sided stimulation alone (interrupted lines) and for both sides combined (continuous line) have been plotted. C, mean (+s.e.m.) magnitudes of the initial force response (hatched bars) and position response (filled bars) for the 5 head positions. No significant effect of head position was observed.

Comparison with galvanic vestibular stimulation

There were a number of similarities between the responses to unilateral bone-conducted sound and unilateral GVS (cathodal), as shown in Fig. 7. Both caused the body to sway away from the side of stimulation with a similar time course and similar kinematic profile. Thus, higher body markers displaced further than lower sites and there was an overall shift in the centre of pressure (CoP) of the ground reaction force, which when the body is in a quasi-static state reflects displacement of the body's centre of mass (CoM). This pattern suggests that for both stimuli a major component of the response consisted of body sway about the feet and ankle joints.

Figure 7. Comparison of temporal fossa vibration and galvanic vestibular stimulation (GVS).

Figure 7

Open in a new tab

Group mean raw records comparing the effects of vibration (black lines) and GVS (grey lines). A, traces show the mediolateral and anteroposterior components of body horizontal position and centre of pressure before, during and after 3 s stimulation. Each trace represents mean responses in 10 subjects. The vertical dashed lines mark stimulus onset and cessation. Traces have been aligned at stimulus onset. B, the group mean sway path for vibration (black) and GVS (grey). The dotted and continuous lines represent the on and off responses, respectively.

The magnitudes of the two responses were well matched (force: 1.11 ± 0.21 N for vibration, 1.62 ± 0.17 for GVS; velocity: 27.4 ± 3.08 mm s−1 for vibration, 30.9 ± 4.71 mm s−1 for GVS; P = 0.14 and 0.26, respectively, on paired t tests). When the four measures of position change (occiput, neck, thorax, pelvis) at 2 s were compared in a 4 × 2 factor general linear model, there was a significant main effect of marker location (F3,27 = 49.09, P < 0.001) but no effect of stimulus type (F1,9 = 0.45, P = 0.52).

The major distinguishing feature between the two stimuli was in the direction of the evoked response (Fig. 7B). The mean directions of the on-response initial force, peak velocity and position were significantly clustered for both vibration (force: −56.7 deg., r = 0.89, P < 0.001; velocity: 47.1 deg, r = 0.93, P < 0.001; position: 52.7 deg., r = 0.94, P < 0.001) and GVS (force: −86.6 deg, r = 0.97, P < 0.001; velocity: −78.3 deg, r = 0.98, P < 0.001; position: −79.3 deg., r = 0.97, P < 0.001) For all three measures the mean response directions were significantly different for the two stimuli (force: P < 0.01; velocity: P < 0.001; position: P < 0.005; Moore's method of comparing paired angular data). The linearity of the mean sway path also appeared to differ for the two responses with GVS producing a more curved path (Fig. 7B). However, this may have been a consequence of the difference in response directions. The sway vector to GVS was such that subjects' CoM moved further laterally taking them to a position of greater instability. This would have been signalled by other sensory systems, e.g. proprioceptors, which are known to modify the developing GVS-evoked response (Day & Cole, 2002), causing the sway path to be modified.

Discussion

Previous work has shown that short-duration (7 ms) 250–1000 Hz vibration of the mastoid process evokes myogenic potentials in sternocleidomastoid muscles of the neck (Sheykholeslami et al. 2000; Welgampola et al. 2003). Clinical evidence suggests that these potentials have a vestibular origin. They are absent in subjects with selective vestibular neurectomy but preserved in subjects with severe sensorineural hearing loss (Welgampola et al. 2003; Brantberg & Mathiesen, 2004). One aim of the present study was to investigate whether it is possible to obtain a whole-body response to this form of vestibular stimulation. The results show that a 500 Hz stimulus applied for a relatively long period (2 s) is indeed capable of evoking a whole-body sway response in standing subjects deprived of vision. When the subject faces forward the mean direction of sway is oblique with a forward component and a lateral component away from the stimulated ear. Rotation of the head in yaw causes the response direction to rotate by the same amount indicating a craniocentric organization of the response. We hypothesize that the whole-body sway represents a balance response to the vibration-evoked vestibular input.

Other investigators have reported that, although neck muscle vibration evokes measurable sway, mastoid vibration does not (Andersson & Magnusson, 2002; Magnusson et al. 2004). Our stimulus differed from their's in that it was generated by a different stimulus source with a higher stimulus frequency. Stimuli used in these previous studies had a frequency of 120 Hz or less. For myogenic potentials evoked by bone-conducted tones, well-formed responses are obtained using stimuli of 250–1000 Hz (Welgampola et al. 2003) with maximal amplitudes at 200–400 Hz (Sheykholeslami et al. 2001). Vibration at 500 Hz has been shown to be an effective stimulus for activating vestibular afferents in guinea pig (Curthoys et al. 2006). Our choice of stimulus frequency was governed by these observations and by the output of our stimulator, which is maximal at 500 Hz. Was our stimulus source better suited to evoke a sway response since it generated a signal that is more lateralized? Using the vestibular-evoked myogenic potential as a marker of vestibular input, we suspect that vibration delivered via a bone conductor is also transmitted bilaterally but not symmetrically since the response is 30% larger ipsilaterally (Welgampola et al. 2003). Our measures of head acceleration also indicate asymmetrical stimulation.

Does muscle spindle input contribute to the response?

It is well established that vibration of posterior neck muscles can evoke a forward whole-body sway response in standing subjects (Gregoric et al. 1978; Lund, 1980). Furthermore, the sway response direction changes with head yaw position indicating organization in a craniocentric reference frame (Ivanenko et al. 1999). The vibration frequencies used in their experiments were an order of magnitude lower than the frequency used in the present study, but we were able to replicate forward sway behaviour using 500 Hz vibration applied directly to posterior neck muscles. The precise mechanisms underlying the whole-body sway responses to posterior neck muscle vibration are not clear. Responses are either abolished or dramatically reduced in subjects with bilateral loss of vestibular function (Lekhel et al. 1997). In subjects with unilateral vestibular lesions the sway response is smaller and in a different direction compared with normal (Popov et al. 1996; Lekhel et al. 1998). A simple explanation for the absence or reduction of sway in these lesions would be that vibration-evoked vestibular input normally contributes to the sway response. An alternative explanation, and one that is favoured by Lekhel et al. (1998) and Popov et al. (1996), is that the sway response is driven exclusively by vibration-evoked muscle spindle input but modified by concurrent vestibular information. Their argument is that the change in muscle spindle input generated by vibration mimics a stretch of the posterior neck muscle, as though the neck were flexed, but the vestibular system signals that the head has remained upright. The brain therefore interprets the situation as a backward lean of the body together with a neck flexion that keeps the head upright. The apparent unplanned backward lean of the body is compensated by a forward directed whole-body sway.

Could our mastoid sway response have this mechanism? Mastoid vibration could potentially be transmitted to nearby anterior or posterior neck muscles. The sternocleidomastoid (SCM), which inserts over the mastoid process, contributes to contralateral rotation of the head, ipsilateral lateral flexion and forward flexion of the neck. The splenius, which also inserts over the mastoid, contributes to ipsilateral rotation of the head, ipsilateral lateral flexion and extension of the neck (Gray, 1918). If SCM and splenius were activated together then most of these actions would cancel out to leave lateral neck flexion. Vibration-evoked muscle spindle input from both muscles would therefore mimic the muscle lengthening associated with contralateral lateral neck flexion. Using the argument outlined above, this would be interpreted as an unplanned ipsilateral lean of the body demanding a body sway away from the stimulated side. This is close to the observed behaviour. The additional forward component of the observed sway response could be simply explained by an asymmetrical signal from the two muscles with splenius providing the stronger input.

The evidence that favours more a vestibular rather than muscle spindle origin of the mastoid response comes from the results of stimulating at other sites. When the stimulator was moved off the bone and placed directly on the SCM muscle its spindle input should have increased. The direction of the response might be expected to change since the posterior neck muscles would contribute less to the input, but the direction should be just as consistent between subjects. However, we found this was not the case. The response magnitude became smaller and the response direction lost its consistency as the stimulator was moved further from the mastoid. Presumably by stimulating the soft tissue of muscle there was less transmission of vibration to the vestibular organs. In contrast, when we moved the stimulator off the mastoid to a point 4 cm above the external acoustic meatus the response was unchanged. The natural action of the nearby muscles (auricularis superior and temporalis) do not involve head or neck movements, therefore activation of their primary afferents should not evoke a sway response. A transmitted response by propagation of the signal to the posterior neck muscles is possible, but not likely to be the dominant mechanism since the average magnitude of displacement evoked by temporal fossa vibration was twice the displacement evoked by posterior neck vibration. The temporal fossa location, by its ability to generate well-formed vestibular-evoked myogenic potentials (Welgampola et al. 2003) has been shown to be an optimal site (as is the mastoid process) for vestibular activation by bone-conducted sound in humans. The sway responses evoked by temporal or mastoid stimulation are therefore likely to be predominantly vestibular in origin.

Does cochlear stimulation contribute to the response?

Bone-conducted sound activates both vestibular and cochlear afferents. The dependency of sway upon head orientation and the similarity of the initial rapid force responses observed at the onset and offset of GVS and vibration may be more indicative of a vestibular-evoked response. However, a cochlear contribution to the vibration-evoked sway response cannot be excluded until similar responses are recorded from subjects with isolated profound hearing loss.

Comparison with sway evoked by air-conducted sound

Lower limb EMG responses and sway evoked by air-conducted sound have been described by Dieterich et al. (1989) in a subject presenting with the Tullio phenomenon. They reported anterolateral displacement of the body towards the stimulus. Russolo et al. (2002) also reported mediolateral sway towards the stimulated ear in response to air-conducted tone bursts of 500 Hz in healthy subjects. These findings differ from ours and raise the possibility that sway responses to long duration air- and bone-conducted sound may differ in direction, thus implying activation of different vestibular afferents. However, the studies performed by Watson & Colebatch (1998), who reported soleus EMG responses evoked by intense auditory clicks, are contrary to these findings. The soleus EMG responses to monaural clicks were of similar polarity to soleus EMG responses evoked by monopolar cathodal stimulation and consisted of an initial short latency component and an oppositely directed medium latency component. Since the direction of the medium latency component in galvanic-evoked soleus EMG responses usually reflects the direction of sway (away from the cathodal ear), the findings of Watson and Colebatch can be extrapolated to suggest that air-conducted sound also evokes sway away from the stimulated ear. This question is best resolved by studies using air- and bone-conducted stimuli of similar intensity and duration in the same subjects.

Origin of bone-conducted sway

Cathers et al. (2005) suggested that the whole-body sway response evoked by bilateral bipolar GVS consists of a small otolith-mediated component plus a larger and more dominant semicircular canal-mediated component. The semicircular canal input produced by unilateral cathodal GVS used in the present study can be calculated from the model proposed by Fitzpatrick & Day (2004) using known canal coordinates (Blanks et al. 1975) and the assumption that afferents from all three semicircular canals are equally weighted and equally activated by GVS. This calculation yields an expected sway direction of −79 deg in response to a left-sided cathodal stimulus. This predicted sway direction agrees well with the measured sway direction (−79.3 deg for the position response) and suggests that the GVS-evoked response is indeed dominated by inputs from the semicircular canals. The bone-conducted sway response was not in the same direction as the GVS response implying that the afferent input was different for the two types of stimulation. This is in agreement with the recent work of Curthoys et al. (2006) who showed that the dominant response to bone-conducted sound in the guinea pig comes from the otoliths, with little if any response from the semicircular canals.

Vestibular-evoked myogenic potentials (VEMPs) generated by air-conducted clicks and tones (Colebatch et al. 1994) are thought to represent sacculocollic pathways (McCue & Guinan, 1994, 1997). VEMPs evoked by bone-conducted tones demonstrate partial phase cancellation by air-conducted tones, indicating that the two stimuli may activate common receptors (Welgampola et al. 2003). Loss of VEMPs evoked by both air- and bone-conducted sound following inferior vestibular nerve section (Brantberg & Mathieson, 2004) also points to significant saccular activation by both stimuli. However, it is unlikely that our whole-body responses to bone-conducted tones arise from a pure saccular input. The saccular maculae lie predominantly in the sagittal plane and so a pure saccular stimulus should result in a whole-body response also predominantly in the sagittal plane. If our sway responses are mediated exclusively by otolith afferent input, the lateral component of sway direction suggests there is likely to be a significant utricular component to the input, which is consistent with the afferent responses recorded in guinea pig (Curthoys et al. 2006). If the response is otolith mediated it is not clear why bone vibration transmitted to the saccular and utricular maculae, with their multidirectionally aligned hair cells, would produce such a consistent sway response direction. Although there was appreciable inter- and sometimes intrasubject variability, the response was far from being randomly represented in all possible directions. Even when the stimulation site was moved from the mastoid to the temporal fossa a similar mean sway direction was obtained. One explanation could be that non-specific activation of the total population of unilateral otolith afferents (plus possibly a weaker but similar contribution from the opposite side) is equivalent to a consistently directed linear acceleration through vector summation of the individual hair cells' preferred directions. Alternatively, there could be a specific activation of otolith hair cells with a preferred orientation with respect to the axis of the applied vibratory stimulus.

In summary, bone-conducted sound evokes consistent craniocentric whole-body responses in standing subjects. The characteristics of the response are compatible with it being mediated by vestibular input, although the sway direction is different to that evoked by galvanic vestibular stimulation. This suggests that different patterns of input are produced by the two types of stimulation, possibly involving different proportions of afferents from the otoliths and semicircular canals. If so, bone-conducted sound, used either in isolation or in combination with GVS, may enable investigation of hitherto unexplored aspects of vestibular function in intact freely behaving human subjects.

Acknowledgments

This work was supported by the Medical Research Council. M.W. was supported by the Garnett Passe and Rodney Williams Memorial Foundation, Melbourne, Australia and the JJ Billings Trust of the Royal Australasian College of Physicians. We thank Dr Hilary Watt for advice on statistical analyses and Mr Edward Bye for design, construction and maintenance of the tone burst generator. The bone conductors were calibrated by the National Physical Laboratory, UK.

References

  1. Andersson G, Magnusson M. Neck vibration causes short-latency electromyographic activation of lower leg muscles in postural reactions of the standing human. Acta Otolaryngol. 2002;122:284–288. doi: 10.1080/000164802753648169. [DOI] [PubMed] [Google Scholar]
  2. Batschelet E. Circular Statistics in Biology. London: Academic Press; 1981. [Google Scholar]
  3. Blanks RH, Curthoys IS, Markham CH. Planar relationships of the semicircular canals in man. Acta Otolaryngol. 1975;80:185–196. doi: 10.3109/00016487509121318. [DOI] [PubMed] [Google Scholar]
  4. Brantberg K, Mathiesen T. Preservation of tap vestibular evoked myogenic potentials despite resection of the inferior vestibular nerve. J Vestib Res. 2004;14:347–351. [PubMed] [Google Scholar]
  5. Brown MC, Engberg I, Matthews PBC. The relative sensitivity to vibration of muscle receptors of the cat. J Physiol. 1967;192:773–800. doi: 10.1113/jphysiol.1967.sp008330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Burke D, Hagbarth KE, Lofstedt L, Wallin BG. The responses of human muscle spindle endings to vibration of non-contracting muscles. J Physiol. 1976;261:673–693. doi: 10.1113/jphysiol.1976.sp011580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cathers I, Day BL, Fitzpatrick RC. Otolith and canal reflexes in human standing. J Physiol. 2005;563:229–234. doi: 10.1113/jphysiol.2004.079525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Colebatch JG, Halmagyi GM, Skuse NF. Myogenic potentials generated by a click-evoked vestibulocollic reflex. J Neurol Neurosurg Psychiatry. 1994;57:190–197. doi: 10.1136/jnnp.57.2.190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Curthoys IS, Kim J, McPhedran SK, Camp AJ. Bone conducted vibration selectively activates irregular primary otolithic vestibular neurons in the guinea pig. Exp Brain Res. 2006 doi: 10.1007/s00221-006-0544-1. DOI: 10.1007/s00221-006-0544-1. [DOI] [PubMed] [Google Scholar]
  10. Day BL, Cole J. Vestibular-evoked postural responses in the absence of somatosensory information. Brain. 2002;125:2081–2088. doi: 10.1093/brain/awf212. [DOI] [PubMed] [Google Scholar]
  11. Day BL, Fitzpatrick RC. Virtual head rotation reveals a process of route reconstruction from vestibular information. J Physiol. 2005;567:591–597. doi: 10.1113/jphysiol.2005.092544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Day BL, Severac Cauquil A, Bartolomei L, Pastor MA, Lyon IN. Human body-segment tilts induced by galvanic stimulation: a vestibularly driven balance protection mechanism. J Physiol. 1997;500:661–672. doi: 10.1113/jphysiol.1997.sp022051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dieterich M, Brandt T, Fries W Otolith function in man. Results from a case of otolith Tullio phenomenon. Brain. 1989. pp. 1377–1392. [DOI] [PubMed]
  14. Fitzpatrick RC, Day BL. Probing the human vestibular system with galvanic stimulation. J Appl Physiol. 2004;96:2301–2316. doi: 10.1152/japplphysiol.00008.2004. [DOI] [PubMed] [Google Scholar]
  15. Goldberg JM, Smith CE, Fernandez C. Relation between discharge regularity and responses to externally applied galvanic currents in vestibular nerve afferents of the squirrel monkey. J Neurophysiol. 1984;51:1236–1256. doi: 10.1152/jn.1984.51.6.1236. [DOI] [PubMed] [Google Scholar]
  16. Gray H. Gray's Anatomy of the Human Body. 20. New York: Lea & Febiger; 1918. [Google Scholar]
  17. Gregoric M, Takeya T, Baron JB, Bessineton JC. Influence of vibration of neck muscles on balance control in man. Agressologie. 1978;19:37–38. [PubMed] [Google Scholar]
  18. Hudspeth AJ. Mechanoelectrical transduction by hair cells of the bullfrog's sacculus. Prog Brain Res. 1989;80:129–135. doi: 10.1016/s0079-6123(08)62206-2. [DOI] [PubMed] [Google Scholar]
  19. Hudspeth AJ, Corey DP. Sensitivity, polarity, and conductance change in the response of vertebrate hair cells to controlled mechanical stimuli. Proc Natl Acad Sci U S A. 1977;74:2407–2411. doi: 10.1073/pnas.74.6.2407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Ivanenko YP, Grasso R, Lacquaniti F. Effect of gaze on postural responses to neck proprioceptive and vestibular stimulation in humans. J Physiol. 1999;519:301–314. doi: 10.1111/j.1469-7793.1999.0301o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lekhel H, Popov K, Anastasopoulos D, Bronstein A, Bhatia K, Marsden CD, Gresty M. Postural responses to vibration of neck muscles in patients with idiopathic torticollis. Brain. 1997;120:583–591. doi: 10.1093/brain/120.4.583. [DOI] [PubMed] [Google Scholar]
  22. Lekhel H, Popov K, Bronstein A, Gresty M. Postural responses to vibration of neck muscles in patients with uni- and bilateral vestibular loss. Gait Posture. 1998;7:228–236. doi: 10.1016/s0966-6362(98)00012-5. [DOI] [PubMed] [Google Scholar]
  23. Lowenstein O. The effect of galvanic polarization on the impulse discharge from sense endings in the isolated labyrinth of the thornback ray (Raja clavata) J Physiol. 1955;127:104–117. doi: 10.1113/jphysiol.1955.sp005241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lowenstein O, Roberts TDM. The localisation and analysis of the responses to vibration from the isolated elasmobranch labyrinth. A contribution to the problem of the evolution of hearing in vertebrates. J Physiol. 1951;114:471–489. doi: 10.1113/jphysiol.1951.sp004638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lund S. Postural effects of neck muscle vibration in man. Experientia. 1980;36:1398. doi: 10.1007/BF01960120. [DOI] [PubMed] [Google Scholar]
  26. McCue MP, Guinan JJ., Jr Acoustically responsive fibers in the vestibular nerve of the cat. J Neurosci. 1994;14:6058–6070. doi: 10.1523/JNEUROSCI.14-10-06058.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. McCue MP, Guinan JJ., Jr Sound-evoked activity in primary afferent neurons of a mammalian vestibular system. Am J Otol. 1997;18:355–360. [PubMed] [Google Scholar]
  28. Magnusson M, Andersson G, Martensson A, Fransson P, Karlberg M, Gomez S. Vibration to the posterior neck evokes fast EMG responses of the lower leg, but mastoid vibration does not. J Vest Res. 2004;14:158. [Google Scholar]
  29. Mardia KV, Jupp PE. Directional Statistics. UK: John Wiley & Sons Ltd; 2000. [Google Scholar]
  30. Moffat AJM, Capranica RR. Auditory sensitivity of the saccule in the american toad (Bufo americanus) J Comp Physiol. 1976;105:1–8. [Google Scholar]
  31. Moore BR. Modification of the Rayleigh test for vector data. Biometrika. 1980;67:175–180. [Google Scholar]
  32. Murofushi T, Curthoys IS, Topple AN, Colebatch JG, Halmagyi GM. Responses of guinea pig primary vestibular neurons to clicks. Exp Brain Res. 1995;103:174–178. doi: 10.1007/BF00241975. [DOI] [PubMed] [Google Scholar]
  33. Murofushi T, Matsuzaki M, Wu CH. Short tone burst-evoked myogenic potentials on the sternocleidomastoid muscle: are these potentials also of vestibular origin? Arch Otolaryngol Head Neck Surg. 1999;125:660–664. doi: 10.1001/archotol.125.6.660. [DOI] [PubMed] [Google Scholar]
  34. Popov K, Lekhel H, Bronstein A, Gresty M. Postural responses to vibration of neck muscles in patients with unilateral vestibular lesions. Neurosci Lett. 1996;214:202–204. doi: 10.1016/0304-3940(96)12909-8. [DOI] [PubMed] [Google Scholar]
  35. Rao JS, Sengupta S. Topics in Circular Statistics. Singapore: World Scientific Press; 2001. [Google Scholar]
  36. Russolo M. Sound-evoked postural responses in normal subjects. Acta Otolaryngol. 2002;122:21–27. doi: 10.1080/00016480252775689. [DOI] [PubMed] [Google Scholar]
  37. Schneider E, Glasauer S, Dieterich M. Comparison of human ocular torsion patterns during natural and galvanic vestibular stimulation. J Neurophysiol. 2000;87:2064–2073. doi: 10.1152/jn.00558.2001. [DOI] [PubMed] [Google Scholar]
  38. Sheykholeslami K, Habiby Kermany M, Kaga K. Frequency sensitivity range of the saccule to bone-conducted stimuli measured by vestibular evoked myogenic potentials. Hear Res. 2001;160:58–62. doi: 10.1016/s0378-5955(01)00333-1. [DOI] [PubMed] [Google Scholar]
  39. Sheykholeslami K, Murofushi T, Kermany MH, Kaga K. Bone-conducted evoked myogenic potentials from the sternocleidomastoid muscle. Acta Otolaryngol. 2000;120:731–734. doi: 10.1080/000164800750000252. [DOI] [PubMed] [Google Scholar]
  40. Sparto PJ, Schor RH. Directional statistics. In: Stergiou N, editor. Innovative Analysis of Human Movement. Leeds, UK: Human Kinetics; 2004. pp. 121–161. [Google Scholar]
  41. Watson SR, Colebatch JG. Vestibular-evoked electromyographic responses in soleus: a comparison between click and galvanic stimulation. Exp Brain Res. 1998;119:504–510. doi: 10.1007/s002210050366. [DOI] [PubMed] [Google Scholar]
  42. Welgampola MS, Day BL. Vestibular-evoked postural responses to bone conducted sound. J Vestib Research. 2004:O165. abstract. [Google Scholar]
  43. Welgampola MS, Rosengren SM, Halmagyi GM, Colebatch JG. Vestibular activation by bone conducted sound. J Neurol Neurosurg Psychiatry. 2003;74:771–778. doi: 10.1136/jnnp.74.6.771. Erratum in J Neurol Neurosurg Psychiatry (2005) 76, 1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Young ED, Fernandez C, Goldberg JM. Responses of squirrel monkey vestibular neurons to audio-frequency sound and head vibration. Acta Otolaryngol. 1977;84:352–360. doi: 10.3109/00016487709123977. [DOI] [PubMed] [Google Scholar]
  45. Zar JH. Biostatistical Analysis. 4. Upper Saddle River, NJ: Prentice Hall, Inc.; 1999. [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES